Biological system's dynamics are increasingly studied with nonlinear ordinary differential equations, whose parameters are estimated from input/output experimental data. Structural identifiability analysis addresses the theoretical question whether the inverse problem of recovering the unknown parameters from noise-free data is uniquely solvable (global), or if there is a finite (local), or an infinite number (non identifiable) of parameter values that generate identical input/output trajectories. In contrast, practical identifiability analysis aims to assess whether the experimental data provide information on the parameter estimates in terms of precision and accuracy. A main difference between the two identifiability approaches is that the former is mostly carried out analytically and provides exact results at a cost of increased computational complexity, while the latter is usually numerically tested by calculating statistical confidence regions and relies on decision thresholds. Here we focus on local identifiability, a critical issue in biological modeling. This is the case when a model has multiple parameter solutions which equivalently describe the input/output data, but predict different behaviours of the unmeasured variables, often those of major interest. We present theoretical background and applications to locally identifiable ODE models described by rational functions. We show how structural identifiability analysis completes the practical identifiability results. In particular we propose an algorithmic approach, implemented with our software DAISY, to calculate all numerical parameter solutions and to predict the corresponding behaviour of the unmeasured variables, which otherwise would remain hidden. A case study of a locally identifiable HIV model shows that one should be aware of the presence of multiple parameter solutions to comprehensively describe the biological system and avoid biological misinterpretation of the results.
1.
Introduction
Nonlinear differential equation models are extensively used in mathematical systems biology, as well as in many biomedical research areas, for describing and predicting dynamic biological phenomena. An indispensable step for model development is parameter estimation, obtained by adjusting model parameters to best fit input-output (I/O) data. By optimising some cost function of the prediction error, accurate data fitting does not guarantee, however, uniqueness of the obtained parameter estimates [1,2,3]. The question whether equal model predictions can be provided by different parameter values is adressed by the identifiability analysis. Two identifiability approaches have been proposed which are normally regarded as disjoint because structural identifiability (S-ID) analysis is applicable a priori and is based on analytic calculations [4,5,6,7,8,9,10], while practical identifiability (P-ID) analysis is based on sensitivity analysis and numerical simulations of system's equations [11,12,13], see also [14,15,16,17,18] for some interesting specific models in different application areas. In this study, we propose a unified viewpoint of two different identifiability analysis approaches and motivate their joint use for studying local identifiability, in particular to calculate all the numerical solutions of a local identifiable model.
More specifically, S-ID addresses the theoretical question whether the inverse problem of recovering the unknown parameters from ideal, noise-free experimental data is: (ⅰ) uniquely solvable, or if there are (ⅱ) a finite, or (ⅲ) an infinite number of parameter vectors that generate identical output trajectories. These three identifiability properties are traditionally referred to as global; local; and non S-ID, respectively.
In contrast, P-ID aims to assess whether given experimental data provide information on the parameter estimates in terms of precision and accuracy. Typically, statistical confidence regions are calculated in terms of probability levels of the Likelihood function [19,20].
In this paper we recall the theoretical background of S-ID analysis and apply a differential algebra method to a model for the study of the HIV virus dynamics. We will discuss how conclusions drawn by considering only one of the possible multiple parameter solutions can be misleading. To avoid such potential pitfalls we propose an algorithmic approach to determine all possible solutions of ODE models described by rational functions, by illustrating how S-ID analysis integrates with and completes the P-ID results. In particular we will:
1. numerically calculate all the solutions of a locally identifiable model;
2. show all the possible different behaviours of the internal, unmeasured variables corresponding to each of the previous solutions;
3. show how to possibly reject some of them based on existing constraints on parameters.
2.
Problem Statement
2.1. The nonlinear ODE model
This Section provides the reader with the definitions that are necessary to set the notations used in the paper. Consider a nonlinear dynamic system described in state space form as
where state x(t)∈Rn; input u(t)∈Rq ranging on some vector space, U, of piecewise smooth (infinitely differentiable) functions; output y(t)∈Rm; functions f and g are vectors of rational functions of variable x; and constant unknown parameter vector θ belonging to some admissible subset Θ⊆Rp.
It is assumed that there is no feedback and at least one admissible parameter θ∗ exists.
Whenever the initial state is specified, the equation x(0)=x0 is added to the system of equations (2.1, 2.2). In presence of equality constraints on the parameters of the form
where h is a rational polynomial, Eq (2.3) is added to system of equations as well.
With these notations, the I/O map of system (2.1, 2.2) with initial state x0 will be denoted with
This equation has at least one solution if evaluated in θ∗. The goal of the structural identifiability analysis is to count the number of solutions of Eq (2.4).
2.2. Structural Identifiability via Differential Algebra
The I/O map of system (2.1, 2.2) represents the object of study of structural identifiability analysis. In the following we focus on local identifiability (the reader is referred to [6] for the definitions of global identifiability and non identifiability).
Definition 1. The system (2.1, 2.2) is locally identifiable at θ∗∈Θ from I/O data, if there exists (at least) one input function u and an open neighborhood Uθ∗ of θ∗, such that equation
has a unique solution θ∈Uθ∗ for all initial states x0∈X⊆Rn.
Note that this definition deals with the case of Eq (2.5) having a finite number (but more than one) of solutions in Cp, provided that alternative solutions be isolated points. These solutions can be viewed as belonging to an equivalence class in the sense they equivalently describe the I/O map of the model. More formally:
Definition 2. Let R be the equivalence relation on Θ defined by Eq (2.5) and let θ∗∈Θ, then the equivalence class of θ∗ under R is the set
then each θ∈[θ∗]R is called a R-relative of θ∗. That is, the equivalence class of θ∗ under R is the set of all R-relatives of θ∗.
In case of locally identifiable models the goal should be to determine the whole above equivalence class. It is important to stress that multiple solutions are not rare, even in unsophisticated models, and are typically, but not exclusively, associated with symmetries in the system dynamics that allow permutation of subsystems without affecting I/O relations. Non-trivial multiple solutions for Eq (2.5) can be encountered also with simple, seemingly tractable models as we will show in the following with our example and with the case study in Section 4.
In order to this, we will apply a structural identifiability method implemented in the software DAISY (Differential Algebra Identifiability of SYstems) [21]. The method is summarized below, while the reader is referred to [22] for a formal treatment of differential algebra, and to [6,23,24] for a detailed explanation of the theory behind the software tool.
The basic idea of the above differential algebra method is to look at the n+m differential polynomials defining the dynamic system (2.1, 2.2) as the generators of a differential ideal I in the differential ring R(θ)[u,y,x], i.e., containing polynomials in the inputs, outputs, states and their derivatives with respect to time as variables, with multiplicative coefficients being polynomials in the unknown model parameters. First of all the method finds a basis of this differential ideal.
By applying the pseudodivision algorithm among polynomials suggested by Ritt [22], the characteristic set of the ideal I is calculated. This is a basis of the above ideal. It is formed by a finite set of n+m nonlinear differential polynomials A1,...,Am+n satisfying certain minimal condition, which describes exactly the same solution set of the original system. In particular, the characteristic set of a dynamic system described in state space form (2.1, 2.2), after a suitable normalization, is unique and has the following triangular form:
In the first m polynomials the state variable x(t) has been eliminated from the system, hence they are free of x(t). These are polynomials only in the variables (u(t),y(t)) that, in the working hypothesis of structural identifiability, are perfectly known from the experiment. Thus they represent exactly the I/O map of the original dynamic model. These polynomials are linear in their coefficients. In particular each of their coefficients is formed by a rational algebraic function c(θ) of the unknown parameter θ. Formally, the set of these algebraic functions represents the so-called exhaustive summary of the model. If parameter equality constraints (2.3) are present in the model, these have to be added to the above exhaustive summary.
Identifiability is tested by checking injectivity of the exhaustive summary with respect to parameter θ. In order to do this, the I/O map is evaluated at enough time points to calculate its linear coefficients, which will be denoted by c∗. Nonlinear algebraic equations are obtained by equating the polynomials forming the exhaustive summary to this set of symbolic (known) points:
This algebraic nonlinear system in the unknown θ is solved by applying the Buchberger's computer algebra algorithm, which represents a common generalization for nonlinear equations and for more variables of the Gaussian and the Euclidean algorithm, respectively. Buchberger's algorithm calculates a Gröbner basis of the system which is in general represented as:
where nG is a finite number and Gi(θ,θ∗), i=1,...,nG are vectors of algebraic polynomials. The Gröbner basis, Eq (2.9) allows to count the number nθ of solutions of system (2.1, 2.2) in the complex space. In particular whenever Eq (2.5) has one and only one solution, say θ1, the Gröbner basis, Eq (2.9) simply becomes G(θ,θ∗)={θ−θ1}, where nθ=1, showing that the model (2.1, 2.2) is (structurally) globally identifiable.
If Eq (2.5) has nθ finitely multiple solutions the Gröbner basis equation (2.9), in general, has the following form:
Note that if the k-th components of θi are equal for all i=1,...,nθ, the k-th parameter component is globally identifiable (see, for example, parameter k21 of the locally identifiable model (3.1)).
If specific initial conditions x0 are present, after having checked the accessibility of the system from the given initial condition [6], the initial conditions have to be included as well, in a suitable way, in the exhaustive summary.
Thus in case of local identifiability, the above method provides the following relevant information:
– the cardinality nθ of the equivalence class of the parameter solutions, definition (2), i.e. the finite number of solutions equivalently describing the experimental I/O data,
– a means for analytically calculating all other solutions, that would otherwise remain ``hidden", as illustrated in the next Section.
3.
The joint identifiability method to calculate all the solutions of a locally identifiable model
In this Section it is shown how, in case of local identifiability, practical identifiability tests based on model output sensitivities, can be combined with the information provided by structural identifiability analysis based on differential algebra. In particular, we want to show how the specific value simulated or estimated with the practical approach, together with the exhaustive summary of the model, allows to calculate all the other candidate solutions and, possibly, by checking the known physical constraints on these solutions, to accept or reject some of them.
The problem of multiple solutions in parameter estimation is traditionally associated with the idea that local search optimisation algorithms can get trapped, referring to minimisation problems, by local minima with unsatisfactory model predictions of experimental data. Cost functions in presence of multiple (isolated) local minima can be represented as basins of attraction whose nadirs are the optimal candidate solutions, e.g. local minima of the opposite Likelihood function. Common practice for estimating model parameters with multiple local optimal points is to use global optimisers, or multi-start methods combined with local optimiser, e.g. [25]. Local solutions found by such algorithms can be independent from each other, in which case selection of the global optimum by direct comparison of multiple candidate solutions is justified. By using global search and multi-start algorithms, the search for best-fit model parameters is extended to the whole admissible parameter space by increasing the probability to hit the true global minimum.
In case of local identifiable models (checked by structural identifiability analysis) approaches as the multi-start searches can certainly find additional multiple solutions but without guaranteeing to find all of them. By combining the S-ID with the P-ID results we arrive to calculate them all. In particular, the Gröbner basis (2.10) provides their exact number together with the analytic relations among them [26]. This relations define the equivalence class containing all the solutions with respect to their ability to describe the experimental data. Parameters belonging to the same equivalence class will produce equivalent I/O predictions thus the corresponding value of the cost function will be identical. Now we applied a P-ID algorithm to provide the numerical value of an accepted global minimum. This represents the element θ∗ defining the equivalence class, definition (2), by using the relation R, definition (1), we calculate all the R-relatives of θ∗, that is the numerical values of all the multiple solutions of the model. These, by definition, equivalently describe the I/O map of the model but, they in general predict different trajectories of the unmeasured variables whose knowledge is often the goal of the modeling.
For this purpose, we propose to adopt the following methodological steps:
1. calculate the exact number of the parameter solutions and the I/O map of the model;
2. generate or estimate the numerical value of a global minimum of a cost function;
3. go back to the input-output map and substitute the just estimated value in order to provide the known coefficients of Eq (2.7);
4. by solving the corresponding equations, calculate all the remaining solutions;
5. check the known physical constraints on these solutions, i.e. reality and positivity, in order to reject some of them, possibly arriving at a unique solution.
To show the practical consequences of the joint use of structural and practical identifiability for local identifiable models, a simple example is illustrated in the following.
3.1. A simple model with three parameter solutions
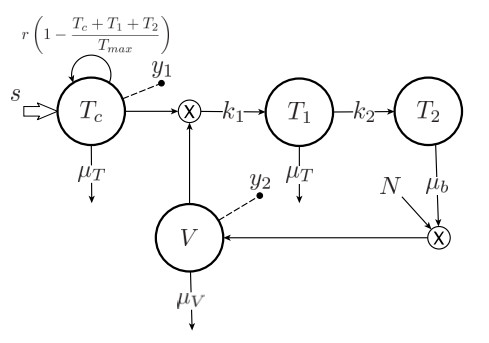
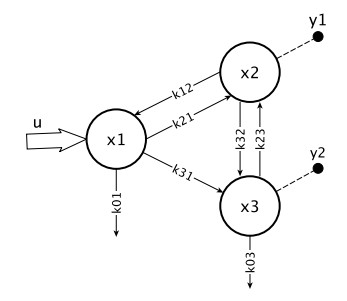
We consider as a benchmark example the three compartment model depicted in Figure 1. It is described by the following ODE's:
where θ=[k03,k01,k12,k32,k31,k23,k21] is the unknown constant parameter vector, x=[x1,x2,x3] the states vector, u the input, y1 and y2 the measured outputs of the model. The initial condition x1(0) is supposed to be known while the others are known from the outputs y1 and y2.
The first question to be addressed is whether the unknown parameter vector θ is structurally identifiable from an experiment in which the output function y(t) is measured exactly.
According to the differential algebra method described in Section 2.2, the pseudodivision algorithm is applied to calculate the characteristic set of the dynamic model (3.1):
Polynomials A1 and A2 are free of x and exactly describe the interdependence between model inputs, outputs and their derivatives. By following the method previously described we should equate these coefficients, known functions of θ∗, to a set of points c∗. It is worth noting that in the structural identifiability context, the parameter vector θ∗, Eq (2.9), can in principle assume any admissible value, thus it can be described by a (known) symbolic value. The exhaustive summary is then:
This system of algebraic nonlinear equations in the unknown model parameters defines the equivalence class to which the solutions belong, and will be used in the practical identifiability test, to find all the numerical solutions, starting from the value estimated from the simulated or measured I/O data. For this simple example one can analytically (symbolically) solve the above system (3.3) and count its solutions in the complex space. However, in general, to speed up calculations, it is convenient to skip the symbolic calculations simply by assigning to the parameters randomly chosen numerical values, see details in [6]. In this case, for example, by substituting the random numerical value θ∗=[27,14,20,7,36,12,1] and calculating the corresponding numerical value of the known coefficients c∗, we obtain an algebraic nonlinear system with real coefficients in the unknowns kij. We solve this system with the Buchberger algorithm which provides the following Gröbner basis (corresponding to Eq (2.10) of Section 2.2):
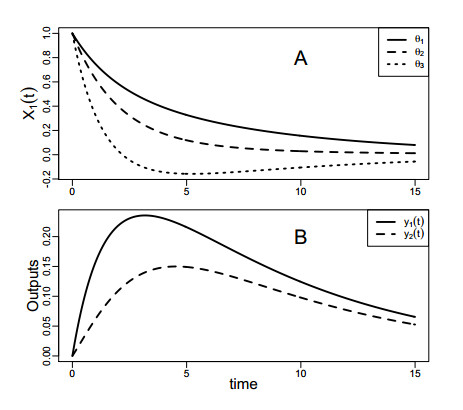
which shows that the original model is locally identifiable, in particular it has three solutions (the only globally identifiable parameters are k21 and k31) all being equivalently able to describe the output function of the model. More important the fact that in correspondence of each of these three solutions, the behaviour of all unmeasured variables is different.
This will be the starting point to provide a method able to numerically calculate all the model solutions describing the I/O experimental data. Typically, local optimisation algorithms for estimating the model parameters calculate one local solution, and need more runs from different initial points to capture additional solutions. The relevant finding of this work is to show how analytically calculate all the multiple solutions of a locally identifiable model.
We move now to the practical context and consider the I/O relationship by assuming a nominal value θ∗ for discussing different possible scenarios. In particular, by imposing θ∗=[k03=0.458,k01=0.022,k12=0.22,k32=0.32,k31=0.06,k23=0.16,k21=0.23] in the exhaustive summary equations (3.3) to calculate c∗, we are able to analytically calculate the other two equivalent numerical solutions, reported in Table 1. For sake of clarity, in the following we will denote θ∗ as θ1 and the two remaining solutions as θ2 and θ3, respectively.
This shows that the numerical solution θ∗ estimated by using an optimisation algorithm (the plausible solution) has nothing more or special with respect to those that remain hidden. The relevant fact is that the two solutions θ2 and θ3 predict the output function of the model exactly as the selected θ∗ does (see Figure 2). In this particular case, by assuming as admissible parameter space Θ the real and positive space, besides the first imposed solution θ1, only θ2 is admissible (non-negative), whereas θ3 shows two negative components.
We would like to emphasize that an optimisation algorithm would normally be able to find arbitrarily only one of these three solutions, if unconstrained optimisation is applied, or one of the two positive alternatives with positive constrained optimisation.
In addition one can see from Figure 2 that, while the evolution of the measured variables x2 and x3 is invariant, the trajectory of the unmeasured variable x1 markedly changes for each solution. More specifically, the decay of x1(t) is the slowest with θ1; decays more rapidly, yet remaining positive, with θ2; and decays fastest with θ3 with negative undershoot. Irrespective of the latter, a practical misleading impact of these findings could be, for instance, the model-based inference of a bioavailability metric, e.g. the area under the curve (AUC), for the unaccessible target compartment x1, obtained by estimating the model parameter from measurements of the other two compartments.
Thus, the measured curves can be equivalently described by the three different parameter sets, but not all of them may be possible candidates to be the true one. In conclusion, the correct way to proceed would be to consider and discuss all of the calculated solutions. Since in biological and biomedical studies, the goal of model identification is usually to estimate variables that are not directly measurable but whose distinct values can discriminate a pathological from a normal state, neglecting the hidden solutions could lead to completely erroneous conclusions. Note that, in this case, the only way to reject some solutions, possibly arriving at only one acceptable solution, is to check if the behaviours of the unobservable variables are physically acceptable. If not, the corresponding parameter value can be rejected.
By observing Table 1 and imposing positivity, we can see that two out of three solutions belong to the admissible parameter space Θ and allow to conclude that two out of three parameterisations are equally plausible. However, in general, the qualitative results just described lead to different conclusions depending on the values of the nominal parameter vector θ∗. Nonetheless, only at this practical stage of rejecting the non admissible parameters, is one allowed to consider the numerical results as global solutions. For the example considered this can be ascertained very easily, i.e. very often the model turns out to be uniquely identifiable under positivity constraints of the parameters. This is a favourable situation in which additional solutions can be rejected demonstrating, in practice, global identifiability of the model. The new method is based on the analytic calculation of all numerical solutions of a locally identifiable model in the whole parameter space. We can also have the chance of discarding some of them and show that the model has only one solution in the admissible parameter space, which is of interest in applications. This opens up new perspectives in theoretical and practical identifiability analysis with important practical implications as shown by applying this joint methodology to a benchmark biological model.
4.
Case study. A locally identifiable HIV model with two solutions
In order to show the relevance of the above methodology in biological applications, we shall analyze a nonlinear model proposed for the study of HIV virus dynamics [28] and schematically depicted in Figure 3. It represents the theoretical formulation on which many of the recently developed HIV models are based. In particular the model examines the interaction of HIV with CD4+ T cells and is described by the following polynomial nonlinear ODEs:
where Tc is the population size of uninfected CD4+ cells; T1 is the population size of latently infected cells; T2 is the population size of productively (or actively) infected cells; and V is the population size of free HIV virus particles. θ=[s,r,Tmax,μT,μb,μv,k1,k2,N] is the unknown parameter vector, and y1 and y2 are measured outputs in blood. One of the relevant goals of the model is that of predicting, from the experimental data, the time-course of the unmeasured, hidden, state variables, that are the population sizes of latently (T1) and of productively infected cells (T2). On the basis of these results, in fact, the optimal therapeutic decision could be taken.
We apply the differential algebra method and check the local identifiability of the model. Note that this is an uncontrolled model, thus in the characteristic set of equations (3.2) the variable u disappears. In particular we show that parameters k1,μT,μv,r,s and Tmax are globally identifiable, while the remaining ones have two different solutions. Now we are aware that there are two distinct parameter vectors equivalently describing the experimental data, up to the measurement error.
By joining the two structural and practical identifiability approaches we are able to analytically calculate the second parameter solution, θ2, corresponding to the parameter estimate provided in [28]: θ∗=[10,0.03,1500,0.02,0.24,2.4,0.000024,0.003,1400]. In fact, as illustrated in the previous example, we can calculate the known coefficients of the exhaustive summary as functions of the estimated θ∗ and solve the provided algebraic nonlinear system in the unknowns k1,μT,μv,r,s and Tmax. The calculated Gröbner basis is the following
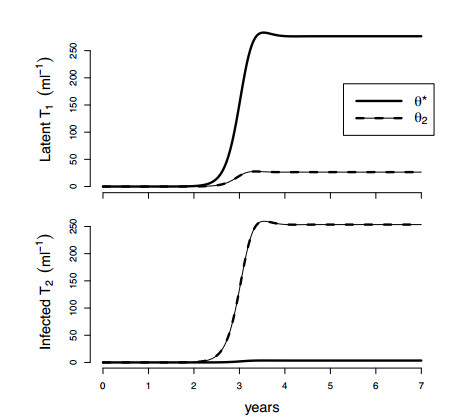
The two solutions θ∗ and θ2 are reported in Table 2. Note that only μb,k2 and N have two solutions while the remaining parameters are globally identifiable. The relevant fact is that these two solutions are equivalent in the sense that they equivalently describe the data (with the model starting from the same given initial conditions Tc(0)=1000,T1(0)=0,T2(0)=0,V0(0)=0.001 [28]). However these equivalent solutions are different even by an order of magnitude and, not surprisingly, they lead to two different predictions of the unmeasured state variables T1 and T2. In particular we refer to the parameters μb, k2 and N which have a central role in the possible interpretations of the model and of its results. In fact, by considering θ∗, one can see that the model predicts a very high viral cell production N and a very low conversion rate k2 of latent T1 cells to infected T2 cells, and a high rate constant μb. Conversely, θ2 provides a much smaller value for N together with a k2 two order of magnitude larger than before, and μb one order of magnitude smaller than before. This means that the same time-course of V and Tc are due to both a high value of k2 and a small value of μb and of N, or viceversa. Maybe it could be of interest for a physician to know which is the situation in order to correctly address the therapy choice. Furthermore, by looking at Figure 4, one can easily realize that not only these predictions are quite different, but the difference appears only after two years.
It is interesting to observe that the product of all rate constants which is representative of the closed loop gain, i.e. k2⋅μb⋅N, must be invariant for both the solutions θ∗ and θ2. In this case the above product is equal to 1.008 corresponding to a fractional daily growth rate of 0.8% (day−1).
The model prediction provided by the estimated parameter vector θ∗ are widely discussed in [28] where the following features are stressed:
1. after an initial phase of infection in which the number of T1 and T2 increases over time, a quasi-steady state is reached
2. the curves of T1 and T2 over the time are essentially identical, up to a scale factor.
The authors stated that many findings were expected and consistent with a number of quantitative observations. However some features did not match these observations. In order to correct this deficiency, the authors proposed further modifications of the model that include more realistic assumptions about the biology of HIV. Very interesting is the observation of Perelson et al. (1993) regarding the number of latently infected cells: "the number of latently infected cells grows to unrealistically high levels, ...".
These interpretations have been obtained without the knowledge of the second solution θ2, which possibly could be the more realistic one. From the joint identifiability method, presented here, we know exactly the numerical value of both the "candidates" θ∗ and θ2. This knowledge completes the results obtained in [28] and would allow a correct discussion on them. In principle, in fact, the two solutions are equivalent with respect to the description of the experimental data, thus the model predictions provided by θ2 should be discussed on the same terms as done for those provided by θ∗. Maybe θ2 should be rejected in favour of θ∗, maybe it could better match the model independent known clinical data, providing the correct solution and avoiding the introduction of assumptions made only to correct the model predictions.
In this case study, it is interesting to observe that the "hidden" solution θ2 predicts:
1. a number of latently infected cells, appearing only after two years, very different from that predicted by using θ∗, and
2. a number of free virus produced by lysing a CD4+ T cell about seven times smaller than that predicted by using θ∗, which could be a more plausible result.
By ignoring this possible solution can lead the physician to possibly erroneous decisions given that depletion values are used in a clinical setting as indicators of the disease stage.
We can conclude that the knowledge of each of the finite number of parameter vectors of a locally identifiable model is essential to provide a complete picture for a correct interpretation of results.
5.
Discussion
In this Section some specific aspects related to the proposed methodology will be discussed further.
Global structural identifiability is a prerequisite for the related optimisation problem to be well-posed. In particular, for well-posedness according to Hadamard it is assumed that a solution of the optimisation problem: (ⅰ) exists; (ⅱ) is unique; and (ⅲ) continuously depends upon the data [29]. Our method calculates one optimal solution of a locally identifiable model and then all its R-relatives that represent an equivalence class, definition (2), defined in the complex space. Thus, in this perspective, by relaxing the uniqueness requirement, also the identification of locally structurally identifiable models can be viewed as a well-posed problem in the generalised sense of Tykhonov [29].
To check the uniqueness of parameter solution, structural identifiability analysis solves a system of nonlinear algebraic equations with real coefficients. Thus the answer holds in the whole complex space Cp, i.e. the solutions can be either real positive; real negative; or complex conjugate [17]. In particular, when the model is globally identifiable, the unique solution corresponds to the real one, but when the model is locally identifiable, we know the number of solutions in Cp but not in the admissible parameter space Θ⊂Rp, as we would be practically interested. Typically, for biological and biomedical models, reality and positivity are required. By applying the joint method proposed in this paper, all the model parameter solutions are numerically calculated and it can happen that some of these solutions are not admissible. At this stage, we can select the solutions belonging to the admissible parameter space Θ. The numerical solutions which are not admissible can be discarded possibly arriving at an a posteriori uniquely identifiable system.
We successfully apply our method to many biological and biomedical models recently published in the literature. Being based on analytic calculations, the method may be limited by its computational complexity and it can not tackle with overly complex model structures. On the other hand multi-start local optimization methods allow to explore the parameter space by starting from multiple points thus they can be easily parallelised and less computationally demanding. However, when applicable, only by preceding these last methods by a structural identifiability test the investigator becomes aware of the presence of all multiple solutions and can directly proceed to their calculations.
Some existing numerical optimisation algorithms, such as multi-start methods combined with local search, are able to determine multiple optimal solutions. However, to the best of our knowledge, no algorithms have been developed to explicitly find the equivalence classes of parameters introduced in this study. Bayesian inference algorithms, implementing Markov-Chain Monte Carlo (MCMC) simulation, may be able to detect multiple solutions that characterize local identifiability. However, since equivalent parameterisations generate identical model outputs, no difference in Likelihood are expected between different equivalent parameters. Thus it is difficult to predict the behaviour of an MCMC simulation run.
It is important to outline that structural identifiability analysis can be viewed as a tool for checking the adequacy of the designed experiment, possibly before collecting experimental data. This is crucial in biomedical studies where severe experimental limitations are imposed for ethical and practical reasons.
Finally, it is worth noting that if a model is structurally identifiable, it may nevertheless turn out to be practically non-identifiable. In this case the inability to unequivocally estimate model parameters may be caused by a number of distinct reasons, among which: (1) excessive noise in the measurements, (2) poor or very sparse sampling schedules, (3) poorly designed experiments, where measurement locations or inputs are missing or insufficiently informative. However, if the model turns out to be practically non identifiable, only by first checking structural identifiability it is possible to know if the problem lays on a too complex model-experiment structure or on the above reasons related to experimental data. Our proposed method allows for this distinction, thus providing the investigator a useful suggestion on how to proceed to make the model identifiable.
6.
Conclusion
We motivate here a joint use of two different identifiability techniques which guarantees to find all the numerical parameter solutions of a dynamic model described by rational ODE's. As demonstrated in a simple three compartment model, by neglecting possible parameter solutions one can erroneously predict the behaviour of some unmeasured variables leading to ambiguous interpretations of model results.
The two methodologies, namely structural identifiability and practical identifiability, are traditionally regarded as disjoint because they are based, in turn, on differential algebraic manipulations and on numerical simulation of systems equations. In this study we propose to apply first the structural identifiability test to count the parameter solutions and also to provide their analytic relations. In fact, the method gives the polynomials defining the class of equivalence of the parameter solutions with respect to their ability to describe the I/O experimental data. Second, to apply the practical identifiability to simulating/estimating one numerical parameter value and to go back to the structural results, in order to analytically calculate all the equivalent parameter solutions of the dynamic model. This is a relevant result in biological/biomedical modeling where often the goal is that of predicting the behaviour of the variables not directly accessible to the measure. By neglecting some possible parameter solutions describing the same I/O data, one cannot predict the corresponding internal variables behaviours which remain hidden. Finally, to assess all the admissible parameter estimates by rejecting the non admissible ones, possibly arriving at a globally identifiable model.
We claim that by implementing this joint method which guarantees to find all the model parameter solutions makes the identification process from real data more rigorous and reliable. In order to show the relevance of these ideas in the biological areas, we applied them to a model of HIV virus dynamics by showing that, without calculating all the equivalent parameter solutions, there is a risk of large bias in the biological interpretation of the results.
Acknowledgments
We would like to show our gratitude to Leontina D'Angiò, Giuseppina Bellu and Stefania Audoly for their always helpful comments and discussions.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: