Models for liquid relative permeability of cementitious porous media at elevated temperature: comparisons and discussions

1.   Introduction

It is well known that many nonlinear phenomena in physics, chemistry and biology are described by dynamics of shapes, such as curves and surfaces, and the time evolution of a curve and a surface has significations in computer vision and image processing. The time evolution of a curve and a surface is described by flows, in particular inextensible flows of a curve and a surface. Physically, inextensible flows give rise to motion which no strain energy is induced. The swinging motion of a cord of fixed length or of a piece of paper carried by the wind, can be described by inextensible flows of a curve and a surface. Also, the flows arise in the context of many problems in computer visions and computer animations ^[2,7]

In ^[5], Hasimoto studied the relation between integrable systems and geometric curve flows and he showed that the non linear Schrödinger equation is equivalent to the binormal notion flow of space curves by using a transformation relating the wave function of the Schrödinger equation to the curvature and torsion of curves (so-called Hasimoto transformation). In particular, Lamb ^[8] proved that the mKdV equation and the sine-Gordon equation arise from the invariant curve flows by using the Hasimoto transformation. After, Mohamed ^[9] investigated the general description of the binormal motion of a spacelike and a timelike curve in a 3-dimensional de-Sitter space and gave some explicit examples of a binormal motion of the curves. Schief and Rogers ^[11] investigated binormal motions of inextensible curves with a constant curvature or a constant torsion, and introduced two new examples of integrable equations which are derived from the binormal motion of curves and established the Bäcklund transformation and matrix Darboux transformations of the extended Dym equation and the mKdV equation. In ^[1] the authors studied curve motions by the binormal flow with the curvature and the torsion depending velocity and sweeping out immersed surfaces and obtained filaments evolving with a constant torsion which arise from extremal curves of curvature energy functionals. Curve flows have been studied by many experts and geometers ^[4,6,13].

The outline of the paper is organized as follows: In Section 2, we give some geometric concepts of curves and surfaces in an isotropic 3-space. In Section 3, we study inextensible flows of a space curve and give time evolutions of the Frenet frame, the curvature and the torsion of the curve. In the last section, we construct the Bäcklund transformations of the Schrödinger flows and the extended Harry-Dym flows as the binormal flows and give a nonexistence of bi-harmonic Hasimoto surfaces in an isotropic 3-space.

2.   Isotropic space

The three dimensional isotropic space $\Bbb I^3$ has been developed by Strubecker in the 1940s, and it is based on the following group $G_6$ of an affine transformations $(x, y, z) \rightarrow(\bar x, \bar y, \bar z)$ in $\Bbb R^3$,

where $a, b, c, c_1, c_2, \phi \in \Bbb R$. Such affine transformations are called isotropic congruence transformations or isotropic motions of $\Bbb I^3$, in this case $\mathcal{B}_6$ is denoted by the group of isotropic motions (cf. ^[12]). Observe that on the $xy$ plane this geometry looks exactly like the plane Euclidean geometry. The projection of a vector ${\bf x} = (x_1, y_1, z_ 1)$ in $\Bbb I^3$ on the $xy$ plane is called the top view of $\bf x$ and we shall denote it by $\widehat{ {\bf x} } = (x_1, y_1, 0)$. The top view concept plays a fundamental role in the isotropic space $\Bbb I^3$, since the $z$ direction is preserved under action of $\mathcal {B}_6$. A line with this direction is called an isotropic line and a plane that contains an isotropic line is said to be an isotropic plane.

In the sequel, many of metric properties in isotropic geometry (invariants under $\mathcal{B}_6$) are Euclidean invariants in the top view such as the isotropic distance, so call $i$-distance. The isotropic distance of two points ${P} = (x_1, y_1, z_1)$ and ${Q} = (x_2, y_2, z_2)$ is defined as the Euclidean distance of the their top views, i.e.,

As a fact, two points $(x, y, z_i)$ $(i = 1, 2)$ with the same top views have isotropic distance zero, they called parallel points.

Let $\mathbf{x} = (x_1, y_1, z_1)$ and $\mathbf{y} = (x_2, y_2, z_2)$ be vectors in $\Bbb I^3$. The isotropic inner product of $\mathbf{x}$ and $\mathbf{y}$ is defined by

We call vector of the form ${\bf x} = (0, 0, z)$ in $\Bbb I^3$ isotropic vector, and non-isotropic vector otherwise.

Now we introduce some terminology related to curves. A regular curve $C : I \rightarrow \Bbb I^3$, i.e., $C' \neq 0$, is parametrized by an arc-length $s$ if $|| C'|| = 1.$ In the following we assume that all curves are parametrized by an arc-length $s$. In addition, a point $\alpha(s_0)$ in which $\{ C'(s_0), C''(s_0)\}$ is linearly dependent is an inflection point and a regular unit speed curve $C(s) = (x(s), y(s), z(s))$ with no inflection point is called an admissible curve if $x' y'' - x'' y' \neq 0$.

On the other hand, the (isotropic) unit tangent, principal normal, and curvature function of the curve $C$ are defined as usual

respectively. As usually happens in isotropic geometry, the curvature $\kappa$ is just the curvature function of its top view $\hat{ C}$ and then we may write $\kappa(s) = (x' y''- x'' y')(s).$ To compute the moving trihedron, we define the binormal vector as the vector ${\bf b} = (0, 0, 1)$ in the isotropic direction. The Frenet equation corresponding to the isotropic Frenet frame $\{ {\bf t}, {\bf n}, {\bf b} \}$ can be written as (^[12])

where $\tau$ is the (isotropic) torsion, that is,

Consider a $C^r$-surface $M$, $r\geq 1$, in $\Bbb I^3$ parameterized by

A surface ${M}$ immersed in $\Bbb I^3$ is called admissible if it has no isotropic tangent planes. We restrict our framework to admissible regular surfaces.

For such a surface, the coefficients $g_{ij}$ $(i, j = 1, 2)$ of its first fundamental form are given by

where $X_u = \frac {\partial X}{\partial u}$ and $X_v = \frac {\partial X}{\partial v}.$ The coefficients $h_{ij}$ $(i, j = 1, 2)$ of the second fundamental form of $M$ are calculated with respect to the normal vector of $M$ and they are given by

The isotropic Gaussian curvature $K$ and the isotropic mean curvature $H$ are defined by

The surface ${M}$ is said to be isotropic flat (resp. isotropic minimal) if ${K}$ (resp.${H}$) vanishes (cf. ^[12,14]).

3.   Inextensible flows of a space curve

We assume that $C : [0, l] \times [0, w] \rightarrow M \subset \Bbb I_3$ is a one parameter family of a space curve in $\Bbb I_3$, where $l$ is the arc-length of a initial curve. Let $u$ be the curve parametrization variable, $0 \leq u \leq l.$ We put $v = || \frac {\partial C}{\partial u}||$, from which the arc-length of $C$ is defined by $s(u) = \int_0^u v d u.$ Also, the operator $\frac {\partial }{\partial s}$ is given in terms of $u$ by $\frac {\partial }{\partial s} = \frac 1 v \frac {\partial }{\partial u}$ and the arc-length parameter is given by $ds = v du.$

On the Frenet frame $\{ \bf t, \bf n, \bf b \}$ of the curve $C$ in $\Bbb I_3$, any flow of $C$ can be given by

where $\alpha, \beta, \gamma$ are scalar speeds of the space curve $C$, respectively. We put $s(u, t) = \int ^u _0 v du$, it is called the arc-length variation of $C$. From this, the requirement that the curve not be subject to any elongation or compression can be expressed by the condition

for all $u \in [0, l].$

Definition 3.1. A curve evolution $C(u, t)$ and its flow $\frac {\partial C}{\partial t}$ in $\Bbb I_3$ are said to be inextensible if

Theorem 3.2. If $\frac {\partial C}{\partial t} = \alpha {\bf t} + \beta {\bf n} + \gamma {\bf b}$ is a flow of $C$ in an isotropic 3-space $\Bbb I_3$, then we have the following equation:

Proof. Since $v^2 = \left \langle \frac {\partial C}{\partial u}, \frac {\partial C}{\partial u} \right \rangle$ and $u$, $t$ are independent coordinates, $\frac {\partial}{\partial u}$ and $\frac {\partial}{\partial t}$ commute. So by differentiating of $v^2$ with respect to $t$ and using (2.4) and (3.1) we can easily obtain (3.3).

Now, we give necessary and sufficient condition for a inextensible flow in an isotropic space and it is useful to get our results.

Theorem 3.3. Let $\frac {\partial C}{\partial t} = \alpha {\bf t} + \beta {\bf n} + \gamma {\bf b}$ be a flow of a space curve $C$ in $\Bbb I_3$. Then the flow is inextensible if and only if

Proof. Suppose that the curve flow of a space curve $C$ is inextensible. From (3.2) and (3.3) we have

It follows that

Since $\frac {\partial }{\partial s} = \frac 1 v \frac {\partial }{\partial u}$, we can obtain (3.4).

Conversely, by following a similar way as above, the proof is completed.

Theorem 3.4. Let $\frac {\partial C}{\partial t} = \alpha {\bf t} + \beta {\bf n} + \gamma {\bf b}$ be a flow of a space curve $C$ in $\Bbb I_3$. If the flow is inextensible, then a time evolution of the Frenet frame $\{ \bf t, \bf n, \bf b \}$ along a curve $C$ is given by

where

Proof. Noting that

Also,

which imply that a time evolution of the principal normal vector $\bf n$ can be expressed as

This completes the proof.

Now, we give time evolution equations of the curvature $\kappa$ and the torsion $\tau$ of the inextensible space curve $C$ in $\Bbb I_3$.

Theorem 3.5. Let $\frac {\partial C}{\partial t} = \alpha {\bf t} + \beta {\bf n} + \gamma {\bf b}$ be a flow of a space curve $C$ in $\Bbb I_3$. Then, the time evolution equations of the functions $\kappa$ and $\tau$ for the inextensible space curve $C$ are given by

Proof. It is well known that the arc length and time derivatives commute. That is,

and

Comparing two equations, we find

Also by using $\frac {\partial }{\partial s } \left(\frac {\partial {\bf n}}{\partial t} \right) = \frac {\partial }{\partial t } \left(\frac {\partial {\bf n}}{\partial s} \right)$ and following a similar way as above, we can obtain the second equation of (3.8). The proof is completed.

Remark 3.6. Taking $\beta = -\kappa_s$, by (3.4) one find $\alpha = - \frac 1 2 \kappa^2$. From the time evolution of the curvature (3.8) we get

it follows that the curvature $\kappa$ evolves according to the mKdV equation

where $\kappa_s = \frac {\partial \kappa }{\partial s}$ and $\kappa_t = \frac {\partial \kappa }{\partial t}$. The corresponding flow of a curve is

which is the so-called modified KdV flow ^[3].

We give a example of inextensible flow of a curve with constant torsion as follows:

Example 3.7. Taking $\tau = \tau_0$ = constant. If we consider

where $\alpha_0, \beta_0, \gamma_0$ are non zero constants, then the PDE system (3.8) takes the form

it follows that one solution of the last equation is

Thus, (2.4) and (3.5) imply $\alpha_0 {\bf t}_s = {\bf t}_t$ and ${\bf n} = e^{-(s + \alpha_0 t)} {\;\bf t}_s$. If we take

the vector ${\bf n}$ is given by

Thus, we can get the family of curves $C_t$, so we can determine the surface that is generated by this family of curves.

4.   Binormal flows of a space curve

Qu et al. ^[10] studied the Bäcklund transformations of geometric curve flows in a Euclidean 3-space $\Bbb R^3$. In this section, we aim to give the Bäcklund transformations of integrable geometric curve flows by using time evolutions of a curve in an isotropic 3-space $\Bbb I^3$.

4.1.   The Schrödinger flows

It is well-known that the Schrödinger flow in a 3-space is given by ^[5]

In this case we take $(\alpha, \beta, \gamma) = (0, 0, \kappa)$ in (3.1), it follows that (3.5) and (3.8) imply the following theorem:

Theorem 4.1. The Schrödinger flow (4.1) implies the time evolutions of frame fields, the curvature and the torsion of a space curve $C$ in an isotropic 3-space $\Bbb I_3$ as follows:

We now construct the Bäcklund transformation of the Schrödinger flow (4.1). Considering another curve in $\Bbb I^3$ related $C$ by

where $\mu, \nu$ and $\xi$ are the smooth functions of $s$ and $t$. Using (2.4), (4.1) and (4.2), a direct computation leads to

Let $\tilde{s}$ be the arclength parameter of the curve $\tilde{C}$. Then

where $\Omega$ is a non zero smooth function. It follows that the unit tangent vector of the curve $\tilde{C}$ is determined by

where $\Phi_1 = \Omega^{-1} (1 + \mu_s - \kappa \nu), \Phi_2 = \Omega^{-1} (\nu_s + \kappa \mu)$ and $\Phi_3 = \Omega^{-1} (\xi_s + \tau \nu)$. Differentiating (4.5) with respect to $\tilde{s}$, we get

which gives the curvature of the curve $\tilde{C}$:

Thus form (2.3) the Frenet frames of the curve $\tilde{C}$ are given by

Assume that the curve $\tilde{C}$ also fulfills the Schrödinger flow, that is,

The Bäcklund transformation of the Schrödinger flow with the help of (4.5), (4.8) and (4.9) turns out to be the following result (cf. ^[10]):

Theorem 4.2. The Schrödinger flow (4.1) is invariant with respect to the Bäcklund transformation (4.4) in an isotropic 3-space $\Bbb I_3$ if $\mu, \nu$ and $\xi$ satisfy the system

4.2.   The extended Harry-Dym flows

The extended Harry-Dym flow ^[11]

is obtained by setting $\alpha = 0$, $\beta = 0$ and $\gamma = \tau^{-\frac 12}$ in a space curve flow (3.1).

Theorem 4.3. The extended Harry-Dym flow (4.10) implies the time evolutions of frame fields, the curvature and the torsion of a curve $C$ in an isotropic 3-space $\Bbb I_3$ as follows:

We consider the Bäcklund transformation of the extended Harry-Dym flow (4.10)

where $\mu, \nu$ and $\xi$ are the smooth functions of $s$ and $t$. Differentiating (4.13) with respect to $s$ and $t$ and using (4.11) we get

Let $\tilde{s}$ be the arclength parameter of the curve $\tilde{C}$. Then the unit tangent vector of the curve $\tilde{C}$ is given by

where we put

Differentiating (4.15) with respect to $\tilde{s}$, we get

it follows that the curvature of the curve $\tilde{C}$ leads to

Thus form (2.3) the Frenet frames of the curve $\tilde{C}$ are given by

Assume that the curve $\tilde{C}$ also fulfills the extended Harry-Dym flow, that is,

The Bäcklund transformation of the extended Harry-Dym flow with the help of (4.14) and (4.17) turns out to be the following result:

Theorem 4.4. The extended Harry-Dym flow (4.10) is invariant with respect to the Bäcklund transformation (4.13) in an isotropic 3-space $\Bbb I_3$ if $\mu, \nu$ and $\xi$ satisfy the system

4.3.   Hasimoto surfaces

Definition 4.5. The surface $C(s, t)$ wiped out by the Schrödinger flow (4.1) is called a Hasimoto surface.

Sometimes, Eq. (4.1) is called the vortex filament or smoke ring equation, and can be viewed as a dynamical system on the space curves. Since ${C}_s = {\bf t}$ and ${C}_t = \kappa {\bf b},$ the first and second fundamental forms of the Hasimoto surface are given by

In this case $\kappa$ is non-vanishing everywhere. Thus, we have

Theorem 4.6. Let ${C}(s, t)$ be a Hasimoto surface such that ${C}(s, t)$ is a unit speed curve for all $t$ in an isotropic 3-space $\Bbb I_3$. Then the surface has zero Gaussian curvature and the mean curvature $H = -\frac 1 2 \kappa$.

Corollary 4.7. There is no minimal Hasimoto surface in an isotropic 3-space.

Theorem 4.8. Let ${C}(s, t)$ be a Hasimoto surface in an isotropic 3-space $\Bbb I_3$. Then the followings are satisfy:

(1). $s$-parameter curves of the surface are non-asymptotic curves.

(2). $s$-parameter curves of the surface are geodesic curves.

Proof. Suppose that ${C}(s, t)$ is a Hasimoto surface such that ${C}(s, t)$ is a unit speed curve for all $t$. It is well known that the normal curvature $\kappa_n$ of a $s$-parameter curve on the surface ${C}(s, t)$ is given by

where $U = \frac {{C}_s \times {C}_t} {||{C}_s \times {C}_t||}$ is a unit normal vector of the surface. Since $\kappa \neq 0$, a $s$-parameter curve is non-asymptotic.

Also, the geodesic curvature $\kappa_g$ of a $s$-parameter curve on the surface ${C}(s, t)$ is

it follows that a $s$-parameter curve is geodesic. The proof is completed.

Theorem 4.9. Let ${C}(s, t)$ be a Hasimoto surface in an isotropic 3-space $\Bbb I_3$. Then the followings are satisfy:

(1). $t$-parameter curves of the surface are asymptotic curves.

(2). $t$-parameter curves of the surface are geodesic curves.

Proof. The normal curvature $\kappa_n$ and the geodesic curvature $\kappa_g$ of a $t$-parameter curve on the surface ${C}(s, t)$ are given by

Thus, a $t$-parameter curve is asymptotic and geodesic. The proof is completed.

On the other hand, the mean curvature vector $\bf H$ is given by

and Laplacian of the mean curvature vector is expressed as

Theorem 4.10. Let ${C}(s, t)$ be a Hasimoto surface such that ${C}(s, t)$ is a unit speed curve for all $t$ in an isotropic 3-space $\Bbb I_3$. If the surface satisfies the condition $\Delta {\bf H} = \lambda {\bf H}$ for some constant $\lambda$, then the curve ${C}(s, t)$ for all $t$ has a constant curvature and a constant torsion. Furthermore, $\lambda = \kappa^2$.

Proof. Suppose that a Hasimoto surface satisfies the condition $\Delta {\bf H} = \lambda {\bf H}$. With the help of (4.19) and (4.20), we obtain the following equations:

which imply $\kappa_s = 0$ and $\tau_s = 0$. From (4.3) we also get $\kappa_t = 0$ and $\tau_t = 0$, that is, $\kappa$ and $\tau$ are constant. Furthermore, from (4.21) $\lambda = \kappa^2$. Thus, the proof is completed.

Corollary 4.11. There is no bi-harmonic Hasimoto surface in an isotropic 3-space.

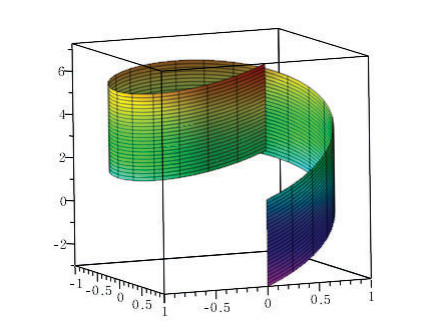
Example 4.12. Let us consider the surface in $\Bbb I^3$ parametrized by

with $0 \leq s \leq 2 \pi$ and $-2 \leq t \leq 2$. Then, we have

On the other hand, we can check the following:

Thus the surface is a Hasimoto surface (Figure 1) and it satisfies $\Delta {\bf H} = {\bf H}.$

Acknowledgments

The authors would like to thank the anonymous referee for useful comments and suggestions that helped for a significant improvement of the exposition.

This paper was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education (NRF-2018R1D1A1B07046979).

Conflict of interest

The authors declare no conflicts of interest.