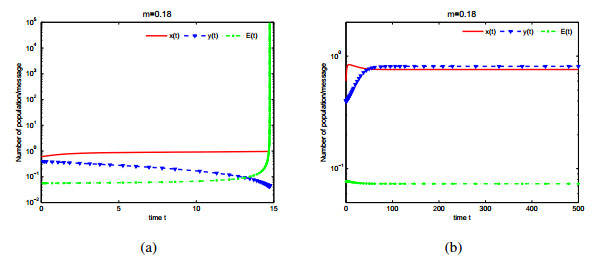
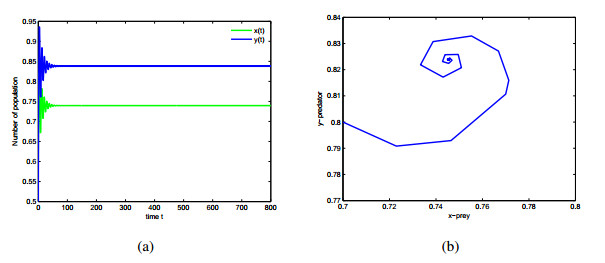
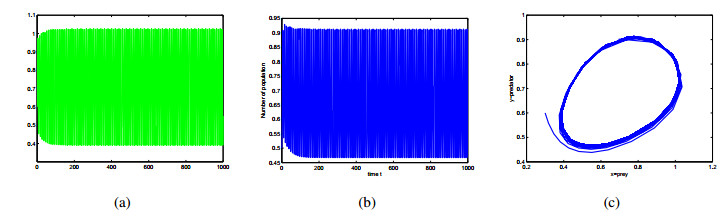
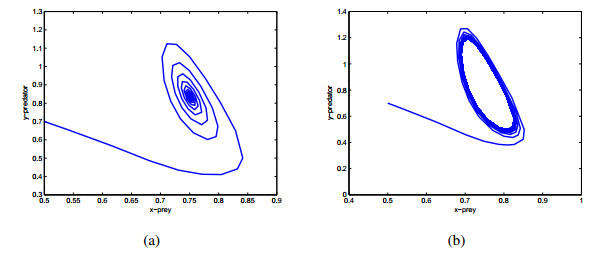
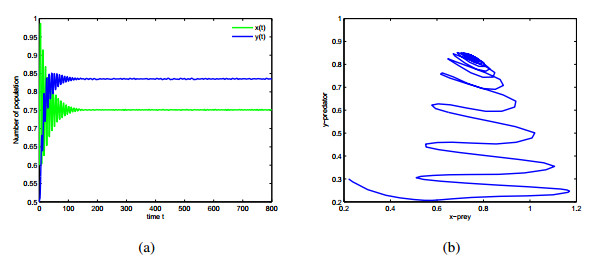
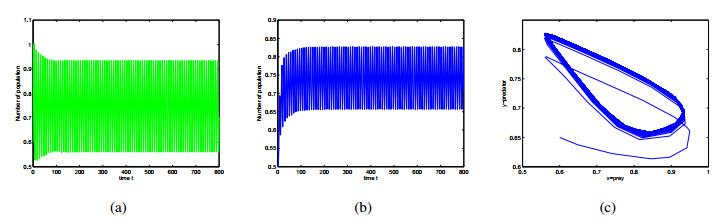
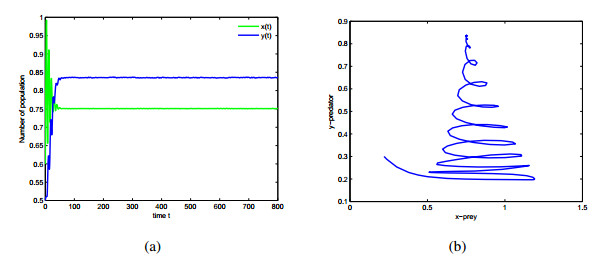
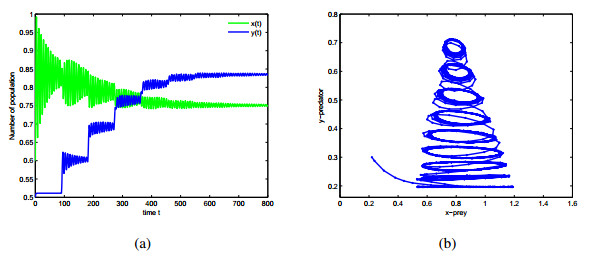
In this paper, a differential algebraic predator-prey model including two delays, Beddington-DeAngelis functional response and nonlinear predator harvesting is proposed. Without considering time delay, the existence of singularity induced bifurcation is analyzed by regarding economic interest as bifurcation parameter. In order to remove singularity induced bifurcation and stabilize the proposed system, state feedback controllers are designed in the case of zero and positive economic interest respectively. By the corresponding characteristic transcendental equation, the local stability of interior equilibrium and existence of Hopf bifurcation are discussed in the different case of two delays. By using normal form theory and center manifold theorem, properties of Hopf bifurcation are investigated. Numerical simulations are given to demonstrate our theoretical results.
1.
Introduction
Deep learning becomes one of the most important technologies in the field of artificial intelligence [1,2,3]. CNN is the most representative model of deep learning [4]. In 1989, Yann LeCun [5] proposes CNN model and applies CNN to handwritten character recognition. Yoshua Bengio presents the Probabilistic models of sequences and proposes generative adversarial networks [6]. Geoffrey Hinton et al. present a deep brief net [7] and apply CNN in Image Net game. The advantages of CNN against traditional methods can be summarized as follows [4].
(1) Hierarchical feature representation.
(2) Compared with traditional shallow models, a deeper architecture provides an exponentially increased expressive capability.
(3) The architecture of CNN provides an opportunity to optimize several related tasks together.
(4) Benefiting from the large learning capacity of CNNs, some classical computer vision challenges can be recast as high-dimensional data transform problems and solved from a different viewpoint.
Due to these advantages, CNN has been widely applied into many research fields [8,9,10,11,12,13,14]. However, the CNN has some disadvantages. Many Parameters need to be adjusted in CNN. It needs many training samples and the GPU is preferred for training CNN.
Extreme learning machine (ELM) [15] is a kind of feed-forward neural network in essence. ELM generates input layer weights and bias values at random, directly solves the least square solution of the output weights, and obtains the final training model at the same time. ELM has the advantages such as no iterative calculation, fast learning speed and strong generalization ability. Many scholars pay close attention to ELM and have achieved good results [16,17,18,19,20]. A fast kernel ELM combining the conjugate gradient method (CG-KELM) is presented in [16] and the kernel ELM is applied in image restoration. In [17], the paper further studies ELM for classification in the aspect of the standard optimization method and extends ELM to a specific type of "generalized" single-hidden layer feedforward networks-support vector network. An improved meta-learning model of ELM is proposed in [18]. Chunmei He et al. [19] propose a fast learning algorithm for the regular fuzzy neural network based on ELM which has good performance and approximation ability. Since ELM is based on the principle of empirical risk minimization which may lead to over-fitting problem. In [20], the scholars combine the structural risk minimization theory and weighted least square method and present RELM. RELM considers both the structural risk and the empirical risk and balances the two risks using the risk ratio parameter. RELM is widely used in the fields of classification, regression and prediction. RELM has the advantage of fast learning speed and further improves the generalization performance of ELM.
Motivated by the remarkable success of CNN and RELM, RELM is introduced into CNN and an effective classifier CNN-RELM is proposed in this paper. In CNN-RELM, CNN can extract the deep feature of the input, while RELM have fast learning speed and good generalized ability to acquire better recognized accuracy. The rest paper is organized as follows. Section 2 introduces the basic theory of CNN, ELM and RELM. The CNN-RELM model and learning algorithm are presented in section 3. The experiment simulations show the excellent performance of the CNN-RELM in section 4. Section 5 summarizes the study and discusses the future work.
2.
Brief reviews of CNN, ELM and RELM
2.1. Convolutional Neural Network
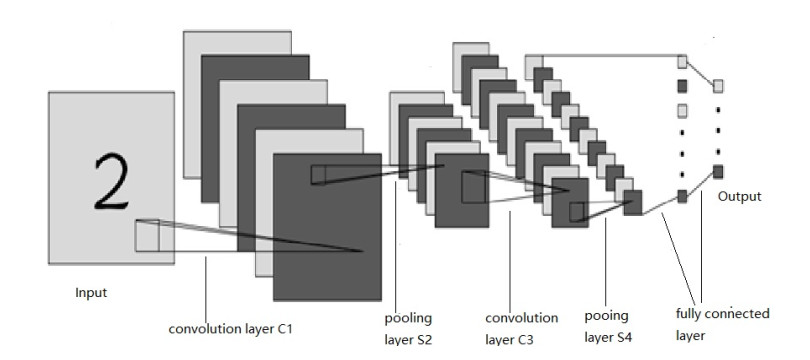
A typical CNN is simply introduced here. The CNN topological model is shown in Figure 1.
In the CNN, the convolution layer and pooling layer extract the features and input into the fully connected layer to obtain the classification results. The feature extraction process is as follows.
In the convolution layer, convolution is performed on the input, and the output is
where Mj is the input set and b is the bias of the convolution layer.
The gradient of the convolution layer is defined by δlj=βl+1j(f′(ulj)∘up(δl+1j)).
The output of the pooling layer is
where down(⋅) is the pooling function, b is the bias, and β is the weight.
In the fully connected layer, the output of the l-th layer is xl=f(ul), where ul=wlxl−1+bl, wl is the weight and bl is the bias of the l-th layer.
2.2. ELM and RELM
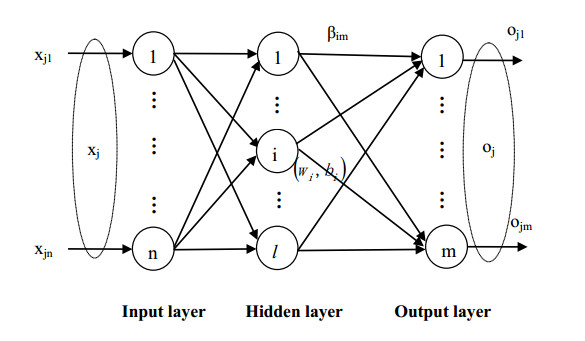
We simply introduce ELM and RELM. For more details, please refer to [15,20]. The topology of ELM is shown in Figure 2.
Different from other feed-forward neural networks, the input weight wi and bias bi of the ELM are generated randomly in the training. After the input sample set (xj,yj) is processed by the hidden layer neurons, the hidden layer output matrix H of ELM can be fixed. The goal of ELM is to adjust the weight ˆβ satisfying the following equation.
where β=[βT1,⋯,βTl]Tl×m, Y=[yT1,⋯,yTN]TN×m is the expected output and
The solution of Eq (3) is the least normal square solution as follows.
where H+ is the Moore-Penrose generalized inverse matrix.
ELM only considers the empirical risk and doesn't consider the structural risk. ELM directly calculates the least squares solution, and users can't make fine-tuning according to the characteristics of the database, these results in poor control ability and over-fitting problems. Therefore, the structural risk minimization theory is introduced into ELM, and RELM is proposed [20]. The RELM model is as follows. When γ→∞, the RELM degenerates into the ELM, that is, ELM is a special case of the RELM.
where ‖β‖2 is the structural risk, ε is the error, ‖ε‖2 is the empirical risk, γ is the proportion parameters to balance empirical risk and structural risk. The Eq (6) is a conditional extreme problem, which is solved by converting Lagrange equation into an unconditional extreme problem as follows.
where αj∈Rm(j=1,⋯,n) is Lagrange operator. Let the gradient of the Lagrange equation be 0 and compute the weight β as follows.
3.
An effective classifier: CNN-RELM
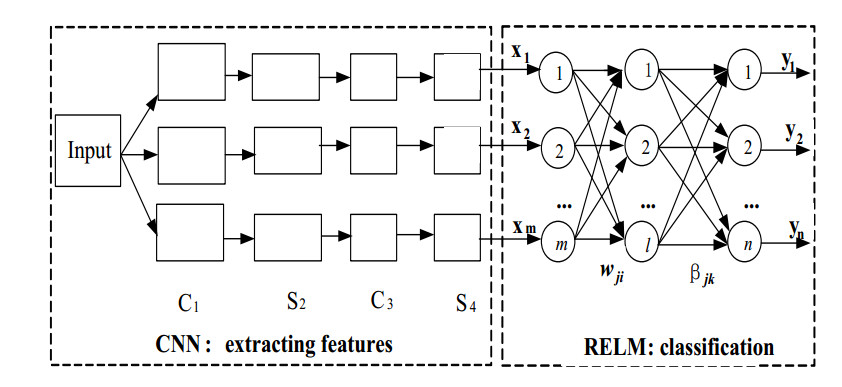
In this section, the CNN-RELM model and learning algorithm are presented. In CNN-RELM, the convolutional hidden layer and the pooling layer in CNN extract deep features from the original input and then RELM are used for feature classification. The CNN-RELM model is changed in the two steps of training period. And in testing period, there is no fully connected layer in CNN which is replaced by the RELM.A trained CNN-RELM used for testing is as in Figure 3. The training of CNN-RELM model is divided into two steps: The training of CNN and the merger of CNN and RELM. These two steps are presented in detail as follows.
3.1. The training of CNN
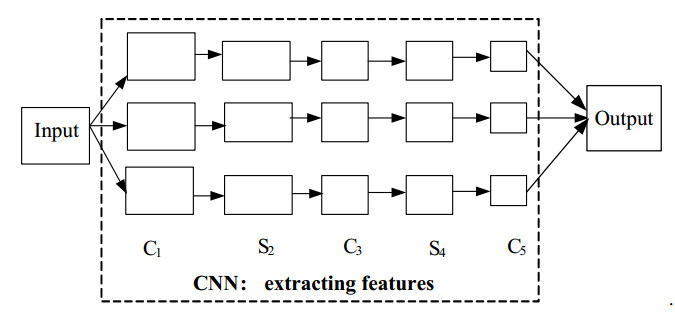
In this step, the CNN model is trained. The CNN model in this step is as in Figure 4. The related parameters in CNN are adjusted by the gradient descent method according to the errors between the actual output and the expected output. The training of the CNN stops if the minimum error reaches or the maximum number of iterations reaches. Then the CNN is saved for the next step.
The feature map in the CNN is adjusted as follows.
(a) If the m-th layer is a convolution layer, the n-th feature map is
where Mn is the input set; f is a nonlinear active function; kmin is the convolution kernel; bmn is bias.
(b) If the m-th layer is a pool layer, its n-th feature map is
where wmn is weight, bmn is bias and down(⋅) is pooling function. The two pooling methods: The max pooling and the mean pooling are used here.
3.2. The merger of CNN and RELM
In this step, we firstly acquire the RELM which is optimized by genetic algorithm. And then the convolutional layers and pooling layers of the CNN is fixed while the full-connected layer of the CNN is replaced by the RELM. The topology of RELM is also shown as in Figure 3. The optimal risk ratio parameters γ in the RELM are optimized by genetic algorithm. The RELM mathematical model is the same as Eq (6). The weight β is computed by Eq (8). The fully-connected layer of CNN is replaced by the RELM. In other words, the feature images trained by CNN are considered as the input of RELM, and the desired classification results are obtained through RELM. The role of RELM is to act as a classifier in CNN-RELM model.
3.3. The learning algorithm of CNN-RELM
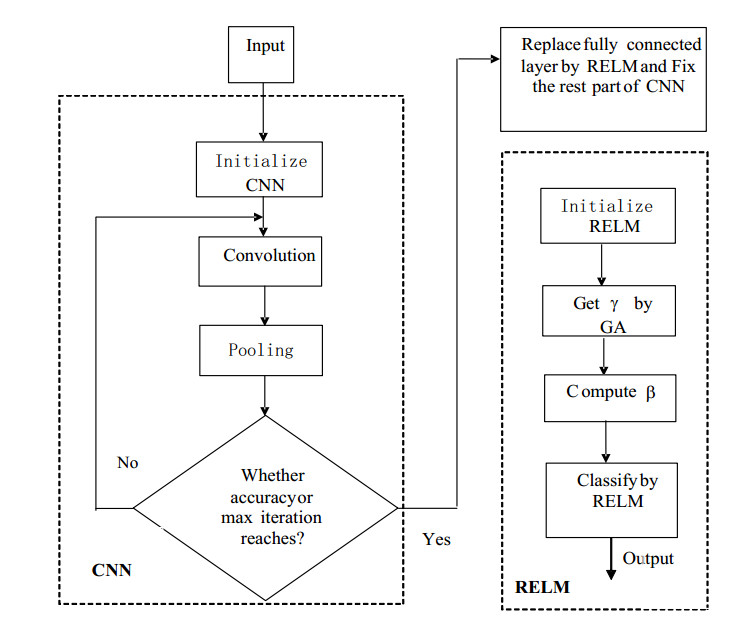
The learning algorithm of CNN-RELM is outlined in Algorithm 1. The learning algorithm flow chart of CNN-RELM is shown as in Figure 5.
Algorithm 1
Step 1. Initialize the CNN parameters, expected target and maximum iteration times.
Step 2. Compute the actual output of the network by Eqs (9), (10).
Step 3. If the predetermined target precision reaches or the maximum number of iterations reaches, then go to Step 5, else go to Step 4.
Step 4. Adjust the parameters of CNN by the gradient descent method and go to Step 2.
Step 5. Initialize RELM. Randomly initialize the weights and biases. Get the regularized parameters by GA.
Step 6. Let the feature vectors obtained by CNN into RELM and Compute β by Eq (8).
Step 7. Save the CNN-RELM and classify by the CNN-RELM.
4.
Simulation experiments
In this section, we present the face recognition experiment to verify the feasibility of CNN-RELM and compare it with RELM and CNN. The impacts of different pooling methods and different number of training samples on the performance of CNN-RELM are also presented.
4.1. Face databases and experiment environments
Two face databases: ORL and NUST are used in the simulations. The detailed database information is shown in Table 1. The ORL face database is founded by the Olivetti research laboratory in Cambridge, England. The ORL face database can be downloaded in the following website: http://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html. The NUST face database is made by Nanjing University of Science and Technology, China.
The experimental execution environment is as follows. Software environment: Matlab-R2014a. Operation system: Windows 8. Hardware environment: Dell PC. CPU: Intel(R) Core(TM) i5-6500 CPU @ 3.20GHz. Hard disk: Seagate ST500DM002-1SB10A (500 GB /7200 rpm). Memory: 32 GB (Samsung DDR4 2666MHz).
4.2. Face recognition experiment by CNN-RELM
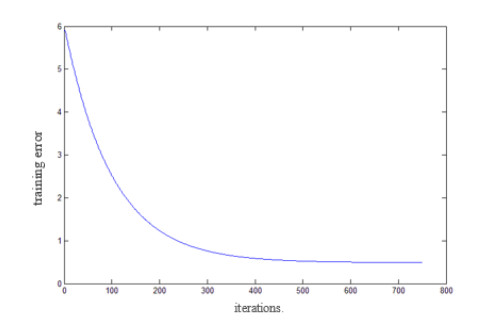
To evaluate the performance of CNN-RELM, some simulations on the ORL face databases are given. In training of the CNN, there are two convolution layers: C1, C3 and two pool layers: S2, S4. The convolution kernel of convolution layer C1 and C3 are all set as 9×9 matrix. In pooling layer S2 and S4, max-pooling is used and the window size is 3×3. The gradient descent algorithm is used to train the CNN. The error function of CNN in the training is shown in Figure 6. As the number of iterations increases, the training error gradually decreases.
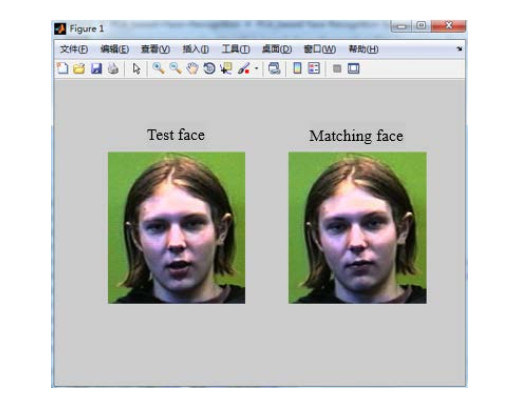
After the CNN is trained, the fully connected layer is replaced by RELM for classification. The feature images obtained by the pooling layer S4 are converted into column vectors and stored in matrix. Moreover, the RELM model is used for classification. When initializing RELM, we obtain the input weight and bias in a random way. At the same time, we use the optimal risk ratio parameter mentioned in [21], and the hidden layer nodes are set to 200. The test results are shown in Figure 7. The experimental results show that the proposed algorithm is feasible in face recognition.
4.3. Comparison experiments to other methods
In this section, we compare the performances of CNN-RELM, RELM and CNN in face recognition experiments. The parameters in the CNN and the risk ratio parameter of RELM are similar to that in [21]. Two standard face databases: ORL and NUST as in Table 1 are used in the comparative experiments. In the experiment, we select seven images of each person as training samples, and the remaining three images as test samples. All hidden layer node number of neural networks is set to 200. The recognition results of the three algorithms are shown in Table 2.
As seen from Table 2, the CNN-RELM model proposed in this paper has the best recognition accuracy. In next section, an experiment is given to study the influence of different pooling methods and number of the training sample on CNN-RELM.
4.4. Impact of different pooling methods and number of training samples on the performance of CNN-RELM
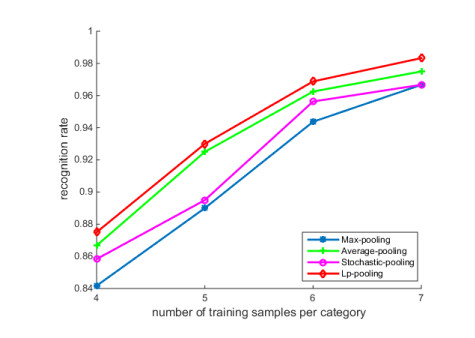
In order to evaluate how different pooling methods and different training samples impact on the performance of the CNN-RELM, the experiment is conducted in this section. The ORL face database is selected here. The parameters of the CNN-RELM model are selected as the same as those in section 4.2. The pooling method respectively uses Max-pooling, Average-pooling, Stochastic-pooling and Lp-pooling. Figures 4–7 are selected for each class's training samples and the rest pictures are taken as test samples. The experimental results are shown in Table 3 and Figure 8.
4.5. Discussion and result analysis
By the experiment in Figures 6 and 7, it's known that the CNN-RELM is feasible in classification. From Table 2, we can concluded that the CNN-RELM outperform CNN and RELM in classification. The CNN-RELM model combines CNN with RELM and overcomes the deficiency of the two models. The CNN-RELM can also be used in other application tasks such as remote sensing and object shape reconstruction and the process is similar to that of classification.
From Table 3 and Figure 8, we can see that the recognition rate increase at the same pooling strategy as the selected training samples increase. When the same number of training samples is selected, the Lp− pooling strategy has the highest recognition rate. The recognition rate corresponding to the average pooling strategy, the statistics pooling strategy and the maximum pooling strategy are sequentially reduced.
Seen from Figure 8, the selection of different pooling methods has an impact on the performance of CNN-RELM. In practical applications, the selection of appropriate pooling methods according to the actual situation of data is conducive to achieving better application results.
5.
Conclusions
An effective classifier CNN-RELM is proposed in this paper. Firstly, the CNN-RELM trains the convolutional neural network using the gradient descent method until the learning target accuracy reaches. Then the fully connected layer of CNN is replaced by RELM optimized by genetic algorithm and the rest layers of the CNN remain unchanged. A series of experiments conducted on ORL and NUST databases show that the CNN-RELM outperforms CNN and RELM in classification and demonstrate the efficiency and accuracy of the proposed CNN-RELM model. Meanwhile, we also verify that the selection of different pooling methods has an impact on the performance of CNN-RELM. When the same number of training samples is selected, the pooling strategy has the highest recognition rate. In practical applications, the selection of appropriate pooling methods according to the actual situation of data is conducive to achieving better application results. Due to the uniting of CNN and RELM, CNN-RELM have the advantages of CNN and RELM and it is easier to learn and faster in testing. The future work includes improve the generalized ability and further reduce the training time.
Acknowledgement
This work is supported by the National Natural Science Foundation of China (Grant No. 61402227), the Natural Science Foundation of Hunan Province (No.2019JJ50618) and the project of Xiangtan University (Grant No. 11kz/kz08055). This work is also supported by the key discipline of computer science and technology in Hunan province, China.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: