Reimagining multiplication as diagrammatic and dynamic concepts via cutting, pasting and rescaling actions

1.   Introduction

Quick advancements in technology, drastic global competition, and growing client expectations have all put massive pressure on manufacturers to deliver high-quality products. Clients anticipate high-reliability products. Enhancing reliability is a significant part of the overall vision of improving product quality. For modern products, there is a longer lifespan with higher reliability, which means it is not beneficial to test products under normal-use circumstances, where the evaluation procedure may be overly long and excessive. In this case, accelerated life tests (ALTs) have been presented to gather failure information quickly within a reasonable testing time frame. In ALTs, items are subjected to higher-than-normal amounts of stress (for example, temperature or pressure) to lead to a quicker failure. The data acquired from such ALTs is then examined to determine the life characteristics under typical circumstances of operation. Employing the constant-stress ALTs (CSALTs), the test objects are under continual severe stress until failure occurs or the test is finished. The mechanism of CSALTs is explained in detail in the next section. It is vital to highlight that there are other types of ALTs, such as step-stress ALTs. Many authors have considered ALTs in their studies; see, for example, Balakrishnan and Han^[1], Nelson^[2], Kateri and Kamps^[3], Mohie El-Din et al.^[4], Wang^[5], Nassr and Elharoun ^[6], Nassar et al. ^[7,8], Dey and Nassar^[9], Feng et al.^[10], Balakrishnan et al.^[11], Alotaibi et al.^[12], Kumar et al. ^[13], Manal et al. ^[14], and Wu et al. ^[15].

In life testing and reliability analysis, collecting data from all tested units is unrealistic because of its high cost and duration. Accordingly, the use of censoring schemes is naturally utilized in reliability and lifetime investigations, where the experiment will end when a portion of the units fail. Type-Ⅰ and Type-Ⅱ censoring strategies are the most commonly utilized plans in publications. Nevertheless, these plans do not permit the experimenters to discard items from the experimentation at any moment until the investigation is completed. To overpower this disadvantage, a progressive Type-Ⅱ censoring (PT2C) procedure is suggested, in which the experimenters can remove live units in various testing phases. The lifespan of items is increasing due to technological advancements, and even when the PT2C scheme is used, this results in increased test time frames. In certain cases, no failure occurs within the test period. Therefore, Kundu and Joarder^[16] suggested the progressive Type-Ⅰ hybrid censoring strategy, which is a combination of PT2C and hybrid censoring plans. The major weakness of this plan is that the number of failures is arbitrary and occasionally low or zero, which delivers outcomes of statistical deduction that may be inappropriate or inadequate. To improve this shortage, Ng et al. ^[17] introduced an adaptive PT2C (APT2C) plan that adapts the test procedure according to the trial improvement to achieve the desired pre-fixed number of failures. Because of the advantages of this scheme, numerous researchers have explored the estimation problems of some lifetime models in the presence of APT2C data, see, for example, Ismail^[18], AL Sobhi^[19], Nassar and Abo-Kasem^[20], Nassar et al^[21], Elshahhat and Nassar^[22], Abu El Azm et al^[23], and Nassr et al^[24], among others. Nevertheless, as indicated by Ng et al. ^[17], the APT2C is efficient in parameter evaluation when the full period of the trial is not a significant matter. On the other hand, if the products being studied are exceptionally reliable, the assessment process may require a lengthy period, and the APT2C plan cannot ensure that the total test duration is suitable. To overcome this limitation, Yan et al. ^[25] proposed an improved-APT2C (IAPT2C). It guarantees that the assessment ends in the allotted amount of time. It can also be viewed as a generalization of many plans. Therefore, if the investigator aims to finish the test within a designated time frame, the IAPT2C may be applied. The description of the IAPT2C plan is presented in the next section. Recently, some studies considered this scheme; see for example Elbatal ^[26] and Dutta and Kayal ^[27].

In this study, we utilize the IAPT2C under the CSALTs when the tested failure times follow the Weibull model. This work's motivation comes from: (1) The popularity and flexibility of the Weibull distribution in modeling various data types; (2) the effectiveness of combining CSALTs with the IAPT2C plan in cutting the test time and estimating the product's performance under regular usage circumstances; (3) it is the first time that the product of spacings (PS) function has been used in the case of the IAPT2C with CSALTs, so we are interested to see how it performs when compared with other classical and Bayesian methods; (4) the reliability function (RF) estimation under normal use situations was researched in a few studies, despite many examining the estimation issues in the presence of CSALTs. To put it another way, the vast majority of the studies have only focused on the estimation issues of unknown parameters and have said nothing about the estimation of the RF under normal operational settings. We believe it is important for reliability engineers and other practitioners to identify the RF for the Weibull distribution under normal operating conditions. For more detail about the importance of the reliability estimation, see Xu et al. ^[28] and Wang et al. ^[29]. To achieve our objectives, the unknown parameters are estimated using two classical approaches, namely maximum likelihood and maximum product of spacings (MPS) methods. Moreover, the Bayesian method via the Markov chain Monte Carlo (MCMC) sampling technique is considered to get different estimates when the observed data are evaluated using the two classical approaches. Based on the different estimation methods, the scale and reliability parameters are estimated at the designed stress level. In addition, the approximate confidence intervals (ACIs) and the Bayes credible intervals (BCIs) are acquired. As far as we are aware, this is the first time that the various estimation approaches to the Weibull distribution under the IAPT2C with CSALTs have been studied. Another important motivation for this paper is to compare the maximum likelihood estimators (MLEs) with the MPS estimators (MPSEs), as well as the corresponding Bayesian ones. To assess our findings, an extensive simulation study is implemented. It is very interesting for statisticians and applied researchers to see the applicability of the different methods offered in real-life cases. Consequently, two groups of real-world data are explored to demonstrate how the suggested methodologies may be applied in reality.

This study is arranged as follows: In Section 2, we provide the model and basic assumptions. In Section 3, the point and interval estimates of the unknown subjects are obtained using the maximum likelihood method. The various estimates using the MPS method are provided in Section 4. The Bayes' method is utilized in Section 5. In Section 6, the various estimation methods are compared via a simulation study. Two real CSALT data sets are analyzed in Section 7. Section 8 ends the study.

2.   Model description

In this work, we make the assumption that the lifespan of products follows the Weibull distribution. It is favoured because it is a logical generalization of the exponential distribution and hence recreates a critical role in many applications in different fields, including analyzing engineering, biological, and medical data sets. Here, we consider the Weibull CSALTs model with the next two assumptions:

$(1)$ The unit lifetime associated with each stress level $s_{i}, i = 1, \dots, k$ is Weibull, and the corresponding probability density function (PDF) and cumulative distribution function (CDF) are outlined below:

and

where $\lambda_{i}$ and $\theta$ are the scale and shape parameters, respectively.

$(2)$ The relationship between stress and life is proposed to be expressed in the log-linear model as follows:

where $\beta_{0}$ and $\beta_{1}$ are unknown parameters to be estimated.

The Weibull log-linear model for the scale parameter has been extensively investigated in the literature, see, for example, Wang and Kececioglu ^[30]. It is known that the ALTs are often performed in the context of stress factors such as temperature, voltage or pressure. Because the main objective of executing the ALTs is to deduce reliability at a normal level of stress, the statistical model employed for this goal must have some technical foundation as well. As a result, the use of the log-linear model described in assumption 2 allows some conventional engineering models, including inverse power, Arrhenius, and exponential models to be readily acquired as special instances. See for more detail Roy ^[31].

Based on the CSALTs, assume $k$ accelerated stress levels $s_1 < s_2 < \dots < s_k$ and the designed stress level is denoted by $s_u$. Also, suppose that there are $N$ similar test units splited into $k$ sets of size $n_1, n_2, \dots, n_k$, where $\sum_{i = 1}^{k} n_i = N$. Before starting the experiment, the number ($m_{i} < n_{i}$), $i = 1, \dots, k$, the progressive censoring plan $R_{i, 1}, \dots, R_{i, m_{i}}$ such that $n_{i} = m_{i}+\sum_{j = 1}^{m_{i}}R_{i, j}$ and two thresholds $T_{i, 1}, T_{i, 2}\in (0, \infty)$, where $T_{i, 1} < T_{i, 2}, i = 1, \dots, k$ are determined in advance, taking into account that some values of $R_{i, j}$'s, $i = 1, \dots, k, j = 1, \dots, m_{i}$ may be changed during the experiment. Then, the IAPT2C with CSALTs can be stated as follows: At the stress level $s_{i}, i = 1, \dots, k$, when the first failure arises, designated by $X_{i, 1}$, $R_{i, 1}$ (surviving units) are randomly discarded. At $X_{i, 2}$, $R_{i, 2}$ units are randomly withdrawn from the remaining surviving units, and so on. Here, we have three possible cases outlined as follows:

$(1)$ Case Ⅰ: If $X_{i, m_{i}} < T_{i, 1}$, the test stops at the time of $m_{i}-{th}$ failure with $R_{i, m_{i}} = n_{i}-m_{i}-\sum_{j = 1}^{m_{i}-1}R_{i, j}$ are withdrawn. In this case, we have PT2C with CSALTs.

$(2)$ Case Ⅱ: If $X_{i, d_{i}} < T_{i, 1} < X_{i, d_{i}+1}$, where $d_{i}$ is the size of failures at $T_{i, 1}$ and $(d_{i}+1) < m_{i}$, with $X_{i, m_{i}} < T_{i, 2}$, then we set $R_{i, d_{i}+1} = \dots = R_{i, m_{i}-1} = 0$ and end the test at the time of $m_{i}-{th}$ failure and at which point all the remaining $R_{i, m_{i}} = n_{i}-m_{i}-\sum_{j = 1}^{d_{i}}R_{i, j}$ units are removed. In this case, we have APT2C with CSALTs.

$(3)$ Case Ⅲ: If $X_{i, m_{i}} > T_{i, 2}$, the experiment terminates at $T_{i, 2}$, with the understanding that no units will be discarded from the experiment when the test time passes the threshold $T_{i, 1}$. In this case, we have $d_{i}^{*} < m_{i}$ number of observed failures, where $d_{i}^{*}$ is the number of failures before the time $T_{i, 2}$. At the time $T_{i, 2}$, all remaining units are withdrawn, i.e., $R^{*}_{i} = n_{i}-d_{i}^{*}-\sum_{j = 1}^{d_{i}}R_{i, j}$. This describes the IAPT2C with CSALTs.

We can express the likelihood function (LF) of the observed data as follows, ignoring the normalized constant, based on the aforementioned scenarios

where

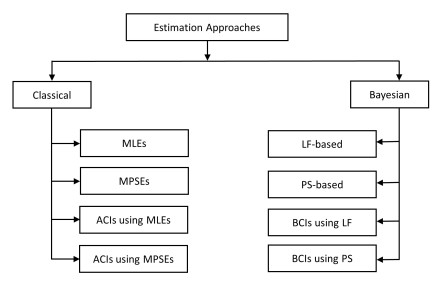
and $T_{i}^{*} = 0, x_{i, m_{i}}$ and $T_{i, 2}$ for Cases Ⅰ, Ⅱ and Ⅲ, respectively. Before proceeding, for clarity, Figure 1 depicts the various point and interval estimations considered in this work.

3.   Maximum likelihood approach

In this part, the MLEs of $\theta, \ \beta_0$ and $\beta_1$ are discussed using IAPT2C with CSALTs data. Under typical use settings, the MLEs of the scale parameter $\lambda_{u}$ and RF $R_{u}(x_{0})$ are provided. Moreover, the interval estimations of the different parameters are formed through the asymptotic theory of the MLEs.

3.1.   Point estimation

From (2.1)–(2.3), we can express the LF of $\theta, \ \beta_0$ and $\beta_1$ as

where $J = \sum\nolimits_{i = 1}^{k}J_{i}$ and $\Psi_{i}(\theta) = \sum\nolimits_{j = 1}^{J_{i}}x_{i, j}^{\theta}+ \sum\nolimits_{j = 1}^{D_{i}}R_{i, j}x_{i, j}^{\theta}+R_{i}^{*}T_{i}^{*\theta}$. The log-LF of (3.1) of $\theta, \ \beta_0$ and $\beta_1$ can be expressed as

where $\delta = \sum\nolimits_{i = 1}^{k}J_{i}s_{i}$. The MLEs $\hat{\theta}, \hat{\beta_{0}}$ and $\hat{\beta_{0}}$ of $\theta, \ \beta_0$ and $\beta_1$ can be inferred as

and

where $\Psi_{i}^{'}(\theta) = \sum\nolimits_{j = 1}^{J_{i}}x_{i, j}^{\theta}\log(x_{i, j})+ \sum\nolimits_{j = 1}^{D_{i}}R_{i, j}x_{i, j}^{\theta}\log(x_{i, j})+R_{i}^{*}T_{i}^{*\theta}\log(T_{i}^{*})$. Using (3.4), the MLE of $\beta_{0}$ can be obtained as a function of the other two parameters as follows

Substituting $\hat{\beta}_{0}(\theta, \beta_{1})$ in (3.3) and (3.5), the MLEs of $\theta$ and $\beta_1$, denoted by $\hat{\theta}$ and $\hat{\beta}_1$, can be reached by solving the subsequent normal equations

and

Clearly, there are no closed-form solutions to obtain the MLEs of $\theta$ and $\beta_1$. Therefore, one could direct oneself to numerical iterative procedures like the Newton-Raphson method to acquire the needed estimates from (3.7) and (3.8). Upon the MLEs of $\theta$ and $\beta_1$ being obtained, the MLE $\hat{\beta}_0 = \hat{\hat{\beta}}_{0}(\hat{\theta}, \hat{\beta}_{1})$ of $\beta_0$ can be obtained directly from (3.6).

Since $\log(\lambda_{i}) = \beta_{0} +\beta_{1} s_i$, one can derive the MLE of $\lambda_{i}$ as a function of $\theta$ as $\hat{\lambda}_{i}(\theta) = J_{i}/\Psi_{i}(\theta)$. Therefore, we can conclude that $\hat{\lambda}_{i}$ exists and is unique if $\theta$ exists and is unique. Substitute $\hat{\lambda}_{i}(\theta)$ in (3.2), the profile log-LF at stress level $i$ can be written as

From Lemma 1 in Wang ^[5], one can conclude that the profile log-LF $\varpi(\theta)$ is concave with respect to $\theta$. Consequently, at stress level $i$, the MLE of $\theta$ can be found as

It is simple to demonstrate that $1/\theta$ is a monotone decreasing function in $\theta$ using (3.10). Conversely, the right-side in (3.10) is monotone increasing in $\theta$, as shown by Lemma 2 in Wang ^[5]. As a result, there is a clear interaction location for the slopes of both variables from both directions in (3.10). This suggests that the MLE of $\theta$ exists and is unique.

Remark 1. A number of previous studies are expanded upon and readily transformed into special scenarios based on the findings obtained in this investigation. Examples of these include:

● The results of Cui et al. ^[32], by setting $T_{i, 2}\rightarrow \infty$ for $i = 1, 2, \dots, k$, in the case of APT2C data.

● The results of Ismail ^[33], by setting $T_{i} = T_{i, 1} = T_{i, 2}$ for $i = 1, 2, \dots, k$, in the case of Type-Ⅰ progressive hybrid censored data.

● The results of Wang et al. ^[34], by setting $T_{i, 1}\rightarrow \infty$ for $i = 1, 2, \dots, k$, in the case of PT2C data.

● The results of Watkins and John ^[35], by setting $T_{i, 1}\rightarrow \infty$, $R_{i, j} = 0$ and $R_{i, m_{i}} = n_{i}-m_{i}$ for $i = 1, \dots, k, \ j = 1, \dots, m_{i}-1$, in the case of Type-II censored data.

It is important to estimate the scale parameter at the designed stress level as well as the RF. To get such estimates, one can utilize the invariance property of the MLEs. Let $\lambda_u$ be the scale parameter under the designed stress level $s_u$, then the MLE of $\lambda_u$, denoted by $\hat{\lambda}_u$, can be obtained as

Similarly, the MLE of the RF at time $x_{0}$ under the designed stress level can be acquired as follows

where $R(\cdot) = 1-F(\cdot)$ and $\hat{\lambda}_{u}$ is evaluated from (3.11).

3.2.   Asymptotic interval estimation

Based on the MLEs' asymptotic normality, the interval estimates for the unknown parameters are given in this subsection. Furthermore, we employ the delta method to approximate the variances of the estimators of the scale parameter and the RF at the designed stress level to obtain the related interval ranges.

In order to accomplish our goals, we first need to get the expressions of the second derivatives obtained from the log-LF in (3.2) as

and

where $\Psi_{i}^{''}(\theta) = \sum_{j = 1}^{J_{i}}x_{i, j}^{\theta}\log^{2}(x_{i, j})+$ $\sum_{j = 1}^{D_{i}}R_{i, j}x_{i, j}^{\theta}\log^{2}(x_{i, j})+R_{i}^{*}T_{i}^{*\theta}\log^{2}(T_{i}^{*})$. The complex nature of the expectations of the second partial derivatives makes it evident that the asymptotic variance-covariance matrix (AV-CM) of the MLEs of $\theta, \ \beta_0$, and $\beta_1$ cannot be constructed. Therefore, by obtaining the inverted observed Fisher information as follows, we are able to obtain the approximate AV-CM for the MLEs

Obviously, the asymptotic distribution of $(\hat{\theta}, \hat{\beta}_{0}, \hat{\beta}_{1})$ is $N\left[(\theta, \beta_{0}, \beta_{1}), I_{0}(\hat{\theta}, \hat{\beta}_{0}, \hat{\beta}_{1})\right]$, where $I_{0}(\hat{\theta}, \hat{\beta}_{0}, \hat{\beta}_{1})$ is determined by (3.13). Hence, the $100(1-\alpha)\%$ ACIs of $\hat{\theta}, \hat{\beta}_{0}$ and $\hat{\beta}_{1}$ can be computed as

where $\widehat{var}(\hat{\theta}), \widehat{var}(\hat{\beta_{0}})$ and $\widehat{var}(\hat{\beta_{1}})$ are the main diagonal elements of $I_{0}(\hat{\theta}, \hat{\beta}_{0}, \hat{\beta}_{1})$ given by (3.13), respectively, and $z_{\alpha/2}$ is the higher $(\alpha/2)-{th}$ percentile standard normal level.

In order to construct the ACIs for the $\lambda_{u}$ and the RF under the designed stress level, we require getting the variances of their estimators. To obtain such variances, we suggest using the delta method to compute the approximate estimates of these variances; see Greene^[36] for complete details about the delta method. Let $\widehat{var}(\hat{\lambda}_{u})$ and $\widehat{var}(\widehat{R}_{u})$ denote the approximate estimates of the variances of the MLEs of the scale parameter and RF, respectively. Then, based on the delta method, we have

where

with the following elements

and

Now, the $100(1-\alpha)\%$ ACIs for the scale parameter and the RF under the designed stress level can be obtained, respectively, as follows:

4.   Maximum product of spacings approach

The MPS estimation approach is proposed as a competitive approach to the usual maximum likelihood method by Cheng and Amin^[37] and Ranneby^[38], independently. Using this approach, the MPSEs are attained using the same logic as the MLEs by maximizing the PS function. Let $\Delta_{i, j} = F(x_{i, j})-F(x_{i, j-1}), i = 1, \dots, k, j = 1, \dots, J_{i}$ be the uniform spacings of an IAPT2C random sample of size $J_{i}$ from the Weibull distribution under CSALTs with $x_{i, 0} = 0$, $x_{i, J_{i}+1} = \infty$ and $\Delta_{i, J_{i}+1} = 1-F(x_{i, J_{i}})$ such that $\sum_{j = 1}^{J_{i}+1}\Delta_{i, j} = 1$. For more studies about the MPS procedure, one can refer to Basu et al.^[39], Volovskiy and Kamps ^[40], and Chaturvedi et al. ^[41]. However, we can write the PS function of the IAPT2C with CSALTs data as follows:

In this section, we study the MPSEs of $\theta, \beta_0$ and $\beta_1$ using IAPT2C with CSALTs data. Utilizing the invariance trait of the MPSEs, the estimates of $\lambda_u$ and RF at the designed stress level are also computed. Likewise, the ACIs of the different parameters are created using the asymptotic normality of the MPSEs. For more detail regarding the properties of the MPSEs, one can see Ranneby ^[38], Cheng and Traylor ^[42], Ghosh and Jammalamadaka ^[43], and Anatolyev and Kosenok ^[44].

4.1.   Point estimation

Suppose we have an IAPT2C sample taken from the Weibull population with CDF given by (2.2), the PS function of $\theta, \ \beta_0$ and $\beta_1$ can be expressed using (2.2) and (4.1) as follows:

where $Q_{i}(\theta) = \sum_{j = 1}^{D_{i}}R_{i, j}x_{i, j}^{\theta}+R_{i}^{*}T_{i}^{*\theta}$. The log-PS function of (4.2) takes the form

The MPSEs $\tilde{\theta}, \tilde{\beta}_0$ and $\tilde{\beta}_1$ of $\theta, \ \beta_0$ and $\beta_1$ can be obtained by maximizing the objective function in (4.3) with respect to $\theta, \ \beta_0$ and $\beta_1$, or equivalently by solving the following three normal equations:

and

where

and

It is clear from (4.4)–(4.6) that the MPSEs cannot be obtained in closed-form solutions, similar to the case of the MLEs. Accordingly, one can employ an iterative technique to attain the needed estimates numerically. Consequently, employing the invariance property of the MPSEs, we can get the MPSEs of $\lambda_{u}$ and RF under the designed stress level, respectively, as

and

4.2.   Interval estimation

In this subsection, we use the asymptotic features of the MPSEs to create the ACIs of $\theta, \ \beta_0$ and $\beta_1$ as well as $\lambda_{u}$ and RF at the designed stress level. Firstly, from (4.3), we require obtaining the next quantities

and

where

The expectations of the expressions of the second derivatives are not straightforward to obtain. Thus, the AV-CM of the MPSEs of $\theta, \ \beta_0$, and $\beta_1$ cannot be obtained in closed structures. So, we use the approximate AV-CM for the MPSEs as

Following the MPSE's asymptotic features, similar to the case of the MLEs, the $100(1-\alpha)\%$ ACIs of $\theta, \ \beta_0$ and $\beta_1$ can be constructed as

where $\widetilde{var}(\tilde{\theta}), \widetilde{var}(\tilde{\beta_{0}})$ and $\widetilde{var}(\tilde{\beta_{1}})$ are the main diagonal elements of $I_{0}(\tilde{\theta}, \tilde{\beta}_{0}, \tilde{\beta}_{1})$ presented by (4.9).

Now, we need to build the ACIs of the $\lambda_{u}$ and the RF under the designed stress level. To achieve this purpose, we first consider using the delta method to compute the approximate estimates of the variances $\widetilde{var}(\tilde{\lambda_{u}})$ and $\widetilde{var}(\widetilde{R}_{u})$ as follows:

where $\Lambda_{\lambda_{u}}$ and $\Lambda_{R_{u}}$ are as defined in (3.14). Then, the $100(1-\alpha)\%$ ACIs of $\lambda_{u}$ and RF under the designed stress level are computed, respectively, by

5.   Bayesian approach

When the sample size is large enough or there is no censoring of the data, classical estimation procedures usually produce highly precise results. However, in experiments with small sample sizes or when there is censored data, these classical procedures can sometimes lead to misleading and incorrect conclusions. The Bayesian approach offers a solution by incorporating additional prior information, such as historical data or existing knowledge, into the statistical inference process. This allows for more accurate estimations. In this section, we will discuss Bayesian estimations of $\theta$, $\beta_0$, and $\beta_1$. We will also examine $\lambda_{u}$ and RF under the designated stress level. To investigate the Bayesian estimates, both points and intervals, we will derive the posterior distributions based on the LF and PS functions, respectively.

5.1.   Prior information and loss function

In this subsection, it is considered that the parameters $\theta, \ \beta_0$ and $\beta_1$ are statistically independent. It is observed from (3.1) or (4.2) that no conjugate prior distributions are available for the unknown parameters due to the complex expressions of the LF or PS function. Furthermore, it is to be mentioned here that it is not straightforward to involve Jeffrey's priors because of the complicated form of the Fisher information matrices using both classical approaches. Therefore, we assume that the parameters $\theta$ and $\beta_1$ have gamma PDFs, i.e., $\theta\sim Gamma(c_{1}, w_{1})$ and $\beta_1\sim Gamma(c_{2}, w_{2})$. We consider the gamma prior distributions since they adjust the support of the unknown parameters $\theta$ and $\beta_1$ and are fairly straightforward. They are also flexible and incorporate a wide range of prior knowledge. Furthermore, the usage of gamma prior distributions may not result in much complexity in posterior evaluation or calculation scenarios, particularly when employing the MCMC technique. On the other hand, it is known that the parameter $\beta_{0}$ can be positive (or negative) depending on the nature of the product. Therefore, we adopted this information and assumed that the parameter $\beta_{0}$ has a normal prior distribution, i.e., $\beta_{0}\sim N(\mu, \sigma^{2})$. Here, we select the normal distribution due to its popularity and flexibility with the understanding that some other distributions like generalized logistic type-Ⅰ or Gumbel distributions can be used. So, the joint prior distribution becomes

where $c_{1}, c_{2}, w_{1}, w_{2}, \sigma > 0$ and $-\infty < \mu < \infty,$ are the associated hyper-parameters and are considered to be known. The joint prior in (5.1) reduces to the case of non-informative prior when $c_{1} = c_{2} = w_{1} = w_{2} = \mu = 0$ and $\sigma = \beta_{0}/\sqrt{2\log(\beta_{0})}$.

From a Bayesian perspective, the choice of loss function plays a crucial part in the inference issues. Since there is no precise analytical method for determining which loss function should be used, most studies on estimating problems have assumed that the underlying loss function, which is a symmetric loss function, is the squared error loss function (SELF). Assuming $\check{\tau}$ represents the parameter $\tau$'s Bayesian estimator, then the SELF can be expressed as

From (5.2), the Bayes estimator $\check{\tau}$ of $\tau$ is the posterior mean of $\tau$.

5.2.   Bayesian estimation via likelihood-based

Combining the LF in (3.1) with the joint prior distribution in (5.1), the joint posterior PDF of $\theta, \ \beta_0$, and $\beta_1$ can be expressed as

where $A$ is the normalized constant. Let $\eta(\theta, \beta_{0}, \beta_{1})$ be any parametric function of $\theta, \ \beta_0$ and $\beta_1$, then the Bayesian estimator using likelihood-based, denoted by $\check{\eta}(\theta, \beta_{0}, \beta_{1})$, using the SELF is the expectation of the posterior distribution in (5.3), which is given by

From (5.4), it is obvious that it is not probable to acquire an exact expression for the Bayesian estimator $\check{\eta}(\theta, \beta_{0}, \beta_{1})$ because it is depicted as the ratio of three intractable integrals. Accordingly, the MCMC technique is implemented to calculate the required estimates. To do the steps of the MCMC technique, we first need to derive the conditional distributions of $\theta, \ \beta_0$ and $\beta_1$ as

and

Clearly, the conditional distributions of $\theta, \ \beta_0$, and $\beta_1$ in (5.5)–(5.7) cannot be described by any well-known distributions. Thus, to get the Bayes estimates, the Metropolis-Hastings (M-H) procedure is operated to yield random samplings from these distributions. However, to perform Bayesian estimation by performing the M-H algorithm, the stages of the sample generation procedure in Algorithm 1 have to be completed.

Consequently, the Bayesian estimates of $\theta, \ \beta_0$ and $\beta_1$ under the SELF can be obtained as follows:

where $M$ is the burn-in period. Also, the Bayesian estimates of $\lambda_{u}$ and RF at the designed stress level can be computed, respectively, as

Moreover, Algorithm 2 offers the steps for creating a $100(1-\alpha)\%$ BCI of $\xi$, where $\xi = [\theta, \beta_{0}, \beta_{1}, \lambda_{u}, R_{u}(x_{0})]$.

5.3.   Bayesian estimation via product of spacings-based

The Bayesian estimators of $\theta, \ \beta_0$, and $\beta_1$ as well as $\lambda_{u}$ and RF at the usual stress level are obtained using PS-based estimation. Merging the PS function in (4.2) with the joint prior distribution given by (5.1), the joint posterior distribution of $\theta, \ \beta_0$, and $\beta_1$ takes the following form

where $B$ is the normalized constant. Using the SELF (5.2) and the joint posterior PDF (5.8), one can obtain the Bayesian estimator using the PS-based of $\eta(\theta, \beta_{0}, \beta_{1})$, denoted by $\breve{\eta}(\theta, \beta_{0}, \beta_{1})$, as follows:

Similar to the case of Bayesian estimation using the likelihood-based method, it is not achievable to obtain (5.9) analytically. Hence, we suggest approximating it by employing the MCMC technique. To apply the MCMC steps, we first derive the conditional distributions of $\theta, \ \beta_0$ and $\beta_1$, respectively, as

and

where $\Delta_{i, j}(\theta, \beta_{0}, \beta_{1}) = \Delta_{i, j}$.

Remark 2. The conditional distributions in (5.10)–(5.12) cannot be presented by any known distribution, hence samples from these distributions can be gained via the M-H technique. This enables the acquisition of the necessary Bayesian estimates for the various parameters. For this goal, the same procedures as are listed in Algorithms 1 and 2 can be carried out.

6.   Simulation outcomes

By considering two sets of stress levels $s_{i}, \ i = 1, 2$, namely Stress-Ⅰ:(0.25, 0.75) and Stress-Ⅱ:(1.5, 2.5), a number of 1,000 IAPT2C samples are generated when the true value of parameters $(\theta, \beta_0, \beta_1)$ is taken as (0.8, 0.5, 0.2) for different combinations of $(T_{i, 1}, T_{i, 2})$, namely (0.1, 0.3) and (0.3, 0.7). To analyze the efficiency of the proposed estimators of $\theta$, $\beta_0$, $\beta_1$, $\lambda_u$, $\lambda_1$, $\lambda_2$ and $R_u(x_0)$, we perform comparisons based on different choices of complete (effective) sample sizes $n_i(m_i)$, two time thresholds $T_{i, 1}$ and $T_{i, 2}$, censoring schemes $R_{i, j}$'s for $i = 1, 2, \dots, k$ and $j = 1, 2, \dots, m_i$. The design scenarios of this study are presented in Table 1. Here, we assume that the predetermined times $T_{i, 1}$ and $T_{i, 2}$ are equal for the different stress levels. Therefore, we use the notation $(T_{1}, T_{2})$ instead of $T_{i, 1}$ and $T_{i, 2}$ in this section. For each scenario, the actual values corresponding to the unknown parameters $(\lambda_{1}, \lambda_{2})$ with respect to stress sets Ⅰ and Ⅱ are $(1.7333, 1.9155)$ and $(2.2255, 2.7182)$, respectively. Furthermore, using $s_{u} = 0.1$, the proposed estimates of $\lambda_{u}$ and $R_{u}(x_0)$, for distinct time $x_0$, are evaluated, while their true values are 1.6820 and 0.7660, respectively.

To run a life-test experiment based on the IAPT2C with CSALTs, follow the steps in Algorithm 3.

The specification of hyper-parameter values is the main issue in a Bayesian setup. It is known that if improper prior knowledge on the unknown subjects is available, then the objective's posterior density goes down to its matching LF (or PS). Consequently, it is preferable to estimate the unknown parameters by any frequentist approach rather than the Bayesian approach due to the computational exhaustion of the latter. So, we take $(c_{1}, c_{2}) = (8, 2)$ and $w_{i} = 10, \ i = 1, 2,$ for $\theta$ and $\beta_1$ also take $(\mu, \sigma) = (0.5, 1)$ for $\beta_0$. Alternatively, one could determine the hyper-parameter values for the unknown parameters of interest using "past sample". Following Section 5, we set $H = 12,000$ and $M = 2,000$. Here, the MLE and MPSE are used as initial guesses for running the MCMC sampler. However, the average estimates (AvEs), root mean squared-errors (RMSEs), mean relative absolute biases (MRABs), average confidence lengths (ACLs), and coverage probabilities (CPs) of $\theta$, $\beta_0$, $\beta_1$, $\lambda_u$, $\lambda_1$, $\lambda_2$, and $R_u(x_0)$ are calculated.

All necessary computational algorithms are coded in $\textsf{R}$ statistical programming language software version 4.0.4 via three packages: (ⅰ) 'coda' package proposed by Plummer et al.^[45], (ⅱ) 'maxLik' package by Henningsen and Toomet^[46], (ⅲ) 'GoFKernel' package by Pavia^[47].

The simulation results of $\theta$, $\beta_0$, $\beta_1$, $\lambda_u$, $\lambda_1$, $\lambda_2$, and $R_u(x_0)$ are reported in the supplementary material. Briefly, the first part of the simulated results, when $S_{15, 20}^{[1]}$ and $S_{20, 20}^{[1]}$ for each $T_i, \ i = 1, 2,$ values, is reported in Tables 2 and 3. In each Monte Carlo output table, for each scenario, the corresponding estimates of each parameter based on stresses Ⅰ and Ⅱ are tabulated in the first and second lines, respectively.

Now, the following conclusions on the unknown parameters $\theta$, $\beta_0$, $\beta_1$, $\lambda_u$, $\lambda_1$, $\lambda_2$, and $R_u(x_0)$ are made:

● Both frequentist and Bayesian estimates of $\theta$, $\beta_0$, $\beta_1$, $\lambda_u$, $\lambda_1$, $\lambda_2$, and $R_u(x_0)$ are showing satisfactory behavior based on minimum RMSEs, MRABs, and ACLs as well as maximum CPs.

● As $\sum_{i}^{k}n_i$ (or $\sum_{i}^{k}m_i$) increases, the RMSEs and MRABs decrease of all estimates in most cases as expected.

● As $T_i, \ i = 1, 2,$ increase, the RMSEs and MRABs of $\theta$ and $\beta_0$ decrease while those associated with others increase.

● As $T_i, \ i = 1, 2,$ increases, in almost all cases, the ACLs narrow down while the CPs achieve the specified nominal level for all unknown parameters.

● As $s_i, \ i = 1, 2,$ grow, the RMSEs and MRABs of $\theta$ and $\beta_1$ decrease while those associated with others increase.

● As $s_i, \ i = 1, 2,$ grow, the ACLs decreased while the CPs increase for $\theta$ and $\beta_1$ unlike other unknown parameters.

● Comparing the investigated techniques, the simulation results showed that:

– The LF (along with the MCMC-LF) method is the best for estimating $\theta$, $\beta_0$, $\beta_1$, and $R_u(x_0)$.

– The LF of $\lambda_u$, $\lambda_1$, and $\lambda_2$ performs satisfactorily compared to the PS in respect of classical estimates, while the MCMC-PS performs better compared with the MCMC-LF in respect of Bayes' estimates.

– Comparing the performance of the interval methodologies on the basis of smallest ACLs and highest CPs, in most cases, it can be seen that the LF (along with MCMC-LF) method is the best for estimating all unknown parameters except $R_u(x_0)$.

– Because prior knowledge about the unknown parameters is available, the Bayes estimates as well as associated BCI estimates outperform those obtained using the frequentist methods. As a result, the investigated priors are very adaptable in both nature and application.

● To appreciate the convergence of the simulated MCMC draws, Brooks–Gelman–Rubin (BGR) diagnostic (when $S_{15, 20}^{[1]}$, $(T_{1}, T_{2}) = (0.1, 0.3)$, and $(s_{1}, s_{2}) = (0.25, 0.75)$ as an example) is plotted in Figure 2. The BGR assesses the degree of convergence of Markovian sequences by comparing the variance-within and variance-between chains for each model parameter simultaneously. Recently, this diagnostic has also been discussed by Nassar and Elshahhat^[48]. We found that the BGR metric indicates that there are certainly no significant variations within the replicated chains. Therefore, one can conclude that the MCMC draws are appropriately mixed.

● Ultimately, depending on different accuracy criteria, namely: RMSE and MRAB (for point estimate) as well as ACL and CP (for interval estimate), simulation findings showed that the proposed Bayes (using LF) method via the M-H sampler is significantly better than other competitive methods.

7.   Real-life applications

We analyzed two data sets to determine the practicality of the inferred strategies. The functionality and user-friendliness of these examples have validated the effectiveness of the suggested techniques in practical usage.

7.1.   M00071 white OLED data

This application deals with the analysis of the lifetime (in hours) of the M00071 white organic light-emitting diode (OLED) mixed with different colors; see Zhang et al.^[49]. Recently, OLED data was also discussed by Lin et al.^[50] and Nassar et al.^[8]. The calculations involved subtracting 1500 and 500 from the lifetime points at ${{s}_{1}}$ and ${{s}_{2}}$, and then dividing the results by their standard deviations. Table 4 presents the newly updated OLED information. According to Zhang et al.^[49], there are two stress levels, namely $s_{1} = 9.64$ mA and $s_{2} = 17.09$ mA. At each stress level, the MLEs with their standard-errors (SEs) of $\theta$ and $\lambda_{i}, \ i = 1, 2,$ as well as the Kolmogorov-Smirnov (KS) with its $P$-value are calculated; see Table 4. This result indicates that the Weibull distribution fits the OLED data set well. In order to prove the existence and uniqueness of the MLEs $\hat\theta$ and $\hat\lambda_{i}, \ i = 1, 2,$ the contours of $\theta$ and $\lambda_{i}, \ i = 1, 2,$ are provided in Figure 3. It indicates that the MLEs of $\theta$ and $\lambda_{i}, \ i = 1, 2,$ exist and are also unique. The likelihood ratio (LR) test can be used to evaluate the assumption of a common shape parameter across data collected at different stress levels. The test statistic in this case is $\Lambda^{*} = 2(\ell_{1}+\ell_{2}-\ell_{c})$, where $\ell_{1}$ and $\ell_{2}$ correspond to the likelihood values acquired at stress levels 1 and 2, respectively, and $\ell_{c}$ is the likelihood value achieved by fitting a model with a common shape parameter $\theta$. The distribution of $\Lambda^{*}$ is approximately chi-square with $1$ degree of freedom. From the original data, we have $\Lambda^{*} = 1.283$ with $P$-value = 0.257. This result indicates that shape parameters do not differ significantly for any significance level less than 0.257.

Now, from the complete failure times at both stress levels $s_{i}, \ i = 1, 2,$ two IAPT2C samples using $m_{i} = 5, \ i = 1, 2,$ $R_{i, j} = 1, \ j = 1, \dots, m_{i},$ and some choices of $T_{i, 1}$ and $T_{i, 2}, \ i = 1, 2,$ are generated and reported in Table 5.

Using information in Table 5, the various estimations of $\theta$, $\beta_0$, $\beta_1$, $\lambda_u$, $\lambda_1$, $\lambda_2$, and $R_u(x_0)$ are computed. Using the design stress level $s_u = 5$ mA, the different estimates of $\lambda_u$ and the RF (for $x_{0} = 1$) are obtained. Following Section 5, the first 5000 samples are removed out of 30,000 MCMC draws. Furthermore, we computed all Bayes estimates using non-informative priors. We chose to use 0.001 for all the hyper-parameters in our calculations. However, Tables 6 and 7 display the calculated classical/Bayes estimates (along their SEs) and 95% asymptotic/credible interval estimates (along their lengths) of $\theta$, $\beta_0$, $\beta_1$, $\lambda_u$, $\lambda_1$, $\lambda_2$, and $R_u(x_0)$. Since Bayes' findings are calculated without any additional information, Tables 6 demonstrates the similarity between the frequentist and Bayes estimates. Additionally, BCIs of all parameters perform better than others; see Table 7. Moreover, in terms of the lowest SE and shortest interval length values, the Bayes' results reported in Tables 6 and 7 showed that Bayesian point (or credible) estimates outperformed compared to others. Some important statistics of $\theta$, $\beta_0$, $\beta_1$, $\lambda_u$, $\lambda_1$, $\lambda_2$, and $R_u(x_0)$ are computed and provided in Table 8.

Furthermore, to show the convergence of drawn samples from both types of 25,000 MCMC variates, the trace and marginal density plots (with their histograms using the Gaussian kernel) of $\theta$, $\beta_0$, $\beta_1$, $\lambda_u$, $\lambda_1$, $\lambda_2$, and $R_u(x_0)$ are displayed in Figure 4. In each trace (or density) plot, the Bayes estimate of each subject is displayed as a horizontal solid line, while its BCI limits are represented with horizontal dotted lines. It indicates that all the generated samples collected from the MCMC-LF (or MCMC-PS) sampler converged satisfactorily. Furthermore, Figure 4 shows that the generated variates of $\theta$ and $\beta_0$ are fairly symmetric, those of $\beta_1$ and $R_u(x_0)$ are negatively skewed, while those of $\lambda_u$, $\lambda_1$ and $\lambda_2$ are positively skewed. Also, Figure 4 supports our numerical findings presented in Table 8. In Figure 5, based on both stress (9.46 mA and 17.09 mA) data, the plots of fitted and empirical RFs of the Weibull life distribution using the proposed methodologies are provided.

7.2.   Pump motor data

This application considers an engineering data set to examine the practical utility of the proposed methodologies. This data demonstrates the operational lifespan (in hours) of a pump motor. It was originally reported by the ReliaSoft website (http://www.reliasoft.com/newsletter/1q2002/qalt.htm) and later analyzed by Dey and Nassar ^[9]. The data were obtained based on two specified stress levels of the liquid density, namely $s_{1} = 1.0$ g/mL and $s_{2} = 1.4$ g/mL, where the failure times at each stress level are recorded. For computational convenience, we simplified the numbers by subtracting 500 from each data point and then dividing the result by 1000. This subtraction is done for computational purposes, because dealing with the same actual time points for the pump motor is not appropriate. The transformed data values are listed in Table 9.

Table 9 provides evidence that the Weibull model fits the pump motor data sets well. Contour plots, based on two stress levels, are plotted in Figure 6. It indicates that the MLEs $\hat\theta$ and $\hat\lambda_{i}, \ i = 1, 2,$ exist and are also unique. Using the LR test, we compute $\Lambda^{*} = 4.179$ with $P$-value$= 0.041$. This finding indicates that the shape parameters do not differ significantly at any significance level lower than 0.041. Although the $P$-value is small, we can continue our analysis by assuming common shape parameters, especially for illustration purposes, taking into account the lack of available data sets in the literature.

Using $m_{i} = 5, \ i = 1, 2,$ and $R_{i, j} = 1, \ j = 1, \dots, m_{i}$, two IAPT2C samples, for various choices of $(T_{i, 1}, T_{i, 1}), \ i = 1, 2,$ are gathered; see Table 10. The calculated estimates of $\theta$, $\beta_0$, $\beta_1$, $\lambda_u$, $\lambda_1$, $\lambda_2$ and $R_u(x_0)$, based on the data sets reported in Table 10, are obtained. Also, by running the MCMC algorithm 30,000 times (when $M = 5000$), using non-informative priors, the Bayesian calculations of the considered parameters are developed. The estimated RF (for $x_{0} = 1$) using both classical and Bayes methods, when the normal stress level $s_u$ is taken as 0.75 g/mL, is obtained. All point and interval estimates of $\theta$, $\beta_0$, $\beta_1$, $\lambda_u$, $\lambda_1$, $\lambda_2$ and $R_u(x_0)$ are presented in Tables 11 and 12, respectively. These tables showed that Bayesian point (or interval) estimates perform better than other frequentist point (or interval) results in terms of minimum SEs and interval lengths. Several statistics for MCMC posterior distributions of $\theta$, $\beta_0$, $\beta_1$, $\lambda_u$, $\lambda_1$, $\lambda_2$ and $R_u(x_0)$ are also computed; see Table 13. In this table, the statistics MCMC drawn based on LF and PS approaches are listed in the first and second rows, respectively.

The density and histogram plots of $\theta$, $\beta_0$, $\beta_1$, $\lambda_u$, $\lambda_1$, $\lambda_2$ and $R_u(x_0)$ from MCMC-LF and MCMC-PS approaches are displayed in Figure 7. It represents that the offered MCMC-LF (or MCMC-PS) sampler converges adequately. It is also noted, for both MCMC-LF and -PS approaches, that variates of $\theta$, $\beta_0$, $\beta_1$ are fairly symmetric; the generated posterior estimates of $\lambda_u$, $\lambda_1$, $\lambda_2$ are positively skewed, while the generated posterior estimates of $R_u(x_0)$ are negatively skewed. Figure 8 shows the plots of fitted and empirical RFs (for 1.0 g/mL and 1.4 g/mL data sets) using the computed estimates based on each considered method.

8.   Conclusions and recommendations

In this paper, through a constant-stress accelerated life test model based on improved Type-Ⅱ adaptive progressive censoring, various estimation challenges for the Weibull parameters of lifetime have been investigated. Assuming a log-linear acceleration model, different point estimations of the Weibull's parameters and its reliability at normal use conditions have been studied using two classical methods, namely the maximum likelihood and the maximum product of spacings approaches. The approximate confidence intervals of all unknown subjects have been obtained using the asymptotic properties of the two frequentist estimation methods. Also, Bayesian point and interval estimators have been studied using both likelihood and the product of spacings functions. It has been observed that Bayes' results cannot be acquired in explicit expressions; therefore, the Metropolis–Hastings technique has been employed to get the required estimates. To highlight the behavior of the various estimates proposed in this study, a wide simulation comparison has been implemented. Additionally, two actual sets of data were used to show how the different approaches can be used. These applications support the numerical findings of the proposed estimators obtained from simulation studies in terms of the estimated standard errors. Generally, Bayes' setup using the likelihood function has been recommended to evaluate the shape parameter and reliability function under normal use conditions, while Bayes estimates using the product of spacings function have also been recommended to evaluate the scale parameters, which behave well compared with their counterparts. For future work, it is of interest to investigate the estimation methods for Weibull distribution using other kinds of accelerated life tests, for example, step-stress-accelerated life tests using improved Type-Ⅱ adaptive progressive censoring data

Author contributions

Mazen Nassar: Conceptualization, Methodology, Investigation, Writing-review & editing; Refah Alotaibi: Methodology, Investigation, Funding acquisition, Writing-original draft; Ahmed Elshahhat: Methodology, Software, Data curation, Writing-original draft. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to express their gratitude to the editor and the five anonymous referees for their helpful suggestions and valuable comments. This research was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R50), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

There is no conflict of interest.