1.
Introduction
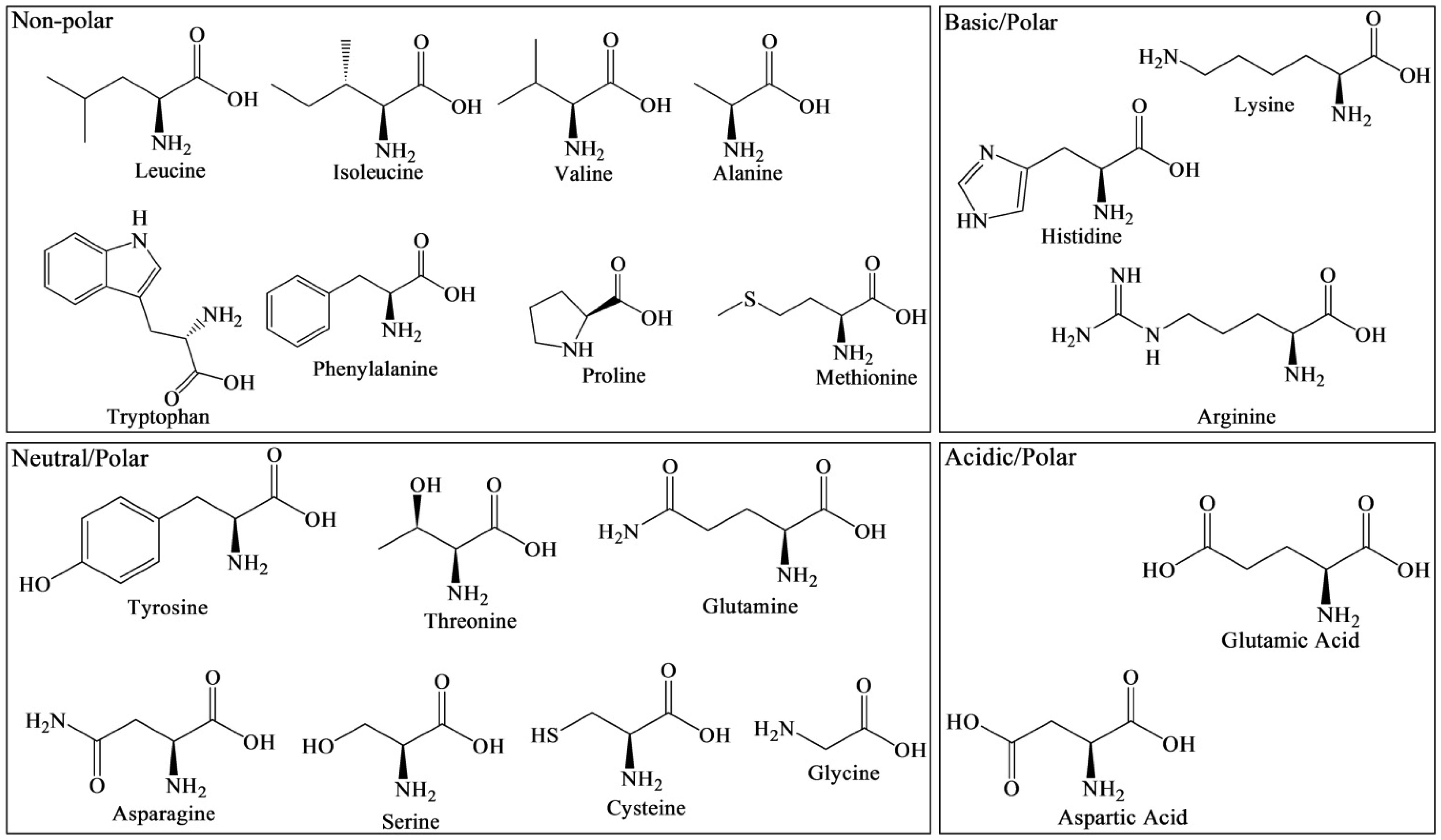
Proteins are integral part of living organisms that play critical roles in numerous biological processes including the proper functioning, survival and adaptation to changes in external atmosphere. Proteins differ from one another in their sequence of amino acids, which is directed by genetic materials i.e. nucleotides. In living organisms, protein synthesis occurs in a cellular organelle called ribosomes, which links amino acids in an order dictated by messenger RNA (mRNA). Transfer RNA (tRNA) carries amino acids specified by the three nucleotides RNA codon that connect to each other through peptide bond and finally leads to synthesis of proteins [1]. Amino acids are small molecule metabolites containing an amine (–NH2) and a carboxyl (–COOH) functional groups and are present in all living things [2]. To date, 22 amino acids are found to be present in proteins, among which 20 appear in the genetic code and known as proteinogenic amino acids or standard/canonical amino acids and play a central role in cellular metabolism [3]. The remaining two amino acids, selenocysteine and pyrrolysine can be incorporated into proteins by special translational mechanism [4]. Selenocysteine can be found in both eukaryotes and prokaryotes [5], whereas pyrrolysine is only been reported in prokaryotes [6]. Besides 11 non-essential amino acids, which the human body can synthesize, there are 9 amino acids which are known as essential amino acids as they can only be obtained from exogenous sources. The common essential and non-essential amino acids are listed in Table 1 and their structures are summarized in Figure 1. These 20 proteinogenic amino acids showed higher polymerization reactivity and fewer side reactions, which are believed to have contributed towards their appearance in the genetic codes and translation to proteins [7]. The 20 proteinogenic amino acids, also termed as proteinaceous amino acids spontaneously link to form polymers (proteins) through a nucleophilic attack, and often time it proceeds without the aid of any other biological molecules or catalyst.
All proteinogenic amino acids (except Gly) exist in two stereoisomeric forms and studies report that, all proteins are primarily made up of L-AAs. However, D-AAs are reported to play important biological functions in both prokaryotic and eukaryotic systems. Therefore, it is imperative to be able to accurately distinguish and measure the correct stereoisomeric version of the proteinogenic amino acids in a given system to explain their role. Due to difference in polarity and acid-base characteristics, it has been a challenge to analytically resolve and quantitate all proteinogenic amino acid stereoisomers (39 species, 38 isomeric AAs and Gly) in a single analytical run. Liquid and gas chromatography have been used for chiral analysis of amino acids using both direct and indirect approach, the later requires derivatization that is time consuming [10]. Tremendous advancements in the field of stationary phases [11],[12], availability of numerous chiral derivatizing reagents [13] and instrumentations [14]–[17] have tremendously contributed to chiral analysis of amino acids in a much more straightforward fashion [18]. In this review, a comprehensive discussion of numerous biological functions and chromatography coupled to mass spectrometry (MS) based analytical methods for chiral analysis of proteinogenic amino acids and their stereoisomers are outlined.
2.
Structural features and stereochemistry
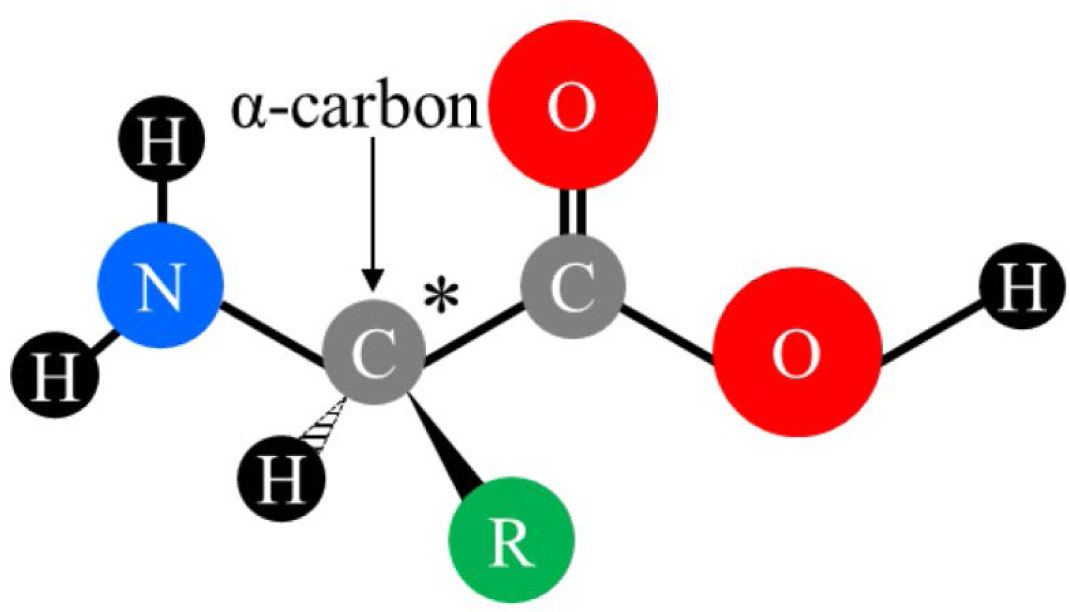
Structural features play a direct role in explaining the physicochemical properties displayed by different amino acids and also direct their classification. Based on the location of core structure, amino acids can be classified into four groups such as alpha- (α-), beta- (β-), gamma- (γ-) or delta- (δ-) amino acids. Certain other criteria such as polarity (polar and non-polar), pH level (positively charged, neutral, negatively charged), and side chain group type (aliphatic, acyclic, aromatic, hydroxyl or sulfur containing etc.) play crucial role in determining the types, characteristic features, behavior, reactivity and functions of the amino acids. Amino acids are primarily composed of carbon, hydrogen, nitrogen, oxygen and sulfur; the carbon atom next to the carboxyl group is called the α-carbon as showed by asterisk (*) in Figure 2.
Amino groups when connected to α-carbon referred to as α-amino acids, which is the most common form of amino acids found in nature. Except for proline, all other amino acids contain a primary amino group (NH2). The α-carbon is chiral when the side chain is not a hydrogen (glycine). Therefore, except for glycine, remaining 19 proteinogenic amino acids exist in two stereoisomeric forms, known as D- and L-amino acids, which are mirror images of each other. Most of the proteins are predominately comprised of L-amino acids except for few proteins found in bacteria and cone snails [19]. D-amino acids play a major role in bacterial cell wall biosynthesis [20]. Several D-amino acids have reported to serve important roles in different branches of sciences including food, agriculture, pharmaceutical, microbiology, cosmetic, extraterrestrial etc. Due to presence of the carboxylic acid and amino functional groups, the amino acids are amphiprotic and can coexist as zwitterion within various range of pH. Therefore, the charge distribution on the amino acid molecules largely depends on the pH of the environment, which can also be exploited to ionize them in mass spectrometry-based detection.
3.
Physicochemical properties of amino acids
Amino acids are colorless, non-volatile crystalline solids, which have a melting point above 200°C as their inorganic salts. Several factors play important role in determining the nature and physicochemical properties of these amino acids including charge, polarity, size and functional groups as discussed earlier. Properties of the amino acids ultimately contribute to the properties and functions of the proteins they form. For examples, proteins that will bind to negatively charged molecules will have surfaces rich with positively charged amino acids such as lysine, arginine and histidine. Whereas proteins binding to positively charged molecules will have surfaces rich with negatively charged amino acids such as glutamic acid and aspartic acid. Similarly, water-soluble proteins tend to have the hydrophobic amino acids buried in the core, which is inaccessible to water whereas the hydrophilic amino acids remain accessible. Water insoluble or limited water-soluble proteins, on the other hand, have their hydrophobic amino acid residues exposed, for example, lipid membrane bound proteins. There are amino acids with other specific properties such as, cysteine can form covalent disulfide bonds to other cysteines, proline can form a cyclic polypeptide backbone etc. In aqueous solutions, amino acids can exist as dipolar ions and can react with strong acids or bases. Due to these neutralization reactions, amino acids can also be used as a buffer. Depending on the solution pH, amino acids can have a predominating charged form, which determines their movement in an electric environment. The pH at which amino acids do not migrate in an electrical field is called their isoelectric point, which can be manipulated to improve the solubility and stability of the proteins they form [21]. In general, amino acids have good stability in different solution strength, pH and radiation, although glutamic acid is reported to have significant degradation in 0.1 N HCl with time [22] and phenylalanine and tryptophan are reported to degrade when exposed to UV and gamma radiation [23]. It has been reported that, non-proteinogenic amino acids are relatively more stable than proteinogenic amino acids, which also explains why non-proteinogenic amino acids can be found in meteorites as part of terrestrial biochemistry whereas proteinogenic amino acids as part of life biochemistry [24].
4.
Synthesis and reactivity of proteinogenic amino acids
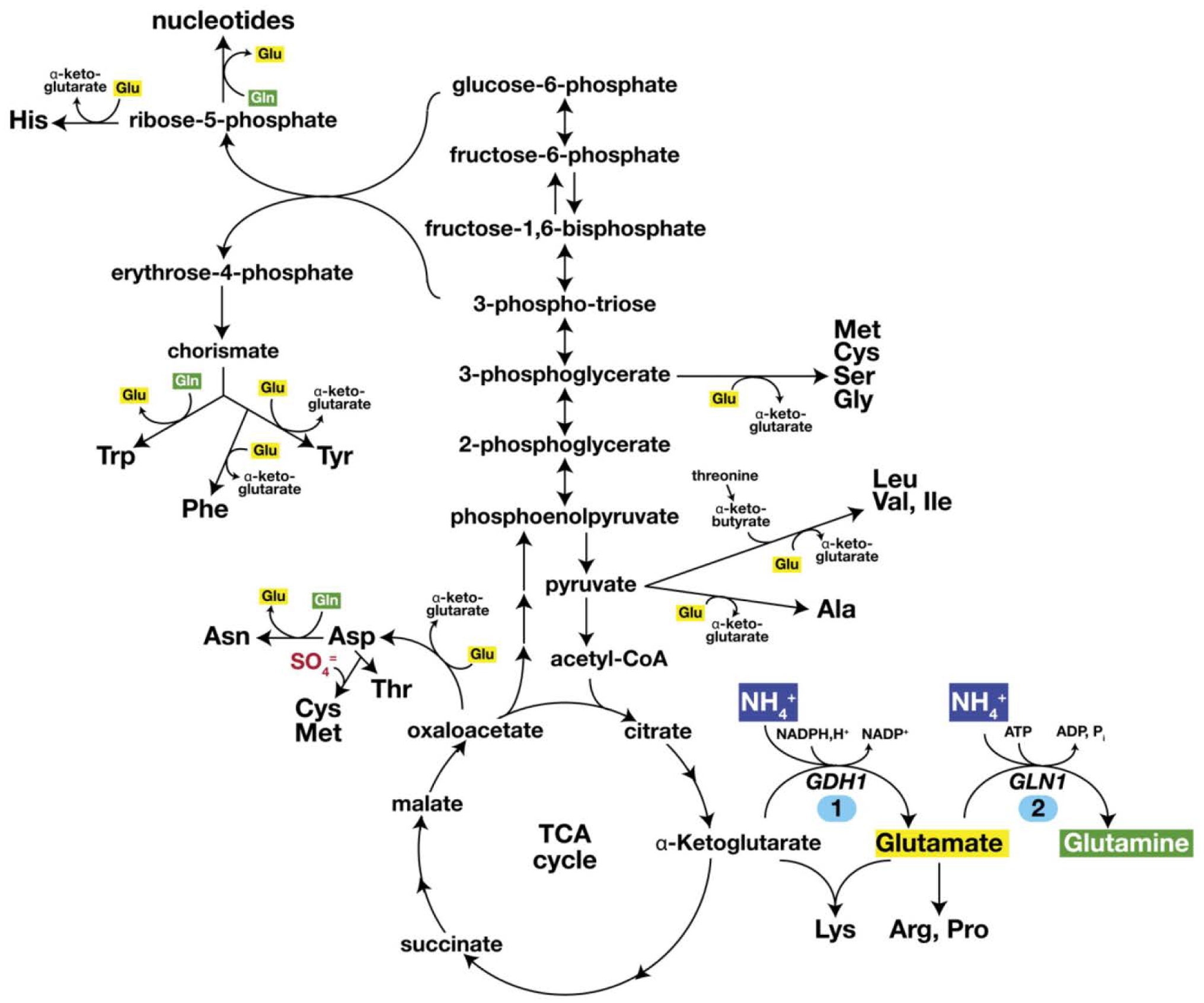
Commercial production of amino acids is primarily dependent on bacterial synthesis in expense of glucose utilization or enzymatic conversion of amine metabolites. Chemically, amino acids can be synthesized using Strecker synthesis reaction by reacting aldehyde with ammonium chloride in presence of potassium cyanide [25]. Most bacteria and plants can synthesize all 20 common proteinogenic amino acids, whereas humans can only synthesize 11 which are also known as non-essential amino acids [26]. Biosynthetically, amino acids are derived from various intermediates of glycolysis, citric acid cycle and pentose phosphate pathway [27] (Figure 3). Biosynthetic pathways for non-essential amino acids are fairly straightforward, however, the pathways involved for the essential amino acids can be more complex [28]. For example, glutamate is synthesized by reductive amination of α-ketoglutarate with the aid of glutamate dehydrogenase, which is then transaminated to other α-ketoacid to form other non-essential amino acids including proline, glutamine, histidine and arginine [29]. Alanine, leucine and valine can be synthesized from pyruvate and aspartate can be synthesized from transamination of oxaloacetate. Serine is synthesized from 3-phosphoglycerate which then act as a precursor for glycine. Other amino acids go through complex multi-step biosynthesis pathway as can be seen in Figure 3. From this discussion, it can be realized how studying proteinogenic amino acid level can provide important information and insights on activity and function of different pathways and enzymes between a normal vs dysregulated biological system.
The types and reactivity of various reactions different amino acids undergo depend on their functional groups and side chain properties [31]. The most common reaction that amino acids undergo is peptide bond formation by which amino acids can be connected to each other through an amide linkage, which leads to formation of peptides and finally grows in length to form a polymer called protein. Inside cells, proteins are translated from RNA inside ribosome and the synthesis starts at their N-terminal. Similar to metabolism of drugs and xenobiotics, amino acid metabolism and excretion also occur in liver and in kidney respectively, finally entering into urea cycle to be removed from the body. Detection and quantitation of free amino acids are thus important to evaluate and determine the progress of numerous reactions they undergo.
5.
Functions of proteinogenic amino acids in biology
Proteinogenic amino acids are integral part of almost all biological functions as proteins are ubiquitous and responsible for plethora of important roles. Non-proteinogenic amino acids on the other hand can be a part of proteins through post-translational modification and can be of various uses such as defense mechanism of fungi, synthesis of peptide antibiotics, components of meteorite and inhibition of neurotransmission [32],[33]. Proteinogenic amino acids play a critical role in various pathways of human metabolism such as urea cycle, citric acid cycle, gluconeogenesis as a source of energy [27],[28]. Several amino acids also act as precursors of important bioactive molecules as listed in Table 2.
However, it should be noted that, not all non-protein functions of proteinogenic amino acids are known until today. Free essential amino acids contribute to glycolytic and Krebs cycle and are used as a source of energy during depletion of carbohydrate and fat [55]. Muscle can catabolize the branched chain amino acids (BCAA), valine, leucine and isoleucine [56]. Imbalance in amino acid levels is also reported to be observed in various diseases due to changes in metabolic capacity including cancer [57], liver cirrhosis [58], neurological [59]–[62] and metabolic disorder [63]. In plant biology, amino acids are reported to have roles in production of chlorophyll, hormones and growth factors; stimulation of vitamin and enzyme synthesis, mineral chelation, and increased pest and pathogen resistance [64],[65]. D-amino acids exhibit both inhibitory effect (D-Ser, D-Ala and D-Arg) and positive effect (D-Ile, D-Val) on Arabidopsis growth [66], whereas D-Lys promoted growth of both Arabidopsis and tobacco [67].
6.
Proteinogenic amino acids as biomarkers
Amino acids have been marked by significant dysregulation in more than 50 disorders till date due to mutant genes resulting in abnormal enzymes leading to metabolic errors [68]. Hence, amino acid profiling has been a focus of biomarker study [69],[70] and some of the most important amino acid biomarkers and the associated diseases are listed in Table 3.
The major caveat of using amino acids as biomarkers is that they are vital to many biological processes and their pool might be dysregulated for various other reasons, which need to be carefully considered before using them diagnostically as biomarkers. However, presence of D-amino acids can be a good indication of bacterial infection; although it cannot help in determining the type of bacteria involved, at least not yet. Besides, due to physiological and biochemical differences between different biological systems; and difference in number of subjects in studies, results need to be carefully interpreted to establish suitability of use between species.
7.
Therapeutic roles of proteinogenic amino acids
Amino acids and their intermediates have remained of keen interest to scientists across the globe because of their critical role in important biochemical pathways in different biological systems. Both essential and non-essential amino acids are reported to play important roles in array of different physiological and biochemical models across several different species. Numerous therapeutic applications of proteinogenic amino acids have been reported in respiratory physiology, cardiology, nephrology, neurology, immunology, reproductive system, cell signaling, growth and differentiation, gene expression, acid base balance, systemic circulation, metabolic, bone and congenital disorders among others [68],[83]. Role of non-essential amino acids in cancer biology has also been comprehensively discussed [84]. Some of the key therapeutic roles of various proteinogenic amino acids are discussed in Table 4.
It can be realized that, several amino acids have key therapeutic and diagnostic roles in plethora of diseases. Roles of amino acids as precursors of important bioactive molecules, biomarkers and clinically important agents emphasize why robust analytical methods are required to accurately measure their levels in different biological matrices.
8.
Industrial application of proteinogenic amino acids
Besides having numerous roles in different biological systems, proteinogenic amino acids have several industrial applications including use in human nutrition such as parenteral nutrition, dietary supplements for athletes, use in animal feed additives to help improve the health and production of animals [117]. Glutamic acid and aspartame (L-aspartyl-L-phenylalanine-1-methyl ester) are used as flavor enhancer [118] and artificial sweetener [119] in food industry. In agriculture industry, metal chelating amino acids are used in case of mineral deficiencies and help in improving plants' health [120]. Besides, proteinogenic amino acids are regularly used in pharmaceutical and cosmetic industries for various applications [121] such as environmental friendly packaging, in drug delivery and prosthetic implants due to biodegradable characteristics [122]. Polyaspartate due to its water solubility, biodegradable features and metal chelating ability, is used in disposable diapers [123], anti-scaling agent and corrosion inhibitor [124],[125]. Tyrosine on the other hand is reported to be used as an alternative to phenol in polycarbonate synthesis which has various construction and engineering applications [126].
9.
Stereospecific roles of proteinogenic amino acids
L-amino acids are primarily present in various prokaryotic and eukaryotic protein. Participation of D-amino acids in protein synthesis is very limited, although some D-amino acids have been detected in bacteria, some vertebrates, marine invertebrates and plants as part of peptide antibiotics, hormones, neuropeptides, opioids and toxins [127]. Proteins have ubiquitous roles in animal and plant kingdom including structural integrity, metabolic functions and transport of necessary entities. The role of L-amino acids is limitless as they make proteins, which are responsible for performing plethora of functions in biology, hence are related to the evolution of life. Reasons for the selection of only one isomer of amino acids are not well established, but it can be understood that a mix of both will hinder proper folding of the proteins and might render them inactive. In general, D-amino acids cannot be digested well as peptide bonds containing D-L, L-D and D-D configurations offer resistance to proteolytic enzymes [127], hence it says homochirality is essential for life. Except for threonine and isoleucine which have stereogenic center and glycine which is achiral, remaining 17 proteinogenic amino acids have similar physicochemical properties but vary in biological functions. Conversion of L- to D-amino acids is primarily carried out by D-amino acid racemase via formation of α-iminoacid. L-amino acid oxidase can also participate in this conversion through α-ketoacid formation. In mammals, oxidase predominates over the racemase pathway; the latter is more common in bacteria. Heat and alkaline treatment can also cause this conversion. Historically, D-amino acids are studied only in the context of microorganisms, but in last few decades, their presence have been found in higher organisms as well. As D-amino acids are less frequently present in nature and biology, curiosity developed in studying these stereoisomers. Several D-amino acids have been reported to be identified in human, mouse, rat, chicken, frog, snail, lobster and spider in free form or part of peptides and proteins and thought to be the result of racemization during development and aging [128], although in general racemase pathway is considered dominant in microorganisms. Table 5 enlists presence of several D-amino acids in different higher organisms.
The biggest source of D-amino acids is the food industry and its been reported that in general we consume more than 100 mg of D-amino acids everyday [13]. D-amino acids are reported to provide varying taste and flavor besides providing antimicrobial and antiaging effect. Marcone GL et al. discussed elaborately the different D-amino acids present in different food products naturally or due to processing or contamination [13]. Naturally, fruits and vegetable contain some D-amino acids. Till today various D-amino acids such as D-Asn, D-Asp, D-Ala, D-Arg, D-Gln, D-Glu, D-Val, D-Leu, D-Lys and D-Ser have been found in milk, apple, pineapple, papaya, mango, clementine, orange, pear, lemon, passion fruit, grape fruit, cabbage, water melon, tomato, carrot, celery, rice, meat, fish, liquid spice, peanuts, honey etc. [13],[148]. Alcoholic beverages are reported to contain D-Phe and D-Pro in addition to the already stated ones. Coffee has been another major source of D-amino acids containing D-Asp, D-Glu, D-Pro and D-Phe [149]. Soy and corn based meals are reported to contain D-Met in addition to other commonly present D-amino acids in food. Fermented dairy products such as yogurt and cheese are reported to contain several D-amino acids due to lactic, acetic or bacterial fermentation [150]. Finally, temperature and pH induced racemization can also cause formation of certain D-amino acids in processed food items and can be used as a marker for such treatment. But abnormal or higher than normally reported amount of D-amino acids in food items warrants to check the quality as it is often indicative of microbial contamination especially increased level of D-Asp, D-Glu and D-Ala [151].
D-amino acids have important application in biomedicine as bioactive compounds, biomarkers, essential peptides and proteins. Besides an indicator of bacterial infection, several free and bound D-amino acids have been reported to act as biomarkers, e.g. D-Ser, D-Pro and D-Asn for kidney disease [69],[152],[153], D-amino acid oxidase for post-stroke dementia [154] and cellular senescence [155], D-amino acid peptide for better cellular retention on monoclonal antibody for tumor targeting [156] and D-Glu in heart diseases [157]. Other important D-amino acid containing enzymes includes: D-Pro reductase, D-Glu cyclase, D-Cys desulfhydrase, D-arginase, D-Ser dehydrase and D-Met aminotransferase [158]. There are also reports where the presence of D-amino acid is found to be important for the biological activity, both of therapeutic and adverse origin e.g. D-Ala for analgesic activity of demorphine [137], D-Phe for antibacterial activity of gramicidin S [159], D-Ser for calcium channel blocking activity [160], D-Met for toxicity of defensin like peptide 2 [161], D-Val for cancer therapy [162], D-Tyr for hypertension [163], D-Trp for effect of growth hormone Auxin in plants [164] etc.
10.
Role of proteinogenic amino acids in microbial world
Prokaryotes especially bacteria are a great source of D-amino acids. D-amino acids are present in peptidoglycan (PG) layer of the cell wall, and participate in cell wall biosynthesis and remodeling, spore germination, biofilm formation etc. [165]. Studying bacterial D-amino acid contents can help in better understanding of their cellular adaptation and behavior under stress, which can further aid in antibacterial drug discovery and development. Both gram-positive and gram-negative bacteria have a cell wall and one of the major components of the cell wall is the PG layer, which is thicker in the former and thinner in the later (Figure 4). But in both systems, various D-amino acids participate in the formation of the PG layer [20].
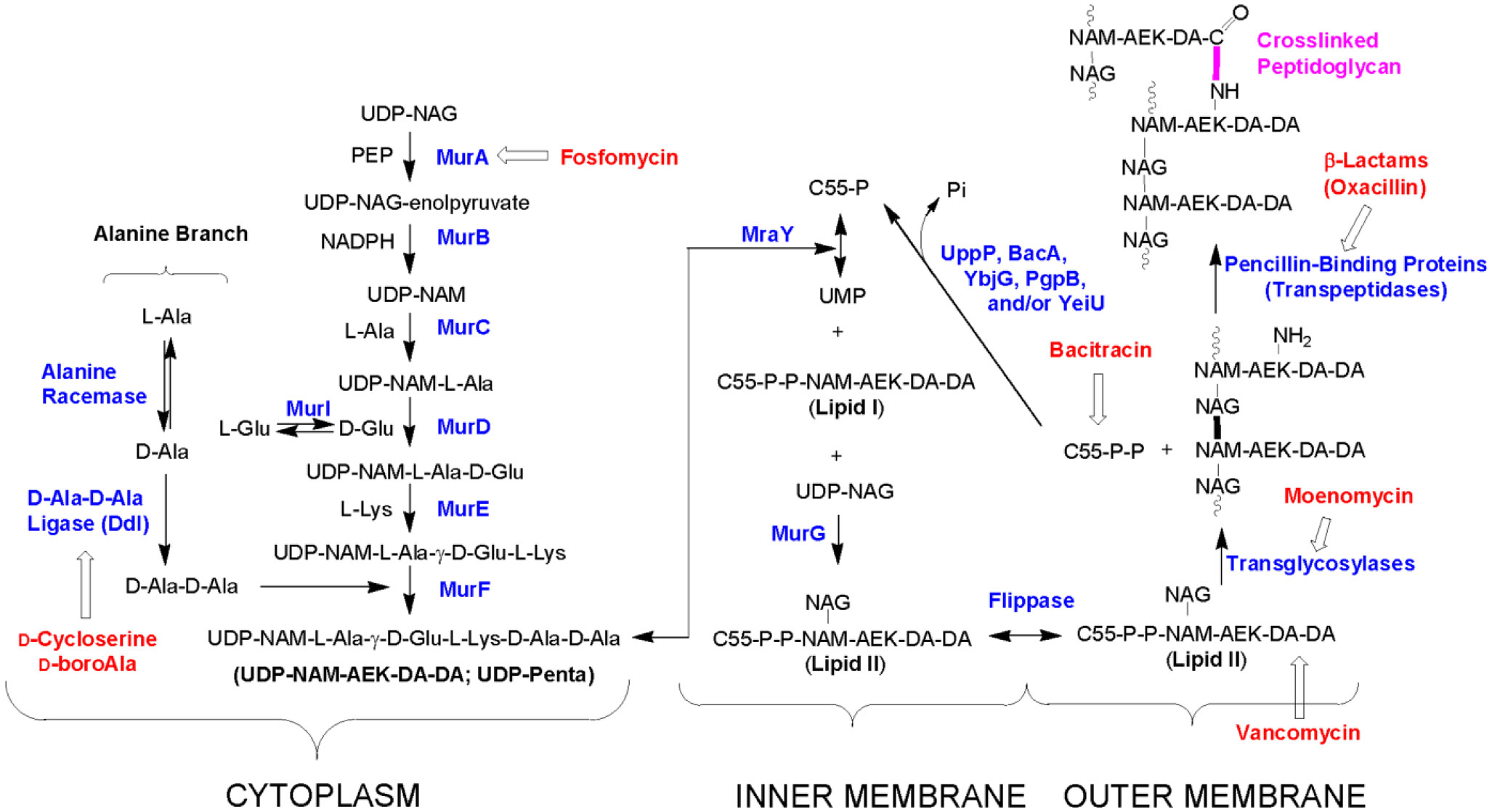
The peptidoglycan layer contributes to the morphology, strength and resistance to stressors, which is primarily composed of linear glycan strands cross-linked by short peptides. The D-amino acids are primarily present in those short-peptides connecting the sugar chains and play important roles in the biosynthesis of the PG i.e. cell wall and are an imperative part of bacterial survival. The linear glycan chain is made up of either N-acetyl glucosamine (GlcNAc, NAG) or N-acetylmuramic acid (MurNAc, NAM). Bacterial PG synthesis occurs in three phases, each of which consists of multiple steps [166] (Figure 5).
D-amino acids participate in the very early stage i.e. phase I where several D-amino acids such as D-Ala, D-Ala-D-Ala and D-Glu along with L-Ala, L-Lys and L-Glu take part to synthesize the core UDP linked intermediates: UDP-GlcNAc (UDP-NAG), UDP-NAG-enolpyruvate (UDP-EP), UDP-MurNAc (UDP-NAM), UDP–NAM–L-Ala (UDP-Mono), UDP–NAM–L-Ala–D-Glu (UDP-Di), UDP–NAM–L-Ala–γ-D-Glu–L-Lys (UDP-Tri), and UDP–NAM–L-Ala–γ-D-Glu–L-Lys–D-Ala–D-Ala (UDP-Penta) [169]. All these steps take place in the cytoplasm during phase I leading to synthesis of UDP-Penta and phosphor-NAM-pentapeptide, which are then transferred to lipid carrier for further elaboration during phase II on the inner membrane to form lipid I and then ultimately to lipid II by incorporation of NAG from UDP-NAG intermediate. Finally, during phase III, lipid II undergo transglycosylation and transpeptidation by penicillin-binding proteins (PBPs) and are assembled into mature peptidoglycan on the outer membrane.
D-amino acids are also believed to participate in PG remodeling and metabolism as reported in various studies e.g. effect of D-Met, D-Leu, D-Val and D-Ile in rod-to-sphere shape transition of mrcA type Vibrio cholera [170], negative regulation of PG synthesis on V. cholerae and B. subtilis upon D-amino acids exposure specially D-Arg targeting cell wall independent pathways [171], incorporation of D-Cys by several bacteria from the nutrient media supplemented with D-Cys [172]. A very recent study discussed the role of D-Met and D-Phe in maintaining cell wall integrity during acid stress in Lactococcus lactis strain F44 [173]. Exact mechanism by which D-amino acids participate in bacterial PG remodeling is yet to be determined but it is hypothesized that D-amino acids regulate the periplasmic enzymes responsible for synthesis and modification of PG polymer and by modulating PBPs activity [165]. In addition, Cava P et al discussed about the possibility that presence of D-amino acid in a nutrient-depleted bacterial culture might be indicative of downregulation of PG synthesis i.e. biomarker of stress condition for bacterial population [165]. D-Ala and D-His are reported to act as germination inhibitor for Bacillus species during high spore population and can alter kinetics of germination to enhance infection [174]. On the other hand, D-amino acids containing peptides (D-Ala-D-Lac and D-Ala-D-Met) can also help bacteria to develop resistance e.g. resistance against vancomycin by Enterococcus, by preventing binding of drugs to the PG precursor leading to cell wall inhibition or by making cell wall resistant to various protease enzymes [175].
D-amino acids are also involved in biofilm formation providing protection to the bacterial cell against antimicrobials and host's immune system and make treatment challenging [176]. Bacterial biofilm is primarily composed of polysaccharides, proteins and/or DNA [177]. Several D-amino acids namely D-Leu, D-Met, D-Trp, D-Tyr, D-Pro and D-Phe are reported to induce dissolution of biofilm produced by B. subtilis, S. aureus, S. epidermidis and P. aeruginosa, an effect which was not observed with L-amino acids [178]–[180], although there are some contradictions to these conclusions [181], that are believed to have occurred due to variation in experimental setup [182]. Interestingly these roles of D-amino acids such as negative metabolism on PG synthesis and biofilm dispersal effect have been reported to potentiate the antibacterial activities of other agents [183]. For example, D-amino acids are reported to enhance the activity and stability of several peptide antibiotics such as penicillin, cephalosporin, cycloserine, gramicidin, actinomycin, bacitracin and polymyxin [184]. D-amino acids are also present in a metal scavenging agent known as Staphylopine which is derived from S. aureus and can trap various metals including nickel, zinc, cobalt, copper and iron [185].
11.
Analytical methods for separation and quantification of proteinogenic amino acids
Myriad roles and functions of different amino acids have warranted for ways to accurately distinguish and quantify them in a system of interest. Amino acids analysis is also used for quantification and characterization of peptides and proteins [186]. Moreover, important functions attributed to a specific stereoisomer of an amino acid clearly indicates the necessity of accurate identification of the correct stereoisomers to be able to study, predict, explore and explain important phenomena. There are various analytical technologies available to separate and detect the amino acid stereoisomers including chromatographic, spectrometric, fluidics, electrophoretic, microbiological or enzymatic methods. At any given time, complete separation and quantification can be challenging as racemization can occur due to various physical and chemical factors [187]. Frequency of spontaneous racemization has been reported to decrease in the following order [188]: Cys>Asp>Pro>Glu>Met>His>Leu>Lys>Phe>Ala>Tyr>Arg>Trp>Val>Ile>Ser>Thr.
Microbiological amino acid analysis methods were popular in the primitive days [189] and currently are taken over by other more sensitive and accurate methods. Enzymatic assays and biosensors on the other hand require specific enzymes for total amino acid analysis hence are not very convenient [190]. Chromatographic techniques, including the simple thin layer chromatography [191],[192] or the advanced multidimensional chromatography [193], are the most common platform for amino acid analysis and with the advent of mass spectrometry based detection, this has remained the popular method of choice for analysis of proteinogenic amino acid stereoisomers [194]–[196]. A carefully developed and optimized chromatography coupled to mass spectrometry based analytical method can provide baseline separation, superior sensitivity and high throughput at analyzing all proteinogenic amino acid stereoisomers [197]. Microfluidics and nanofluidics based devices, such as lab-on-a-chip also enables chiral separation, offers portability and faster analysis [198]. Capillary electrophoresis (CE) on the front end for separation has been recently used due to its reliability, automation and robustness [199] and showed successful chiral analysis of amino acid (non-proteinogenic and proteinogenic) in extraterrestrial [200] and biological [201] samples. It uses various chiral selectors for derivatization such as cyclodextrins, naphthalene dicaroboxaldehyde (NDA), 4-fluoro-7-nitro-2,1,3-benzoxadiazole (NBD-F) and Fluorescein isothiocyanate (FITC) with capillary zone electrophoresis or micellar electrokinetic chromatography [202]–[204].
12.
Chiral analysis of proteinogenic amino acids by chromatography coupled to mass spectrometry
Greatest performance in separation and detection of amino acid stereoisomers can be obtained by combining the resolution power of various chromatographic techniques such as liquid chromatography, gas chromatography, supercritical fluid chromatography etc. to the sensitivity power of mass spectrometry. Sample preparation is a very critical step in chromatographic method especially when the matrix is of complex origin such as plasma, serum, urine, cerebrospinal fluid or cellular extract. In addition, careful selection of solvent, buffer, pH, stationary phase and derivatization reagents is very critical in achieving utmost analytical performance. Chiral analysis of amino acids from proteins or peptides can be more complex than from a system rich in D-amino acids. Acid hydrolysis has been the primary way to obtain free amino acids from proteins and peptides since 1954 [205],[206]. The strength, temperature and duration of reaction are constantly studied and modified to get a stable pool of amino acids for accurate analysis [205]. Microwave assisted acid hydrolysis is reported to reduce time during acid hydrolysis while preserving stability and coverage [207].
The most commonly used chromatography in amino acid analysis is ion exchange chromatography (IEC) which is an indirect method and requires pre-column derivatization using o-phthalaldehyde (OPA), phenylisothiocyanate (PITC) or post-column derivatization using ninhydrin [208]. Detection on IEC has been traditionally performed with UV detector using a wavelength of 570 nm and 440 nm, which is great for absolute quantification but might not provide sufficient sensitivity for trace level analysis. Additionally, co-eluting peaks cannot be always resolved by manipulating mobile phase compositions, gradients and stationary phases and is a serious limitation of UV based analysis. Chiral ligand exchange chromatography (CLEC) on the other hand is a direct analysis method which does not require any derivatization and utilize chiral stationary phases (CSPs) for enantioseparation of the proteinogenic amino acids [209]. However, CLEC requires non-volatile mobile phase which is not compatible if mass spectrometry or evaporative light scattering based detection are to be used on the back end [210].
High performance liquid chromatography (HPLC) can significantly improve the throughput of amino acid analysis over IECs and CLECs [211]. HPLC can provide better analysis with both pre- and post-column derivatization, where derivatization provide stable chromophore, for example 260 nm for 6-aminoquinolyl-N-hydroxysuccinimidyl carbamate derivatives [212] or 340 nm for 1-fluoro-2-4-dinitrophenyl-5-L-alalnine amide derivatives [213],[214]. It can also enable chiral amino acid analysis in underivatized i.e. in their natural form using modern stationary phases such as hydrophilic interaction chromatography (HILIC) [215] or in reverse phase (RP) with ion pairing reagent [216]. Still, such advancements cannot allow separation of co-eluting peaks and create challenges for quantitation of such amino acids. Using mass spectrometers for detection can tremendously help with sensitivity and allow accurate detection of co-eluting peaks due to different mass to charge ratio irrespective of derivatization and/or chromatographic techniques [12],[217]–[220]. Use of mass spectrometer as a detection tool however incur some challenges such as variability due to ionization efficiency, matrix effect and ion suppression which if not carefully monitored and controlled can affect the accuracy. This can be solved by using stable isotopically labeled internal standard or isobaric tag, which can take recovery of amino acids into consideration for data correction as well as allow separation of isobaric amino acids [221]. Liquid chromatography coupled to mass spectrometry (LC-MS) although seems like an outstanding option, still has some limitations such as use of ion pairing reagents that are not recommended for mass spec detection. On traditional C18 analytical columns, polar amino acids do not retain well hence cannot provide a quantitation. In addition, in HILIC chromatography some amino acids still do not separate well (D-alloisoleucine from isoleucine) and suffer from lack of reproducibility [218]. All these limitations however points out towards derivatized amino acid analysis with traditional analytical columns as a feasible option, which allows use of both liquid chromatography (LC) and gas chromatography (GC). Inclusion of metals with magnetic properties, namely high performance magneto-chromatography and HPLC coupled to a circular dichroism detector also reported to offer faster and highly reproducible amino acid analysis [222],[223]. Moreover, state of the art technologies on separation science and mass spectrometry such as multi-dimensional separation and ion mobility spectrometry (IMS) brings a paradigm shift to utilize modern approaches to achieve faster, accurate and super sensitive analysis of proteinogenic amino acid stereoisomers [14],[150],[211],[224].
Gas chromatography coupled to mass spectrometry, on the other hand provides better reproducibility however is restricted to volatile analytes hence chemical derivatization (silylation and alkylation) is a must [225]. Chiral and capillary columns are widely used in GC-MS based amino acids analysis [226]. GC coupled to flame ionization detector (FID), along with GC-MS and LC-MS have also been reported in chiral amino acid analysis from beer [226] and coffee [227]. With the advent of high resolution mass spectrometer and inclusion of machine learning and bioinformatics, amino acids are currently analyzed as part of global metabolome of a biological system that has enabled their identification and quantification in variety of matrices [228]. Comprehensive review of various chromatographic techniques for amino acid analysis can be found in Kasper H et al. 2009 [229], Schurig V et al. 2011 [230], Otter DE 2012 [194] and Szoko E et al. 2016 [231].
13.
Analysis of proteinogenic amino acids in underivatized form
Chiral analysis of amino acids in underivatized form i.e. in their native form is the straightforward way, which does not involve any type of derivatization techniques. Wide difference in polarity among different proteinogenic amino acids holds a chromatographic challenge making the separation difficult using a single chromatographic technique i.e. stationary phase and solvent system. For example, a traditional C18 analytical column (non-polar stationary phase) will not retain the polar amino acids such as Arg, His, Lys, Asp and Glu, on the other hand a HILIC column (polar-stationary phase) will not retain the remaining 15 non-polar amino acids well. Even if a variety of amino acids is retained well in either column, the relative difference between retention times might not be large enough for baseline separation of all the amino acid stereoisomers. Thus, analysis of these proteinogenic amino acids in their underivatized from can be a challenging task. Besides, most of the proteinogenic amino acids do not have any chromophore and cannot be detected using UV detector. However, chiral stationary phases (CSPs) such as α-cyclodextrin, crown ether, zwitterionic selector, teicoplanin, etc. based chiral columns can enable separation of underivatized proteinogenic amino acids. It can be argued that, with mass spectrometry based detection, separation might not be always needed for accurate quantification. However, a good chromatography provides confidence in the accuracy of the mass spectrometry based quantification. Moreover, smaller molecules are difficult to fragment in mass spectrometer and hence are difficult to analyze in tandem mass spectrometry mode (MS/MS). In spite, due to tremendous advancements in stationary phases, chromatographic strategies and mass spectrometers, some tremendously facile routes for underivatized amino acid analysis have been reported to date (Table 6). It should be noted that, amino acids cannot be analyzed by GC without derivatization; chiral ligand exchange chromatography and RP-HPLC require non-volatile solvent and ion-pairing reagents respectively for direct analysis, which are not recommended for mass spectrometry based detection, hence, are not part of Table 6.
14.
Analysis of proteinogenic amino acids in derivatized form
Indirect analysis of proteinogenic amino acid utilizes various chemical reagents, which react with amino acids and form derivatives that can offer potential advantages such as chromophore for UV-Vis detection, changes in polarity etc., and can help with better resolution and detection. There are pre-column derivatization and post-column derivatization techniques; former is more popular as post column derivatization cannot be controlled and prone to inconsistency in quantitation between samples during analytical run [245],[246]. Chemical derivatization has some drawbacks such as variation in reaction kinetics between amino acids and their isomers with the derivatizing reagents, stability of the derivatives, removal of excess derivatizing reagents, introduction of racemization due to temperature and pH required for certain derivatization reactions, derivatization time etc. However, this approach allows using the traditional, most reliable and most economic reverse-phase chromatography coupled to mass spectrometry based techniques. Additionally, this offers the flexibility in choosing a suitable derivatizing reagent from a plethora of different reagents that is feasible for a lab. Upon stringent validation in terms of robustness, reproducibility and performance, this approach can be one of the best approaches for targeted amino acid analysis. An exhaustive list of different derivatizing reagents for chiral amino acid analysis can be found in Bhushan R et al. 2004 [247], Ilisz I et al. 2008 [248], Tanwar S et al. 2015 [249], Szoko E et al. 2016 [231] and Marcone GL et al. 2020 [13]. A few notable chiral amino acid analyses using various derivatization techniques are discussed in Table 7.
15.
Conclusion
Amino acids are important biomolecules, which either play important biochemical roles in different biological systems or indicate occurrence of different biological phenomena. Due to stereochemistry, it is crucial to successfully distinguish the specific stereoisomer responsible for a certain event, for which, an accurate, robust, sensitive, fast and reproducible analytical method is a must. Due to their small size, diverse polarity and absence of chromophore, it is a challenge to achieve baseline separation for different amino acids in a single analytical run using chromatography coupled to mass spectrometry based approaches. Significant advancement in stationary phases, chromatographic and mass spectrometric platforms made direct analysis of amino acids in their native form achievable. However, direct analysis requires specialized stationary phases, such as chiral columns, which might not be feasible or economic in all laboratory settings. Additionally, success of direct analysis utilizing chiral mobile phase additives with an achiral stationary phase depends on the purity of the chiral selectors. Lack of a chromophore does not allow analysis of these amino acids in their native form without a specialized detector such as mass spectrometer. On the other hand, indirect analysis offers selection of plethora of derivatizing reagents, which allows use of traditional stationary phases, chromatographic and mass spectrometric platforms. Although, indirect analysis offers flexibility, it needs to be carefully optimized and monitored routinely to obtain accurate results, as derivatization reactions and derivatives are extremely prone to degradation due to changes in temperature, pH, reaction and storage condition. Both direct and indirect approaches have proven advantages and pitfalls, and the right approach needs to be carefully selected based on the aim of the study, type of samples and the available resources. Myriad analytical methods have been developed till date using various platforms such as IEC, LC-MS, GC-MS, SCF, CE, metal-assisted chromatography, biosensors, multidimensional chromatography and IMS; all have their pros and cons. Direct analysis with chiral mobile phase-achiral stationary phase suffers from lack of control and selectivity of interaction between chiral selector and amino acids. On the other hand, indirect analysis with an ion-pairing reagent-achiral stationary phase requires ion-pairing reagents, which can contaminate the mass spectrometer. In lights of these, direct analysis with a chiral stationary phase and indirect analysis with a chiral derivatizing reagent, provide better analytical performance and could be adopted based on feasibility. However, a carefully developed and validated method using any analytical platform can aid in analyzing proteinogenic amino acid stereoisomers and solely depends on the knowledge, skills and experience of the analytical scientist.
This review paper discusses important roles of proteinogenic amino acids and their stereoisomers and different analytical approaches to accurately analyze them. In a targeted study, where chiral analysis of amino acids is the primary focus to answer important questions, an indirect approach with chemical derivatization using reverse phase HPLC or GC coupled to mass spectrometry can provide feasible route of their analysis. For example, roles of amino acid stereoisomers in bacterial cell wall biosynthesis can be accurately studied using chemical derivatization with Marfey's reagent and liquid chromatography tandem mass spectrometry technique. However, in global analysis of a physiological model where amino acids are part of the whole metabolome with different other endogenous molecules such as lipids, nucleic acids and sugars in an untargeted manner, such a chemical derivatization is not feasible as a single derivatizing agent might not react to all molecules that belong to different chemical classes. In such cases, direct analysis might be a feasible approach given that the chromatographic performance on the front end is satisfactory and high resolution mass spectrometer is available on the back end to confidently identify the amino acids and their stereoisomers. Now a days, untargeted analysis is often done followed by targeted analysis of the analytes of interest in order to confirm the findings in the former. It is imperative to adhere to strict validation to ensure optimum performance of the analytical platform and sample preparation workflow to accurately and confidently analyze these important biomolecules to identify their functions and explore their roles in different physiological model systems.









 DownLoad:
DownLoad: