Mathematical modelling of a mushy region formation during sulphation of calcium carbonate

1.   Introduction

Water resource management is a crucial component of the water supply chain, ensuring the sustainable distribution and availability of water resources for various ecological and/or human needs. In today's world, environmental management is critical because it aims to maintain natural resource availability and durability while also promoting human progress. Population growth, urbanization, and industrialization have increased the water demand ^[1], emphasizing the importance of effective management strategies. Protecting river basins is a significant challenge because they are critical for a variety of reasons, including biodiversity, water supply, and the maintenance of ecosystem services ^[2]. In countries where freshwater resources are limited and cannot meet the needs, a balance must be struck between water extracted for human activities and water stored for managing the river or watershed system ^[3,4,5]. In many developing countries, due to the lack of minimum required information about rivers, there are no comprehensive and flexible methods available to determine the environmental flow (EF) ^[6,7]. It is a challenging task to manage and preserve the ecosystems of these rivers ^[8].

The EF's mission, as Arthington et al. ^[9] explain, is to protect the biodiversity of rivers, lakes, and estuaries by managing river basins and implementing environmental conservation measures. A specific quantity, frequency, and quality of water flow, commonly referred to as EF, is required for the survival of freshwater and estuarine ecosystems, as well as the preservation of human lifestyles ^[10]. EF refers to the water regime that is implemented to protect the ecosystems and their associated benefits in river, wetland, or coastal area ^[11,12]. The flow regime, according to the IFC definition, refers to the hydrological characteristics of a river, which encompass four flow levels, including the life flow of a period of drought ^[13], basal flow as a natural flow to maintain river habitat in healthy conditions ^[14,15], high flow that removes sediment in the environment ^[16], and overflow bank that connects the main river to the floodplain, which has significant morphological significance ^[17]. The EF is higher than the waterways' minimum water level; this involves managing water regimes to mimic natural flow patterns as closely as possible ^[18]. The migration and spawning of fish are dictated by these patterns; and understanding ecosystem needs, water flow, ecological health, and socioeconomic interdependence is the first step toward achieving proper ecological functioning. By maintaining environmental flows, we aim to achieve a sustainable balance that supports ecosystems while accommodating human uses (i.e., agriculture, industry, and recreation). As a matter of fact, this balance is crucial for preserving biodiversity, ensuring water quality, and sustaining the services provided by aquatic ecosystems to communities and economies. As a result, by striking a balance between ecological preservation and human water needs, this article emphasizes the importance of interdisciplinary collaboration in environmental problem-solving; this emphasizes the importance of long-term solutions that benefit the environment and people.

The purpose of methods designed to preserve river ecosystems is to maintain one or more parts of the mentioned flow regimes ^[19,20]. The compromise between the economic benefits of rivers such as hydropower potential and environmental protection must be considered in estimating the EF ^[21,22,23]. There are different divisions to determine the EF of rivers. The numerical method of habitat simulation modeling was used to study how water flow affects the conditions of the environment for aquatic life ^[24]. The United States Wildlife Service developed the Physical Habitat Simulation (PHABSIM) model during the 1970s (https://www.usgs.gov/node/279289). This model consists of a range of tools that can be used to simulate the appropriateness of hydraulic habitats for aquatic species ^[25]. The simulation model for aquatic habitats gauges the standard of the habitat by taking into account physical alterations, like the depth, flow velocity, and channel conditions ^[26,27]. The process of simulating a habitat involves two stages, namely habitat simulation and hydraulic simulation ^[28,29]. The PHABSIM model was used for suitable ecological water demand ^[30,31], quantifying the hydrological requirements for fish ^[32], and modeling fish habitat conditions in ice-affected rivers ^[33]. Nikghalb et al. ^[28] conducted a comparison of two hydrologic techniques, namely Tennant and Q95, with a PHABSIM. The comparison was conducted under conditions of data shortage. The results showed that the PHABSIM model was able to provide valid outcomes even when the input data was imprecise. Peng and Sun ^[34] utilized the PHABSIM models to prevent the river ecosystem from hydroelectric exploitation. They clarified that the PHABSIM models establish a relationship between habitat and flow that maximizes instream flow releases while reducing ecological disturbances. The outcome of the research indicates that the PHABSIM model is effective in optimizing the flow release schemes of hydropower stations in the southwestern region of China. Gholami et al. ^[35] estimated the EF for the wetland's river system using various models, including the PHABSIM model, the Tenant model, the Wetted-Perimeter method, and the flow duration curve. The study concluded that the Wetted-Perimeter and the PHABSIM model were the most effective in estimating the EF for the rivers in the wetland, considering the river's seasonality and hydro-climatic condition of the study area. Using the PHABSIM model, Miao et al. ^[30] showed that land use change can decrease the urban water supply and the quality of fish habitat. The PHABSIM model necessitates extensive hydrological and ecological data over an extended period. Obtaining such data is both time-consuming and expensive. However, accurate employment of the model for estimating EF allows for the generalization of data obtained for one river to surrounding rivers with similar ecological conditions. Therefore, utilizing the appropriate model reduces the time and cost involved in estimating EF for rivers. Im et al. ^[36] utilized fuzzy neural network models to create habitat-suitable indexes (HSI) which were then used as input data for the PHABSIM model. They showed that fuzzy neural network models can consider uncertainties in complex ecosystems. Recently, the Adaptive Neuro-Fuzzy Inference System (ANFIS) was used in environmental studies ^[37,38,39] and it seems it can accurately predict the environmental variables ^[40,41]. Therefore, it seems that the ANFIS model can predict the EF using HSI data. Thus, our purpose is to simulate the PHABSIM model to determine the EF of a river and predict the EF of the other rivers using a linear model, Multilayer Perceptron neural network (MLP), as a nonlinear model, and ANFIS as a hybrid model. By using the mentioned models, the impact of changes in river flow on the ecosystem will be evaluated, and the discharge needed to maintain the river's potential biodiversity will be determined.

2.   Materials and methods

2.1.   Study area

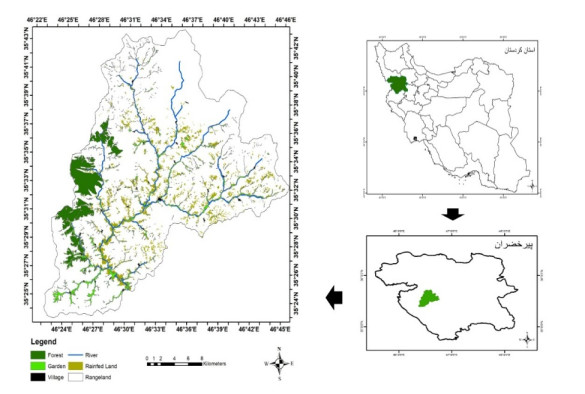
The Pir Khezran River, which is in the western part of Kurdistan province, is the subject of this research. It is one of the sub-basins of the Azad River (Figure. 1) and covers an area of 4.70220 hectares with 632 mm rainfall. The basin is of significant importance to Azad Dam and is one of the sub-basins of the Sirvan River in western Iran.

Figure 1.  Geographical location of Pir Khezran river.

DownLoad: Full-Size Img PowerPoint

2.2.   Data

The required data for the study was collected in January 2018, with measurements taken across the river's cross-section. The processes of sampling, transporting, storing, and receiving samples were carried out according to the international standards of American Public Health Association (APHA). The hydrology team recorded water velocity, depth, and discharge ^[42], while the fisheries team gathered data for various fish species, including their numbers, ages, sexual maturity, densities, and diversities ^[43]. In the realm of these studies, there are several methods that can be utilized for capturing and gathering fish. The electrofishing method, as defined by the EPA ^[44], is a more extensive approach. Fish sampling will entail the use of an electroshock device with a power rating of 2 kilowatts, a potential difference of 200-300 volts, a current intensity of 0-10 amps, and an anode opening length of 40 cm. Each sampling station will be positioned 20 to 50 meters from the river, in line with the Standard method ^[45]. Following capture, the fish samples from each station will be placed into containers with a 10% formaldehyde solution before being transported to the Fish Biology Laboratory of Kurdistan University. To determine channel index variables ^[46], substrate materials were sampled from each location, with three samples collected from the bed floor. The channel index was then calculated based on the sizes of sand, gravel, and stones. One of the most important steps in EF modeling is the production of HSI data ^[43]. The appropriate HSI shows the living conditions of the index species at the sampling site ^[12]. For example, by analyzing the water depth variable, it is possible to identify the optimal depth range for the index species' living conditions ^[47]. This information can then be used to predict how the living conditions will be affected when the depth deviates from the optimal range ^[48]. Data from all the studies mentioned was used to create habitat suitability curves.

2.3.   Estimation of EF using the PHABSIM model

The PHABSIM model is essentially a combination of hydraulic and habitat models. It establishes a relationship between flow conditions and the appropriateness of physical habitats for index species in the river ecosystem ^[30]. The method is divided into cells based on diversity. Each section has suitability functions for depth, velocity, and channel index that determine the cell's degree of suitability based on its current state ^[43]. The suitability index of the composite for each cell in each section is determined by combining the calculated scores for each of the mentioned parameters. The Weight Usable Area (WUA) is the final index used to determine EF, which is calculated by multiplying the HSI for each cell at the relevant available level ^[28]. A WUA versus discharge map can be generated using the overall WUA amount for a particular section of a river. This map provides a clear illustration of the correlation between discharge and the quality and quantity of habitat available. The index is used as a guide to analyze alterations in habitats due to evacuation. It's essential to acknowledge that there have been objections regarding the correlation between fish biomass and the availability of habitat or WUA ^{[30,31,32,33]}.

2.4.   Environmental water flow prediction models

2.4.1.   ANFIS model

The ANFIS model was executed using Matlab version 14a during the simulation and testing phases. Jung's ANFIS method is an algorithm that merges fuzzy logic with an artificial neural network (ANN) for hybrid learning. This approach offers the benefits of both ANN and fuzzy models, allowing for the optimization of nonlinear problems and the acquisition of imprecise and ambiguous information ^[36]. The Fuzzy Inference System (FIS) was initially introduced by Mamdani and Assilian. Afterwards, Sugeno presented the Sugeno model, which enhanced the computational efficiency of the previous FIS ^[49]. The fuzzy approach offers a significant benefit by allowing for the direct integration of non-numerical information, such as specialized knowledge, into rules. This is particularly useful when there is a lack of field data. Furthermore, membership rules and functions can be defined in such a way as to consider the inherent uncertainty of environmental variables ^[50,51]. The ANFIS method was tested using the observed data set for validation ^[49]. The construction of the HSI model has also been achieved by utilizing fuzzy neural network models ^[52,53] and the results indicate that the evaluation of ecosystems demands the use of fuzzy neural network models, particularly when dealing with intricate ecosystems ^[49]. The least squares method and multiplication algorithm are used to predict output values and optimize the parameters of membership functions in this approach. The Sugeno inference system is employed to enhance the efficiency of optimization. The ANFIS network is composed of five layers, which include the fuzzy layer, product layer, normalized layer, de-fuzzy layer, and output layer. Each layer's output variables are determined by the input variables from the previous layers and the parameters in each node ^[36].

2.4.2.   Multilayer perceptron neural network MLP

Matlab version 14a was utilized to run the MLP model in the simulating and testing phases. The most famous, adaptable, and uncomplicated form of artificial neural network is MLP. This approach is extensively employed to articulate the nonlinear correlation between anticipated and recorded information ^[54]. The primary objective of the neural network is to enhance the efficiency of the predicted and observed values. MLP is specifically engineered to excel in modeling nonlinear phenomena. An MLP network that is forward-facing comprises an input layer as well as an output layer, both of which are flanked by one or more hidden layers in the middle. Within each layer, there are a predetermined number of artificial neurons.

2.4.3.   Linear regression model LR

SPSS version 22 was used to run the LR model in the simulating and testing phases. Regression analysis is a statistical technique used to investigate the connections between variables. It involves an independent variable and a dependent variable, with the researchers generally seeking to determine the impact of the independent variable Y on the dependent variable xi. All of these components, including the dependent and independent variables and the error, are part of the regression analysis process, and the resulting equation for prediction is commonly referred to as a regression model ^[55]. It should be kept in mind that prior to analyzing the correlation between the dependent and independent variables, it is recommended to use a distribution diagram to assess the noteworthy correlation between them. Furthermore, it is important to determine whether there exists a significant association between these variables. The statistical technique of linear regression holds a crucial position in statistical methods.

In the research, the prediction quality of MLP, ANFIS, and LR neural network models was assessed using various performance indicators. The assessment criteria included statistical measures such as the R² correlation coefficient, root mean square error (RMSE), and mean absolute error (MEA). The objective was to enhance the efficiency, speed, and accuracy of the models, with a focus on minimizing RMSE and MEA while maximizing the correlation coefficient to ensure high accuracy and close alignment between predicted and actual values at each stage of the model.

3.   Results and discussion

3.1.   Estimating EF of Pir Khezran river

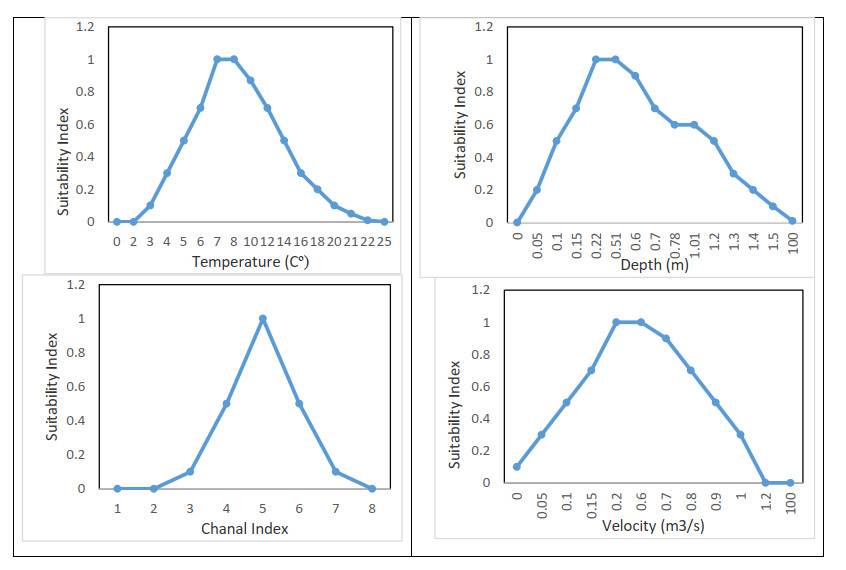
Habitat suitability curves in January for Pir Khezran River and surrounding rivers are shown in Figure 2.

Figure 2.  Flow Depth, flow velocity, channel index, and suitable temperature for the life of index species in Pir Khezran River in January.

DownLoad: Full-Size Img PowerPoint

As Figure 2 shows, the appropriate flow velocity for the Pir Khezran River and the surrounding rivers in January is between 0.2 and 0.6 (m/s), i.e. in this range, the maximum rate of fishing and benthos, and the highest rate of diversity was obtained. At the flow velocity higher or less than this range, habitat suitability for the index species gradually tends to zero. The appropriate flow depth, according to figure 2, is between 0.22 to 0.51 m, which, as stated for the flow velocity, in this depth range, was the highest catch of index species.

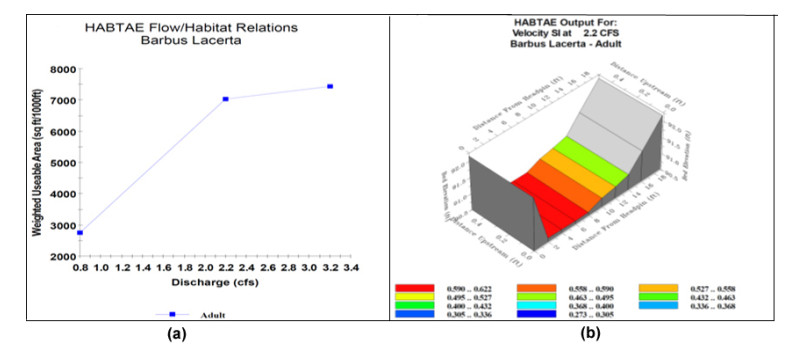
Habitat suitability decreases at a very high depth of river but will not be zero because the index species studied in this research has also been seen in the Azad dam, which has a depth of nearly 85 m, so the highest depth has 0.1 value in the flow depth suitability index. Habitat suitability for the channel index is highest at 5 and tends to zero at lower and higher than this rate. Also, the appropriate temperature in the best biological condition was 7 to 10 ℃. In order to obtain the EF of the rivers of the study area in January, the PHABSIM model developed HIS indexes. As Figure 3a shows, the amount of EF in this river in January is equal to 2.2 m³/s. since then, the habitat suitability does not change and remains the same, but reducing the volume of water from this amount causes a reduction in the habitat suitability.

Figure 3.  (a) EFR in Pirkhezran River in January, (b) Habitat suitability at the flow velocity of 2.2 m3/s in Pir Khezran River in January.

DownLoad: Full-Size Img PowerPoint

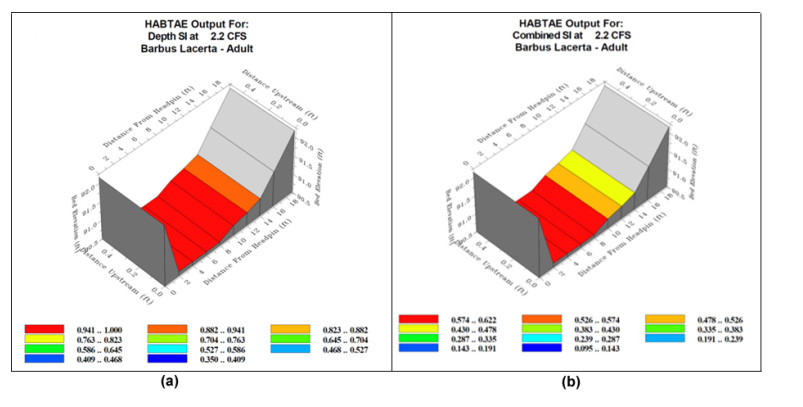
The desirability of habitats in different parts of the Pir Khezran River for flow velocity, flow depth, and channel index are shown separately below. Habitat suitability for the flow velocity variable is shown in Figure 3b. The legend section is stated and different numerical ranges are given for each color. As this figure shows, the habitat suitability in the left part of the river has the highest rate, and moving from left to right reduces the habitat suitability. Figure 4a shows the desirability of habitat at different flow depths in the Pir Khezran River in January. As this figure shows, most parts of the river are suitable for fish life.

Figure 4.  (a) Habitat suitability at flow depths between 0.22 to 0.51 m of Pirkhezran River in January, (b) Habitat suitability based on a combination of flow velocity and flow depth variables in Pir Khezran River in January.

DownLoad: Full-Size Img PowerPoint

Figure 4b indicates the habitat suitability for the indicator species based on a combination of the flow velocity and flow depth variables. In this figure, the left side of the river has good desirability, and in only two parts of the left side did the desirability decrease. This is also observed in Figures 3b and 4a.

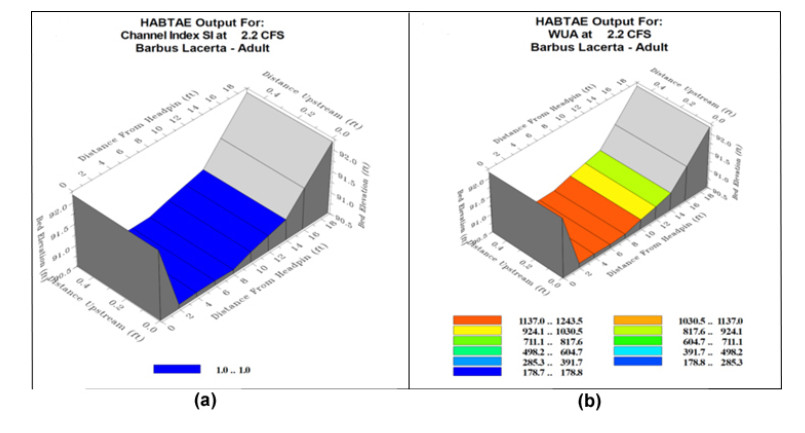
Figure 5a shows the extent of habitat desirability based on the channel index, in which the expression of the degree of desirability for the channel index is equal to 5, which is the highest. Then, this rate gradually tends to zero. As Figure 5a shows, all the different parts of the river have the highest habitat quality at this range, and therefore it can be said that the river does not limit the life of the indicator species at this range of channel index.

Figure 5.  (a) Habitat suitability in Pir Khezran river based on substrate index, (b) Different desirability of Pir Khezran river at the 2.2 m3/s of EFR.

DownLoad: Full-Size Img PowerPoint

Finally, the habitat suitability of the index species is modeled by the PHABSIM model based on all the variables shown in Figure 5b. As this figure shows, the Pir Khezran River has different ranges of habitat suitability for the indicator species.

3.2.   Predicting environmental water requirement using ANFIS, MLP, and LR models

In this study, the data were divided into 80% and 20% for the training and testing phases, respectively. In order to eliminate the alignment effect on the modeling results, the VIF and Tolerance tests were performed and the results are shown in Table 1.

Table 1.  Tolerance and VIF results of independent variables for estimation EFR.

Test	V min	V max	D min	D max	Ch min	Ch max	T min	T max
VIF	4.418	4.638	4.328	4.863	4.856	4.871	5.500	5.700
Tolerance	0.208	0.216	0.202	0.206	0.010	0.211	0.185	0.171

---

 | Show Table

DownLoad: CSV

The results of Table 1 show that the appropriate water temperature for indicator species in both minimum and maximum conditions has a high correlation with other parameters, so these two variables were not used in modeling. The mean, minimum, maximum, and standard deviation of independent and dependent variables used in modeling are shown in Table 2.

Table 2.  Descriptive statistics of independent and EFR data.

	No.	Min	Max	Mean	SD
V min	100	0.20	0.80	0.48	0.13
V max	100	0.30	0.97	0.60	0.15
D min	100	0.10	0.95	0.57	0.18
D max	100	0.22	1.35	0.70	0.22
Ch min	100	5.00	5.50	5.25	0.02
Ch max	100	6.00	6.50	6.25	0.03
EFR	100	7.00	3.20	2.10	0.49

---

 | Show Table

DownLoad: CSV

As Table 2 shows, by increasing the value of the independent variables to its maximum value, the minimum amount of EF increased. Results can indicate that there is a strong relationship between increasing EF and the increase of independent variables. However, the linearity or nonlinearity of this relationship is not yet clear which were tested using the linear model LR and nonlinear model such as MLP and hybrid model like ANFIS.

3.3.   Predicting the minimum environmental water requirement using the LR model

The LR model is a linear regression model that has many applications in environmental studies ^[56,57,58]. The obtained LR model is shown using independent and dependent variables in Eq 1.

EWF = 0.115-0.13 * (V min) -0.597 * (V max) + 0.155 * (D min) + 0.197 *(D max) + 0.01 * (Ch min) +0.02 (Ch max) (1)

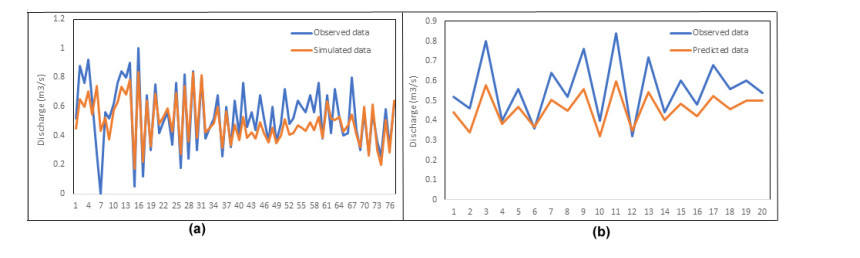
As equation 1 shows, the minimum EF has an inverse relationship with the flow velocity at both the lowest and highest levels and a direct relationship with the flow depth and channel index at both the lowest and highest levels. The results of the LR model training phase are shown in Figure 6a.

Figure 6.  (a) Observed and simulated data of EFR in LR model, (b) Observed and predicted data of EFR in LR model.

DownLoad: Full-Size Img PowerPoint

The correlation between the observed and simulated data is equal to R² = 0.67 and also RMSE = 0.1301 and MAE = 0.0191. As Figure 6a shows, there is no high correlation between the observed and simulated data. Figure 6b shows the results of the test phase of the LR model in which R² = 0.81, RMSE = 0.1233, and MAE = 0.0152. As Figure 6b shows, the correlation between the observed and predicted data at this phase is greater than at the training phase.

3.4.   Predicting the minimum environmental water requirement using the MLP model

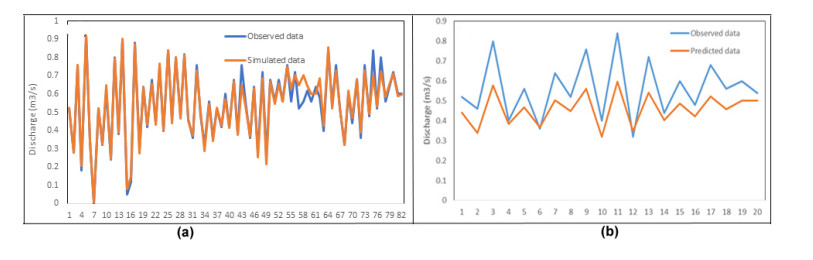
The MLP model is one of the most common artificial neural network models that is widely used in natural resource studies ^[59,60,61]. The results of the MLP model in the training stage of determining the EF of Pir Khezran River are shown in Figure 7a, where R² = 0.96, RMSE = 0.0370, and MAE = 0.0014. As Figure 7a shows, the correlation coefficient between the observed and simulated data in the MLP model is greater than the results of the LR model in the training phase.

Figure 7.  (a) Observed and simulated data of EFR in the MLP model, and (b) Observed and predicted data of EFR in MLP model.

DownLoad: Full-Size Img PowerPoint

The results of the testing phase of the MLP model (R² = 0.92, RMSE = 0.0026, and RME = 0.0027) in predicting the EF of Pir Khezran River are shown in Figure 7b. According to Figure 7b, the correlation coefficient between the observed and predicted data at this phase is more than the results of the LR model, which are consistent with the results ^[62,63,64].

3.5.   Prediction of minimum environmental water requirement using ANFIS model

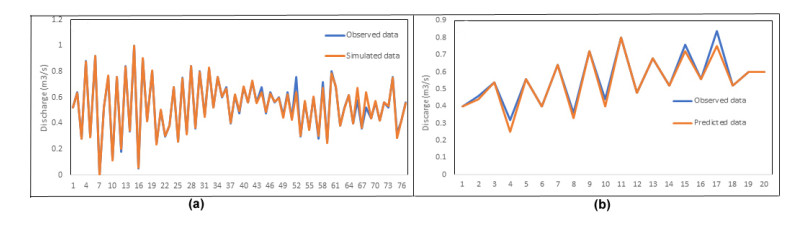
As stated in the methodology section, the ANFIS model is a hybrid nonlinear model that has more advantages than the nonlinear models ^[40,41,65]. Figure 8a indicates the results of the ANFIS model in the training phase (R² = 0.98, RMSE = 0.0248, and MAE = 0.0006) to determine the EF.

Figure 8.  (a) Observed and modeled data on environmental water demand in ANFIS model, (b) Observed and predicted data of EFR in the testing phase of ANFIS model.

DownLoad: Full-Size Img PowerPoint

A comparison of Figure 8a with the previous figures related to the models training phases (LR and MLP models) shows that the correlation coefficient of the ANFIS model is the highest. The results of the testing phase of the ANFIS model (R² = 0.97, RMSE = 0.0295, and MAE = 0.0008) in predicting the EF of the Pir Khezran River are shown in Figure 8b. A comparison of the results of the ANFIS model in the testing phase to the results of the other two models shows that the ANFIS model has a higher accuracy in predicting the amount of EF in the Pir Khezran River.

The comparison between the training and test phases revealed these findings. This research aligns with previous studies by Klaus Jorde et al. ^[66,67,68]. Their results indicated that the fuzzy method, with minimal field data, offers greater flexibility and predictive ability compared to other hybrid methods. It also appears capable of identifying critical situations more effectively than the conventional IFIM method. This is supported by the work of Junga and Choib ^[69], who utilized the ANFIS model to predict the composite suitability index (CSI) for simulating the physical habitat of the Dal River in Korea. In their study, utilizing two 2D hydraulic models to simulate the habitat, it was found that the ANFIS model accurately predicted the distribution of the suitability index. They also suggested the potential for utilizing monitoring data with ANFIS in other watershed areas.

It has been found that fuzzy neural network models, as used by Dongkyun et al. ^[70], are suitable for addressing uncertainties in complex ecosystems. Additionally, the ANFIS method can be utilized to predict CSI in habitat simulation models by directly using data from the PHABSIM model, including depth, velocity, and channel index. This suggests that implementing the ANFIS model to estimate environmental damage could simplify and enhance the accuracy of environmental modeling. These findings align with a study conducted by Elkiran et al. ^[71], which compared artificial neural network models, linear regression models, and neural-fuzzy inference system models, demonstrating the superiority of the ANFIS model over the others.

4.   Conclusion

An essential link in the water supply chain, water resource management guarantees that water resources will be distributed and made available sustainably to meet various human and environmental demands. The main objective in writing this article, thus, was to offer practical advice for river basin conservation and environmental management by evaluating different modeling approaches to EF determination. To estimate EF using data from the HSI and river discharge, for the case of Pir Khezran River, we utilized the PHABSIM model. The necessity for more efficient and cost-effective modeling techniques is highlighted by the resource-intensive field sampling that is required for PHABSIM. This research showed that nonlinear modeling approaches, especially the ANFIS model, can be effective at predicting EF. When tested against more traditional models like MLP and LR, the ANFIS model outperformed them due to its fuzzy logic neural network integration. The results show that optimizing EF in river basin management can be achieved through interdisciplinary approaches that combine fuzzy logic with machine learning.

This research, however, has broader implications for environmental management practices as it provides a methodology for managing river ecosystems in a sustainable way. This work helps policymakers and practitioners find a balance between human water needs and ecological conservation goals by demonstrating how well ANFIS generalizes EF estimates across rivers and watersheds. This highlights the significance of working together across disciplines to tackle intricate environmental issues. Nonetheless, proposing and validating more models in a variety of river basins and environmental settings could remain a subject for future research. To further improve our ability to manage and conserve freshwater resources, we should investigate how ANFIS can be integrated with other modeling techniques and decision support systems. In addition, studies should be conducted to examine the monetary and social effects of EF optimization methods, considering the costs and benefits of balancing human progress with environmental preservation. Moreover, by outlining a solid modeling strategy for optimizing EF in river basin management, our study helps to progress environmental management practices. We can enhance our knowledge of river ecosystems and promote evidence-based decision-making for sustainable environmental management by utilizing advanced modeling techniques such as ANFIS.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence tools in the creation of this article.

Acknowledgments

We would like to express our gratitude to the Iran Water and Power Resources Development Company for providing us with the data necessary for this research.

Conflict of interest

The authors have declared that no competing interest exists.