Mathematical modelling of a mushy region formation during sulphation of calcium carbonate

1.   Introduction

Recently, the recurrence phenomenon has received great attention, in particular, in the areas of biological and medical science. For example, Zhang et al. ^[1] studied a $ 4 $-dimensional ($ 4 $-d) autoimmune disease model, which exhibits recurrent dynamics and is preserved in reduced $ 3 $-d and $ 2 $-d models, and further proved that the recurrence behavior is induced from Hopf bifurcation. This recurrence behavior has also been found in other diseases such as multifocal osteomyelitis ^[2,3], eczema ^[4] and subacute discoid lupus erythematosus ^[5], etc. Actually, the subtypes of some diseases are clinically classified based on the patterns of this recurrence behavior ^[6]. Thus, an improved understanding of recurrence phenomenon in autoimmune diseases is important to promoting correct diagnosis, patient management, and treatment decisions.

The recurrence phenomenon belongs to a more general class of so-called "slow-fast" motions in many physical and engineering systems. A slow-fast system usually involves at least two kinds of dynamical variables, evolved on very different time scales. The ratio between the slow and fast time scales is measured by a small parameter. When attention is focused on periodic oscillations, a slow-fast motion implies that the motion is slow on a part of a solution trajectory while fast on the remaining part of the trajectory. In general, for a given dynamical system such as an HIV model, identifying the special periodic solution – recurrence oscillation is not an easy task. The well-know Geometric Singular Perturbation Theory (GSPT) ^[7] can be applied to consider slow-fast motions in singularly perturbed systems, which are characterized by slow and fast motions along particular system coordinates. Consider the following $ 2 $-d singular perturbation system (here choosing a $ 2 $-d system for convenience of illustration):

where $ (x, y) \! \in \! R^2 $, $ 0 \! < \! \varepsilon \! \ll \! 1 $, and $ f, g \! \in \! C^k, \, k \! \ge \! 3 $, $ x $ and $ y $ are called fast and slow variables. Introducing $ \tau = \varepsilon t $ into (1.1), we have

where $ t $ and $ \tau $ are called fast and slow times, respectively, and the systems (1.1) and (1.2) are called fast and slow systems, respectively.

The basic idea to study slow-fast motions in systems (1.1) and (1.2) is to first consider the limiting systems as $ \varepsilon \rightarrow 0 $, which results in the fast subsystem:

and the slow subsystem:

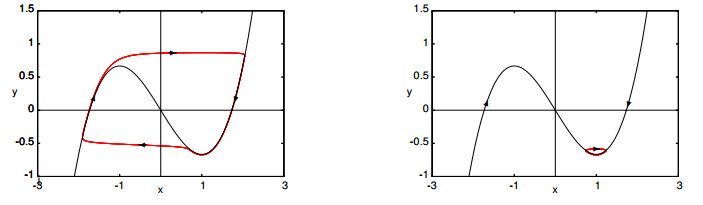
respectively. The equation $ f(x, y, 0) = 0 $, which generates the singular points for the fast subsystem, defines a critical manifold, also called slow manifold. It is obvious that the fast subsystem defines fast manifolds in the horizontal direction. Thus, if the fast and slow manifolds can form a closed loop, then the system (1.1) may exhibit slow-fast motions (e.g., canard cycle) under a small perturbation. For example, consider the well-known van der Pol's equation,

where $ a $ is a constant. This model can be rewritten in the form of singular perturbation equations ^[8]:

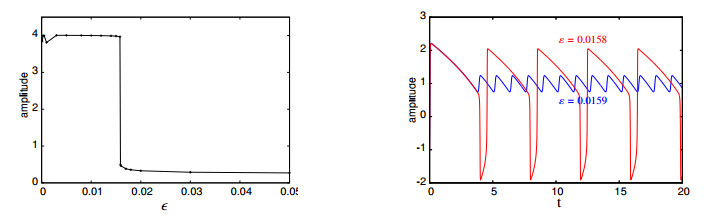
The system has a Hopf bifurcation at the critical point $ a = 1 $. The critical (slow) manifold is defined by the cubic polynomial equation $ y = \frac{1}{3}\, x^3- x $, and it indeed can form closed loops with fast manifolds (in the horizontal direction). For a fixed $ a = 0.998 $, the simulated phase portaits and time histories for different values of $ \varepsilon $ are shown in Figures 1 and 2, respectively. The slow-fast motions are observed from these two figures, which are usually called canard cycles with a head for $ \varepsilon < 0.0158 $ and without a head for $ \varepsilon > 0.0158 $.

Therefore, in order to apply the GSPT to study slow-fast motions, one needs to put one's system in the "shoe" of the GSPT frame. However, in reality it has been found that many physical or biological systems cannot be transformed to ones in the form of singularly perturbed system, but they still exhibit slow-fast motions, like recurrence phenomenon. For example, consider the following $ 2 $-d HIV in-house disease model ^[9,10]:

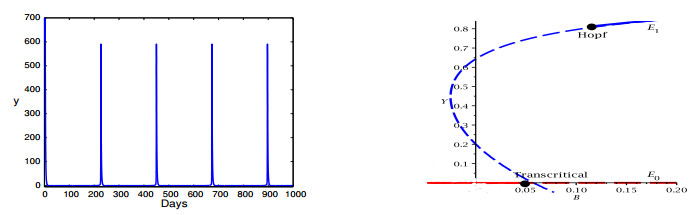
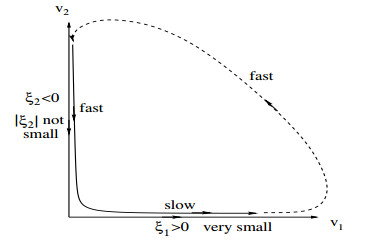
where $ X $ and $ Y $ are the dimensionless healthy and infected cells, respectively, and $ A $, $ B $, $ C $ and $ D $ are normalized parameters, all of them take positive real values. It has been shown in ^[9,10] that this model exhibits recurrence behaviour, namely a slow-fast motion, see the simulated oscillation depicted in Figure 3(a). Such sustained oscillation cannot be analyzed by the GSPT since one cannot obtain an $ \varepsilon $ for one of the equations in (1.6). But it is easy to use dynamical system theory to explain how such a special oscillation occurs. The model (1.6) has two equilibrium solutions: infection-free equilibrium $ {\rm E_0} $ and endemic equilibrium $ {\rm E_1} $; and there exists a transcritical bifurcation between them, see the bifurcation diagram in Figure 3(b). It is seen from Figure 3(b) that the transcritical bifurcation happens at $ B = 0.057 $, and $ B = 0.060 $ is chosen for simulating recurrence (or viral blips). It can be seen from the bifurcation diagram that both equilibria $ {\rm E_0} $ and $ {\rm E_1} $ are unstable between the transcritical point and Hopf bifurcation point (marked by two black circles), but the solutions of the system are bounded and so the motion induced by the Hopf bifurcation must be persistent. Moreover, we can see that the point defined by $ B = 0.060 $ at which the system exhibits recurrence behaviour, is a saddle point and close to the transcrtical bifurcation point, and thus one of the eigenvalues is positive and very small (in order $ \varepsilon $), while the other one is negative in the order $ O(1) $. Thus, one can image that when a trajectory moves around this saddle point, it moves very slow in the direction of the eigenvector associated with the small positive eigenvalue and fast in the direction of the eigenvector associated with the negative eigenvalue, yielding the slow-fast motion. This is shown in Figure 4, where $ v_1 $ and $ v_2 $ denote the two eigenvectors associated with the two eigenvalues $ 0 < \xi_1 \ll 1 $ and $ \xi_2 < 0 $, respectively.

So how do we apply the dynamical system approach to identify such slow-fast motions? Recently, four conditions were proposed and a new method was developed in ^[9,10,11] to study such slow-fast motions. These conditions have been further improved. Roughly speaking, for a given dynamical system, if the following conditions are satisfied:

$ \rm C _1 :$ there exists at least one equilibrium solution;

$ \rm C _2 : $ there exists a transcritical or saddle-node bifurcation;

$ \rm C _3 : $ there is a Hopf bifurcation; and

$ \rm C _4 : $ there is a "window" between the Hopf bifurcation point and the transcritical/saddle-node bifurcation point in which oscillation continuously exists,

then the system exhibits slow-fast motions. To verify these conditions for higher dimensional dynamical systems, identifying Hopf bifurcation (condition $ {\rm C}_3 $) becomes crucial.

In this paper, we will apply our new method to study the recurrence phenomenon which occurs in an oscillating network model related to organic reactions ^[12]. The recurrence behaviour for this network model has been shown by numerical simulations. We will use our approach to prove the existence of such phenomenon and determine the parameter values under which such slow-fast motions can occur. To achieve this, we first study stability and bifurcation of the equilibrium of the system, in particular, find the condition under which Hopf bifurcation occurs, and then verify the four conditions $ {\rm C_1} $-$ {\rm C_4} $.

The rest of the paper is organized as follows. In the next section, the oscillating network model is described. Then, in section 3, we present a theorem which can be used to identify Hopf bifurcation for general $ n $-dimensional dynamical systems. In section 4, we derive explicit conditions for saddle-node and Hopf bifurcations arising from the equilibrium of the oscillating network model and find the conditions which generate the recurrence phenomenon. Also, we use simulations to verify the analytical predictions, showing that they agree very well with the experiment results reported in ^[12]. In section 5, a further analysis is given on the Hopf bifurcation to explore the post-critical oscillating behavior. Conclusion and discussion are given in Section 6.

2.   An oscillating network model related to organic reactions

Organic chemical reaction networks have recently become more and more important in life and played a central role in their origins ^[13,14,15]. Network dynamics regulates cell division ^[16,17,18], circadian rhythms ^[19], nerve impulses ^[20] and chemotaxis ^[21], and provides guidelines for the development of organisms ^[22]. In chemical reactions, out-of-equilibrium networks have the potential to display emergent network dynamics such as spontaneous pattern formation, bistability and periodic oscillations. However, it has been noted that the principle of organic reaction networks developing complex behaviors is still not completely understood. In ^[12], a biologically related network organic reaction was developed, exhibiting bistability and oscillations in the concentrations of organic thiols and amides. Oscillations are generated from the interaction between three sub networks: an autocatalytic cycle that produces thiols and amides from thioesters and dialkyl disulfides; a trigger that controls autocatalytic growth; and inhibitory processes that remove activating thiol species that are generated during the autocatalytic cycle. Previous studies proved oscillations and bistability using highly evolved biomolecules or in organic molecules of questionable biochemical relevance (for example, those used in Belousov-Zhabotinskii-type reactions)^[23,24], while the organic molecules used in ^[12] are related to metabolism, which is similar to those found in early Earth. The network considered in ^[12] can be modified to study the influence of molecular structure on the dynamics of reaction networks, and may possibly lead to the design of biomimetic networks and of synthetic self-regulating and evolving chemical systems.

Simulations given in ^[12] have shown that space velocities (defined as the ratio of the flow rate and the reactor volume and given in units of per second) in the range $ 0.0001 $-$ 0.01 $/s would produce hysteresis. In order to test the result of simulations, the authors of ^[12] studied the total concentration of thiols during stepwise changes. In particular, they started from a low flow rate, then raised to a high flow rate, and finally returned to the low flow rate. To activate the autocatalytic pathway, one needs to use high thiol concentrations which are generated through self-amplification [of Cysteamine (CSH)], requiring the space velocities to be lowered to $ 0.0005 $/s. It has been observed that when the space velocity reaches $ 0.006 / $s, the system transitions will be out of the self-amplifying state. Such limits may explain the self-amplification which requires maleimide to be removed from the Continuously Stirred Tank Reactor (CSTR) more rapidly than it is added through the inlet port; while when the termination of self-amplification starts, free thiols should be removed from the CSTR by transporting out from the outlet port more rapidly than they are produced. Noticed from the model prediction, an increase of maleimide concentration reduced the bistable limit flow velocity. This chemical reaction network shows a general process to convert any quadratic autocatalytic system into a bistable switch. In ^[25], Epstein and Pojman found that bistable systems could generate oscillations in the presence of an inhibition reaction. In the system studied in ^[12], they chose acrylamide as an inhibitor, and tested this system with acrylamide in batch, which exhibited an oscillation (that is, one peak) in the concentration of free thiols. Moreover, Nuclear Magnetic Resonance (NMR) analysis has shown that the oscillation is triggered when the maleimide is removed. With a combination of numerical simulations and experiments in the CSTR under different flow rates, they found the conditions under which the addition of acrylamide can produce sustained oscillations in Organic Thiols (RSH). Sustained oscillations are often called recurrent oscillations in disease models, which may generate complex dynamical behaviors. To determine how the changes in flow rate affect such oscillations, the authors of ^[12] further examined the influence of flow rate on the stability, period and amplitude of oscillations. It showed that period increases nonlinearly with space velocity, while the amplitude increases linearly.

In ^[12], the authors examined how changes in flow rate affect oscillations and found that sustained oscillations (recurrence) occurred for certain space velocities. In order to explain the trends in period and amplitude of oscillating networks, and the nature of bifurcations at low and high limiting space velocities, a simple kinetic model has been established ^[12] to enable qualitative analysis on dynamic behaviors. The model simplifies the autocatalytic thiol network to bimolecular autocatalytic production of thiols from thioester, and considers the concentrations of Cystamine (CSSC) and acrylamide as constants. The simple model is described by three ordinary differential equations:

where $ A $, $ I $ and $ S $ represent the concentrations of organic thoils (RSH), maleimide and L-alanine ethyl thioester (AlaSEt), respectively, $ I_{0} $ and $ S_{0} $ are the concentrations of maleimide and AlaSEt fed into the reactor, respectively, $ k_{i}, \, i = 1, 2, 3, 4, $ are rate constants and $ k_{0} $ is the space velocity. From a linear analysis of this model ^[25], it has been found in ^[12] that increasing $ k_{0} $ from low to high values causes two transitions. Firstly, the system takes the transition from having a stable focus (damped oscillations) to a stable orbit (sustained oscillations) via a Hopf bifurcation ^[26]. Secondly, the system transits from having a stable orbit to a single stable equilibrium via a saddle-node or fold bifurcation ^[26]. The sustained oscillations between the two transitions, found numerically and experimentally in ^[12] indeed show the interesting recurrence phenomenon. In this paper, we will use our method to prove the existence of the recurrence behavior and determine the parameter values underlying this phenomenon.

3.   Criterion for Hopf bifurcation in general $ n $-dimensional dynamical systems

In this section, we present a theorem for identifying Hopf bifurcation in general $ n $-dimensional dynamical systems, which are assumed to be described by the following nonlinear differential equation:

where the dot denotes differentiation with respect to time $ t $, $ x $ and $ \mu $ are the $ n $-dimensional state variable and $ m $-dimensional parameter variable, respectively. Assume that the nonlinear function $ f(x, \mu) $ is analytic with respect to $ x $ and $ \mu $, and suppose that an equilibrium solution of Eq (3.1) is given in the form of $ x_e = x_e(\mu) $, which is determined from $ f(x, \mu) = 0 $. In order to analyze the stability of $ x_e $, evaluating the Jacobian of system (3.1) at $ x = x_e(\mu) $ yields $ J(\mu) = D_xf|_{x = x_e(\mu)} $. If all eigenvalues of $ J(\mu) $ have nonzero real parts, then the system is said to be hyperbolic, that means no complex dynamics exists in the vicinity of the equilibrium. Otherwise, at least one of the eigenvalues of $ J(\mu) $ has zero real part at a critical point, defined by $ \mu = \mu_c $, and bifurcations may occur from $ x_e(\mu) $. To determine the stability of the equilibrium, we compute the eigenvalues of the Jacobian $ J(\mu) $, which are the roots of the characteristic polynomial equation:

For a fixed value of $ \mu $, if all roots of the polynomial $ P_n(\lambda, \mu) $ have negative real part, then the equilibrium is asymptotically stable for this value of $ \mu $. If at least one of the eigenvalues has zero real part as $ \mu $ is varied to cross a critical point $ \mu_c $, then the equilibrium becomes unstable and bifurcation occurs from this critical point. When all roots of $ P_n(\lambda, \mu) $ have negative real part, we call $ P_n(\lambda, \mu) $ a stable polynomial.

In general, for $ n\geqslant 3 $, it is hard to find the roots of $ P_n(\lambda, \mu) $. Thus we use the Routh-Hurwitz Criterion ^[27] to analyze the local stability of the equilibrium solution $ x = x_e(\mu) $. The criterion gives sufficient conditions under which the equilibrium is locally asymptotically stable, i.e., all roots of the characteristic polynomial $ P_n(\lambda, \mu) $ have negative real part. These conditions are given by

where $ \Delta_i(\mu) $ is called the $ i $th-principal minor of the Hurwitz arrangements of order $ n $, defined as follows (here, order $ n $ means that there are $ n $ coefficients $ a_i $ ($ i = 1, 2, \ldots, n $) in Eq (3.2), which construct the Hurwitz principal minors):

Assume that as $ \mu $ is varied to reach a critical point $ \mu = \mu_{c} $, at least one of $ \Delta_{i} $'s becomes zero. Then the fixed point $ x_{e}(\mu_{c}) $ loses stability, and $ \mu_{c} $ is called a critical point. It can be seen from Eq (3.3) that if $ a_{n}(\mu_c) = 0 $, but other Hurwitz arrangements are still positive (i.e., $ \Delta_{n}(\mu_c) = 0 $, $ \Delta_i(\mu_c) > 0 $, $ i = 1, 2, \ldots, (n-1) $), then $ P_n(\lambda, \mu_c) = 0 $ has one simple zero root. In this case, system (3.1) has a simple zero singularity and a static bifurcation occurs from $ x_e $, usually causes a "jump" from one equilibrium to another one. In other cases, for example, Hopf bifurcation may occur at a critical point when $ P_n(\lambda, \mu) = 0 $ has a pair of purely imaginary eigenvalues $ \pm i\omega $ $ (\omega > 0) $ at this point. However, the pair of purely imaginary eigenvalues are often difficult to be determined explicitly for high dimensional systems. Here, we present a theorem which can be used to determine the necessary and sufficient conditions under which Hopf bifurcation occurs in general $ n $-dimensional dynamical systems. Its proof can be found in ^[28].

Theorem 1. ^[28] The necessary and sufficient conditions for system (3.1) to have a Hopf bifurcation from an equilibrium solution $ x = x_e $ are $ \Delta_{n-1} (\mu_c) = 0\, $ and $ \, \left. \frac{d \Delta_{n-1} (\mu)}{d \mu} \right|_{\mu = \mu_c} \ne 0 $, with other Hurwitz conditions being still held, i.e., $ a_n (\mu_c) > 0 $ and $ \Delta_i(\mu_c) > 0 $, for $ i = 1, \ldots, n-2 $.

Note that suppose $ \, P(\lambda, \mu) = 0 \, $ has a complex conjugate eigenvalue, $ \, \alpha(\mu) \pm \omega(\mu) \, $ near $ \, \mu = \mu_c $. Then, $ \Delta_{n-1} (\mu_c) = 0\, $ is equivalent to $ \, \alpha(\mu_c) = 0 $, and $ \, \left. \frac{d \Delta_{n-1} (\mu)}{d \mu} \right|_{\mu = \mu_c} \ne 0 \, $ is equivalent to the transversality condition ^[29]: $ \, \left. \frac{d \alpha (\mu)}{d \mu} \right|_{\mu = \mu_c} \ne 0 $.

4.   Bifurcation analysis and recurrence phenomenon

In this section, we present a bifurcation analysis for model (2.1) based on the results established for general nonlinear dynamical systems in the previous section and show that the model exhibits recurrence phenomenon.

We start from finding the equilibrium solution of model (2.1), which can be simply obtained by setting $ \dot{A} \! = \! \dot{I} \! = \! \dot{S} \! = \! 0 $ and solving the resulting algebraic equations, and obtain the equilibrium solution $ E_1 $, given by

where $ A_1 $ is determined from the equation:

which is equivalent to the following cubic polynomial equation:

The typical parameter values obtained from experiments for the model are given below ^[12]:

which are substituted into (4.3) to yield

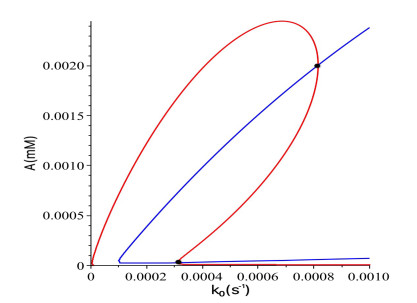
Note that the rational numbers given in (4.5) are obtained from transforming the numbers in digital format for convenience of symbolic computation. The graph depicted in Figure 5 shows the component $ A_1 $ of the equilibrium solution $ E_1 $, satisfying $ F_1(A_1, k_0) = 0 $.

Next, we consider the stability of the equilibrium solution $ E_1 $, and give a complete bifurcation classification. Evaluating the Jacobian of (2.1) at $ E_1 $ yields a cubic characteristic polynomial, given by

where the coefficients $ a_1(A_1, k_0) $, $ a_2(A_1, k_0) $ and $ a_3(A_1, k_0)\, $ are expressed in terms of $ A_1 $ and $ k_0 $ as

Based on the characteristic polynomial (4.6), we consider possible bifurcations from $ E_1 $, including both static (saddle-node) and dynamical (Hopf) bifurcations. First, we consider static bifurcation, which occurs when $ P_3(\lambda, A_1, k_0) = 0 $ has zero roots (zero eigenvalues). The simplest case is single zero, i.e., when $ a_3(A_1, k_0) = 0 $, and $ A_1 $ should simultaneously satisfy $ F_1(A_1, k_0) = 0 $ (see Eq (4.5)). Thus, we obtain

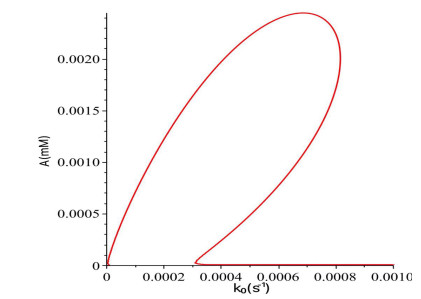
where $ k_{0s} $ is determined from the $ 8 $th-degree polynomial equation,

Solving $ F_2(k_{0s}) = 0 $ for $ k_{0s} $ yields four positive real solutions. Then, substituting the four solutions into $ A_{1s}(k_{0s}) $ using (4.7), we get four values of $ A_{1s}(k_{0s}) $, and two of them are positive, which yield two critical values (see the two black circles in Figure 6): $ (k_{0sn}, A_{1sn}) \! \approx \! (3.0827 \! \times \! 10^{-4}, \, 2.6398 \! \times \! 10^{-5}) $ and $ (8.1553 \times 10^{-4}, \, 2.0062 \times 10^{-3}) $. By verifying the changes of the stability on both sides of the critical points on the curve $ F_1(A_1, k_0) = 0 $, we find that the first one defines a saddle-node bifurcation. For example, we select $ A_1 \! = \! 2.7 \! \times \! 10^{-5} $ (above the critical point), the corresponding value of $ k_0 $ is equal to $ 3.0827 \! \times \! 10^{-4} $, under which the eigenvalues defined by equation (4.6) are $ 1.99 \! \times \! 10^{-5} $, $ -2.49 \! \times \! 10^{-4} $ and $ -0.1124 $, implying that the corresponding equilibrium solution is unstable. When we select $ A_1 \! = \! 2.5 \! \times \! 10^{-5} $ (below the critical point), the corresponding $ k_0 $ is equal to $ 3.0831 \! \times \! 10^{-4} $, for which the eigenvalues are $ -4.61\times 10^{-5} $, $ -2.45\times 10^{-4} $ and $ -0.12014 $, indicating that the corresponding equilibrium solution is locally asymptotically stable.

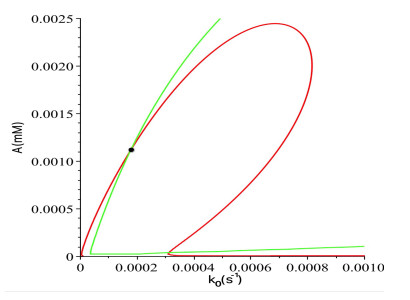
Next, we turn to consider Hopf bifurcation which may occur from the equilibrium $ E_1 $. To achieve this, we apply Theorem 1 to the equilibrium $ E_1 $, where $ A_1 $ satisfies the polynomial equation $ F_1(A_1, k_0) \! = \! 0 $ in (4.5). Based on the cubic characteristic polynomial $ P_3(\lambda, A_1, k_0) \! = \! 0 $, we apply the formula, $ \Delta_2(A_1, k_0) \! = \! a_1a_2 \!-\! a_3 $, to solve the two polynomial equations, $ \Delta_2(A_1, k_0) \! = \! 0 $ and $ F_1(A_1, k_0) \! = \!0 $, together with the parameter values given in (4.4), yielding three candidates for Hopf critical points: $ (k_{0H1}, \, A_{H1}) \! \approx \! (1.7681 \! \times \! 10^{-4}, \, 1.1148 \! \times \! 10^{-3}) $, $ (2.5483 \! \times \! 10^{-4}, \, -2.9768 \! \times \! 10^{-5}) $ and $ (3.0912\times 10^{-4}, \, 3.3790\times 10^{-5}) $. We only consider the biologically meaningful points with two positive entries to get two candidates for Hopf critical points: $ (k_{0H1}, A_{H1}) $ and $ (k_{0H3}, A_{H3}) $. For these two solutions, we need to check if the eigenvalues defined by equation (4.6) contain a pair of purely imaginary eigenvalues. By a simple calculation, we find that the unique Hopf critical point is $ (k_{0H}, A_{H})\approx(1.7681\times 10^{-4}, 1.1148\times 10^{-3}) $, which is shown in Figure 7. Note that at the critical point $ (k_{0H}, A_{H}) $, other stability conditions given in Theorem 1 are still satisfied. Moreover, it can be shown that

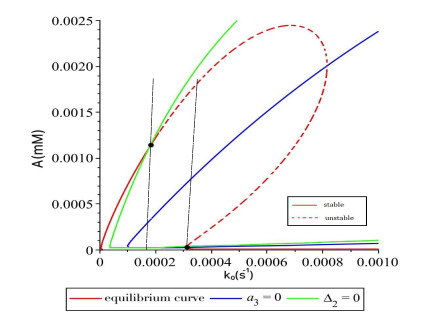
As a matter of fact, by using the Hopf critical value, we may numerically compute the Jacobian of system (2.1) at the equilibrium $ E_1 $ to get a purely imaginary pair and one negative real eigenvalues: $ \pm 1.0879 \! \times \! 10^{-3}\, i $ and $ -0.3362 $. Therefore, on the equilibrium solution curve defined by $ F_1(k_0, A_1) \! = \! 0 $ (see Figure 8), the equilibrium $ E_1 $ is stable from the origin to the Hopf critical point $ (k_{0H}, A_{H}) $, and unstable from $ (k_{0H}, A_{H}) $ to the saddle-node bifurcation point $ (k_{0sn}, A_{1sn}) $, and then returns to stable from the saddle-node bifurcation point, as shown in Figure 8. This agrees with that observed in experiments and numerical simulations ^[12].

We have also used the MATCONT software package in Matlab to obtain the numerical bifurcation diagram, as depicted in Figure 9, which confirms our bifurcation diagram as given in Figure 8.

It is seen that all the four conditions $ \, {\rm C}_1 $-$ {\rm C}_4 $ (given in the section of introduction) are satisfied for the network oscillating model (2.1). In particular, it is observed that there exists a "window", as shown in Figure 8 bounded by two vertical lines, between the Hopf and saddle-node bifurcation points. Therefore, the recurrence phenomenon occurs in this model when the values of the bifurcation parameter $ k_0 $ are chosen from the interval $ \, k_0 \! \in \! (k_{0H}, \, k_{0sn}) \! = \! (1.7681 \! \times \! 10^{-4}, \, 3.0827 \! \times \! 10^{-4}) $.

Next, we present simulations to demonstrate the behavior changes of the solutions, showing a good agreement, in particular for the recurrence behavior as reported in ^[12]. With the parameter values given in (4.4), system (2.1) becomes

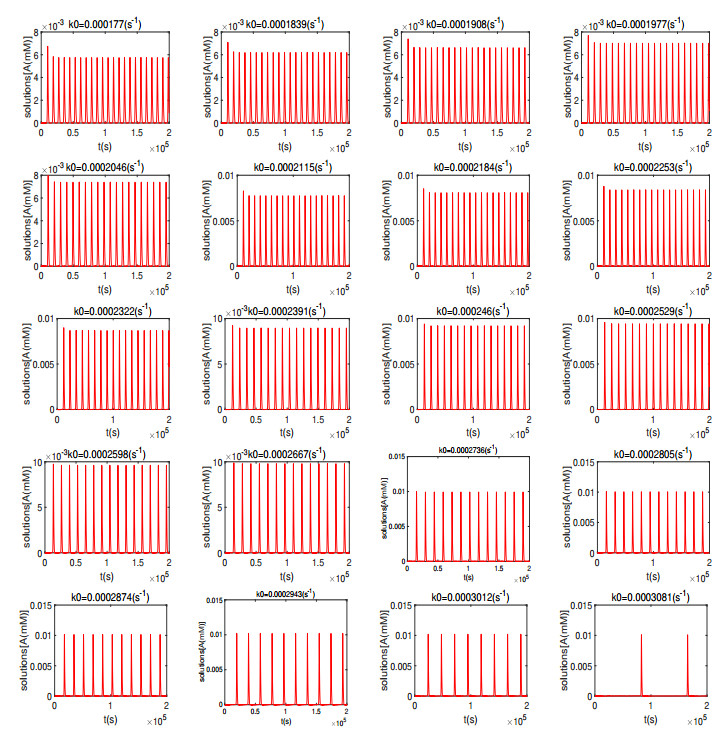
We have used the ode45 solver in Matlab for differential equations to simulate system (4.10) by varying the values of $ \, k_0\, $ in the interval $ \, k_0 \! \in\! (1.7681 \! \times \! 10^{-4}, \, 3.0827 \! \times \! 10^{-4}) \, $ to obtain the results, as shown in Figure 10.

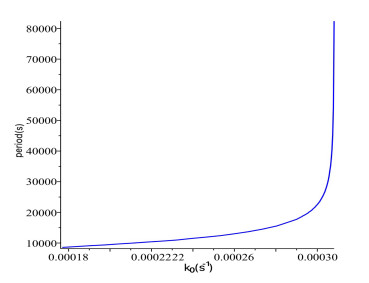
It is seen from Figure 10 that the solutions of $ A $ are oscillating when the values of $ k_0 $ are chosen between $ k_{0H} $ and $ k_{0sn} $ to exhibit the relaxation behavior, showing that the method developed in ^[9,10,11] with the four conditions $ {\rm C_1} $-$ {\rm C_4} $ to study recurrence phenomenon is an efficient approach. The period of oscillation increases with the increase of $ k_0 $, as shown in Figure 11, indicating that the period goes to infinity as $ k_0 $ is varied towards the saddle-node bifurcation point, as expected. From a biological point of view, certain subtypes of some diseases are classified based on the patterns of this recurrent behavior ^[6]. Therefore, an improved understanding of recurrence phenomenon in autoimmune diseases is crucial in promoting correct diagnosis, patient management and treatment decisions. For the recurrence phenomenon studied in this paper, our method can be used to realistically explain complex dynamics in organic reactions and improve correct classification, management and utilization of energy resources.

5.   Further study on the Hopf bifurcation and limit cycles

Although in the previous section, we have identified the Hopf bifurcation and the transversality condition (see equation (4.9)) for model (2.1), we do not know whether the Hopf bifurcation is supercritical or subcritical, as well as post-critical behavior of the model. To answer this question, in this section we give a further study on the Hopf bifurcation from the equilibrium $ E_1 $ of the model, and use normal form theory to study stability of the bifurcating limit cycles. Assume that $ k_0 = k_{0H}+\mu = 0.000176806\cdots+\mu $, where $ \mu $ is a small perturbation (bifurcation) parameter. Using the values given in (4.4), we introduce the following transformation,

where

into system (2.1) to obtain

where $ G_{1} $, $ G_{2} $ and $ G_{3} $ are rational functions in $ x_{1} $, $ x_{2} $, $ x_{3} $, $ \mu $ and $ A_{1} $, as listed in Appendix.

Note in the above equations that we have used decimal points for convenience. Now, the relation between $ A_1 $ and $ \mu $ can be still determined by (4.5) with $ k_0 = k_{0H}+\mu $. The Jacobian of system (5.3) evaluated at the origin, $ x_i = 0, \ i = 1, 2, 3 $, and critical point, defined by $ \mu = 0 $, with $ A_1 = 1.1147\cdots \times \! 10^{-3} $ (corresponding to the positive equilibrium $ E_1 $ for model (2.1)) is then in the Jordan canonical form:

where $ \omega_c = 1.0878\cdots \times 10^{-3} $ and $ \alpha = -0.3361\cdots $. Next, by applying center manifold theory and normal form theory, one can obtain the normal form of the Hopf bifurcation for system (5.3), given in polar coordinates:

where $ r $ and $ \theta $ represent the amplitude and phase of oscillating motions (limit cycles), respectively. The coefficients $ v_0 $ and $ \tau_0 $ can be found from a linear analysis, while computing $ v_k $ and $ \tau_k $ ($ k \ge 1 $) needs a nonlinear analysis. The $ v_k $ is called the $ k $th-order focus value. The following theorem provides explicit formulas for computing $ v_0 $ and $ \tau_0 $.

Theorem 2. ^[31] For the two-dimensional linear system,

the following formulas hold:

Based on the center manifold theory, in the vicinity of the Hopf critical point, the system is described on the center manifold of system (5.3) by a two-dimensional dynamical system. Then, applying the formula (5.7), we obtain

Next, letting $ \mu\! = \!0 $, and $ A_1 \! = \! A_H = 0.001114785 $ in system (5.3), and then applying the Maple program ^[30] to the resulting system yields

Therefore, the normal form associated with this Hopf bifurcation, up to third-order terms, is given by

Note in (5.9) that $ v_0 = 1.4557 > 0 $, which is indeed equivalent to the condition given in (4.9).

The steady-state solutions of Eq (5.9) are determined from $ \dot{r} = \dot{\theta} = 0 $, yielding

The solution $ \bar{r} = 0 $ represents the equilibrium $ E_1 $ of model (2.1). A linear analysis on the first differential equation of (5.9) shows that $ \frac{d}{dr}(\frac{dr}{dt})|_{\bar{r} = 0} = v_0\mu $, and thus $ \bar{r} = 0\ $ (i.e., the equilibrium $ E_1 $) is stable (unstable) for $ \mu < 0\ (>0) $, as expected. When $ \mu $ is decreased from positive to cross zero, a Hopf bifurcation occurs and the amplitude of the bifurcating limit cycles is approximated by the nonzero steady state solution,

Since $ \frac{d}{dr}(\frac{dr}{dt})|_{ (5.11)} = 2v_1\bar{r}^2 = -2v_0\mu > 0\ \ (\mu < 0, v_0 > 0, v_1 > 0) $, the Hopf bifurcation is subcritical and so the bifurcating limit cycles are unstable. Equation (5.11) gives the approximate amplitude of the bifurcating limit cycles, while the phase of the motion is determined by $ \theta = \omega t $, where $ \omega $ is given by

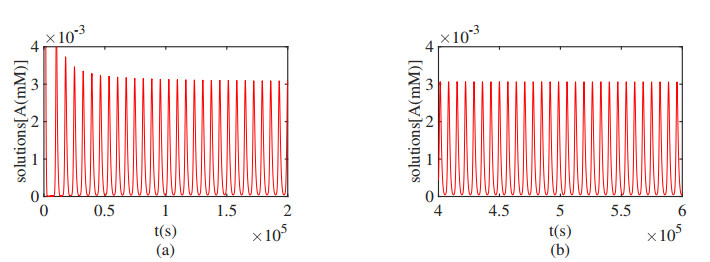
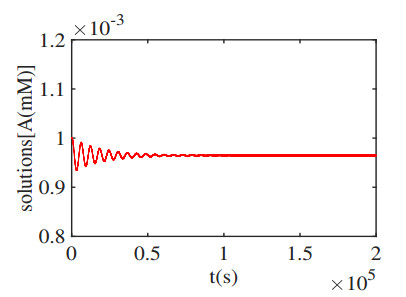
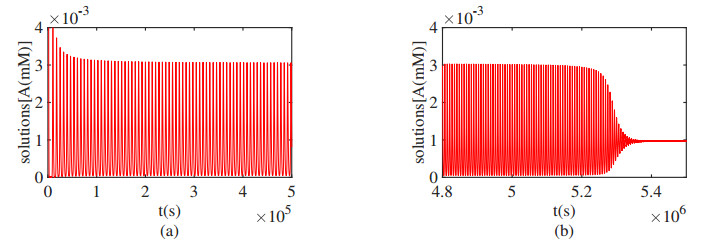
Further, by simulation we find that the stable region before the Hopf critical point as shown in Figure 8 (i.e., for $ k_0 \! \in \! (0, \, k_{0H}) $) can be divided into two parts for the equilibrium: globally asymptotically stable and locally asymptotically stable. The approximate value of the dividing point can be obtained as follows: Recalling $ k_{0H} \! = \! 0.000176806 $, we choose $ k_0 \! = \! 0.00014466350 $ and two initial points $ (A, I, S) \! = \! (1, 1, 1) $ and $ (0.001, \, 0.000005, \, 0.016) $ for simulation and obtain the results as shown in Figures 12 and 13, respectively. It is seen that the trajectory starting from the first initial point converges to a stable limit cycle, while that starting from the second critical point converges to the equilibrium $ E_1 $. Moreover, we choose $ k_0 \! = \! 0.00014466348 $ and the initial point $ (A, I, S) = (1, 1, 1) $ to obtain the result, as depicted in Figure 14, showing that the trajectory eventually converges to the equilibrium $ E_1 $ even from a far away initial point, which implies that the equilibrium $ E_1 $ is globally asymptotically stable for this value of $ k_0 $. Thus, the approximate value of the point dividing global stability and local stability is $ k_0 \approx 0.00014466348 $.

The subcritical Hopf bifurcation found above implies that there exists an unstable limit cycle, restricted on a local invariant manifold, between the stable equilibrium $ {\rm E_1} $ and a stable (outer) limit cycle. This yields a different bistable phenomenon due to bifurcation of multiple limit cycles, which involves a stable equilibrium and a stable periodic motion, different from the classical bistable phenomenon which only contains two stable equilibria.

6.   Discussion and conclusion

In this paper, we have introduced a new method to study certain type of slow-fast motions in dynamical systems. This approach is based on dynamical system theory and can be easily applied to identify sustained oscillations. In particular, when the geometric singular perturbation theory (GSPT) fails to investigate such slow-fast motions, our method may work quite well. The basic idea of this new method is to identify a "window" in bifurcation diagrams between Hopf bifurcation and saddle-node/transcritical bifurcation. This approach has been applied to many biological systems to study such slow-fast motions (e.g., see ^{[1,9,10,11,31]}). It has been shown that this approach is quite convenient in application and works well for higher-dimensional dynamical systems which involve multiple parameters. The key step is to determine Hopf critical points.

In this work, the new method has been applied to analyze an oscillating network model of biologically relevant organic reactions and confirmed the recurrence behaviour found in ^[12] based on numerical simulations and experiments. Bifurcation analysis is given to identify saddle-node and Hopf bifurcations and particularly to determine the bifurcation window, which yields the recurrence phenomenon. Simulations are also present to verify the analytical predictions, showing a very good agreement between the simulations and predictions. Moreover, normal form theory is applied to determine that the Hopf bifurcation is subcritical and the equilibrium is locally asymptotically stable near the Hopf critical point, yielding an unstable limit cycle, restricted on an invariant manifold, between the stable equilibrium and the outer stable limit cycle. This bistable phenomenon may explain some special complex dynamics occurring in this model. Further, a critical point is numerically identified, which divides the equilibrium solution into two parts: one is globally asymptotically stable and the other is locally asymptotically stable. The recurrence phenomenon studied in this paper for this kinetic model may be one of the sources of generating complex dynamics in biological systems or even more generally in real physical systems. It is anticipated that the method used in this paper can be applied to study other nonlinear dynamical systems.

However, even the new method can be applied to consider higher-dimensional dynamical systems, it may not applicable for some simple systems such as the van der Pol's equation (1.6). This implies that a slow-fast motion in dynamical systems can be in general very complex, which may involve several "modes" in different time scales. The GSPT can be used to analyze a part of such systems if such a system can be put in the form of singularly perturbed differential systems, while our method can solve a part of such systems if the four conditions $ {\rm C_1} $-$ {\rm C_4} $ are satisfied for such a system, which does not need the singular perturbation frame. We have shown that the two approaches can work for different systems: the slow-fast motion in the van der Pol's equation (1.5) can be analyzed by the GSPT, but not by our method; while the slow-fast motion in the 2-d HIV model (1.6) can be investigated by our method, but not by the GSPT. We also found that for some systems, both methods are applicable. For example, consider the following SIS epidemic model ^[32]:

which, by taking $ N = S+I $, can be put in the following form,

Here, $ S $ and $ I $ denote the numbers of susceptible and infected individuals, respectively, and $ N $ is the total population size. $ b_1 $ is the per-capita maximum birth rate, and $ K_1 $ reflects the effect of total population size on the birth. $ d_1 $ and $ \alpha_1 $ are the per-capita natural and disease-related death rates respectively, and $ \gamma_1 $ is the per-capita recovery rate. All the parameters take real positive values. In ^[32], it is assumed that $ b_1 $, $ d_1 $ and $ \alpha_1 $ are small, compared with other parameters, and so letting

and introducing

into (6.2) yields

which now becomes a singularly perturbed system, where $ \lambda_1 $ may be negative, $ \varepsilon_1 $ and $ |\lambda_1 | $ are chosen small enough so that $ \gamma_2 > 0 $. Further, applying the scaling:

to (6.3) yields the following dimensionless system:

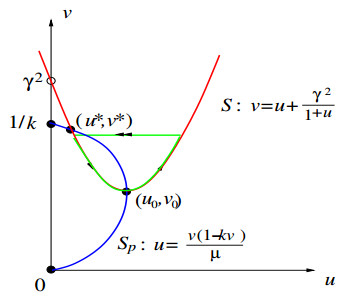
where $ u $ and $ v $ are the fast and slow variables, respectively. Then, the critical manifold (slow manifold) is given (setting $ \varepsilon = 0 $) by

which indeed, together with fast manifolds, can form closed loops, as shown in Figure 15.

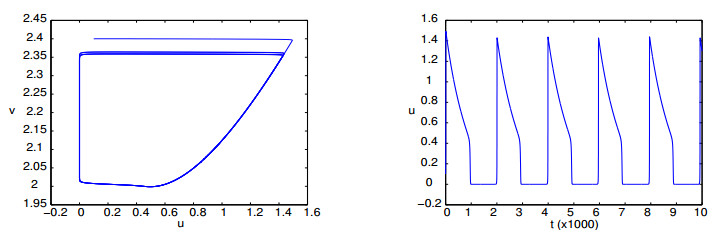
Numerical simulations for $ \varepsilon = 0.001, \, \gamma = \mu = \lambda = 3, \ k = 0.101074 $ are depicted in Figure 16, which clearly shows a slow-fast motion – canard cycle. This result can also be obtained by applying our method to the non-scaled system (6.2).

Finally, we should point out that unlike the GSPT theory which has been developed for more than 40 years and established a fundamental mathematical theory, our new method needs further research to develop a rigorous mathematical theory, in particular, for the existence of the "window". In other words, how to define/obtain the exact conditions under which the window exists and oscillations continuously exist for the whole window, from the Hopf critical point (which induces oscillations) to the saddle-node/transcritical bifurcation point (which ends the oscillation)? Further study is needed to improve our simple and efficient method with a well established mathematical theory.

Acknowledgments

This work was partially supported by the Natural Sciences and Engineering Research Council of Canada (No. R2686A2). The comments and suggestions received from the anonymous reviewer is greatly appreciated.

Conflict of interest

All authors declare no conflicts of interest in this paper.

Appendix

The rational functions $ G_{1} $, $ G_{2} $ and $ G_{3} $ in (5.3) are given below. In Maple calculation, the accuracy is taken up to $ 100 $ digits, but here only up to 6 digits are present for brevity.