1. Introduction
The Atlantic Forest is a megadiverse biome which forest cover was strongly reduced as a function of historical crop expansion and urbanization [1]. Originally, the Atlantic Forest was one of the largest rainforests of the Americas, covering around 1.5 million km2. Today, only 11.7% of its original forest cover remains [2]. In order to promote the biodiversity conservation and re-establish environmental services, several restoration projects have been carried out [3]. Nevertheless, the technical basis of the restoration methods is still controversial, especially as to the selection of species to be reintroduced [4,5].
1.1. Forest restoration and seedling planting
Seedling planting and direct seeding of tree species are methods employed for tropical and subtropical forest restoration. Seedling planting could significantly increase the success of forest recovery in abandoned pastures when compared to spontaneous regeneration or direct seeding [6], in spite of higher costs [7]. For long-term viability of these processes, species selection is a critical issue [3,5,7,8,9]. In addition, previous intensive land use tends to impose greater difficulty for forest restoration [6,10], with an emphasis in abandoned pastures in which exotic grass species are the main obstacle to overcome [11,12]. In order to reinstate the original diversity and allow the formation of self-perpetuating forests, many restoration initiatives have utilized a great diversity of tree species (usually more than 15) from different successional groups [6,12,13]. Additionally, high-diversity plantings with different successional guilds have been highly recommended for areas with reduced capacity for self-regeneration, such as abandoned pastures and intensive crop fields [5]. An additional argument for high-diversity restoration models is the inhibition of secondary succession and forest recovery promoted by monospecific plantings of fast-growing pioneer tree species [14,15,16]. However, the effectiveness of the high-diversity model for seedling planting has been scarcely studied. In some cases the observed diversity has been considered low even after 10 years of planting [17].
1.2. The successional guilds
Species differ in their ability to occupy areas in different successional stages, according to physiological, morphological and ontogenetic traits [18]. Pioneer species are able to occupy disturbed areas such as forest gaps but have reduced ability to germinate and establish in late successional stages of the forest. In turn, late successional species (or non-pioneer) can regenerate in mature areas, with low recruitment in disturbed areas [19]. Budowski [20] identified four successional stages, outlining the features expected for the species of each phase. However, the number of guilds is controversial, given that it is always a relatively arbitrary generalization. Denslow [21] admitted three categories (large-gap, small-gaps specialists, and understory specialists) while Swaine and Whitmore [19] point out only two categories: pioneer and non-pioneer. In the Atlantic Forest context, the authors are divided adopting between two [22] and four categories [23,24]. Although there is a certain degree of divergence among authors regarding the criteria and number of guilds, the classification of the species in these groups allows for a generalization which is usually applied in forest restoration plans. Notwithstanding, if plantings should be restricted to early successional species in order to obtain fast colonization and biomass increment [25,26] or include all the guilds as a way to recompose the diversity of late successional stages of the forest more quickly [5,27] still remains a question to be clarified.
1.3. Seed mass and tree species regeneration
Seed mass is positively correlated with early survival and has been indicated as a standard for species selection [28,29]. In general, species with a large mass of nutritional reserves tend to present higher survival in seedling phase, particularly in environments with restricted nutrients, light, or water. They also overcome better defoliation (herbivory) and litter inhibition [30]. Large seeds originate large seedlings [31,32] which decrease the mortality caused by herbivores [33]. Moreover, resprouting capability at seedling stage is directly correlated with seed size [32]. At seedling stage, the amount of reserves is positively correlated with tolerance to shading and inversely correlated with growth rate [34]. Insofar seeds size increases seedling sizes, survival expectancy in forest environments is enlarged, in spite of low growth rates [35]. However, adult trees in forest environments (DBH > 10 cm) present growth and survival rates negatively correlated with seed sizes [36]. In addition, survival of species with large seeds is higher in more advanced successional stages than in recently abandoned pastures [37]. Degraded areas with a history of intensive land use are very distinct environments in relation to mature forests, in which natural selection promotes the evolution of ecophysiological traits. Succession in these sites has unique characteristics, and for this reason, it has been called anthropic succession [27]. Large seeds could be related to late-successional species, with seedlings of higher survival in shaded conditions in mature or advanced secondary forests, at the same time as they present low tolerance to open sites in early successional stages, such as in abandoned croplands or pastures.
Our investigation was aimed at measuring growth and survival of seedlings in a high-diversity planting of tree species. In addition, differences among successional guilds were evaluated as well as a correlation between seed mass, growth, and survival. Experiment sites were highly degraded croplands, in a region previously covered by Semideciduous Atlantic Forest similar to those described by Benvenuti-Ferreira et al. [38].
2. Materials and Methods
A total of 36 native tree species from the Atlantic Forest biome were included in the study, from different successional groups and seed size classes as described in Table 1. Seed mass values were obtained from the specialized literature or the authors. The successional classification was based on three categories according to two criteria: growth rate (following the specialized literature, when available) and occurrence in different successional stages on the forests within the region (Table 2). Our classification was verified with reference literature, particularly Carvalho et al. [39]. Considering divergences on its classification, Inga marginata Willd was excluded from the analysis.
Table 1.Tree species with successional group and average seed mass
| Species
|
Family
|
Successional group
|
Seed mass (mg)
|
|
Trema micrantha (L.) Blüme
|
Cannabaceae
|
Pioneer
|
4.6
|
|
Heliocarpus americanus L.
|
Malvaceae
|
Pioneer
|
7.0
|
|
Schinus terebinthifolius Raddi
|
Anacardiaceae
|
Pioneer
|
10.5
|
|
Mimosa scabrella Bentham
|
Fabaceae
|
Pioneer
|
14.7
|
|
Schinus molle L.
|
Anacardiaceae
|
Pioneer
|
30.4
|
|
Vasconcellea quercifolia A. St.-Hilaire
|
Caricaceae
|
Pioneer
|
43.4
|
|
Ateleia glazioveana Baill.
|
Fabaceae
|
Pioneer
|
44.5
|
|
Sesbania virgata (Cav.) Pers.
|
Fabaceae
|
Pioneer
|
72.3
|
|
Enterolobium contortisiliquum (Vell.) Mor.
|
Fabaceae
|
Pioneer
|
180.2
|
|
Luehea divaricata Mart.
|
Malvaceae
|
Secondary
|
4.0
|
|
Jacaranda micrantha Cham.
|
Bignoniaceae
|
Secondary
|
8.0
|
|
Tabebuia alba (Cham.) Sandwith
|
Bignoniaceae
|
Secondary
|
10.8
|
|
Patagonula americana L.
|
Boraginaceae
|
Secondary
|
27.2
|
|
Cedrela fissilis Vellozo
|
Meliaceae
|
Secondary
|
27.5
|
|
Cordia trichotoma (Vell.) Arrab. & Steud.
|
Boraginaceae
|
Secondary
|
30.8
|
|
Parapiptadenia rigida (Benth.) Brenan
|
Fabaceae
|
Secondary
|
33.4
|
|
Tabebuia heptaphylla (Vell.) Toledo
|
Bignoniaceae
|
Secondary
|
41.2
|
|
Erythroxylum deciduum A.St.-Hilaire
|
Erythroxylaceae
|
Secondary
|
51.4
|
|
Rupretchia laxiflora Meissner
|
Polygonaceae
|
Secondary
|
66.7
|
|
Machaerium stipitatum Vogel
|
Fabaceae
|
Secondary
|
158.7
|
|
Pelthophorum dubium (Spreng.) Taubert
|
Fabaceae
|
Secondary
|
189.4
|
|
Inga sessilis (Vellozo) Martius
|
Fabaceae
|
Secondary
|
250.0
|
|
Eugenia uniflora L.
|
Myrtaceae
|
Secondary
|
353.3
|
|
Ilex paraguariensis A.St.-Hilaire
|
Aquifoliaceae
|
late successional
|
6.7
|
|
Campomanesia xanthocarpa Berg
|
Myrtaceae
|
late successional
|
33.0
|
|
Myrocarpus frondosus Freire Allemão
|
Fabaceae
|
late successional
|
101.0
|
|
Myrcianthes gigantea (Legr.) Legr.
|
Myrtaceae
|
late successional
|
114.0
|
|
Allophylus edulis (A.St.-Hilaire) Radlk.
|
Sapindaceae
|
late successional
|
125.0
|
|
Pliniaperuviana (Poir.) Govaert
|
Myrtaceae
|
late successional
|
215.0
|
|
Myrcianthes pungens (Berg.) Legr.
|
Myrtaceae
|
late successional
|
230.0
|
|
Cabralea canjerana (Vellozo) Mart.
|
Meliaceae
|
late successional
|
271.8
|
|
Eugenia pyriformis Camb.
|
Myrtaceae
|
late successional
|
305.0
|
|
Eugenia involucrata DC.
|
Myrtaceae
|
late successional
|
403.0
|
|
Chrysophyllum gonocarpum (Mart.& Eichler) Engler
|
Sapotaceae
|
late successional
|
410.0
|
|
Balfourodendron riedelianum (Engler) Engler
|
Rutaceae
|
late successional
|
416.7
|
|
Plinia rivularis (Camb.) Rotman
|
Myrtaceae
|
late successional
|
1250.0
|
Table 2.Criteria for species classification in the successional groups
|
|
Growth
|
Predominant occurrence
|
| Pioneer
|
Fast, reaching height >1.0 m in the first year; high volumetric increments (>15m3 ha−1 year−1) in monocultures
|
Forest clearings, borders, spontaneous regeneration in open areas
|
| Secondary
|
Moderate, reaching height >0.7 m in the first year; medium volumetric increments (5-15 m3 ha−1 year−1).
|
Juveniles at early secondary forests and emergent or in intermediary strata within old-growth forests
|
| Late successional
|
Slow growing, volumetric increments lower than 5 m3 ha−1 year−1
|
Intermediary strata or understory of advanced secondary forests or
old-growth forests
|
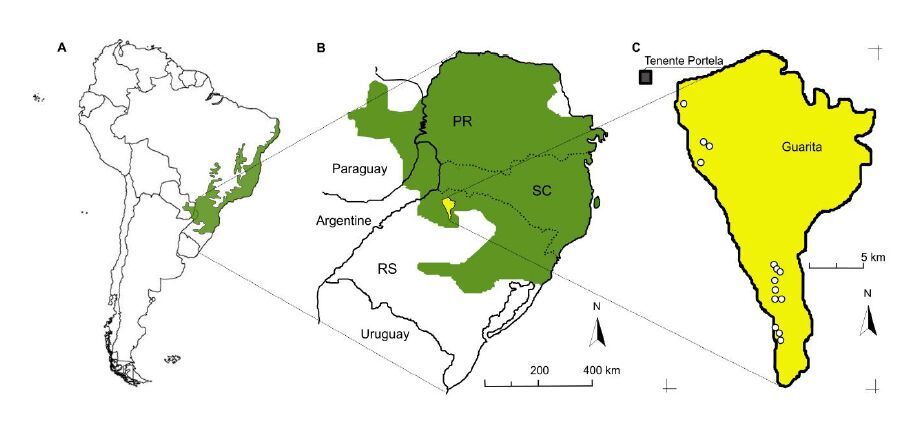
The study was performed in the Guarita Indigenous Area (230 km2), in Rio Grande do Sul state, Brazil (Figure 1). The outermost coordinates of the Guarita Indian Area are 27°20’ N, 27°35’ S, 53°44’ W and 53°32’E. Planting sites (n = 14; Table 3) present low-fertility soils [38] mainly of the Oxisols class, with some transition to Mollisols (Lithic Hapludoll). The climate presents yearly average temperatures between 18-19 °C and average yearly rainfall between 1700 and 1900 mm. The coldest month (July) has average temperatures close to 10 °C and the average temperatures of the warmest month (January) reaches 22 °C.
As a function of latitudinal and altitudinal amplitude, climatic conditions along the Atlantic Forest Biome is highly variable. Average yearly temperatures range between 12-25 °C and average yearly rainfall ranges between 1300 and 2800 mm [40]. Thus, the experimental sites correspond to a typical and median climate condition within the range of the Atlantic Forest Biome.
Seedlings were grown in a nursery using conical containers, being planted in the field with 3-4months of age. Planting was carried out between July and August 2004 with a density of 1475seedlings·ha−1. Three hectares were planted on each site. All species were planted on every site, and the composition included the same number of seedlings of each species on each site. The assemblage was composed by 67% of pioneer, 21% of secondary, and 12% of late successional species. The density of each species was considered according to nursery availability, ranging between 17 and 1477 ha−1 (Appendix 1). All measurements were obtained after seedling planting, therefore excluding the early stage of development in the nursery.
Planting time (August 2014) was considered as t = 0. Survival was calculated as the proportion of individuals remaining after 8 and 15 months since seedling planting, expressed as a mean percentage of sites (n = 14) for each species. Height was measured after 8 months for two individuals of each species on each site (n = 28). These individuals were evaluated after 15 months for height measurements and to calculate Relative Growth Rate between 8-15 months (RGR8-15). Relative Growth Rate between t = 0 and 8 months (RGR0-8) was calculated from height at t = 0 and 8 months after planting. RGR values were thus obtained with the equation RGR = (ht+1 − ht)/ ht。
Since mortality was high at 15 months, several plants measured at 8 months died. Therefore, the number of replications at 15 months was variable among species and local factors were not considered for the analysis of RGR8−15.
Prior to planting, the terrain subsoil was plowed and 5000 kg of dolomitic lime were added at 20cm depth using a grid of disk plows. A fertilizer (NPK-04-14-08) was applied at 100 g for each seedling and mixed to the soil in each planting furrow.
In order to allow for comparison among successional groups, survival percentage data was transformed according to the arcsin of the square root of x + 0.5. The Bonferroni test was applied for pairwise tests (P < 0.05). Statistics were carried out using the software Prism 3.0 (GraphPad Software Inc. 1999).
Table 2.Afforestation sites in the Guarita Indigenous Area
| Site code
|
Area sector
|
Coordinates
|
| DS
|
Bananeira
|
27°29’56” S, 53°38’59” W
|
| AM
|
Estiva
|
27°33’39” S, 53°38’46” W
|
| JG
|
Estiva
|
27°33’50” S, 53°38’33” W
|
| PA
|
Estiva
|
27°33’57” S, 53°38’17” W
|
| AF
|
Irapuá
|
27°31’22” S, 53°38’31” W
|
| LM
|
Irapuá
|
27°32’04” S, 53°39’16” W
|
| PKE
|
Irapuá
|
27°32’01” S, 53°39’26” W
|
| DC
|
Km 10
|
27°25’57” S, 53°42’06” W
|
| Os
|
Missão
|
27°28’42” S, 53°38’45” W
|
| PAm
|
Missão
|
27°28’50” S, 53°37’12” W
|
| RC
|
Missão
|
27°29’46” S, 53°37’37” W
|
| VR
|
Pedra Lisa
|
27°23’04” S, 53°43’44” W
|
| FFF
|
Três Soitas
|
27°24’12” S, 53°42’07” W
|
| JR
|
Três Soitas
|
27°24’50” S, 53°42’17” W
|
3. Results
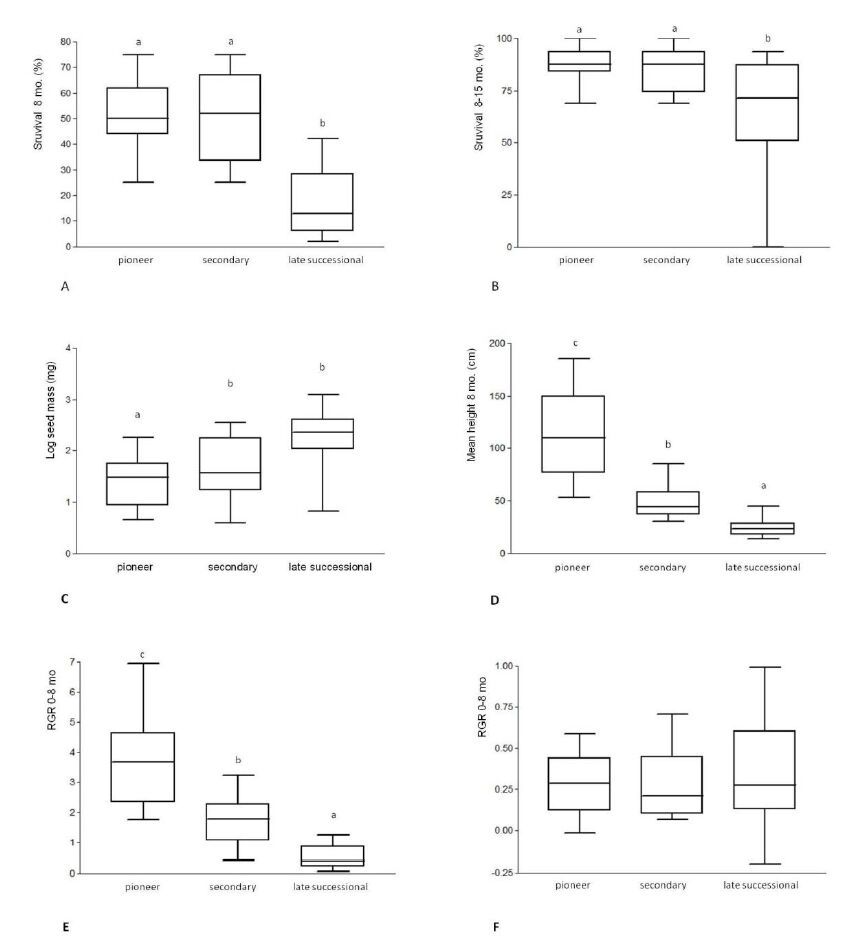
Average survival for all species after 15 months was 32.5%. However, the number of individuals was 40.9% as a function of disparity in the initial number of seedlings among the species, with a predominance of pioneers. The late successional species had a mean survival rate of 12.0% after 15 months. Survival was lower for the late successional species in the first period (8 months) than in the second period (8-15 months) (Figure 2A, B). Three late successional species showed 100% of mortality after 15 months: Pliniaperuviana (Poir.) Govaert, P. rivularis (Camb.) Rotman and Balfourodendron riedelianum (Engler) Engler.
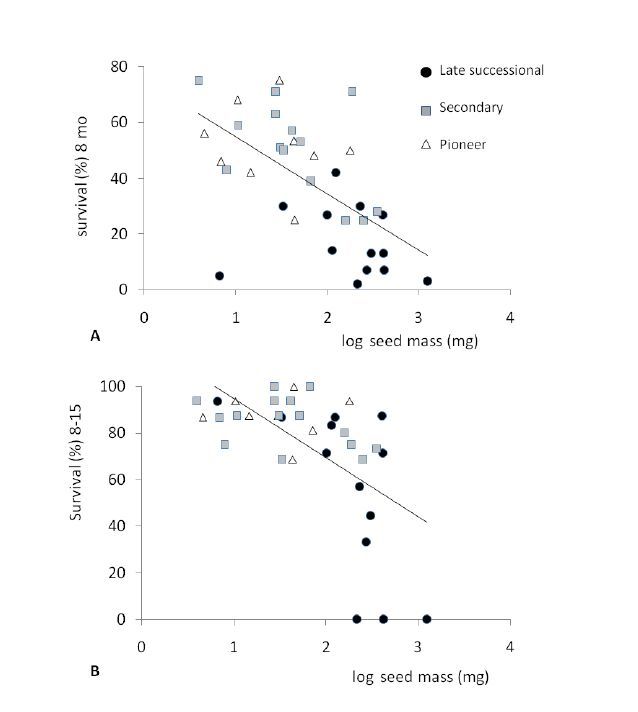
The seed mass of late successional species was higher than the seed mass of pioneers and secondary species (Figure 2C). For all species, survival at 8 months was inversely correlated to the log of seed mass (Figure 3). The general average seed mass was 153.9 mg. Every species with seeds weighing more than 200 mg each presented a mean survival rate ≤30%. Among these, 8 out of 11 were late successional species (Figure 3A). On the other hand, among the 12 species with survival rates higher than 50% at 8 months, 9 of them are secondary and 3 are pioneer (Figure 3A). Among them, only 2 presented seed masses higher than 50 mg. Height at 8 months and RGR0-8 were also inversely correlated with the log of seed mass (Table 3).
The successional guilds were significantly different in respect to the height at 8 months and RGR0-8: pioneers presented the highest values and the late successional species presented the lowest (Figure 2D, E). Notwithstanding, the successional groups did not differ as to RGR8-15 (Figure 2F). In addition, RGR 8-15 did not correlate with any of the other variables (Table 3).
Table 3.Correlations among parameters of growth and survival
|
height 8 months
|
RGR (0-8)
|
RGR (8-15)
|
Survival after 8 months
|
Survival between 8-15 months
|
| log seed mass
|
−0.430*
|
−0.536**
|
−0.044
|
−0.595**
|
−0.601**
|
| height 8 months
|
|
0.798**
|
−0.185
|
0.529**
|
0.335**
|
| RGR (0-8)
|
|
|
−0.037
|
0.580**
|
0.362**
|
| RGR (8-15)
|
|
|
|
−0.080
|
0.215
|
| Survival 8 months
|
|
|
|
|
0.545**
|
| * P< 0.01; ** P< 0.001 |
The contribution of Myrtaceae, which comprises 50% of the late successional species, could have been determining the difference between the seed mass of this group in relation to the others; however, the average seed mass of late successional Myrtaceae (364 ± 409 mg, n= 7) did not differ from the value of other late successional species (222 ± 171 mg, n= 6; P = 0.46, t-test).
4. Discussion
4.1. Growth and survival
As expected, the successional guilds differed with regard to growth. Pioneers achieved greater height and growth rate in the initial period. In turn, late successional species exhibited the lowest height and RGR0-8. The guilds did not differ in respect to the RGR8-15, possibly because that period corresponds to the colder season, during which growth tends to be reduced. Meanwhile, the survival in the first period was correlated with survival in the later period, indicating that survival continued to be affected independently of growth rate.
Survival in the first period was positively correlated to RGR0-8. However, the secondary species exhibited an equivalent survival rate in spite of having lower growth than the pioneers. Nevertheless, survival of the late successional species was 5 times lower than for the other two guilds. Similar results were achieved by Ramírez-Marcial et al. [41] who observed equivalent survival for pioneers and secondary species, and lower survival rates for the late successional species in a restoration experiment.
Growth rates correlate positively with survival in secondary succession [42]. For restoration efforts, higher growth and survival rates promote more effective colonization as competition with exotic grasses remains even after several years [12,17]. On the other hand, greater growth tends to correspond to higher litter production [38], which contributes effectively to the recovery of the nutrient cycle, highlighting contributions from the Fabaceae with biological fixation of nitrogen [43]. In the face of these aspects, planting late successional species is more reasonable after pioneer and secondary species are established, in later stages of succession [37]. Planting of late successional species is fundamental in hard landscape conditions in which the sources of propagules are insufficient for spontaneous regeneration [5,17].
4.2. Seed mass and survival in juvenile stages
Survival was negatively correlated with seed mass both in the initial period (0-8 months) and in the later period (8-15 months). Our results corroborate findings of Martínez-Garza et al. [44], who observed that growth and survival rates were negatively correlated with seed mass after 30 months of tree seedling planting.
Other studies [36,46] that included early seedling stages tended to indicate a positive correlation between seed mass and survival. In contrast, the influence of early stages is removed when the seedlings were first in nurseries [44]. Higher seed mass is an advantage in light-restricted environments for seedlings [34,35] and for juveniles in a forest environment [45]. Additionally, Tunjai & Elliot [46] reported higher survival of larger-seeded species after 12 months in a direct seed experiment. However, these authors measured survival as the ratio between surviving plants and the number of planted seeds. Therefore, small-seed species which usually present high mortality in the transition between seed germination and seedling [44] tend to exhibit lower values of survival. In nature, low probability of survival for individual seeds tends to be compensated by higher seed production [44]. In the present study, the positive effect of larger seed mass in the survival of the seedlings and in the growth of early phases of the seedling stage was minimized by the use of seedlings grown in a nursery. Theoretically, the main effects of seed mass took place during the nursery period. After that, the effect of seed reserves no longer interferes directly.
Our findings indicate that survival in the juvenile phase is negatively correlated with seed mass, at least in a highly degraded environment context. Similarly, a negative correlation between recruitment of tree species and seed mass was observed in forest areas after severe perturbation caused by logging operations [47]. In forest borders of the Atlantic Forest remnants, recruitment of large-seeded species was at least one degree of magnitude lower than in the forest interior [48]. However, it could be emphasized that the influence of seed sizes in the juvenile and adult phases is more probably indirect. Small seeds are associated with a suite of ecophysiological traits, such as high specific leaf area and high nutrient content [49], which can favor the juvenile recruitment in early secondary phases [47]. Beyond the classification of species in successional categories, which has been a key concept for the planning of forest restoration in the Atlantic Forest and other tropical biomes, seed mass could be complementary information for guide restorationists and researchers.
4.3. Successional guilds
Successional classification could be a controversial matter [19,23]. Other objective parameters could be useful to guide the selection of species in megadiverse biomes. The Atlantic Forest has more than 13,700 angiosperm species [50]. The southern sector of the Atlantic Forest has more than 1500 tree species [51], and higher tree diversity could be expected for the southeast and northeast sectors. Ecophysiological and silvicultural information are lacking for a majority of these species. Seed mass is information that can be easily obtained by restorationists and nursery managers. Moreover, the data presented here serves as a warning for the technical staff of tree nurseries, who may be tempted to prioritize large-seeded species due to their easy handling.
5. Conclusions
The growth and survival rates of pioneer and secondary species were higher than for late successional species. The survival of late successional species was so low that their inclusion in early phases of forest restoration is considered questionable.
In addition to guild classification, seed mass proved to be a strong indicator of long-term survival in the context of restoration sites with a history of intense degradation. Although large seed mass is an advantage for early seedling phases, such functional trait is related to lower survival and growth rates in the later stages, at least in the conditions evaluated in this study. The use of seedlings grown in nurseries cancels the positive influence of seed mass on survival and growth of trees in the field.
Acknowledgements
To FAPERGS (ProCoredes 04/0556.3) and CNPq (477.973 2012-4) for research grants; To the Guarita Indigenous Community for the permission to perform the study; To UNIJU—Universidade Regional do Noroeste do Estado do Rio Grande do Sul for research support; To Jorge Thiesen and Rosângela Pöersh for logistical support and assistance in the field work; To Meggie Fornazari for the English review.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: