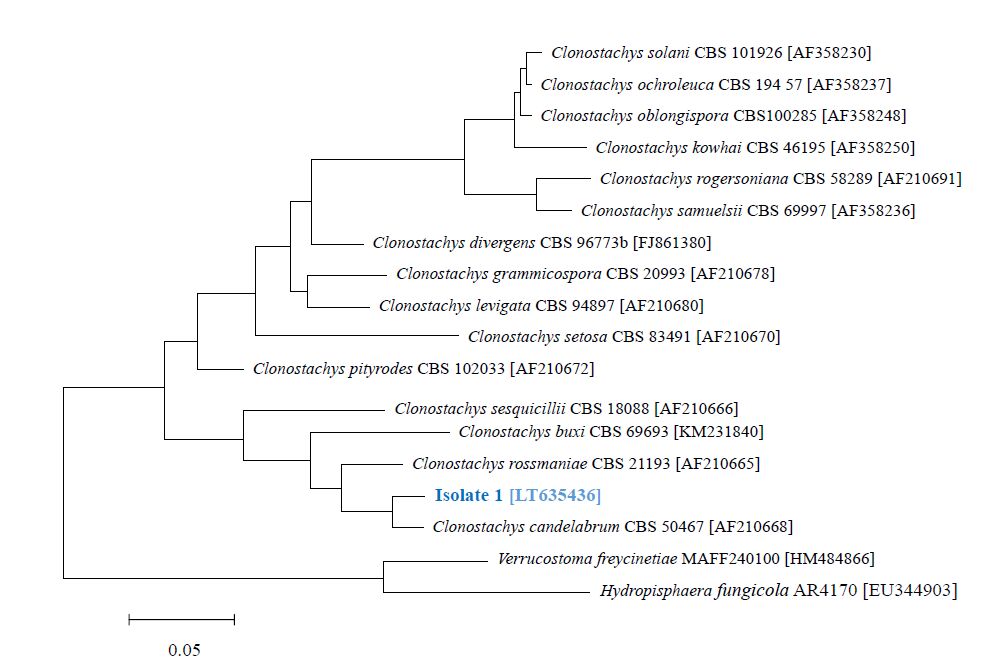
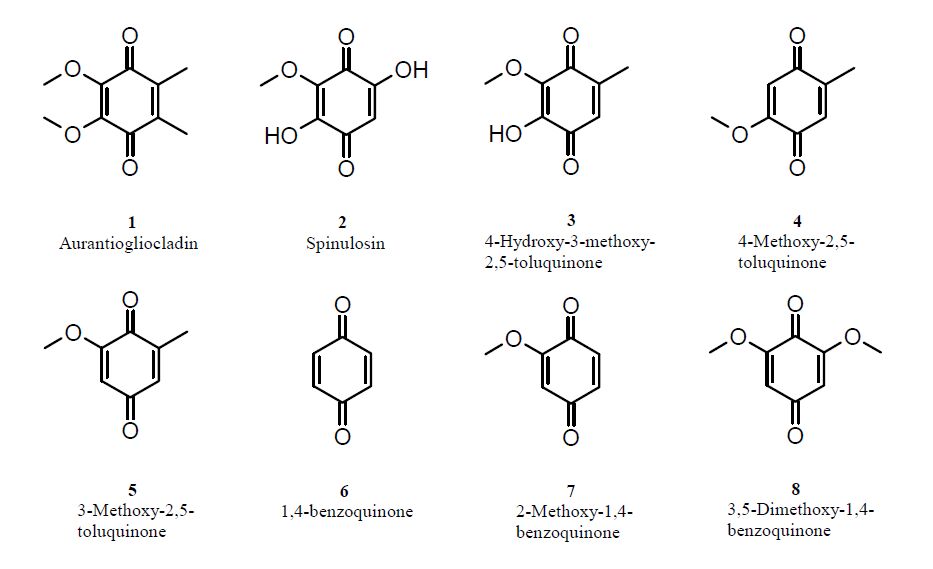
Infections where pathogens are organized in biofilms are difficult to treat due to increased antibiotic resistances in biofilms. To overcome this limitation new approaches are needed to control biofilms. One way is to screen natural products from organisms living in a wet environment. The rational is that these organisms are preferentially threatened by biofilm formation and may have developed strategies to control pathogens in these biofilms. In a screen of fungal isolates obtained from the Harz mountains in Germany several strains have been found producing compounds for the inhibition of biofilms. One of these strains has been identified as Clonostachys candelabrumproducing aurantiogliocladin. Biological tests showed aurantiogliocladin as a weak antibiotic which was active against Staphylococcus epidermidisbut not S. aureus. Aurantiogliocladin could also inhibit biofilm formation of several of the tested bacterial strains. This inhibition, however, was never complete but biofilm inhibition activity was also found at concentrations below the minimal inhibitory concentrations, e. g. Bacillus cereuswith a MIC of 128 μg mL–1showed at 32 μg mL–1still 37% biofilm inhibition. In agreement with this finding was the observation that aurantiogliocladin was bacteriostatic for the tested bacteria but not bactericidal. Because several closely related toluquinones with different antibiotic activities have been reported from various fungi screening of a chemical library of toluquinones is suggested for the improvement of biofilm inhibition activities.
1.
Introduction
This study will address time-optimal solutions of affine systems defined by the pairs (G,K) where G is a semi-simple Lie group and K is a compact subgroup of G with a finite centre. Such pairs of Lie groups are reductive in the sense that the Lie algebra g of G admits a decomposition g=p+k with p the orthogonal complement of the Lie algebra k of K relative to the Killing form in g that satisfies Lie algebra condition [p,k]⊆p. We will then consider time-optimal solutions of affine control systems of the form
where Xo,…,Xem are all left-invariant vector fields on G under the assumption that the drift element X0 belongs to p at the group identity and that the controlling vector fields Xi,i=1,…,m belong to k at the group identity. We will write such systems as
where A=X0(e) and Bi=Xi(e), i=1,…,m.
We will be particularly interested in the pairs (G,K) in which K is the set of fixed points by an involutive automorphism σ on G. Recall that σ≠I is an involutive automorphism on G that satisfies σ2=I where I is the identity map in G. Then, the tangent map σ∗ at e of σ is a Lie algebra isomorphism that satisfies σ2∗=I, where now I is the identity map on the Lie algebra g. Therefore (σ∗+I)(σ∗−I)=0, and g=ker(σ∗+I)⊕ker(σ∗−I), i.e.,
It follows that k={X∈g:σ∗(X)=X} is the Lie algebra of K and that p={X∈g:σ∗(X)=−X} is a vector space in g that coincides with the orthogonal complement of k and satisfies [p,p]⊆k. In the literature of symmetric Riemannian spaces the decomposition g=k⊕p subject to
is called a Cartan decomposition ([5], [6]). A symmetric pair is said to be of compact type if the Killing form is negative definite on p. Compact type implies that G is a compact Lie group (prototypical example G=SU(n),K=SO(n,R)). The pair (G,K) is said to be of non-compact type if the Killing form is positive definite on p (prototypical example G=SL(n,R),K=SO(n,R)) ([5]). We will assume that the pair (G,K) is one of these two types. In either case Kl(X,Y) will denote the Killing form on g. Recall that Kl is non-degenerate on g.
This background information shows that in each affine system (1.1) there is a natural energy function
where the scalar product ⟨,⟩ is the negative of the Killing form.This energy function induces a natural variational problem, called affine-quadratic problem, defined as follows: given two boundary conditions in G and a time interval [0,T], find a solution g(t) of (1.1) that satisfies g(0)=g0, g(T)=g1 whose energy of transfer ∫T0⟨U(t),U(t)⟩dt is minimal. Remarkably, every affine system (1.1) is controllable on G whenever A is regular and the Lie algebra kv generated by B1,…,Bm is equal to k and the corresponding extremal Hamiltonian system obtained by the maximum Principle is completely integrable ([7]).
In contrast to the above energy problem, time-optimal problems are more elusive due to the fact that the reachable sets need not be closed because the control functions are not bounded (it may happen that certain points in G that can be reached in an arbitrarily short time, but are not reachable in zero time, as will be shown later). More generally, it is known that any point of the group Kv generated by the exponentials in the Lie algebra kv generated by B1,…,Bm belongs to the topological closure of the set of reachable points A(e,≤T) in any positive time T, and yet it is not known (although it is generally believed) that each point in Kv can be reached in an arbitrarily short time from the group identity e. This lack of information about the boundary of the reachable sets in the presence of a drift vector still remains an impediment in the literature dealing with time optimality ([1,8,9,10]).
In this paper we will adopt the definition of R. W. Brockett et al. ([1], [2]) according to which the optimal time T that g1 can be approximately reached from g0 is defined as T=inf{t:g1∈ˉA(g0,≤t)}, where ˉA(g0,≤t) denotes the topological closure of the set of points reachable from g0 in t or less units of time by the trajectories of (1.2). Then T(g) will denote the minimal time that g is approximately reachable from the group identity e.
It is evident that Brockett's definition of time optimality is invariant under any enlargement of the system that keeps the closure of the reachable set A(e,≤t) the same. In particular, the optimal time is unchanged if the original system is replaced by
where now U(t) is an arbitrary curve in kv. Let now Kv denote the Lie subgroup generated by the exponentials in kv. We shall assume that Kv is a closed subgroup of K, which then implies that Kv is compact, since K is compact. Recall that every point in Kv belongs to the closure of A(e,≤t) for any t>0. Therefore T(h)=0 for any h∈Kv.
Each affine system (1.5) defines a distinctive horizontal system
These two systems are related as follows: every solution g(t) of (1.5) generated by a control U(t)∈kv defines a solution ˆg(t)=g(t)h−1(t) of the horizontal system whenever dhdt=h(t)U(t). Conversely, every solution ˆg(t) of the horizontal system gives rise to a solution g(t)=ˆg(t)h(t) of the affine system for h(t) a solution of dhdt=h(t)U(t). It follows that T(ˆg)=T(gh−1)=T(g), and that ˉAh(e,≤t)⊆ˉA(e,≤t), where Ah(e,≤t) denotes the reachable set of the horizontal system.
The above horizontal system can be extended to the convexified system without altering the closure of the reachable sets A(g0,≤t). The convexified system is given by
We will think of this system as a control system with h1(t),…hk(t) in Kv and λ1(t),…λk(t) as the control functions, and we will use Aconv(e,≤t) to denote the points in G reachable from e in t or less units of time by the solutions of (1.7).
The following proposition summarizes the relations between (1.5), (1.6) and (1.7).
Proposition 1. Aconv(e,≤T) is a compact set equal to ˉAh(e,≤T) for each T>0. Therefore, Aconv(e,≤t)=ˉAh(e,≤t)⊆ˉA(e,≤t).
This proposition is a paraphrase of the well known results in geometric control theory: Theorem 11 in [11], p. 88 implies that
and Theorem 11 in [11] on p.119 states that Aconv(e,≤t) is compact.
Equation (1.7) may be regarded as the compactification of (1.6). The following proposition captures its essential properties.
Proposition 2. The optimum time T(g) is equal to the minimum time required for a trajectory of the convexified system to reach the coset gKv from the group identity.
Proof. If g∈ˉA(e,≤T) then there is a sequence of trajectories gn(t) of (1.5) and a sequence of times {tn} such that limgn(tn)=g. There is no loss in generality in assuming that {tn} converges to a time t,t≤T. Let ˜gn(t)=gn(t)hn(t),hn(t)∈Kv denote the corresponding sequence of trajectories in (1.6). Since Kv is compact there is no loss in generality in assuming that hn(tn) converges to an element h in Kv. Then lim˜gn(tn)=gh and gh belongs to ˉAh(e,≤t). But then gh is reachable by the convexified system (1.7) since Aconv(e,≤T)=ˉAh(e,≤T).
Conversely if gh∈Aconv(e,≤T), then the same argument followed in reverse order shows that g∈ˉA(e,≤T). Therefore, T(g)=Tconv, where Tconv is the first time that a point of gKv is reachable from e by a trajectory of the convexified system (1.7).
The paper is organized as follows. We begin with the algebraic preliminaries needed to show that the convex hull of {Adh(A),h∈K} contains an open neighbourhood of the origin in p whenever A is regular and Kv=K (an element X in p is regular if the set {P∈p:[P,X]=0} is an abelian subalgebra in g contained in p). This result implies two important properties of the system. First, it shows that the stationary curve g(t)=g(0) is a solution of the convexified system, which it turn implies that any coset gK can be reached in an arbitrarily short time by a trajectory of the convexified system. Second, it shows that the positive convex cone spanned by {Adh(A),h∈K} is equal to p. Therefore, the convexified system is controllable whenever [p,p]=k. These facts then imply that any two points in G can be connected by a time-optimal trajectory of the convexified system, and they also imply that any point g0 in G can be connected to any coset g1K by a time optimal trajectory of the convexified system. We then follow these findings with the extremal equations obtained by the maximum principle. We show that the time- optimal solutions on G are either stationary, or are of the form
for some elements P∈p and Q∈k.
The non-stationary solutions on G/K are of the form
where π denotes the natural projection π(g)=gK. Since π(g(0)etP),P∈p,||P||=1, coincide with the geodesics on G/K emanating from π(g(0)) (relative to its natural G-invariant metric) it follows that t is the length of the geodesic that connects π(g(0)) to π(g(0)etP). Evidently minimal time corresponds to the length of the shortest geodesic that connects these points.
Remark 1. The papers of Brockett et al ([1] and [2]) claim that the time optimal solutions in (1.1) can be obtained solely from the horizontal system (1.6), but that cannot be true for the following reasons: every trajectory g(t) of the horizontal system dgdt=g(t)Adh(t)(A) is generated by a control U(t)=Adh(t)(A) that satisfies ||U(t)||2=||Adh(t)(A)||2=||A||2. Hence U(t) cannot be equal to zero, and g(t) cannot be stationary.
In the second part of the paper we apply our results to quantum systems known as Icing n-chains (introduced in [2]). We will show that the two-spin chains conform to the above theory and that their time-optimal solutions are given by equations (1.8). The three-spin systems, however, do not fit the above formalism due to the fact that the Lie algebra generated by the controlling vector fields does not meet Cartan's conditions (1.4). We provide specific details suggesting why the solutions fall outside the above theory. We end the paper by showing that the symmetric three-spin chain studied by ([3], [4]) is solvable in terms of elliptic functions. The solution of the symmetric three-spin system is both new and instructive, in the sense that it foreshadows the challenges in the more general cases.
2.
Convexified horizontal systems
2.1. Algebraic background
We will continue with the symmetric pairs (G,K), with G semisimple and K a compact subgroup of G subject to Cartan's conditions (1.4). We recall that the Killing form is positive on p in the non-compact cases, and is negative on p in the compact cases. In either case g admits a fundamental decomposition
where each gi is a simple ideal in g and [gi,gj]=0,i≠j ([11], p.123). It then follows that p⊕[p,p]=g, a fact that is important for controllability, as we shall see later on. As before, ⟨,⟩ will denote a suitable scalar multiple of the Killing form.
We recall that an element X in p is regular if the set h={P∈p:[P,X]=0} is an abelian subalgebra in g contained in p. It follows that h is a maximal abelian algebra that contains X. It is easy to verify that the projection of a regular element on each factor pi is non-zero. The following proposition summarizes the essential relations between regular elements and maximal abelian sub-algebras in p.
Proposition 3. i. Every maximal abelian algebra in p contains a regular element.
ii.. Any two maximal abelian algebras h and h∗ in p are K conjugate, i.e., Adk(h)=h∗ for some k∈K.
iii. p is the union of maximal abelian algebras in p.
The above results, as well as the related theory of Weyl groups and Weyl chambers are well known in the theory of symmetric Riemannian spaces ([5], [6]), but their presentation is often directed to a narrow group of specialists and, as such, is not readily accessible to a wider mathematical community. For that reason, we will present all these theoretical ingredients in a self contained manner, and in the process we will show their relevance for the time-optimal problems defined above.
If h is a maximal abelian algebra in p then F={adX:X∈h} is a collection of commuting linear transformations in g because [adX,adY]=ad[X,Y]=0 for any X and Y in h. In the non-compact case, g is a Euclidean space relative to the scalar product ⟨X,Y⟩σ=−Kl(σ∗X,Y) induced by the automorphism σ. Relative to this scalar product each adH,H∈p is a symmetric linear transformation in gl(g). Then, it is well known that F can be simultaneously diagonalized over g. That is, there exist mutually orthogonal vector spaces g0, gα, with α in some finite set Δ such that:
1. g0=∩H∈hker(adH).
2. g=g0⊕∑α∈Δgα,
3. adH=α(H)I on gα for each H∈h, and α(H)≠0 for some H∈h.
Additionally,
which implies that Δ is symmetric, that is −α∈Δ for each α∈Δ. It is not hard to show that each α∈Δ is a linear function on h, i.e., Δ is a subset of h∗. In the literature on symmetric spaces gα are called root spaces, and elements α∈Δ are called roots ([5]).
In the compact case, the Killing form is negative on g. Therefore g is a Euclidean vector space relative to the scalar product ⟨,⟩=−Kl. Since Kl(X,[Y,Z])=Kl([X,Y],Z), ⟨ad(H)X,Y⟩=−⟨X,ad(H)Y⟩. Hence each ad(H) is a skew-symmetric linear operator on g. It follows that F={adH:H∈h} is a family of commuting skew-symmetric operators on g for each maximal abelian algebra h; as such, F can be simultaneously diagonalized, but this time over the complexified algebra gc.
The complexified Lie algebra gc consists of elements Z=X+iY,X,Y∈g with the obvious Lie algebra structure inherited from g. Then gc=pc⊕kc with pc=p+ip and kc=k+ik. It is evident that pc and kc satisfy Cartan's conditions
whenever p and k satisfy conditions (1.4).
In order to make advantage of the corresponding eigenspace decomposition we will regard gc as a Hermitian vector space with the Hermitian product
We recall that Hermitian means that ⟨⟨,⟩⟩ is bilinear and satisfies
for any u and v in gc. One can easily show that for each H∈h
therefore each adH is a skew-Hermitian transformation on gc.
It follows that F={adH,H∈h} becomes a family of commuting skew-Hermitian operators on gc, and consequently can be simultaneously diagonalized. If λ is an eigenvalue of a skew-symmetric transformation T, then λ is imaginary, because Tx=λx means that
Hence λ=−ˉλ. We will write λ=iα. So, if Xα is the eigenvector corresponding to iα≠0 then ad(H)(Xα)=iα(H)Xα, H∈h. It follows that α∈h∗ because
hence α(λH1+μH2)=λα(H1)+μα(H2). Then gcα will denote the eigenspace corresponding to iα for each non-zero eigenvalue iα, that is,
Since
−iα is a non-zero eigenvalue for each eigenvalue α. We will let iΔ denote the set of non-zero eigenvalues of {ad(H),H∈h}. As in non-compact case, Δ is a symmetric and a finite set in h∗. It then follows that the eigenspaces gcα corresponding to different eigenvalues are orthogonal with respect to ⟨⟨,⟩⟩ and gc=gc0+∑α∈Δgcα, where gc0 is given by ∩H∈hker(adH) and where the sum is direct.
Every Z∈gc can be written as Z=Z0+∑α∈ΔZα in which case
Then Z∈g if and only if Zα+ˉZα=0 and ˉZ0=Z0. If H is such that α(H)≠0 for all α, then adH(Z)=0 if and only if Zα=0 for all α.
Suppose now that Z∈g∩gc0 that is, suppose that adH(Z)=0 for all H∈h. Then, Z=X+Y for some X∈p, and Y∈k. Our assumption that adH(X+Y)=0 yields [H,X]=0 and [H,Y]=0. Hence X∈h and Y∈k belongs to the Lie algebra m in k consisting of all elements Y such that [H,Y]=0 for all H∈h.
Proposition 4. For each α∈Δ there exist non-zero elements Xα∈p and Yα∈k such that
and
In either case [Xα,Yα]∈h.
Proof. Let us begin with the compact case with Zα in gcα a non-zero element such that adH(Zα)=iα(H)Zα for some element H∈h such that α(H)≠0. If Zα=Uα+iVα with Uα∈g and Vα∈g, then
These relations imply that neither Uα=0 nor Vα=0. Let now
with Upα,Vpα in p and Ukα,Vkα in k. It follows that
Cartan relations (1.4) imply
which, in turn, imply that both Upα and Vkα are non-zero, and also imply that Ukα and Vpα are non-zero. Then Xα=Upα and Yα=Vkα satisfy
In the non-compact case, Zα=Xα+Yα, Xα∈p and Yα∈k. Then adH(Zα)=α(H)Zα, together with the Cartan conditions yield
In either case,
Hence [Xα,Yα]∈h.
There are many properties that both the compact and the non-compact spaces symmetric spaces share. In particular in both cases each root α defines a hyperplane {X∈h:α(X)=0}. The set ∪α∈Δ{X∈h:α(X)=0} is closed and nowhere dense in h. Therefore its complement R(h), given by R(h)=∩α∈Δ{X∈h:α(X)≠0}, is open and dense in h. It is a union of finitely many connected components called Weyl chambers. Each Weyl chamber is defined as an equivalence class under the equivalence relation in R(h) defined by X∼Y if and only if α(X)α(Y)>0 for all roots α∈Δ. It is evident that each Weyl chamber is an open and convex subset in h.
Proposition 5. An element X∈p is regular in a maximal abelian algebra h in p if and only if X∈R(h). That is, X is regular if and only if α(X)≠0 for every root α∈Δ.
Proof. The proof is almost identical in both the compact and the non-compact case. Suppose that X is regular in h and suppose that α(X)=0 for some α∈Δ. Let Xα∈p and Yα∈k be as in Proposition 4, that is
in the compact case, and
in the non-compact case. If α(X)=0, then adX(Xα)=0 and therefore Xα∈h. Hence 0=adH(Xα)=±α(H)Yα which yields Yα=0 since α≠0, which contradicts our assumption that neither Xα nor Yα are non-zero.
Conversely, assume that X is an element in h such that α(X)≠0 for any α∈Δ. Let Y∈p be such that [X,Y]=0. Then 0=adX(Y)=∑α∈Δα(X)Yα, where Y=Y0+∑Yα. This relation implies that Yα=0 for any α≠0. Hence Y=Y0, Y0∈g0∩h. This shows that Y∈h, therefore X is regular.
Corollary 1. The set of regular elements in p is open and dense in p.
The following proposition is of central importance.
Proposition 6. Let X and X∗ be regular elements in the maximal abelian algebras h and h∗ in p. Consider now functions F(h)=Kl(X∗,Adh(X)),h∈K, in the non-compact case and F(h)=−Kl(X∗,Adh(X) in the compact case. If k∈K yields a critical point for the function F(h), then Adk(X)∈h∗ and Adk(h)=h∗. When k yields the maximum for F then Adk(X)∈C(X∗), and Adk(C(X))=C(X∗), where C(X) and C(X∗) denote the Weyl chambers that contain X and X∗.
Proof. Let ⟨X,Y⟩=±Kl(X,Y). If U∈k then
When k is a critical point of F, then ddtF(ketU)|t=0=0, and when k is a maximal point then in addition d2dt2F(ketU)|t=0≤0. In the first case,
for any U∈k. It follows that [X∗,Adk(X)]=0 because U is arbitrary and Adk is an isomorphism on k. Hence Adk(X) belongs to the Cartan algebra that contains X∗, which is equal to h∗ since X∗ is regular in h∗. If Y∈h then [Adk(Y),Adk(X)]=Adk([X,Y])=0, therefore Adk(Y)∈h∗. Hence, Adk(h)=h∗.
Assume now that F(k) is a maximal point for F. It follows that
If we let Adk(X)=X′ and Adk(U)=U′ then the above can be written as
If T=adX∗adX′ then T is negative semi-definite on k.
In the compact case T is a composition of two commuting skew-symmetric operators, hence is symmetric (relative to ⟨,⟩ which is positive on k). In the non-compact case, T is a composition of two commuting symmetric operators, hence is symmetric again, but this time relative to a negative definite metric- since the Killing form is negative on k. Hence T is negative semi-definite on k in the compact case, and positive semi-definite in the non-compact case. Therefore, the non-zero eigenvalues of T are positive in the non-compact case and negative in the compact case.
We will show now that α(X∗)α(X′)>0 for each α∈Δ(h∗). In the compact case there are elements Xα∈p and Yα∈k such that
for each α∈Δ(h∗). Then,
Since X∗ and X′ are regular α(X∗) and α(X′) are non-zero. We then have
It follows that Yα is an eigenvector for T with −α(X∗)α(X′) the corresponding eigenvalue. Since the non-zero eigenvalues of T are negative we get α(X∗)α(X′)>0.
In the non-compact case
for each α∈Δ(h∗), therefore
Thus α(X)α(X′ are the eigenvalues of T. Since T is positive semi-definite α(X)α(X′>0 (neither α(X) nor α(X′) can be zero because X and X′ are regular.) Therefore X′∈C(X∗) in both cases.
We now return to Proposition 3 with the proofs.
Proof. The first statement is obvious in view of Proposition 5, If h is any Cartan algebra then take any X∈h such that α(X)≠0 for any α∈Δ.
Second statement follows from Proposition 6. To prove the last statement let P be an arbitrary element in p and let X0 be a regular element in h. There is an element k∈K that attains the maximum for the function F(k)=⟨P,AdkX0⟩. Then dF(k)=0 yields [P,AdkX0]=0. Therefore P∈Adk(h). This shows that every element P∈p is contained in some maximal abelian algebra in p.
We are now ready to introduce another important theoretic ingredient, the Weyl group. If h be any maximal abelian subalgebra in p let
These groups are respectively called the normalizer of h and the centralizer of h. Each group is a closed subgroup of K, and consequently, each group a Lie subgroup of K. Moreover, C(h) is normal in N(h). Any element U in the Lie algebra n(h) of N(h) satisfies adU(X)∈h for any X∈h. But then ⟨[U,X],h⟩=⟨U,[X,h]⟩=0. Hence [U,X]=0. Therefore, U belongs to the Lie algebra of the centralizer C(h). It follows that N(h) and C(h) have the same Lie algebra, which then implies that N(h) is an open cover of C(h), that is, the quotient group N(h)/C(h) is finite. This quotient group is called the Weyl group.
We will follow S. Helgason and represent the elements of the Weyl group by the mappings Adk|h with k∈N(h) ([6]) in which case {Adk|h:k∈N(h)} is denoted by W(G,K). An interested reader can easily show that if Wh(G,K) is the Weyl group associated with a Cartan algebra h and Wh∗(G,K) is the Weyl group associated with another Cartan algebra h∗ then
In that sense the Weyl group is determined by the pair (G,K) rather than a particular choice of a Cartan algebra.
Proposition 7. If Adk(C(h))=C(h) for some k∈K, and some Weyl chamber C(h) in h, then Adk|h=Id.
The following lemma is useful for the proof of the proposition.
Lemma 1. Let H be a regular element in a maximal abelian algebra h in p. Then
Proof. If Z=P+Q,P∈p,Q∈k, then [Z,H]=0 if and only if [P,H]=0 and [Q,H]=0. Therefore, P∈h because H is regular. It follows that {Z∈g:[Z,H]=0}=h+{Q∈k:[Q,H]=0]}.
Now let V be an arbitrary point in h. Then for any Q∈k such that [Q,H]=0, [[Q,V],H]=−[[H,Q],V]−[[V,H],Q]=0. Therefore [Q,V]∈h since [Q,V]∈p and H is regular. But then⟨[Q,V],h⟩=⟨Q,[V,h]⟩=0 and hence [Q,V]=0.
We now return to the proof of Proposition 7.
Proof. Since C(h) is open in h and the set of regular elements is dense, there is a regular element X in C(h). Then Adk(X)=X∗ belongs to C(h). If Z∈h then [X∗,AdkZ]=[AdkX,AdkZ]=Adk[X,Z]=0 and therefore AdkZ∈h. This shows that k∈N(h) that is, Adk|h∈W(G,K). Since W(G,K) is finite, the orbit {Adnk(X∗),k=0,1,…} is finite, and therefore there is a positive integer N such that AdNk(X∗)=X∗. If N is the smallest such integer then let H=1N−1(X∗+AdkX∗+⋯+AdN−1kX∗). It follows that Adk(H)=H. Since Adk(C(h))=C(h), AdnkX∗∈C(h), and since C(h) is convex, H∈C(h).
The above implies that k belongs to the centralizer of H. The Lie algebra of the centralizer in K is given by {U∈k:[U,H]=0}. But this Lie algebra coincides with {U∈k:[U,V]=0,V∈h} as shown in the Lemma above. Since Adk(H)=H, ketHk−1=etH. Therefore k belongs to the centralizer of the one parameter group {etH,t∈R}. Let T be the closure of {etH,t∈R}. Then, T is a connected abelian subgroup in G, i.e., T is a torus. Its centralizer in G is the maximal torus that contains T. Every maximal torus is connected, and consequently is generated by the exponentials in its Lie algebra. The Lie algebra of this centralizer is given by L={Z∈g:[Z,H]=0}, which is equal to h+{U∈k:[U,h]=0} by the lemma above.
We now have AdetUX=X for each U∈L and each X∈h. Since k=∏mi=1eUi for some choice of U1,…,Um in L, Adk|h=Id, and therefore X∗=X.
Propositions 6 and 7 can be summarized as follows:
Proposition 8. Let C(h) be a Weyl chamber in h. Then {Adk(C(h)):k∈W(G,K)} acts simply and transitively on the set of Weyl chambers in h. Here acting simply means that if some k∈W(G,K) takes a Weyl chamber C(h) onto itself, then k=e.
Corollary 2. If X0 is any regular element in p and if C(h) is a Weyl chamber associated with any maximal abelian subalgebra in p then there is a unique k∈K such that Adk(X0)∈C(h).
The Weyl group could be also defined in terms of the orthogonal reflections in h around the hyperplane {X∈p:α(X)=0},α∈Δ. The reader can readily verify that this reflection is given by sα(H)=H−2α(H)α(A)A where A∈h is the unit vector such that α(H)=⟨A,H⟩,H∈h. The following proposition is basic.
Proposition 9. There exists k∈N(h) such that Adk|h=sα.
Proof. Let Xα and Yα be non-zero vectors in g as in Proposition 4 such that
in the compact case, and
in the non-compact case. We have already shown [Xα,Yα]∈h. Since
Xα could be rescaled so that ⟨H,[Yα,Xα]⟩=α(H).
Let Aα∈h be such that α(H)=⟨Aα,H⟩,H∈h. Then [Yα,Xα]=Aα. We now have
Therefore
Hence,
where θ=√α(Aα). When tθ=π then AdetY(Aα)=−Aα.
Moreover, if H∈h is perpendicular to Aα then α(H)=0 and therefore, adY(H)=α(H)X=0. Hence AdetY(H)=H, and AdetY|h=sα.
Proposition 10. The Weyl group W(G,K) is equal to the group generated by the reflections Adk|h=sα,α∈Δ.
Proof. Let Ws be the group generated by sα, α∈Δ. Then Ws is a subgroup of W(G,K). We will show that for any Adk in W(G,K) there exists an element Adh in Ws such that Adk(X)=Adh(X) for any X∈h. It suffices to show the equality on regular elements in h.
If X is a regular element in h, then let C∗ be the Weyl chamber in h∗=Adk(h) that contains X∗=Adk(X). Let Adh∗ be the element of Ws that minimizes ||X∗−Adh(X)|| over Ws. Then the line segment from Adh∗(X) to X∗ cannot cross any hypersurface α=0. Hence α(X∗) and α(Y) have the same signature at any point Y on the line segment from X∗ to Adh∗(X). It then follows that Adh∗(X) and X∗ belong to the same Weyl chamber. Then Adk(X)=Adh∗(X) by the previous proposition.
2.2. Weyl group and controllability
Let h be any maximal abelian algebra in g contained in p, and let α1,…,αn be any basis in Δ. Then let A1,…,An be the corresponding vectors in h defined by ⟨X,Ai⟩=αi(X),X∈h. If X is a an element in h that is orthogonal to each Ai, then αi(X)=0 for each αi∈Δ. That means that ad(X)=0. Therefore X=0, since the centre in g consists of 0 alone. Hence A1,…,An form a basis in h. With these observations at our disposal we now return to the convexified horizontal control system
with X0∈p regular, controlled by the coefficients λ1,…,λk and the curves h1(t),i=1,…,k in K. There will be no loss in generality if the curves hi(t) are restricted to the solutions of dhdt=U(t)h(t) with U(t) transversal to the Lie algebra {V∈k:[V,X0]=0}.
Proposition 11. The convex hull of {Adh(X0),h∈N(h)} contains an open neighbourhood of the origin in h.
Proof. Let O(X0)={AdhiX0,i=0,1,…,m} denote the orbit of W((G,K) through X0. Assume that Adh0(X0)=X0 and that Adhi(X0)=sαi,i=1,…,n. We know that O acts simply and transitively on the Weyl chambers in h. Let
It follows that X is in the convex hull of the orbit {AdhX0,h∈N(h)}. Since AdhjAdhiX0=AdhjhiXo=AdhkX0, where k∈K, each Adhj permutes the elements in O(X0), which in turn implies that AdhjX=X for each j=1,…,m. Therefore, X=0. Let now
where ε0,ε1,…,εn are arbitrary numbers such that ∑ni=0εi=0. Let
Then, ∑mi=0λi(t)=1, and for sufficiently small t, λi>0,i=0,…,m. It follows that σ(t) is contained in the convex hull of the Weyl orbit through X0 for small t and satisfies σ(0)=0. Then dσdt(0)=−∑ni=1εiαi(X0)α(Ai)Ai and therefore the mapping F(λ0(t),…,λm(t))=∑mi=1λi(t)AdhiX0 is open at λ1=λ2=⋯=λm=1m.
Corollary 3. The convexified horizontal system (2.9) admits a stationary solution g(t)=g0.
Proposition 12. The convexified horizontal system is controllable.
Proof. We will first show that the Lie algebra L generated by {AdhX0:h∈K} is equal to g. Let V denote the vector space spanned by {Adh(X0),h∈K} and let L be the Lie algebra generated by V. If U1,…,Uj are arbitrary elements in k then Adh1(t1)⋯hj(tj)(X0) is in V where hi(ti)=etiUi. Since V is a vector space, ∂∂tiAdh1(t1)⋯hj(tj)(X0) is in V. Therefore,
Further differentiations yield ad(U1∘ad(U2)∘⋯ad(Uj)(X0)∈V. This can be also written as adjk(X0)⊂V.
Let now ˆV be the vector space spanned by ⋃∞j=0adjk(X0). It follows that ˆV⊆V. Let now ˆV⊥ denote its orthogonal complement in p. Both ˆV and ˆV⊥ are ad(k) invariant. If Z∈ˆV, W∈ˆV⊥ and Y∈k, then
Since Y is arbitrary [Z,W]=0. Therefore [ˆV,ˆV⊥]=0, and hence ˆV+[ˆV,ˆV] is an ideal in g. Let us now use the fundamental decomposition
defined in (2.1). It follows that the projection of ˆV+[ˆV,ˆV] on each simple factor is equal to gi (since X0∈ˆV, and the projection of X0 on each factor gi is non-zero). So ˆV+[ˆV,ˆV]=g. But then ˆV+[ˆV,ˆV]⊆L yields L=g. Since ˆV+[ˆV,ˆV]⊆V+[V,V]=g, V=ˆV and V=p.
To prove controllability it would suffice to show that the affine cone {∑ki=1λiAdhi(X0),λi≥0,hi∈K,i=1,…,k} is equal to V which by the above is equal to p. Let P be an arbitrary point in p. Then, P belongs to some maximal abelian algebra h. By the preceding proposition the convex hull of {AdhX0:h∈K} covers a neigborhood of the origin in h. If ε>0 is any scalar such that εP is in this neighborhood, then −εP is also in this neghborhood, and hence is reachable by the convex hull of {AdhX0:h∈K}. But then −P=1ε(−εP) is in the above affine cone.
The preceding results show that the convex cone spanned by Adh(X0) is a neighbourhood of the origin in p. It then follows that the positive cone ∑λiAdhi(X0),λi≥0, is equal to p. This implies that any time optimal trajectory of the compactified horizontal system is generated by a control on the boundary of the convex cone defined by {Adh(X0),h∈K}. For if g(t) is a trajectory generated by a control U(t)=∑ki=1λi(t)Adhi(t)(X0) in the interior of the convex set spanned by Adh(X0), then ρU(t) is in the same interior for some ρ>1. But then g(t) reparametrized by s=ρt steers e to g(T) in s=Tρ units of time violating the time optimality of g(t).
The time-optimal problem for the convexified system is related to the sub-Riemannian problem of finding the shortest length of a horizontal curve that connects two given points in G. In fact any horizontal curve g(t) is a solution of dgdt=g(t)U(t) with U(t)=Adh(t)X0 and inherits the notion of length from G given by ∫T0√⟨U(t),U(t)⟩dt, where ⟨,⟩ denotes a suitable scalar multiple of the Killing form. Since U(t)=Adh(t)(X0) satisfies ⟨U(t),U(t)⟩=||X0||2=1 when X0 is a unit vector, the length of g(t) in the interval [0,T] is equal to the time it takes to reach g(T) from g(0). Therefore, the shortest time to reach a point g1 from g0 is equal to the minimum length of the horizontal curve to reach g1 from g0. As we showed above, the horizontal system is controllable, therefore any two points in G can be connected by a horizontal curve. But then any two points in G can be connected by a horizontal curve of minimal length by a suitable compactness argument.
3.
Necessary conditions of optimality
3.1. Generalities-left-invariant Hamiltonians
We will now use the maximum principle to obtain the necessary conditions of optimality on the cotangent bundle T∗G. We recall that each optimal solution is the projection of an integral curve in T∗G of the Hamiltonian vector generated by a suitable Hamiltonian obtained from the maximum principle. To preserve the left-invariant symmetries, we will regard the cotangent bundle T∗G as the product G×g∗ via the left-translations. In this formalism tangent vectors v∈TgG are identified with pairs (g,X)∈G×g via the relation v=Lg∗X, where Lg∗ denotes the tangent map associated with the left translation Lg(h)=gh. Similarly, points ξ∈T∗gG are identified with pairs (g,ℓ)∈G×g∗ via ξ=ℓ⋅Lg−1∗. If the optimal problem was defined over a right-invariant system, then the tangent bundle would be trivialized by the right translations, in which case the ensuing formalism would remain the same as in the left-invariant setting.
Then, T(T∗G), the tangent bundle of the cotangent bundle T∗G, is naturally identified with (G×g∗)×(g×g∗), with the understanding that an element ((g,ℓ),(A,a))∈(G×g∗)×(g×g∗) stands for the tangent vector (A,a) at the base point (g,ℓ).
We will make use of the fact that G×g∗ is a Lie group in its own right since g∗, as a vector space, is an abelian Lie group. Then left-invariant vector fields in G×g∗ are the left-translations of the pairs (A,a) by the elements (g,ℓ) in G×g∗. The corresponding one-parameter groups of diffeomorphisms are given by (gexp(tA),ℓ+ta),t∈R. In terms of these vector fields the canonical symplectic form on T∗G is given by
for any V1=(gA1,a1) and V2=(gA2,a2). ([7]).
The above differential form is invariant under the left-translations in G×g∗, and is particularly revealing for Hamiltonian vector fields generated by the left-invariant functions on G×g∗. A function H on G×g∗ is said to be left-invariant if H(gh,ℓ)=H(g,ℓ) for all g,h∈G and all ℓ∈g∗. It follows that the left-invariant functions are in exact correspondence with functions on g∗. Each left-invariant vector field X(g)=(Lg)∗A, A∈g, lifts to a linear function ℓ→ℓ(A) on g∗ because
Any function H on g∗ generates a Hamiltonian vector field →H on G×g∗ whose integral curves are the solutions of
For when H is a function on g∗, then its differential at a point ℓ is a linear function on g∗, hence is an element of g because g∗ is a finite dimensional vector space. If →H(g,ℓ)=(A(g,ℓ),a(g,ℓ)) for some vectors A(g,ℓ)∈g and a(g,ℓ)∈g∗, then
must hold for any tangent vector (B,b) at (g,ℓ). This implies that A(g,ℓ)=dHℓ, and a=−ad∗dHℓ(ℓ), where (ad∗A)(ℓ)(B)=ℓ[A,B] for all B∈g. This argument validates equations (3.2).
The dual space g∗ is a Poisson space with its Poisson structure {f,h}(ℓ)=ℓ([dh,df]) inherited from the symplectic form (3.1). Recall that a manifold M together with a bilinear, skew-symmetric form
that satisfies
for all functions f,g,h on M, is called a Poisson manifold.
Every symplectic manifold is a Poisson manifold with the Poisson bracket defined by {f,g}(p)=ωp(→f(p),→g(p)),p∈M. However, a Poisson manifold need not be symplectic, because it may happen that the Poisson bracket is degenerate at some points of M. Nevertheless, each function f on M induces a Poisson vector field →f through the formula →f(g)={f,g}. It is known that every Poisson manifold is foliated by the orbits of its family of Poisson vector fields, and that each orbit is a symplectic submanifold of M with its symplectic form ωp(→f,→h)={f,h}(p) (this foliation is known as a the symplectic foliation of M ([7])).
It follows that each function H on g∗ defines a Poisson vector field →H on g∗ through the formula →H(f)(ℓ)={H,f}(ℓ)=ℓ([dH,df]). The integral curves of →H are the solutions of
That is, each function H on g∗ may be considered both as a Hamiltonian on T∗G, as well as a function on the Poisson space g∗; the Poisson equations of the associated Poisson field are the projections of the Hamiltonian equations (3.2) on g∗.
Solutions of equation (3.3) are intimately linked with the coadjoint orbits of G. We recall that the coadjoint orbit of G through a point ℓ∈g∗ is given by Ad∗g(ℓ)={ℓ∘Adg−1,g∈G}.
The following proposition is a paraphrase of A.A. Kirillov's fundamental contributions to the Poisson structure of g∗ ([12]).
Proposition 13. Let F denote the family of Poisson vector fields on g∗ and let M=OF(ℓ0) denote the orbit of F through a point ℓ0∈g∗. Then M is equal to the connected component of the coadjoint orbit of G that contains ℓ0. Consequently, each coadjoint orbit is a symplectic submanifold of g∗.
The fact that the Poisson equations evolve on coadjoint orbits implies useful reductions in the theory of Hamiltonian systems with symmetries. Our main results will make use of this fact.
On semi-simple Lie groups the Killing form, or any scalar multiple of it ⟨,⟩ is non-degenerate, and can be used to identify linear functions ℓ on g with points L∈g via the formula ⟨L,X⟩=ℓ(X), X∈g. Then, Poisson equation (3.3) can be expressed dually on g as
The argument is simple:
Since X is arbitrary, equation (3.4) follows.
With the aid of Cartan's conditions (1.4) equation (3.4) can be written as
where dHp, dHk, Lp and Lk denote the projections of dH and L on the factors p and k.
Under the above identification coadjoint orbits are identified with the adjoint orbits O(L0)={gL0g−1:g∈G}, and the Poisson vector fields →fX(ℓ)=−ad∗X(ℓ) are identified with vector fields →X(L)=[X,L]. Each vector field [X,L] is tangent to O(L0) at L, and ωL([X,L],[Y,L])=⟨L,[Y,X]⟩, X,Y in g is the symplectic form on each orbit O(L0).
3.2. Time-optimal extremals
Let us now turn to the extremal equations associated with the time-optimal problem for the convexified horizontal system (1.7). The Hamiltonian lift is given by
Suppose now that g(t) is a time-optimal curve generated by the controls λλi(t),hi(t),i=1,…,k. According to the maximum principle g(t) is the projection of an extremal curve (λλ0,ℓ(t))∈R×g∗, ℓ(t)≠0 when λλ0=0, that satisfies H0(ℓ(t))=0 and is further subject to:
for any μi(t)≥0, ∑ki=1μi(t)=1, and any hi(t)∈K.
The extremal curve ℓ(t) is called abnormal when λλ0=0. In such a case, H(ℓ(t))=∑mi=1λλi(t)ℓ(Adhi(t)X0)=0. In the remaining case, λλ0=1, H(ℓ(t))=1, and ℓ(t) is called a normal extremal. In either case,
or, dually,
When the terminal point is replaced by a terminal manifold S then a time-optimal trajectory must additionally satisfy the transversality condition ℓ(T)(V)=0 for all tangent vectors V in Tg(T)S. In particular, when S=gK, and when the tangent space TgK is represented by TgK=g×k, then the transversality condition becomes ℓ(T)V=0 for all V∈k.
We will find it more convenient to work in g rather than g∗. So, if L in g corresponds to ℓ in g∗, then L=Lp+Lk where Lp∈p and Lk∈k.
Proposition 14. Suppose that a time optimal control X(t)=∑ki=1λi(t)Adhi(t)X0 is the projection of an extremal curve L(t). If L(t) is abnormal, then Lp(t)=0 and Lk(t) is constant. In particular, the stationary solution X(t)=0 is the projection of an abnormal extremal curve.
If L(t) is a normal extremal curve then X(t)=Adh(t)X0 for some curve h(t) in K.
Proof. If L(t) is abnormal then
for arbitrary controls ∑ki=1μi(t)=1, and h1(t),…,hk(t) in K. This can hold only when Lp(t)=0 (due to Proposition 11). But then equations (3.7) become
Evidently these equations hold when X(t)=0. So the stationary solution is the projection of an abnormal extremal.
In the normal case
So Lp(t)≠0. Let h(t)∈{h1(t),…,hk(t)} corresponds to the maximal value of ⟨Lp(t),Adhi(t)(X0)⟩, i=1,…,k. Then,
can hold only if X(t)=Adh(t)(X0).
It follows that the normal extremals are the solutions of the following system of equations:
subject to the inequality
3.3. Time-optimal solutions
Let us first note that there is no loss in generality in assuming that ||Lp(t)||=1 for the following reasons: since h(t) is a critical point of H, [Adh(t)(X0),Lp(t)]=0. Then,
Therefore ||Lp(t)|| is constant. Hence the extremal equations are unaltered if Lp is replaced by 1||Lp||Lp and Lk is replaced by 1||Lp||Lk.
Proposition 15. Suppose that (Lp(t),Lk(t)) is a normal extremal curve generated by h(t) with ||Lp(t)||=1. Then, Lp(t)=Adh(t)X0 and Lk(t) is constant.
Proof. According to the Cauchy-Schwarz inequality, ⟨X,Y⟩≤1 for any unit vectors X and Y in a finite dimensional Euclidean vector space, with ⟨X,Y⟩=1 only when X=Y. In our case, ||AdhX0||=1 and ||Lp||=1, hence ⟨Lp,Adhh(X0)⟩=1 occurs only when Lp=Adh(X0). But then dLkdt=[Adh(t)(X0),Lp(t)]=0, and Lk is constant.
Proposition 16. The normal extremal curves project onto
The solutions that satisfy the transversality condition Lk=0 are given by g(t)=g0etP for some P∈p such that ||P||=1.
Proof. Since Adh(t)X0=Lp(t), Lp(t) is a solution of dLpdt=[Lp(t),Lk]. Since Lk is constant, Lp(t)=AdetLkLp(0). Then ˜g(t)=g(t)etLk satisfies d˜gdt=˜g(t)(Lp(0)+Lk), from which (3.10) easily follows. Since Lk is constant, it is zero whenever it is zero at the terminal point. So the solution satisfies the transversality condition Lk(T)=0 whenever Lk=0 in the above formula.
Remark 2. Formula (3.10) is not new. As far as I know, it appeared first in 1990 in ([13]) and it has also appeared in various contexts in my earlier writings ([11], [7]). But it has never before been obtained directly from the affine system (1.1) with controls in the affine hull ∑ki=1λiAdhiA,hi∈K,∑ki=1λi=1.
Corollary 4. Let π denote the natural projection from G onto G/K. Then π(g0etP) is a geodesic in G/K that connects π(g0) to π(g(t),g(t)=g0etP. Therefore T(g) is equal to the shortest length of a geodesic that connects π(I) to π(g).
3.4. Fundamental example (SU(2),SO(2))
This example is not only typical of the general situation, but is also a natural starting point for problems in quantum control. Recall that SU(2) consists of matrices (ab−ˉbˉa) with a and b complex numbers such that |a|2+|b|2=1. It follows that g∈G whenever g−1=g∗, where g∗ is the matrix transpose of the complex conjugate of g. Hence the Lie algebra su(2) of G consists of matrices 12(ix3x1+ix2−x1+ix2−ix3). We will assume that su(2) is endowed with the trace metric ⟨X,Y⟩=−2Tr(XY), in which case the skew-Hermitian matrices
form an orthonormal basis in su(2). If X=12(izx+iy−x+iy−iz) is represented by the coordinates (xyz)∈R3 then the adjoint representation X→Adg(X) is identified with rotations in R3. If Gx,Gy,GZ denote the rotations around the axes (100),(010),(001), then Ax,Ay,Az are the infinitesimal generators of Gx,Gy,Gz which explains the motivation behind the terminology. Relative to the Lie bracket [A,B]=BA−AB, Ax,Ay,Az conform to the following Lie bracket table:
The automorphism σ(g)=(gT)−1 identifies SO(2) as the group of fixed points by σ, and induces a Cartan decomposition g=p+k with p the linear span of Ay and Az, and k the linear span of Ax. Relative to the above decomposition,
is a prototypical affine system in G.
Since [Az,Ax]]=−Ay, G=A(e,≤T) for some T>0, and since SU(2) is simple, A(e,T)=G for some T>0 ([14]). However, not all points of G can be reached from the identity in short time as noticed in [14]. For instance, points g=(x0+ix1x2+ix3−x2+ix3x0−ix1) in SU(2) with x21+x23>0 cannot be reached from the identity in time less than 2(x21+x23). The argument is simple:
Therefore,
and hence
because (x0−x1)2+(x2+x3)2=1−2(x0x1−x2x3)≥0 implies that 2(x0x1−x2x3)≤1. So if a point g can be reached in time T, then T≥2(x21+x23).
However, not all points of SU(2) can be reached in the shortest time. Below we will show that −I can be reached in any positive time, but is not reachable at T=0. To demonstrate, note that for any X∈su(2), X2=−14||X||2I, and therefore,
In particular when X=Az+uAx,u∈R, then ||X||=√1+u2, and
For any t>0 there exists u∈R such that t√1+u2=2π, and therefore, etX=−I. Therefore, −I can be reached in any positive time t but is not reachable at T=0.
The preceding formula can be used to show that any element of SO(2) lies in the closure of A(e,≤t) for any t>0. To do so, let θ be any number, and then let un=2nθ, Then, e1nX(un)∈A(e,≤T) for any T>0, provided that n is sufficiently large. An easy calculation shows that
Hence g=(cosθsinθ−sinθcosθ) belongs to ˉA(e,≤T). It seems likely that g∈A(e,≤T), but that has not been verified, as far as I know.
Let us now return to the horizontal system given by
It follows that
and therefore
To pass to the convexified horizontal system we need to enlarge the controls to the sphere u21+u22≤1. It then follows that the time-optimal extremals are given by equation (3.10) except for the stationary extremal g(t)=g0.
Let us interpret the above results in slightly different terms with an eye on the connections with quantum control. If X=x1Ax+x2Ay+x3Az and Y=y1Ax+y2Ay+y3Az, then Z=[X,Y]=z1Ax+z2Ay+z3Az is given by the vector product z=y×x, where x=(x1,x2,x3), y=(y1,y2,y3), and z=(z1,z2,z3). Hence [X,Y]=0 if and only if x and y are co-linear. Therefore, maximal abelian algebras in p are one dimensional, and every non-zero element in p is regular. It follows that the Weyl group consists of ±I.
The equation AdhX0=Lp is solvable for each Lp∈p such that ||Lp||=1. Then the line segment that connects −Lp and Lp is in the convex hull defined by AdhX0. This shows that {AdhX0:h∈K} is the unit circle in p and the corresponding convex hull is the unit ball {Lp∈p:||Lp||≤1}. The coset extremals are given by
These extremals reside on a two dimensional sphere S2 because
for any matrix iP=(iaibib−ia) with a and b real. If x=cost√a2+b2, y=a√a2+b2sint√a2+b2, and z=b√a2+b2sint√a2+b2, then x2+y2+z2=1. The decomposition g=eiPR corresponds to the Hopf fibrationS3→S2→S1.
Hopf fibration has remarkable applications in quantum technology due to the fact that a two level quantum system, called qubit, can be modelled by points in SU(2), whereby all possible states of a particle are represented by complex linear combinations α(|0>)+β(|1>0), where |0> and |1> denote the basic levels (states) and where α and β are complex numbers such that |α|2+|β|2=1. In this context, the particle can be either in state |0> with probability |α|2, or in state |1> with probability |β|2. For this to make mathematical sense, the basic states are represented by two orthonormal vectors in some complex Hilbert space. Then, the states α|0>+β|1>0 are identified with matrices (αβ−ˉβˉα) in SU(2).
In this setting, the quotient space G/K is called the Bloch sphere (see for instance [15]). In quantum mechanics points in G/K represent the observable states. It follows that each point g in a given coset is reached time-optimally according to the formula g=eT(Q+P)e−QT,||P||=1 for some T>0, but the coset itself is reached time-optimally in the time equal to the length of a geodesic that connects π(I) to π(g) where π stands for the natural projection from G to G/K.
For instance, if gf=−I, then gfK=K. Therefore, g(t)=I, generated by u(t)=0, is the only trajectory of the convexified horizontal system that reaches the coset K in zero time. Any other optimal trajectory is of the form g(t)=et(Q+P)e−Qt, and such trajectories cannot reach points in zero time.
4.
Notable Riemannian symmetric pairs
4.1. (SL(n),SO(n)) and (SU(n),SO(n))
Each of these pairs of Lie groups is symmetric relative to the automorphism σ(g)=(gT)−1 where gT denotes the matrix transpose. It follows that K=SO(n) is the group of points in G fixed by σ. Then, g is equal to sl(n) when G=SL(n) and is equal to su(n) when G=SU(n). In the first case the Lie algebra is equal to the space of n×n matrices with zero trace, while in the second case the Lie algebra consists of n×n complex skew-symmetric matrices with zero trace. Then, g=p⊕k, where p is equal to the space of symmetric matrices in sl(n) and the space of symmetric matrices with imaginary entries in su(n). These two Lie algebras are dual in the sense that the Cartan decomposition p+k in sl(n) corresponds to the Cartan decomposition k+ip in su(n) (see [6] for further details). In each case, the Killing form is equal to 2nTr(XY). It follows that it is positive on p in sl(n) and negative on p in su(n). Therefore, the pair (SL(n),SO(n)) is non-compact, while the pair (SU(n),SO(n)) is compact.
In sl(n), each matrix X in p can be diagonalized by some Adh,h∈K, and the set of all diagonal matrices D in p forms an n−1 dimensional abelian algebra, which is also maximal since [D,X]=0 can only hold only if X is diagonal. It follows that n−1 is the rank of the underlying symmetric space. If X is a diagonal matrix with its diagonal entries x1,…,xn then ad(X)Y=∑ni,j(xi−xj)Yijei⊗ej for any matrix Y=∑ni,jYijei⊗ej. Hence
that is, α(X)=xi−xj are the non-zero roots in D. This implies that X is regular if and only if the diagonal entries of X are all distinct.
Weyl chambers in D are in one to one correspondence with the elements of the permutation group on n letters. For if X=diag(x1,…,xn) and Y=diag(y1,…,yn) are any regular elements in D then there exist unique permutations α and β on n letters such that xα(1)>xα(2)>⋯>xα(n) and yβ(1)>yβ(2)>⋯>yβ(n). If X and Y are in the same Weyl chamber, then (xi−xj)(yi−yj)>0 for all i and j. It then follows by an easy argument that α=β. The reasoning on su(n) with diagonal matrices having imaginary entries is similar and will be omitted.
It follows that the Weyl orbit Adh(X0) in D consists of the diagonal matrices with diagonal entries a permutation of the diagonal entries of X0. The convex hull spanned by these matrices coincides with the controls of the convexified system that reside in D.
4.2. Self-adjoint subgroups of SL(n)
A subgroup G of SL(n) is called self-adjoint if the matrix transpose gT is in G for any g in G. Any self-adjoint group G admits an involutive automorphism σ(g)=gT−1,g∈G, with K=SO(n)∩G equal to the group of its fixed points.
It follows that the Lie algebra g of G admits a Cartan decomposition g=k+p where k=g∩so(n) and p=Sym(n)∩g with Sym(n) the space of symmetric matrices in sl(n). Since ⟨X,Y⟩=2nTr(XY) inherited from sl(n) is positive on p the pair (G,K) is a symmetric Riemannian pair of non-compact type.
One can show that SO(p,q),p+q=n, the group that preserves the scalar product (x,y)p,q=∑pi=1xiyi−∑ni=p+1xiyi is self-adjoint, as well as Sp(n), the group that leaves the symplectic form ∑ni=1xiyn+i−yixi+n,x,y∈Rn invariant.
When G=SO(p,q) the Lie algebra g consists of block matrices M=(ABBTC) with A and C skew-symmetric p×p and q×q matrices and B an arbitrary p×q matrix.Then M∈p if A=C=0, and M∈k if B=0. The quotient space SO(p,q)/K can be identified with an open subset of Grassmannians consisting of all q-dimensional subspaces in R(p+q) on which (x,x)p,q>0, while the quotient spaces Sp(n)/K can be identified with the generalized Poincaré plane Pn={X+iY,XT=X,YT=Y,Y>0} ([7], pages 126,127).
4.3. Rank one symmetric spaces
In rank-one symmetric spaces the Weyl group is minimal (it consists of two elements ±I)), which accounts for an easier visualization of the general theory. We will use (SO(1,n),K) together with its compact companion (SO(n+1),K), K={1}×SO(n) to illustrate the relevance of the rank for the general theory. Both of the above cases can be treated simultaneously in terms of the parameter ε=±1 and the scalar product (x,y)ε=x0y0+ε∑ni=1xiyi. In that spirit, SOε(n+1) will denote SO(1,n) when ε=−1, and SO(n+1) when ε=1.
Each group SOε(n+1) acts on points of Rn+1 by the matrix multiplication and this action can be used to identify the quotient space SOε(n+1)/K with the orbit O(e0)={ge0:g∈SOε(n+1)} where e0=(1,0,…,0)T. Since SOε(n+1) preserves (,)ε, O(e0) is the Euclidean sphere Sn when ε=1 and the hyperboloid Hn when ε=−1.
Let now gε=soε(n+1) denote the Lie algebra of SOε(n+1) equipped with its natural scalar product ⟨X,Y⟩=12Tr(XY), and let k denote the Lie algebra of K. It is easy to check that the orthogonal complement pε of k is given by ={e0∧εu,u∈Rn+1,(u,e0)ε=0}, and that k itself is given by k={(u∧εv):(u,e0)ε=(v,e0)ε=0}, where
with u⊗εv the rank-one matrix defined by (u⊗εv)x=(v,x)εu,x∈Rn+1.
It follows that Cartan's relations
hold, as can be readily verified through the following general formula
Since ⟨e0∧εu,e0∧εv⟩=−ε∑ni=1uivi, the bilinear form ⟨,⟩ is positive on pε when ε=−1 and is negative when ε=1. It follows that the pair (Gε,K) is a compact type when ε=1 and a non-compact type when ε=−1.
We now return to time optimality. The space pε={u∧εe0:⟨u,e0⟩ε=0} is n-dimensional. If U=u∧εe0 and V=v∧εe0 are arbitrary elements in pε then [U,V]=u∧εv. Hence [U,V]=0 if and only if u and v are parallel. Thus each maximal abelian algebra is one-dimensional and each non-zero element U in pε is regular. The Weyl group consists of two elements I1 and I2 such that AdI1U=U and AdI2U=−U.
If h={1}×R for some R∈SO(n), then AdhX0=Rx0∧εe0. Since SO(n) acts transitively on the spheres Sn, AdKX0=Sn∧εe0. If Lp=l∧εe0 then Rx0=l yields AdhX0=Lp. The above shows that {AdhX0,h∈K}={x∧εe0,||x||=||x0||} and the convex hull is equal to {x∧εe0:||x||≤||x0||}.
4.4. Compact Lie groups
Each semi-simple compact Lie group K is a symmetric space realized as the quotient G/˜K, with G=K×K and ˜K={(g,g):g∈K} under the automorphism σ(g1,g2)=(g2,g1).
If k denotes the Lie algebra of K then g=k×k is the Lie algebra of G, and ˜k={(X,X),X∈k} is the Lie algebra of ˜K. Then, p={(X,−X):X∈k} is the orthogonal complement of ˜k in g relative to the natural bi-invariant metric inherited from K. It then follows that ˜k and p satisfy Cartan's decomposition (1.4). To pass to the quotient space G/˜K, note that G acts on K by the natural action
Since h2h1h−11=h2 the action is transitive. In particular the orbit through the group identity is identified with K.
Maximal abelian algebras in p are in exact correspondence with maximal abelian algebras in k. Any ˜X0∈p is of the form ˜X0=(X0,−X0) for some X0∈k. If h∈˜K is of the form h=(g,g), then Adh˜X0=(Adg(X0),−AdgX0). Therefore, time-optimal solutions associated with
are given by
for some elements P∈k and Q∈k, with h(t)=g1(0)et(P+Q)et(−P+Q)g−12(0) the projection on K in accordance with equation (3.10).
5.
Applications to quantum control-n chains
5.1. Finite dimensional Schrödinger equation and the associated control systems
In non-relativistic quantum mechanics, time evolution of a finite dimensional quantum system is governed by a time dependent Schrödinger equation
in an n-dimensional complex Hilbert space Hn, where H(t) is a fixed time varying Hermitian operator in Hn ([1]). Recall that H(t) is Hermitian if ⟨H(t)z,w⟩=⟨z,H(t)w⟩ for z,w in Hn where ⟨,⟩ denotes the Hermitian quadratic form on Hn.
In what follows, points in Hn will be represented by the coordinates z1,…,zn relative to an orthonormal basis in Hn, and Hn will be identified with Cn with the Hermitian scalar product ⟨z,w⟩=∑ziˉwi for any z and w in Cn, with ˉwi the complex conjugate of wi. Then, a matrix H is Hermitian if H∗=H, where H∗ is equal to the complex conjugate of the matrix transpose of H.
Equation (5.1) is subordinate to the master equation
in the unitary group U(n), in the sense that every solution z(t) of (5.1) that satisfies z(0)=z0 is given by z(t)=g(t)z0. Recall that iH is skew-Hermitian for each Hermitian matrix H, hence every solution g(t) of equation (5.2) that originates in U(n) evolves in U(n). It follows that ||z(t)||=||z0||, i.e., the reachable sets of (5.1) evolve on the spheres S2n−1.
To be consistent with the first part of the paper, we will focus on the left-invariant form of the master equation
Of course, it is easy to go from one form to the other; if g(t) is a solution of (5.2), then g−1(t) is a solution of (5.3) and vice versa.
As a way of bridging the language gap between quantum control literature and mainstream control theory, we will make a slight detour into the Kronecker products of matrices and the associated operations. For our purposes it suffices to work with square matrices. Then the Kronecker product U⊗V of any n×n matrix U and any m×m matrix V is equal to the nm×nm matrix with block entries (uijV),i,j≤n. The Kronecker product enjoys the following properties:
It follows that (U⊗V)∈U(nm) for any U∈U(n) and V∈U(m): similarly, U⊗V is in SU(mn) whenever U∈SU(n) and V∈SU(m) and n and m are of the same parity. It can be easily shown that
for any matrices U1,U2 of the same size, and any matrices V1,V2 also of the same size (recall our convention [X,Y]=YX−XY).
The following proposition assembles some facts that are relevant for the n-spin chains.
Proposition 17. If U∈u(n) (resp. U∈su(n)) and Ik is the k-dimensional identity matrix. then both Ik⊗U and U⊗Ik belong to u(nk) (resp. su(nk)).
However, if U∈u(n) and V∈u(m), then i(U⊗V)∈u(nm). Similarly, i(U⊗V) is in su(nm) whenever U∈su(n) and V∈su(m).
Proof. (Ik⊗U)∗=I∗k⊗U∗=Ik⊗(−U)=−(Ik⊗U). Hence Ik⊗U∈u(n). If Tr(U)=0 then Tr(Ik⊗U)=0. In addition,
We will now direct our attention to the n-spin chains introduced in [1] and [2]. These chains are defined in terms of the Kronecker products of Pauli matrices
The n-spin chains oriented in the z-direction are defined by the Hamiltonians
where Jij are the coupling constants, and where Iix,Iiy,Iiz denotes the matrix X1⊗X2⊗⋯⊗Xn where Xi=Ix (resp. Xi=Iy,Xi=Iz) in the i-th position and where all the remaining elements Xj are equal to the identity I2. This kind of spin-chains are known as the Ising spin chains ([16], [17]). We will now address time optimality of the associated left-invariant master system (5.3). Each chain defines a pair of Lie algebras (L,kv) where kv, the vertical algebra, is the Lie algebra generated by the controlling vector fields Iix and Iiy, i=1,…m, and where L is the controllability algebra generated by the drift element ∑nj=2J(j−1)jI(j−1)zIjz and kv.
We will now consider two and three spin chains with a particular interest on the cases where L=su(n) for some integer n and where kv is a subalgebra of L such that the Cartan conditions (1.4) hold for the pair (p,kv) with p equal to the orthogonal complement of kv in L. For the sake of uniformity with the first part of the paper, we will work with the matrices Ax,Ay,Az introduced in equations (3.11) rather than with the Pauli matrices Ix,Iy,Iz. Recall that
In this notation then
As a preliminary first step, let us single out the symmetric (irreducible) Riemannian pairs (G,K) in which G=SU(n) for some n. It is known that there are only three such Riemannian spaces
where S(U(p)×U(q))=SU(p+q)∩(U(p)×U(q)) ([6], p. 518).
The first symmetric space (SU(n),SO(n)), known as Type AⅠ, has already been discussed in the preceding section. The second symmetric space, Type AⅡ, occurs on SU(2n) and is induced by the automorphism
Then σ(g)=g if and only if g−1TJn=Jng, or Jn=gTJng, which in turn means that g∈Sp(n), where Sp(n)=SU(2n)∩Sp(2n,C). Then
It follows that k={X∈su(2n):JnˉXJ−1n=X} and p={X∈su(2n):JnˉXJ−1n=−X}. If X=(X11X12−ˉXT12X22) is the decomposition of X into the n×n blocks, then
Therefore, X∈k if and only if
and X∈p if and only if
The remaining symmetric space, Type AⅢ, is associated with the automorphism
The induced automorphism on su(p+q) is given by σ∗(X)=Ip,qXI−1p,q. Then
where A is a p×p matrix and B is a q×q matrix such that Tr(A+B)=0, and where C is an arbitrary p×q matrix with complex entries. Then S(U(p)×U(q)) denotes the subgroup of SU(p+q) whose Lie algebra consists of matrices X=(A00B), with A∈u(p), B∈u(q) such that Tr(A+B)=0.
In all these cases the metric on p coincides with the restriction of the canonical metric on su(n) given by ⟨X,Y⟩=−12Tr(XY)=12Tr(XˉYT).
The relevance of these classical classifications for the problems of quantum control has already been noticed in the existing literature ([1] and [2] in regard to Type AⅠ, and [18] in regard to Type AⅢ).
5.2. Two-spin chains
The two-spin chains given by
give rise to the rescaled left-invariant master equation (J(j−1)j=1)
where now Aix and Aiy are the chains with Ax and Ay in the i-th position.
Let now kv denote the vertical subalgebra generated by the controlling vector fields Aiy,Aix,i=1,…,m. For m=1 there are two controls u and v associated with the controlling matrices Ax⊗I2 and Ay⊗I2, and for m=2 there are four controls u1,u2,v1,v2 associated with matrices Ax⊗I2,I2⊗Ax,Ay⊗I2,I2⊗Ay.
It is easy to verify that kv={X⊗I2:X∈su(2)} for m=1, and kv={X⊗I2+I2⊗Y:X∈su(2),Y∈su(2)} for m=2. In the first case kv is a three-dimensional algebra isomorphic to su(2), and in the second case it is a six dimensional Lie algebra isomorphic to su(2)×su(2).
Lemma 2. If A and B are any matrices in su(2), then
The mapping ϕ defined by ϕ(iX⊗Y)=iY⊗X,
ϕ(X⊗I2)=I2⊗X,ϕ(I2⊗X)=X⊗I2, X,Y in su(2) is a Lie algebra isomorphism on su(4).
Proof. If A=(ia3a−ˉa−ia3) and B=(ib3b−ˉb−ib3) then
Hence 2AB=−2⟨A,B⟩I2+[B,A]. This proves the first part of the lemma.
Then
and
Hence ϕ is an isomorphism.
Proposition 18. Let L denote the Lie algebra generated by i(Az⊗Az) and kv. When m=1, L=p⊕k, p=i(su(2)⊗Az) and k=su(2)⊗I2. If ϕ is the isomorphism from the previous lemma then ϕ(L)=(su(2)00su(2)) and
Proof. Evidently, k=kv. Secondly, [i(Az⊗Az),X⊗I2]=i([Az,X]⊗Az) for any X in su(2). This implies that both i(Ay⊗Az) and i(Ax⊗Az) are in L. Therefore p⊂L. Since ⟨X⊗I2,Y⊗Az⟩=−12Tr(XY)Tr(Iz)=0, kv and p are orthogonal. Also, [i(X⊗Az),i(Y⊗Az)]=−[X,Y]⊗A2z=14[X,Y]⊗I2. Therefore [p,p]⊆kv L=p⊕k. Hence p and k satisfy Cartan's conditions (1.4) and consequently L=p⊕kv.
If ϕ is the isomorphism from the preceding lemma, then ϕ(−2iX⊗Az))=−2iAz⊗X=(X00−X) for any −2iX⊗Az in p, and ϕ(X⊗I2)=I2⊗X=(X00X) for X⊗I2∈k. The linear span of these matrices is equal to (X00Y), X,Y in su(2).
The above shows that the m=1 chain can be represented on G=SU(2)×SU(2) as
The time-optimal solutions are of the form
P∈su(2),Q∈su(2), with h(t)=g1(0)et(P+Q)et(−P+Q)g−12(0) the projection on SU(2) (in accordance with (4.2)).
Proposition 19. For m=2, L=su(4). If
then L=p+kv and
Proof. Let p={i(X⊗Y):X∈su(2),Y∈su(2)}. It then follows that su(4)=p⊕kv by an easy dimensionality argument. Straightforward calculations shows that p and kv satisfy Cartan's conditions
So it suffices to show that p⊂L.
Since i(Az⊗Az) is in p,
is in L for any X and Y in su(2). Therefore both i[Az,X]⊗Az and i(Az⊗i[Az,Y]) are in L, which then implies that i(X⊗Az) and i(Az⊗Y) are in L for any X,Y in su(2) (because i(Az⊗Az) is in L).
But then [i(X⊗Az),I2⊗Y]=X⊗i[Az,Y] and [i(X⊗Az),Y⊗I2]=i([X,Y]⊗Az yields that i(X⊗Y) is in L for any X and Y in su(2).
Corollary 5. The reachable set from the identity is equal to SU(4).
The following lemma reveals the connection to the appropriate symmetric Riemannian space.
Lemma 3. Let h=√2(−AzAyAx−12I2). Since h∗=ˉhT=√2(Az−Ax−Ay−12I2)=h−1, and Det(h)=1, h belongs to SU(4). Then
Also, Adh(i(A⊗B))=14i(C1C2CT2C3), C1=(−a1b1+a2b2−a3b3a3b2+a2b3a3b2+a2b3−a1b1−a2b2+a3b3),
for any matrices A=12(ia3a−ˉa−ia3) and B=12(ib3b−ˉb−ib3), a=a1+ia2 and b=b1+ib2. We leave these verifications to the reader.
It then follows that
which then yields that the quotient space SU(4)/Kv is isomorphic to the symmetric space SU(4)/SO(4). The above formulas also show that the two-spin system with m=2 is conjugate to
where
For m=1 the controls are reduced to U=U1=U2 and V=V1=V2.
Corollary 6. The time optimal solutions for the two-spin chains are given by the same formulas as in Proposition 16.
5.3. The three-spin chains
Let us now consider the three-spin systems
in G=SU(8).
It follows that A1zA2z=(Az⊗I2⊗I2)(I2⊗Az⊗I2)=(Az⊗Az)⊗I2. Similarly, A2zA3z=I2⊗(Az⊗Az). So the drift Hamiltonian Hd is of the form
where a and b are arbitrary non-zero constants. In the case that m=3, the controlled Hamiltonians are given by
It is easy to verify that the vertical algebra kv generated by the controlled Hamiltonians is equal to
Case m=1 is similar to its two spin analogue and will be omitted. The remaining cases m=2 and m=3, however, show new phenomena that take their solutions outside the general framework described earlier in the paper.
The following lemma highlights some of the calculations in m=2.
Lemma 4. Let k=kv+kh where kv=su(2)⊗I2⊗I2+I2⊗su(2)⊗I2 and kh=su(2)⊗su(2)⊗Az. Then k is a Lie subalgebra in su(8), ⟨kv,kh⟩=0 and
The proof follows by simple calculations which we leave to the reader..
Proposition 20. For m=2, the Lie algebra L generated by Hd and the controlled Hamiltonians H1,H2,H3,H4 contains the Lie algebra k in the preceding lemma. If p denotes the orthogonal complement of k in L then L=k+p and [p,k]⊆p,[p,p]⊆k,[k,k]⊆k.
Proof. For m=2, kv=su(2)⊗I2⊗I2+I2⊗su(2)⊗I2 is a subalgebra in L. If X1 and X2 are any elements in su(2) let ˜X1=X1⊗I2⊗I2 and ˜X2=X2⊗I2⊗I2. Then,
Therefore su(2)⊗Az⊗iI2 is in L since X1,X2 are arbitrary and a≠0. In particular, −a(Az⊗Az⊗iI2)⊆L, and consequently b(iI2⊗Az⊗Az)⊆L.
Let now ˜Y1=I2⊗Y1⊗I2 and ˜Y2=I2⊗Y2⊗I2 with Y1 and Y2 arbitrary elements in su(2). Then
show that Az⊗su(2)⊗iI2 is in L. Similar calculation with iI2⊗Az⊗Az in place of Az⊗Az⊗iI2 shows that iI2⊗su(2)⊗Az is also in L. But then
Hence Az⊗su(2)⊗Az is in L. Finally,
shows that su(2)⊗su(2)⊗Az is in L. Therefore k of the preceding lemma in L.
Let now p=su(2)⊗su(2)⊗iI2+iI2⊗su(2)⊗Az+su(2)⊗iI2⊗iAz. We showed above that iI2⊗su(2)⊗Az is in L. Since [iI2⊗su(2)⊗Az,kh] is in L, [iI2⊗Z⊗Az,X⊗Y⊗Az]=−14X⊗[Z,Y]]⊗iI2 is in L for any X,Y, and Z in su(2). That is, su(2)⊗su(2)⊗iI2 is in \mathcal{L} .
An easy calculation with [\mathfrak{su}(2)\otimes \mathfrak{su}(2)\otimes iI_2, \mathfrak {k}_h] shows that \mathfrak{su}(2)\otimes iI_2\otimes A_z belongs to \mathcal{L} . Therefore \mathfrak {p}\subset \mathcal{L} .
It follows from above that both \mathfrak {p} and \mathfrak {k} are in \mathcal{L} . Since \mathfrak {p} and \mathfrak {k} are orthogonal, \mathfrak {p}\cap \mathfrak {k} = \{0\} , and [\mathfrak {p}, \mathfrak {k}]\subseteq \mathfrak {p} . The reader can readily show that [\mathfrak {p}, \mathfrak {p}]\subseteq \mathfrak {k} . Therefore \mathfrak {k} and \mathfrak {p} satisfy Cartan's conditions (1.4), and consequently \mathfrak {k}+ \mathfrak {p} is a Lie algebra. Since \mathcal{L}\subseteq(\mathfrak {k}+ \mathfrak {p})\subseteq \mathcal{L} , \mathcal{L} = \mathfrak {k}+ \mathfrak {p} .
Proposition 21. \mathcal{L} is isomorphic to \mathfrak{su}(4)\times \mathfrak{su}(4) , and \mathfrak {k} is isomorphic to \mathfrak{su}(4) .
Proof. First, let us note that \mathfrak {k} and \mathfrak{su}(4) are isomorphic under the isomorphism
Indeed F([U, V]) = [F(U), F(V)] for any U and V in \mathfrak {k}_v by a straightforward calculation. If U and V are in \mathfrak {k}_h then U = X_1\otimes X_2\otimes A_z and V = Y_1\otimes Y_2\otimes A_z . It follows that [U, V] = \frac{1}{4}(\langle X_2, Y_2\rangle [X_1, X_2]\otimes I_2+\langle X_1, Y_1\rangle I_2\otimes [X_2, Y_2])\otimes)I_2 , and hence F([U, V]) = \frac{1}{4}(\langle X_2, Y_2\rangle [X_1, X_2]\otimes I_2+\langle X_1, Y_1\rangle I_2\otimes [X_2, Y_2]) = [F(U), F(V)] . The remaining case U\in \mathfrak {k}_v , V\in \mathfrak {k}_h also yields F([U, V]) = [F(U), F(V)] which shows that F is an isomorphism whose range is \mathfrak{su}(4) . Thus \mathfrak {k} is isomorphic to \mathfrak{su}(4) .
Then \mathfrak {p} can be identified with the Hermitian matrices in \mathfrak{sl}(4, {\mathbb C}) via the identification
Now \mathfrak{su}(4) is a compact real form for \mathfrak{sl}(4, {\mathbb C}) ( \mathfrak{sl}(4, {\mathbb C}) = \mathfrak{su}(4)+i \mathfrak{su}(4) ). It follows that \mathcal{L} and the real Lie algebra generated by \mathfrak{sl}(4, {\mathbb C}) are isomorphic, (since \mathfrak{sl}(4, {\mathbb C}) is the complexification of \mathfrak{su}(4) ).
The above calculations show that the horizontal systems associated with three-spin systems starting with m = 2 exhibit notable differences from the horizontal systems associated with two-spin systems that considerably complicate the time-optimal solutions. As demonstrated above, the reachable set G is isomorphic to SU(4)\times SU(4) and K is isomorphic to SU(4) , hence M = SU(4)\times SU(4)/SU(4) is the associated symmetric Riemannian space. However, the Lie algebra generated by the controlled vector fields is a proper subalgebra of the isotropy algebra \mathfrak {k} ( \mathfrak {k}_v = \mathfrak{su}(2)\times \mathfrak{su}(2) and \mathfrak {k} = \mathfrak{su}(4) ), and therefore the associated homogeneous manifold G/K_v does not admit a natural metric compatible with the decomposition \mathfrak {k}_v^\perp+ \mathfrak {k}_v . As a consequence, the time optimal solutions of the horizontal system
are no longer given by the exponentials of matrices in \mathfrak {p} mainly because K is no longer the symmetry group for the horizontal system.
The same phenomena occur in the three-spin chains with m = 3 . For then
is contained in the Lie algebra \mathfrak {k} equal to the linear span of \mathfrak {k}_v and matrices of the form X\otimes Y\otimes Z where each of X, Y, Z range over the matrices in \mathfrak{su}(2) . A simple count shows that dim(\mathfrak {k}) = 36 . Then \mathfrak {p} , the linear span of matrices X\otimes Y\otimes Z , where one of the matrices X, Y, Z is equal to iI_2 and the remaining two are in \mathfrak{su}(2) , is orthogonal to \mathfrak {k} . Since dim(\mathfrak {p})) = 27 , dim(\mathfrak {p}+ \mathfrak {k}) = 63 = dim(\mathfrak{su}(8)) . Hence \mathfrak{su}(8) = \mathfrak {p}\oplus \mathfrak {k} .
Proposition 22. The preceding decomposition \mathfrak {p}\oplus \mathfrak {k} is a Cartan decomposition of Type AⅡ associated with the symmetric space SU(8)/Sp(4) .
Proof. Let us recall h = {\sqrt{2}} \begin{pmatrix}-A_z&A_y\\ A_x & -\frac{1}{2}I_2 \end{pmatrix} from Proposition 3. Since h is a point in SU(4) , \Psi = \begin{pmatrix} h & 0\\0&h \end{pmatrix} is a point in SU(8) and hence Ad_\Psi is an isomorphism on \mathfrak{su}(8) .
Let Ad_\Psi(X\otimes Y\otimes Z) = M = \begin{pmatrix} M_{11}&M_{12}\\-M^*_{12}&M_{22} \end{pmatrix} where M_{ij} are 4\times 4 matrices. To show that Ad_\Psi(\mathfrak {k}) and Ad_\Psi(\mathfrak {p}) correspond to a Cartan pair of type {\bf{AII}} we need to show that Ad_\Psi(\mathfrak {k}) satisfies M_{11} = \bar M_{22}\text{ and }M_{12} = M_{12}^T, and Ad_\Psi(\mathfrak {p}) satisfies M_{11} = -\bar M_{22}, Tr(M_{11}) = 0, \text{ and }M_{12}^T = -M_{12}.
When X = \frac{1}{2} \begin{pmatrix} ix_3&x\\-\bar x & -ix_3 \end{pmatrix} , Y = \frac{1}{2} \begin{pmatrix} iy_3&y\\-\bar y & -iy_3 \end{pmatrix} , Z = \frac{1}{2} \begin{pmatrix} iz_3&z\\-\bar z & -iz_3 \end{pmatrix} , X\otimes Y\otimes Z belongs to \mathfrak {k} and
The formulas in Lemma 3 show that Ad_h(Y\otimes Z) is a symmetric matrix with real entries. Hence \bar{M}_{22} = M_{11} and M_{12}^T = M_{12} .
If one of X, Y, Z is equal to iI_2 then X\otimes Y\otimes Z belongs to \mathfrak {p} . When X = iI_2 then
Evidently, \bar{M}_{22} = -M_{11} .
In the complementary case when Y or Z is iI_2 and X = \frac{1}{2} \begin{pmatrix} ix_3&x\\-\bar x & -ix_3 \end{pmatrix} , M_{11} = ix_3Ad_h(Y\otimes Z) , M_{22} = -ix_3Ad_h(Y\otimes Z) , and M_{12} = xAd_h(Y\otimes Z) . It follows that Ad_h i(Y\otimes Z) is a skew-symmetric matrix and therefore, \bar{M}_{22} = -M_{11} and M_{12}^T = -M_{12} .
In the remaining cases two elements in X\otimes Y\otimes Z are equal to I_2 and X\otimes Y\otimes Z belongs to \mathfrak {k} . If Y = Z = I_2 then M_{11} = ix_3I_4, M_{22} = -ix_3I_4 and M_{12} = xI_4 . Evidently M_{11} = M_{22} and M_{12}^T = M_{12}
When X = I_2 then either Y or Z is equal to I_2 . But then Ad_h(Y\otimes Z) is a skew-symmetric matrix, and therefore M_{11} = iAd_h(Y\otimes Z) = M_{22} = -iAd_h(Y\otimes Z) , and M_{12} = 0 . Hence Ad_\Psi(\mathfrak {k}) and Ad_\Psi(\mathfrak {p}) correspond to the Cartan factors of Type AⅡ.
Proposition 23. For m = 3 the three spin system (56) is controllable in SU(8) .
Proof. Let \mathcal{L} denote the Lie algebra generated by H_d and \mathfrak {k}_v . Then, [H_d, \mathfrak{su}_2\otimes I_2\otimes _2] = a(A_z^\perp\otimes A_z\otimes iI_2) , and [A_z^\perp\otimes A_z\otimes iI_2, I_2\otimes \mathfrak{su}_(2)\otimes I_2] = A_z^\perp\otimes A_z^\perp\otimes I_2 , where A_z^\perp denotes the orthogonal complement of A_z in \mathfrak{su}(2) .
Similarly, [H_d, I_2\otimes I_2\otimes \mathfrak{su}(2)] = b(iI_2\otimes A_z\otimes A_z^\perp) , and [iI_2\otimes A_z\otimes A_z^\perp, I_2\otimes \mathfrak{su}(2)\otimes I_2] = iI_2\otimes A_z^\perp\otimes A_z^\perp . Therefore, both iI_2\otimes A_z^\perp\otimes A_z^\perp and A_z^\perp\otimes A_z^\perp\otimes iI_2 belong to \mathcal{L} . In particular A_x\otimes A_x\otimes iI_2 , A_y\otimes A_y\otimes iI_2 , iI_2\otimes A_x\otimes A_x , and iI_2\otimes A_y\otimes A_y all belong to \mathcal{L} .
Analogous calculations with A_x\otimes A_x\otimes iI_2 , iI_2\otimes A_x\otimes A_x , A_y\otimes A_y\otimes iI_2 , and iI_2\otimes A_y\otimes A_y show that A_x^\perp\otimes A_x^\perp\otimes iI_2 , iI_2\otimes A_x^\perp\otimes A_x^\perp belong to \mathcal{L} , as well as A_y^\perp\otimes A_y^\perp\otimes iI_2 and iI_2\otimes A_y^\perp\otimes A_y^\perp .
Therefore, \mathfrak{su}(2)\otimes \mathfrak{su}(2)\otimes iI_2 and iI_2\otimes \mathfrak{su}(2)\otimes \mathfrak{su}(2) belong to \mathcal{L} . But then [\mathfrak{su}(2)\otimes \mathfrak{su}(2)\otimes iI_2, iI_2\otimes \mathfrak{su}(2)\otimes \mathfrak{su}(2)] = \mathfrak{su}(2)\otimes \mathfrak{su}(2)\otimes \mathfrak{su}(2) . Hence \mathfrak {k}\subset \mathcal{L} . But then, \mathfrak{su}(2)\otimes iI_2\otimes \mathfrak{su}(2) is contained in
and therefore, \mathfrak {p}\subset \mathcal{L} .
The above suggests that one cannot expect time optimal solutions of three-spin chains to have a simple and computable form. However, there are some solvable cases that shed light on the general situation. One such case is a three-spin chain defined by the drift H_d = 2(J_{12}(I_z\otimes I_z\otimes I_2)+J_{21}(I_2\otimes I_z\otimes I_z)) controlled by a single Hamiltonian H_c = I_{2y} = I_2\otimes I _y\otimes I_2 . This system first appeared in studies on nuclear magnetic resonance spectroscopy ([3]), ([19]), ([4]).
Let us first make some introductory remarks on the results presented in ([3], [4]). The aforementioned studies begin with the density equation
associated with a right-invariant affine system
with H_d = 2(J_{12}I_z\otimes I_z\otimes I_2+J_{21}I_2\otimes I_z\otimes I_z) and H_c = I_2\otimes I_x\otimes I_2 .
The density equation is assumed to evolve in the Hilbert space \mathcal{H} of Hermitian matrices in i \mathfrak{su}(8) endowed with its natural scalar product \langle X, Y\rangle = \frac{1}{2}Tr(XY) . Recall that iX is Hermitian for each X\in \mathfrak{su}(n) .
Rather than studying the density equation directly, the above papers consider instead the time-optimal evolution of the expectation values of certain elements in \mathcal{H} , where the expectation value of an element X along a solution \rho (t) is defined by \langle X, \rho(t) \rangle . It then follows that the expectation value of X evolves in time according to
In particular when X = X_1 = (I_x\otimes I_2\otimes I_2) , then \langle [X_1, i(H_d+u(t)H_c)], \rho(t)\rangle = -J_{12}\langle 2(I_x\otimes I_z\otimes I_2), \rho\rangle . Hence the expected value x_1 = \langle X_1, \rho\rangle evolves according to
where x_2(t) is the expected value of X_2 = 2(I_y\otimes I_z\otimes I_2) . Continuing this way one obtains new elements X_3 and X_4 whose expectation values x_3(t) and x_4(t) together with x_1(t) and x_2(t) satisfy a closed differential system
with the time rescaled by a factor J_{12} , where x(t) is the column vector in R^4 with the coordinates x_1, x_2, x_3, x_4 . In fact, x_3 = -\langle 2I_x\otimes I_y\otimes I_2, \rho\rangle, \text{ and }x_4 = \langle 4iI_x\otimes I_x\otimes I_z, \rho\rangle ([4]). The above authors then pose the time-optimal problem of reaching (0, 0, 0, 1)^T from (1, 0, 0, 0)^T in the least amount of time. We will refer to this problem as the Yuan's optimal problem since it was originated in ([3]).
Rather than tackling this problem directly, the papers ([3]), ([19]), ([4]) concentrate on certain lower dimensional approximations and then show that these approximations are integrable in terms of elliptic functions. As far as I know, the original problem remained open.
We will show that Yuan's problem and the time optimal problem associated with the affine system (5.18) are essentially the same and both can be integrated in terms of elliptic functions.
5.4. Symmetric three-spin systems
For the sake of consistency with the rest of the paper we will formulate (5.18) in the left-invariant way as
with iH_d = 2(J_{12}(I_z\otimes I_z\otimes iI_2)+J_{21}(iI_2\otimes I_z\otimes I_z)) and H_c = I_{2y} , which we will write as iH_d = 2a (A_z\otimes A_z\otimes iI_2)+2b(iI_2\otimes A_z\otimes A_z) , a = -J_{12}, b = -J_{23} , and iH_c = iI_{2y} = I_2\otimes A_x\otimes I_2 . We will refer to the above system as a symmetric three-spin system.
Proposition 24. If \mathcal{L} denotes the Lie algebra generated by iH_d and iH_c then \mathcal{L} is the vector space spanned by
Proof.
Therefore H_2 = a(A_z\otimes A_y\otimes iI_2)+b(iI_2\otimes A_y\otimes A_z) is in \mathcal{L} . Then
hence H_3 = A_z\otimes A_x\otimes A_z belongs to \mathcal{L} . Continuing,
is in \mathcal{L} . But then
and hence, H_5 = A_z\otimes A_z\otimes iI_2 , and H_6 = iI_2\otimes A_z\otimes A_z are in \mathcal{L} .
Finally, [H_5, H_c] = [A_z\otimes A_z\otimes iI_2, I_2\otimes A_x\otimes I_2] = A_z\otimes A_y\otimes iI_2 , which it turn implies that iI_2\otimes A_y\otimes A_z is in \mathcal{L} . We have now shown that
are contained in \mathcal{L} .
Let now
It is now easy to verify that the above matrices satisfy the following Lie bracket table
Let \mathcal{L}_0 denote the linear span of matrices U_i, V_i, i = 1, 2, 3 . It follows from the above table that \mathcal{L}_0 is a Lie subalgebra of \mathfrak{su}(8) . Since iH_d and iH_c belong to \mathcal{L}_0 , \mathcal{L}\subseteq \mathcal{L}_0 . But then \mathcal{L}_0\subseteq \mathcal{L} by our construction. Therefore \mathcal{L}_0 = \mathcal{L} .
Corollary 7. \mathcal{L} is isomorphic to \mathfrak{so}(4).
Proof. Let \hat U_1 = e_4\wedge e_3, \hat U_2 = e_2\wedge e_4, \hat U_3 = e_2\wedge e_3, \hat V_1 = e_2\wedge e_1, \hat V_2 = e_3\wedge e_1, \hat V_3 = e_4\wedge e_1 . Then \hat U_i, \hat V_i, i = 1, 2, 3 is a standard basis in \mathfrak{so}(4) that conforms to the same Lie bracket table as displayed in Table 1.
Proposition 25. The set of points reachable from the identity by the trajectories of
is a six dimensional subgroup G of SU(8) isomorphic to SO(4) .
Proof. \mathcal{L} is a Lie algebra isomorphic to \mathfrak{so}(4) , which is also isomorphic to \mathfrak{su}(2)\times \mathfrak{su}(2) . In fact if \mathfrak {g}_1 is the linear span of \frac{1}{2}(U_1+ V_1), \frac{1}{2}(U_2+ V_2), \frac{1}{2}(U_3+ V_3) , and \mathfrak {g}_2 is the linear span of \frac{1}{2}(U_1-V_1), \frac{1}{2}(U_2-V_2), \frac{1}{2}(U_3-V_3) , then \mathcal{L} = \mathfrak {g}_1\oplus \mathfrak {g}_2 , [\mathfrak {g}_1, \mathfrak {g}_2] = 0 and each factor \mathfrak {g}_i is isomorphic to \mathfrak{su}(2) .
Since \mathcal{L} is isomorphic to \mathfrak{su}(2)\times \mathfrak{su}(2) there is a subgroup \tilde G in SU(8) which is isomorphic to SU(2)\times SU(2) (Lie algebras are in one to one correspondence with simply connected Lie groups ([6])). But then SU(2)\times SU(2) is a double cover of SO(4) and SO(4) is the connected component of SU(2)\times SU(2) that contains the group identity (see for instance [11]). Therefore the reachable set of (5.20) is a subgroup G of \tilde G isomorphic to SO(4) .
In terms of the notations introduced above (5.20) can be rewritten as
or as
after suitable reparametrizations ( t\rightarrow \frac{t}{b}, u\rightarrow \frac{u}{b} ).
We will now reformulate Yuan's problem as a variational problem on the sphere S^4 realized as the quotient SO(4)/K, K = \{1\}\times SO(3) under the right action (g, x)\rightarrow g^{-1}x . Then equation (5.19) can be recast as
or as
in terms of the basis \hat U_1 = e_4\wedge e_3, \hat U_2 = e_2\wedge e_4, \hat U_3 = e_2\wedge e_3, \hat V_1 = e_2\wedge e_1, \hat V_2 = e_3\wedge e_1, \hat V_3 = e_4\wedge e_1 introduced in the preceding corollary.
Proposition 26. Yuan's differential system (5.23) is isomorphic to the affine-symmetric system (5.22).
Proof. Let R = \begin{pmatrix} 1 & 0 & 0 & 0\\0 & 0 & 0 & -1\\0 & 0 & 1 & 0\\0 & 1 & 0 & 0 \end{pmatrix} . Then R\in SO(4) and hence, R^{-1} = R^T . If \tilde g(t) = Rg(t)R^{-1} then \tilde g(t) is a solution curve of
for any solution g(t) of equation (5.23). The correspondence U_i\rightarrow \tilde U_i, V_i\rightarrow \tilde V_i is a Lie algebra isomorphism from \mathcal{L} onto \mathfrak{so}(4, {\mathbb R}) . So (5.23) and (5.24) are isomorphic and (5.24) and (5.22) are isomorphic.
It follows that the time optimal solutions of (5.23) and (5.22) are qualitatively the same, apart from the fact that in Yuan's problem time optimality is relative to the cosets gK . We will come back to this point later on in the text. Let us now come to the horizontal three-spin symmetric system
where h(t) is a solution of \frac{dh}{dt} = u(t)h(t)U_1) . Since (2U_1)^2 = -I_8 where I_8 is the identity in SU(8) ,
or e^{U_1t} = I_8\cos \frac{t}{2}+2U_1\sin\frac{t}{2} . Let now \theta (t) = \int_0^tu(s)\, ds+\theta_0. Then
Easy calculations show that
Therefore,
It follows that (5.25) is of the form
where u_1(s) = \cos\theta (s), u_2(s) = -\sin\theta (s) . To pass to its convex extension it is sufficient to enlarge the controls to the ball u_1^2+u_2^2\leq 1 .
We will now consider the time optimal problem in the reachable group G in SU(8) associated with the above convex system.
We remind the reader that \langle\, , \, \rangle is the scalar product on \mathfrak{su}(8) given by \langle A, B\rangle = -\frac{1}{2}Tr(AB) . This scalar product is a multiple of the Killing form and hence satisfies \langle [A, B], C\rangle = \langle A, [B, C]\rangle for any matrices A, B, C in \mathfrak{su}(8) . Relative to \langle\, , \, \rangle matrices U_1, U_2, U_3, V_1, V_2, V_3 constitute an orthonormal basis. Then G with the left-invariant metric induced by the above scalar product becomes a Riemannian manifold as well as a sub-Riemannian manifold with the sub-Riemannian length defined over the horizontal curves by
Thus a horizontal curve g(t) that connects g_0 = I to a point g_1 \in G in T units of time is a curve of minimal length if and only if \int_0^T\sqrt{u_1^2(t)+u_2^2(t)}\, dt is minimal. As expected the non-stationary time optimal horizontal curves coincide with the sub-Riemannian geodesics of shortest length.
The sub-Riemannian metric induces a Riemannian metric on the quotient space M = G/K_v with the geodescs on M equal the projections of the sub-Riemannian geodescs in G that connect the initial coset K_v to the terminal coset g_1K_v . It is important to note that the above sub-Riemannian metric is not of contact type, that is, [\Gamma, \Gamma]\neq \mathcal{L} where \Gamma denotes the vector space spanned by V_2+kU_2 and V_3+kU_3 . Instead,
Secondly, it may be important to note that the induced metric on G/K_v is not symmetric.
Let us now use the maximum principle to get the extremal curves associated with the above time optimal problem.
5.5. The extremal curves
We will follow the formalism outlined in Section 3, in which the cotangent bundle T^*G is trivialized by the left-translations and represented as G\times \mathfrak {g}^* , where \mathfrak {g}^* denotes the dual of \mathfrak {g} ., Then \mathfrak {g}^* will be identified with \mathfrak {g} via \langle\, , \, \rangle with \ell\in \mathfrak {g}^* identified with L\in \mathfrak {g} through the formula \langle L, X\rangle = \ell(X) for any X\in \mathfrak {g} . Every L\in \mathfrak {g} admits a representation L = \sum_{i = 1}^3P_iB_i+M_iA_i where P_i = \ell(B_i) and M_i = \ell(A_i) .
Then the Hamiltonian lift of the horizontal system (5.26) is given by
where P_i = \langle L, V_i\rangle , and M_i = \langle L, U_i\rangle , i = 1, 2, 3 .
We recall that the Hamiltonian equations associated with H are given by the equations
where dH = (V_3+kU_3)u_1(t)+(V_2+kU_2)u_2(t) , or, dually by \frac{dL}{dt} = [dH, L] . In the coordinates, P_i, M_i the preceding equations take on the following form
According to the maximum principle time optimal trajectories are the projections of the extremal curves which can be abnormal and normal. In the abnormal case the maximum principle results in the constraints
while in the normal case the maximum principle singles out the Hamiltonian
generated by the extremal controls u_1 = P_3+kM_3, \, u_2 = P_2+kM_2 , whose integral curves on energy level H = \frac{1}{2} coincide with the normal extremal curves. Let us begin with the abnormal extremals.
Proposition 27. Abnormal extremal curves associated with the time optimal curves g(t) are generated by the controls
and are confined to the manifold
In addition, M_1(t) and P_1(t) are constant. On M_1 = 0 , both u_1 and u_2 are constant, hence g(t) is a Riemannian geodesic in G .
Proof. As stated above, abnormal extremal curves satisfy
and when they correspond to a time optimal curve, then they satisfy another constraint, known as the Goh condition, namely
which yields
Since \dot M_1 = \{H, M_1\} = (P_2+kM_2)u_1-(P_3+kM_3)u_2 = 0 , M_1 is constant, and hence P_1 must be constant also.
Upon differentiating (5.29) along the extremal curve we get
which implies that
since time optimality demands that u_1^2+u_2^2 = 1 whenever u\neq 0 . Then
hence
On M_1 = 0, P_1 = 0 , and \omega = 0 .
We now come to the normal extremals. Let us first note that the Poisson equation \frac{dL}{dt} = [dH, L] that governs the normal extremals is completely integrable on each coadjoint orbit in \mathfrak{so}(4) for the following reasons: \mathfrak{so}(4) is of rank two, and hence admits two universal conservation laws (Casimirs)
Therefore, generic coadjoint orbits are four dimensional, and since coadjoint orbits are symplectic, they admit at most two independent integrals of motion functionally independent from the Casimirs. In the present case, I_3 = M_1 and H = \frac{1}{2}(P_2+kM_2)^2+(P_3+kM_3)^2) are the required integrals. The fact that M_1 is constant was clear from the very beginning since K_v = \{e^{ \varepsilon U_1}, \varepsilon\in {\mathbb R}\} is a symmetry for (5.26).
We will now show that the normal extremals can be integrated by quadrature in terms of elliptic functions on the manifold
Then,
It follows that
We now have
Hence,
where
It is well known that the solutions of \frac{dz}{dt} = \sqrt{P(z)} with P a fourth degree polynomial can be solved in terms of elliptic integrals (for instance, see ([20])).
The remaining variables can be integrated by quadrature through the representation
Then
yields
Hence the extremal controls are now specified and the projected curve g(t) is obtained as a solution of a fixed ordinary differential equation.
In the presence of the transversality conditions, M_1 = 0 , and the above equation simplifies. For when M_1 = 0 ,
Then \xi = P_1^2 is a solution of
The preceding equation can be put in its canonical form \frac{d\xi}{dt} = \sqrt{4\xi^3-g_2\xi-g_1} and then can be solved in terms of the Weierstrass' \wp function ([7]), page 113).
The solutions of Yuan's optimal problem satisfy additional transversality conditions, namely, the extremal curve L(t) is orthogonal to \mathfrak {k} at the initial and the terminal time, where \mathfrak {k} is the Lie algebra spanned by U_1, U_2, U_3 . That means that M_i(0) = 0 and M_i(T) = 0 for i = 1, 2, 3 . Such extremal curves reside on I_2 = 0 .
Use of AI tools declaration
The author declares not having used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
I am grateful to Fatima Silva Leite for her constructive criticisms of an earlier version of the paper as well as for her help with various technical requirements imposed by the publisher.
Conflict of interest
The author declares there is no conflict of interest.









 DownLoad:
DownLoad: