An efficient ECG denoising method by fusing ECA-Net and CycleGAN

1.   Introduction

Electrocardiogram (ECG) denoising is aimed at removing and suppressing baseline drift, motion artifacts, electromyographic interference, power line interference, Gaussian white noise, etc., in order to provide high-quality signals for subsequent feature extraction and classification work ^[1,2].

The frequency analysis technique can convert a time-domain signal into a frequency-domain signal and be used for noise reduction analysis. Wavelet transform is a popular transform domain filtering method. The multi-resolution of wavelet transform can make the signal and noise in multi-scale space, which can be used to process ECG denoising. Singh et al. ^[3] implemented ECG signal denoising using discrete wavelet transform (DWT) and non-local means (NLM) estimation which achieved better results. Hao et al. ^[4] proposed an improved multivariate wavelet denoising technique combining subspace and principal component analysis to improve the output SNR by projecting the observed signal into the subspace using the derived optimal orthogonal matrix and then applying the univariate wavelet shrinkage operator to the projected signal. Wang et al. ^[5] obtained optimized filter coefficients by approximating the amplitude-frequency response of an ideal filter in order to optimize the wavelets, effectively removing high-frequency noise from the ECG. However, due to the limitation of wavelet base function, fixed base function, constant multi-resolution, etc., makes wavelet analysis lack adaptivity.

In addition, signal decomposition-based denoising methods decompose the signal into several frequency band components, and then determine the components to be retained based on the a priori information of the target signal, and finally use these frequency band components to reconstruct the target signal to achieve noise removal ^[6]. Denoising algorithms based on signal decomposition included empirical mode decomposition (EMD) ^[7,8], variational mode decomposition (VMD) ^[9,10] and singular spectrum analysis (SSA) ^[11,12], et al. In processing non-stationary and non-linear ECG signals, compared with wavelet decomposition, although EMD is not affected by the choice of wavelet base and decomposition level, EMD also has end effects and model mixing phenomena in decomposition. Moreover, in practical applications, EMD cannot effectively distinguish frequency-similar bands, such as high-frequency noise and QRS complexes, or lower frequency P-waves and T-waves, which can lead to distortion of the denoised signal. In contrast, the VMD is an adaptive signal decomposition method that uses a set of adaptive Wiener filters to estimate each mode at different center frequencies. Compared with the EMD method, VMD can effectively overcome the end effect and model mixing. However, the optimal values of the decomposed Intrinsic Mode Function k and the penalty factor α are difficult to set.

Sharma and Sharma ^[13] achieved better denoising results by artificially adding baseline drift noise to the ECG and removing this noise using Hilbert vibration decomposition technique. Manju and Sneha ^[14] conducted a noise reduction comparison experiment between the Wiener filter and the Kalman filter for ECG signals, and the results showed that the Wiener filter has better noise reduction performance. Due to the high overlap of the motion artifact band range with the ECG signal, the signal decomposition-based denoising algorithms are difficult to remove the motion artifacts cleanly and sometimes destroy the main morphology of the ECG, and some of the algorithms can only remove for a certain kind of noise ^[15,16], which has poor generalization ability.

Compared with traditional ECG noise reduction methods, deep learning-based denoising methods were widely used in ECG denoising recently. Deep learning-based methods have strong nonlinear modeling and representation abilities, which can learn more complex features in electrocardiogram signals with good generalization capabilities [17−19]. CycleGAN ^[20] was used as a variant of GAN for image-to-image transformations on unpaired datasets. In terms of ECG denoising, Serkan et al. ^[21] proposed a one-dimensional operable CycleGAN for ECG denoising, which replaced the neurons in the convolutional layers of the model with Self-Organized Operational Neural Networks (Self-ONNs) ^[22,23]. Antczak ^[24] proposes a new method for denoising ECG signals using deep recurrent denoising neural networks, and the network is pre-trained with synthetic data generated from a dynamic ECG model through a transfer learning technique and fine-tuned using real data.

The attention mechanism was first introduced in the recurrent neural network model by Mnih et al. ^[25] and can effectively improve the accuracy of image classification. The attention mechanism assigns different weights to different parts of the attention thing to reduce the role of other irrelevant parts. Qiu et al. ^[26] used a convolutional neural network to perform ECG denoising in two stages, with the first stage consisting of a one-dimensional U-Net for ECG denoising and the second stage using a one-dimensional DR-Net to correct the noise-reduced signal obtained in the first stage, adding SENet for further learning of detailed ECG features.

In general, a wide range of noise types, including baseline drift, motion artifacts, myoelectric interference, industrial frequency interference, Gaussian white noise, etc., have varying characteristics. Most of the existing denoising methods are oriented to a single noise type and do not perform denoising experiments for mixed noise, with poor generalization ability. Moreover, the band range of motion artifacts is highly overlapping with the band range of the ECG signal, so it is difficult to remove motion artifacts by using signal decomposition denoising methods alone. To address these issues, the main work in this paper is outlined below:

1) The combination of the ECA-Net and CycleGAN was proposed for ECG denoising. Using the local cross-channel interaction strategy to selectively emphasize informative features and suppress useless features, causes the effective feature map to be weighted more and the ineffective or small effect feature map to be weighted less, so that the critical input features in ECG were preserved and noise information was suppressed.

2) The loss function of the Cycle-GAN was optimized to improve the ECG denoising performance. To further extract global and local features of ECG signals, the L1 norm is combined to minimize the distance between the generated denoised signal and the original signal. The maximum difference function is also incorporated to minimize the maximum difference between each sample point pair between the denoised signal and the original signal, which suppresses the maximum local error.

3) Adding single and mixed noise to the MIT-BIH Arrhythmia database was proposed for training the CycleGAN based ECG denoising model, and some ablation experiments were also used to investigate the denoising performance of the proposed method.

In the following, the proposed methodology will be explained specifically in Section 2. The experimental setting and results are presented in Section 3. Section 4 provides the conclusion.

2.   Proposed method

2.1.   ECA-Net

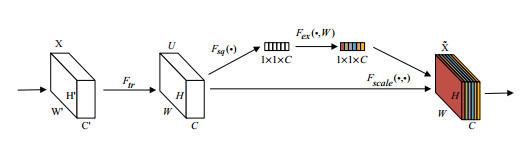
The structure of the SENet is shown in Figure 1, where X denotes the input feature map, for any given transformation, ${F_{tr}}$:$X \to U, X \in {R^{H' \times W' \times C'}}, U \in {R^{H \times W \times C}}$, and $\tilde X$ denotes the final output feature map. The input is a three-dimensional feature tensor, where the first dimension is the height H, the second dimension is the width W and the third dimension is the number of channels C. In SE-Net, ${F_{sq}}$, ${F_{ex}}$ and ${F_{scale}}$ represent three different operations: Squeeze, Excitation and Scale respectively ^[27].

Figure 1.  A Squeeze-and-Excitation block.

DownLoad: Full-Size Img PowerPoint

ECA-Net is a very efficient attention mechanism to learn effective attention channels in a more efficient way, and some other studies have improved SE blocks by capturing more complex channel dependencies or by combining additional spatial attention ^[28].

Figure 2 presents the diagram of ECA module, where GAP represents the global average pooling layer. It can be seen that, unlike SENet, ECA-Net first determines the convolution kernel size $K$ adaptively by a function of the channel dimension C, and then performs a fast one-dimensional convolution of size $K$, before performing a Sigmoid function to learn channel attention.

Figure 2.  Diagram of ECA module.

DownLoad: Full-Size Img PowerPoint

The convolution kernel size $K$ is a key parameter that determines the coverage of the interaction and is related to the channel dimension C, which is usually set to an integer power of 2. The mapping relationship between the two exists as follows:

The size $K$ of the adaptive local convolution kernel is calculated as:

Where ${\left| t \right|_{odd}}$ denotes the nearest odd number $t$.

ECA-Net has no dimensionality reduction, and considers the correspondence between channels, outperforms SENet and CBAM and is designed for lightweight CNN architectures. In this paper, ECA-Net is added to the model to avoid dimensionality reduction while enabling the model to focus on ECG local features and reduce the interference caused by noise, thus improving the noise reduction capability of the model.

While the attention mechanism helps to focus on key information, the ECA mechanism is an effective attention method with fewer parameters and better performance, which can enhance the attention to different pass information features and generate weights between different channels, and the inclusion of ECA can enhance the attention to the local information of ECG.

2.2.   The proposed method framework

The proposed ECG denoising framework was implemented by incorporating ECA-Net with Operational CycleGANs ^[21], as shown in Figure 3, which contains two generators and two discriminators. The generator A2B indicates to generate the corrupted ECG into a clean ECG in the state; the generator B2A means to generate the clean ECG into a corrupted ECG in the same state; discriminator A identifies real corrupted ECG or generated corrupted ECG; discriminator B identifies real clean ECG or generated clean ECG. The cycle consistency loss reduces the gap between the real corrupted ECG and the generated corrupted ECG and reduces the gap between the real clean ECG and the generated clean ECG.

Figure 3.  Overall architecture of the proposed denoising method.

DownLoad: Full-Size Img PowerPoint

The ECG data is a discrete 1D time series, so a one-dimensional convolutional neural network is used to process ECG signal feature extraction, using Self-Organized Operational Neural Networks as convolutional layers of 1D Cycle-GAN.

The architecture diagrams for the generator and discriminator are shown in Figures 4 and 5, respectively. The generator is a U-net structure, containing five cascades of down sampling, and mirrored five cascades of up sampling. Each up sampling block includes a convolutional layer, batch normalization, activation function and Dropout layer, and the down sampling block includes a convolutional layer, batch normalization and activation function. The batch normalization process ensures that all training data are normalized. The addition of activation functions to each 1D convolutional layer to achieve a normalized model that can better mine relevant features and fit the training data; The addition of a Dropout layer for solving the training overfitting problem; The use of skip connection facilitates the propagation of gradients during denoising training. The pooling layer performs the down sampling process by obtaining the maximum or mean value of a range from the mapping space, but the inclusion of the pooling layer also results in a lack of local feature information, so the pooling layer is not included in the model.

Figure 4.  Generators architecture diagram.

DownLoad: Full-Size Img PowerPoint

Figure 5.  Diagram of the discriminator model.

DownLoad: Full-Size Img PowerPoint

In the generator, the corrupted ECG with dimension 4000 is taken as input, and after five layers of down sampling, each with a step size of 2 and a convolutional kernel size of 5, the number of output channels in each layer is 16, 32, 64,128 and 128, respectively, followed by five up-samplings of the mirror image, each with a step size of 2 and a convolutional kernel size of 5 except for the last layer of 6. The final output is the clean ECG with latitude 4000, which is the noise reduction signal generated according to the extracted features. The MSE between the output of the discriminator and the label vector is calculated as the loss function of the discriminator, with an output dimension of 30. It should be noted that in order to address the problem of insufficient ECG feature extraction by existing methods, we added a layer of ECA-Net after each of the first four up samplings, and the model is optimized by calculating the attention probability distribution and highlighting the key input features.

2.3.   Loss function

For the ECG denoising network in this paper, the input is the corrupted ECG signal $\tilde x$ and the output is the denoised clean ECG signal $\hat x$. G is responsible for generating a pseudo-sample that retains the main features of the ECG signal in the output, recovering the original clean ECG signal $x$ from corrupted noisy ECG. D tries to distinguish the difference between the generated samples and the actual data samples. The training process of G is to maximize the probability of D making an error. The objective function is to learn the mapping relationship from the data distribution of the noisy signal $\tilde x \in X$ to the data distribution of the clean data $\hat x \in Y$. The two sets of mapping relations ${G_{X \to Y}}$ and ${G_{Y \to X}}$ in the network are learned according to adversarial loss ^[29] and cycle consistency loss ^[30], respectively, the former makes the mapped data distribution close to that of the target domain, and the latter ensures that the two learned mappings do not contradict each other. It is known from the Operational CycleGANs that ${G_{X \to Y}}$ denotes the generator from the corrupted ECG signal to the clean ECG signal with an adversarial loss as:

Similarly, ${G_{Y \to X}}$ denotes the generator from the clean ECG signal to the corrupted ECG signal with an adversarial loss as:

The cycle consistency loss is:

The identity loss is:

where X_X and X_Y are corrupted and clean ECG signal segments, D_Y is used to distinguish the real noise-free signal from the generated pseudo-noise-free signal, and D_X is used to distinguish the real noise-containing signal from the generated pseudo-noise-containing signal.

In order to better solve the ECG denoising problem under non-parallel data, the following two partial optimizations are made on the basis of the loss function of Operational CycleGANs in this paper. The first part ${l_{dist}}$ is to reduce the difference between the denoised sample and the original sample ^[31]. The second component, ${l_{\max }}$, represents the maximum differential function which is utilized to learn the local characteristics of a signal, maintain consistency of local features and thereby enhance the overall quality of the signal ^[32]. ${l_{dist}}$ and ${l_{\max }}$ are defined by the following equations:

The final objective function is derived as follows:

where N is the number of samples and the hyperparameter ${\lambda _i}(i = 1, 2, 3, 4)$ is used to adjust the weights of the components in the objective function. When tuning hyperparameters, the appropriate weights of each loss function are used to balance the magnitudes of different loss functions. Then, after parameter sweeping, the hyperparameter values with the best denoising performances are used as the weights of the components in the objective function.

2.4.   Performance metrics

In quantitative analysis, the metrics used are: signal-to-noise ratio improvement (SNR_imp), percentage-root-mean-square difference (PRD) and root-mean-square error (RMSE). Ideally, the larger the SNR_imp value, the greater the difference between the SNR of a clean ECG signal and the SNR of a corrupted ECG signal:

where N is the length of the ECG signal, $x$ is the original clean ECG signal, $\tilde x$ is the corrupted ECG signal and $\hat x$ is the denoised ECG signal.

Lower RMSE and PRD values indicate that the closer the denoised signal is to the original signal, the lower the distortion and the better the denoising performance:

2.5.   Experimental setup

In order to obtain the best noise reduction results, we determined the values for each parameter after several experiments. The batch size was equal to 8, the epoch was equal to 2000, the lr was equal to 0.00001, the optimizer for both the generator and discriminator was Adam, and the learning rate optimization strategy was Cosine Annealing. To speed up the convergence of the model and to fit the stylized migration task, Instance Normalization was chosen to do the normalization within a channel and Tanh was used for the activation function.

The datasets from standard MIT-BIH Arrhythmia database were used to investigate the proposed method. Each ECG record was sampled at 360 Hz and contains 650,000 sampling points. The database contains 48 half-hourly ECG records from different patients. All records consisted of two leads, most of which were present in the lead MLII. Noise data EM, BW, MA from the MIT-BIH Noise Stress Test database. All experiments used signals from MLII leads as the original data set, used as a clean training distribution and were divided into two groups: the training set and the test set. The training set used 80% of the data set and the rest was used for the test set. The models in this paper were built on python 3.7 and PyTorch 1.8 and trained on an NVIDIA GeForce RTX 3090 graphics card.

In order to achieve the goal of optimal mapping relationship of signals from noise-bearing space to noise-free space, two types of sample data, noise-bearing and noise-free signals, need to be constructed. Ten records were selected as the original ECG data, including numbers 103,105,111,116,122,205,213,219,223,230. Using the sliding window technique, a sample was set to contain 4000 sampling points, 250 training samples were taken for each record with an overlap rate of 50%, and a total of 2500 training samples were available for the 10 records. The corrupted ECG signal is generated by adding noise to the original ECG signal, and finally the clean ECG and noisy ECG signals are generated as a matrix of size (2500, 4000) and used as the training set. On the test set, the test data are fed into the generator for noise reduction experiments. The test set is generated in the same way as the training set, and there is no data overlap between the test and training sets. To accelerate convergence, the ECG signals were normalized to between 0 and 1 as follows:

where ${x_{\max }}$ and ${x_{\min }}$ denote the maximum and minimum values in each sample, respectively.

3.   Experimental results and discussion

3.1.   Experimental results

The denoising performances of a single noise is evaluated, and the proposed noise reduction method is quantitatively compared and analyzed with the method proposed in ^[21] in three evaluation indexes. The smaller the SNR of the input noise, the greater the damage to the original signal and the more difficult it is to remove the noise. In the experiment, adding noises with different SNR can explore the comprehensive performance of the ECG denoising methods. The 5 and 10 dB EM, BW and MA noise were added to the original clean ECG signal as corrupted ECG, and the average value was taken for multiple experiments, and the specific quantitative comparison data are shown in Tables 1−3.

Table 1.  Noise reduction effect of the model on MA noise.

Records	Operational CycleGANs [21]						Proposed method
	SNRimp		RMSE		PRD		SNRimp		RMSE		PRD
	5 dB	10 dB	5 dB	10 dB	5 dB	10 dB	5 dB	10 dB	5 dB	10 dB	5 dB	10 dB
103	15.69	17.20	0.0182	0.0153	9.47	7.90	18.84	19.91	0.0125	0.0110	6.47	5.72
105	14.06	15.75	0.0292	0.0237	12.18	9.84	18.58	19.97	0.0160	0.0137	6.68	5.69
111	14.35	15.85	0.0365	0.0306	11.14	9.29	19.72	21.25	0.0192	0.0161	5.85	4.91
116	14.86	16.46	0.0296	0.0238	10.98	8.79	19.84	21.09	0.0152	0.0132	5.79	5.01
122	17.32	18.52	0.0181	0.0160	7.79	6.82	19.62	20.73	0.0137	0.0121	5.90	5.20
205	12.69	14.70	0.0524	0.0456	15.36	12.70	19.46	20.70	0.0144	0.0125	6.23	5.40
213	15.22	16.52	0.0352	0.0305	10.00	8.63	20.58	21.97	0.0185	0.0158	5.30	4.51
219	14.97	16.20	0.0266	0.0233	10.38	9.01	18.47	19.74	0.0173	0.0150	6.79	5.87
223	13.71	14.87	0.0374	0.0324	12.21	10.69	19.10	20.44	0.0177	0.0151	6.31	5.41
230	15.08	16.90	0.0446	0.0359	10.33	8.36	22.80	24.29	0.0174	0.0146	4.12	3.47
Average	14.83	16.32	0.0323	0.0276	10.94	9.22	19.67	20.95	0.0160	0.0138	5.95	5.15

---

 | Show Table

DownLoad: CSV

Table 2.  Noise reduction effect of the model on BW noise.

Records	Operational CycleGANs [21]						Proposed method
	SNRimp		RMSE		PRD		SNRimp		RMSE		PRD
	5 dB	10 dB	5 dB	10 dB	5 dB	10 dB	5 dB	10 dB	5 dB	10 dB	5 dB	10 dB
103	16.04	18.84	0.0172	0.0125	8.95	6.47	19.79	21.93	0.0112	0.0087	5.82	4.55
105	15.40	18.58	0.0244	0.0160	10.21	6.68	20.44	22.73	0.0130	0.0100	5.42	4.17
111	15.95	19.72	0.0298	0.0192	9.07	5.85	21.32	23.67	0.0160	0.0122	4.88	3.72
116	16.24	19.84	0.0243	0.0152	9.13	5.79	20.65	23.06	0.0149	0.0105	5.68	4.01
122	18.29	19.62	0.0161	0.0137	6.92	5.90	21.19	23.24	0.0115	0.0091	4.94	3.91
205	14.78	19.46	0.0342	0.0144	11.31	6.23	20.77	23.18	0.0124	0.0094	5.37	4.05
213	16.52	20.58	0.0300	0.0185	8.51	5.30	21.73	23.95	0.0163	0.0126	4.66	3.61
219	15.70	18.47	0.0242	0.0173	9.35	6.79	19.77	22.27	0.0150	0.0113	5.85	4.38
223	15.20	19.10	0.0295	0.0177	9.99	6.31	20.44	22.87	0.0152	0.0115	5.42	4.09
230	17.54	22.80	0.0329	0.0174	7.67	4.12	23.70	25.80	0.0157	0.0123	3.71	2.91
Average	16.18	19.67	0.0259	0.0160	9.11	5.95	20.96	23.26	0.0139	0.0106	5.18	3.94

---

 | Show Table

DownLoad: CSV

Table 3.  Noise reduction effect of the model on EM noise.

Records	Operational CycleGANs [21]						Proposed method
	SNRimp		RMSE		PRD		SNRimp		RMSE		PRD
	5 dB	10 dB	5 dB	10 dB	5 dB	10 dB	5 dB	10 dB	5 dB	10 dB	5 dB	10 dB
103	13.93	14.69	0.0220	0.0202	11.43	10.46	16.39	19.22	0.0165	0.0119	8.58	6.19
105	12.64	13.36	0.0343	0.0315	14.28	13.06	16.42	17.96	0.0205	0.0172	8.54	7.16
111	11.55	12.42	0.0498	0.0449	15.14	13.64	17.57	19.19	0.0245	0.0204	7.48	6.22
116	12.95	13.76	0.0364	0.0319	13.63	11.86	17.80	19.99	0.0192	0.0149	7.30	5.69
122	15.86	16.12	0.0214	0.0209	9.17	8.93	17.43	19.24	0.0176	0.0143	7.58	6.15
205	12.34	12.84	0.0455	0.0450	14.81	14.18	17.11	19.30	0.0190	0.0146	8.05	6.34
213	11.15	13.14	0.0588	0.0447	16.48	12.63	18.31	20.60	0.0240	0.0185	6.85	5.27
219	11.50	12.32	0.0413	0.0369	15.49	13.94	16.00	17.91	0.0231	0.0185	9.00	7.22
223	10.98	11.61	0.0503	0.0476	16.58	15.56	16.54	18.45	0.0238	0.0190	8.45	6.80
230	13.28	14.03	0.0549	0.0498	12.73	11.56	20.44	22.88	0.0228	0.0172	5.39	4.08
Average	12.70	13.53	0.0406	0.0363	13.87	12.44	17.36	19.44	0.0208	0.0164	7.74	6.13

---

 | Show Table

DownLoad: CSV

From Tables 1−3, it can be seen that when the input SNR is low, the SNR_imp of the generated noise reduction signal will be smaller and the RMSE and PRD will be larger. With the increasing of SNR, the SNR_imp gets a relatively larger value and the RMSE and PRD will be relatively smaller. In all the test records, the SNR_imp obtained by the proposed method in this paper is significantly higher than that of the comparison method, and the average values of RMSE and PRD are significantly lower than that of the comparison method. It can be concluded that the proposed ECG denoising method performs better than that of the compared method in the case of single input noise.

In Figure 6, the noise reduction effect of the noise reduction method proposed in this paper is shown for different noises with an input SNR at 10 dB, taking record 213 as an example. For the convenience of display, only 2000 sampling points are plotted for each sample, and in the subplots, from top to bottom, are the original ECG signal, the corrupted ECG signal, the noise reduction signal of Operational CycleGANs and the noise reduction signal output of the proposed method in this paper, respectively. It can be seen from the figure that the P-wave amplitude is generally relatively small, but there is a strong correlation with atrial fibrillation. The noise mainly destroys the P-wave and T-wave of the ECG signal, and the EM noise destroys the main morphology of the ECG, while the denoised signal output from the model trained with the method proposed in this paper is closer to the morphology of the original clean ECG signal, and the characteristic information of the P-wave and T-wave is obviously recovered, which is more medically valuable. The noise reduction signal generated by the Operational CycleGANs method will contain high-frequency noise that is not present in the original signal. This is most obvious when the input noise is EM, and many detailed features of the signal are not generated, and the average value of the metrics obtained from the test samples is low, and the difference in the noise reduction effect is very large between different samples.

Figure 6.  Noise reduction for different single types of input noise at 10 dB input SNR.

DownLoad: Full-Size Img PowerPoint

Considering the acquisition process of ECG signals, the same segment of data should contain multiple noises, i.e., mixed noise EM+BW, EM+MA, BW+MA and EM+BW+MA. Therefore, the denoising of the hybrid noise is also evaluated in this paper, and the specific quantitative comparison data are shown in Table 4. It can be seen that the proposed method has better SNR_imp, RMSE and PRD under different test noise conditions, and also has good noise reduction ability for mixed noise and better generalization ability.

Table 4.  Average noise reduction results obtained by denoising the mixed noise.

		Operational CycleGANs [21]				Proposed method
		EM+BW	EM+MA	BW+MA	EM+BW+MA	EM+BW	EM+MA	BW+MA	EM+BW+MA
5 dB	SNRimp	13.16	13.17	15.78	13.38	17.64	17.70	21.23	17.76
	RMSE	0.0384	0.0386	0.0278	0.0374	0.0202	0.0200	0.0134	0.0199
	PRD	13.16	13.15	9.66	12.82	7.51	7.47	5.00	7.42
7.5 dB	SNRimp	13.39	13.96	15.89	14.01	19.03	18.77	21.15	19.303
	RMSE	0.0372	0.0344	0.0277	0.0340	0.0172	0.0177	0.0135	0.0167
	PRD	12.72	11.90	9.56	11.80	6.42	6.61	5.04	6.2312
10 dB	SNRimp	14.25	14.46	15.59	14.32	18.71	19.75	21.96	19.05
	RMSE	0.0334	0.0329	0.0316	0.0334	0.0179	0.0158	0.0124	0.0172
	PRD	11.51	11.29	10.23	11.44	6.63	5.92	4.59	6.40
15 dB	SNRimp	14.38	14.82	16.02	15.52	19.32	19.23	22.98	19.83
	RMSE	0.0321	0.0301	0.0290	0.0276	0.0166	0.0169	0.0110	0.0157
	PRD	11.16	10.60	9.54	9.72	6.20	6.26	4.07	5.84

---

 | Show Table

DownLoad: CSV

Figure 7 shows the noise reduction effects of different noises when the input SNR is 7.5 dB. It can be seen that the P wave and T wave have also been severely damaged and lost effective medical features. After denoising through the model of this paper, the obtained close to the original ECG signal.

Figure 7.  Noise reduction for different mixed type of input noise at 7.5 dB input SNR.

DownLoad: Full-Size Img PowerPoint

Some traditional signal processing methods were used to denoise ECG signals, especially for processing Gaussian white noise. In order to fully verify the noise reduction performance of the proposed method in the face of different complex situations, the Gaussian white noise reduction experiment is also investigated, and as a comparison with the existing work of AFD method ^[33].

The test results are clearly shown in Figure 8. After all test records are output by the noise reduction model, the SNR has been significantly improved. The noise reduction effect of the method in this paper is more significant, at least 9.45 dB higher than the AFD method at 1.25 dB, at least 8.13 dB higher than the AFD method at 5 dB.

Figure 8.  Noise reduction effect of Gaussian white noise.

DownLoad: Full-Size Img PowerPoint

In all test cases, qualitatively, the noise reduction signal obtained by the method in this paper is smoother, does not generate additional noise, has a higher degree of restoration and is closer to the original ECG signal; quantitatively, the method in this paper can obtain good noise reduction effects for all test samples, and the average values of metrics are better than those of the Operational CycleGANs.

In all, the denoised signal obtained by the ECG noise reduction method proposed in this paper is very close to the original signal, with high SNR_imp, low RMSE and PRD, and can effectively remove four single noises of EM, BW, MA and Gaussian white noise, and four mixed noises of EM+BW, EM+MA, BW+MA and EM+BW+MA.

3.2.   Ablation experiment results and discussion

In order to further investigate the role of the proposed method for ECG denoising, ablation experiments are conducted for different models in this paper. The specific scheme of the model design is shown in Table 5, where '√' indicates that this item is included in the model. The loss function of Operational CycleGANs is $Los{s_{adv1}} + Los{s_{adv2}} + {\lambda _1}Los{s_{cyc}} + {\lambda _2}Los{s_{ide}}$, and new loss is listed as shown in Eq (9). Since the mixed noise is the most common and difficult to remove in ECG, this experiment adds 5, 7.5, 10, 15 dB of mixed noise EM+BW+MA to 10 original ECG records respectively to get the corrupted ECG signal.

Table 5.  Objects included in different models.

Model	Operational CycleGANs	ECA-Net	new Loss
A	√
B	√	√
C	√		√
D	√	√	√

---

 | Show Table

DownLoad: CSV

Figure 9 shows the average SNR_imp, RMSE and PRD values of the test data at 5, 7.5, 10, 15 dB input SNRs. When the input signal-to-noise ratio is small, the noise reduction effect of Model C is better than that of Model B. As the input SNR gradually increases, the denoising performance of Model B has a faster improvement, and the performance exceeds that of Model C at 10 dB. The noise reduction performance of Model C is slightly better than that of Model A, but not nearly as good as that of Model D.

Figure 9.  Comparison of denoising performance of different models at different input SNRs.

DownLoad: Full-Size Img PowerPoint

All in all, adding only ECA-Net or new Loss under different input noise conditions does not lead to a good optimization of the model. Compared with Model A, the proposed method, Model D, has a significant improvement and achieves the optimum in all metrics, with 32.74% relative SNR_imp improvement, 46.79% relative RMSE reduction and 42.12% relative PRD reduction at an input SNR of 5 dB.

Embedding ECA-Net or optimizing the loss function in the model can slightly improve its performance. When both methods are used simultaneously, they can complement each other and further improve the overall performance of the model, achieving better denoising effects. In ECG signal denoising, attention mechanisms can help the model to focus on the key information in the signal, paying more attention to key signal features such as QRS complex, which can accurately separate noise from the signal while retaining important signal characteristics. Optimizing the loss function can enable the model to better learn the features of the data, ensure a better fit with real data, reduce the risk of overfitting and further improve the denoising performance. Therefore, when attention mechanisms and optimized loss functions are used simultaneously, the model can better learn the key features in the signal, achieving better denoising effects.

In this paper, the model generalization performance resulting from manual data screening is approximate to the clinical setting, and it might not be appropriate to use in clinical practice directly. Therefore, in the future work, intra-patient testing protocols will be further verified in clinic practice. Some quantitative metrics, such as SNR_imp, PRD and RMSE, have been provided to assess the superiority of the designed modules. However, the influence of training strategy and model complexity, have not been considered in this work. We will conduct further analysis in subsequent work on the impact of various training strategies on model performance and explore model complexity under different circumstances.

4.   Conclusions

In this paper, we propose a fusion of ECA-Net and CycleGAN for ECG signal noise reduction. The model uses data from the MIT-BIH Arrhythmia database and the MIT-BIH Noise Stress Test database, which constitute the original and corrupted ECG samples. A one-dimensional convolutional neural network was used to extract the time-domain features of ECG data, and the model optimization was achieved by ECA-Net highlighting the key features and introducing a new loss function to further extract the global and local ECG features. The qualitative and quantitative experimental results show that the proposed ECG denoising method can remove a variety of single or mixed noises with higher SNR_imp, as well as lower RMSE and PRD, and has a good reduction of both global and local features with stronger generalization ability. Moreover, the proposed effective end-to-end ECG denoising method is of practical significance and clinical value, which can prevent potential diseases such as stroke and sudden death caused by arrhythmias in a timely and early manner.

Acknowledgments

This work is supported in part by the Key Research and Development Program of Zhejiang Province (2020C03060), the National Natural Science Foundation of China (62011530130, 62272415 and 62101497), Joint Fund of Zhejiang Provincial Natural Science Foundation (LSZ19F010001).

Conflict of interest

The authors declare there is no conflict of interest.