1.
Introduction
Coronary microvascular dysfunction (CMD) is one of the basic mechanisms of myocardial ischemia which can lead to severe clinical events including cardiac infarction and heart attack [1,2]. It is found that, of patients with ischemia with no obstructive coronary disease coronary disease (INOCA), up to 72% have demonstrated coronary microvascular dysfunction [3]. Compared to referent stable coronary artery disease, patients with INOCA reported greater physical limitation, angina frequency, and reduced quality of life. In addition, patients with INOCA reported frequent time missed from work and work limitations, suggesting a substantial economic impact [4]. CMD may result from functional or structural abnormalities occurring at the site of coronary microcirculation, and the relative roles these mechanisms play may vary across different clinical settings [5]. The COVADIS study provides evidence that microvascular angina is an important health problem regardless of sex or ethnicity. A diagnosis of microvascular angina portends a substantial risk for major cardiovascular events associated with hypertension and previous history of coronary artery disease [6,7]. CMD can markedly impair quality of life and prognosis, and represents a substantial cost burden to healthcare systems [6,7].
Since in vivo visualization of the coronary microcirculation is beyond the resolution of coronary angiography, the diagnosis of CMD is based on functional assessment techniques. CMD is usually assessed invasively by measuring the response to vasoactive stimuli of coronary blood flow velocity using intracoronary Doppler-flow wire or thermodilution method [8,9]. Doppler-flow wire method has been reported to have superior agreement with 15O H2O positron emission tomography (PET) in comparison with thermodilution method. However, feasibility of measuring thermodilution-derived coronary flow reserve (CFR) is higher than that of Doppler-derived CFR. In addition, the thermodilution method, allows a simultaneous measurement of fractional flow reserve (FFR), CFR and index of microvascular resistance (IMR).
CFR is measured as the ratio of maximal flow after adenosine induced hyperemia to resting absolute myocardial blood flow [10,11]. CFR provides integrated information of the coronary artery and therefore abnormal values can be seen in diseases affecting both the epicardial and microvascular coronary arteries [12]. Hence, its interpretation needs assessment of FFR, which estimates the severity of epicardial stenosis. Indeed, in patients with high FFR (>0.80), CFR is determined mainly by the status of the microvascular system. Therefore, measurements of CFR and IMR in patients with high FFR are used to assess microvascular function, allowing more accurate risk stratification. In these patients, values of CFR < 2.0 or IMR ≥ 25 units indicate an abnormal microvascular function [13,14,15].
Although invasive methods constitute the gold standard for assessment of CMD, they present obvious limitations, which include prolongation of diagnostic angiography and increase of costs and risks. At present, PET is the mostly used and well-validated non-invasive diagnostic method. It allows quantitative measurements of both global and regional myocardial blood flow (MBF) using intravenous injection of positron-emitting radiotracers that are actively extracted by the myocardial cells (e.g., Rubidium-82, 13N-ammonia) or diffuse in the myocardium (15O-water) proportionally to blood flow. Limitations of this technique include a less than optimal anatomical resolution, limited clinical availability, prolonged examination time, and high cost. Cardiac magnetic resonance (CMR) also allows valuable assessment of global and regional coronary microvascular dilation using gadolinium as contrast medium to measure MBF. Compared to PET, CMR is radiation-free and has a higher spatial resolution. However, several shortcomings of this technique should be noted, including time-consuming for scan and post-processing, interobserver variability, lack of widespread availability and imaging artifacts. Myocardial contrast echocardiography (MCE) is a non-invasive, bedside and inexpensive technique which may also assess MBF using distribution of an echographic contrast medium. Microbubbles are infused at a constant rate to achieve steady-state concentration and then destroyed by acoustic waves. Changes of echo-signal are used to determine MBF. The MBF reserve, dividing the stress MBF by the baseline MBF, indicates coronary flow reserve. Quantitative MCE is better evaluated in the detection of epicardial coronary artery disease, and was correlated with Doppler flow wire, and PET [16,17,18,19]. A recent study also showed that an MBF reserve < 2 by MCE classified 37% of patients with chest pain but no obstructive CAD as having CMD [20,21,22]. However, there was no validation with other coronary microvascular dysfunction assessment methods [22]. There are no current recommended diagnostic thresholds for CMD [23]. Although MCE is a promising and objective echocardiographic method of coronary flow reserve assessment, the evidence is considered inadequate, and there is no consensus regarding whether it will replace any of the present diagnostic tests [19,24,25].
The objective of this study is to investigate the diagnostic performance of MCE for the evaluation of CMD.
2.
Materials and methods
This study was approved by the Institute Review Board of 2nd Affiliated Hospital of Zhejiang University and all patients provided informed consent. From September 2019 to May 2021, 122 patients who were admitted to the Department of Cardiovascular Medicine due to symptoms of myocardial ischemia and met the following inclusion criteria were enrolled prospectively: (1) Older than 18 years with informed consent; (2) With typical or atypical symptoms of chronic and stable myocardial ischemia; (3) Coronary angiography or computed tomography angiography (CTA) showed no obvious coronary stenosis (stenosis ≤ 50%); (4) Coronary stenosis was indicated by previous coronary angiography or CTA, but FFR > 0.8; (5) Chest pain and chest tightness were present, but no clear evidence of myocardial ischemia; (6) Objective evidence of myocardial ischemia. Exclusion criteria: (1) Unable to sign informed consent; (2) Expected survival time less than 1 year; (3) Myocardial infarction or acute cerebrovascular disease within 3 months; (4) Female patients during pregnancy or lactation; (5) Hemodynamically unstable patients (Killip class III-IV); (6) Left ventricular ejection fraction < 30%; (7) Serum creatinine > 150 µmol/L or glomerular filtration rate < 45 ml/kg/1.73 m2; (8) Be allergic to contrast agents; (9) Cannot tolerate decongestants; (10) Be expected to have a pressure guide wire unable to pass through lesions with severe calcification or varicose vessels; (11) Have factors that can seriously affect the quality of angiographic images, such as frequent premature atrial beats or atrial fibrillation.
2.1. Thermodilution: gold standard for CMD diagnosis
In this study, the thermodilution-derived CFR was used as gold standard for assessment of CMD. This technique is based on the principle of Fick's method, which requires the connection of a guide catheter (5- to 7-F) without a side hole to the coronary artery, and a pressure-temperature sensor tip guide wire was used to measure various parameters. Before each measurement, 100 or 200 mg of nitrate was injected into the patient's coronary arteries. During the measurement, the pressure sensor was always placed at the distal end of the target blood vessel, and the physiological salt with the same temperature as room temperature was injected into the vein through catheter, a total of 3 injections, 4 ml each time, to obtain the thermodilution curve in the resting state.
In order to obtain the thermodilution curve under stress, adenosine triphosphate (ATP) vasodilator was injected into peripheral or central vein through a syringe (140 mg/kg/min) first to cause maximum expansion of the blood vessel. After the measurement was complete, the guidewire was pull back into the guide catheter to check pressure drift. When the drift is greater than 3 mmHg, re-measurement is required. The ratio of Tmn at rest and under ATP vasodilator is the CFR.
2.2. CMD diagnosis with MCE
MCE images were acquired and stored for subsequent analysis using a Philips Q7 echocardiography system (Philips Ultrasound, Bothell, WA) at a centerline frequency of 2.0 MHz. MCE was performed at rest and during ATP stress at the same day of thermodilution measurement. ECG triggered real-time frames were acquired in the apical 4-chamber, 3-chamber, 2-chamber, and long-axis imaging planes. Lipid-shelled octafluoropropane microbubbles (SonoVue, Bracco, Milan, Italy) were diluted to 30 mL total volume in normal saline and infused at a constant rate of 4 ml/min. 1.0-1.5 ml of SonoVue ultrasound contrast agent were slowly injected, 5ml of normal saline were then slowly injected to rinse for more than 20 seconds. Using the destruction-reperfusion technique, a five-frame high-power (mechanical index > 0.9) sequence was applied to destroy microbubbles. The adenosine triphosphate (Xuzhou Ryen Pharma, Xuzhou, China) used was 20 mg/2ml of liquid, which was injected intravenously through a syringe to induce maximal increases in blood flow. The infusion rate was 160 ug/kg/min, and the total infusion time was about 6 minutes. Blood pressure and ECG were recorded before, during, and after ATP infusion. At least 15 cardiac cycles for each case were recorded to assess myocardial perfusion.
The Narnar APP (Narnar, LLC) was used to process MCE images. Through image import, frame selection and region division, important parameters such as blood flow velocity and MBF can be quickly fitted and calculated, and rendered on the ultrasound image based on these parameters. The specific steps are as follows: Import the obtained MCE image into the Narnar APP, select the end-systolic frames, circle the ventricular wall contour, draw the region of interest (ROI), and fit the relationship between the ROI perfusion intensity and time. The following four parameters can be calculated automatically: myocardial microbubble velocity (β), microvessel cross-sectional area (A), MBF (A × β) and goodness of fitting (GOF). CMD was defined as MBF reserve < 2 [1]. The MBF reserve equals the quotient of the stress MBF divided by the baseline MBF.
3.
Results
IBM SPSS Statistics 26.0 was used for statistical analysis. The normally distributed measurement data were described by mean ± standard deviation, and the t test was used for the comparison between groups, the non-normally distributed measurement data was described by the median (P25, P75), and the nonparametric test was used for the comparison between groups. Enumeration data were described by the number of cases, constituent ratios or ratios, and the chi-square test was used for comparison between groups. The evaluation indicators mainly include: accuracy, sensitivity, specificity, positive predictive value, negative predictive value, positive likelihood ratio, negative likelihood ratio and Youden index. The Kappa test was used to evaluate the consistency of the MCE method for early diagnosis of CMD and the gold standard CFR test results, and the Clopper-Pearson method was used to calculate the two-sided 95% confidence interval of accuracy. The Pearson correlation coefficient was used to calculate the linear correlation between MCE and the gold standard.
3.1. Baseline participant characteristics
122 patients were recruited initially, of which complete data for MCE, FFR, CFR and IMR for 87 patients were available for assessment. Five patients were excluded due to poor image quality, resulting in a total of 82 patients (65.9 ± 9.1 years, 58 males [70.7%]). The baseline characteristics are listed in Table 1. Most of the 82 patients (75.6%) had clinical manifestations of chest tightness, and a few (34.1%) also had chest pain reactions. 23 patients had a CFR value of 2.0 or less as measured by the gold standard. The probability of CMD associated with diabetes was 28%, the probability of associated hypertension was 25.6%, and the probability of associated smoking history was 37.5%. 62 segments (75.6%) of left anterior descending branch (LAD), 9 segments of left circumflex branch (LCX) and 11 segments of right coronary artery in 82 patients had different degrees of stenosis. It can be found that patients with abnormal CFR have higher IMR than patients with normal CFR (P < 0.001), and there is no statistical difference in FFR, prevalence of hypertension and diabetes, and smoking status between the two groups.
3.2. Image analysis
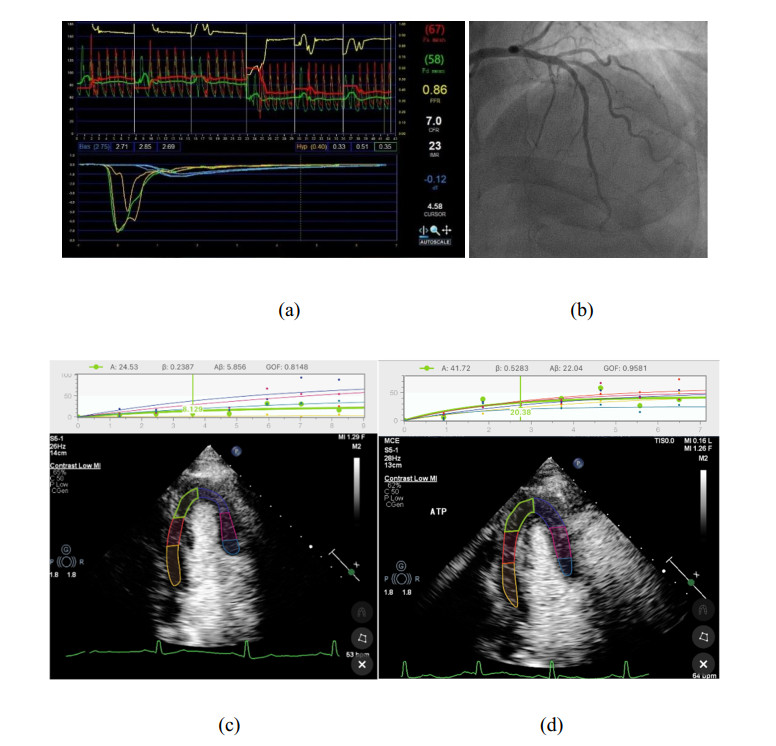
Two typical cases of suspected patients with CMD were shown in Figures 1 and 2. Figure 1 shows a case example of a 74-year-old man with complaints of chest pain and chest tightness. Coronary angiography (b) shows a lesion in the left anterior descending artery. Thermodilution (a) demonstrates FFR = 0.86, CFR = 7.0, and IMR = 23. Through MCE image analysis, as shown in Figure 1(c), (d), it can be found that the patient's time-intensity curve is relatively regular, with a high degree of fit. The MBF reserve was 3.76.
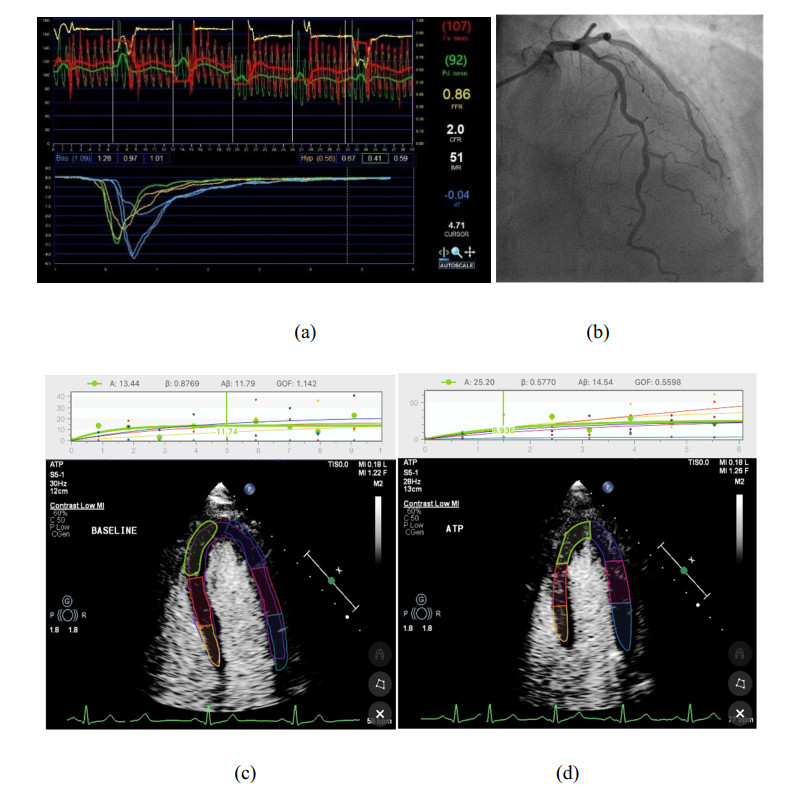
Figure 2 shows a case example of a 72-year-old man with complaints of chest pain and chest tightness for half a year. Coronary angiography (b) shows a lesion in the left anterior descending artery. Thermodilution (a) demonstrates FFR = 0.86, CFR = 2.0, IMR = 51. Through MCE image analysis, as shown in Figure 2(c), (d), the MBF reserve was calculated as 1.23.
3.3. A, β, A × β values
Table 2 shows the A, β, A × β values of patients with normal and abnormal CFR in resting state and ATP stress state. Among them, for patients with normal CFR values, the peak A in the resting state was significantly smaller than that in the stress state (49.91 [29.35, 76.63] vs 54.37 [31.83, 72.15]). For patients with abnormal CFR values, the peak A at rest was significantly greater than that at stress (54.79 [20.20, 109.43] vs 51.94 [24.77, 77.09]). At the same time, the β value of patients with abnormal CFR decreased significantly after stress (0.70 [0.16, 1.06] vs 0.41 [0.27, 0.84], 0.61 [0.33, 1.21] vs 0.35 [0.24, 0.93]), and the A × β value increased significantly (18.63 [15.61, 49.50] vs 35.47 [21.94, 112.24], 25.90 [7.65, 56.16] vs 29.33 [13.76, 61.22]). In the apical four-chamber view, the blood flow velocity β of patients with normal CFR and abnormal CFR was significantly different under stress, and the β value of patients with normal CFR was significantly greater than that of patients with abnormal CFR.
From the above experimental results, it can be found that the changes of the three data of different patient groups A, β, and A × β are different. From this it can be inferred that CMD may be a disease with many different pathobiologies. For many patients, CMD reflects an imbalance of microvascular systolic and diastolic processes in different physiological states, resulting in a reduction in peak blood flow (A). According to the results of some studies, CMD may also reflect the abnormal metabolism of cardiomyocytes. Some CMD patients had reduced high-energy phosphate production, which stimulates myocardial work and increases its perfusion level, which explains the increased resting blood flow in the patients studied by Rinkevich et al. [26].
3.4. ROC curve
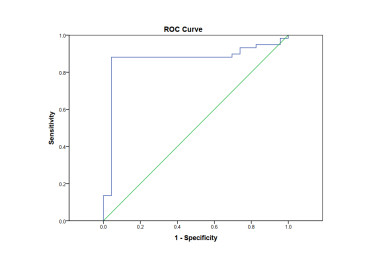
Figure 3 is the ROC curve of the MCE method for early diagnosis of CMD. The Youden index corresponding to the best critical point of the ROC curve was 0.838, and the area under the curve (AUC) was 0.867 (95% CI: 0.773-0.961, P < 0.001).
3.5. Consistency analysis
As shown in the Table 3, compared with the results measured by the gold standard, the MCE method correctly judged 50 normal patients and 22 abnormal patients, and wrongly judged 9 normal patients and 1 abnormal patient. Diagnostic accuracy of MCE at presentation for CMD was 87.8%, the sensitivity was 88.1%, specificity was 95.7%, positive predictive value was 75.9%, and negative predictive value was 98.1%. Considering the influence of chance factors in the two methods, the Kappa coefficient of the two methods was calculated, which was 0.727 (95% confidence interval: 0.57-0.88, P < 0.001), with strong consistency.
3.6. Linear relationship
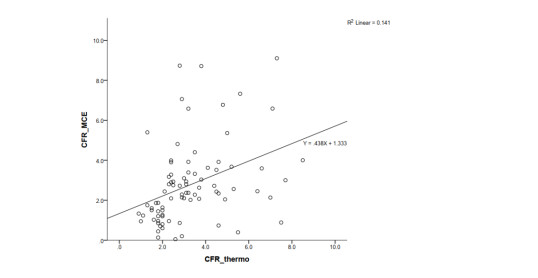
Pearson correlation analysis was used to evaluate the relationship between CFR measured by thermodilution and MCE method. The Pearson correlation coefficient (R = 0.376, p < 0.001) was calculated by drawing the corresponding scatter plot of CFR measured by thermodilution method and MCE method (Figure 4), the results showed that MCE method and gold standard method were moderately correlated. R2 = 0.141, indicating that the CFR value measured by MCE can correspond to the CFR value measured by thermal dilution method in a degree of 14.1%.
4.
Discussion
MCE is an effective and noninvasive method for evaluation of CMD in patients with early coronary artery disease. The statistical results of this study show that the MCE method had a high sensitivity and specificity in the diagnosis of CMD, and was in good agreement with thermodilution method. MCE is not only suitable for early diagnosis of CMD, but also provides a lot of useful information for the determination of subsequent treatment methods and prognosis judgment.
There are some limitations to the present study. There was a modest correlation between CFRthermo and CFRMCE. In the Everaars et al study, CFR was assessed on 98 vessels in 40 patients with suspected coronary artery disease. They considered PET as the gold standard and found only a moderate correlation between thermodilution and PET (R = 0.55; p < 0.001), with thermodilution tending to overestimate CFR at higher values [27]. This will have a certain impact on the diagnostic results of patients with CFR values near the critical value, which may lead to an increase in the number of false-negative patients. In order to decrease the number of false-negative patients, it is suggested that patients suspected of having CMD would be better to be assessed with MCE.
Senior echocardiologists are in charge of acquiring MCE images. Nurses are responsible for preparing relevant consumables and injecting ATP and SonoVue ultrasound contrast agent, and recording the patient's blood pressure during the examination. Communication and cooperation between echocardiologists and nurses during the examination are very important. MCE is a well-established routine test in our hospital, which can be done either in the outpatient clinic or on the ward. It takes about 15-20 minutes to complete an MCE exam. Because steps such as image matching require manual confirmation, and resting and ATP stress images need to be processed separately, it takes about 10 additional minutes to complete offline image post-processing for a case. Therefore, it is urgent to develop fully automated image post-processing software.
In this study, some patients had unclear images. Although this phenomenon is often attributed to motion artifacts, it can also occur from insufficient mixing of microbubble contrast agent (SonoVue in this study) when artificial oscillation is used. The MCE image post-processing software Narnar used in this study only works on the iPad and Macbook, which somewhat limits the clinical application of MCE technology.
Until now, MCE has been used for more than 20 years, however, the clinical use of MCE has been limited to only a handful of experts in the field due in large part to the perceived experience dependence of MCE interpretation. There are some key points that need attention in the image acquisition and post-processing stages when MCE is used for CMD diagnosis. In the image acquisition stage, in order to obtain high quality images, echocardiologists and nurses need to cooperate well, and the infusion rate of SonoVue ultrasound contrast agent and ATP needs to be adjusted appropriately according to the actual situation. In the image post-processing stage, image post-processing is performed by two doctors separately to ensure correct evaluation. For the results of inconsistent assessment, discussion is needed.
The machine learning-based analysis method of cardiac contrast echocardiography can be applied to myocardial segmentation, quantitative analysis and diagnosis of MCE images, it can also greatly improve the efficiency of MCE detection [28,29]. However, there are still many difficulties and challenges in this field. In the future, researchers are expected to solve the problems in this field, and make it one of the effective ways to solve the uneven distribution of medical resources and talents, and bring new changes to clinical practice.
5.
Conclusions
Myocardial contrast stress echocardiography is a non-invasive, bedside and inexpensive technique to early diagnose of coronary microvascular dysfunction. Using thermodilution method as gold standard, CMD was defined as MBF reserve < 2 by MCE. Diagnostic accuracy of MCE for CMD was 87.8%, sensitivity 95.7%, and specificity 84.7%. The Kappa coefficient of MCE and thermodilution was 0.727 (95% confidence interval: 0.57-0.88, P < 0.001), with strong consistency.
Acknowledgments
This work is supported by the Natural Science Foundation of China (NSFC) under grant number 62171408 and the Key Research and Development Program of Zhejiang Province (2020C03060, 2020C03016, 2022C03111, 2023C03088). The authors thank Dr. Jiri Sklenar from Narnar, LLC for helpful instruction of MCE processing.
Conflict of interest
The authors declare that there are no conflicts of interest.









 DownLoad:
DownLoad: