1. Introduction
Approximately one-third of all proteins are integral membrane proteins (MPs) [1,2,3,4], and they comprise more than half of all drug targets due to their prevalence in a wide variety of biological functions [5,6,7,8]. However, of the more than 106,000 proteins with experimentally determined three-dimensional (3D) structures in the Protein Data Bank (PDB) [2,9,10,11,12,13,14], only about 2,300 are MPs [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Further, according to Stephen White’s database of MPs of known structure (http://blanco.biomol.uci.edu/mpstruc/), only approximately 520 unique MP structures have been determined. The disparity between the importance of MPs and the available 3D structures reflects the technical difficulties associated with MP structure determination by X-ray crystallography and nuclear magnetic resonance (NMR) spectroscopy. To study MPs in their biologically relevant native conformation(s), a membrane mimic must be present during the experiment. While exciting progress in the field of crystallography are observed, such as the use of femto-second crystallography [21,22], robotics [23,24], and antibodies [1,3,4], MP crystallization remains a bottleneck. Limiting factors for solution NMR spectroscopy include line-broadening due to slow tumbling times of large MPs embedded in membrane mimics. Cryo-probes, increasingly powerful NMR magnets, selective labeling, and the development of solid-state NMR techniques [5] are continuously pushing the MP NMR field forward, but challenges remain [9,10,13,14].
1.1. EPR spectroscopy can serve as an alternative means of membrane protein structural characterization
Site-directed spin labeling electron paramagnetic resonance (SDSL-EPR) spectroscopy may serve as another means of MP structure determination because it has a number of advantages compared to more traditional methods. For example, proteins can be studied in native-like environments, such as in lipid bicelles or vesicles, and no crystallization is required. Because of the sensitivity of SDSL-EPR relatively small amounts of protein suffice, which is important in the case of MPs that are often difficult to express and purify. As unpaired electrons are only present at the two labeling sites, results are straight-forward to interpret as an error-prone resonance assignment process is omitted, unlike in NMR spectroscopy [8,15,16,17,18,19,20].
However, EPR is not without its disadvantages. Like NMR spectroscopy, structure determination is indirect in that the spectroscopic data are first converted to structural restraints [25,26,27,28]. Also, for distance measurements, SDSL requires the removal of all endogenous reactive cysteines in the protein and the mutation of the residues of interest into cysteines. As a result, in contrast to NMR spectroscopy, only one inter-residue distance can be measured per experiment. This results in low throughput and sparse datasets. In addition, the spin label itself introduces uncertainty, as the distance between the paramagnetic spin labels, which are at the tips of long and flexible side-chains, is measured. This distance then needs to be converted into a structural restraint based on MP backbone coordinates.
There are two principal ways to accomplish this conversion. Explicit approaches such as MMM [29], mtsslWizard [30], PRONOX [31,32], and RosettaEPR [33] model the spin label explicitly. Such programs can predict EPR distances with an accuracy of ~3 Å. Unfortunately, such methods are too slow to be integrated into de novo folding simulations such as RosettaTMH. As a rapid but less precise alternative we also implemented an implicit Knowledge-Based Potential (KBP) into RosettaEPR that computes a likelihood distribution for the Cβ distance based on the observed distance of the unpaired electron in the SDSL-DEER experiment [25,26]. This potential is used in calculations labeled RosettaTMH+EPR in the present manuscript.
1.2. Novel de novo membrane protein structure prediction tools are needed
In order to aid in MP structure determination, several computational methods have been developed. These methods can be divided into two categories: template-based comparative modeling, and de novo folding. Template-based methods, such has Modeller [34,35,36,37], Rosetta [38,39], SWISS-MODEL [40], and I-TASSER [41,42,43], are commonly used when the structure of a homologous protein exists. Template-based modeling methods are so named because they require a structural template onto which a target sequence can be threaded. For the sequence in question, a template structure, whether it is a sequence homolog or a structure exhibiting the same expected fold, must first be identified. Next, often after performing one or more sequence alignments, the target sequence is threaded onto the 3D coordinates of the template structure, thus replacing the sequence of the template with that of the target [44].
Even though significant advances are being made in the structure determination of additional GPCR or LeuT-fold structures, progress is slow when it comes to the determination of new MP folds. Thus, it is often difficult to identify a suitable template structure for MP comparative modeling because there are a limited number unique MP structures available in the PDB. Additionally, even though templates having a similar fold may exist, it is possible that the sequence homology between the target and the template is too low to be confidently detected. For example, of the more than 20 experimentally determined structures of G-protein coupled receptors (GPCRs), the majority are of class A, or class 1 (http://gpcr.scripps.edu/index.html) [45], even though there are five or six classes of GPCRs [46]. Similarly, while there are some structures of transporters, such as LeuT [47], vSGLT [48], BetP [49], and GadC [50], MPs having the LeuT fold perform a large variety of functions, show significant divergence in sequence, and can belong to a number of different protein superfamilies [51]. While comparative modeling based on an evolutionarily distant template can be useful for hypothesis generation, especially when combined with experimental methods in an iterative fashion [52], de novo structure prediction of MPs is needed in the absence of a structural template. Additionally, de novo folding methods allow for an unbiased exploration of the conformational space and can be used to complement comparative modeling in case of low similarity between template and target.
Compared to template-based MP modeling methods, there are only a handful of tools for de novo folding of MPs. RosettaMembrane was introduced in 2006 [53] and was later expanded to include full-atom scoring potentials [54]. Its structure prediction capabilities were limited to MPs of fewer than 150 amino acids. The addition of limited helix-helix contact restraints derived from sequence conservation allowed for accurate modeling of larger MPs - in four of twelve test cases models superimposable below a RMSD of 4 Å were observed [55]. One limitation was that this method could only account for one restraint at a time. Furthermore, the utility of RosettaMembrane in its current state is limited. For technical reasons that originate in the RosettaMembrane code base, it is not possible to de novo fold MPs with multiple restraints, such as those obtained from NMR and EPR.
Other methods to predict MP structure, such as FILM3, exhibit mild success for predicting large MPs, but they rely on correlated mutational information to score MP models. Of 71 MP sequences, FILM3 was able to correctly predict 100% of inter-helix contacts for 17 proteins. Upon comparison with two-dimensional slices of the experimental structures, 9 predicted structures had the correct fold [56,57]. EVfold_membrane is also a promising method for MP structure determination but also relies on information from evolutionary covariation [58]. BCL::MP-Fold, on the other hand, is independent of contacts predicted from correlated mutations. It reduces the conformational search space by assembling secondary structure elements (SSEs) combined with knowledge-based potentials (KBPs) to assess model quality [59]. The disadvantage of BCL-generated models is the lack of inter-helix loop regions. Additionally, it under-predicts secondary structural features often present in MPs, such as helical kinks because models are comprised of idealized α-helices.
1.3. RosettaTMH allows for folding of membrane proteins, both with and without experimental restraints
We have developed RosettaTMH to address the size limitation of other reported MP de novo folding methods. RosettaTMH assembles MP folds via rigid body perturbations of transmembrane helices (TMHs). However, unlike BCL::MP-Fold, 3- and 9-amino acid fragment insertions, as used in the traditional Rosetta de novo folding algorithm [53,55,60], are used to more thoroughly sample helical orientations and introduce bends and kinks. Throughout the de novo folding process, RosettaMembrane’s MP-specific scoring functions are used [53,54]. RosettaTMH can be combined with multiple experimental restraints, such as inter-residue distance information from EPR, which is an advantage compared to previously published RosettaMembrane folding protocols. This additional feature allows for improved sampling of native-like folds that are in agreement with empirical information.
RosettaTMH was benchmarked on 34 MPs of known structure. It was compared to the original RosettaMembrane folding algorithm, “MembraneAbinitio” [53,55] and the traditional fragment assembly-only method used for folding soluble proteins in Rosetta, “ExtendedChain” [61] but using the RosettaMembrane scoring function. In order to assess the performance of combining RosettaTMH with experimentally obtained structural data, EPR distance restraints were simulated for all MPs in the benchmark set. The purpose of the benchmark was to determine if these restraints increase the sampling of native-like MP folds. The simulated distance restraints were generated using the BioChemical Library (BCL, www.meilerlab.org) and the restraint-picking algorithm introduced by Kazmier, et al. [62]. We show that, by implementing the ability to fold MPs with structural restraints, native-like folds can be obtained for 30 MPs in the benchmark set. For the purpose of this manuscript we define a native-like fold as having a RMSD100SSE value smaller than 8 Å (read below).
2. Materials and Methods
2.1. The RosettaTMH de novo folding algorithm
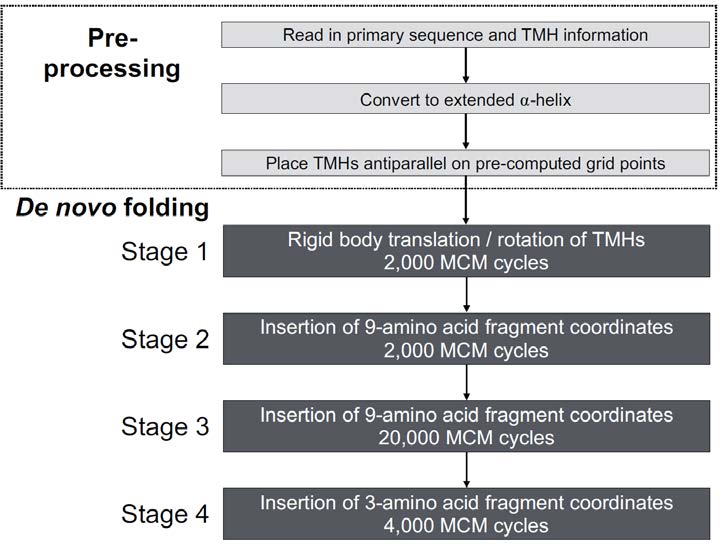
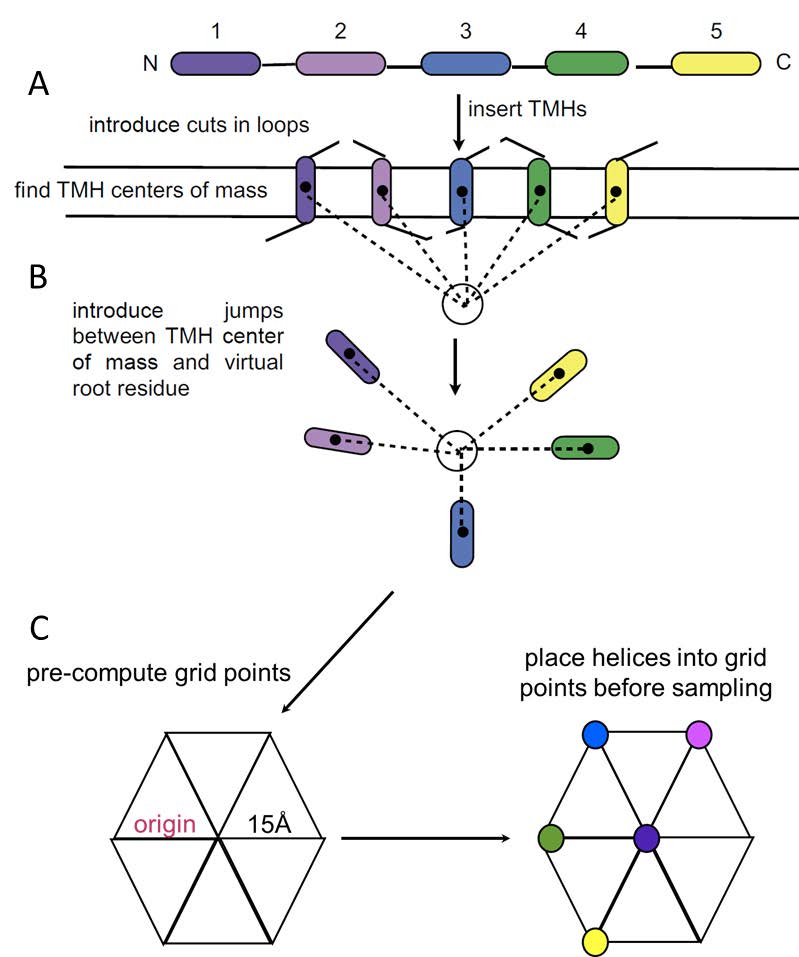
The RosettaTMH MP folding algorithm differs significantly from both the Rosetta folding algorithm for soluble proteins, “ExtendedChain” [61], as well as the published RosettaMembrane folding protocols [53,55]. The primary difference is that RosettaTMH allows for potentially enhanced sampling of MP folds by treating TMHs as rigid bodies. Each TMH can be rotated, translated, or transformed as an independent entity. In order to implement this new algorithm in the overall Rosetta folding framework, the model’s fold tree was modified. The fold tree of a protein model is a directed acyclic graph representing the connectivity of the model in internal coordinate space. This connectivity is distinct from chemical connectivity and enables Rosetta to rapidly move large sections of the protein independently [63,64]. In the case of a helical MP, a radial, or star-shaped, fold tree is used; therefore, the center of mass (CoM) of each TMH is connected to a central node (Figure 1).
Before de novo folding begins, each TMH is inserted into the implicit RosettaMembrane environment [53]. The CoM of each TMH is set at the membrane center, and the helices are aligned to the membrane normal such that each TMH is antiparallel to its sequential neighbors. The helices are arranged in a hexagonal grid and are initially separated from each other by 15 Å. The starting fold of the model is randomized; that is, the arrangement of helices in the hexagonal grid is different for each starting model (Figure 1).
2.2. Stages of de novo folding with RosettaTMH
The pre-processing and de novo folding stages of RosettaTMH are summarized in Figure 2.
Folding begins after the initialization of the model. The first stage of de novo folding consists entirely of rigid body transformations [53] performed in a Monte Carlo Metropolis (MCM) fashion [65,66]. For each MCM move, the TMH is allowed to either rotate by up to 0.1° about any axis or translate up to 0.5 Å in any direction from its current position. The conformation resulting from each transformation is scored according to the RosettaMembrane centroid-based scoring function. Stage 1 of folding consists of 2,000 MCM moves, and the RG and RosettaMembrane-specific “density” term are turned on [53]. These scoring terms aid in improving the compactness of the model. After the first stage, the model undergoes 9- and 3-amino acid fragment insertions using a protocol analogous to the one used for soluble proteins [53,61]. Briefly, in Stage 2,2,000 MCM cycles are performed, during which 9mer fragments are inserted onto the helical protein backbone. The density scoring term is turned off, and residue pairing, membrane environment, and membrane-specific penalties are added [53,54]. The density term is re-introduced in Stage 3, which consists of 10 inner cycles; during these inner cycles, the scoring function can be alternated if desired. However, for MPs, the scoring function is the same for each of two inner cycle sub-stages. Each sub-stage consists of 2,000 MCM cycles for inserting 9mer fragments, resulting in a total of 20,000 fragment insertions. Finally, the density term is up-weighted in Stage 4, and 4,000 MCM cycles of 3mer fragment insertions are performed. Note, that we omitted construction of loops between TMHs as we wanted to test the TMH folding protocol. An inter-helix distance score ensures that TMHs are close enough to allow for construction of loops (red below).
2.3. Setup of RosettaTMH parameterization and benchmarking datasets
The 34-protein benchmarking set exhibits a wide range of sizes and topological complexity. The number of EPR distance restraints simulated was computed as
|
@\# restraints = 0.2 \times \# a{a_{TMH}}@
|
Where
#restraints refers to the number of simulated EPR restraints generated, and
#aaTMH refers to the number of amino acids in TMHs defined in the experimental structures. This number of restraints was chosen because it is on the order of the maximal number of distance restraints that have been obtained for several MPs
[67,68,69,70]. The input files used (i.e., fragments, secondary structure prediction, span, lipophilicity, and native PDB files) were the same or based on those employed for benchmarking of BCL::MP-Fold
[59] and are provided in the Protocol Capture that accompanies this publication.
2.4. Simulation of EPR distance restraints using the BioChemical Library
Ten sets of EPR distance restraints were generated for each protein for the 34-MP benchmark. This was done to avoid bias resulting from using any single restraint set. The restraint selection algorithm developed by Kazmier, et al. [62] was employed. The algorithm optimizes the information content of the restraint set by maximizing the sequence separation between spin labeling sites. At the same time, the algorithm finds restraint sets that link all pairs of SSEs in the protein and excludes positions that are likely buried and unlikely to be labeled without disruption of the tertiary structure. In order to convert the resulting restraint sets to EPR-like distance restraints for testing during de novo folding, the Euclidian distances between the specified residues were determined from the MP experimental structures. Next, a spin label uncertainty was added to each distance, based on the cone model-based spin label statistics generated for the RosettaEPR KBP [26]. These statistics were generated by placing a pseudo-spin label in the form of a right-angle cone (based on methanethiosulfonate, or MTS) on exposed residue pairs in a database of over 3,500 proteins. The frequency of observed values for the calculated difference between spin label distance and Cβ distance (dSL-dCβ) were collected in a histogram, which was shown to match relatively well to experimentally determined dSL-dCβ values for T4-lysozyme and αA-crystallin. This histogram of spin label statistics quantifies the expected uncertainty associated with EPR distances measured on proteins spin labeled with MTS.
2.5. Optimization of EPR distance restraint scoring term weighting
The EPR distances for the residue pairs were simulated as described in the previous section. Preliminary benchmarking indicated that the EPR score used for the folding of T4-lysozyme [26] was insufficient to improve MP model quality of large MPs, such as rhodopsin. Instead, it was determined that a two-component scoring term was needed.
The modified EPR restraint potential for folding MPs consists of an energetic bonus derived from the aforementioned cone model statistics. Indeed, this energetic bonus is the same KBP used in the de novo folding of T4-lysozyme [26]. However, in addition to the KBP energetic bonus, the EPR restraint score contains an energetic penalty characterized by the equation:
|
@f\left( x \right) = \left\{ {(x−lb)2forx<lb0forlb≤x≤ub(x−ub)2forub<x≤ub+rswitchx−ub−rswitch+rswitch2forx>ub+rswitch
} \right.@
|
where
x is the currently measured distance within the model,
lb is the restraint lower bound,
ub is the restraint upper bound, and
rswitch is set to 0.5. This quadratic penalty is similar to that used for NOE-derived distance restraints in NMR structure calculations. The EPR scoring potential is designed such that the quadratic penalty is enforced if, during folding, the simulated model’s d
SL-d
Cβ value for a given residue pair is greater than −12.0 Å and less than 12.0 Å.
The weight of each EPR scoring term component was optimized separately. One thousand models of each of 9 proteins indicated in Table 1 were folded using RosettaTMH for each EPR restraint weighting scheme. Combinations of the weights for both components of the scoring term were systematically tested in a grid search. For each protein and each of 49 weighting schemes, the percentage of models having RMSD100SSE < 8 Å was computed, and the average of these values across the 9 proteins are reported in Table S1. The RMSD100SSE is defined as:
|
@RMS{D_{100}}SSE = RMSD\_SSE/\left( {1 + ln\sqrt {N/100} } \right)@
|
where
RMSD is root mean square distance,
SSE is secondary structural element, and
N is the number of residues. In addition, the enrichment was computed based on the models obtained from each weighting scheme (Table S2). Enrichment was computed as:
|
@enrichment = \frac{{TP}}{{TP + FP}} \times \frac{{P + N}}{P}@
|
where @\left( {P + N} \right)/P@ the ratio is set to 10, limiting the maximum possible enrichment to 10.0. The models were sorted according to Rosetta score. Models that fell within the top 10% by score were counted as “positive, ” (
P), and models whose scores fell into the bottom 90% by score were counted as “negative” (
N). The positives were then sorted by RMSD
100SSE relative to the native structures, and those models that fell within the top 10% by RMSD
100SSE were labeled “true positives” (
TPs). All other low-scoring models were considered “false positives” (
FPs).
Table 1. Proteins used for benchmarking.
| PDB | Chain | Domain | # Res | # TMH | Contact Order | # Restraints |
| 3SYO | | 76–197 | 122 | 2 | 14.4 | 12 |
| 2BG9 | A | 211–301 | 91 | 3 | 6.9 | 16 |
| 1J4N | | 4–119 | 116 | 3 | 15.2 | 17 |
| 2KSF | | 396–502 | 107 | 4 | 11.9 | 13 |
| 1PY6 (1PY7)a | | 77–199 | 123 | 4 | 13.3 | 20 |
| 2PNO | A | 2–131 | 130 | 4 | 13.6 | 22 |
| 2BL2 | | 12–156 | 145 | 4 | 20.7 | 25 |
| 2K73 | | 1–164 | 164 | 4 | 15.5 | 19 |
| 2ZW3 | A | 2–217 | 216 | 4 | 25.7 | 24 |
| 1IWG | | 336–498 | 163 | 5 | 17.4 | 26 |
| 1RHZ | A | 23–188 | 166 | 5 | 19.8 | 21 |
| 2YVX | A | 284–471 | 188 | 5 | 20.6 | 26 |
| 1OCC | C | 71–261 | 191 | 5 | 24.1 | 29 |
| 4A2N | | 1–192 | 192 | 5 | 22.4 | 24 |
| 1KPL | | 31–233 | 203 | 5 | 23.4 | 31 |
| 2BS2 | C | 21–237 | 217 | 5 | 17.5 | 29 |
| 3P5N | | 10–188 | 179 | 6 | 17.9 | 22 |
| 2IC8 | | 91–272 | 182 | 6 | 17.9 | 23 |
| 1PV6 | | 1–190 | 189 | 6 | 28.3 | 33 |
| 2NR9 | | 4–195 | 192 | 6 | 17.6 | 24 |
| 1OKCb | | 2–293 | 292 | 6 | 25.8 | 34 |
| 3B60b | A | 10–328 | 319 | 6 | 25.7 | 52 |
| 2KSY | | 1–223 | 223 | 7 | 20.1 | 37 |
| 1PY6b | | 5–231 | 227 | 7 | 25.2 | 36 |
| 3KCU | | 29–280 | 252 | 7 | 29.7 | 33 |
| 1FX8b | | 6–259 | 254 | 7 | 28.6 | 38 |
| 1U19b | | 33–310 | 278 | 7 | 25.0 | 41 |
| 3KJ6 | A | 35–346 | 311 | 7 | 39.5 | 31 |
| 3HD6b | | 6–448 | 403 | 12 | 43.6 | 59 |
| 3GIAb | | 3–435 | 433 | 12 | 62.5 | 64 |
| 3O0Rb | B | 10–458 | 449 | 12 | 30.6 | 69 |
| 3HFXb | | 12–504 | 493 | 12 | 68.0 | 63 |
| 2XUT | A | 13–500 | 488 | 14 | 42.8 | 71 |
| 2XQ2 | A | 9–573 | 565 | 15 | 71.8 | 79 |
| a Referred to as 1PY7 in this publication |
| b These proteins were used in RosettaTMH parameter optimization |
During EPR restraint weight optimization, the Rosetta radius of gyration (RG) scoring term was used with a weight of 4.25. Each restraint was scored independently, and the sum of individual restraint scores constitutes the total raw restraint score. The total restraint score was multiplied by a normalization factor that is equal to:
|
@weigh{t_{cst}} = \frac{{log\left( {\# cst} \right)}}{{\# cst}} \times \# aa@
|
Where
weightcst is the weight by which the entire restraint score is multiplied before it is added to the total Rosetta score, or energy,
#cst is equal to the number of simulated EPR restraints used, and
#aa is the number of residues in the protein. Because the total restraint score is the sum of individual restraint scores, the weighted restraint score can be represented by:
|
@cst\_scor{e_{weighted}} = average\left( {cst\_scor{e_{weighted}}} \right) \times log\left( {\# cst} \right) \times \# aa@
|
2.6. Benchmarking of RosettaTMH in the absence and presence of simulated EPR restraints
The generation of input files for this benchmark, except for the simulated restraints, is described in the work by Weiner, et al. on BCL::MP-Fold [59]. Briefly, the primary sequence of each protein listed in Table 1 was used to generate 3- and 9-amino acid fragment files required for de novo folding in Rosetta. The Rosetta spanfiles containing the TMH definitions were obtained by using predictions from OCTOPUS [71]. Rosetta lipophilicity files were also generated for each protein using the LIPS algorithm [72]. Five thousand models were folded from the primary sequence, using TMH information and the RosettaMembrane centroid-based scoring function [53]. When multiple EPR restraint sets were used, the number of total models generated per restraint set was equal to the total number of models generated divided by the number of different restraint sets (i.e., 10 sets of 500 models for each protein).
2.7. Computational details
All computations were performed using the Vanderbilt University Advanced Computing Cluster for Research and Education (ACCRE) on a combination of AMD Opteron and Intel Nehalem processor nodes or the Vanderbilt University Center for Structural Biology computing cluster on a variety of x86 computing processors.
2.8. Availability
The RosettaTMH source code is available in the Rosetta master branch, which is available to developers in the RosettaCommons via https://github.com/RosettaCommons. Rosetta revision numbers d592380 and d7b5a70 were used for RosettaTMH parameter optimization and benchmarking, respectively. The software licenses and the complete protocol capture for this work is available from the RosettaCommons (www.rosettacommons.org), as well as in the Supplemental Information. Information for obtaining software licenses for the BioChemical Library is available at www.meilerlab.org/bclcommons.
3. Results
3.1. Rosetta de novo folding benchmarked on 34 helical membrane proteins
Thirty-four α-helical MPs and MP subunits of known structure were chosen to test the RosettaTMH folding algorithm (Table 1). Nine of these proteins (underlined) were used for the initial testing and parameter optimization of the RosettaTMH protocol. These nine proteins were chosen because we wanted to design a method that would be primarily used for folding larger, complex MPs. While many MPs are oligomers, the present benchmarks includes only monomeric MPs or protomeric subunits of oligomeric MPs. Folding as well as EPR labeling strategies need to be adapted when moving to oligomeric MPs which is a focus of ongoing research but beyond the scope of this initial manuscript.
3.2. The optimal EPR restraint potential weighs both knowledge-based potential and quadratic penalty equally
De novo folding of soluble proteins with EPR restraints in Rosetta had been optimized previously [25,26]. However, it was found that, for MPs, a quadratic penalty was needed in addition to the EPR KBP energetic bonus to sufficiently improve conformational sampling of native-like folds where a ‘native-like’ fold is defined as having a RMSD100SSE value smaller than 8 Å. The EPR KBP and the quadratic penalty were weighted equally. The enrichment for folding was 2.93 (Table S2). RMSD100SSE and enrichment are defined in Materials and Methods.
As expected, the enrichment for de novo folding with EPR restraints was generally lower than folding with no restraints. This is because the number of false positives, or low-scoring, high-RMSD models, was higher when folding with simulated restraints. This is perhaps due to the higher promiscuity of the EPR restraints, which are broader than distance restraints resulting from NMR nuclear Overhauser effects (NOEs). Therefore, models that fulfill the simulated restraints and are lower-scoring have not always native-like fold. This phenomenon is generally observed across all 34 benchmarked MPs as well (Table S3).
3.3. Addition of EPR restraints significantly improves sampling for RosettaTMH and ExtendedChain
In order to assess the overall sampling capability of each folding protocol, we computed the percentage of models having an RMSD100SSE < 8 Å (FractionRMSD<8 Å, Table 2), which serves as a cutoff for determining if models have the correct fold. We also report the best RMSD100SSE (RMSD1st RMSD) obtained for each method and the mean RMSD100SSE of the five lowest-scoring models (RMSDtop5 score). As was observed with T4-lysozyme [25,26], the addition of EPR restraints increases the likelihood of obtaining the correct MP fold for both RosettaTMH and ExtendedChain. When looking at FractionRMSD<8 Å, followed by the RMSD10% RMSD and RMSDtop5 score, RosettaTMH performs better than ExtendedChain for 11 of 34 proteins, including the 6 largest proteins. Further, when compared to other Rosetta MP folding methods, RosettaTMH+EPR obtains the highest percentage of correctly folded models for 3 of the 13 medium-sized proteins, 2 of the 8 large proteins, and 3 of the 6 very large proteins. Interestingly, ExtendedChain+EPR performs best for de novo folding of medium-sized proteins (Table 2).
Table 2. Overall performance of de novo folding membrane proteins with Rosetta.
| | RMSDtop5 score | RMSD1st RMSD | FractionRMSD<8 Å |
| average RMSD100SSE to experimental structure of the top five models by score | lowest RMSD100SSE to experimental structure | percentage of models with a RMSD100SSE better than 8 Å |
| PDB | Membrane Ab Initio | Extended Chain | Extended Chain + EPR | Rosetta TMH | Rosetta TMH + EPR | Membrane Ab Initio | Extended Chain | Extended Chain + EPR | Rosetta TMH | Rosetta TMH + EPR | Membrane Ab Initio | Extended Chain | Extended Chain + EPR | Rosetta TMH | Rosetta TMH + EPR |
| 3SYO | 11.0 | 11.8 | 12.3 | 12.6 | 12.4 | 7.1 | 7.2 | 8.5 | 6.4 | 8.0 | 0 | 0 | 0 | 0 | 0 |
| 2BG9 | 6.3 | 9.7 | 9.1 | 12.5 | 8.4 | 4.0 | 4.2 | 4.6 | 5.7 | 4.3 | 0 | 23 | 30 | 2 | 25 |
| 1J4N | 9.7 | 7.8 | 8.0 | 12.9 | 11.3 | 5.0 | 4.7 | 4.4 | 6.7 | 7.4 | 13 | 14 | 28 | 0 | 1 |
| 2KSF | 8.0 | 9.1 | 10.0 | 9.4 | 10.6 | 5.2 | 5.7 | 5.9 | 5.0 | 5.8 | 21 | 10 | 15 | 1 | 9 |
| 1PY7 | 4.9 | 6.1 | 4.2 | 11.1 | 7.7 | 2.2 | 2.4 | 2.5 | 5.6 | 4.5 | 66 | 67 | 58 | 1 | 23 |
| 2PNO | 7.6 | 8.7 | 7.0 | 12.3 | 8.4 | 3.0 | 3.2 | 3.3 | 7.5 | 5.5 | 29 | 21 | 47 | 0 | 11 |
| 2BL2 | 6.1 | 5.5 | 4.7 | 11.5 | 7.0 | 2.4 | 2.5 | 2.8 | 5.5 | 4.0 | 71 | 55 | 68 | 0 | 39 |
| 2K73 | 9.7 | 10.2 | 10.2 | 12.7 | 10.9 | 5.9 | 4.8 | 6.8 | 7.9 | 6.7 | 2 | 1 | 1 | 0 | 2 |
| 2ZW3 | 13.1 | 12.9 | 13.0 | 16.0 | 13.2 | 8.7 | 9.9 | 10.5 | 10.1 | 9.8 | 0 | 0 | 0 | 0 | 0 |
| 1IWG | 7.3 | 9.1 | 7.3 | 12.9 | 8.4 | 5.0 | 5.5 | 4.4 | 8.1 | 5.9 | 16 | 4 | 48 | 0 | 13 |
| 1RHZ | 10.1 | 10.7 | 8.8 | 11.6 | 11.5 | 6.1 | 6.6 | 6.1 | 8.5 | 7.7 | 1 | 1 | 10 | 0 | 1 |
| 2YVX | 9.2 | 9.0 | 7.9 | 14.7 | 9.0 | 5.9 | 6.0 | 5.1 | 8.2 | 6.7 | 5 | 1 | 20 | 0 | 6 |
| 1OCC | 11.3 | 10.4 | 10.4 | 13.1 | 8.4 | 6.7 | 7.0 | 7.2 | 7.9 | 5.4 | 1 | 0 | 1 | 0 | 17 |
| 4A2N | 8.4 | 9.2 | 9.4 | 11.2 | 10.5 | 5.4 | 6.2 | 6.3 | 7.8 | 7.2 | 4 | 1 | 6 | 0 | 2 |
| 1KPL | 13.2 | 14.4 | 11.8 | 15.1 | 12.7 | 10.0 | 10.7 | 7.9 | 11.1 | 9.5 | 0 | 0 | 1 | 0 | 0 |
| 2BS2 | 10.0 | 9.7 | 10.0 | 13.5 | 10.1 | 6.1 | 5.3 | 5.8 | 8.8 | 6.9 | 1 | 1 | 6 | 0 | 3 |
| 3P5N | 9.5 | 10.4 | 9.5 | 12.6 | 11.7 | 5.3 | 6.0 | 6.9 | 9.5 | 9.0 | 2 | 1 | 2 | 0 | 0 |
| 2IC8 | 9.1 | 9.4 | 9.1 | 11.5 | 10.2 | 5.3 | 5.0 | 6.1 | 8.7 | 7.1 | 4 | 1 | 5 | 0 | 1 |
| 1PV6 | 10.4 | 10.1 | 8.1 | 11.5 | 8.1 | 5.7 | 6.4 | 5.1 | 8.0 | 5.4 | 4 | 1 | 18 | 0 | 15 |
| 2NR9 | 10.2 | 10.9 | 9.8 | 12.2 | 11.3 | 5.8 | 6.9 | 6.3 | 8.6 | 7.4 | 2 | 0 | 3 | 0 | 1 |
| 1OKC | 12.3 | 12.5 | 13.1 | 12.6 | 11.9 | 9.0 | 10.8 | 8.9 | 9.2 | 8.7 | 0 | 0 | 0 | 0 | 0 |
| 3B60f | 9.8 | 9.7 | 6.3 | 13.7 | 9.7 | 6.3 | 6.1 | 4.1 | 9.2 | 6.0 | 2 | 1 | 38 | 0 | 10 |
| 2KSY | 8.9 | 8.4 | 6.8 | 12.8 | 8.5 | 3.9 | 4.2 | 4.5 | 7.7 | 5.1 | 30 | 15 | 28 | 0 | 19 |
| 1PY6f | 8.0 | 8.5 | 8.2 | 12.2 | 7.9 | 3.9 | 5.1 | 5.2 | 7.8 | 5.2 | 27 | 9 | 15 | 0 | 18 |
| 3KCU | 10.6 | 10.3 | 9.9 | 11.9 | 10.8 | 6.3 | 6.9 | 6.4 | 9.7 | 7.9 | 1 | 0 | 2 | 0 | 0 |
| 1FX8f | 10.7 | 11.3 | 10.5 | 12.4 | 10.4 | 7.8 | 8.3 | 7.7 | 8.4 | 8.0 | 0 | 0 | 1 | 0 | 0 |
| 1U19f | 12.7 | 14.6 | 11.8 | 12.4 | 8.7 | 9.2 | 11.4 | 8.4 | 8.7 | 6.1 | 0 | 0 | 0 | 0 | 7 |
| 3KJ6 | 14.6 | 15.2 | 15.5 | 15.6 | 15.3 | 11.5 | 12.1 | 12.0 | 12.4 | 12.7 | 0 | 0 | 0 | 0 | 0 |
| 3HD6f | 10.6 | 16.0 | 12.0 | 13.2 | 10.9 | 7.5 | 12.4 | 9.1 | 10.3 | 8.5 | 0 | 0 | 0 | 0 | 0 |
| 3GIAf | 14.1 | 25.5 | 13.9 | 14.2 | 12.0 | 11.8 | 17.2 | 9.2 | 11.6 | 9.5 | 0 | 0 | 0 | 0 | 0 |
| 3O0Rf | 10.1 | 24.0 | 11.2 | 13.0 | 10.0 | 6.4 | 18.6 | 7.6 | 8.9 | 6.5 | 2 | 0 | 1 | 0 | 4 |
| 3HFXf | 13.5 | 29.9 | 13.5 | 13.1 | 11.6 | 10.0 | 22.2 | 10.2 | 10.6 | 8.7 | 0 | 0 | 0 | 0 | 0 |
| 2XUT | 14.3 | 25.1 | 15.1 | 16.2 | 15.0 | 12.4 | 20.2 | 12.6 | 14.6 | 12.9 | 0 | 0 | 0 | 0 | 0 |
| 2XQ2 | 15.8 | 35.9 | 16.0 | 16.6 | 15.7 | 13.6 | 25.5 | 12.9 | 14.8 | 13.7 | 0 | 0 | 0 | 0 | 0 |
| mean | 10.3 | 13.0 | 10.1 | 13.0 | 10.6 | 6.8 | 8.7 | 6.9 | 8.8 | 7.5 | 10 | 7 | 13 | 0 | 7 |
| stddev. | 2.6 | 7.0 | 2.9 | 13.0 | 10.6 | 2.8 | 5.8 | 2.7 | 2.2 | 2.4 | 18 | 15 | 19 | 0 | 10 |
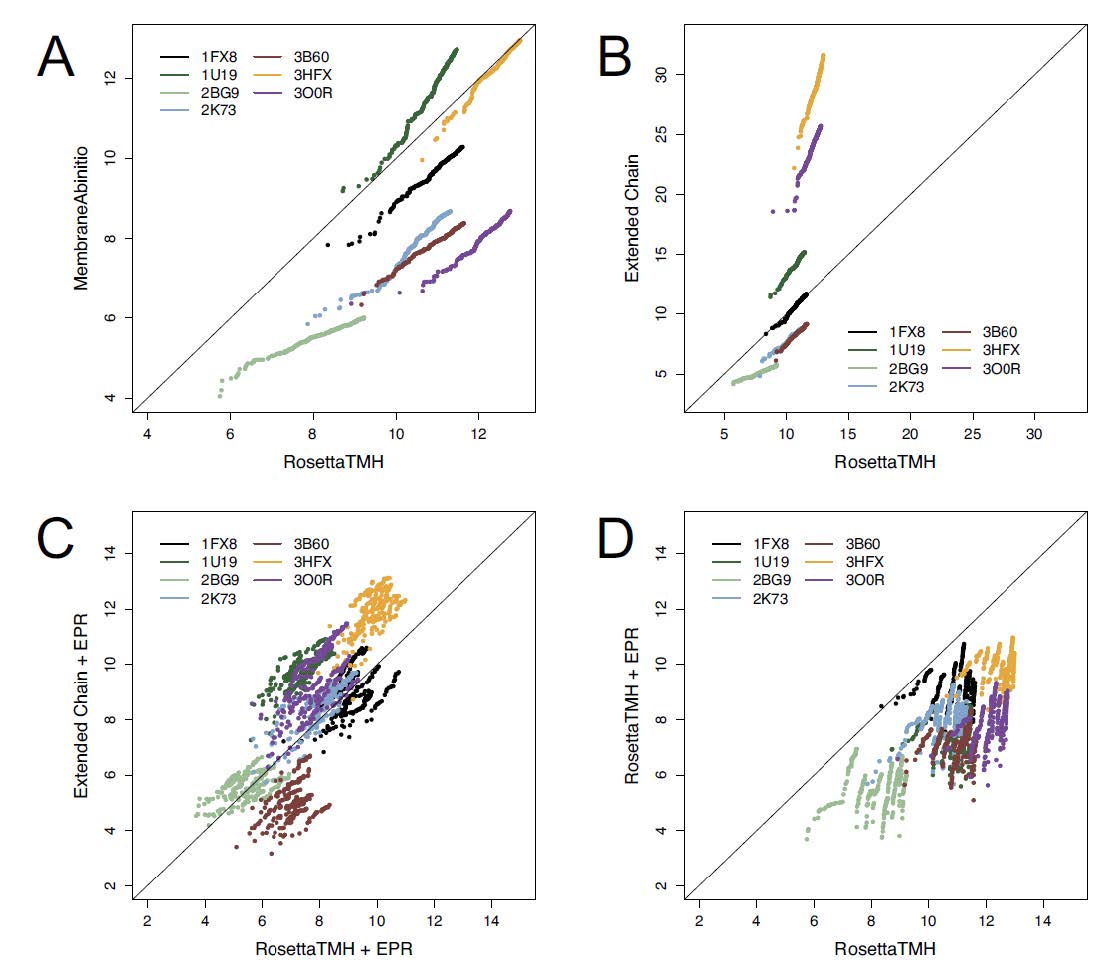
3.4. De novo folding with RosettaTMH for large proteins
A representative subset of 7 proteins was chosen from the 34-protein benchmark set for further RMSD100SSE analysis. For each protein and for each folding method, the RMSD100SSE values were sorted from lowest to highest, and the top 5% of models by RMSD100SSE were selected. Next, RMSD100SSE vs. RMSD100SSE plots comparing RosettaTMH and RosettaTMH+EPR with the other Rosetta MP folding methods were generated. This analysis clarifies a few key conclusions concerning RosettaTMH. First, when no EPR restraints are used, MembraneAbinitio and ExtendedChain outperform RosettaTMH for small- or medium-sized MPs. Second, RosettaTMH+EPR samples more lower-RMSD conformations for larger MPs when compared to RosettaTMH and ExtendedChain (distance restraints cannot be used with MembraneAbinitio). Finally, RosettaTMH performance is comparable to MembraneAbinitio and ExtendedChain for 3HFX and 1FX8, respectively, while RosettaTMH+EPR and ExtendedChain+EPR are comparable when folding 1FX8 (Figure 3).
3.5. Addition of EPR restraints primarily responsible for improvement seen in RosettaTMH folding
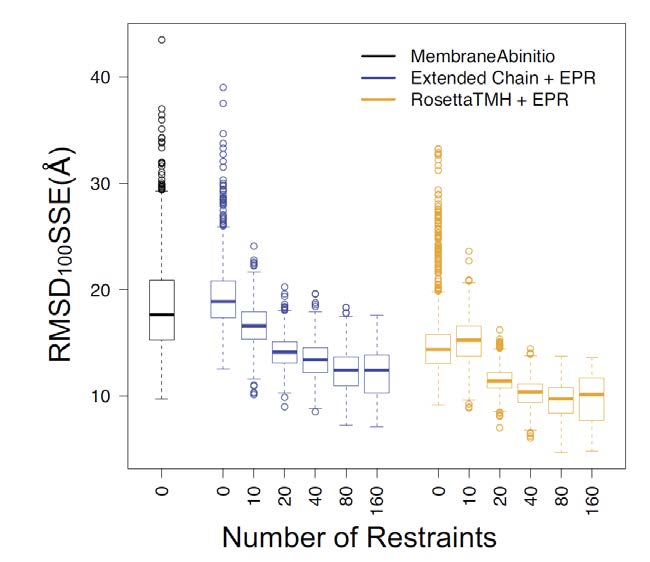
The MembraneAbinitio folding algorithm was first benchmarked on a dataset of relatively small proteins and performed best with small helical bundles [53]. However, it was found that MPs having more complex folds posed a much more difficult challenge, one which folding with experimental restraints and/or a new sampling algorithm could possibly address. Further, the addition of the RosettaEPR distance restraint potential improves sampling of native-like folds significantly. This appears to be primarily due to the influence of the EPR restraints, as folding with ExtendedChain+EPR also increases sampling efficiency to include the correct fold. In order to test this hypothesis, rhodopsin (PDB ID: 1U19 [73]) was selected for an in-depth analysis of the relationship between the number of EPR restraints and overall conformational sampling ability.
Rhodopsin was folded using all of the Rosetta methods listed in Table 2. However, for RosettaTMH+EPR and ExtendedChain+EPR, multiple sets of models were generated based on whether 0, 10, 20, 40, 80, or 160 simulated EPR distance restraints were used. Unlike in the 34-protein benchmark, only one EPR restraint set for each scenario was generated, and 1,000 models were folded for each case. Box-and-whisker plots of the resulting RMSD100SSE distributions are displayed in Figure 4. When no restraints are used, MembraneAbinitio and folding from an extended chain perform similarly, while RosettaTMH generally appears to generate lower-RMSD models. When using 10 restraints, RosettaTMH+EPR and ExtendedChain+EPR exhibit similar median RMSD100SSE values, but RosettaTMH+EPR samples a wider range of conformations. However, when 20 or more restraints are used, RosettaTMH+EPR is consistently better in sampling the correct fold. As expected, the number of outliers correlates inversely with the number of restraints.
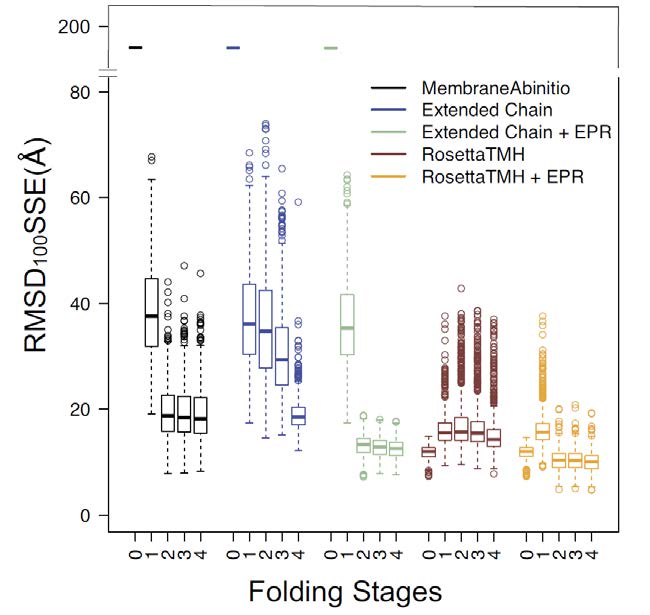
3.6. Detailed analysis of individual de novo folding stages indicate rigid body sampling not necessary
In addition to studying the overall performance of RosettaTMH with and without EPR restraints, the ability of the protocol to sample MP folds during each stage of folding (see Figure 2) was also analyzed. As with the above experiment, rhodopsin was chosen as an example protein, and only one set of 41 optimally weighted restraints was used. For each folding method, 1,000 individual trajectories were run, and the conformations before folding began and after each stage of folding were output. Then, similar to in Figure 4, the RMSD100SSE distributions for each folding stage were plotted. The first step in the Rosetta MembraneAbinitio folding algorithm (Stage 0), samples a single, high scoring, extended-chain conformation. For MembraneAbinitio and ExtendedChain, model quality significantly improves from initiation to Stage 1 and then from Stage 1 to Stage 2. In contrast, RosettaTMH-generated model accuracy decreases during Stage 1 of folding. That is, the rigid body sampling causes the quality of rhodopsin models to decrease. The RMSD100SSE values do not improve significantly for Stages 2-4 when no restraints are used. When EPR restraints are used, the models’ accuracy improves from Stage 1 to Stage 2 but does not change significantly after Stage 2. This was also observed for ExtendedChain+EPR.
3.7. RosettaTMH-generated models exhibit large inter-helical distances
RosettaTMH assembles MP folds by breaking up the proteins into individual TMHs and allowing the helices to move as independent rigid bodies. The resulting arrangements could result in distances between subsequent SSEs that cannot be connected by a loop. In order to determine if the SSEs can be connected by loops, the Euclidian distance between subsequent SSEs was measured for all 34 native MPs, as well as for the 5,000 models for all 34 benchmark MPs folded with and without EPR restraints. For each protein, the percentage of models in which all loops could be theoretically or realistically closed was determined. The maximum Euclidian distance theoretically possible (“Maximum Possible”) was computed as:
|
@Maximum Possible = \left( {3.8*\left( {LoopLength - 1} \right)} \right)@
|
where
LoopLength refers to the number of residues in the inter-helix loop. These percentages were then grouped into four categories based on protein size (see
Table 1) and whether or not EPR restraints were used during
de novo folding. The resulting percentages of models having closeable loops are summarized in box-and-whisker plots in Figure S1.
Generally speaking, RosettaTMH, either with and without EPR restraints, fails to reflect the dependence of Euclidean distance from loop length accurately. Indeed, every protein had at least five models in which all inter-helix distances can theoretically be spanned by a loop, but only a small percentage - if any - exhibit native-like inter-helix distances. Unsurprisingly, the addition of EPR restraints did improve the possibility of generating models with closeable loops in the majority of cases. However, for the very large MPs, no models exhibited native-like loop distances, and of the large MPs, only 0.04% of 1FX8 models had this characteristic, even when restraints were used (S4 Table).
3.8. Guidelines for choosing a Rosetta membrane protein modeling protocol
Based on the analysis presented in this work, we have developed a proximate guide for choosing which Rosetta MP modeling protocol to use based on the protein of interest (Figure S2). First, de novo folding should ideally be used only when there is no protein of ≥ 30% sequence homology for which there is a structure available. Next, Rosetta is currently only capable of de novo folding primarily helical MPs. If the protein of interest has fewer than 200 residues, we recommend folding with MembraneAbinitio (no restraints) or from an extended chain (with restraints). However, if the protein is large and relatively complex, MembraneAbinitio is recommended. Finally, RosettaTMH would be suitable for folding large MPs if experimental restraints, such as those from EPR or NMR, are available.
4. Discussion
We are introducing a new de novo folding algorithm for MPs. This initial implementation is already on par with other methods for folding large MPs within Rosetta. It has some advantages: One advantage is that experimental restraints can be incorporated, a feature that earlier folding protocols lacked. We illustrate this feature using simulated EPR distance restraints. The second advantage is the very short run time and an observed tendency to work better for large MPs.
4.1. EPR restraints significantly assist in obtaining models with the correct fold
The results in Table 2 and Figure 3-5 indicate that, for large and very large MPs, the conformational search space of MP structures must be limited in order to obtain de novo-folded models with native-like folds. The MembraneAbinitio protocol attempts to accomplish this by folding MPs “from the inside out.” That is, a TMH in the middle of the protein sequence is inserted into the implicit membrane environment first. Next, either TMHs N- or C-terminal to the initially inserted TMH are folded into the membrane via fragment-based assembly, beginning with the TMH adjacent to the starting TMH. Then, the TMHs on the other side (in terms of sequence) are folded in the same manner [53].
While MembraneAbinitio was able to generate models with RMSD100SSE < 8 Å for over 26 of the 34 proteins tested. For the remaining 8 cases in which no correctly folded models were obtained, the addition of EPR restraints did enable other folding protocols to do so (Table 2). Indeed, for majority of benchmarked proteins, the MembraneAbinitio protocol performs better than either RosettaTMH or folding from an extended chain when EPR restraints are not used. However, when EPR restraints were used, the additional restraints often resulted in more models having the correct fold. This is important because MembraneAbinitio, unlike RosettaTMH, cannot take EPR restraints into account.
Therefore, for MPs of more than 4 TMHs and 145 residues, it is advantageous to include structural restraints, such as those available from NMR, EPR, etc. If one does employ such restraints, the traditional folding method, ExtendedChain, appears to be better suited for medium-sized MPs. On the other hand, when looking at MsbA (3B60), rhodopsin (1U19), and nitric oxide reductase (3O0R), RosettaTMH shows promise for de novo folding larger MPs, such as GPCRs, channels, and transporters (Table 2).
4.2. Optimization of RosettaTMH folding protocol may lead to further improvement
Even though Rosetta is now capable of folding MPs that have the correct fold and is sometimes able to recover intra-helical features, these models are not yet accurate enough to be used as the input to full-atom refinement using the RosettaMembrane all-atom scoring functions [54]. Typically, models of approximately 2.0 Å RMSD100SSE relative to the native structure are required in order to successfully obtain atomic detail information [74].
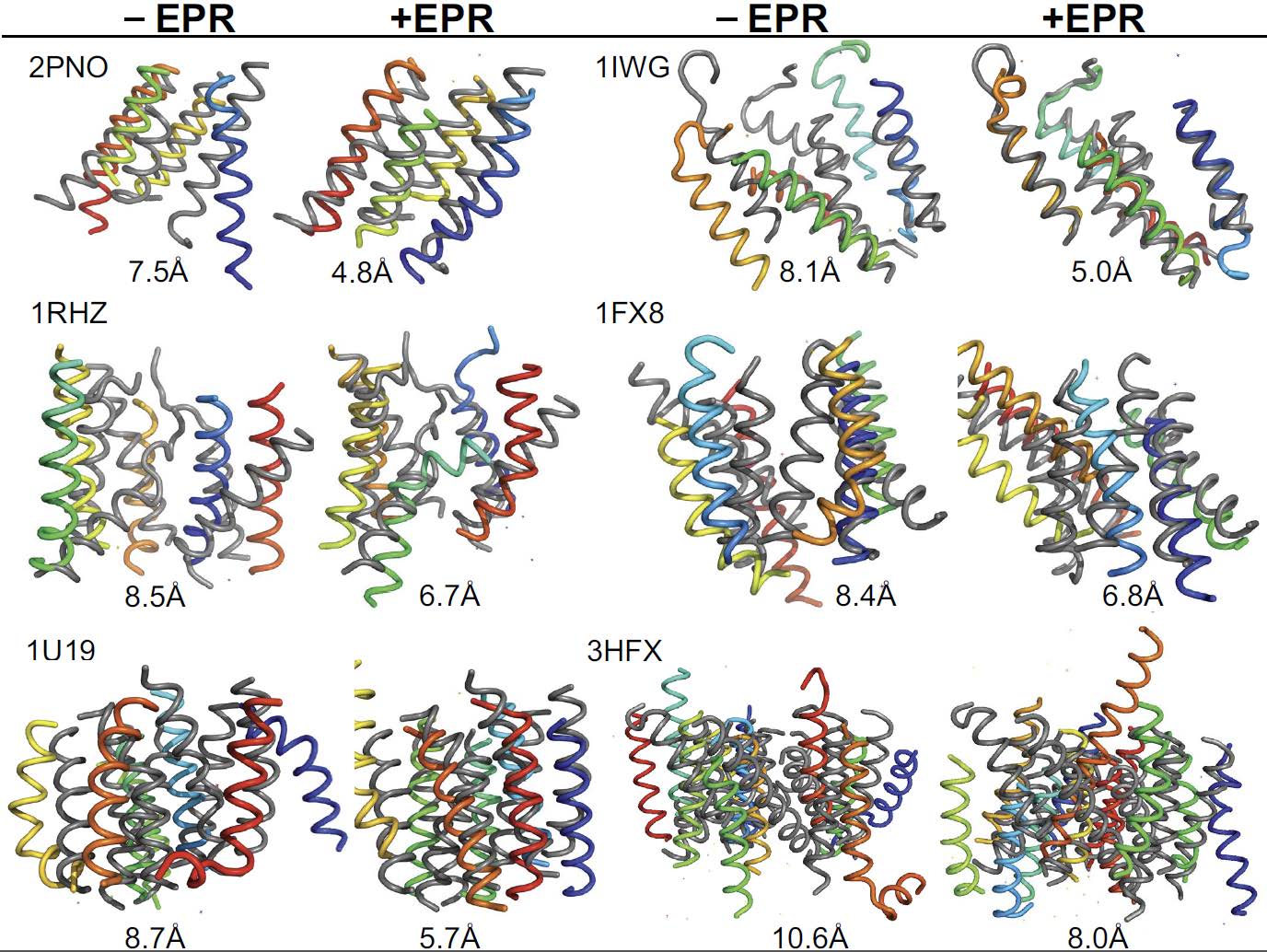
Based on the information in Figure 5, one next step in protocol optimization would be to forego the rigid body sampling in Stage 1 of RosettaTMH folding. It is expected that the initial set of rigid body transformations result in less viable MP conformations (e.g., TMH out of the membrane, lying too orthogonal to the membrane normal, or too far apart in 3D space). The fragment insertions in Stages 2-4 are then not able to recover the correct fold. This is supported by the lowest-RMSD models displayed in Figure 6 and the data in Table S4, which show that there is a general lack of inter-helical packing and native-like placement that is not remedied by fragment insertions. Not surprisingly, the addition of EPR restraints assists in improving packing and in the recovery of helical features (Figure 6).
4.3. Implementation of loop closure filter and knowledge-based potential for de novo folding with RosettaTMH could improve inter-helix packing
In order to create a radial fold tree for each model, the original simple fold tree must be “cut” to maintain the data structure’s acyclic nature. For folding with RosettaTMH, these cutpoints are chosen within the MP loops (Figure 1). However, now that the TMHs can move independently from one another, another external force must be applied to keep the TMHs in relatively close proximity, as they will otherwise drift apart and not exhibit native-like packing (Figure S2 and 6, Table S4). One approach is to integrate a loophash filter, which would ensure that TMHs that would normally be connected by a loop remain close enough in Cartesian space such that the inter-helical loop can be successfully rebuilt at a later stage.
The loophash filter is based on work published by Tyka, Jung, and Baker [75]. In the protocol introduced by the authors, the loophash algorithm allows for extremely fast rebuilding of protein segments by rapidly determining if a loop of a given sequence length can span the distance defined by two endpoints. A hash lookup table is generated for a loop of a given sequence length, and the hashes in the table refer to specific protein segments found in a database of non-homologous proteins of known structure. In addition to the loophash, or loop closure, filter, the implementation of a loop distance KBP, such as that used by BCL::Fold [76,77] could also be beneficial. While the loop closure filter would assist in ruling out models where TMHs could not theoretically be connected, and the loop distance KBP would provide an energetic incentive to place TMHs in more native-like conformations.
4.4. Increased sampling may be needed in order to better observe RosettaTMH’s performance
The RosettaTMH folding protocol appears to be a more rapid means of folding MPs than MembraneAbinitio and fragment-based assembly alone (Figure S3). This is probably a result of the lack of fragment insertions, and thus recalculation of torsion angles, during the first stage of folding. However, this decreased amount of fragment insertion may be the cause of the generation of lower-quality models. In any case, the significant speedup in model production allows for the generation of many more models. This increased sampling speed may be beneficial for obtaining higher quality models of large MPs when using a more optimized RosettaTMH protocol.
5. Conclusion
RosettaTMH is a new de novo folding protocol that assembles MP folds from the rigid body movements of TMHs, followed by peptide fragment insertions. This approach, along with the significantly decreased time required to fold models, allows for increased sampling of conformational space, which is important for the structure prediction of more complex proteins, such as GPCRs, transporters, and channels. RosettaTMH, unlike MembraneAbinitio, allows for the folding of MPs with experimental restraints. Further, while the new folding protocol alone improves sampling, the addition of experimental restraints may be necessary to obtain native-like folds, which is especially important for determination of MPs for which there is no structural template.
Author Contributions
J.M. and S.H.D. conceived the RosettaTMH modeling protocol for use within the Rosetta. S.H.D. was primarily responsible for the implementation and testing of it. S.H.D. created the first version of this manuscript including tables and figures. S.L.D. was involved in the implementation of RosettaTMH within the Rosetta framework, as well as merging the RosettaTMH source code with the publicly released version of Rosetta. A.L.F. performed thorough testing of the RosettaTMH Protocol Capture and provided feedback to S.H.D. J.M. supervised the project and finalized the manuscript.
Acknowledgements
The authors would like to thank Drs. Frank DiMaio, Steven Lewis, and other members of the RosettaCommons for their assistance in the development of RosettaTMH. Axel Fischer was also very helpful in providing protocols on simulating EPR distance restraints in the BCL, and Dr. Brian Weiner provided many of the Rosetta-ready input files for the benchmark set.
Supporting Information
Table S1: Percentage of correctly folded models obtained for folding 1,000 models of 9 membrane proteins with RosettaTMH using a variety of restraint score weighting schemes
Table S2: Enrichment obtained for folding 1,000 models of 9 membrane proteins with RosettaTMH using a variety of restraint score weighting schemes
Table S3: Enrichment obtained for folding 5,000 models of 34 membrane proteins with and without simulated EPR distance restraints
Table S4: RosettaTMH ability to generate models with loops that can or are likely to be closeable
Figure S1: Percentage of models with closeable loops generated by RosettaTMH
Figure S2: General guidelines for membrane protein modeling in Rosetta
Figure S3: Average time required for de novo folding
Protocol: Protocol Capture for the work presented









 DownLoad:
DownLoad: