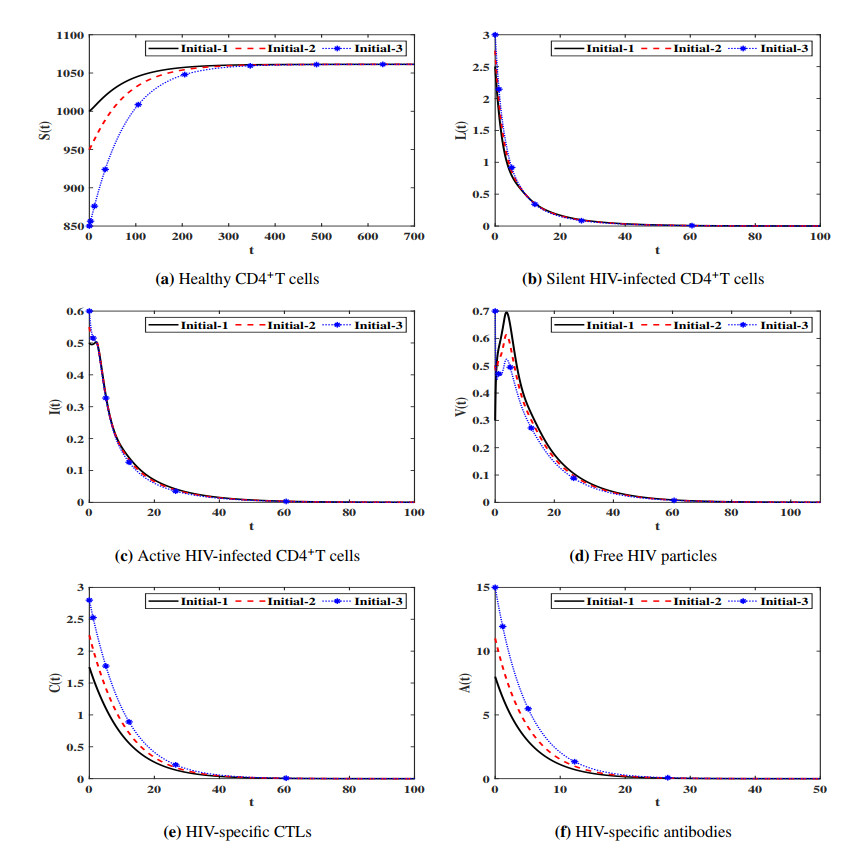
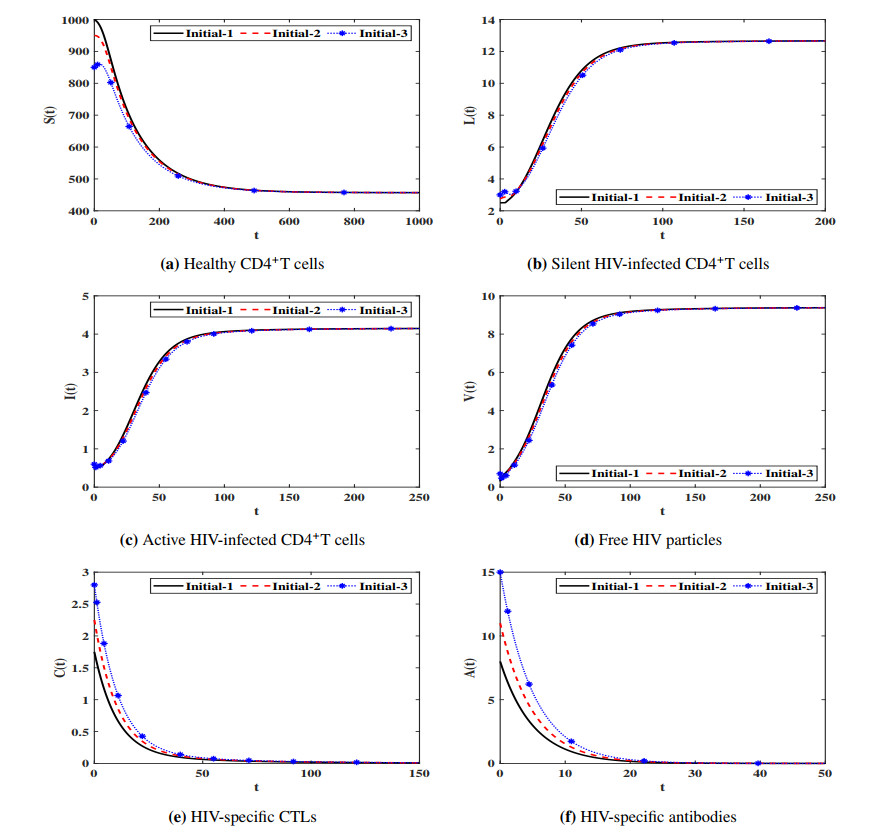
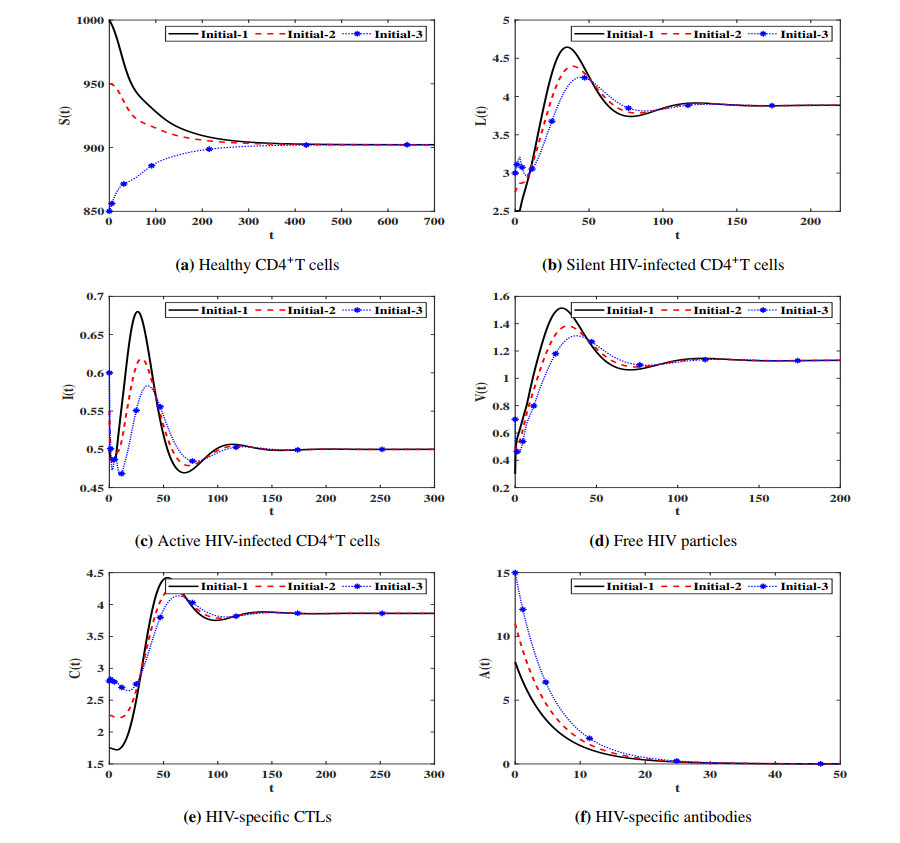
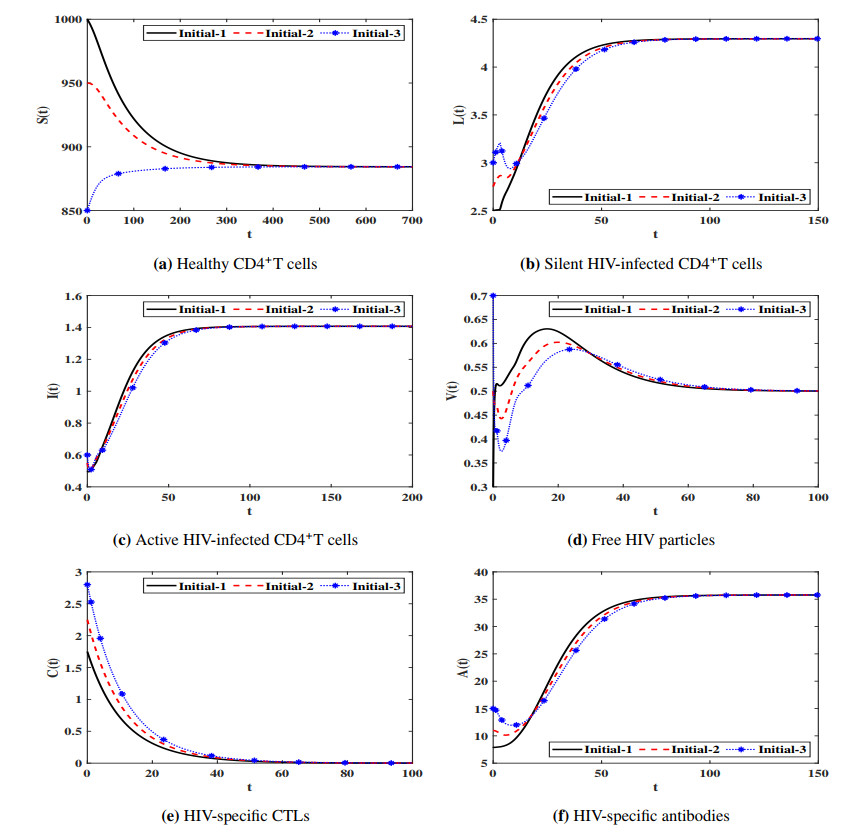
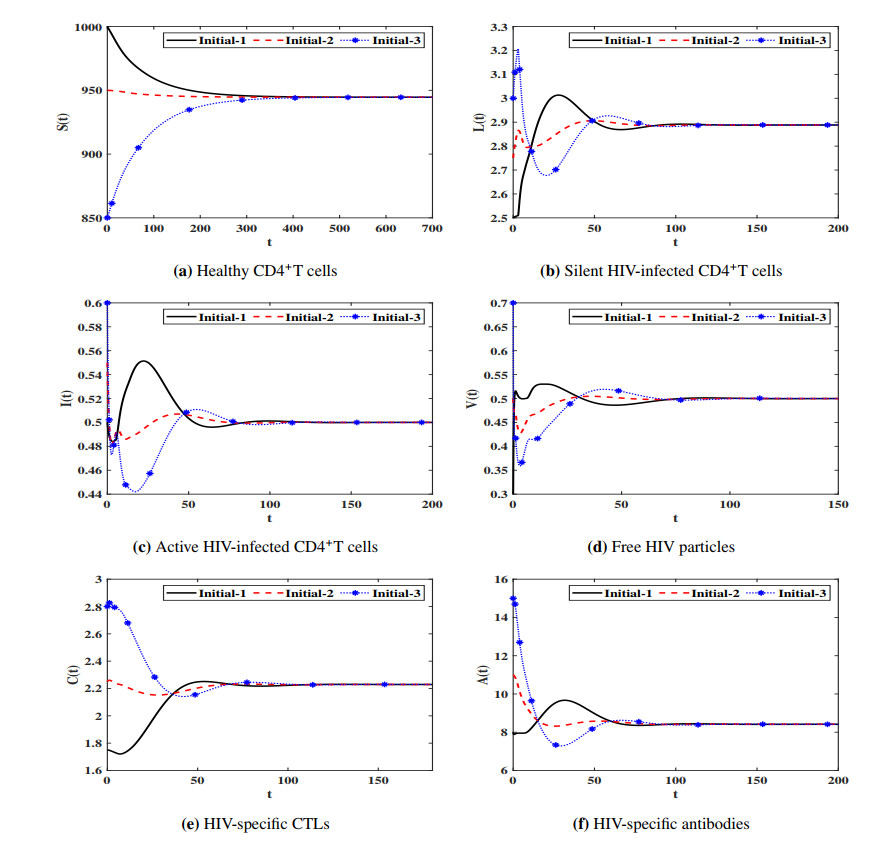
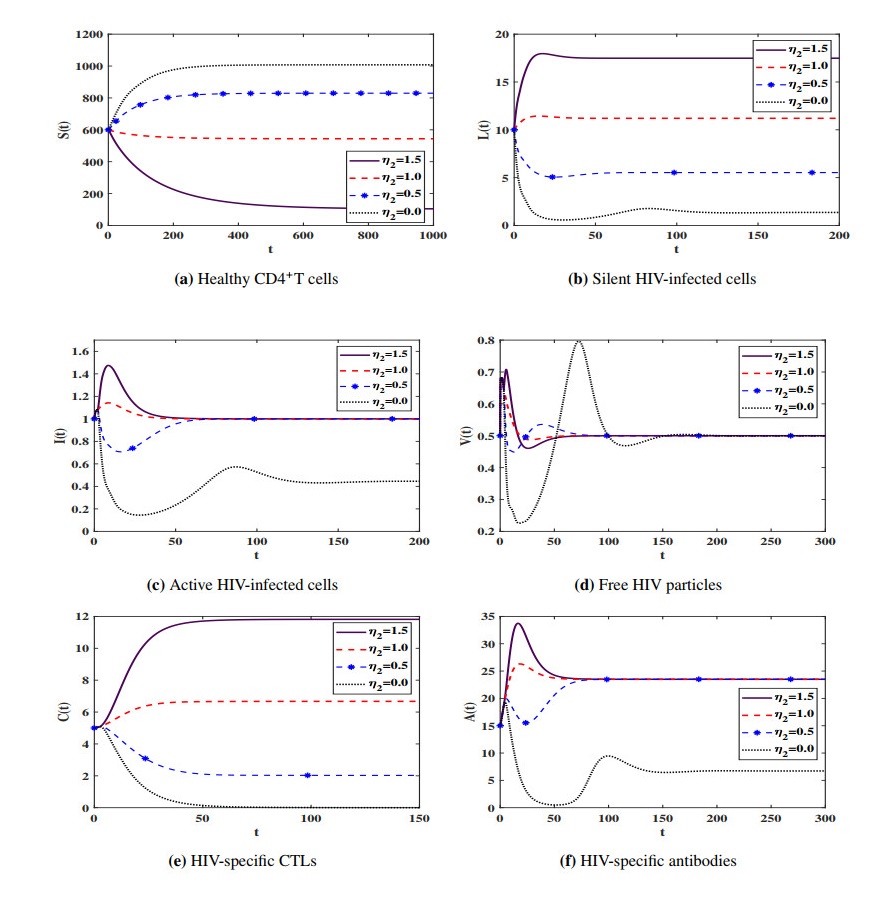
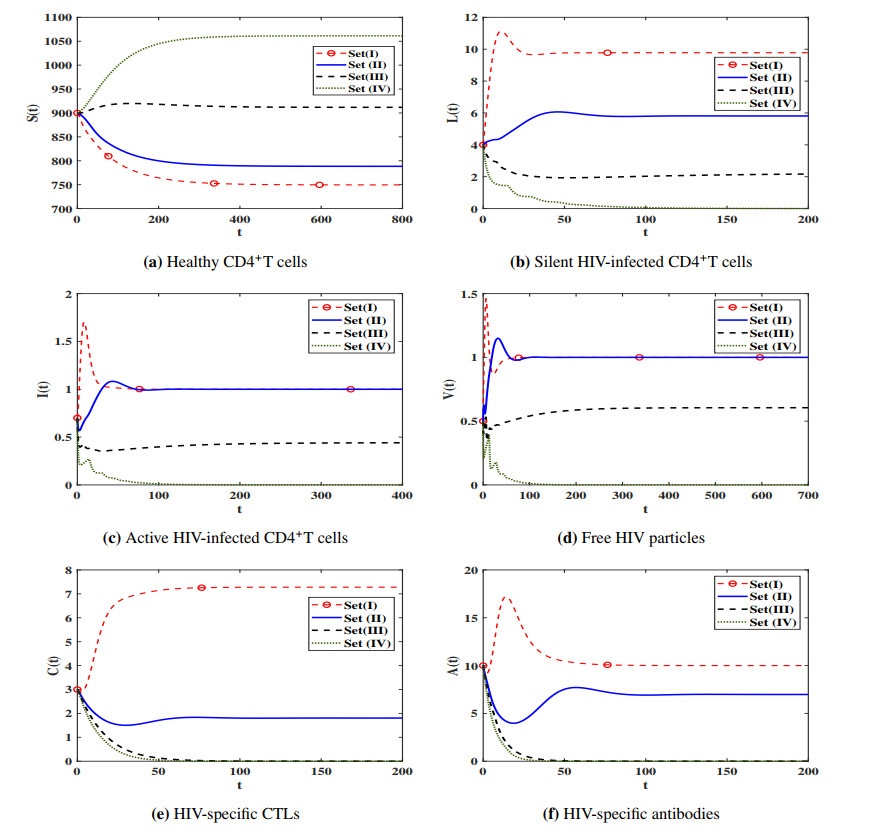
Stability of an adaptive immunity delayed HIV infection model with active and silent cell-to-cell spread

1.   Introduction

High-resolution (HR) magnetic resonance imaging (MRI) unveils enhanced structural details and textures, essential for accurate diagnosis and pathological analysis of bodily organs. However, the resolution of the medical image is often constrained by factors like imaging hardware limitations, prolonged scanning durations, and lower signal-to-noise ratios (SNR) ^[1]. Improving spatial resolution usually involves the sacrifice of decreased SNR and increased scanning time ^[2].

Recently, super-resolution (SR) has emerged as a post-processing technique for upscaling the resolution of MRI images ^[2,3,4]. Existing SR methods include interpolation-based, regularization-based, and learning-based methods ^[5,6]. Interpolation methods usually blur sharp edges and can hardly recover fine details or handle complex textures ^[7]. Using deep convolutional neural networks (CNN) in the SR image has shown notable success in high-quality reconstruction performance ^[8]. After the pioneering work of SRCNN ^[9], a multitude of CNN-based SR models have been proposed, such as EDSR ^[10], RCAN ^[11], and SwinIR ^[12], significantly improving SR performance. The superior reconstruction performance of CNN-based methods, such as SAN ^[13] and HAN ^[14], primarily stems from their deep architecture, residual learning, and diverse attention mechanisms ^[7,15]. Deepening the network's layers can enlarge receptive fields and facilitate its ability to comprehend the intricate mapping between the low-resolution (LR) inputs and HR counterparts. The adoption of residual learning facilitates deeper SR networks, as it effectively mitigates issues associated with gradient vanishing and explosion. Since CNN-based SR methods develop rapidly, transformer-based SR methods emerged to further improve SR performance ^[12,16,17]. As an alternative to CNN, transformer-based methods make full use of long-range dependency information rather than local features, greatly improving SR performance. However, the transformer-based SR model usually has large model parameters and is difficult to train.

Although previous work has made significant progress, the deep SR model is still challenging to train because of its expensive GPU computation and time costs, leading to decreased performance of the state-of-the-art methods ^[18]. Therefore, the SR methods proposed ahead are not suitable for limited computation resources and limited diagnosis time in medical applications.

To tackle the aforementioned issues and challenges, we propose the multi-distillation residual network (MDRN), which has a superior trade-off between reconstruction quality and computation consumption. Specifically, we propose a feature multi-distillation residual block (FMDRB), used in MDRN, which selectively retains certain features and sends others to the subsequent steps. To maximize the feature distillation capability, we incorporate a contrast-aware channel attention layer (CCA) to enhance the aggregation of diverse refined information. Our approach focuses on leveraging more informative features such as edges, textures, and small vessels for MRI image reconstruction.

In general, our main contributions can be summarized as follows:

1) We propose a multi-distillation residual network (MDRN) applied to efficient and fast super-resolution MRI that learns extra discriminative feature representations and is lightweight enough for limited computation costs. Our MDRN is suitable for super-resolution MRI and clinical applications.

2) We introduce a CCA block to our FMDRB that can guide the model to focus on recovering high-frequency information. Based on that, CCA maximizes the power of the MDRN network. Besides, it is suitable for low-level vision and has better performance than the plain channel attention block.

3) Thanks to the unique design of MDRN, it outperforms previous CNN-based SR models even under smaller GPU conditions. The proposed method obtains the best trade-off between inference time and reconstruction quality, showing the competitive advantage of our MDRN over state-of-the-art (SOTA) methods, as supported by quantitative and qualitative evidence.

2.   Methods

We propose a multi-distillation residual network (MDRN) for efficient and fast super-resolution MRI, whose architecture is shown in Figure 1. In Section 2.1, we provide an overview of the MDRN structure. In Section 2.2, we introduce the core module: feature multi-distillation residual block (FMDRB). Drawing inspiration from the common residual block (RB) ^[10] and information multi-distillation block (IMDB) ^[19], our network comprises a series of stacked FMDRBs forming the main chain, as demonstrated in Figure 1.

Figure 1.  The architecture of MDRN.

DownLoad: Full-Size Img PowerPoint

2.1.   Network architecture

Given ${I}_{LR}$ as the LR input of MDRN, the network reconstructs the SR output ${I}_{SR}$ from the LR input. As in previous works, we adopt a shallow feature extraction, deep feature extraction, and post-upsample structure. The process of shallow feature ${F}_{0}$ extracted from the input ${I}_{LR}$ is as follows:

where ${H}_{SF}(\cdot)$ demonstrates the function of shallow feature extractor, specifically one convolution operation.

The subsequent part of MDRN involves the integration of multiple FMDRBs, which are put in a chain manner with feature distillation connections. This design facilitates the gradual refinement of the initial extracted features, culminating in the generation of deep features. The deep feature extraction part can be described as follows:

where ${D}_{D{F}_{k}}(\cdot)$ stands for the function of $k$ -th FMDRB, and ${F}_{k-1}$ and ${F}_{k}$ represent the input and output features of the k-th FMDRB, respectively. After the iterative refinement process by the FMDRBs, one $1\times 1$ convolution layer is put at the end of a feature extraction part to assemble the fused distilled features. Following the fusion operation, a $3\times 3$ convolution layer is put here to smooth the inductive bias of the aggregated features as follows:

where $Concat$ denotes the fusion operation through channel concatenation of all the distillation features, ${D}_{aggregated}$ denotes the operation, which is one $3\times 3$ convolution following one $1\times 1$ convolution, and ${F}_{fusion}$ is the fused and aggregated features. Finally, the SR output ${I}_{SR}$ is generated by the reconstruction module as follows:

where ${D}_{REC}(\cdot)$ denotes the function of the upscale reconstruction part. The initial extracted feature ${F}_{0}$ is added to the assembled features ${F}_{fusion}$ through skip connection, and ${I}_{SR}$ is the output of the network. The upsample reconstruction works through a convolution layer, whose output channels are quadratic in relation to the upscale factor with a $3\times 3$ kernel size and a sub-pixel shuffle operation that is non-parametric.

The shallow extracted features predominantly contain low-frequency information, whereas deep extracted features focus more on restoring fading high-frequency information. The skip connection path enables MDRN to directly transmit low frequencies to the reconstruction process, which can help combine information and achieve more stable training.

2.2.   Feature multi-distillation residual block

Inspired by the concept of feature distillation and residual learning, we designed the core module--feature multi-distillation residual block (FMDRB), which is more efficient and lightweight than the traditional residual modules. Different from the common residual block (two convolutions and one activation with identity connection), FMDRB uses an additional path with convolution for feature distillation and improved residual blocks stacked in the main chain as refinement layers that process coarse features gradually. We describe the complete structure as follows:

where $D$ denotes the distillation operation, $R$ denotes the layer for remaining features, and the subscript number represents the number of layers. The output feature ${F}_{out}$ fuses the right-most features processed in the main chain and distilled features in the distillation paths. As described in the above equations, the distillation operation works concurrently with the residual learning; this structure shows more efficiency and flexibility than the original residual block commonly used. As such, this block is called feature multi-distillation residual block.

As shown in Figure 1 below, the feature distillation path in each level is performed by one $1\times 1$ convolution layer that effectively compresses feature channels at a fixed ratio; for example, we use input channels divided by 2. Although most convolutions in the SR model use $3\times 3$ kernel size, we note that employing the $1\times 1$ convolution for channel reduction, as done in numerous other CNN models, is more efficient. As we replace the convolution in the distillation path, the parameter amount is significantly reduced. The convolutions located in the main body of MDRN still use a $3\times 3$ kernel size, which better refines the features in the main path and more effectively utilizes spatial information in context.

As shown in Figure 1, despite the improvements mentioned above, we also introduce the base unit of FMDRB, named BSRB ^[20], which allows more flexible residual learning than a common residual block. Specifically, it uses a $3\times 3$ Blueprint Separable Convolution (BSConv) ^[21], an identity connection, and the ReLU activation layer. BSConv is a $1\times 1$ pointwise convolution followed by a $3\times 3$ depthwise convolution, which differs from the standard convolution.

2.3.   Contrast-aware channel attention

The initial concept of channel attention, widely recognized as the squeeze-and-excitation (SE) module, has been extensively used in image processing tasks. The significance of a feature map is predominantly determined by the activation of high-value regions, as these areas are critical for classification or detection. Consequently, global average and maximum pooling are commonly utilized to capture global information in these high- or mid-level visions. While average pooling can indeed enhance the PSNR value, it lacks the capability to retain structural, textural, and edge information, which are crucial for improving image detail (as related to SSIM) ^[19]. As illustrated in Figure 1, the contrast-aware channel attention module is specific to low-level vision. Specifically, we replace global average pooling with the summation of standard deviation and mean (evaluating the contrast degree of a feature map). Let us denote $X = \left[{x}_{1}, {x}_{2}, \dots, {x}_{c}, \dots, {x}_{C}\right]$ as the input, which has $C$ feature maps with spatial size of $H\times W$. Therefore, the contrast information value can be calculated by

where ${z}_{c}$ is the c-th element of output. ${H}_{GC}$ indicates the global contrast information evaluation function. With the assistance of the CCA module, our network can steadily improve the accuracy of super-resolution.

3.   Experiments and results

3.1.   Dataset and preprocessing

We used the public clinical dataset from The Cancer Imaging Archive ^[22], which is available at https://www.cancerimagingarchive.net/collection/vestibular-schwannoma-seg/, named MRI-brain below. The dataset contains labeled MRI images obtained from 242 patients who received Gamma Knife radiation treatment and have been diagnosed with vestibular schwannoma. The images were acquired on a 32-channel Siemens Avanto 1.5T scanner. We used 5000 slices in the MRI-brain dataset for the training set. For testing the performance of our method, we used the remaining 1000 slices as the testing set. The dataset is enough for training and testing since one patient has approximately 140-160 slices.

In data preprocessing, first, we converted the DICOM raw files to NumPy files with voxels. Then, the image pixel data was clipped to range below 2000 and normalized to range [0, 1]. Third, we used bicubic interpolation as the degradation function of the original HR image to the LR image. The preprocessing workflow is shown in Figure 2.

Figure 2.  Preprocessing workflow of our data.

DownLoad: Full-Size Img PowerPoint

3.2.   Implementation details

We trained our model with $5\times {10}^{-4}$ learning rate updated by StepLR scheduler and minimizing the L1 loss function. For the purpose of reducing the training burden, we got patches $192\times 192$ from whole HR images as the input to the network. We used the ADAM optimizer with ${\beta }_{1}\text{}\text{ = }\text{}\text{0.9}$, ${\beta }_{2}\text{ = }\text{}\text{0.99}$. The entire MDRN procedure took approximately 48 h (20, 000 iterations per epoch, 200 epochs) for training and evaluation on the MRI dataset on a single GeForce RTX 3090 GPU with 24 GB of memory.

Following previous works, peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM) were used to assess the model's performance. The calculation of these evaluation metrics is written below:

3.3.   Ablation study

We verified the effectiveness of each proposed component in our MDRN introduced before in detail on the same dataset under the same experiment setting. As shown in Table 1, we itemized the performance of specific methods.

Table 1.  Ablation study of the different components. The best PSNR values on the 4× dataset are listed below.

	Base	${R}_{1}$	${R}_{2}$	${R}_{3}$	${R}_{4}$	${R}_{5}$	${R}_{6}$	${R}_{7}$	Ours
Multi-distillation (inside block)		√				√	√	√	√
BSRB			√		√		√	√	√
Using CCA				√	√	√		√	√
Multi-distillation (outside block)					√	√	√		√
PSNR	31.07	31.08	31.26	31.54	31.89	31.89	31.97	31.53	32.46

---

 | Show Table

DownLoad: CSV

The $Base$ refers to the model EDSR, which is a common residual block stacked in one path with one long skip connection, keeping the basic style of the mostly used SR SOTA model. The result of ${R}_{1}$ shows the effectiveness of the distillation path outside the FMDRB. The result of ${R}_{2}$ verifies the effectiveness of the basic unit (BSRB); as we can see, the block used alone enhances the performance, overtaking the model constructed from common residual blocks. The result of ${R}_{3}$ shows the role of CCA in this proposed method. Results from ${R}_{4}$ to ${R}_{7}$ with/without the feature distillation operation outside/inside the proposed FMDRB, BSRB, and CCA obtain different SR results and outperform the before model, which further verifies the effectiveness of each proposed method. When the basic residual units (FMDRBs) are stacked in a chain manner, which is the common structure in the popular SR models, the model gets lower performance. However, when adding the feature distillation connections to the main chain of the residual blocks, which is the so-called FMDRB, the enhanced distillation block gets better performance.

The distillation structure is useful not only inside the enhanced distillation block but also outside the basic block. The result ${R}_{6}$ is without/with the CCA layer; the result using CCA outperforms the result not using CCA, which verifies that the CCA layer maximizes the performance of FDRB.

We put the contrast-aware channel attention block in the tail position of the proposed FMDRB, which maximizes the capability of the proposed module. To prove the effectiveness of the attention module, we used other attention blocks for comparison, such as CA and IIA. As shown in Table 2, the results of the ablation study aiming at attention block show that the CCA is effective and has the best ability for immediate features.

Table 2.  Effects of different attention blocks.

Attention block	w/o	CA	IIA	CCA
PSNR	31.97	31.98	32.12	32.46
SSIM	0.8767	0.8771	0.8778	0.8761

---

 | Show Table

DownLoad: CSV

3.4.   Comparison with other methods

3.4.1.   Quantitative results

The proposed MDRN has inherited the advantages of the residual network and combines the advantages of the feature distillation network. To prove the excellent performance of MDRN, we compared our model with popular state-of-the-art SR models, including NTIRE2017 winner EDSR ^[10], RCAN ^[11], large-scale SAN ^[13], HAN ^[14], novel IGAN ^[15], RFDN ^[23], and the recent DINet ^[24]. Since most SR SOTA models are tested on DIV2K, which are 3-channel natural images, the performance comparison between different methods cannot be directly done from cited papers; they were re-tested on the MRI-brain dataset, composed of single-channel clinical images.

Table 3 demonstrates the comparison of quantitative results for 2×, 4×, and 8× SR. Our MDRN outperforms existing methods on MR-brain test datasets of all scales. Without using tricks like self-ensemble, the proposed MDRN network still achieves significant improvements compared to recent advanced methods. It is notably worth noticing that our model is much better than the EDSR, which shares a similar basic architecture with MDRN and shows some superiority over RFDN, which also uses the feature distillation strategy as MDRN. MDRN outperforms methods such as SAN and IGAN, which have more computationally intensive attention modules. Specifically, MDRN obtains superior results by 1.82 dB improvement in PSNR compared to the base EDSR in 4× scale, and its SSIM wins over previous methods. MDRN gains better results by up to 0.44 dB in terms of PSNR than DIPNet.

Table 3.  Comparison of quantitative results with state-of-the-art SR methods on Brain Vestibular-Schwannoma datasets in 2×, 4×, and 8× scale. The best and second-best performances are in red and blue colors, respectively.

	Memory	Time	Scale 2	Scale 4	Scale 8
	[M]	(ms)	PSNR/SSIM	PSNR/SSIM	PSNR/SSIM
Bicubic	--	--	33.66/0.9299	28.44/0.8159	24.40/0.6580
EDSR [10]	2192.74	72.36	34.98*/0.9025*	30.64*/0.8697*	26.17*/0.7513*
RCAN [11]	2355.20	498.26	38.27*/0.9614*	31.65**/0.9019*	26.21*/0.7778*
SAN [13]	5017.60	805.23	34.85*/0.9318*	31.09*/0.8432*	25.39*/0.7359*
IGAN [15]	2099.20	335.77	33.91*/0.9173*	31.73*/0.8744*	26.32*/0.7804*
HAN [14]	5038.98	719.07	34.97*/0.9576*	31.03*/0.8424*	25.66*/0.7612*
RFDN [23]	813.06	49.51	38.31**/0.9620*	31.98*/0.8795*	26.28*/0.7794*
DIPNet [24]	521.02	28.79	38.27**/0.9614*	32.02**/0.8712*	26.33*/0.7884*
Ours	325.21	27.88	39.19/0.9686	32.46/0.8761	26.47/0.8696
*p < 0.05, **p < 0.001

---

 | Show Table

DownLoad: CSV

The efficiency of a SR model can be assessed through various metrics, such as the number of parameters, runtime, computational complexity (FLOPs), and GPU memory consumption. These metrics play pivotal roles in the deployment of models in different aspects. Among these evaluation metrics, the runtime is the most direct indicator of a network's efficiency and is used as the primary evaluation metric. Memory consumption is also an important metric because it determines whether the model can be deployed to the edge device. In a clinical setting, the SR MRI model will be put into a small GPU, and models needing large-memory GPU will not work as intended. Our MDRN model gets the best PSNR, which is over 32 dB, only using 325.21 M GPU memory and 27.88 ms valid runtime, as shown in Table 3, showing a competitive advantage over other methods. To test the validation of experiment results, we analyzed the statistical significance of the results. As shown in Table 3, we calculated the P value of the results using the data of every epoch as a collection of random variables.

Table 4.  Comparison of quantitative results on other datasets.

	BraTS-Gli	BraTS-Meni
	PSNR/SSIM	PSNR/SSIM
Bicubic	32.94/0.9099	30.25/0.8689
EDSR [10]	36.35*/0.9610*	33.33*/0.9196*
RCAN [11]	36.94**/0.9513*	33.86*/0.9160*
SAN [13]	37.06*/0.9514*	34.02*/0.9191*
IGAN [15]	37.09*/0.9620*	34.13*/0.9217*
HAN [14]	37.33*/0.9521*	33.83*/0.9197*
RFDN [23]	38.17**/0.9600**	34.08**/0.9214*
DIPNet [24]	38.38**/0.9623*	34.17*/0.9218*
Ours	38.92/0.9635	34.25/0.9225
*p < 0.05, **p < 0.001

---

 | Show Table

DownLoad: CSV

3.4.2.   Visual results

For a more intuitive demonstration of the gap between these methods, we show the comparison of zoomed results of various methods. As shown in Figure 3, we randomly select some results from the test set for evaluation. Taking "img_050112" as an example, most SR methods can reconstruct the general composition, but only IGAN and MDRN recover the more detailed textures and sharper edges. In zoomed details of "img_05011", we can see that IGAN, SAN, and RFDN do not clearly restore the small vessels, while our MDRN obviously does (shown in red arrows). Additionally, as seen in "img_05024", MDRN is closer to the ground truth, recovering the cerebrospinal fluid and not generating blurring artifacts (shown in yellow arrows). Our MDRN can output more high-frequency information, like enhanced contrast edges, than other methods. Through the observations of visual results, it is verified that MDRN has superiority in complex feature representations and recovery ability over previous works.

Figure 3.  Visual comparison of SR methods in 4× scale on the MRI-brain dataset. Zoomed details for observation. Colored visualization below for better comparison.

DownLoad: Full-Size Img PowerPoint

4.   Discussion

4.1.   Cost and performance analysis

Deep learning-based methods have been proven to work effectively in the domain of medical image processing, including SR reconstruction for MR images. Based on the bottleneck of the SR task, we propose a novel lightweight and fast SR model named MDRN using multi-distillation residual learning.

Figure 4 provides an overview of the comparison of the performance and computation efficiency of the proposed method and other methods. It is evident that MDRN achieves the best execution time. Except for SAN and HAN using transformer structure, the computation complexity of SAN and HAN is $O\left({n}^{2}\right)$ and of other models is $O\left(n\right)$. The quadratic computation complexity $O\left(n\right)$ in relation to the query/key/value sequence length $n$ leads to high computation costs when using self-attention with a global receptive field. For a precise assessment of the computation complexity of our method, we compare it using quantitative metrics with several representative open-source models, as shown in Table 3. Quantitative results show that our MDRN consumes lower computation resources while maintaining 32+ PSNR. MDRN has a better trade-off between performance and cost.

Figure 4.  Comparison of computation efficiency and performance between our method and other methods.

DownLoad: Full-Size Img PowerPoint

4.2.   Generalization analysis

We conducted generalization experiments by applying the super-resolution model trained on head and neck magnetic resonance imaging (MRI) images to pelvic CT images, aiming to validate the model's generalization performance on different datasets (Table 5). The results demonstrate that our model achieves a PSNR of 31.4 dB on the pelvic dataset at a 4× magnification factor. This outcome indicates that our MDRN exhibits favorable generalization performance and is capable of completing super-resolution tasks on new datasets. Visual quality is shown in Figure 5.

Table 5.  Generalization analysis on pelvic CT images.

Scale	2×	4×	8×
PSNR	36.55	32.35	27.79
SSIM	0.8882	0.8938	0.8928

---

 | Show Table

DownLoad: CSV

Figure 5.  Visual quality of SR results on pelvic CT images for generalization study.

DownLoad: Full-Size Img PowerPoint

5.   Conclusions

In this paper, we propose the MDRN, a lightweight CNN model, for efficient and fast super-resolution MRI tasks using the innovative multi-distillation strategy. Our findings show remarkable superiority of MDRN over current SR methods, supported by both quantitative metrics and visual evidence. Notably, MDRN excels at learning discriminative features and striking a better balance between computational efficiency and reconstruction performance by integrating the feature distillation mechanism into the network architecture. Extensive evaluations conducted on an MRI-brain dataset underline the favorable performance of MDRN over existing methods in both computational cost and accuracy for medical scenarios.

Use of AI tools declaration

We declare that we have not used generative AI tools to generate the scientific writing of this paper.

Conflict of interest

We declare that we have no known financial interests or personal relationships that could have appeared to influence the work reported in this paper. There is no professional or other personal interest of any kind in any product, service or company that could influence the work reported in this paper.