Modeling Citrus Huanglongbing transmission within an orchard and its optimal control

1.   Introduction

Citrus Huanglongbing (HLB) is a global citrus disease occurring in almost all citrus-growing regions ^[1,2]. HLB was first reported in southern China in 1919, and now it is discovered and spread in 50 different countries ^[1]. It causes substantial economic burdens to individual growers, citrus industries and governments ^[2]. A large number of countries, such as the United States, Brazil and China, are severely affected by the disease. In Florida, America, the commercial citrus acreage has reduced to 531,493 acres in the fall of 2012, a $28\%$ decrease from 748,555 acres in 2004 ^[3]. In S$\tilde{a}$o Paulo, Brazil, a heavy toll has been taken by HLB. $6.9\%$ of the citrus trees, and even $64.1\%$ of the commercial citrus orchards were affected by HLB in 2012 ^[4]. Till now, in China, the damaged product of citrus is more than $85\%$ of the total product ^[5]. Due to the great harm of HLB to public society, it is significant to increase understanding of HLB transmission dynamics and to take some measures in curbing its transmission.

Mathematical models have been playing a great role in understanding the epidemiology of vector transmitted plant pathogens ^{[6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]}. In recent years, several mathematical models explored how HLB transmits within individual citrus trees, within a citrus orchard, or among orchards ^{[2,6,15,19,25]}. For the purpose of highlighting the role of flush for Asian citrus psyllid (ACP) dynamics, Chiyaka et al. ^[6] proposed a mathematical model of differential equations to describe and investigate the spread of HLB within a tree. Jacobsen et al. ^[19] developed a model for the transmission of HLB within a single citrus orchard, which included the control strategy of roguing. Vilamiu et al. ^[26] proposed a deterministic mathematical model with delay times and human intervention for the transmission of HLB between citrus plants, and the dynamical characteristics of ACP and the development of disease were investigated. In ^[15], Gao et al. investigated a stage-structured mathematical model of HLB with time delay. These models are of great help to our understanding of the law of transmission of HLB.

Most of the HLB models mentioned above does not consider a variety of control measures for the comprehensive management of the transmission of HLB. Thus, in order to fight HLB and protect citrus plants, various control strategies are needed. Currently, there are a variety of feasible control strategies, including antibiotics, insecticides, biological control agents, physical methods, nutritional supplements, etc. Perhaps it is partly because of the simplification of control measures that HLB still remains a major plant disease in China, despite the control program of HLB in China launched in 2005 and sustained over 10 years. Therefore, in order to control the transmission of HLB effectively, a variety of control strategies should be considered simultaneously. Simultaneous implementation of multiple control strategies may help guide us to reduce and eliminate the incidence of HLB in orchards.

Motivated by the above researches, in this paper, we formulate a compartmental mathematical model to describe the transmission dynamics of HLB within a single orchard of citrus trees. The model represents healthy, infected and asymptomatic, infectious and asymptomatic, and infectious and symptomatic individuals in the citrus trees and healthy, infected individuals vector populations. We derive the basic reproductive ratio, a threshold value below which the HLB disease can be eliminated but above which the HLB disease will persist. The global dynamics of the HLB model are further studied. Then, optimal control method is applied to the HLB model to discuss the corresponding optimal control problems.

This article is organized as follows. In section 2, we introduce the deterministic mathematical model to describe the transmission dynamics of HLB which incorporates citrus trees and ACP. In section 3, we compute the basic reproduction ratio and local stability analysis of the six dimension HLB system. Moreover, the global dynamics of the HLB model are discussed. In section 4, optimal control problem of HLB is performed. Furthermore, in section 5, we propose some numerical simulations, and summarize some suggestions for HLB prevention and control. The paper ends with a brief discussion of the results in section 6.

2.   Model formulation

In this section, we mainly formulate the mathematical model to describe the transmission dynamics of HLB.

HLB, a bacterial disease of citrus, mainly transmitted by the insect, i.e., ACP ^[27]. ACP is the most important source of infection for HLB. In addition, Citrus HLB can also be spread by means of grafting and dodder, but it contributes little to the overall transmission. ACP damages citrus directly by feeding on new leaf growth (flush). It takes the bacteria into its body when it feeds on bacteria-infected plants. The disease spreads when a bacteria-carrying ACP flies to a healthy plant and injects bacteria into it as it feeds. In this article, we only consider the scenario that HLB are transmitted between citrus trees and ACP.

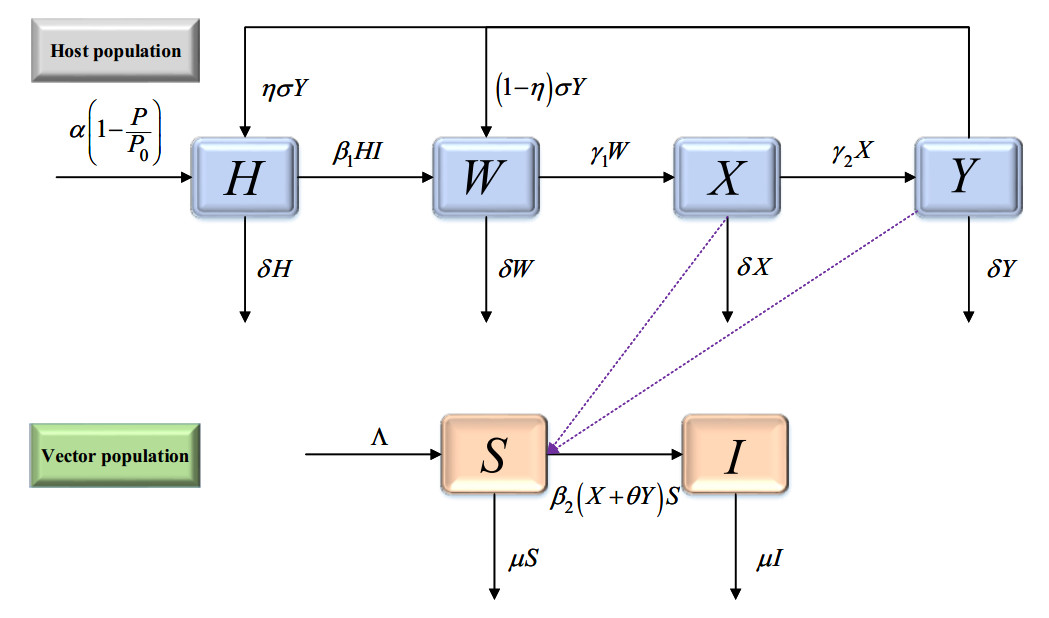
According to the transmission of Citrus HLB, the citrus tree population is assumed to divide into four different classes, namely, healthy individuals, $H(t)$, infected and asymptomatic individuals, $W(t)$ (which are not yet infectious), infectious and asymptomatic individuals, $X(t)$, and infectious and symptomatic individuals, $Y(t)$, at any time $t$. Let $P(t)$ be the total number of citrus tree population, i.e., $P(t) = H(t)+W(t)+X(t)+Y(t)$. The population of ACP is similarly divided into two different classes, namely, susceptible ACP ($S(t)$) and infected ACP ($I(t)$), respectively. The total population of ACP is denoted by $N(t),$ i.e., $N(t) = S(t)+I(t)$.

The transition diagram for the transmission of HLB pathogens is shown in Figure 1. Based on the above transition diagram, the model for HLB transmission is described by:

In system (2.1), $\alpha$ denotes the number of new citrus trees replanted. The maximum number of citrus trees that can be planted in the grove is represented by $P_0$ ($P(t)\leq P_0$). $\beta_1$ is the HLB bacterial transmission probability from ACP to citrus tree. $\beta_2$ is the HLB bacterial transmission probability from citrus tree to ACP. The natural mortality of citrus tree population is denoted by $\delta$. $\sigma$ denotes the removal rate of symptomatic citrus trees. $\eta$ represents the proportion of healthy trees in replanted citrus trees. $\gamma_1$ represents the conversion rate from non-infectious citrus to infectious citrus trees, and $\gamma_2$ represents the conversion rate from asymptomatic citrus trees to symptomatic citrus trees. $\Lambda$ is the recruitment rate of ACP, and $\mu$ is the death rate of ACP. $\theta$ denotes the increased infectiousness of $Y(t)$. All parameters and its biological interpretation of the HLB model (2.1) are summarized in Table 1.

Let

where

Then it follows from the above discussion that all solutions of the system (2.1) starting in $\Omega$ remain in $\Omega$ for all $t\geq0$. Therefore, $\Omega$ is a positively invariant, and it is sufficient to consider only the solutions in the region $\Omega$. In this region, the usual existence, uniqueness, and continuation results hold for the system (2.1). In what follows, we always assume that the initial conditions of system (2.1) lie in $\Omega$.

3.   Model analysis

In this section, we mainly investigate the dynamics of the model (2.1).

The model (2.1) always has the disease-free equilibrium (DFE), namely $E^0 = (H^0, W^0, X^0, Y^0, S^0, I^0) = \left(\frac{\alpha P_0}{\alpha+\delta P_0}, 0, 0, 0, \frac{\Lambda}{\mu}, 0\right).$

It is noted that system (2.1) has four infected individuals, namely $W(t)$, $X(t)$, $Y(t)$, and $I(t)$. Using the notations in ^[29,30], the matrices $F$ and $V$, for the new infection terms and the remaining transfer terms respectively, are given by

It follows that the basic reproduction number of the model (2.1), denoted by $\mathscr{R}_0$, is

where $\rho(FV^{-1})$ is the spectral radius of the matrix $FV^{-1}$. Using Theorem 2 in ^[30], we have

Theorem 3.1. The DFE ($E^0$) of the system (2.1) is locally asymptotically stable (LAS) if $\mathscr{R}_0 < 1$, and unstable if $\mathscr{R}_0 > 1$.

In what follows, we show that the global stability of DFE ($E^0$) when $\mathscr{R}_0 < 1$.

Theorem 3.2. If $\mathscr{R}_0 < 1,$ then the system (2.1) is globally asymptotically stable (GAS).

Proof. If $\mathscr{R}_0 < 1$, by Theorem 3.1, it follows that the DFE ($E^0$) is LAS. Next, we only need to prove that the DFE ($E^0$) is a global attractor.

It follows from system (2.1) that we have

Consider the following auxiliary equations

From the system (3.3), we can easily verify that the system is an irreducible cooperative system in $\mathbb{R}^4_+$. Furthermore, it follows from Theorem 11.3 in ^[31] that the global stability of the origin of system (3.3) is entirely determined by the stability of the Jacobian matrix $J_{E^0} = F-V$. If $\mathscr{R}_0 < 1$, it follows from Theorem 2 in ^[30] that $J_{E^0}$ is stable. Then we have

By the comparison principle ^[32], it follows that

Then, substituting them into model (2.1), the limiting system can be obtained as follows:

Solving the equations of system (3.4), we have $\lim_{t\rightarrow \infty} H(t) = \frac{\alpha P_0}{\alpha+\delta P_0},$ and $\lim_{t\rightarrow \infty} S(t) = \frac{\Lambda}{\mu}.$ Since the system (3.4) is the limiting system of (2.1), from the Theorem 2.3 in the ^[33], we further obtain that the DFE ($E^0$) is the global attractor of the model (2.1). This completes the proof of Theorem 3.2.

In what follows, we investigate the uniform persistence of system (2.1) when $\mathscr{R}_0 > 1$.

Theorem 3.3. If $\mathscr{R}_0 > 1$, then the system (2.1) is uniformly persistent, i.e., there is a positive constant $\xi$ such that every positive solution $(H(t), W(t), X(t), Y(t), S(t), I(t))$ of (2.1) satisfies

Proof. Define

In order to show that the system (2.1) is uniformly persistent, we only need to demonstrate that $\partial \chi_{0}$ repels uniformly the solutions of $\chi_{0}.$

First, it follows from system (2.1) that both $\chi$ and $\chi_{0}$ are positively invariant. Clearly, $\partial\chi_{0}$ is relatively closed in $\chi$ and (2.1) is point dissipative. Set

We now show that

Assume $(H(0), W(0), X(0), Y(0), S(0), I(0))\in M_{\partial}.$ It suffices to demonstrate that $W^2(t)+X^2(t)+Y^2(t)+I^2(t) = 0$ for all $t\geq0.$ Suppose not . Then there exists a $t_0\geq0$ such that $W^2(t_0)+X^2(t_0)+Y^2(t_0)+I^2(t_0) > \; 0.$ Without loss of generality, we only discuss the case $I(t_0) > 0,$ $H(t_0) = 0,$ $W(t_0) = 0,$ $X(t_0) = 0,$ $Y(t_0) = 0,$ $S(t_0) = 0.$ Analogously, the other cases can be derived in the same way. Since

and

it follows that there is an $\epsilon_0$ small enough such that $H(t) > 0, S(t) > 0, I(t) > 0$ for all $t_0 < t < t_0+\epsilon_0.$ Furthermore, let $t_1 = t_0+\frac{\epsilon_0}{2}$, then we have $H(t_1) > 0$ and $I(t_1) > 0.$

If $W(t_1) > 0$, we have

This means that $W(t) > 0$ for all $t\geq t_1;$ if $W(t_1) = 0$, we get

It then follows that there is an $\epsilon_1 < \frac{\epsilon_0}{2}$ such that $W(t) > 0$ for all $t_1 < t < t_1+\epsilon_1.$ Similarly, there exists $\epsilon_2 < \frac{\epsilon_1}{2}$ and $\epsilon_3 < \frac{\epsilon_2}{2}$ such that $X(t) > 0$ for all $t\in(t_1+\frac{\epsilon_1}{2}, t_1+\frac{\epsilon_1}{2}+\epsilon_2)$ and $Y(t) > 0$ for all $t\in(t_1+\frac{\epsilon_1}{2}+\frac{\epsilon_2}{2}, t_1+\frac{\epsilon_1}{2}+\frac{\epsilon_2}{2}+\epsilon_3),$ respectively. Thus, for all $t_1+\frac{\epsilon_1}{2}+\frac{\epsilon_2}{2} < t < t_1+\frac{\epsilon_1}{2}+\frac{\epsilon_2}{2}+\epsilon_3$ we have $H(t) > 0,$ $S(t) > 0,$ $I(t) > 0,$ $W(t) > 0,$ $X(t) > 0$ and $Y(t) > 0$. This contradicts the assumption that $(H(0), W(0), X(0), Y(0), S(0), I(0))\in M_{\partial}.$ This proves (3.5).

It is obvious that $E^0 = \left(\frac{\alpha P_0}{\alpha+\delta P_0}, 0, 0, 0, \frac{\Lambda}{\mu}, 0\right)$ is the unique equilibrium in $M_{\partial},$ where $P^0 = \frac{\alpha P_0}{\alpha+\delta P_0}$ and $N^0 = \frac{\Lambda}{\mu}$. We now demonstrate that $E^0$ repels the solutions in $\chi_{0}$. It can be seen that

We can choose $\zeta_1 > 0$ small enough such that

If (3.6) holds, i.e., $\det(J_{E^0}) < 0$, we can also select $\zeta_1 > 0$ small enough such that

By calculations, we can select $\xi_1 > 0$ small enough such that

Suppose $(H(t), W(t), X(t), Y(t), S(t), I(t))$ is a solution of system (2.1) with $(H(0), W(0), X(0), Y(0), S(0), I(0))\in \chi_0$. We now claim that

For the sake of contradiction, suppose that there is a $T_0 > 0$ such that $W(t)\leq \xi_1,$ $X(t)\leq \xi_1,$ $Y(t)\leq \xi_1,$ $I(t)\leq \xi_1,$ for all $t\geq T_0$. By the first and fifth equations of the model (2.1), we have

for $t\geq T_0$. Consider the following system

As in our previous analysis of the model (3.4), we can restrict $\xi_1$ to be small enough such that (3.11) admits a positive equilibrium $(\bar{H}^0, \bar{S}^0)$, where

Moreover, the unique positive equilibrium $(\bar{H}^0, \bar{S}^0)$ is GAS for system (3.11). By (3.9) and the comparison principle, there is a $\tau_0 > 0$ such that $H(t)\geq P^0-\zeta_1,$ $S(t)\geq N^0-\zeta_1$ for $t > T_0+\tau_0$. Consequently, for $t\geq T_0+\tau_0$, we get

Consider an auxiliary system

The coefficient matrix $\widehat{J}_{E^0}$ of the right hand of (3.12) is given by

Since $\widehat{J}_{E^0}$ admits positive off-diagonal elements, Perron-Frobenius Theorem indicates that there is a positive eigenvector $\nu_M$ for the maximin eigenvalue $\lambda_M$ of $\widehat{J}_{E^0}$. Extensive calculations yield that $\lambda_M > 0$ since (3.7) and (3.8) hold. Based on the linear system theory, it is clear that $\lim_{t\rightarrow \infty} \widehat{W}(t) = \infty,$ $\lim_{t\rightarrow \infty} \widehat{X}(t) = \infty,$ $\lim_{t\rightarrow \infty} \widehat{Y}(t) = \infty,$ $\lim_{t\rightarrow \infty} \widehat{I}(t) = \infty.$ Then by the comparison principle, we get $\lim_{t\rightarrow \infty} W(t) = \infty,$ $\lim_{t\rightarrow \infty} X(t) = \infty,$ $\lim_{t\rightarrow \infty} Y(t) = \infty,$ $\lim_{t\rightarrow \infty} I(t) = \infty.$ This contradicts $W(t)\leq \xi_1,$ $X(t)\leq \xi_1,$ $Y(t)\leq \xi_1,$ $I(t)\leq \xi_1$ for all $t\geq T_0$. This proves (3.10). Thus $W^s(E^0)\cap\chi_0 = \emptyset$. Obviously, every forward orbit in $M_{\partial}$ converges to $E^0$. By Theorem 4.6 of ^[34] we can draw a conclusion that the system (2.1) is uniformly persistent with respect to $(\chi_0, \partial\chi_0)$. This completes the proof of Theorem 3.3.

Remark 3.1. By Theorem 3.3, it follows from Theorem 2.3 in ^[31] that the system (2.1) has at least one positive solution when $\mathscr{R}_0 > 1.$ Furthermore, let $E^* = (H^*, W^*, X^*, Y^*, S^*, I^*)$ be any endemic equilibrium of the system (2.1). By setting the right equations of model (2.1) equal to zero, we can obtain

where

It is obvious to follow that $I^{*} > 0$ if and only if $\mathscr{R}_0 > 1$. By the expressions of $H^*$, $W^*$, $X^*$, $Y^*$, $S^*$ and $\mathscr{R}_0 > 1$, there is only one $E^* \in \Omega$ for the system (2.1). We have the following result.

Theorem 3.4. The system (2.1) has at most one endemic equilibrium. More precisely,

(1) If $\mathscr{R}_0 > 1,$ there exists a unique endemic equilibrium $E^*$.

(2) If $\mathscr{R}_0 < 1,$ there is no endemic equilibrium.

Remark 3.2. Although we do not have an analytic result for the global stability of the positive equilibrium $E^*,$ our numerical studies indicate that $E^*$ is GAS whenever it exists, i.e., when $\mathscr{R}_0 > 1$.

4.   Optimal control

In this section, we try to implement anti-HLB control to protect healthy citrus trees while minimizing the total cost. As a matter of fact, this problem is a representative optimal control problem.

First, we assume the set of control variables as:

where $T_f$ is the final time. Then, it is hypothesised that all control strategies are bounded and Lebesgue measurable in this paper. The upper bound of control variable is defined by $U_i$ (i = 1, 2, 3). The control function $u_1(t)$ indicates the reduction of the HLB bacterial transmission probability from ACP to citrus trees. Some specific control measures can be taken such as injecting nutrient solution. $u_2(t)$ represents an increase in the rate of removal of the infected and symptomatic citrus trees by fruit growers. $u_3(t)$ shows the eradication effort of insecticide spraying.

In this paper, we consider the following objective function

subject to

where $H(0)\geq 0, W(0)\geq0, X(0)\geq 0, Y(0)\geq 0, S(0)\geq 0, I(0)\geq 0$. The coefficients $a_i$ (i = 1, 2, 3) are positive constants indicating the weight of the total number of citrus trees, the number of the infectious and asymptomatic trees, and the number of the infectious and symptomatic trees. $b_i$ (i = 1, 2, 3) are weight constants represent for the costs of injecting nutrient solution, removing the infected and symptomatic trees, and spraying insecticide. The cost of a quarantine survey of all the citrus trees in the grove is represented by $a_1 P(t)$, the number of infectious citrus trees are represented by $a_2 X(t)+a_3 Y(t)$, and the total cost of implementing control measures is represented by $\sum^{3}_{i = 1}b_i u_i^2 (t)$.

The ultimate goal of HLB control is to protect the citrus trees health, and to minimize the diseased trees and the cost of implementing the control, by using the possible minimal control variables $u_i(t)$ (i = 1, 2, 3), such that

subject to the model given by (4.2).

Now the necessary conditions that $(u_1^*(t), u_2^*(t), u_3^*(t))$ and corresponding states must satisfy is derived. The existence of optimal control can be demonstrated by using the Pontryagin's Maximum Principle ^[35]. In this problem, we can prove that the control set $\Phi$ is convex and closed and the objective function is convex on $\Phi$. To determine compactness for the existence of the optimal control, the optimal system (4.2) is bounded.

To obtain the optimal solution, the Lagrangian and Hamiltonian function of the optimal control system (4.2) need to be found. Firstly, the Lagrangian function $\mathscr{L}$ for (4.2) can be defined as

In order to get the optimal solution of the model (4.2), we define the Hamiltonian function $\mathscr{H}$ as follows:

where

Theorem 4.1. Given optimal controls $u_1^*$, $u_2^*$, $u_3^*$ and solutions $H^*$, $W^*$, $X^*$, $Y^*$, $S^*$, $I^*$ of the corresponding state system (4.2). Then there exists adjoint variables $\lambda(t) = (\lambda_1(t), \lambda_2(t), \lambda_3(t), \lambda_4(t), \lambda_5(t), \lambda_6(t))$ satisfying the equations as follows:

with transversality conditions $\lambda_i(t) = 0\; (i = 1, 2, 3, 4, 5, 6)$. Furthermore, the optimal control are given by

Proof. Based on Pontryagin's Maximum Principle, we obtain

Applying the adjoint conditions to $\mathscr{H}\big(t, Z(t), U(t), \lambda(t)\big)$ with $Z = Z^*$, that is

The Eq (4.1) are obtained. The optimal conditions at $U^*$ can be calculated as follows:

that is

Using the lower and upper bounds of the controls, the optimal solutions of model (4.2) can be obtained. This completes the proof of Theorem 4.1.

5.   Numerical simulation

In this section, we mainly present some numerical simulation results, confirm or extend the analysis results, which assess the impact of ACP on the transmission of HLB, and explore the effects of various control strategies against HLB.

It follows from ^[28] that the average life expectancy of citrus trees is from 20 to 30 years. Based on this, we assume an average life span of citrus trees is $1/\delta = 25 year$, i.e., $\delta = 0.04(year^{-1}).$ According to the implementation of control strategies for HLB, all citrus trees infected by HLB must be removed. However, HLB has an incubation period during which the infected citrus trees do not show symptoms, thus we take the removal rate $\sigma = 0.6$ by empirical estimation. Assume that the maximum number of citrus trees that can be planted in the orchard is 1000, i.e., $P_0 = 1000.$ It is reported by Taylor et al. ^[2] that average nature death rate of ACP is $\mu = 5.9441(year^{-1}).$ The other parameter values in the model (2.1) are shown in Table 1. To examine the sensitivity of model results to the uncertainty of parameters, we conducted sensitivity and uncertainty analysis.

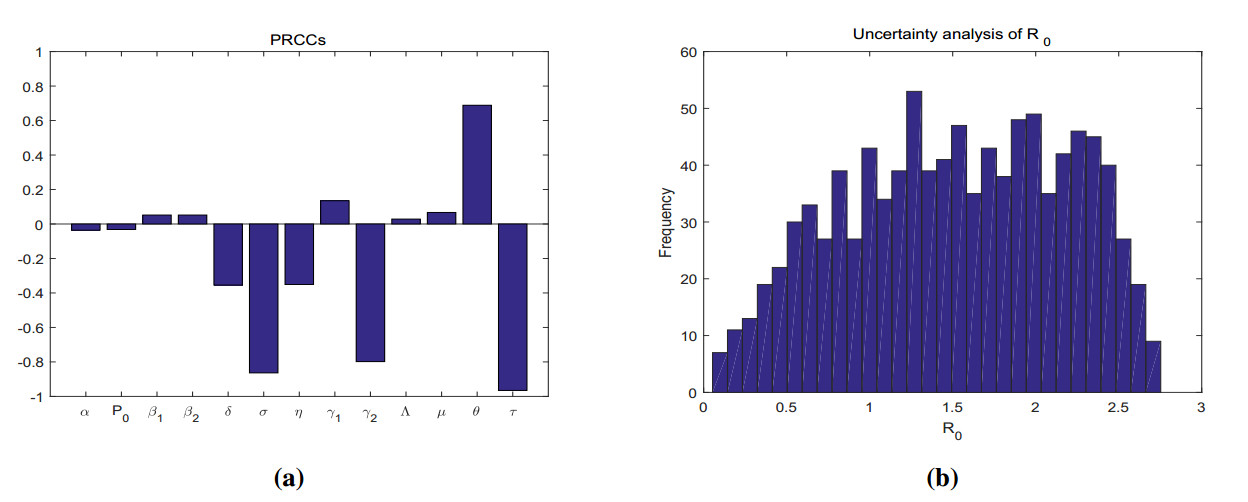
Based on the above parameters of the model (2.1), we perform a global sensitivity analysis on the basic reproductive number $\mathscr{R}_0$. Figure 2a, b present our sensitivity and uncertainty analysis, which involved computing the Partial Rank Correlation Coefficients (PRCCs) of $\mathscr{R}_0$ using the Latin Hypercube Sampling (LHS) method ^{[36,37,38,39]}. It indicates how uncertainty in model parameters may influence $\mathscr{R}_0$. We observe in Figure 2a that $\mathscr{R}_0$ is very sensitive to the conversion rate ($\tau$), the removal rate of symptomatic citrus trees ($\sigma$), and the infectious enhancement coefficient ($\theta$) of $Y(t)$, but not sensitive to the maximum number of citrus trees that can be planted in the grove ($P_0$) and the recruitment rate of ACP ($\Lambda$). For both transmission probabilities, $\beta_1$ has a greater impact on $\mathscr{R}_0$. Thus, decreasing $\beta_1$ is more effective in reducing $\mathscr{R}_0$ in terms of controlling the disease. For uncertainty analysis, according to Figure 2b, about $70\%$ of the distribution of $\mathscr{R}_0$ is greater than 1, indicating that persistent HLB bacterial infection is likely to occur. Furthermore, the mean and standard deviation of $\mathscr{R}_0$ can be obtained to be 1.5159 and 0.6591, respectively.

In what follows, using the numerical methods in ^[40], we explore the optimal solution of the optimality system (4.2), the corresponding optimal control, and a reasonable explanation for each case. The objective of this paper is to analyze the effect of three controls (i.e., injection of nutrient solution, removal of diseased trees and application of insecticides) on the transmission of HLB. The initial numbers of susceptible citrus trees and ACP are assumed that $H(0) = 658$, $S(0) = 332280$. Then we assume that the initial numbers of infectious citrus trees and ACP are $W(0) = 191$, $X(0) = 78$, $Y(0) = 73$, and $I(0) = 250$, respectively. In the simulations, the values of other parameters are derived from Table 1.

In practice, the ideal weights are difficult to obtain. It requires an amount of work on data analysis and fitting. Therefore, finding the right weights in practical problems is a very difficult task that requires further research ^[41]. The costs associated with $u_1$ mainly include the costs of nutrient solutions and fruit growers injecting nutrient solutions into citrus trees. The costs associated with $u_2$ mainly involve the costs of fruit growers removing some of the symptomatic citrus trees. Then the costs associated with $u_3$ mainly include the costs of insecticides and fruit growers spraying insecticides. According to these practical conditions, we consider that the weights in the objective function are $a_1 = 2$, $a_2 = 10$, $a_3 = 2$, $b_1 = 10$, $b_2 = 2$ and $b_3 = 2$, respectively. It should be pointed out that the weights in the simulations here are only of theoretical sense to illustrate the control strategies proposed in this paper ^[42].

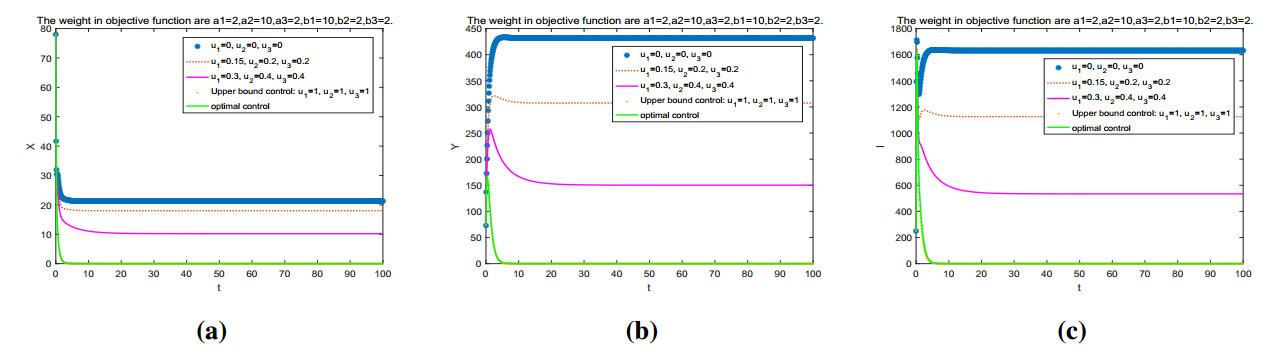
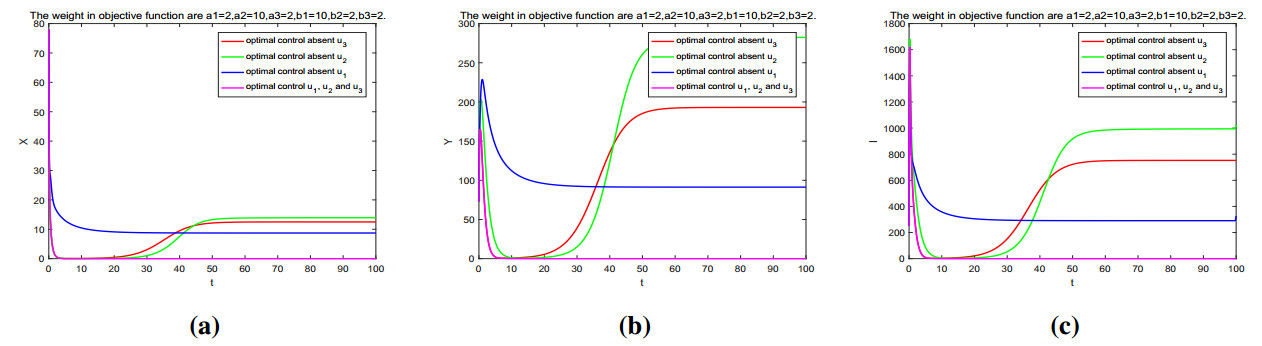
Figure 3a, b and Figure 3c depict the number of infectious citrus trees and the number of infectious ACP under different control levels, respectively. In terms of reducing the total number of the diseased citrus trees (or the diseased ACP), the optimal control strategy is consistent with the upper bound control strategy and is superior to the constant control. Furthermore, as shown in Table 2, we can conclude that the cost of the optimal control is less than the cost of the upper bound control. The enhancement of the level of control can achieve significant effects on both the number of hosts and vectors.

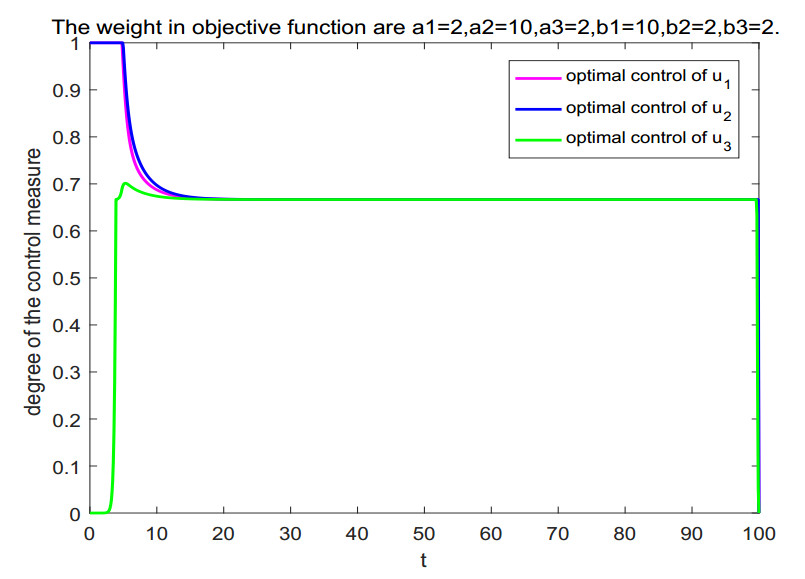
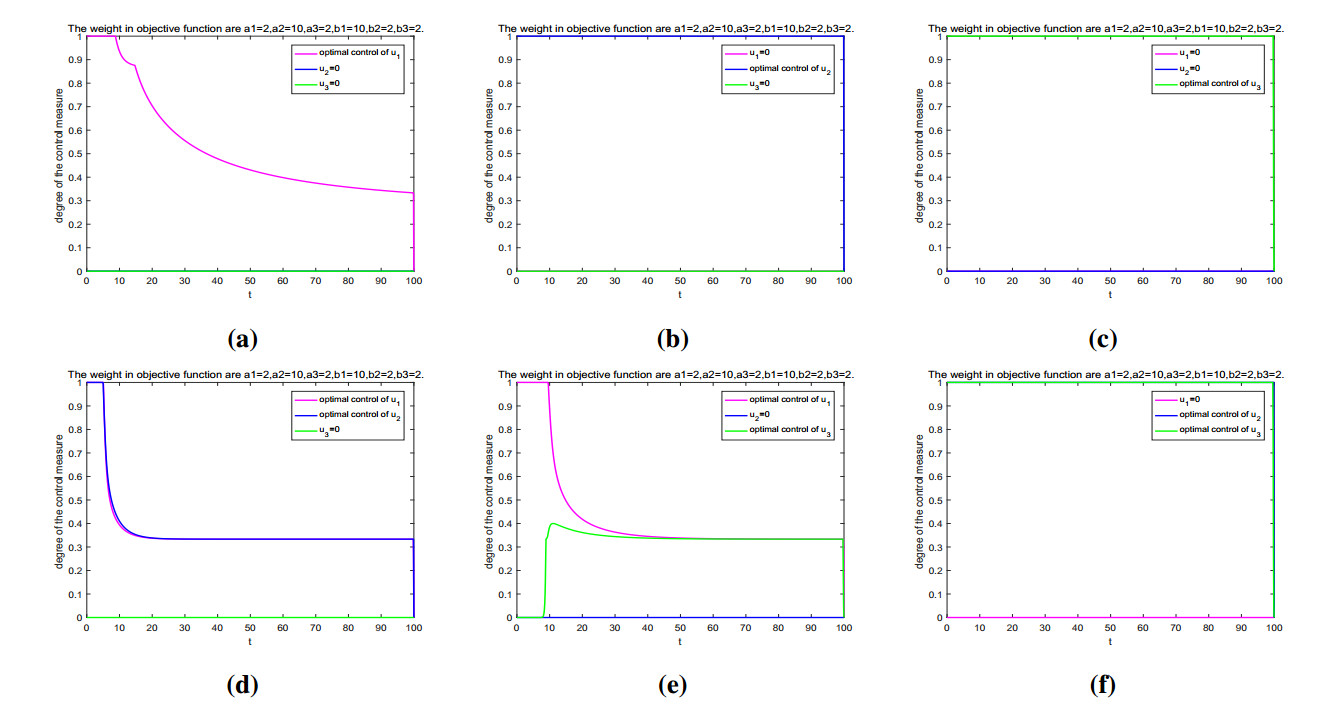
Figure 4 illustrates the optimal control law of $u_1$, $u_2$, and $u_3$. At the beginning of simulation, the control variables $u_1$ and $u_2$ maintain the upper bound, and then gradually decrease to 0 until the end of simulation. However, the control variable $u_3$ is 0 in simulation of the initial stage, then rises vertically, and then remains horizontal, and finally drops vertically to 0.

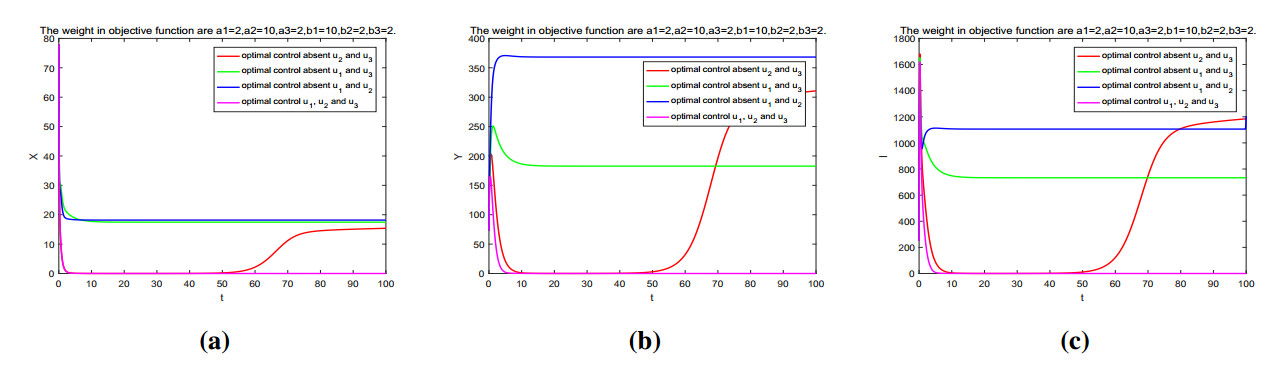
Figures 5 and 6 present the number of infectious citrus trees and infectious ACP under different control strategies. These control strategies are : (Ⅰ) $u_1$, $u_2$, $u_3$; (Ⅱ) $u_1$ ($u_2$ = $u_3$ = 0); (Ⅲ) $u_2$ ($u_1$ = $u_3$ = 0); (Ⅳ) $u_3$ ($u_1$ = $u_2$ = 0); (Ⅴ) $u_1$, $u_2$ ($u_3$ = 0); (Ⅵ) $u_1$, $u_3$ ($u_2$ = 0); (Ⅶ) $u_2$, $u_3$ ($u_1$ = 0). Firstly, the cost of executing strategy (Ⅱ) is lower than that of executing strategy (Ⅲ) or (Ⅳ); the cost of executing strategy (Ⅴ) is less than that of executing strategy (Ⅵ) or (Ⅶ). Moreover, the cost of executing strategy (Ⅴ) is less expensive than executing strategy (Ⅱ). Secondly, the number of infectious citrus trees is the smallest when implementing strategy (Ⅰ), while the number of infectious citrus trees is the largest when implementing strategy (Ⅳ). Thirdly, in addition to strategy (Ⅰ), the final number of diseased ACP is the least when applying strategy (Ⅶ); and the final number of diseased ACP is the most when applying strategy (Ⅱ). Therefore, it is suggested that multiple control strategies should be adopted simultaneously to inhibit the spread of HLB.

Figure 7 shows the optimal control trajectories under different control measures. It can be seen from Figures 4 and 7 that in the early phase of HLB outbreak, the upper bound control strategies should be adopted in most cases to suppress the transmission of the disease.

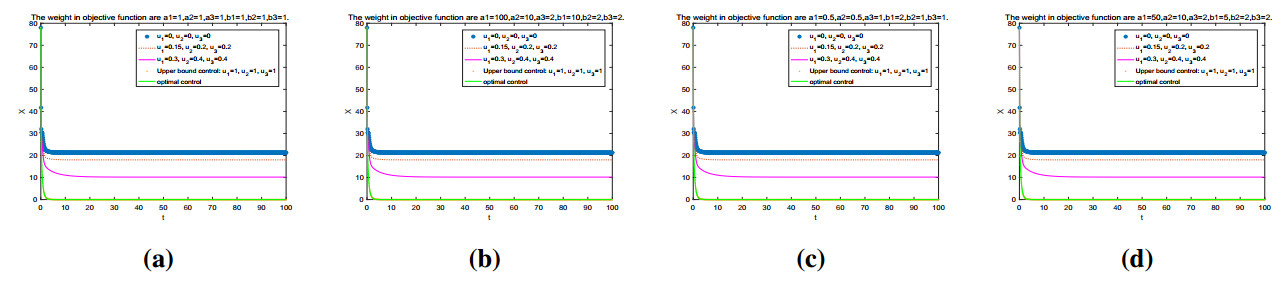
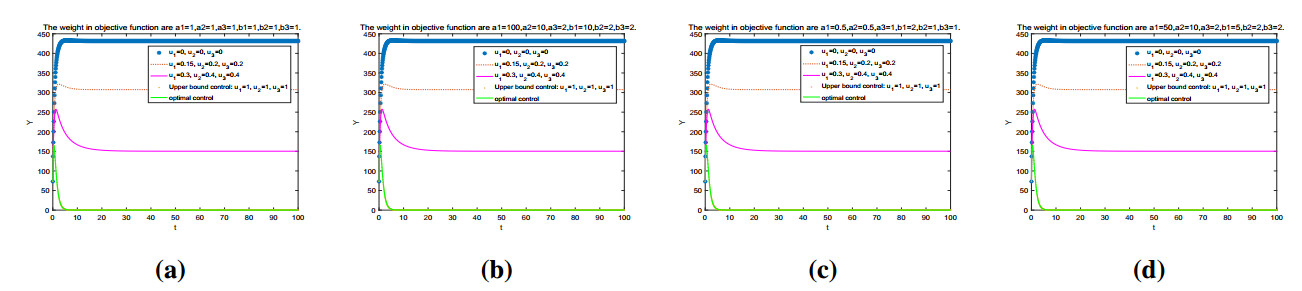
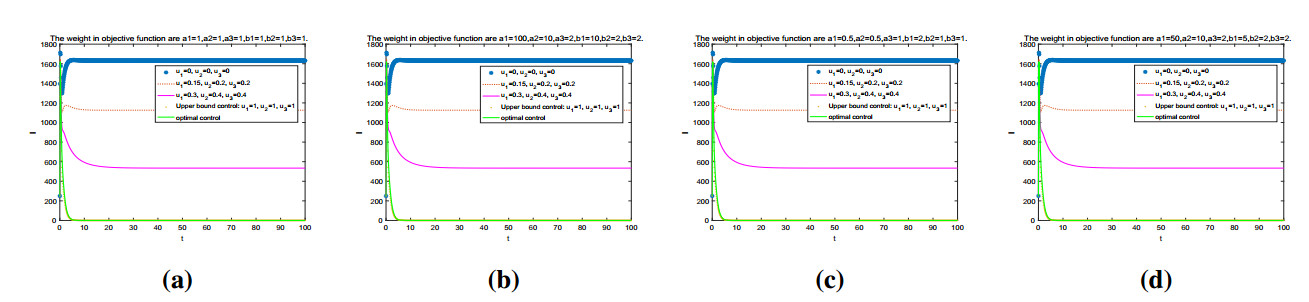
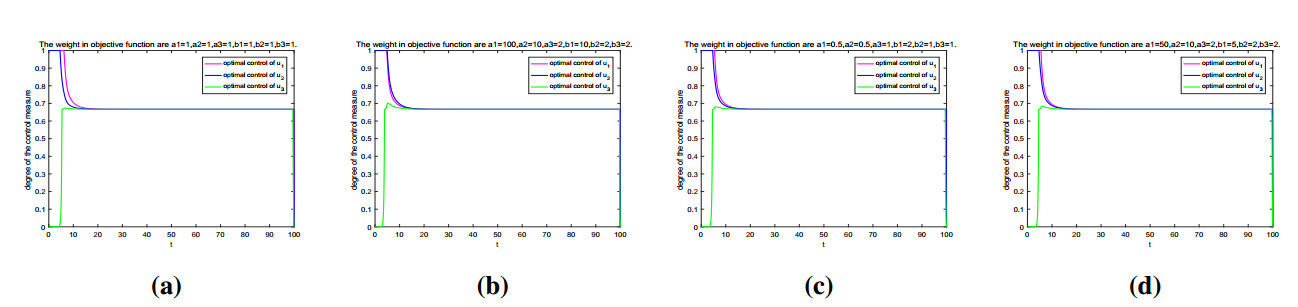
Figures 8 and 9, Figure 10, and Figure 11 depict the trajectories of the diseased citrus trees, the diseased ACP, and the optimal controls with different weights in objective function, respectively. Based on the simulation results, we can get that the weights in the objective function have little or no effect on the spread of HLB (Figures 8–10). However, the weights have a great impact on the control cost (Table 2). They have little impact on the control strategy (Figure 11).

6.   Conclusion

In this paper, the deterministic mathematical model is developed to depict the transmission dynamics of HLB which incorporates citrus trees and ACP. According to the method of the next-generation matrix, we obtain the expression of the basic reproductive ratio $\mathscr{R}_0$ and explain $\mathscr{R}_0$ from the biological point of view. Based on the above previous results, the dynamic behavior of the six-dimensional nonlinear system is strictly analyzed by dynamic system theory. Theoretical results indicate that if $\mathscr{R}_0 < 1$, the DFE ($E^0$) is GAS and if $\mathscr{R}_0 > 1$, there is only one endemic equilibrium point in the system. In addition, if $\mathscr{R}_0 > 1$, the HLB system (2.1) is persistent.

Moreover, the theory of optimal control is applied to the HLB model with vector and host to investigate the corresponding problems of optimal control. The necessary conditions for the existence of optimal solution of optimal control problems are obtained according to Pontryagin's Maximum Principle. Finally, we validate the theoretical results analyzed by numerical simulation, and explore and compare the effects of various control strategies on the transmission of HLB. Based on analytical and the numerical simulation results, the main conclusions can be summarized as follows:

(1) The infected ACP plays a decisive role in the transmission of HLB, and eliminating the infected ACP will be helpful to curtail the spread of HLB in citrus trees.

(2) The optimal control strategy is superior to the constant control strategy in decreasing the prevalence of the infected citrus trees, and the cost of implementing optimal control is much lower than that of the constant control strategy.

(3) In the early phase of the transmission of HLB, spraying insecticides is more effective than other control strategies in reducing the number of the infected ACP.

In this paper, we formulate a compartmental mathematical model to describe the transmission dynamics of HLB in a single orchard of citrus trees. The dynamic model of HLB with optimal control strategy can be useful for fruit growers in the comprehensive control of HLB. Our model is depicted by the ordinary differential equations that do not include the stage-structure of the insect vector population. However, some existing literature indicates that the stage-structure of ACP has a certain influence on the transmission dynamics of HLB ^[6]. Therefore, we should incorporate the stage-structure of the ACP population into the transmission dynamics model of HLB and consider it in our future work.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (No. 11671206, 11971232, 11961003, 11561004), Key Project of Jiangxi Natural Science Foundation (No. 20192ACBL20004), the Earmarked Fund for Jiangxi Agriculture Research System (No. JXARS-07-diseaes and pests management), the Science and Technology Research Project of Jiangxi Provincial Education Department (No. GJJ170815), the Scholarship Foundation of China Scholarship Council (No. 201806840120), the Fundamental Research Funds for the Central Universities (No. 30918011339), the outstanding Chinese and Foreign Youth Exchange Program of China Association of Science and Technology and the Bidding Project of Gannan Normal University (No. 16zb02). The authors would like to thank anonymous referees for their suggestions which helped to improve the presentation of the manuscript.

Conflict of interest

The authors declare no competing interests.