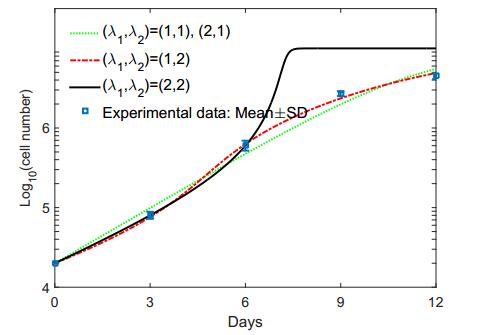
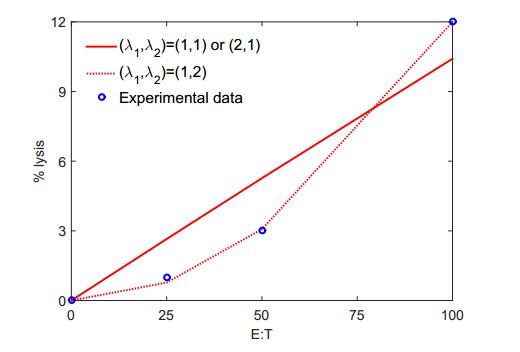
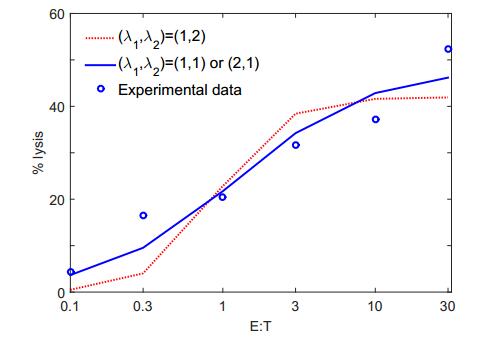
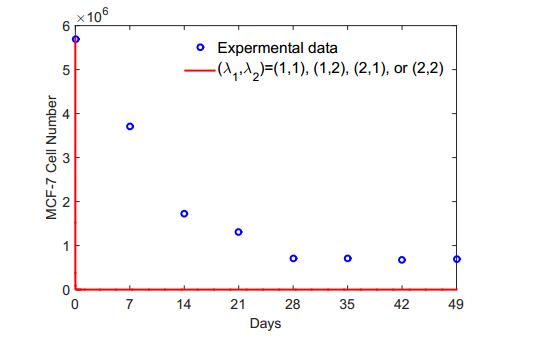
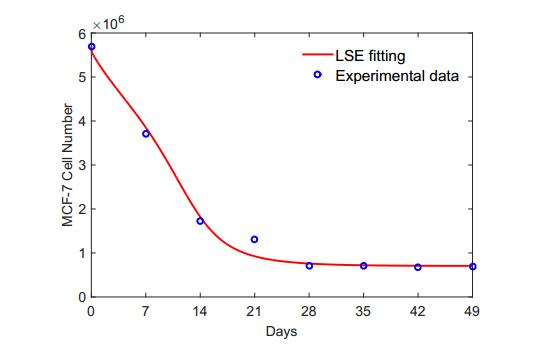
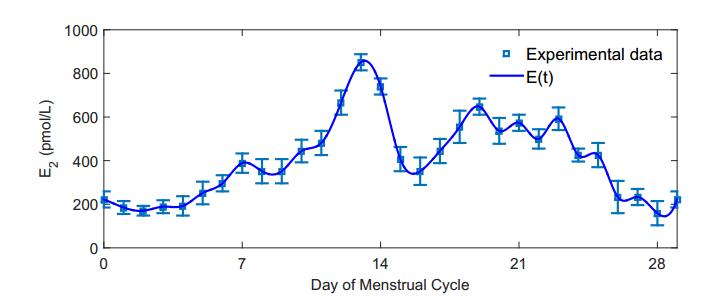
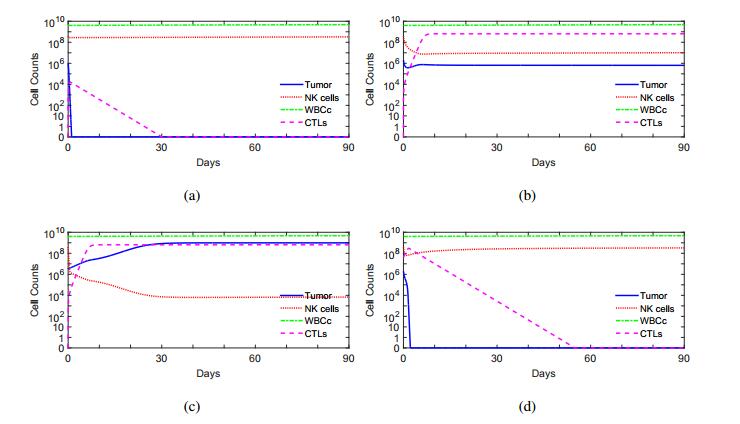
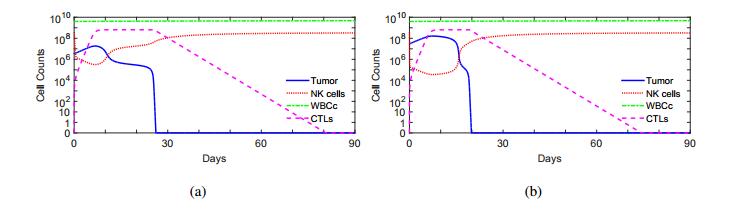
Breast cancer is the second most commonly diagnosed cancer in women worldwide. MCF-7 cell line is an extensively studied human breast cancer cell line. This cell line expresses estrogen receptors, and the growth of MCF-7 cells is hormone dependent. In this study, a mathematical model, which governs MCF-7 cell growth with interaction among tumor cells, estradiol, natural killer (NK) cells, cytotoxic T lymphocytes (CTLs) or CD8+ T cells, and white blood cells (WBCs), is proposed. Experimental data are used to determine functional forms and parameter values. Breast tumor growth is then studied using the mathematical model. The results obtained from numerical simulation are compared with those from clinical and experimental studies. The system has three coexisting stable equilibria representing the tumor free state, a microscopic tumor, and a large tumor. Numerical simulation shows that an immune system is able to eliminate or control a tumor with a restricted initial size. A healthy immune system is able to effectively eliminate a small tumor or produces long-term dormancy. An immune system with WBC count at the low parts of the normal ranges or with temporary low NK cell count is able to eliminate a smaller tumor. The cytotoxicity of CTLs plays an important role in immune surveillance. The association between the circulating estradiol level and cancer risk is not significant.
1.
Introduction
The most important tumor suppressor p53 has a key role in regulating a number of cellular responses upon various stresses including DNA damage and oncogene activation [1,2]. Depending on the type and severity of the damage, p53-mediated responses include cell cycle arrest, cellular senescence and apoptosis, which can be triggered through regulating the expression of different downstream genes [3,4]. These responses are closely related to p53 dynamics, where p53 keeps low level in unstressed cells, whereas a high level of p53 induces apoptosis to destroy irreparably damaged cells [5,6]. More interestingly, the oscillation dynamics of p53 may initiate cell cycle arrest or apoptosis depending on the number of p53 pulses [7,8]. Therefore, it is meaningful to explore p53 dynamics for understanding cellular response in response to different conditions. Furthermore, p53 dynamics can be investigated through simulating the mathematical models of p53 gene regulatory network with p53, it upstream regulators, downstream target genes and feedback loops [9,10].
A number of mathematical models depicting p53 gene regulatory network have been established to explore p53 dynamics in response to different conditions from theoretical analyses and numerical simulations [7,8,11]. Typically, an integrated model of p53 gene regulatory network with four modules was proposed by Zhang et al., who demonstrated that the number of p53 pulses determined cell fates upon DNA damage [7,8]. Based on the integrated model and experiment results, a mathematical model of p53 gene regulatory network regulated by Programmed Cell Death 5(PDCD5) has been developed so as to reveal that PDCD5 modulates cell fate decisions as a co-activator of p53 [12,13]. Furthermore, the effects of rate constants in the p53 gene regulatory network on p53 dynamics are explored through bifurcation analyses and potential landscapes [14,15]. However, the transcriptional and translational processes in the model are seen as instant. Actually, slow and complex transcriptional and translational processes as the basic steps of gene expression in cells are usually related to long time delay [16]. Time delays in various networks, such as neural networks and disc dynamos with viscous friction, have important impact on the dynamics in the network, which are explored through stability and bifurcation analyses [17,18,19,20]. Also, more researches explore the effect of time delays in some p53 gene regulatory networks on p53 oscillation [21]. However, the effect of time delay on p53 oscillation in p53 gene regulatory network regulated by PDCD5 has not been considered.
Inspired by these considerations, we introduce a time delay of the transcriptional and translational processes of Mdm2 activated by p53 into p53 gene regulatory network regulated by PDCD5 in ref. [22]. The local stability of positive equilibrium of the model are demonstrated through analyzing the characteristic equations of the corresponding linearized system for two cases without and with time delay. Also, these stability are verified through time series, the distribution of characteristic roots, one-parameter bifurcation diagram and potential landscapes. Then, two-parameter bifurcation diagrams of time delay with the concentration of PDCD5 and four typical rate parameters, vp53, dp53, vMdm2 and dMdm2 are carried out to explore their effect on the oscillation dynamic of p53.
This paper is organized as follows. The p53 gene regulatory network regulated by PDCD5 is given in Section 2. In Section 3, we analyze the local stability of positive equilibrium of the model by means of stability theory for two cases without and with time delay. Then numerical simulations and bifurcation analyses are given in Section 4. Finally, we conclude the paper in Section 5.
2.
A model of p53 gene regulatory network with time delay
The model of p53 gene regulatory network regulated by PDCD5 is illustrated in Figure 1, which was established in Ref. [22]. Double strand breaks (DSBs) induced by various stresses activate ATM monomers, which further phosphorylate p53 at Ser-15 in the nucleus(p53) and Mdm2 at Ser-395 in the cytoplasm (Mdm2395Pcyt). Phosphorylated p53 in the nucleus inhibits ATM activity through activating it inhibitor Wip1 [23,24,25]. Additionally, Mdm2 protein in the cytoplasm(Mdm2cyt) transforms with Mdm2395Pcyt and Mdm2 protein in the nucleus (Mdm2nuc). Furthermore, Mdm2395Pcyt stimulates p53 translation through interacting with p53 mRNA while Mdm2nuc promotes p53 degradation by binding p53 and increasing it ubiquitination [26]. Besides, PDCD5 functions as a positive regulator of p53 through accelerating the degradation of Mdm2nuc and inhibiting the degradation of p53 by Mdm2nuc [22]. Here, phosphorylated p53 accelerates the production of Mdm2cyt through promoting the expression of Mdm2 gene. As we know, it takes some time from gene transcription to protein production, so we introduce a time delay into the interaction of p53 with Mdm2cyt. The model equations of the p53 gene regulatory network with time delay are given as follows.
where
Here x(t), y(t), z(t), w(t) and m(t) represent the concentration at time t of active p53, Mdm2cyt, Mdm2395Pcyt, Mdm2nuc and ATM proteins. The biological significance and values of all parameters in the model are given in Table 1.
3.
Local stability analysis
In this section, the local stability of positive equilibrium E∗=(X∗,Y∗,Z∗,W∗,M∗) are analyzed through stability theory for without and with time delay. Let ¯x(t)=x(t)−X∗, ¯y(t)=y(t)−Y∗, ¯z(t)=z(t)−Z∗, ¯w(t)=w(t)−W∗, ¯m(t)=m(t)−M∗, the linearization of system (2.1) at E∗ is given as follows,
where
The system (3.1) can be written as the form of matrix:
where
Using Laplace transform,
Eq (3.2) can be given as follows:
Without loss of generality, let
Then, the characteristic equation of the linear system (3.1) is give as follows:
That is:
where
3.1. The case τ=0
For τ=0, Eq (3.5) becomes
The conditions for local stability of E∗=(X∗,Y∗,Z∗,W∗,M∗) are give in Theorem 3.1 according to the Routh-Hurwitz criterion [27].
Theorem 3.1. E∗=(X∗,Y∗,Z∗,W∗,M∗) is locally asymptotically stable when all roots of Eq (3.6) have negative real parts, the following conditions (H) should be satisfied.
(H):
3.2. The case τ≠0
For τ≠0, let iω(ω>0) be a root of Eq (3.5), so ω satisfies the following equation:
Separating the real and imaginary parts, we have
Squaring both sides of each equation and then adding them up leads to
Let z=w2, p=a21−2a2, q=a22+2a4−2a1a3, r=a23−2a2a4+2a1a5−A22, u=a24−2a3a5−A21+2A0A2 and v=a25−A20. Then Eq (3.8) can be written as
Some lemmas for establishing the distribution of positive real roots of Eq (3.9) are given as follows [28].
Lemma 3.2. If v<0, then Eq (3.9) has at least one positive root.
Proof. Denote h(z)=z5+pz4+qz3+rz2+uz+v. Since h(0)=v<0 and limz→+∞h(z)=+∞. Hence, there exists a z0>0 such that h(z0)=0. The proof is complete.
For v≥0, considering the following equation:
Let z=y−p5, then Eq (3.10) is changed into:
where
If q1=0, then the four roots of Eq (3.11) are as follows:
where Δ0=p21−4r1. Thus zi=yi−p5, i=1,2,3,4 are the roots of Eq (3.10). Then we have the following lemma.
Lemma 3.3. Suppose that v≥0 and q1=0.
(i) If Δ0<0, then Eq (3.9) has no positive real roots.
(ii) If Δ0≥0, p1≥0 and r1>0, then Eq (3.9) has no positive real roots.
(iii) If (i) and (ii) are not satisfied, then Eq (3.9) has positive real roots if and only if there exists at least one z∗∈{z1,z2,z3,z4} such that z∗>0 and h(z∗)≤0.
Proof. (ⅰ) If Δ0<0, then Eq (3.10) has no real roots. Since limz→+∞h′(z)=+∞, so h′(z)>0 for z∈R. Hence, h(0)=v≥0 leads to h(z)≠0 when z∈(0,+∞).
(ⅱ) If Δ0≥0, p1≥0 and r1>0, then h′(z) has no zero in (−∞,+∞). It is similar to (ⅰ) that h(z)≠0 for any z∈(0,+∞).
(ⅲ) The sufficiency holds obviously. We will prove the necessity. If Δ0≥0, then Eq (3.11) has only four roots y1,y2,y3,y4, so Eq (3.10) has only four roots z1,z2,z3,z4 at least z1 is a real root. We assume that z1,z2,z3,z4 are all real. This means that h(z) has at most four stationary points at z1,z2,z3,z4. If it is not true, we will have that either z1≤0 or z1>0 and min{h(zi):zi≥0,i=1,2,3,4}>0. If z1≤0, then h′(z)≠0 in (0,+∞). Since h(0)=v≥0 is the strict minimum of h(z) for z≥0 which means h(z)>0 when z∈(0,+∞). If z1>0 and min{h(zi):zi≥0,i=1,2,3,4}>0, since h(z) is the derivable function and limz→+∞h(z)=+∞, then we have minz>0h(z)=min{h(zi):zi≥0,i=1,2,3,4}>0. The proof of the necessity is done. We finish the proof.
If q1≠0. Thinking about the solution of Eq (3.11):
that is
Let
So, Eq (3.12) has the following three roots
Let s∗=s1≠p1 (since p1 is not a root of Eq (3.12)). Equation (3.11) is equivalent to
For Eq (3.13), Eq (3.12) indicates that the formula in square brackets is a perfect square.
If s∗>p1, then Eq (3.13) is
After factorization, we get
and
Let
Then we obtain the four roots of Eq (3.11)
So zi=yi−p5, i=1,2,3,4 are the roots of Eq (3.10). Thus we can get the following lemma.
Lemma 3.4. Suppose that v≥0, q1≠0 and s∗>p1.
(i) If Δ2<0 and Δ3<0, then Eq (3.9) has no positive real roots.
(ii) If (i) is not satisfied, then Eq (3.9) has positive real roots if and only if there exists at least one z∗∈{z1,z2,z3,z4} such that z∗>0 and h(z∗)≤0.
Proof. We omit the proof since it is similar to Lemma 3.3.
Finally, if s∗<p1, then Eq (3.13) is
Let ¯z=q12(p1−s∗)−p5, we have the following lemma.
Lemma 3.5. Suppose that v≥0, q1≠0 and s∗<p1, then Eq (3.9) has positive real roots if and only if q214(p1−s∗)2+s∗2=0, ¯z>0 and h(¯z)≤0.
Proof. If Eq (3.13) has a real root y0, which satisfies
so
Therefore, Eq (3.13) has a real root y0 if and only if q214(p1−s∗)2+s∗2=0. The rest of the proof is similar to Lemma 3.3, we omit it.
Lemmas 3.2, 3.3, 3.4 and 3.5 give the sufficient and necessary conditions of existence of positive roots of Eq (3.9).
Suppose that Eq (3.9) has five positive roots zk,i=1,2,3,4,5. Then Eq (3.8) has five positive roots ωk=√zk, i=1,2,3,4,5. From Eq (3.8), we obtain the corresponding τ(k)j>0 and the characteristic equation (3.5) has purely imaginary roots.
It is obvious that limj→∞τ(k)j=∞ for k=1,2,3,4,5. Next we can define
On the basis of the above analysis, we obtain the conditions that all roots of Eq (3.5) have negative real parts in the following lemma.
Lemma 3.6. (i) If one of the followings holds:(a) v<0; (b) v≥0, q1=0, Δ0≥0 and p1<0 or r1≤0 and there exist z∗∈{z1,z2,z3,z4} such that z∗>0 and h(z∗)≤0; (c) v≥0, q1≠0, s∗>p1, Δ2≥0 or Δ3≥0 and there exist z∗∈{z1,z2,z3,z4} such that z∗>0 and h(z∗)≤0; (d) v≥0, q1≠0, s∗<p1, q214(p1−s∗)2+s∗2=0, ¯z>0 and h(¯z)≤0, then all roots of the characteristic equation (3.5) have negative real parts when τ∈(0,τ0).
(ii) If the conditions (a)-(d) of (i) are all not satisfied, then all roots of Eq (3.5) have negative real parts for all τ>0.
Proof. Lemmas 3.2, 3.3, 3.4 and 3.5 shows that Eq (3.5) has no roots with zero real part for all τ>0 if the conditions (a)–(d) of (ⅰ) are not satisfied. If one of (a)–(d) holds, when τ≠τ(k)j, Eq (3.5) has no roots with zero real part and τ0 is the minimum value of τ, which make equation (3.5) has purely imaginary roots. We get the conclusion of the lemma.
Next, we want to prove the system (2.1) can undergo Hopf bifurcation at τ=τ0.
Let
be the root of Eq (3.5) satisfying α(τ0)=0, ω(τ0)=ω0. We have the next lemma.
Lemma 3.7. Suppose h′(z0)≠0. If τ=τ0, then ±iω0 is a pair of simple purely imaginary roots of Eq (3.5).
Proof. If iω0 is not simple, then ω0 must satisfy
This implies that
Meanwhile, from Eq (3.7) we konw that ω0 satisfies
Thus, we have
According to Eq (3.9) and ω20=z0, Eq (3.19) becomes
Notice that h(z)=z5+pz4+qz3+rz2+uz+v and h′(z)=5z4+4pz3+3qz2+2rz+u, Eq (3.20) becomes ((A0−A2z0)2+A21z0)h′(z0)=0. we obtain a contradiction to the condition h′(z0)≠0. This proves the conclusion.
Next, we will get the conditions for dRe(λ(τ0))dτ>0 in Lemma 3.8.
Lemma 3.8. If the conditions of Lemma 3.6 (i) are satisfied, then dRe(λ(τ0))dτ>0.
Proof. Differentiating both sides of Eq (3.5) with respect to τ gives
Therefore
If dReλ(τ0)dτ<0, then equation (3.5) has a root with positive real part for τ<τ0 and close to τ0, which contradicts Lemma 3.6 (ⅰ). This completes the proof.
To sum up, we get the following theorems.
Theorem 3.9. Let ω0, z0, τ0, and λ(τ) be defined by Eq (3.15) and (3.16), respectively.
(i) If the conditions (a)–(d) of Lemma 3.6 are not satisfied, then all the roots of Eq (3.5) have negative real parts for all τ>0.
(ii) If one of the conditions (a)–(d) of Lemma 3.6 is satisfied, then all the roots of Eq (3.5) have negative real parts when τ∈(0,τ0); when τ=τ0 and h′(z0)≠0, then ±iω0 is a pair of simple purely imaginary roots of Eq (3.5) and all other roots have negative real parts. In addition, dReλ(τ0)dτ>0 and Eq (3.5) has at least one root with positive real part when τ∈(τ0,τ1), when τ1 is the first value of τ>τ0 such that Eq (3.5) has purely imaginary root.
Theorem 3.10. Let ω0, z0, τ0, and λ(τ) be defined by Eq (3.15) and (3.16), respectively.
(i) If the conditions (a)–(d) of Lemma 3.6 are not satisfied, then the positive equilibrium point E∗=(X∗,Y∗,Z∗,W∗,M∗) of system (2.1) is asymptotically stable for all τ>0;
(ii) If one of the conditions (a)–(d) of Lemma 3.6 is satisfied, then the positive equilibrium point E∗=(X∗,Y∗,Z∗,W∗,M∗) of system (2.1) is asymptotically stable when τ∈(0,τ0);
(iii) If conditions (a)–(d) of Lemma 3.6 is satisfied, and h′(z0)≠0, system (2.1) undergoes a Hopf bifurcation at E∗=(X∗,Y∗,Z∗,W∗,M∗) when τ=τ0.
In summary, Theorems 3.1 and 3.10 give the local stability of positive equilibrium E∗=(X∗,Y∗,Z∗,W∗,M∗) of system (2.1) and the conditions undergoing Hopf bifurcation without and with time delay, respectively. In the following, some numerical simulations are given to verify the correctness of these theorems.
4.
Numerical simulation and bifurcation analysis
4.1. Numerical simulation
In this section, Theorems 3.1 and 3.10 are verified through time series of the concentrations of active p53(x), total Mdm2(y+z+w), ATM(m) and the eigenvalues of Eq (3.5) for τ=0 and τ≠0. Besides, one-parameter bifurcation diagram of the concentrations of active p53(x) with respect to τ and potential landscapes of active p53(x) and total Mdm2(y+z+w) are given to verify the correctness of Theorem 3.10. These figures are realized by MATLAB software.
In case Ⅰ of τ=0, a positive equilibrium E∗=(3.0492,0.0770,0.1184,0.0858,2.2877) of system (2.1) is obtained for parameters in Table 1. Substituting these parameters into Δi(i=1,2,3,4,5), we have Δ1=1.9910>0, Δ2=2.2370>0, Δ3=0.6136>0, Δ4=0.0197>0 and Δ5=0.0134>0. The condition (H) in Theorem 3.1 is satisfied, so the positive equilibrium E∗ is asymptotically stable, which is verified through numerical simulations in Figure 2. Figure 2(a) shows that the concentrations of x, y+z+w and m firstly increase and then converge to the positive equilibrium E∗. Also, all roots of the characteristic equation (3.6) at the positive equilibrium point E∗ have negative real parts, as shown in Figure 2(b).
For case Ⅱ τ≠0, substituting the same positive equilibrium E∗ with τ=0 and the parameters in Table 1 into Eq (3.8), we get
Equation (4.1) has a positive root ω0=0.2342, then z0=ω20=0.0548 and τ0=2.1217 from Eq (3.8). Note that v=−1.2282×10−4<0 and h′(z0)=0.0065≠0, the conditions (ⅱ) and (ⅲ) in Theorem 3.10 are satisfied, so the positive equilibrium E∗ is asymptotically stable when τ∈(0,τ0) and system (2.1) undergoes Hopf bifurcation at τ0=2.1217, where E∗ loses stability and a stable limit cycle appears. The correctness of Theorem 3.10 is verified by the following numerical simulations in Figures 3–6. Figure 3(a) describes one-parameter bifurcation diagram of x with respect to τ, where black solid and dashed lines are stable and unstable equilibria, and green solid dots are the maxima and minima of the stable limit cycle. As is shown in Figure 3(a), system (2.1) converges to the positive equilibrium E∗ for τ<τ0 and undergoes Hopf bifurcation at HB point with τ=τ0, then the positive equilibrium E∗ loses stability and a stable limit cycle appears for τ>τ0. Also, the stability of the positive equilibrium E∗ is further verified through the maximum real part of the eigenvalues of the characteristic equation (3.5) in Figure 3(b), where maximum real part is negative for τ<τ0 and zero at τ=τ0 then positive for τ>τ0.
Next, Figures 4 and 5 show time series of the concentrations of active p53(x), total Mdm2(y+z+w), ATM(m) and the eigenvalues of Eq (3.5) for three typical time delays τ=1<τ0, τ=2.1217=τ0 and τ=2.5>τ0 to further verify the stability of system (2.1). As shown in Figure 4, system (2.1) converges to the stable equilibrium E∗ at τ=1 (Figure 4(a)) and shows damped oscillation at τ=τ0 (Figure 4(b)), then is in a continuous oscillating state at τ=2.5 (Figure 4(c)). Accordingly, all roots of the characteristic equation (3.5) have negative real part at τ=1 (Figure 5(a)), and a pair of roots with zero real part appear at τ=2.1217 (Figure 5(b)), and some roots have positive real part at τ=2.5(Figure 5(c)).
Furthermore, the global stability of p53 dynamics are explored through the potential landscapes of active p53(x) and total Mdm2(y+z+w) in Figure 6. The potential landscape U=−ln(Pss) proposed by Wang et al. is related with the the steady state probability distribution Pss of the system (2.1) [29]. Pss can be obtained through simulating the corresponding stochastic differential equations of system (2.1) for a long time over many independent runs. The stochastic differential equations are obtained through adding Gaussian and white noise ζ(t) into right hand of each equation of system (2.1), where <ζ(t)ζ(t′)>=2Dδ(t−t′), and <ζ(t)>=0, D is noise strength.As shown in the Figure 6(a), the potential landscape has a global minimum that corresponds to the global stable steady state. However, the potential landscapes in Figure 6(b) and 6(c) exhibit closed ring valleys which correspond to the stable limit cycle in system (2.1). The potential landscape at τ=2.1217 has wider attractive regions than the one at τ=2.5 since system (2.1) shows damped oscillation at τ=2.1217 and continuous oscillation at τ=2.5>τ0.
Numerical simulations in this section are in agreement with the theoretical results in Section 3. In the following, we will further explore the effect of time delay τ and typical parameters on the oscillation dynamics of p53 from bifurcation perspective.
4.2. Bifurcation analyses
To investigate how time delay τ affect p53 oscillation, we perform two-parameter bifurcation analyses with respect to time delay τ and several typical parameters, including the concentration of PDCD5(p), maximum production and degradation rates of p53 and Mdm2: vp53, dp53, vMdm2, dMdm2. Figures 7–11(a) show two-parameter bifurcation diagrams, where black solid lines hb represent Hopf bifurcation curves. For each two-parameter bifurcation diagram, several typical one-parameter bifurcation diagrams are given in Figures 7–11(b)–(e), where black solid and dashed lines are stable and unstable steady states, respectively, and green solid dots are maxima and minima of stable limit cycles.
Figure 7(a) shows two-parameter bifurcation diagram with time delay τ and the concentration of PDCD5(p). Hopf bifurcation curves hb1 and hb2 on the figure divide the parameter region into three parts. p53 reaches a lower stable steady state for parameters on the left of the curve hb1, where p is less than 0.710 regardless of the value of τ. Then p53 oscillation appears for parameters between these two curves hb1 and hb2, where p53 always oscillates for any τ when 0.710<p<0.974 while p53 can oscillate when τ increases to certain value for 0.974<p<11.9. Also the value of τ on Hopf bifurcation curve is more larger for larger p. However, p53 reaches a higher stable steady state for any τ when p>11.9. For intuitiveness, one-parameter bifurcation diagrams of p53 concentration with respect to τ for four typical p are given in Figure 7(b)–(e).
Figures 8–10(a) show similar two-parameter bifurcation diagrams with respect to τ and vp53, dp53, vMdm2, respectively, where the Hopf bifurcation curves hb divides the parameter plane into two parts. p53 exhibits oscillation inside the curve hb and reaches a stable steady state outside the curve hb. As shown in Figures 8–10(a), time delay can induce p53 oscillation for moderate value of the rate constants while it has no effect on p53 dynamics for smaller and larger value of these parameters. Also, the value of time delay on Hopf bifurcation curve increases with the increase of vp53 and vMdm2 while the value of time delay decreases with the increase of dp53. Furthermore, from one-parameter bifurcation diagrams in Figures 8–10(b)–(d), p53 reaches a lower stable steady state for smaller vp53 and vMdm2 and a higher stable steady state for larger vp53 and vMdm2, while the case is opposite for dp53.
Besides, two-parameter bifurcation diagram with respect to τ and dMdm2 is shown in Figure 11(a), where p53 exhibits oscillation for any τ when dMdm2 is less than 0.0146 and reaches a stable steady state for any τ when dMdm2 is larger than 0.0355 while p53 changes from a stable steady state to oscillation with the increase of τ when dMdm2 varies between 0.0146 and 0.0355. These dynamics are shown on one-parameter bifurcation diagrams in Figure 11(b)–(d).
Therefore, bifurcation analyses further explore the effect of time delay τ on p53 oscillation.
5.
Conclusions
The oscillation dynamics of p53 plays a key role in deciding cell fate after DNA damage. The time delay in transcriptional and translational processes is an important factor to induce oscillation. In this study, we explore the effect of time delay of Mdm2 gene express in p53 gene regulatory network regulated by PDCD5 on p53 oscillation through stability theory and bifurcation analyses. Firstly, we give theorems that provide the conditions on the appearance of p53 oscillation for without and with time delays through stability analysis theory. Then, these theorems are verified through numerical simulations, including time series of p53 concentrations, one-parameter bifurcation diagram of p53 concentration versus time delay, the roots of the characteristic equations, and the potential landscapes of p53 and total Mdm2 concentrations. Furthermore, the effect of time delay and several typical parameters p, vp53, dp53, vMdm2 and dMdm2 in system (2.1) on p53 oscillation are explored through two-parameter bifurcation diagrams, which give boundary curves of p53 oscillation. Our results show that time delay can induce p53 oscillation for moderate value of most parameters while it has no effect on p53 dynamics for smaller and larger value of these parameters. Taken together, analyzing the effect of time delay on p53 oscillation will help us understand the mechanism of p53 oscillation.
In this study, we explore the effect of time delay of Mdm2 gene express in p53 gene regulatory network regulated by PDCD5 on p53 oscillation. Our results have demonstrated that suitable time delay can induce p53 oscillation for moderate value of most parameters. However, the effect of multiple time delays in p53 gene regulatory network on p53 oscillation should be further explored. Besides, noise is common in gene regulatory work, it is worthwhile to explore the combined effect of noise and time delay on p53 dynamics. Also, it is meaningful to investigate the dynamics of the other gene regulatory networks or neural networks with time delay and noise for understanding their biological mechanism.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Nos. 12062017 and 11702149), Natural Science Foundation of Inner Mongolia Autonomous Region of China (Grant 2021ZD01) and Collaborative Innovation Center for Grassland Ecological Security (Jointly Supported by the Ministry of Education of China and Inner Mongolia Autonomous Region). The authors acknowledge the reviewers for their valuable reviews and kind suggestions.
Conflict of interest
The authors declare there is no conflicts of interest.










 DownLoad:
DownLoad: