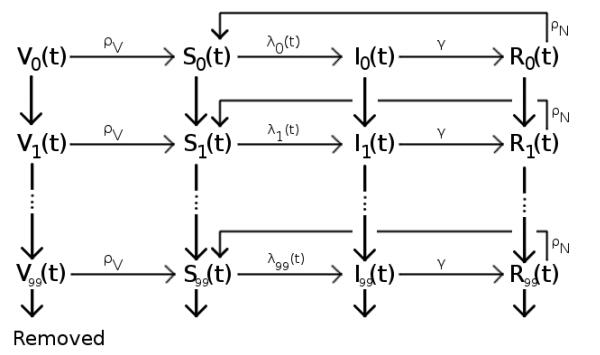
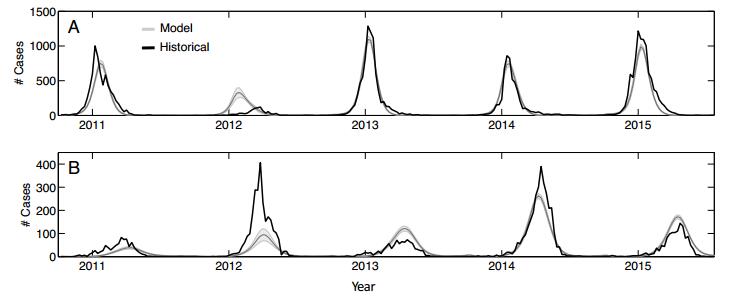
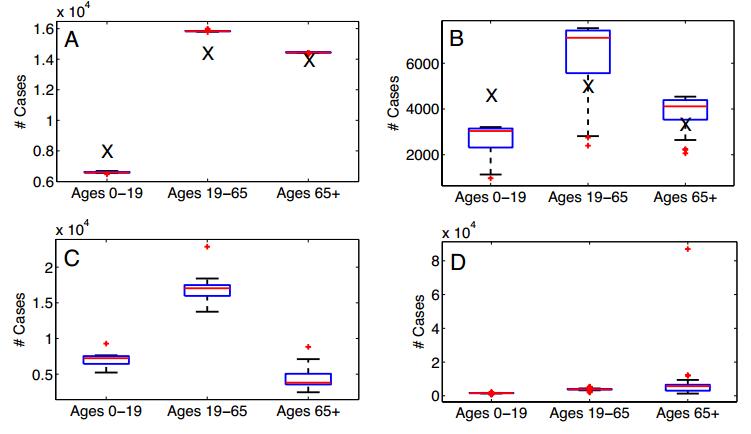
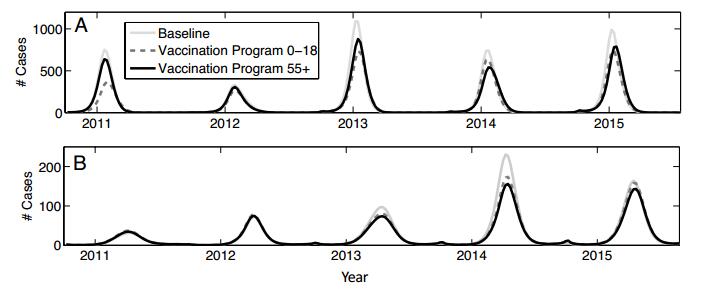
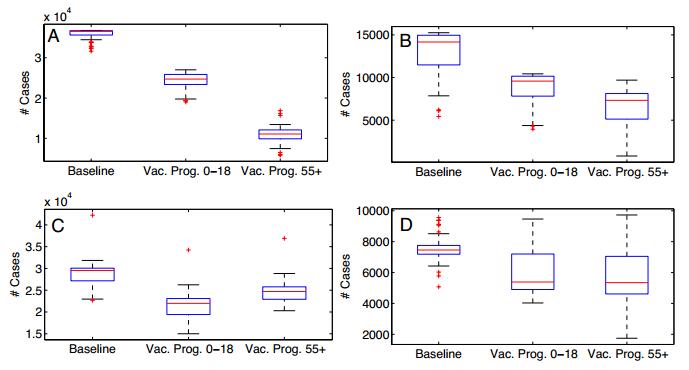
Dynamic transmission models of influenza are sometimes used in decision-making to identify which vaccination strategies might best reduce influenza-associated health burdens. Our goal was to use laboratory confirmed influenza cases to fit model parameters in an age-structured, two-type (influenza A/B) dynamic model of influenza. We compared the fitted model under two fitting methodologies: using longitudinal weekly case notification data versus using cross-sectional age-stratified cumulative case notification data. The longitudinal data came from a Canadian province (Ontario) whereas the cross-sectional data came from the national level (all of Canada). We find that the longitudinal fitting method provides best fitting parameter sets that have a higher variance between the respective parameters in each set than the cross-sectional cumulative case method. Model predictions--particularly for influenza A--are very different for the two fitting methodologies under hypothetical vaccination scenarios that expand coverage in either younger age classes or older age classes: the cross-sectional method predicts much larger decreases in total cases under expanded vaccine coverage than the longitudinal method. Also, the longitudinal method predicts that vaccinating younger age groups yields greater declines in total cases than vaccinating older age groups, whereas the cross-sectional method predicts the opposite. We conclude that model predictions of vaccination impacts under different strategies may differ at national versus provincial levels. Finally, we discuss whether using longitudinal versus cross-sectional data in model fitting may generate further differences in model predictions (above and beyond population-specific differences) and how such a hypothesis could be tested in future studies.
Abbreviations: FASRM: Ferrite-Assisted Synchronous Reluctance Motor; SyncRelM: Synchronous Reluctance Motor; SMPMSM: Surface-Mounted Permanent Magnet Synchronous Motor; WFSM: Wound-Field Synchronous Motor; IM: Induction Motor; DoE: Design of Experiments; ELM: Extreme Learning Machine; EV: Electric Vehicle; IPM: Interior Permanent Magnet; HEVs: Hybrid Electric Vehicles; TEFC: Total Enclosed Fan Cooling; CPSR: Constant Power Speed Range; CCD: Central Composite Designs; DSD: Definitive Screening Design; LHC: Latin Hyper Cube; OFAT: One-Factor-At-A-Time; L-BFGS: Limited-memory Broyden-Fletcher-Goldfarb-Shanno; EDM: Electrical Discharge Machining; CRNO: Cold-Rolled Non-Grain-Oriented; CNC: Computer Numerical Control
1.
Introduction
With the increasing vehicular pollution levels across the globe, rigorous rules are being implemented by various countries. In order to comply with these regulations, automobile manufacturers invest in fuel-saving technologies. This has led to a rejuvenated interest in vehicle electrification, which is a grand overarching strategy. Since electric vehicles offer higher power train efficiency and zero tailpipe emissions, they are considered carbon dioxide neutral in many regulations. Of all available means of road transport, three-wheeled vehicles are considered as the most suitable for last-mile connectivity and are good candidates for building a complete Electric Vehicle (EV) ecosystem. Also, due to their lower total cost of ownership, electrification of the three-wheeler segment is expected to grow faster than the other segments. Hence, a comprehensive analysis is required for the design and development of electric trikes. While power trains form the core of EVs, the electric motor is their heart, and an in-depth analysis becomes essential for choosing the motor. While there are several solutions available currently in the market for three-wheelers with induction and synchronous machines, significant research efforts are being made on reluctance machines. The proper choice of a motor [1] contributes to an appropriate size, rating, power density, driving range, cooling aspects etc. Therefore, there is a need for comparative electromagnetic and multiphysics analysis along with sensitivity analysis and optimization.
While Induction Motors (IM) [2,3,4] have been widely used in many EV and traction applications due to their robustness and cost-effective commissioning and maintenance, the Surface-Mounted Permanent Magnet Synchronous Motor (SMPMSM) [5] has proven to be a promising candidate with higher torque density, efficiency, and much-acquainted design methodology. Another potential candidate is a Wound-Field Synchronous Motor (WFSM) due to the absence of permanent magnets, the complete control of field excitation from the rotor side with the possibility of optimal field weakening, and loss minimization over driving cycles. Recently, the Synchronous Reluctance motor (SyncRel) has received research attention due to its robustness, non-dependency on magnets, and, hence, its reduced cost. The Ferrite-Assisted Synchronous Reluctance (FASR) motor [6] has a higher reluctance torque than magnet torque. A further increase in torque is obtained by optimal sizing and positioning of ferrite magnets. Presently, the power density of the rare-earth PMSM is comparable to a Spoke-Type Ferrite Magnet Motor and seems to be one of the most promising motors for EVs; they also have higher overload capacity and higher power density.
The literature is rich with comparisons of various types of 48-slot/8-pole electric machines suited for four-wheeler EV applications [7]. However, there is a lack of comparative configuration analysis for lower-power ratings suited to trike applications. In [8], the Toyota Prius 2017 IPM is compared with the 2016 BMW i3 and the 2013 Nissan Leaf. Total torque for a wide speed range, torque per volume, and efficiency are used as the performance indicators. PM-assisted SyncRelMs [6] are seen as an alternative to Interior Permanent Magnet (IPM) machines, with the advantages of lower cost and high overall efficiency. IPM machine is found to be a good candidate from the efficiency point of view. However, the dependency on rare earth magnets makes the motor costly, and adequate cooling arrangements are required to get the desired performance. Although different motor types and performance indicators are analyzed in the literature, a common and systematic approach is lacking. This has led to the use of Induction Motors [2,3,4] and Switched Reluctance Motors [9,10,11,12] in American and European markets and the PMSM [7] in Japanese markets for Hybrid Electric Vehicles (HEVs). The lack of agreement on the optimal type of motor for a specific application can essentially be attributed to the use of different sets of parameters for comparative evaluations. A broad compilation of this topic has not been found in the literature. Furthermore, there is a dearth of evaluations of electric motor's thermal and vibration capabilities for such vehicular applications.
This paper focuses initially on six different motor types, namely IM, WFSM, SMPMSM, Synchronous Reluctance, FASR, and Spoke Type, and their impact on various design choices. Their electromagnetic performances are compared for the same power rating of 1.2 kW. All motors with the same diameter and inverter ratings are considered for evaluation; the magnets used are of non-rare earth ferrite type [6] and are designed and characterized by Finite Element Analysis (FEA). The thermal performance [13] and mechanical stresses [14] are also evaluated. Along with comparative analysis, there is a need for establishing a design procedure [15,16,17] for the motor best suited to trike application. Hence, for the FASR motor, one of the most promising candidates for EV application, a Design of Experiments (DoE) approach is used to analyze its design parameters [18,19] for sensitivity toward performance parameters [20]. A neural network-based interpolation tool, Extreme Learning Machine (ELM) [21], is used to map the design parameters with respect to target performance measures. Further, the Basin-hopping optimization algorithm is used to obtain optimal designs achieving application-specific requirements.
The paper is organized as follows. Section 2 proposes the requirements for electric motors suited to trike applications. Vehicular specifications are proposed in Section 3. Electromagnetic performance analysis for different motor configurations is presented in Section 4. Thermal and stress analyses are conducted in Section 5. Section 6 details the discussion on results, and Section 7 discusses the drive cycle analysis for the FASR motor. Design optimization of the FASR motor is detailed in Section 8, with the experimental study in Section 9.
2.
Requirements of electric three-wheeler motor design and selection criteria
The common design targets [1,7,15] essential for electric motors suited to trike applications considered in this work are:
1. High efficiency over a wider speed and torque range.
2. Low weight, volume, and cost.
3. Low torque ripple and low acoustic noise for comfort.
4. High power/torque density.
5. High starting torque at low speeds.
6. High torque per current capability.
7. Lower mechanical stress on rotor for improved life.
8. Good thermal capabilities for longevity.
3.
Vehicular and motor specifications
The three-wheeler model of Reep vehicle [22] is taken as a reference. The specifications considered for a light electric trike in this work are given in Table 1. The estimated motor power rating based on the traditional tractive effort [23,24] calculation is 1.2 kW. For all motors considered in this work, the power rating of 1.2 kW is taken for evaluating the electromagnetic [25] and multi-physics [26] performances. Motor type and ratings are significant in a drive train, helping in deciding the cost and mileage of the vehicle. A typical three-wheeler vehicle has a low-speed driving profile [27] compared to cars. Even so, if its motor is underrated, then the vehicular requirements may not be met; if it is overrated, there is a possibility of the motor not being fully utilized, reducing its efficiency and increasing its cost.
Six typical EV motors are selected for comparison: IM, WFSM, SPM, SyncRel, FASR, and Spoke motor. The main parameters and specifications of the motors are given in Table 2, which are arrived based on tractive effort calculation as in [5]. The CAD-based FEA software tools MagNet 2212 and MotorSolve 2212 are utilized for the electromagnetic field analysis. Transient 3D analysis is employed in obtaining the performance curves. Stress analysis results are obtained using FEA. Thermal analysis results are acquired to analyze their thermal behavior with Total Enclosed Fan Cooling (TEFC). All the motors are designed with the same outer diameter of the stator, steel lamination material, and ferrite magnet. The common parameters used are given in Table 2.
4.
Comparison of electromagnetic performance
All motor geometry models considered for the feasibility study are analyzed using a 3D FEA [3,4,15] simulation. The stator structure remains the same throughout the analysis.
4.1. Stack length
Analysis based on the same torque developed by all selected motors is done by appropriately adjusting the stack length of the motor. The stator outer diameter of all motors is maintained at 159 mm and the stack length varies to get 8 nm as the desired torque for 1.2 kW at the rated speed. The current density chosen is 6 A/mm2 for continuous operation. The flux saturation is 2.1 T, for the chosen electromagnetic steel, M1000-65A. Space factor/slot fill factor is kept at 40%. Table 3 gives the stack lengths of various motors for obtaining the desired torque. Figure 1 shows all the motors with variable stack lengths. It can be seen that the FASR and spoke-type motors produce the desired torque for the same stack length of 64 mm, while all the other four motors require an increase in stack length. The stack length of WFSM is found to be maximum, indicating poor power density and more space required for the motor casing.
4.2. Power density, torque density, torque ripple, and torque-current capability
A motor with higher power density makes the EV compact and lightweight. Hence, power density serves as an important selection index. Even motors of the same type and rating are designed and manufactured differently by various manufacturers. Hence, there can be a slight difference in their weights. For various types of electric motors with the same voltage, power, and speed ratings, the mean weight of the electric motor is used to determine the power/weight ratio. Table 4 defines the volume of the stator and rotating parts of various candidate motors. The air gap length of these motors is maintained at 0.52 mm. The total mass of these motors is in the range of 8.7–9.9 kg and their active rotor volume is in the range of 250–370 cm3. Figures 2–4 show various torque components, instantaneous torque characteristics and torque-speed characteristics with respect to efficiencies of the various motors. The synchronous and induction motors are found to have lower power density than the others. The Spoke and SyncRel types are found to have almost the same power density, while a slight improvement is seen in FASR because of ferrite magnets. The torque density of FASR is found to be higher than SyncRel and Spoke motors, while the synchronous and induction motors have only 60–70% values. The torque per unit current of FASR and spoke motors is found to be the same because of the presence of magnets with a higher volume in the spoke motor.
The characteristics of these machines challenge their selection due to the high complexity, interdependence of parameters, and mixed advantages or disadvantages. From Table 4, it is evident that, as compared to the synchronous and induction machines, the size of reluctance and spoke-type motors is reduced. Since the spoke motor can hold a larger number of permanent magnets, it can effectively use magnet torque and reluctance torque. However, it has to be noted that the spoke motor has a higher torque ripple, which may lead to vibration and premature failure of the drive train components.
4.3. Efficiency map
An efficiency map provides the efficiency for the speed and torque combinations and is a contour plot of efficiency with torque and speed axes. The efficiency maps of all investigated motors are represented in Figure 4 and are obtained by 3D FEA analysis in motor solve.
5.
Mechanical stress and thermal analysis
The mechanical stress and thermal analysis provide relevant comprehensive information on the mechanical stability and thermal longevity of the machine.
5.1. Von Mises stress analysis
To determine the factor safety of electric motors, Von Mises stress analysis is done for maximum torque and maximum speed [14] using FEA. The safety factor is defined as the ratio of yield stress to maximum stress and should be close to 1.5. The conditions for analysis are detailed in Table 5.
For the structural steel of all motors, the tensile strength of 250 MPa was taken; for Y30 ferrite, it was 34 MPa, and for copper, it was 33.3 MPa. Von Mises stresses for FASRM is shown in Figure 5.
Maximum Von Mises stress is found as 149.61, 63.507, 54.768, 31.16, 18.86, and 4.9 MPa for SyncRel, spoke, IM, FASR, and WFSM, respectively, at their core. The highest stresses occur at the sharp edges of all motors and near the ribs for the FASR motor. PM motors like spoke, FASR, and SPM have their stress at the magnets and are of the order of 40.67, 24.97, and 3.780 MPa, respectively. The fatigue analysis and safety factor details for all motors are given in Table 6. A minimum safety factor of 0.84 is found on the magnet of the spoke motor. Since the hypothetical condition of maximum torque at maximum speed is considered, the stress exceeds the yield value for the spoke motor. However, this would decrease when the actual torque at maximum speed is considered.
5.2. Thermal analysis
Heat distribution information in the electric motor is very valuable at the design stage. High temperature indicates the need of decrement in losses, a change of cooling type, adjustments in the fins and frame, and optimization of the motor. The mechanical losses in the motor include bearing loss and windage/drag loss. The electromagnetic losses, which are associated with the active parts of the motor like iron, winding, and magnets, tend to affect the thermal analysis heavily. FE analysis results provide the losses in the machine. These results are used as input to the thermal analysis software. Also, the hottest spot in the EM can also be located with this FEA-based thermal analysis [13]. Based on the loss calculations, the dynamic temperature distribution under the driving duty cycle is predicted for a totally enclosed fan-cooled model with a coolant speed of 12.8 m/s. The motor insulation class chosen is F. The temperature distribution of all the motors after a steady operation of 1 hour is shown in Figure 6. For the maximum power, the maximum temperature is well within the allowable temperature rise of insulation, and the motor life will be extended for all motor types. The maximum temperature rise of approximately 90 ℃ is found in the stator winding for the motors and in the rotor bar for induction motors. For SyncRel, FASR, and spoke motors, the rotor core also experiences higher temperatures in the range of only 85 ℃. The difference in temperature between the stator and rotor hotspots is in the range of 1–5 ℃. The WFSM has hotspots only on the stator winding.
6.
Discussion and results
In order to find out the most suitable drive motor for electrical trikes, six machine types were compared. To have good comparability, a numerical FE simulation for a nominal power of 1.2 kW is performed. The applicability of all selected motors is compared for power/torque density, efficiency values, range of speed, mechanical safety factors, and temperature rise. The following inferences are drawn from various analyses.
•The reluctance and spoke motors have higher torque density. The presence of magnets contributed to their higher torque. However, the torque ripple of reluctance-type motors is very small compared to spoke-type motors. The efficiency of these types at rated speed is also higher compared to the other machines.
•The torque density, power density, and torque/current capability of reluctance and spoke motors are higher than the other types, making them promising candidates for EVs to get a compact drive space.
•SyncRel and FASR motors outperform others in terms of efficiency at higher torque speed range, field weakening at speed range of 8500 rpm, and wide Constant Power Speed Range (CPSR).
•Thermal analysis after 1 hour of steady run reveals that all motors experience thermal stress on the upper stator winding; the choice of proper cooling means will keep this temperature rise under control.
•Von Mises analysis reveals that the factor of safety of Spoke type is poor, as the stress both on the core and magnets are maximum. Design optimization may help in achieving a good overall design and improved safety factor. The safety factor of SyncRel and FASR motors is good.
•SyncRel machines have low-cost construction since there are no magnets and conductors in the rotor structure. This is of prime interest in EVs. Though the presence of magnets in SMPMSM provides improved torque, their CPSR is very narrow. They can be considered for low -speed trikes as they have a good constant torque characteristic and a high factor of safety.
7.
Drive cycle modeling of FASR motor
The investigations reveal that the FASR motor is one of the best-suited motors for trike applications. A simple kinematic vehicle model is used to convert the standard Indian drive cycle (IDC) [15] into time/speed vehicle profiles into a time/torque/speed profiles for the motor. The vehicle parameters are given in Section 3. The IDC points are plotted onto the torque-speed curve as in Figure 7.
8.
Design optimization of FASR motor
Achieving an optimal motor configuration requires a design optimization step based on the geometric design parameters. However, this high-dimensional multi-objective problem [5,11,12,18] has inherently high computational costs owing to the large search space of design parameters and stipulated performance objectives. Thus, a DoE-based statistical analysis methodology [20] is used in this paper to identify the vital parameters that can then be effectively searched for robust motor performance in the optimization step.
A multi-level sensitivity analysis is a proven way to exploit this inherent stratification of design parameters to quickly arrive at a robust motor design. Few recent research papers have reported the same approach. However, these approaches employ One-Factor-At-A-Time (OFAT) methodologies, which can fall short of the optimal settings of factors, and more specifically, the two-factor and other interaction effects between design variables are usually unaccounted for. An alternate statistical analysis tool for multivariate optimization problems is the DoE, which attempts to delineate significant parameters using single-factor effects as well as multi-factor interaction effects. Besides, DoE methodologies have led to new designs that require fewer experimental runs than the classical Central Composite Designs (CCD).
In this section, the DoE technique used to extract the vital parameters from the 13 design parameters of a FASR motor is detailed along with the sensitivity indices and inference charts. Also, the variation of the sensitivity index for geometrical parameters with a change in the choice of objectives is emphasized.
The DoE techniques can broadly be classified as full factorial techniques and partial factorial techniques, with the latter having many sub-designs that have iteratively less experiment cycles. A straightforward approach would be to use a full factorial design, which requires kn total experimental runs for n design parameters and k parameter levels and has an exponential growth factor. For a FASR motor with n = 13 parameters and a two-level design of k = 2, a total of 8192 experiments must be run to ascertain the geometric influence.
For a 13-dimensional optimization problem of the FASR motor, one factorial design, two response surface designs, and one randomized design were selected and analyzed: Plackett-Burman design, Box-Behnken (3-level) design, Definitive Screening Design (DSD), and Latin Hyper Cube (LHC) design. Considering a two-level design constraint for 13 design parameters, Plackett-Burman requires 16 experimental runs, Box-Behnken requires 325 runs, DSD-O (2n + 1) requires 27 runs, and LHC-O (4n) requires 52 runs. The DSD design was eventually chosen due to its tested capability to capture nonlinearity across design parameters and relatively shorter experiment cycles. To examine the sensitivity of our FASR motor design objectives to the design variables, experiments need to be performed to examine the design variables for different levels. For running the DoE experiments, 13 geometric parameters of the FASR motor, shown in Figure 8, were selected, with their low and high bounds as specified in Table 7. These values correspond to the 0-level and 1-level in its DoE design matrix and vice versa. The bounds of the design variables were chosen based on manufacturing constraints.
8.1. Sensitivity analysis
For the FASR motor, torque average (Tav), torque ripple percentage (Tr%), and motor efficiency (ƞ) are selected as performance objectives for which the motor has to be optimized. The average torque and torque ripple are calculated using FEA software and analytical methods.
Once the sensitivity index for each of these three design objectives is calculated from the DoE matrix, a composite sensitivity function Sspt is then calculated as follows,
where, λ1 + λ2 + λ3 = 1 and Sav(xi), Sripple(xi), and Seff(xi) are the absolute values of the sensitivity indices of Tav, Tripple%, and efficiency, respectively. λ1, λ2, and λ3 are the weighted coefficients of Tav, Tripple%, and efficiency, which satisfy Eq (1).
The values λ1, λ2, and λ3 are chosen as 0.333 for equal significance of optimization objectives. In multi-level optimization, the design parameters are then stratified into two levels, as follows:
● Highly sensitive (Level 1), considering the parameters with G(xi) > δ.
● Mildly sensitive (Level 2), considering the parameters with G(xi) < = δ,
where δ is the average sensitivity value.
8.2. Results of sensitivity analysis through interaction measures
The sensitivity indices and composite sensitivity function calculated as per the above equations for the three design objectives of Tav, Tripple%, and efficiency are listed in Table 8.
From the Table 8, it is observed that θ1, θ3, δ1, δ2, and δ3 are the highly sensitive design variables out of the 13 geometric parameters of a FASR motor.
The sensitivity results also expose additional information on whether a design variable aids in/suppresses a particular design objective.
To ensure that these observations are devoid of approximation errors and not biased from only the first-order effects of design variables, they need to be verified by calculating higher-order interaction effects of the design variables on our design objectives. A k-factor interaction effect simply denotes that k of the n-design parameters varied together at a time and the corresponding output response change is observed. For a given n-factor experiment, the output objective can be influenced by 1-factor, 2-factor, 3-factor, … n-factor interaction effects. It should be noted that 1-factor effects in this n-term series were the individual factor effects tested by OFAT methods, while the rest are usually unaccounted for. As the number of factors (n) increases, the number of interactions increases exponentially too, as the total number of possible interactions = 2n – n – 1. Thus, for our 13-factor FASR experiment, there are a total of 8178 possible interactions that could influence the output variable. However, not all these interactions are worthwhile/significant enough to deduct through experimental runs, as most of them wield a negligible influence on the output design variable. Aside from individual effects, the second-order (2-factor) interaction effects are the next most significant data points that can help verify/nullify the hypothetical results derived from first-order effects. It must be noted that for an n-factor experiment, there are n × (n – 1)/2 two-factor interaction effects. The second-order normalized sensitivity measures of the 13 design variables for each of the three design objectives are represented as heat maps in Figure 9 (a–c).
From the interaction effects matrix, important conclusions can be drawn regarding the most significant factors, how they are coupled with the design objective, the best setting for each factor, and the confounding structure of the design variables. Since all second-order effects have been normalized to a common {–1, +1} scale, determining the relatively significant parameters is equivalent to determining the parameters with the most extreme correlation values (values close to +1 or –1). The second-order effects are mere extensions of first-order effects, therefore they behave similarly in that the factor pairs with high absolute values, suggesting that they influence the output response more than the factor pairs with interaction measures closer to zero. The sign of the measure also corresponds to whether it aids in/suppresses the design objective as before.
It can be inferred from the graph that δ1, δ2, and δ3 variables exhibit high positive correlation values > 0.90 in line with the high positive sensitivity measures observed in Table 8. The magnet lengths are the next design variables with high positive correlation among them and they were the most influential of the weakly sensitive parameters classified from Table 8. The θ1, θ2, and θ3 variables, on the other hand, exhibit high negative correlation with each of the other variables, in line with the high negative sensitivity measure observed in Table 8. It is also interesting to note that the interaction measures of θ1 and θ2 are negative for all variables except for the θ1 – θ2 interaction measure, as they both work simultaneously in suppressing the design objective instead of working against each other. The other design parameters reveal a similar behavior. These inferences imply that the observed first-order effects were not spurious correlations, and the second-order interaction measures corroborate with first-order results for significant parameters.
8.3. Inferences for design ranking
The sensitivity and interaction measures are a major step in building the definitive list of ranked factors for each of the design optimization routines, as explained by Figure 10.
The multi-column chart in Figure 10 lists the normalized sensitivity measures of 13 design parameters for each of the three design objectives of Tripple, efficiency, and Tavg. These normalized values give a good sense of each factor's relative importance with respect to each design objective. For example, if a designer's only objective is to tune torque ripple, then one should go about fine-tuning the variables with the highest normalized S values in the chart, as the normalized values are ranked in increasing influence from 0 to +1/–1.
The same ranking can also be done vice-versa by normalizing each design objective's relative importance with respect to each design parameter. Those results for the significant level-1 parameters are shown in Figure 11 in the nested pie chart. Any given ring in the chart shows the corresponding factor's relative influence on the three design objectives. For example, by comparing the θ1 and θ3 rings, one can infer that the θ1 variable has a negligible effect on efficiency compared to θ3, but it also has a far higher effect on average torque than θ3. So, if one were to fine-tune any of the significant variables, a measure of each of the three design objectives and their interdependencies affected can be evaluated from this graph.
8.4. Extreme learning machine-based performance prediction
A typical motor design optimization routine requires the estimation of performance objectives during every step. This requires close coupling of the FEA, a time-expensive process, with the optimization routine for each of the given optimization objectives to simulate the motor performance under said conditions. However, this FEA can be replaced by equally precise statistical feature-learning models, with much lower computing time costs. This work proposes the use of a subclass of machine learning models, called an Extreme Learning Machine (ELM) [21], which utilizes pseudo-inverse of n-dimensional matrices to update the layer weights instead of backpropagation. This network is chosen to model the FASR motor due to its efficient hyper-parameter tuning process as well as a low training/inference time that speeds up the subsequent optimization routine. ELM, despite being a single-layer network, can provide good model generalization for a lower number of data points compared to conventional data-intensive neural network models, further adding to its suitability for our requirements.
The comparison between ELM and FEA is shown in Figure 12. The close correlation of FEA and ELM values from Figure 12 further validates the choice of using an ELM network to model FEA. Using FEA, data for the FASR performance objectives are collected with each run taking ~15 min. These data are then used for ELM training, with the resulting model having an average inference time of ~500 mS.
Once a reasonably accurate ELM model is obtained, the Basin-hopping optimization technique is run with this model to obtain optimal motor designs. Basin-hopping is a global optimization [28] framework that finds the global minimum of a polynomial function by making use of local optimization. The algorithm involves three major steps—a local search step to choose the nearest minima in the search space followed by an acceptance test and a final counteracting perturbation step to pull the model toward the global minima.
In the local search step, a quasi-Newton algorithm is used for finding the nearest minima. In this method, the Hessian matrix (Bk), which holds the information of second-order derivatives of a multivariable function, is approximated at the beginning and updated at each step of the iteration. This is suitable for optimization algorithms where the Hessian matrix cannot be calculated since the nature of the objective function is not known beforehand. The particular type of quasi-Newton method that we have adopted is the Limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithm.
The Hessian approximation (Bk) in quasi-Newton methods must adhere to the below quasi-Newton condition,
where yk=∇f(Xk+1)−∇f(Xk)andΔXk=Xk+1−Xk.
Hessian with updating is given as
The expressions for constants a and b are arrived at by imposing the quasi-Newton condition and setting u and v to u = yk and v = BkΔxk.
Now, we have the expression for Hessian update as follows,
The nearest minima are now calculated with this approximation of Hessian. In the subsequent acceptance test, the new solution is accepted if the new objective value (fj) is lesser than the previous objective value (fi). If not, the new solution is accepted if it satisfies the metropolis criteria, i.e., e-| fi - fj | ≥ 0.5. In the final perturbation step, a random perturbation that follows a uniform distribution between ±stepsize is added to the minima found in the local search step. In our implementation, the step size is set to be 0.2 × |MAXi – MINi|, ∀i ∈ {1, 2, 3…, N}, where N is the number of design variables. These three steps are iteratively repeated until the preset MAX_ITERATIONS count is reached. The results of ELM-Basin-hopping optimization are shown in Figure 13.
This end-end optimization process for optimal FASR design selection is described in the flowchart in Figure 14.
9.
Experimental study
In this study, a FASR motor is designed for electric vehicle traction applications [29,30] for a rating of 1.2 kW. The optimized design parameters used for the fabrication of the motor are given in Table 9, and the fabricated prototype is represented in Figure 15.
A prototype has been developed for the optimized design of 1.2 kW FASR motor. The manufacturing process of Wirecut - Electrical Discharge Machining (EDM) is used to shape the flux barrier in the ferrite-assisted synchronous reluctance motor, involving the utilization of electric current to cut Cold-Rolled Non-Grain-Oriented (CRNO) steel. The process takes place in a tank filled with deionized water for cooling the work piece. Varnish is applied between the laminations of the rotor before stacking in order to reduce iron loss. Stacking, stamping, press fitting, and shaft insertion, which is done by a Computer Numerical Control (CNC) machine, are all part of the manufacturing process. Additionally, ferrite magnets are filed and inserted inside the flux barrier using araldite as an adhesive. Balancing is conducted to maintain the center of gravity and minimize rotor vibrations.
The experimental setup [16] to verify the performance of the developed optimized motor is shown in Figure 16. The experiments were done for rated operating conditions of 1.2 kW power and 8 nm torque requirement. The RMS voltage for the motor is 42.43 V and RMS current is 21.2 A on full load. The generator load is coupled to the motor with a shaft-to-shaft coupling containing a torque sensor in between.
The experimental results are compared with the analytical and simulation results and are presented in Table 10 and Figures 17 and 18.
Analyses show that the designed motor satisfies the desired electromagnetic requirements, with a good match among FE, analytical, and hardware results.
Additionally, torque vs. rotor angle plot and instantaneous torque response from FEA and torque sensor are also shown in Figures 17 and 18, providing insights into the validity of the FEA model with respect to the experimental results.
10.
Conclusions
The performances of electromagnetic, thermal, and stress analyses were compared between six EV motors. SyncRel, Spoke, and FASR motors were found to have good torque density and higher efficiency, being compact solutions for trike applications. They also have a wide CPSR. The thermal analysis revealed that the upper stator winding is subjected to a maximum of 90 ℃ and should be brought down by proper cooling methods. The FASR motor was selected among all motors and its parameters were optimized using sensitivity analysis, DoE- and ELM-based interpolation techniques. A prototype FASR was tested, and the test results closely matched the simulation results. Drive cycle investigations also revealed that the operating points of FASR are well within the capabilities of the machine. This work also provides guidelines for electric motor designers, exhibiting various tradeoff criteria and performance measures with respect to trike application.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
Mohan Lal Kohle is a guest editor for AIMS Energy and was not involved in the editorial review or the decision to publish this article. All authors declare that there are no competing interests.
Author contributions
V. Rajini: Conceptualization, Methodology, Validation, Investigation, Supervision, Writing Original draft preparation.
V.S. Nagarajan: Methodology, Validation, Investigation, Data curation, Writing—Original draft preparation.
Karunya Harikrishnan: Methodology, Validation, Visualization, Investigation, Writing—Original draft preparation.
Mohan Lal Kolhe: Investigation, Formal Analysis, Supervision, Writing—Reviewing and Editing.









 DownLoad:
DownLoad: