1. Introduction
This manuscript extends a previous work [20] which examined how variability of the latent and infectious periods of an infectious disease could affect the threshold value $\rho>0$ by assuming an intervention against transmission applied homogeneously across individuals at a rate $\phi$ so that, when $\phi\geq\rho$, the controlled reproduction number, as defined in [20], would be kept below unity. The objective here is to address how between-individual variability in adherence makes the theoretically proven effective control measure less effective when $\phi\geq\rho$.
1.1. Brief review of the previous work
A branching process is often used to approximate the cumulative number of infected individuals during the initial phase of an epidemic, when an infectious "seed" is planted in an infinitely large susceptible population [2]. The basic reproduction number $R_{0}$ is the mean value of the branching process and plays a very important role. According to theory ([19], [17]), if $R_{0}\leq1,$ the branching process will become extinct with certainty. If $R_{0}>1,$ there exists a positive probability that the branching process will grow infinitely large. The branching process approximation is valid only for the establishment phase during which the depletion of the susceptible individuals is negligible and no intervention has taken place.
Assuming a very large population with homogeneous mixing, the infectious contact process (as defined in [3]) is a Poisson process with constant rate $\beta.$ If an infected individual has a random infectious period with finite mean $\mu_{I},$ the basic reproduction number is $R_{0}=\beta\mu_{I}$ (see [1]).
This paper only considers the case $R_{0}>1.$ If the branching process does not die out during the establishment phase, the epidemic does not grow infinitely large. The depletion of the susceptible population depletes the reproduction number over time according to $R_{t}=R_{0}\frac{S(t)}{n}$ where $S(t)$ is the expected number of susceptible individuals and $n$ is the total population size, which is assumed to be constant. $R_{t}$ will be depleted to a threshold value $1$ at some point of time. After that, two scenarios might happen.
1. $R_{t}$ remains less than 1. The result is an end of the epidemic with a positive proportion $0<\eta<1$ of the population cumulatively infected. Under certain circumstances (e.g. closed population, no death), $\eta$ satisfies a final size equation $1-\eta=s_{0}e^{-R_{0}\eta},$ $\eta>0,$ where $s_{0}$ is the initial proportion of susceptible individuals in the population at the beginning of the epidemic. This equation holds true in a very large population with homogeneous mixing so that the infectious contact process is a Poisson process. It holds true for arbitrarily distributed latent and infectious periods, regardless whether there is a latent period [10].
2. Due to loss of immunity of recovered individuals or by demography, there is replacement of susceptible individuals so that $R_{t}$ is sustained at $R_{t}\approx1$ in the long run, resulting an asymptotic equilibrium condition $\frac{S(t)}{n}\approx\frac{1}{R_{0}}.$
In both scenarios, $R_{0}$, defined at the very beginning of the outbreak, transcends to the long run outcome, in theory.
In practice, $R_{0}$ is not only depleted by the transmission dynamics, but also by interventions during the outbreak. The long run outcome, such as the final size $\eta$, does not transcend back to $R_{0}.$ It is manifested as if the reproduction number had been $R_{c}<R_{0}$ at the very beginning and there had been no intervention. Such an analogy is appropriate given the generality of the transcendental relationships between $R_{0}$ and the final size or the asymptotic equilibrium level, as proven in [10].
In [20], $R_{c}$ is called the controlled reproduction number and modelled in a quarantine-isolation paradigm. Infected individuals are quarantined (or isolated) at a constant rate $\phi>0,$ assuming that the intervention is applied homogeneously across individuals. This is the idealized situation.
A latent period is a random duration $T_{E}$ during which an individual is infected but not yet able to infect other susceptible individuals through contact. With quarantine rate $\phi,$ the probability that an individual during the latent period escapes from being quarantined and becomes infectious is $\int_{0}^{\infty}e^{-\phi x}f_{E}(x)dx$ where $f_{E}(x)$ is the probability density function (p.d.f.) of $T_{E}.$ The infectious contact process is a "thinned" Poisson process with rate $\beta\int_{0}^{\infty }e^{-\phi x}f_{E}(x)dx$ which returns to $\beta$ when $\phi=0.$ The infectious period $T_{I}$ has survival function $\overline{F}_{I}(x).$ Infectious individuals are isolated at rate $\phi$ from contacting other individuals. The effective mean duration of infectiousness among infectious individuals is $\int_{0}^{\infty}e^{-\phi x}\overline{F}_{I}(x)dx$ which returns to $\mu _{I}=\int_{0}^{\infty}\overline{F}_{I}(x)dx$ when $\phi=0.$ Using Laplace transform notations $\mathcal{L[}f_{E}](s)=\int_{0}^{\infty}e^{-sx}f_{E}(x)dx$ and $\mathcal{L[}\overline{F}_{I}](s)=\int_{0}^{\infty}e^{-sx}\overline{F}_{I}(x)dx,$ $R_{c}$ is expressed by
|
$
R_{c}(\phi)=\beta\mathcal{L[}f_{E}](\phi)\mathcal{L[}\overline{F}_{I}](\phi).
\label{Yan 2010}
$
|
(1)
|
The threshold condition is $\beta\mathcal{L[}f_{E}](\rho)\mathcal{L[}\overline{F}_{I}](\rho)=1$ so that $R_{c}(\phi)\leq1$ when $\phi\geq\rho.$
Define a new p.d.f. $f_{W}(x)=\frac{1}{\mu_{I}}\overline{F}_{I}(x)$ which is recognized as the equilibrium distribution in renewal process theory. At a randomly chosen time $t,$ "currently" infectious individuals form a prevalence cohort. The infectious period of individuals in this cohort is length-biased because those with longer infectious period have a large probability of being included. If the system is under equilibrium (i.e. the prevalence proportions for susceptible, latent, infectious, recovered and immune individuals are approximately constant), the length-biased infectious period is on average longer than $\mu_{I},$ which is $\mu_{I}(1+cv^{2})$ and $cv$ is the coefficient of variation of the infectious period $T_{I}$ defined as the ratio of standard deviation to its mean. The corresponding length-biased p.d.f. is $\frac{x}{\mu_{I}}f_{I}(x)$. Meanwhile, the time from the beginning of infectiousness of these individuals in the prevalence cohort to the observation time $t,$ is identically distributed, denoted by $W,$ with mean equals to $\frac{1}{2}\mu_{I}(1+cv^{2})$ and the corresponding p.d.f. is $f_{W}(x)=\frac{1}{\mu_{I}}\overline{F}_{I}(x).$
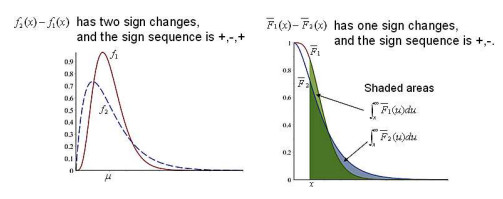
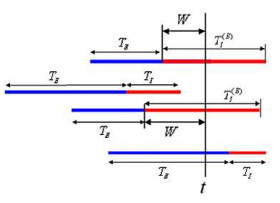
Under equilibrium, if an individual at a randomly chosen time $t,$ assuming susceptible at $t-\Delta t,$ comes in contact with any of the infectious individuals in the prevalence cohort, $G=T_{E}+W$ is the total latent period plus part of the length-biased infectious period, where $W$ is the duration between the time of infection of individuals who are in the prevalence cohort and time $t$. An illustration is given in Figure 1 in which the red line is the infectious period and the blue line is the latent period. In this figure, only two of the four individuals are in the prevalence cohort and $W$ is defined. The mean value for $G$ is $\mu_{E}+\frac{1}{2}\mu_{I}(1+cv^{2}).$
Assuming independency, the p.d.f. for $G=T_{E}+W$, denoted by $f_{G}(x)$, is defined by the convolution between $f_{E}(x)$and $f_{W\text{ }}(x)$. Its Laplace transform is the product $\mathcal{L[}f_{G}](s)=\mathcal{L[}f_{E}](s)\mathcal{L[}f_{W}](s),$$s>0,$where $\mathcal{L[}f_{W}](s)=\frac{1}{\mu_{I}}\mathcal{L[}\overline{F}_{I}](s).$ Thus (1) becomes $R_{c}(\phi)=R_{0}\mathcal{L[}f_{G}](\phi)$and the threshold condition is
|
$
R_{0}\mathcal{L[}f_{G}](\rho)=1. \label{threshold eqn}
$
|
(2)
|
1.2. Highlights of this paper
The quarantine-isolation paradigm in [20] is for the convenience of discussion. In this manuscript, the control measure is generalized into many types of intervention applied to individuals during their latent period and/or their infectious period. Such interventions include, but are not limited to, condom use for the reduction of sexual transmission of diseases, prophylactic intervention and use of antiviral drugs to reduce transmission, and so on.
Several factors may influence the risk of infection separately from any impact of the intervention. One of them is between-individual heterogeneity in compliance that individuals may not fully comply with the intervention. When individuals fully comply with the intervention and the exposure to the infectious agent is comparable across all individuals being studied, this is the idealized situation. The impact of an intervention is sometimes called the efficacy of the intervention. Since some level of non-compliance is likely where an intervention is widely implemented, the focus will be on effectiveness that provides a more accurate view of possible effects population-wide.
Throughout the paper, the notation $\rho$ is the threshold parameter calculated by solving (2)$.$ The condition $R_{c}(\rho)=1$ is a reflection of efficacy under the idealized situation. In the presence of between-individual heterogeneity in the implementation, at the calculated threshold value $\rho,$ the actually realized controlled reproduction number, denoted by $R_{v}(\rho),$ will be in the range $1<R_{v}(\rho)<R_{0}.$ This is a reflection of effectiveness.
Section 2 is a qualitative analysis. A frailty model, with a random effect $z>0,$ is used to characterize unobservable heterogeneity. The variability of $z$ is measured according to the convex order given by Definition 2.2, which is a more natural way to describe dispersion and a more general definition than variance. It shows that the more variable the frailty $z$ according to convex order, the larger the value of $R_{v}(\phi).$ The control measure is most effective if applied homogeneously across all individuals. It also contains an important finding that, given the threshold $\rho$ under the idealized situation$,$ the value of $R_{v}(\rho)>1$ is invariant with respect to the time scale of disease progression, regardless if the disease is acute (e.g. measured in days like influenza) or chronic (e.g. HIV, viral hepatitis). Given the model for frailty, $R_{v}(\rho)$ only depends on $R_{0}$ and $f_{G}.$ The latter includes assumptions on the existence of the latent period and the distributions of the latent and the infectious periods.
Section 3 is a quantitative analysis to evaluate how much influence $f_{G}$ has on $R_{v}(\rho).$ It turns out that the influence is quite weak under the numerical results calculated in 32 different cases. Detailed calculation formula and associated tables are given in Appendix.
The results presented in this paper are not only invariant to the time scale of the disease progression, but also robust with respect to model assumptions in the disease progression.
2. Model intervention heterogeneity as frailty
2.1. The frailty model, efficacy and effectiveness
In survival analysis, the frailty model is a random effect model to account for unobservable heterogeneity between individuals [7]. In the proportional hazard model $h(x|z)=zh_{0}(x),$ $z>0,$ where $h_{0}(x)>0$ is the baseline hazard function, $z>0$ is called the frailty parameter and is assumed to be random with mean value $E(z)=1$ and p.d.f. $\xi(z).$ It can be alternatively written in terms of survival functions $\overline{F}(x|z)=e^{-zH_{0}(x)},$ where $H_{0}(x)=\int_{0}^{x}h_{0}(u)du$ is the cumulative baseline hazard. If there is no heterogeneity, then $\xi(z) $ degenerates to $z\equiv1$ without variation and the survival function is $\overline{F}_{0}(x)=e^{-H_{0}(x)}.$ In the presence of unobserved heterogeneity, the frailty model has the survival function
|
$
\overline{F}^{(frailty)}(x)=\int_{0}^{\infty}\overline{F}(x|z)\xi
(z)dz=\int_{0}^{\infty}e^{-zH_{0}(x)}\xi(z)dz=\mathcal{L[\xi]}(H_{0}(x))
\label{frailty}
$
|
(3)
|
where $\mathcal{L[\xi]}(s)=\int_{0}^{\infty}e^{-zs}\xi(z)dz$ is the Laplace transform of $\xi(z)$ and $\mathcal{L[\xi]}(H_{0}(x))$ is $\mathcal{L[\xi]}(s)$ evaluated at $s=H_{0}(x).$ The importance of Laplace transform in the context of frailty modelling in survival analysis was pointed out in [6].
In the current context, the intervention is associated with a rate $\phi>0$ under the idealized situation. The baseline hazard function is $h_{0}(x)=\phi,$ $H_{0}(x)=\phi x$ and $\overline{F}_{0}(x)=e^{-\phi x}.$ If there is no heterogeneity in control measures, $R_{c}$ is a fraction of $R_{0}$ and this fraction is $\int_{0}^{\infty}e^{-\phi x}f_{G}(x)dx.$ The controlled reproduction number is
|
$
R_{c}(\phi)=R_{0}\int_{0}^{\infty}e^{-\phi x}f_{G}(x)dx=R_{0}\mathcal{L[}
f_{G}](\phi). \label{Rc baseline}
$
|
(4)
|
In the presence of frailty with a non-degenerated p.d.f. $\xi(z)$, replacing $e^{-\phi x}$ with $\mathcal{L[\xi]}(\phi x)>e^{-\phi x},$ the following inequality is established
|
$
R0∫∞0e−ϕxfG(x)dx<R0∫∞0L[ξ](ϕx)fG(x)dx<R0∥∥Rc(ϕ)Rv(ϕ)
\label{frailty 2}
$
|
(5)
|
where $R_{c}(\phi)$ reflects the efficacy in the idealized situation and $R_{v}(\phi)$ reflects the effectiveness in the presence of frailty when the intervention is applied in a large population. The inequalities are mathematical phrases that qualitatively describe the conventional wisdom, that, the control measure is most effective if applied homogeneously across all individuals.
2.2. Variability of the frailty parameter according to convex order
Unobservable heterogeneity is measured by variability for $z.$ The order of variability for two non-negative random variables is described based on "marjorization" and defined in [11]. If $X_{1}$ and $X_{2}$ have equal mean value $\mu_{1}=\mu_{2}$ (should they exist)$,$ corresponding to p.d.f. $f_{1}$ and $f_{2},$ respectively, the verbal description for $X_{2}$ being more dispersed (spread out) than $X_{1}$ is about the change of signs between. $f_{1}$ and $f_{2}$ and their corresponding survival functions $\overline{F}_{1}$ and $\overline{F}_{2}$ as shown in Figure 2 This is the definition of the convex order $X_{1}\underset{cv}{\leq}$ $X_{2}.$
Definition 2.1. $X_{1}\underset{cv}{\leq}$ $X_{2}$ if and only if $\mu_{1}=\mu_{2}$ plus the following two statements:
1. $f_{2}(x)-f_{1}(x)$ has two sign changes and the sign sequence is: $+,-,+$.
2. $\overline{F}_{1}(x)-\overline{F}_{2}(x)$ has one sign change and the sign sequence is: $+,-$.
By this definition, the larger the distribution in convex order, the more it "spreads out" around its mean value. It is mathematically equivalent [11] to the following definition.
Definition 2.2. $X_{1}\underset{cv}{\leq}$ $X_{2}$ if $E[\Psi(X_{1})]\leq E[\Psi(X_{2})]$ for all convex functions $\Psi(x)$ for which these expectations exist.
The convex order is stronger than variance comparison as the choice of a convex function $\Psi(x)=x^{2}$ leads to the conclusion that $X_{1}\leq_{cx}X_{2}\Rightarrow$ $var[X_{1}]\leq var[X_{2}]$.
The following identity, first proven in [5],
|
$
\int_{0}^{\infty}\mathcal{L[\xi]}(\phi x)f_{G}(x)dx=\int_{0}^{\infty}\int
_{0}^{\infty}e^{-\phi xz}\xi(z)f_{G}(x)dzdx=\int_{0}^{\infty}\mathcal{L[}
f_{G}\mathcal{]}(\phi z)\xi(z)dz
$
|
leads to
|
$
R_{v}(\phi)=R_{0}\int_{0}^{\infty}\mathcal{L[\xi]}(\phi x)f_{G}(x)dx=R_{0}
\int_{0}^{\infty}\mathcal{L[}f_{G}\mathcal{]}(\phi z)\xi(z)dz.
$
|
It can be shown that $\mathcal{L[}f_{G}](z)$ is log-convex with respect to $z.$ This gives additional insight into (5), that, the more variable the frailty $z$ according to convex order, the larger the value of $R_{v}(\phi).$
2.3. Scale invariance with respect to disease natural history
The natural history in the current context refers to assumptions in $f_{G},$ which include the existence of the latent period and the distributions of the latent and the infectious periods. Assuming $f_{G}^{\ast}(y)$ is the p.d.f. for $G$ according to the standard time scale $\lambda=1,$ on a transformed time by a scale parameter $\lambda,$ $x=y/\lambda,$ $f_{G}(x;\lambda)=\lambda f_{G}^{\ast}(\lambda x).$
Because the Laplace transform of a p.d.f. of a non-negative random variable is a survival function (arising from the mixture of an exponential survival function with the p.d.f. as the mixing distribution, see [11]), $\mathcal{L[\xi]}(x)$ is a survival function. Under the scale transform $x=y/\lambda,$ $\mathcal{L[\xi]}(y)=\mathcal{L[\xi]}(\lambda x)$ and $e^{-y}=e^{-\lambda x}.$ Therefore
|
$
R_{v}(\phi) =R_{0}\int_{0}^{\infty}\mathcal{L[\xi]}(\phi y)f_{G}^{\ast }(y)dy=R_{0}\int_{0}^{\infty}\mathcal{L[\xi]}(\lambda\phi x)f_{G} (x;\lambda)dx,
$
|
(6)
|
|
$
R_{c}(\phi) =R_{0}\int_{0}^{\infty}e^{-\phi y}f_{G}^{\ast}(y)dy=R_{0} \int_{0}^{\infty}e^{-\lambda\phi x}f_{G}(x;\lambda)dx.
$
|
(7)
|
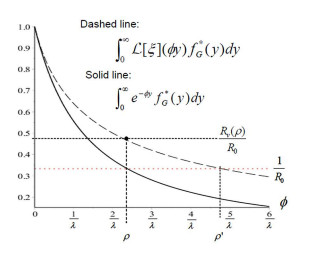
Both $R_{v}(\phi)$ and $R_{c}(\phi),$ divided by $R_{0},$ are plotted in Figure 3, re-scaled by $\lambda.$ The following statements hold.
1. The solid line is $\mathcal{L[}f_{G}^{\ast}\mathcal{]}(\phi)=\int_{0}^{\infty}e^{-\phi y}f_{G}^{\ast}(y)dy.$ It is a survival function (of $\phi$) constructed from a mixture of the exponential survival function $e^{-sy}$ with the mixing function $f_{G}^{\ast}(y).$ The threshold condition $R_{0}\mathcal{L[}f_{G}](\rho)=1$ is equivalent to say that $\rho$ is the $\left( 1-R_{0}^{-1}\right) ^{th}$ percentile corresponding to this survival function. This percentile is unchanged with respect to the scale transformation $x=y/\lambda.$
2. The dashed line is $\int_{0}^{\infty}\mathcal{L[\xi]}(\phi y)f_{G}^{\ast}(y)dy=\int_{0}^{\infty}\mathcal{L[}f_{G}^{\ast}\mathcal{]}(\phi z)\xi(z)dz$ in the presence of frailty. In order to achieve $R_{v}(\phi)=1,$ a new threshold value $\rho^{\prime}$ is the $\left( 1-R_{0}^{-1}\right)^{th}$ percentile corresponding to the survival function (of $\phi$) given by the dashed line. The ratio $\rho^{\prime}/\rho$ does not depend on $\lambda.$
3. $R_{v}(\rho)=R_{0}\int_{0}^{\infty}\mathcal{L[}f_{G}\mathcal{]}(\rho z)\xi(z)dz$ and $R_{0}\mathcal{L[}f_{G}](\rho)=1$ yield
|
$
R_{v}(\rho)=\int_{0}^{\infty}\frac{\mathcal{L[}f_{G}](\rho z)}{\mathcal{L[}
f_{G}](\rho)}\xi(z)dz\equiv R_{v}(R_{0},f_{G}) \label{Goldstein Rv}
$
|
(8)
|
where $\rho$ is a function of $(R_{0},f_{G})$ and depends on $\lambda.$ Meanwhile, $\mathcal{L[}f_{G}](\rho z)$ is $\mathcal{L[}f_{G}](z)$ scaled by its $\left( 1-\frac{1}{R_{0}}\right) ^{th}$ percentile $\rho$ and the ratio
|
$
G(z;R_{0},f_{G})=\frac{\mathcal{L[}f_{G}](\rho z)}{\mathcal{L[}f_{G}](\rho)}
\label{Gfunc}
$
|
(9)
|
is independent of $\lambda.$ Thus $R_{v}(\rho)=\int_{0}^{\infty} G(z;R_{0},f_{G})\xi(z)dz$ only depends on the basic reproduction number $R_{0}$, independent of $\lambda.$
Both $\mathcal{L[}f_{G}^{\ast}\mathcal{]}(\phi)$ and $\int_{0}^{\infty}\mathcal{L[}f_{G}^{\ast}\mathcal{]}(\phi z)\xi(z)dz$ in Figure 3 are heavy tailed because the class of distributions with decreasing hazard rates are closed under mixtures (see [15], pp. 407-409 for details). $\mathcal{L[}f_{G}^{\ast}\mathcal{]}(\phi)$ arises from a mixture of the exponential distribution. $\int_{0}^{\infty}\mathcal{L[} f_{G}^{\ast}\mathcal{]}(\phi z)\xi(z)dz$ is a mixture of $\mathcal{L[} f_{G}^{\ast}\mathcal{]}(\phi)$ with $\xi(z).$ Both correspond to decreasing hazard functions. Because $\rho$ and $\rho^{\prime}$ are the $\left(1-R_{0}^{-1}\right) ^{th}$ percentiles corresponding to these survival functions, if $R_{0}$ is large, these threshold values take place on the far right end of these tails. Numerical results will show that, when the variance of $z$ is getting large, the ratio $\rho^{\prime}/\rho$ increases steeply, highlighting the difficulty in achieving the same objective if there is frailty in the implementation of intervention measures.
3. Robustness of $R_{v}(\rho)$ with respect to the assumed distribution $f_{G}(x)$
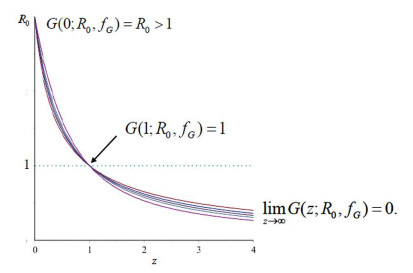
The equation (8) shows that $R_{v}(\rho)$ is a function of $(R_{0},f_{G}),$ of which, $f_{G}$ incorporates assumptions about whether there is a latent period and assumptions of distributions for the latent and the infectious periods. The integrand in (8), $G(z;R_{0},f_{G})\xi(z),$ separates $f_{G}$ from the frailty distribution $\xi(z)$, where $G(z;R_{0},f_{G})$ is given by (9). $R_{v}(R_{0},f_{G})$ depends on $f_{G}$ only through $G(z;R_{0},f_{G}).$
$G(z;R_{0},f_{G})$ is a log-convex function of $z,$ monotonically decreasing, satisfying: $G(0;R_{0},f_{G})=R_{0},$ $G(1;R_{0},f_{G})=1$ and $\lim_{z\rightarrow\infty}G(z;R_{0},f_{G})=0.$ Figure 4 gives a schematic presentation. The dependence on $f_{G}$ mainly shows on the right hand tails. Another log-convex function with a simple Pareto form
|
$
G^{\ast}(z;R_{0})=\frac{R_{0}}{1+\left( R_{0}-1\right) z} \label{G-star}
$
|
(10)
|
has the same features as $G(z;R_{0},f_{G})$ but no longer depends on $f_{G}.$
On the other hand, the p.d.f. $\xi(z)$ for frailty, satisfying $E[z]=1,$ tends to decrease to zero quickly when $z$ is getting large, such as the Gamma distribution given below. Intuitively, $R_{v}(R_{0},f_{G})=\int_{0}^{\infty}G(z;R_{0},f_{G})\xi(z)dz$ is the area under the product $G(z;R_{0},f_{G})\xi(z)$ and is expected to be in close agreement. For numerical demonstration, we choose the Gamma distribution $E[z]=1,var[z]=v$ and
|
$
\xi(z;v)=\frac{1/v}{\Gamma(1/v)}\left( z/v\right) ^{1/v-1}e^{-z/v}
\label{Gamma pdf}
$
|
(11)
|
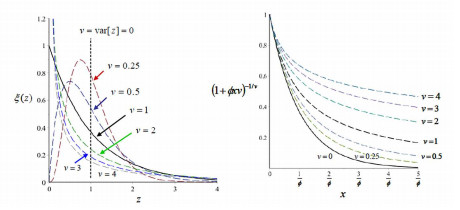
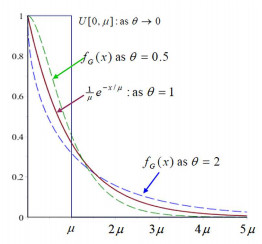
The Laplace transform is $\mathcal{L[\xi]}(s)=\left( 1+sx\right) ^{-1/v}.$ As illustrated in Figure 5, the shape of $\xi(z;v)$ changes dramatically at $v=1.$ When $0<v<1$, $z$ is "more or less" concentrated at $E[z]=1.$ One may loosely call this as "almost homogeneous" in the control measure with some mild variability. When $v>1,$ it is "highly heterogeneous".
When $\xi(z)$ is given by (11), $\overline{F}^{(frailty)}(x)=\mathcal{L[\xi]}(\phi x)=$$\left( 1+\phi xv\right) ^{-1/v}.$ The limiting cases are $\lim_{v\rightarrow0}\left( 1+\phi xv\right) ^{-1/v}=e^{-\phi x}$ and $\lim_{v\rightarrow\infty}\left( 1+\phi xv\right) ^{-1/v}=1.$ For any $x, $ $\overline{F}^{(frailty)}(x)$ is an increasing function of $v.$ The variance $v$ ranks the frailty variable $z$ according to stochastic order. According to (5),
|
$
R_{v}(\phi)=R_{0}\int_{0}^{\infty}\left( 1+\phi xv\right) ^{-1/v}f_{G}(x)dx.
\label{frailty gamma}
$
|
(12)
|
When $\phi=\rho,$ based on (8)-(9), $R_{v}(\rho)=R_{v}(R_{0},f_{G})$ which is
|
$
R_{v}(R_{0},f_{G})=\frac{1/v}{\Gamma(1/v)}\int_{0}^{\infty}G(z;R_{0}
,f_{G})\left( z/v\right) ^{1/v-1}e^{-z/v}dz. \label{Goldstein Rv Gamma}
$
|
(13)
|
We also compare it with the approximation
|
$
R_{v}^{\ast}(R_{0})=\frac{1/v}{\Gamma(1/v)}\int_{0}^{\infty}G^{\ast}
(z;R_{0})\left( z/v\right) ^{1/v-1}e^{-z/v}dz. \label{weighted}
$
|
(14)
|
$G(z;R_{0},f_{G})$ will be specified by assumptions for $f_{G}$ and $G^{\ast}(z;R_{0})$ is given by (10). We restrict discussions to distributions of the latent and the infectious periods that their Laplace transforms can be expressed explicitly.
3.1. In the absence of a latent period
Assuming the infectious period has a finite mean $\mu,$ $f_{G}(x)=\frac{1}{\mu}\overline{F}_{I}(x).$ According to (9),
|
$
G(z;R_{0},f_{G})=\frac{\mathcal{L[}\overline{F}_{I}](\rho z)}{\mathcal{L[}
\overline{F}_{I}](\rho)}. \label{G without latent}
$
|
(15)
|
We consider two parametric models for the infectious period, both with mean $\mu\ $and $var[T_{I}]=\theta\mu^{2}.$ The first model is the Gamma distribution. In this case, $\mathcal{L[}\overline{F}_{I}](s)=\frac{1}{s}\left[ 1-\left( 1+s\theta\mu\right) ^{-1/\theta}\right] $ when $0<\theta<\infty$. Hence (15) becomes
|
$
G_{Gamma}(z)=\frac{1}{z}\frac{1-\left( 1+y(R_{0},\theta)z\right) ^{-\theta}
}{1-\left( 1+y(R_{0},\theta)\right) ^{-\theta}},\text{ }\theta>0
\label{GGamma}
$
|
(16)
|
where $y(R_{0},\theta)=\rho\theta\mu.$ It is a function of $\theta$ and $R_{0}$ because the threshold $\rho$ must satisfy $\frac{R_{0}}{\rho\mu}\left[ 1-\left( 1+\rho\theta\mu\right) ^{-1/\theta}\right] =1.$ Then (13) is written as
|
$
R_{v}(R_{0},\theta)=\frac{\left( 1/v\right) ^{1/v}}{\Gamma(1/v)}\int
_{0}^{\infty}\frac{1-\left( 1+y(R_{0},\theta)z\right) ^{-1/\theta}
}{1-\left( 1+y(R_{0},\theta)\right) ^{-1/\theta}}z^{\frac{1}{v}-2}e^{-z/v}dz
\label{Gamma frailty}
$
|
(17)
|
where $y(R_{0},\theta)=Root\_of\left( R_{0}\theta\left[ 1-\left(1+y\right) ^{-1/\theta}\right] =y,\text{ }y>0\right) .$
The second model is the inverse-Gaussian distribution$.$ In this case, $\mathcal{L[}\overline{F}_{I}](s)=\frac{1}{s}\left( 1-\exp\left\{\frac{1-\sqrt{1+2\theta\mu s}}{\theta}\right\} \right) .$ In this case, $\rho$ satisfies $R_{0}\left( 1-\exp\left\{ \frac{1-\sqrt{1+2\rho\theta\mu}}{\theta}\right\} \right) =\rho\mu.$ In a similar manner, the expression for (15) is
|
$
G_{inv-Gaussian}(z)=\frac{1}{z}\frac{1-e^{\theta\left( 1-\sqrt{1+2y(R_{0}
,\theta)z}\right) }}{1-e^{\theta\left( 1-\sqrt{1+2y(R_{0},\theta)}\right)
}},\text{ }\theta>0 \label{GinvG}
$
|
(18)
|
and (13) is expressed as
|
$
R_{v}(R_{0},\theta)=\frac{\left( 1/v\right) ^{\frac{1}{v}}}{\Gamma(1/v)}
\int_{0}^{\infty}\frac{1-e^{\frac{1-\sqrt{1+2y(R_{0},\theta)z}}{\theta}}
}{1-e^{\frac{1-\sqrt{1+2y(R_{0},\theta)}}{\theta}}}z^{\frac{1}{v}-2}e^{-z/v}dz
\label{invG frailty}
$
|
(19)
|
where $y(R_{0},\theta)=Root\_of\left( R_{0}\theta\left( 1-\exp\left\{\frac{1-\sqrt{1+2y}}{\theta}\right\} \right) =y,\text{ }y>0\right) $.
When $\theta\rightarrow0,$ the infectious period degenerates to a fixed point $\mu$ and $f_{G}(x)=\frac{1}{\mu}\overline{F}_{I}(x)$ is the p.d.f. of the uniform distribution $U[0,\mu].$ In this case,
|
$
R_{v}(R_{0},0)=\frac{\left( 1/v\right) ^{1/v}}{\Gamma(1/v)}\int_{0}^{\infty
}\frac{1-e^{-y(R_{0},0)z}}{1-e^{-y(R_{0},0)}}z^{\frac{1}{v}-2}e^{-z/v}dz.
\label{degenerated frailty}
$
|
(20)
|
The corresponding expression for (9) is $G_{Deg}(z)=\frac{1}{z}\frac{1-e^{-y(R_{0},0)z}}{1-e^{-y(R_{0},0)}}$ where $y({{R}_{0}},0)=Root\_of\left( {{R}_{0}}\left( 1-{{e}^{-y}} \right)=y \right.,$$\left. y>0 \right).$
The Gamma distribution includes the exponential distribution as a special case when $\theta=1,$ the inverse-Gaussian distribution does not include the exponential distribution as a special case.
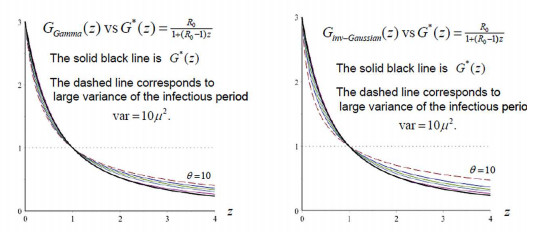
$G_{Gamma}(z)$ and $G_{inv-Gaussian}(z)$ can be numerically calculated for each $R_{0},$ $\theta.$ Figure 6 presents the case when $R_{0}=3$ with $\theta$ ranging from $0$ (i.e. the special case $G_{Deg}(z)$) to $\theta=10.$ They include a wide range of the infectious period distributions for a constant point $\mu$ with no random variation to very large variance $10\mu^{2}.$ Figure 6 also includes the Pareto function $G^{\ast}(z;R_{0})$ given by (10) as the approximation, shown as the dark thick line.
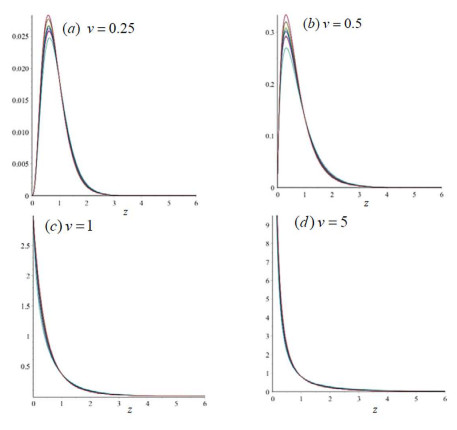
In spite of the differences shown in Figure 6 when $z$ becomes large, the product $G_{Gamma}(z)$ $z^{\frac{1}{v}-1}e^{-z/v}$ gives the integrand in (17) and the product $G_{inv-Gaussian}(z)$ $z^{\frac{1}{v}-1}e^{-z/v}$ gives the integrand in (19)$.$ Figure 7 presents plots of these integrands corresponding to $R_{0}=3$ as function of $z$ for $v=0.25,0.5,1$ and $5$ in the four panels. Within each panel, both $G_{Gamma}(z)$ $z^{\frac{1}{v}-1}e^{-z/v}$ and $G_{inv-Gaussian}(z)$ $z^{\frac{1}{v}-1}e^{-z/v}$ are plotted together for a very wide range of $\theta$ from $0.1$ to $\infty.$
Figure 7 shows close agreements among the integrands in (17) and (19) in a very wide range of $\theta$ at each $v.$ One expects $R_{v}(R_{0},\theta),$ as areas covered by these curves, to be robust with respect to $f_{G}$ and in close agreement with the approximation $R_{v}^{\ast}(R_{0})$ given by (14). Table 1 shows the numerical results for $\theta=0,$ $0.2$, $1,2$ and $10$ at $R_{0}=2$ and $R_{0}=3.$ Although $R_{v}(R_{0},\theta)$ depends on the choice of the distribution family as well as the shape parameter $\theta$, they all fall into a very narrow range around $R_{v}^{\ast}(R_{0})$ for each $R_{0}$ and $v$, and $R_{v}^{\ast}(R_{0})$ does not involve any assumption of the distribution $f_{G}.$
Table 1. Tabulation of $R_{v}^{\ast}(R_{0})$ in (14) along with $R_{v}(R_{0},\theta)$ with respect to Gamma and inverse-Gaussian distributed infectious period at $R_{0}=2$ and $R_{0}=3,$ noticing that $R_{v}^{\ast}(R_{0})$ is identical to Gamma distributed infectious period with $\theta=1.$
| $R_{0}=2$ |
| $v$ |
$R_{v}^{\ast}$ |
$\theta$ |
$\theta>0:$ Gamma |
$\theta>0:$ inv-Gaussian |
|
|
$\rightarrow0$ |
$0.2$ |
$1$ |
$2$ |
$10$ |
$0.2$ |
$1$ |
$2$ |
$10$ |
| $0.25$ |
$1.059$ |
$1.061$ |
$1.061$ |
$1.059$ |
$1.057$ |
$1.055$ |
$1.060$ |
$1.056$ |
$1.054$ |
$1.049$ |
| $0.50$ |
$1.109$ |
$1.113$ |
$1.112$ |
$1.109$ |
$1.108$ |
$1.105$ |
$1.112$ |
$1.106$ |
$1.103$ |
$1.095$ |
| $1.00$ |
$1.193$ |
$1.196$ |
$1.195$ |
$1.193$ |
$1.191$ |
$1.188$ |
$1.195$ |
$1.189$ |
$1.185$ |
$1.176$ |
| $2.00$ |
$1.311$ |
$1.313$ |
$1.313$ |
$1.311$ |
$1.310$ |
$1.308$ |
$1.312$ |
$1.308$ |
$1.304$ |
$1.297$ |
|
| $R_{0}=3$ |
|
$R_{v}^{\ast}$ |
$\theta$ |
$\theta>0:$ Gamma |
$\theta>0:$ inv-Gaussian |
|
|
$\rightarrow0$ |
$0.2$ |
$1$ |
$2$ |
$10$ |
$0.2$ |
$1$ |
$2$ |
$10$ |
| $0.25$ |
$1.109$ |
$1.132$ |
$1.123$ |
$1.109$ |
$1.103$ |
$1.095$ |
$1.123$ |
$1.105$ |
$1.095$ |
$1.077$ |
| $0.50$ |
$1.211$ |
$1.244$ |
$1.232$ |
$1.211$ |
$1.201$ |
$1.188$ |
$1.231$ |
$1.204$ |
$1.187$ |
$1.156$ |
| $1.00$ |
$1.384$ |
$1.425$ |
$1.411$ |
$1.384$ |
$1.372$ |
$1.355$ |
$1.410$ |
$1.374$ |
$1.352$ |
$1.308$ |
| $2.00$ |
$1.637$ |
$1.677$ |
$1.663$ |
$1.637$ |
$1.624$ |
$1.606$ |
$1.662$ |
$1.626$ |
$1.603$ |
$1.554$ |
Incidentally, $G^{\ast}(z;R_{0})$ given by (10) is a special case of $G_{Gamma}(z)$ when $\theta=1,$ that is, exponentially distributed infectious period.
3.2. In the presence of a latent period
In this case, $f_{G}(x)$ is the convolution between $f_{E}(x)$ and $f_{W}(x)=\frac{1}{\mu}\overline{F}_{I}(x).$ From (8) and (13)
|
$
Rv(R0,θ_)=∫∞0L[fG](ρz)L[fG](ρ)ξ(z)dz=(1/v)1vΓ(1/v)∫∞0L[fE](ρz)L[¯FI](ρz)L[fE](ρ)L[¯FI](ρ)z1v−1e−z/vdz,
$
|
(21)
|
where $\underline{\theta}$ may involve parameters that specifies the latent and the infectious period distributions. For notations, $\mu_{E}$ is the mean latent period and $\theta_{E}$ is the shape parameter of the latent period distribution. Without index, $\mu$ is the mean infectious period and $\theta$ is the shape parameter of the infectious period distribution. For the chosen distributions of the latent period and infectious period with explicit Laplace transforms, the variance of the latent period is $\theta_{E}\mu_{E}^{2}$ and the variance of the infectious period is $\theta\mu^{2}.$ In the following combination of latent period and infectious period distributions, $\mathcal{L[}f_{E}](s)$ and $\mathcal{L[}\overline{F}_{I}](s)$ have analytic forms and (21) can be straightforwardly computed.
1. Gamma latent period + Gamma infectious period (including degenerated and exponential distributions):
|
$L[fE](s)=(1+θEμEs)−1/θE,L[¯FI](s)=1s[1−(1+θμs)−θ]
$
|
where $\mu_{E}$ is the mean latent period and $\theta_{E}$ is the shape parameter of the latent period distribution and $\mu$ is the mean latent period and $\theta$ is the shape parameter of the infectious period distribution.
2. Gamma latent period + inverse-Gaussian infectious period
|
$L[fE](s)=(1+θEμEs)−1/θE,L[¯FI](s)=1s(1−e1−√1+2θμsθ).
$
|
3. Inverse-Gaussian latent period + Gamma infectious period
|
$L[fE](s)=exp(1−√1+2θEμEsθE), L[¯FI](s)=1s[1−(1+θμs)−1/θ]
$
|
4. Inverse-Gaussian latent period + inverse-Gaussian infectious period
|
$L[fE](s)=exp(1−√1+2θEμEsθE), L[¯FI](s)=1s(1−e1−√1+2θμsθ).
$
|
Without repeating the investigation for robustness in the previous subsection, numerical results from selected special cases when both the latent and infectious period distribution are chosen from the Gamma family are presented.
3.3. Numerical results for special cases
For these numerical results, 16 distribution models for $f_{G\text{ }}$will presented at two level of $R_{0}.$ In total, there are 32 sets of special cases.
The first 4 models assume Gamma distributed infectious period without the latent period. In particular, The p.d.f. for the infectious period $T_{I}$ is
|
$
f_{I}(x)=\frac{1}{\theta\mu\Gamma(\frac{1}{\theta})}\left( \frac{x}{\theta
\mu}\right) ^{1/\theta-1}e^{-\frac{1}{\theta\mu}x}
$
|
by mean value $\mu$ and variance $\theta\mu^{2}.$ The p.d.f. for $G=W$ is
|
$
f_{G}(x)=\frac{1}{\mu}\overline{F}_{I}(x)=\frac{1}{\mu}\int_{x}^{\infty}
f_{I}(s)ds,
$
|
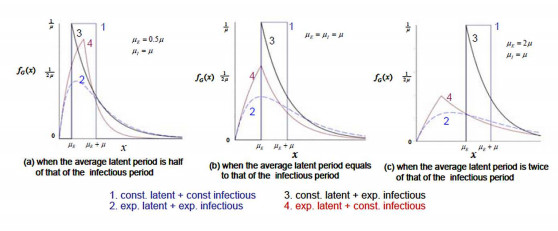
involving the incomplete Gamma function. The mean value for $G$ is $E[G]=\frac{\mu}{2}\left( 1+\theta\right) $. The shapes of $f_{G}(x)$ is illustrated in Figure 8, which includes the following two special cases.
1. When $\theta\rightarrow0,$ $T_{I}$ has a degenerated distribution with mass at a constant $\mu.$ The survival function is $\overline{F}_{I}(x)=1$ if $x\leq\mu$ and $\overline{F}_{I}(x)=0$ otherwise. $G$ corresponds to the uniform distribution $U[0,\mu]$ with $E[G]=\frac{\mu}{2} $ and p.d.f. $f_{G}(x)=\frac{1}{\mu}\overline{F}_{I}(x)=\frac{1}{\mu}$ when $x\leq\mu$ and $f_{G}(x)=0$ otherwise.
2. When $\theta=1,$ $G=W$ is identically distributed as the infectious period $T_{I}$ with $f_{G}(x)=\frac{1}{\mu}e^{-x/\mu}.$
The scale parameter in Figure 8 is $\mu^{-1}.$ Numerical calculation for $R_{v}(\rho),$ with $\xi(z;v)$ defined in (11) is given by (17) for $0<\theta<\infty.$ Table 1 contains results corresponding to $\theta\rightarrow0,$ $\theta=1$ and $\theta=2$.
The next 12 models include a latent period so that $G=T_{E}+W.$ Four special cases are considered: (ⅰ) constant latent period+constant infectious period, (ⅱ) exponentially distributed latent period + exponentially distributed infectious period, (ⅲ) exponentially distributed latent period + constant infectious period, and (ⅳ) exponentially distributed latent period + constant infectious period. The mean latent period is parameterized as $\mu_{E}=l\mu,$ $l\geq0$ and $\mu$ is the mean infectious period. The shapes of $f_{G}(x)$ from combinations of assumed latent period and infectious period distributions are displayed in Figure 9(a)-(c) with respectively assumed relative length of the average latent period to the average length of the infectious period $l=0.5,1$ and $2.$
Numerical calculation for $R_{v}(\rho),$ with $\xi(z;v)$ given by (11), can be derived from (21) applied to each of the special cases. Detailed calculation formula and corresponding tables are given in Appendix.
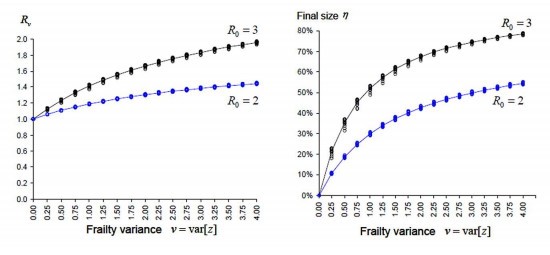
The left panel of Figure 10 provides a comparison of the results for $R_{v}(\rho)$ at $v$ in the range from $0$ to $4$ by $0.25$ increment. For each $v,$ there are 16 points (in black) corresponding to $R_{0}=3$ and 16 points (in blue) corresponding to $R_{0}=2.$ The trends representing $R_{v}(\rho)$ as functions of $v$ are calculated as average and plotted as lines. It shows that assumptions on the structure (e.g. with or without latent period), on the types of distributions of these periods as well as the relative lengths between the latent and the infectious periods have little influence on $R_{v}(\rho).$ The predominant parameters are $R_{0}$ and $v.$ For example: If $R_{0}=3$, a control measure at intervention rate $\rho$ that in theory could have made the epidemic under control (i.e. $R_{c}(\rho)=1$), may result in an outbreak as if manifested by a reproduction number $R_{v}\approx1.4.$
The right panel of Figure 10 is analogous to the left panel, representing the final size $\eta$ through the approximate final size equation $1-\eta=\exp(-R_{v}\eta).$ The final size, as a measure, is only applicable in certain epidemics, typically without replacement of the susceptible population and recovered individuals have immunity. However, unlike $R_{v}(\rho),$ which is mainly a theoretical parameter, the final size (where applicable) is also an observable quantity, also known as the infection attack rate. Once again, assumptions on the structure (e.g. with or without latent period), on the types of distributions of these periods as well as the relative lengths between the latent and the infectious periods have little influence on $\eta.$
Remark 1. It is well known that univariate frailty models are not identifiable from the survival information alone. In the current context, the true value of control rate $\phi$ is not identifiable from $v$ in $\xi(z;v).$ Meanwhile, $.$the basic reproduction number $R_{0}$ is a theoretical value that is difficult to estimate. The observed (or estimated) parameters during or after the outbreak, such as $R_{v}$ or $\eta$, cannot identify $R_{0},$ $\phi$ and $v.$ If one follows some guidelines with a given control rate at a threshold $\phi=\rho$ with proven (in theory) efficacy to get the epidemic under control and if one has observed an outbreak the ends with final size about $35\%$ of the population, it could arise from an outbreak with $R_{0}=3$ and the control measure implemented with relatively good but not perfect adherence at $v=0.5$, or from an outbreak with $R_{0}=2$ and the control measure implemented with poor adherence at $v=1.25,$ or an outbreak with $R_{0}=1.23$ with no intervention at all. An outbreak with infection attack rate $35\%$ is nonetheless a large outbreak. In the absence of knowledge of $R_{0}$ along with unobservable frailty, it leaves impression as if the control measure that looks good on paper "does not work at all" in practice.
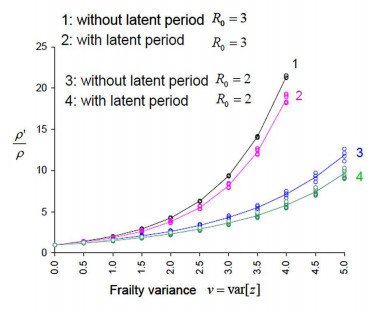
Figure 11 echoes the comments made at the end of Section 2 that, if $R_{0}$ is large, the control thresholds $\rho$ and $\rho^{\prime}$ take place on the far right end tails of the survival functions corresponding to $\mathcal{L[}f_{G}^{\ast}\mathcal{]}(\phi)$ and $\int_{0}^{\infty}\mathcal{L[}f_{G}^{\ast}\mathcal{]}(\phi z)\xi(z)dz$ and both are heavy tailed. Consequently, the ratio $\rho^{\prime}/\rho$ increases steeply if the variance of $z$ is getting large. Of all the $32$ cases examined, the predominant parameters are $R_{0}$ and $v.$ The assumptions on distributions of the latent period and/or infectious period have very little effect on the quantitative results. However, the assumption on whether there is a latent period does have some influence. Generally speaking, the presence of a latent period somewhat make the control efforts easier. The ratio $\rho^{\prime}/\rho$ does not depend on the time scale on disease progression. Figure 11 demonstrates that it is important to ensure strong adherence to minimize the frailty. When $v>1$, in order to get the outbreak under control, the level of difficulty, represented by the ratio $\rho^{\prime}/\rho$, increases steeply. For instance, at $v=4,$ it requires increasing to the control threshold by $7$ folds at $R_{0}=2$ and by $20$ folds at $R_{0}=3$.
4. Discussions and limitations
4.1. On the use of frailty model versus more structured models for intervention heterogeneity
The idealized situation, assuming homogeneous intervention effect at rate $\phi$ on all individuals, is the null hypothesis. The frailty model by introducing a random effect $z$ with $E[z]=1$ is one of the many alternative hypotheses. One could argue the choice of this alternative hypothesis versus more structured hypotheses, such as spatial structure and time-dependence. Indeed, different alternative hypotheses need to be evaluated and some need more complex models. They also lead to different answers to different questions.
The frailty model addresses unobservable (and even un-quantifiable) heterogeneity that could arise in many situations, such as non-adherence (e.g. condom use), "leakage" (e.g. imperfect quarantine or isolation), or, in a prophylactic intervention, individuals may not take the prescribed dose of the medication provided. The frailty model in this paper provides some qualitative insights. More in-depth questions could be posed in each of the situation as alternative hypotheses and targeted models can be developed and applied. Even with that, there will still be unobservable part of heterogeneity and some random effect model may need to be added on top of the structured models. Take the condom use example, condom coverage can be explicitly modelled by space and time, yet there is still unobservable heterogeneity between and within individuals in adherence.
A related issue is the dependence between individuals. Under the null hypothesis, the intervention is applied homogeneously, and independently, on all individuals. Alternatively, one could question about independency and model correlation such as in a spatial structured model. The frailty model also introduces dependency. If a random effect $\xi(z)$ is introduced in $\overline{F}^{(frailty)}(x)=\int_{0}^{\infty}e^{-z\phi x}\xi(z)dz,$ the intervention is no longer applied independently on all individuals. The proof of this is similar to the proof that a mixed Poisson process no longer preserves the independent increment property. Structured models can explicitly describe dependency and provide answers to targeted questions. The frailty model addresses the unobservable aspect and provides qualitative insight for more general questions.
An important aspect of model is to order thoughts and sharpen vague intuitive notions. Empirical wisdom has told us that the control measure is most effective if applied homogeneously across all individuals and the more variable in adherence, the less the effectiveness. The first half of the sentence is mathematically expressed by (5). The notion variability is vague and intuitive. Definition 2.1 provides a verbal description and an illustration of the general concept of variability, which is sharpened in its mathematical equivalence, Definition 2.2. In return, variability according to Definition 2.2 leads to the order of $R_{v}(\phi)=R_{0}\int_{0}^{\infty}\mathcal{L[}f_{G}\mathcal{]}(\phi z)\xi(z)dz,$ corresponding to the second half of the sentence.
The findings that $R_{v}(\rho),$ along with its derived quantities, is scale invariant and robust to the disease progression natural history $f_{G}$ have wide application importance. Although quantitative analysis is used to investigate the robustness, the emphasis of the value of these results should be on the qualitative aspect. The frailty model is aimed to draw general conclusions and is complementary to models for specific questions on spatial-temporal heterogeneity and spatial dependence.
4.2. Non-identifiability and challenges in the design of intervention studies
The non-identifiability problem in Remark 1 poses challenges in the design of intervention studies at the population level. They are confounding factors that hinders the ability to distinguish the 'pure' impact of the intervention without the distorting influence of compliance from the effectiveness since some level of non-compliance are likely. Both the pure impact (efficacy) and population level effectiveness are important objectives in intervention studies.
4.3. Relation to other disciplines in science
The concept of frailty goes back to Greenwood and Yule [4] on accident proneness. The term frailty was introduced in demography [18]. It has been widely used to model heterogeneity in life insurance [13]. As extensions of the proportional hazard model [7], frailty models and are widely used in clinical applications where the study population must be considered as a heterogeneous sample, i.e. a mixture of individuals with different hazards.
When $\xi(z)$ is Gamma distributed, $\overline{F}^{(frailty)}(x)=\left(1+\phi xv\right) ^{-1/v}$ is a special case of the Pareto-II distribution [11] or the Lomax distribution [9]. Re-written as $e_{q}^{-x}\equiv\left[ 1+(q-1)x\right] ^{-\frac{1}{q-1}},$ $x\geq0,$ $q>1,$ it is called as the $q$-exponential distribution [14] with the exponential distribution $e_{1}^{-x}\equiv e^{-x}$. The transform $\int_{0}^{\infty}\left( 1+sxv\right) ^{-1/v}f_{G}(x)dx,$ $s>0$ in (12) has found its applications in astrophysics and statistical mechanics.([8], [12]). It is usually called the generalized Stieltjes transform, but also referred to as the $q-$Laplace transform $\int_{0}^{\infty}e_{q}^{-sx}f(x)dx$ ([8], [12]) by its connection with the $q$-exponential function.
Application of frailty models has been employed in a growing number of empirical works on a large variety of themes, including scale-free networks and dynamic systems. Examples include the population of cities, the study of stock markets, DNA sequences, family names, human behavior, geomagnetic records, train delays, reaction kinetics, air travel networks, hydrological phenomena, earthquakes, world bank records, voting processes, internet, citation of scientific papers, among others. A brief review of this distribution and a list of references of these studies are provided in Picoli et al. [14]. This manuscript adds another application field in this growing theme.
Acknowledgments
The author sincerely thank two anonymous referees for their useful comments and discussions which helped to re-develop the Discussions and limitations section.
Appendix
Tables 2-8 contain numerical values for $R_{v}(\rho),$ the final size $\eta$ (where applicable) and the ratio $\rho^{\prime}/\rho$ corresponding to Figures 10-11, arising from 16 different types of distributions with p.d.f. $f_{G}(x)$ as illustrated in Figures 8 and 9 at two levels $R_{0}=2$ and $R_{0}=3.$
Table 2. Constant infectious period without latent period.
| $R_{0}=2,$ $\rho=1.594/\mu$ |
|
$R_{0}=3,$ $\rho=2.821/\mu$ |
| $v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
|
$v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
| $0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
|
$0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
| $0.25$ |
$1.061$ |
$0.113$ |
$1.120$ |
|
$0.25$ |
$1.132$ |
$0.224$ |
$1.190$ |
| $1.00$ |
$1.196$ |
$0.309$ |
$1.577$ |
|
$1.00$ |
$1.426$ |
$0.531$ |
$2.024$ |
| $2.00$ |
$1.313$ |
$0.436$ |
$2.510$ |
|
$2.00$ |
$1.678$ |
$0.681$ |
$4.253$ |
| $3.00$ |
$1.394$ |
$0.506$ |
$4.056$ |
|
$3.00$ |
$1.847$ |
$0.750$ |
$9.352$ |
| $4.00$ |
$1.454$ |
$0.551$ |
$6.668$ |
|
$4.00$ |
$1.971$ |
$0.789$ |
$21.512$ |
Table 3. Exponential infectious period without latent period.
| $R_{0}=2,$ $\rho=1/\mu$ |
|
$R_{0}=3,$ $\rho=2/\mu$ |
| $v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
|
$v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
| $0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
|
$0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
| $0.25$ |
$1.059$ |
$0.108$ |
$1.133$ |
|
$0.25$ |
$1.109$ |
$0.190$ |
$1.186$ |
| $1.00$ |
$1.193$ |
$0.305$ |
$1.639$ |
|
$1.00$ |
$1.384$ |
$0.498$ |
$2.022$ |
| $2.00$ |
$1.311$ |
$0.434$ |
$2.670$ |
|
$2.00$ |
$1.637$ |
$0.661$ |
$4.257$ |
| $3.00$ |
$1.393$ |
$0.506$ |
$4.370$ |
|
$3.00$ |
$1.811$ |
$0.737$ |
$9.325$ |
| $4.00$ |
$1.454$ |
$0.552$ |
$7.229$ |
|
$4.00$ |
$1.940$ |
$0.780$ |
$21.295$ |
Table 4. Gamma distributed infectious period in four scenarios.
| Gamma distributed infectious period, variance/mean ratio =2 |
| $R_{0}=2,$ $\theta=0.5,$ $\rho=0.719/\mu$ |
|
$R_{0}=3,$ $\theta=0.5,\rho=1.5/\mu$ |
| $v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
|
$v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
| $0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
|
$0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
| $0.25$ |
$1.057$ |
$0.106$ |
$1.136$ |
|
$0.25$ |
$1.103$ |
$0.181$ |
$1.185$ |
| $1.00$ |
$1.191$ |
$0.303$ |
$1.660$ |
|
$1.00$ |
$1.372$ |
$0.488$ |
$2.030$ |
| $2.00$ |
$1.310$ |
$0.433$ |
$2.731$ |
|
$2.00$ |
$1.624$ |
$0.655$ |
$4.295$ |
| $3.00$ |
$1.393$ |
$0.505$ |
$4.501$ |
|
$3.00$ |
$1.800$ |
$0.732$ |
$9.425$ |
| $4.00$ |
$1.454$ |
$0.551$ |
$7.481$ |
|
$4.00$ |
$1.930$ |
$0.777$ |
$21.507$ |
| Gamma distributed infectious period, variance/mean ratio =0.5 |
| $R_{0}=2,$ $\theta=2,$ $\rho=1.236/\mu$ |
|
$R_{0}=3,$ $\theta=2,\rho=2.372/\mu$ |
| $v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
|
$v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
| $0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
|
$0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
| $0.25$ |
$1.060$ |
$0.110$ |
$1.129$ |
|
$0.25$ |
$1.116$ |
$0.201$ |
$1.186$ |
| $1.00$ |
$1.194$ |
$0.306$ |
$1.618$ |
|
$1.00$ |
$1.397$ |
$0.509$ |
$2.017$ |
| $2.00$ |
$1.312$ |
$0.435$ |
$2.611$ |
|
$2.00$ |
$1.650$ |
$0.668$ |
$4.234$ |
| $3.00$ |
$1.393$ |
$0.506$ |
$4.249$ |
|
$3.00$ |
$1.823$ |
$0.741$ |
$9.272$ |
| $4.00$ |
$1.454$ |
$0.552$ |
$7.006$ |
|
$4.00$ |
$1.950$ |
$0.783$ |
$21.215$ |
Table 5. Constant latent period and constant infectious period in six scenarios.
| The latent period is half the infectious period: $l=1/2$ |
| $R_{0}=2,$ $l=0.5,$ $\rho=0.714/\mu$ |
|
$R_{0}=3,$ $l=0.5,\rho=1.153/\mu$ |
| $v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
|
$v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
| $0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
|
$0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
| $0.25$ |
$1.057$ |
$0.105$ |
$1.097$ |
|
$0.25$ |
$1.136$ |
$0.229$ |
$1.156$ |
| $1.00$ |
$1.184$ |
$0.294$ |
$1.463$ |
|
$1.00$ |
$1.428$ |
$0.533$ |
$1.842$ |
| $2.00$ |
$1.298$ |
$0.421$ |
$2.209$ |
|
$2.00$ |
$1.676$ |
$0.680$ |
$3.685$ |
| $3.00$ |
$1.378$ |
$0.493$ |
$3.444$ |
|
$3.00$ |
$1.844$ |
$0.748$ |
$7.968$ |
| $4.00$ |
$1.438$ |
$0.540$ |
$5.537$ |
|
$4.00$ |
$1.967$ |
$0.788$ |
$18.345$ |
| The latent period equals to the infectious period: $l=1$ |
| $R_{0}=2,$ $l=1,$ $\rho=0.468/\mu$ |
|
$R_{0}=3,$ $l=1,\rho=0.748/\mu$ |
| $v$ |
$R_{c}(\rho,\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
|
$v$ |
$R_{c}(\rho,\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
| $0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
|
$0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
| $0.25$ |
$1.056$ |
$0.104$ |
$1.094$ |
|
$0.25$ |
$1.136$ |
$0.230$ |
$1.153$ |
| $1.00$ |
$1.182$ |
$0.292$ |
$1.451$ |
|
$1.00$ |
$1.429$ |
$0.533$ |
$1.829$ |
| $2.00$ |
$1.296$ |
$0.419$ |
$2.182$ |
|
$2.00$ |
$1.677$ |
$0.681$ |
$3.658$ |
| $3.00$ |
$1.376$ |
$0.491$ |
$3.398$ |
|
$3.00$ |
$1.845$ |
$0.749$ |
$7.919$ |
| $4.00$ |
$1.436$ |
$0.539$ |
$5.461$ |
|
$4.00$ |
$1.968$ |
$0.788$ |
$18.257$ |
| The latent period is twice the infectious period: $l=2$ |
| $R_{0}=2,$ $l=2,$ $\rho=0.279/\mu$ |
|
$R_{0}=3,$ $l=2,\rho=0.443/\mu$ |
| $v$ |
$R_{c}(\rho,\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
|
$v$ |
$R_{c}(\rho,\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
| $0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
|
$0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
| $0.25$ |
$1.056$ |
$0.103$ |
$1.093$ |
|
$0.25$ |
$1.136$ |
$0.230$ |
$1.152$ |
| $1.00$ |
$1.182$ |
$0.291$ |
$1.446$ |
|
$1.00$ |
$1.430$ |
$0.534$ |
$1.823$ |
| $2.00$ |
$1.295$ |
$0.418$ |
$2.170$ |
|
$2.00$ |
$1.678$ |
$0.681$ |
$3.647$ |
| $3.00$ |
$1.375$ |
$0.491$ |
$3.377$ |
|
$3.00$ |
$1.845$ |
$0.749$ |
$7.899$ |
| $4.00$ |
$1.435$ |
$0.538$ |
$5.428$ |
|
$4.00$ |
$1.968$ |
$0.788$ |
$18.222$ |
Table 6. Exponentially distributed latent period and exponentially distributed infectious period.
| Mean latent period equals to the mean infectious period: $l=1$ |
| $R_{0}=2,$ $\rho=0.414/\mu$ |
|
$R_{0}=3,$ $\rho=0.732/\mu$ |
| $v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
|
$v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
| $0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
|
$0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
| $0.25$ |
$1.059$ |
$0.110$ |
$1.116$ |
|
$0.25$ |
$1.126$ |
$0.215$ |
$1.174$ |
| $1.00$ |
$1.191$ |
$0.303$ |
$1.548$ |
|
$1.00$ |
$1.413$ |
$0.521$ |
$1.930$ |
| $2.00$ |
$1.307$ |
$0.430$ |
$2.414$ |
|
$2.00$ |
$1.663$ |
$0.674$ |
$3.923$ |
| $3.00$ |
$1.387$ |
$0.501$ |
$3.831$ |
|
$3.00$ |
$1.833$ |
$0.745$ |
$8.463$ |
| $4.00$ |
$1.447$ |
$0.547$ |
$6.209$ |
|
$4.00$ |
$1.958$ |
$0.785$ |
$19.310$ |
| Either $\mu_{E}=\mu,$ $\mu_{I}=2\mu$ or $\mu_{E}=2\mu,$ $\mu_{I}=\mu$ |
| $R_{0}=2,$ $\rho=0.281/\mu$ |
|
$R_{0}=3,$ $\rho=0.5/\mu$ |
| $v$ |
$R_{c}(\rho,\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
|
$v$ |
$R_{c}(\rho,\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
| $0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
|
$0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
| $0.25$ |
$1.059$ |
$0.109$ |
$1.117$ |
|
$0.25$ |
$1.124$ |
$0.213$ |
$1.174$ |
| $1.00$ |
$1.191$ |
$0.302$ |
$1.552$ |
|
$1.00$ |
$1.410$ |
$0.519$ |
$1.931$ |
| $2.00$ |
$1.307$ |
$0.430$ |
$2.425$ |
|
$2.00$ |
$1.660$ |
$0.673$ |
$3.926$ |
| $3.00$ |
$1.387$ |
$0.501$ |
$3.851$ |
|
$3.00$ |
$1.831$ |
$0.744$ |
$8.463$ |
| $4.00$ |
$1.448$ |
$0.547$ |
$6.242$ |
|
$4.00$ |
$1.956$ |
$0.784$ |
$19.298$ |
Table 7. Constant latent period and exponentially distributed infectious period.
| The latent period is half the infectious period: $l=1/2$ |
| $R_{0}=2,$ $\rho=0.53249/\mu$ |
|
$R_{0}=3,$ $\rho=0.90659/\mu$ |
| $v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
|
$v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
| $0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
|
$0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
| $0.25$ |
$1.057$ |
$0.106$ |
$1.106$ |
|
$0.25$ |
$1.127$ |
$0.216$ |
$1.160$ |
| $1.00$ |
$1.186$ |
$0.296$ |
$1.501$ |
|
$1.00$ |
$1.413$ |
$0.521$ |
$1.855$ |
| $2.00$ |
$1.301$ |
$0.424$ |
$2.289$ |
|
$2.00$ |
$1.661$ |
$0.673$ |
$3.701$ |
| $3.00$ |
$1.381$ |
$0.495$ |
$3.581$ |
|
$3.00$ |
$1.831$ |
$0.744$ |
$7.953$ |
| $4.00$ |
$1.441$ |
$0.542$ |
$5.757$ |
|
$4.00$ |
$1.956$ |
$0.784$ |
$18.210$ |
| The latent period equals to the infectious period: $l=1$ |
| $R_{0}=2,$ $\rho=0.3748/\mu$ |
|
$R_{0}=3,$ $,\rho=0.61764/\mu$ |
| $v$ |
$R_{c}(\rho,\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
|
$v$ |
$R_{c}(\rho,\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
| $0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
|
$0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
| $0.25$ |
$1.057$ |
$0.105$ |
$1.100$ |
|
$0.25$ |
$1.131$ |
$0.223$ |
$1.156$ |
| $1.00$ |
$1.184$ |
$0.294$ |
$1.476$ |
|
$1.00$ |
$1.421$ |
$0.527$ |
$1.840$ |
| $2.00$ |
$1.298$ |
$0.421$ |
$2.232$ |
|
$2.00$ |
$1.669$ |
$0.6769$ |
$3.673$ |
| $3.00$ |
$1.378$ |
$0.493$ |
$3.482$ |
|
$3.00$ |
$1.838$ |
$0.746$ |
$7.921$ |
| $4.00$ |
$1.438$ |
$0.540$ |
$5.596$ |
|
$4.00$ |
$1.962$ |
$0.786$ |
$18.201$ |
| The latent period is twice the infectious period: $l=2$ |
| $R_{0}=2,$ $\rho=0.2393/\mu$ |
|
$R_{0}=3,$ $\rho=0.386/\mu.$ |
| $v$ |
$R_{c}(\rho,\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
|
$v$ |
$R_{c}(\rho,\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
| $0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
|
$0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
| $0.25$ |
$1.056$ |
$0.104$ |
$1.096$ |
|
$0.25$ |
$1.134$ |
$0.227.$ |
$1.154$ |
| $1.00$ |
$1.183$ |
$0.292$ |
$1.458$ |
|
$1.00$ |
$1.426$ |
$0.531$ |
$1.831$ |
| $2.00$ |
$1.297$ |
$0.420$ |
$2.196$ |
|
$2.00$ |
$1.674$ |
$0.679$ |
$3.658$ |
| $3.00$ |
$1.377$ |
$0.492$ |
$3.421$ |
|
$3.00$ |
$1.842$ |
$0.748$ |
$7.909$ |
| $4.00$ |
$1.437$ |
$0.539$ |
$5.498$ |
|
$4.00$ |
$1.966$ |
$0.787$ |
$18.215$ |
Table 8. Exponentially distributed latent period and constant infectious period.
| The latent period is half the infectious period: $l=1/2$ |
| $R_{0}=2,$ $\rho=0.7788/\mu$ |
|
$R_{0}=3,$ $\rho=0.1325/\mu$ |
| $v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
|
$v$ |
$R_{c}(\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
| $0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
|
$0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
| $0.25$ |
$1.059$ |
$0.109$ |
$1.109$ |
|
$0.25$ |
$1.131$ |
$0.222$ |
$1.169$ |
| $1.00$ |
$1.189$ |
$0.300$ |
$1.517$ |
|
$1.00$ |
$1.422$ |
$0.528$ |
$1.907$ |
| $2.00$ |
$1.304$ |
$0.427$ |
$2.340$ |
|
$2.00$ |
$1.671$ |
$0.678$ |
$3.865$ |
| $3.00$ |
$1.385$ |
$0.499$ |
$3.694$ |
|
$3.00$ |
$1.840$ |
$0.747$ |
$8.351$ |
| $4.00$ |
$1.445$ |
$0.545$ |
$5.972$ |
|
$4.00$ |
$1.964$ |
$0.787$ |
$19.123$ |
| The latent period equals to the infectious period: $l=1$ |
| $R_{0}=2,$ $\rho=0.5432/\mu$ |
|
$R_{0}=3,$ $,\rho=0.9426/\mu$ |
| $v$ |
$R_{c}(\rho,\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
|
$v$ |
$R_{c}(\rho,\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
| $0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
|
$0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
| $0.25$ |
$1.058$ |
$0.108$ |
$1.112$ |
|
$0.25$ |
$1.127$ |
$0.216$ |
$1.168$ |
| $1.00$ |
$1.189$ |
$0.300$ |
$1.528$ |
|
$1.00$ |
$1.414$ |
$0.522$ |
$1.903$ |
| $2.00$ |
$1.304$ |
$0.427$ |
$2.362$ |
|
$2.00$ |
$1.664$ |
$0.674$ |
$3.849$ |
| $3.00$ |
$1.385$ |
$0.499$ |
$3.731$ |
|
$3.00$ |
$1.834$ |
$0.745$ |
$8.298$ |
| $4.00$ |
$1.445$ |
$0.545$ |
$6.030$ |
|
$4.00$ |
$1.958$ |
$0.785$ |
$18.965$ |
| The latent period is twice the infectious period: $l=2$ |
| $R_{0}=2,$ $\rho=0.3455/\mu$ |
|
$R_{0}=3,$ $\rho=0.6186/\mu$ |
| $v$ |
$R_{c}(\rho,\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
|
$v$ |
$R_{c}(\rho,\rho)$ |
$\eta$ |
$\rho^{\prime}/\rho$ |
| $0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
|
$0.00$ |
$1.000$ |
$0.000$ |
$1.000$ |
| $0.25$ |
$1.058$ |
$0.108$ |
$1.116$ |
|
$0.25$ |
$1.122$ |
$0.209$ |
$1.170$ |
| $1.00$ |
$1.189$ |
$0.300$ |
$1.548$ |
|
$1.00$ |
$1.405$ |
$0.515$ |
$1.910$ |
| $2.00$ |
$1.305$ |
$0.428$ |
$2.410$ |
|
$2.00$ |
$1.655$ |
$0.670$ |
$3.860$ |
| $3.00$ |
$1.386$ |
$0.500$ |
$3.816$ |
|
$3.00$ |
$1.826$ |
$0.742$ |
$8.301$ |
| $4.00$ |
$1.446$ |
$0.546$ |
$6.173$ |
|
$4.00$ |
$1.951$ |
$0.783$ |
$18.915$ |
Constant infectious period, no latent period
The survival function for $T_{I}$ is $\overline{F}_{I}(x)=1$ if $x\leq\mu$ and $\overline{F}_{I}(x)=0$ otherwise. $G$ corresponds to the uniform distribution $U[0,\mu]$ with p.d.f. $f_{G}(x)=\frac{1}{\mu}\overline{F}_{I}(x)=\frac{1}{\mu}$ when $x\leq\mu$ and $f_{G}(x)=0$ otherwise. $E[G]=\frac{\mu}{2}$. $R_{v}(\rho)$ is calculated according to
|
$
R_{v}(\rho)=\left\{
R0(1−(1+ρμv)1−1vρμ(1−v)),v≠1R0log(ρμ+1)ρμ,v=1
\right. ,\label{case 1 frailty}
$
|
(22)
|
of which, $\rho$ is calculated by solving $R_{0}\left( 1-e^{-\rho\mu}\right)=\rho\mu$. The scale parameter for the uniform distribution $U[0,\mu]$ is $\lambda=\mu^{-1}.$ Given any $\mu,$ the threshold $\rho$ is scaled according to $\mu^{-1}.$ $R_{v}(\rho)$ is invariant to the length of the infectious period. With respect to $R_{0}=2$ and $R_{0}=3,$ the threshold $\rho$ is calculated as $\rho=1.594/\mu$ at $R_{0}=2$ and $\rho=2.821/\mu$ at $R_{0}=3.$ Results are presented in Table 2.
Exponentially distributed infectious period, no latent period
In this case, $G=W$ is identically distributed as the infectious period $T_{I}$ with $f_{G}(x)=\frac{1}{\mu}e^{-x/\mu}.$ The scale parameter is $\mu^{-1}.$ The threshold $\rho=\mu^{-1}\left( R_{0}-1\right) $ is a function of $R_{0},$ scaled according to $\mu^{-1}.$ For each of the two scenarios $R_{0}=2$ and $R_{0}=3$, $\rho=1/\mu$ at $R_{0}=2$ and $\rho=2/\mu$ at $R_{0}=3.$ $R_{v}(\rho)$ is calculated according to
|
$
R_{v}(\rho)=\frac{\left( 1/v\right) ^{1/v}}{\Gamma(1/v)}\int_{0}^{\infty
}\left( \frac{zR_{0}}{zR_{0}-z+1}\right) z^{\frac{1}{v}-2}e^{-z/v}dz.
\label{case 2 frailty 1}
$
|
(23)
|
The quantities are presented in Table 3.
Gamma distributed infectious period, no latent period
The calculation of $R_{v}$ as a function of $R_{0}$ and $\theta$ was given by (17) and extensively covered in the previous section. $R_{v}(\theta;R_{0})$ according to selected values for $\theta$ and $v,$ stratified by $R_{0}=2$ and $R_{0}=3$ presented in Table 1. Table 4 add the final size $\eta$ (when applicable) and the ratio $\rho^{\prime}/\rho$ for the following two scenarios:
1. $T_{I}$ with larger than exponential variance at $\theta=2.$ The threshold is calculated as $\rho\mu=0.719$ at $R_{0}=2$ and $\rho\mu=1.5$ at $R_{0}=3,$ respectively.
2. $T_{I}$ with smaller than exponential variance at $\theta=0.5.$ The threshold is calculated as $\rho\mu=1.236$ at $R_{0}=2$ and $\rho\mu=2.372$ at $R_{0}=3,$ respectively.
Constant latent period+constant infectious period
In this case, $T_{E}\equiv l\mu$ and $T_{I}\equiv\mu$ without random variation. Although the sum of the latent and the infectious period is constant$,$ the sum $G=T_{E}+W$ is random, which is the constant $l\mu$ plus an uniformly distributed $W$ between $0$ and $\mu.$ The mean of $G$ is $E[G]=\left( l+\frac{1}{2}\right) \mu.$ The p.d.f. for $G$ is $f_{G}(x)=\frac{1}{\mu},$ if $l\mu<x\leq\left( l+1\right) \mu$ and $f_{G}(x)=0$ otherwise. The threshold condition is $R_{0}e^{-l\rho\mu}\left( 1-e^{-\rho \mu}\right) =\rho\mu.$ When $l$ is given, the threshold $\rho$ is scaled according to $\mu^{-1}.$ At the threshold $\rho,$ $R_{v}(\rho)$ is calculated by
|
$
R_{v}(\rho)=R_{0}\int_{l}^{l+1}\left[ 1+\left( \rho\mu\right) yv\right]
^{-1/v}dy. \label{case 3 frailty}
$
|
(24)
|
Although $\int_{l}^{l+1}\left[ 1+\left( \rho\mu\right) yv\right]
^{-1/v}dy$ does not give explicit mathematical forms, it is easy to evaluate numerically. The preserved quantity is the product $\rho\mu.$ Let us consider $l=0.5,$ $1$ and $2$ at $R_{0}=2$ and $R_{0}=3$. At $l=0.5,$ $\rho=0.714/\mu$ when $R_{0}=2$ and $\rho=1.153/\mu$ when $R_{0}=3$; at $l=1,$ $\rho=0.468/\mu$ when $R_{0}=2$ and $\rho=0.748/\mu$ when $R_{0}=3;$ at $l=2,$ $\rho=0.279/\mu$ when $R_{0}=2$ and $\rho=0.443/\mu$ when $R_{0}=3.$ Numerical results under each of these are displayed in Table 5.
Exponentially distributed latent period + exponentially distributed infectious period
We assume that $\mu_{E}=E[T_{E}]=l\mu$ and $\mu_{I}=E[T_{I}]=\mu,$ In this special case, $W$ is identically distributed as $T_{I}.$ The p.d.f. for $G=T_{E}+W$ is
|
$
f_{G}(x)=\left\{
1(1−l)μ(e−xμ−e−xlμ),l≠11μ2xe−xμ,l=1
\right. .
$
|
The mean value of $G$ is $E[G]=\left( l+1\right) \mu.$ The threshold condition is $\frac{R_{0}}{\left( 1+l\rho\mu\right) \left( 1+\rho \mu\right) }=1.$ When $l$ is given, the threshold $\rho$ is scaled according to $\mu^{-1}.$ At the threshold $\rho,$ $R_{v}(\rho)$ is calculated by
|
$
R_{v}(\rho)=\left\{
R0∫∞0[1+(ρμ)yv]−1/vye−ydy,l=1R0(1−l)∫∞0[1+(ρμ)yv]−1/v(e−y−e−1ly)dy,l≠1
\right. \label{exp-exp frailty}
$
|
(25)
|
The quantity $\rho\mu$ is preserved. In addition, the relative lengths of the latent period and the infectious period can be reversed, without changing the numerical results for $R_{v}(\rho)$ in (25). In other words, the re-parametrizations
|
$
\left\{
μE=lμ,l>0μI=μ
\right. \text{ and }\left\{
μE=μ,μI=lμ,l>0
\right.
$
|
give identical results. When $l=1,$ the product $\rho\mu$ satisfies $R_{0}=\left( 1+\rho\mu\right) \left( 1+\rho\mu\right) ,$ such that $\rho=0.414/\mu$ when $R_{0}=2$ and $\rho=0.732/\mu$ when $R_{0}=3.$ If either $\mu_{E}=\mu,$ $\mu_{I}=2\mu$ or $\mu_{E}=2\mu,$ $\mu_{I}=\mu,$ $\rho\mu$ satisfies $R_{0}=\left( 1+2\rho\mu\right) \left( 1+\rho\mu\right) ,$ such that $\rho=0.281/\mu$ when $R_{0}=2$ and $\rho=0.5/\mu$ when $R_{0}=3.$ Thus numerical values for $R_{v}(\rho)$ are identical when the mean latent period is half of that of the infectious period, and when the mean latent period is twice as long as the mean infectious period. Results are presented in Table 6.
Constant latent period+exponentially distributed infectious period
The mean value for $G=T_{E}+W$ is $E[G]=\left( l+1\right) \mu$ with p.d.f.
|
$
f_{G}(x)=\left\{
0 if x≤lμ1μe−x−lμμ if lμ<x
\right. .
$
|
The Laplace transform for $G$ is $\int_{0}^{\infty}e^{-sx}f_{G}(x)dx=e^{-ls\mu }\left( 1+s\mu\right) ^{-1}.$ The threshold condition is $R_{0}e^{-l\rho\mu }=1+\rho\mu.$ When $l$ is given, $\rho$ is scaled according to $\mu^{-1}.$ Let us consider $l=0.5,$ $1$ and $2$ at $R_{0}=2$ and $R_{0}=3$. At $l=0.5,$ $\rho=0.53249/\mu$ at $R_{0}=2$ at $\rho=0.90659/\mu$ at $R_{0}=3;$ at $l=1,$ $\rho=0.3748/\mu$ at $R_{0}=2$ and $\rho=0.61764/\mu$ at $R_{0}=3;$ at $l=2,$ $\rho=0.2393/\mu$ at $R_{0}=2$ and $\rho=0.386/\mu$ at $R_{0}=3.$ At the threshold $\rho,$ $R_{v}(\rho)$ is calculated by
|
$
R_{v}(\rho)=R_{0}\left( \int_{l}^{\infty}\left[ 1+\left( \rho\mu\right)
yv\right] ^{-1/v}e^{-\left( y-l\right) }dy\right) .\label{case 5 frailty}
$
|
(26)
|
The preserved quantity is $\rho\mu.$ Results are given in Table 7.
Exponentially distributed latent period + constant infectious period
In this setting, $G=T_{E}+W$ has the mean $E[G]=\left( l+\frac{1}{2}\right)\mu$ with p.d.f.
|
$
f_{G}(x)=\left\{
1μ(1−e−x/lμ),x≤μ1μe−x/lμ(e1/l−1),x>μ
\right. .
$
|
The Laplace transform is $\mathcal{L[}f_{G}](s)=\mathcal{L[}f_{E}](s)\mathcal{L[}f_{W}](s)=\frac{1}{1+l\mu s}\frac{1-e^{-s\mu}}{s\mu}.$ The threshold condition is $R_{0}\left( 1-e^{-\rho\mu}\right) =\left(1+l\rho\mu\right) \rho\mu.$ $R_{v}(\rho)$ is calculated by
|
$
R_{v}(\rho)=R_{0}\left(
∫10[1+(ρμ)yv]−1/vdy+e1l∫∞1[1+(ρμ)yv]−1/ve−y/ldy−∫∞0[1+(ρμ)yv]−1/ve−y/ldy
\right) . \label{case 6 frailty}
$
|
(27)
|
The preserved quantity is $\rho\mu.$ At $l=0.5,$ $\rho=0.7788/\mu$ when $R_{0}=2$ and $\rho=0.1325/\mu$ when$R_{0}=3;$ at $l=1,$ $\rho=0.5432/\mu$ when $R_{0}=2$ and $\rho=0.9426/\mu$ when $R_{0}=3;$ at $l=2,$ $\rho =0.3455/\mu$ when $R_{0}=2$ and $\rho=0.6186/\mu$ when $R_{0}=3.$ Results are given in Table 8.









 DownLoad:
DownLoad: