FitzHugh-Nagumo equations with generalized diffusive coupling

1.   Introduction

Generally, it is difficult to control and identify MIMO nonlinear systems as there exists some complex structures, coupling variables, unknown parameters and uncertainty in the dynamical processes ^[1]. At the same time, most techniques related to advanced control analysis and synthesis are studied based on the accurate modeling of complex systems ^[2]. Therefore, the construction of precise mathematical models for MIMO systems is always an open problem in engineering theories and applications ^[3]. Fortunately, in order to relieve this conflict, the adaptive controller is a suitable identification and control strategy to estimate unknown parameters in MIMO nonlinear systems ^[4,5]. Specifically, the adaptive fuzzy control systems have recently been more applied to complex multivariable systems with uncertain parameters ^[6,7]. The control structures of fuzzy logic models are more suitable to the practical systems with uncertainty and unknown parameters as a fuzzy logic reasoning model can make good advantage of operating experience and knowledge from human beings, while linguistic knowledge cannot be sufficiently considered in traditional adaptive control systems ^[8,9,10]. Moreover, the neural networks are employed to approximate unknown functions or terms ^[11,12]. However, in most existing fuzzy adaptive control systems, the traditional rules-based fuzzy systems are mainly employed to design controllers for multi-input-and-single-output (MISO) or single-input-and-single-output (SISO) fuzzy systems ^[13,14,15]. Meanwhile, as the conventional fuzzy models are constructed on uncertain knowledge representation related to fuzzy set and fuzzy inference, it is challenging to describe the entire closed-loop control system by global digital expression, especially for MIMO controlled systems.

With the increasing development of big data and digital technology, it is necessary to find suitable mathematical tools to describe the traditional fuzzy logic rules and reasoning process digitally. In order to construct the matrix expression of multivariable fuzzy language logic and reasoning, a STP algorithm for conventional matrices was introduced to general MIMO fuzzy variables and reasoning operations ^[16,17]. Because of its special properties ^[18], the STP operation has been imported to the related research of engineering fields, to convert a multi-valued logic and reasoning relationship into different applications, such as standard finite dynamic algebra operators ^[19,20], logic analysis ^[21,22], Boolean control networks ^[23,24,25], variety of system analysis ^[26], systems synthesis ^{[27,28,29,30]}, algebraic state space theory ^[31] and so on.

The first author and her research group have worked on applying the STP theory to the fuzzy logic inference systems since 2012. Our target is the matrix representation of conventional fuzzy logic systems and some valuable creative results have been obtained, such as both fuzzy sets and fuzzy reasoning processes expressed by FRM. The traditional fuzzy logic system can be represented by the matrices and STP algorithms, but in previous research ^{[16,17,32,33]}, only an original FRM model was constructed as the matrix description of general multivariable fuzzy systems without considering the design of the fuzzy controller for practical applications. These related results provide theoretical foundations for possible applications of the MIMO FRM models. However, FRM models lack parameter optimization and adaptive capability in applications as a fuzzy controller. Hence, in this manuscript the authors tried to extend our related theoretical results to further possible applications of the MIMO FRM models so that FRM models are used to realize the parameter optimization and adaptive capability in applications as a fuzzy controller.

To implement matrix expression of traditional adaptive fuzzy control systems and online optimization of parameters of FRM models, in this work the objective is to propose the MIMO adaptive FRM control models based on the fuzzy STP algorithms. The major contributions are as follows:

1) The matrix description of general multivariable fuzzy systems is extended to the conventional multiple-variables adaptive fuzzy control systems.

2) FRMs and fuzzy STP are realized for both local and global fuzzy models in the traditional fuzzy adaptive systems. The unknown parameters in MIMO FRM models are identified by the online adaptive FRM laws for the fuzzy systems with varying and uncertain variables.

3) The entire design process of general fuzzy adaptive control systems are reconstructed in the perspective of matrix and STP as the theoretical extension and the applications of multivariable FRMs, and then the control performance can be online analyzed.

The rest is organized in this paper as follows. First, the preliminaries are introduced with the relevant FRM and fuzzy STP algorithms in Section 2. Second, Section 3 gives some descriptions of FRM models for MIMO adaptive fuzzy control systems and universal approximation. Third, the detailed modeling process of indirect adaptive FRM controller is given in Section 4 for continuous nonlinear MIMO systems, and the adaptive FRM control design and convergence of tracking errors are investigated. Finally, in Section 5, the effectiveness is investigated for the proposed adaptive FRM control strategies by some simulations.

2.   Preliminaries

Some related notational descriptions will be introduced for multiple-variable fuzzy relation models in this section, and then the fuzzy theoretical extension will be obtained based on the STP of matrices. In the remainder of this paper, the scalars in the STP and FRM models will be represented in $ \mathfrak{R} $, the space with the $ n\times1 $ real vector or the $ m\times n $ matrix, without considering the complex space.

Definition 2.1. ^[18] Given two arbitrary real matrices $ A = (a_{i, j})\in\mathfrak{R}^{m\times n} $ and $ B = (b_{i, j})\in\mathfrak{R}^{p\times q} $, the STP of $ A $ and $ B $ is defined as

where $ t $ is the least common multiple (LCM) of $ n $ and $ p $, $ I_{t/n} $ and $ I_{t/p} $ are identity matrices and $ \otimes $ is the Kronecker product.

Consider $ R(X, Y) $ as a multivariable fuzzy relation on a universe of discourse (UOD) $ \prod\limits_{i = 1}^n E_i\times\prod\limits_{j = 1}^m F_j $ among multiple continuous fuzzy variables $ X = (x_1, x_2, \dots, x_n) $ and $ Y = (y_1, y_2, \dots, y_m) $. The continuous multivariable fuzzy relationship between $ X $ and $ Y $ has been defined by authors in ^[32] as the following $ (N_1\times \dots, N_n)\times (M_1\times \dots, M_m) $ FRM:

In raditional fuzzy theory, for continuous fuzzy variables it is difficult to describe their fuzzy relationship using a matrix. However, the FRM models in Eq (2.2) are implemented for general continuous multivariable fuzzy equation relations when each pair of variables $ (X, Y) $ is considered as a sampling data pair at any moment $ t $. Correspondingly, it also can be extended in a similar way to the construction of continuous fuzzy MIMO systems on basic conventional fuzzy relations.

In general, the conventional fuzzy logical operators include AND, OR, IMPLICATION, etc., which are defined by algebraic functions $ T $-norm or $ S $-norm. Each of the $ T $-norm and $ S $-norm has some unique properties and operators. In order to formulate a general matrix description of a fuzzy reasoning operation, the STP of algebra matrices is employed to extend the fuzzy implication by introducing the fuzzy logical operators into the STP. For the original STP in Definition 2.1, if $ A $ and $ B $ are two arbitrary FRMs instead of two common matrices, the algebraic addition and algebraic product can be replaced by the $ S $-norm and $ T $-norm operators, respectively. Therefore, the fuzzy STP can be defined for the universal implication operator of general MIMO fuzzy systems as follows.

Definition 2.2. (Fuzzy STP of FRMs) Given two arbitrary FRMs $ A = (a_{i, j})\in\mathfrak{R}^{m\times n} $ and $ B = (b_{i, j})\in\mathfrak{R}^{p\times q} $, the fuzzy STP between $ A $ and $ B $ is defined as

where $ t $ is the LCM of $ n $ and $ p $ and $ I_{t/n} $ and $ I_{t/p} $ are identity matrices. The algebraic addition and product in conventional matrices are substituted by fuzzy logic operators, respectively, in Eq (2.3), so the fuzzy logic reasoning can be realized digitally through the fuzzy STP operations between FRM models.

3.   Description of FRM models for MIMO systems

Let's consider a fuzzy $ n $-inputs-$ m $-outputs system based on FRM models. Assume the complete fuzzy rule base is

where the $ i $-th input is $ x_i $ and the $ k $-th output is

$ A_i^1, \cdots, A_i^{N_i} $ and $ B_k^1, \cdots, B_k^M $ represent the fuzzy input and output variables' sets, respectively,

Generally, Eq (3.1) can be equivalent to a group of $ m $ MISO fuzzy systems. Without loss of generality, consider one following FRM model

Suppose that in each fuzzy rule Eq (3.2), membership functions (MFs) of the output

are symmetrical and normal. Assume on each fuzzy set $ B_k^l $, parameters $ c_k^l $ are the MF centers of $ y_k $. The center points of the fuzzy sets for output variables in the FRM model can be represented as

Given an input value

with fuzzy sets

similar to the operation of fuzzification, the input vector can be described as

where

Assume the FRM with parameters $ c_k^l, l = 1, \cdots, M $ can be estimated by

then the estimated output vector can be obtained from Eqs (3.4) and (3.5), such as

According to the definition of $ V_{F_k}(\hat{y}_{k0}) $, Eq (3.6) can also be expressed as

where the vector $ V_{F_k} $ of the estimated output can be determined by the real-valued FRM $ M_R $ with the input

Based on Eq (3.7), the output $ \hat{y}_{k0} $ can be estimated by the FRM model in Eq (3.5) and can be obtained through defuzzification.

Assume that each output set is a singleton. Since $ B_k^1, \cdots, $ $ B_k^M $ are normalized fuzzy sets with the centers

using the center-average defuzzifier and $ V_{F_k}(\hat{y}_{k0}) $ in Eqs (3.6) and (3.7), we can obtain the real value of $ \hat{y}_{k0} $

where

Denote

and

then,

where $ C_k $ is a constant vector and $ \overline{R}_{x_{0}} $ is the function of input variable $ x_0 $.

It is seen from Eq (3.10) that $ \hat{y}_{k0} $ can be estimated by the FRM $ M_R $, input variable $ x_0 $ and the output parameters $ C_k $.

If for each input variable $ x_i $, through FRM fuzzification on

based on its MFs, the vector expression of $ x_i $ can be determined by

then the fuzzy input vector can be obtained by the formula

As the set $ B_k^l $ in Eq (3.2) is a fuzzy number with $ c_k^l $ as its center, let

Using an appropriation fuzzy STP algorithm and a central defuzzifier, the output from the FRM model for the system Eq (3.2) is

where

Similarly, in the matrix representation of MIMO FRM in Eq (3.1), if $ B_k^l $ is normal and its center is denoted by

the FRM output can be obtained with max-min operator and the central defuzzification

where

Remark 3.1. In order to guarantee the feasibility of adaptive FRM controllers, the approximation analysis results of MISO and MIMO FRM systems are employed from our previous research in ^[33]. This paper focuses on continuous fuzzy variables even though the proofs of approximation theorems always exist for both FRM models on continuous and discrete UOD.

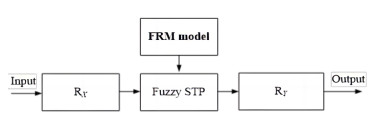
Remark 3.2. In the fuzzy systems based on FRM models, there are no specific limitations for fuzzification, defuzzification, $ T $-norm and $ S $-norm reasoning operators and MFs of all fuzzy variables ^[29]. The processing structure of a common FRM is demonstrated in Figure 1 for multivariable fuzzy systems.

In this paper, both the structure and the basic parameters are supposed to be specified properly in advance, i.e., the designers' decision is needed to determine relevant inputs, MFs parameters, numbers of MFs and rules for the fuzzy system. On the other hand, the consequent parameters, i.e., $ \theta $ need to be obtained by some parameter training algorithms.

4.   Construction of MIMO adaptive FRM controllers

4.1.   The structure and classification of MIMO adaptive FRM control systems

The structure to track outputs is shown for a MIMO adaptive FRM output tracking system in Figure 2. Compared with the conventional fuzzy adaptive control systems, the biggest difference of the adaptive FRM controller is to be designed based on FRM models and fuzzy STP operations, which can implement the matrix expression of multivariable adaptive fuzzy control systems. As we know, the general control system is composed of at least a plant and a controller. In order to construct the matrix expression of human experience, FRM models in a control system can be categorized to two types: control experience and plant knowledge. Therefore, based on the structure of the fuzzy logic controller, the adaptive FRM control strategy is classified into the three categories as follows.

(ⅰ) Indirect adaptive FRM controller: The FRM model comprises some fuzzy systems constructed initially from plant knowledge.

In this work, the basics of indirect adaptive fuzzy control schemes will be developed for nonlinear MIMO FRM systems based on the fuzzy STP algorithms.

(ⅱ) Direct adaptive FRM controller: The FRM control model is a single fuzzy controller constructed initially based on control experience.

(ⅲ) Hybrid FRM controller: The FRM control model is a combined system of the indirect and direct adaptive FRM controllers.

4.2.   Problem formulation

Suppose one MIMO nonlinear dynamical system is described by a set of one-order equations as follows:

where

denotes

as the state vector, which is supposed to be measureable;

and

are the input and output vectors of the plant, respectively. Here, $ D_x $ is a compact set as the UOD of the state variables, and

are smooth unknown nonlinear multivariable functions.

Denote

and the plant Eq (4.1) is able to be rewritten as

Assume that $ G(x) $ is not zero for any $ x\in{D_x} $ to keep the plant controllable. In this paper, $ G(x) $ is assumed nonsingular and

The control objective is to design an adaptive FRM feedback controller $ u = u\left(x\; \middle\vert\; \theta\right) $ on the fuzzy STP operation and an adaptation law to real-time to adjust the parameter $ \theta $, such that:

(1) All internal variables in the closed-loop fuzzy control system $ x(t), \, \theta(t) $ and $ u = u\left(x\; \middle\vert\; \theta\right) $ are uniformly two-norm bounded, i.e.,

and

for all $ t\geq 0 $, where $ M_x $, $ M_{\theta} $ and $ M_u $ are parameters depending on the controlled plants.

(2) The plant output $ y $ follows the ideal trajectory

which its time derivatives are known and bounded.

Since $ F(x) $ and $ G(x) $ are nonlinear and unknown in the plant, we are dealing with a quite general MIMO nonlinear control problem. Consequently, the control objective $ y $ is only required to track $ y_d $ as close as possible instead of asymptotical convergence. Throughout the whole paper, in order to design adaptive FRM controllers, the following assumptions are supposed.

A1: ^[34] $ G(x) $ is a positive definite matrix, then it exists $ \sigma_0 > 0 $, $ \sigma_0\in\mathfrak{R} $ such that $ G(x)\geq\sigma_0I_p $, $ I_p\in\mathfrak{R}^{p\times p} $ is an identity matrix. It is obvious that A1 is a sufficient condition to ensure $ G(x) $ is always regular, then Eq (4.3) is feedback linearizable.

A2: ^[34] The ideal trajectory $ y_d(t) $ and the derivatives of each

are always known bounded, and each $ y_{di}(t) $ is assumed to be $ r_i $-times differentiable.

Next, let us define the following tracking errors

and the filtered tracking errors

where $ i = 1, 2, \cdots, p $. From Eq (4.5), when $ s_i(t)\to 0, $ $ e_i(t)\to 0 $ asymptotically. Now, the objective is to design a controller to satisfy $ s_i(t)\to 0, i = 1, 2, \cdots, p $.

The time derivatives of the filtered errors can be written as

where $ v_i $ are given as:

where $ i = 1, 2, \cdots, p $,

From Eqs (4.6) and (4.7), the time derivatives of the filtered errors can become

If both $ F(x) $ and $ G(x) $ are known, we can design the following nonlinear control law as

where

with $ k_{0i} > 0 $ for $ i = 1, \cdots, p $. Substitute Eq (4.9) in Eq (4.8) and we can obtain

or

which implies that $ s_i(t)\to 0 $ as $ t\to\infty $. Hence, $ e_i(t) $ and all of its derivatives converge to zero, $ t\to\infty $, which means the output $ y $ converges to the ideal value $ y_d $ asymptotically ^[35].

As $ F(x) $ and $ G(x) $ are considered to be unknown in this paper, the above design technique cannot be realized. That is, the ideal controller $ u^{*} $ in Eq (4.9) cannot be implemented. However, we can employ the multiple-variable FRM systems to approximate the nonlinear function matrix $ F(x) $ and $ G(x) $.

4.3.   Design of adaptive FRM control systems

In order to realize the adaptive control based FRM models for the plant in Eq (4.3), in this subsection, two steps are taken to express and approximate matrix functions $ F(x) $ and $ G(x) $ by MIMO FRM models. First, for each entry of matrix $ F(x) $ and $ G(x) $, a set of MISO fuzzy systems as the local FRM models, respectively, $ R_{f_i} $ and $ R_{g_{ij}} $ are constructed to approximate $ f_i $ and $ g_{ij}, i, j = 1, 2, \cdots, p $. Then, for $ F(x) $ and $ G(x) $, the global MIMO FRM models $ R_F $ and $ R_G $ are obtained by the combination of $ R_{f_i} $ and $ R_{g_{ij}}, $ respectively. Finally, in order to obtain the corresponding objectives, these two global fuzzy matrices as approximators ^[32] are developed to a well-defined adaptive controller with its adaptive laws.

Assume nonlinear functions $ f_i $ and $ g_{ij}, i, j = 1, 2, \cdots, p $ can be approximated by the complete fuzzy rule sets. Construct the local FRM models $ \hat{f}_i\left(x\; \middle\vert\; \theta_{f_i}\right) $ from the $ \prod\limits_{k = 1}^n p_k $ rules

where

Similarly, construct the local FRM models $ \hat{g}_{ij}\left(x\; \middle\vert\; \theta_{g_{ij}}\right) $ from the $ \prod\limits_{k = 1}^n q_k $ rules:

where

Specifically, using the fuzzy STP operation, singleton fuzzification and central defuzzifier, the corresponding FRM estimation models of fuzzy systems in Eqs (4.12) and (4.13) are as follows:

Here, $ \overline{y}_{f_i}^{l_1\cdots l_n} $ and $ \overline{y}_{g_{ij}}^{l_1\cdots l_n} $ are the center points of each $ E_i^{l_1\cdots l_n} $ and $ H_{ij}^{l_1\cdots l_n} $, respectively. In order to realize online optimization and adaptive control, let $ \overline{y}_{f_i}^{l_1\cdots l_n} $ and $ \overline{y}_{g_{ij}}^{l_1\cdots l_n} $ be the free parameters. Denote

and

and then $ \xi_{f_i}(x) $ and $ \eta_{g_{ij}}(x) $ are the following $ \prod_{k = 1}^n p_k $-dimensional and $ \prod_{k = 1}^n q_k $-dimensional vectors with its $ l_1\cdots l_n $-th element, respectively

Denote

then the approximation matrices of $ F(x) $ and $ G(x) $ are

Since the matrix parameters $ \theta_F $ and $ \theta_G $ change along with online operation, only the initial parameters are set for both local and global FRM models. Therefore, the following task is to construct a global adaptation law for $ \theta_F $ and $ \theta_G $, such that $ e(t) $ is minimized.

Define the following optimal parameters for $ \theta_F(x) $ and $ \theta_G(x) $ ($ \theta_{f_i} $ and $ \theta_{g_{ij}} $) as

where $ i, j = 1, 2, \cdots, p $, $ D_x $ is a compact set and the nonlinear functions $ f_i(x) $ and $ g_{ij}(x) $ are approximated by fuzzy systems Eqs (4.16) and (4.17) over $ D_x $. Notice that $ \theta_{f_i}^{*} $ and $ \theta_{g_{ij}}^{*} $ in $ \theta_F(x) $ and $ \theta_G(x) $ are artificial constant quantities only in the analytical meaning.

Define parameter estimation errors as:

because of

and minimum fuzzy approximation errors as

because of

and

which are corresponding to the parameters in Eq (4.20).

In this case, since $ D_x $ is a compact set, assume that $ D_x $ is large enough to remain state variables in $ D_x $. Accordingly, it is reasonable for each minimum approximation error bound for each $ x\in D_x $ as follows:

where $ \overline\vartheta_{f_i} $ and $ \overline\vartheta_{g_{ij}} $ are known constants as bounds.

Denote

then we obtain

Next, by using the FRM approximation models $ \hat{F}\left(x\; \middle\vert\; \theta_F\right) $ and $ \hat{G}\left(x\; \middle\vert\; \theta_G\right) $ in Eq (4.9), respectively, the global FRM model of the fuzzy controller is obtained

Generally, it should guarantee that $ \hat{G}\left(x\; \middle\vert\; \theta_G\right) $ is always nonsingular because when $ \hat{G}\left(x\; \middle\vert\; \theta_G\right) $ is singular the certainty equivalent controller (4.25) is not well defined. As $ \hat{G}\left(x\; \middle\vert\; \theta_G\right) $ is defined by the online estimation parameter $ \theta_G $, suitable matrix parameters $ \theta_G $ have to be chosen in a feasible region to guarantee that $ \hat{G}\left(x\; \middle\vert\; \theta_G\right) $ is regular and nonsingular to implement this controller. For solving this problem, the design of the certainty controllers in Eq (4.25) is modified as follows:

where the compensation parameter $ \vartheta_0 $ is a small positive real number. Correspondingly, the regularized inverse of $ \hat{G}^{-1}\left(x\; \middle\vert\; \theta_G\right) $ defined as

Hence, even though $ \hat{G}\left(x\; \middle\vert\; \theta_G\right) $ is singular, Eq (4.27) is defined well and, therefore, the control signal in Eq (4.26) guarantees to be always well defined.

Factually, in the closed-loop system, the stability cannot be guaranteed even though Eq (4.26) is always defined well. It is due to both the approximation of $ \hat{G}\left(x\; \middle\vert\; \theta_G\right) $ by the regularized inverse and the reconstruction errors of the unknown functions $ F(x) $ and $ G(x) $. Hence, in order to cancel these approximation errors, an appending control term $ u_r $ is considered in Eq (4.26) as follows:

The controller in Eq (4.26) can be the summation of both control parts: a modified certainty equivalent control signal $ u_c $ in Eq (4.26) and an adjusting control term $ u_r $, where

where $ u_0 $ can be obtained by

and $ \delta $ is a time-varying parameter defined below.

Eventually, to minimize the tracking error $ e(t) $ and the parameter estimation errors $ \tilde{\theta}_F $ and $ \tilde{\theta}_G $, according to the Lyapunov synthesis approach ^[6], the adaptive parameters $ \theta_{f_i} $, $ \theta_{g_{ij}} $ and the design parameter $ \delta $ are updated by the adaptive laws as follows:

where

and $ \delta(0) > 0. $

4.4.   Lyapunov analysis of adaptive FRM controllers

On basis of the analysis process above, the following theorem can be obtained.

Theorem 4.1. Suppose that A1 and A2 are satisfied for Eq (4.1) as two assumptions. The control law Eq (4.28) together with adaptation laws in Eq (4.31) guarantees the properties:

(1) All signals are bounded in the closed-loop system.

(2) The tracking errors and its derivatives decrease to zero asymptotically.

Proof. The time derivatives of the filtered errors can be written as follows by substituting Eq (4.28) into Eq (4.8),

Using the control term Eqs (4.26)–(4.29), we obtain

Here, we have used the fact that

From Eqs (4.23) and (4.24), one can write Eq (4.33) as

Left multiply $ s^T $ to Eq (4.35) to obtain

The target for an adaptation law is to adjust both $ \theta_F $ and $ \theta_G $ so that $ e(t), \theta_F-\theta_F^{*} $ and $ \theta_G-\theta_G^{*} $ are minimized. Now, let's consider the following Lyapunov function

whose time derivative can be given by

which can be expressed with Eq (4.36) as

where

Substitute Eqs (4.21) and (4.22) into Eq (4.31), then

Using Eqs (4.22) and (4.29), we can obtain

as the following inequality is used,

which is from assumption A1, i.e., $ G(x) $ is assumed to be a positive definite and satisfies $ G(x)\ge\sigma_0 I_p $.

Therefore,

By substitute Eq (4.43), Eq (4.45) becomes

then by using Eq (4.31) in Eq (4.46), we obtain

Finally, we obtain

As a result, $ \dot{V} $ is semi-definite negative and $ V\in L_{\infty} $, which means that the parameters $ s_i(t), \tilde{\theta}_{f_i}(t) $ and $ \tilde{\theta}_{g_{ij}}(t) $ are bounded. i.e., $ \theta_F, \theta_G, x(t), u(t) $ and $ s(t) $ are $ L_2 $ bounded. $ \theta_{f_i}(t) and \theta_{g_{ij}}(t), \dot{s}(t) $ as $ V(t) $ is a bounded nonincreasing function,

exists and we develop

From Eq (4, 49) we know $ s_i(t)\in L_2 $, and by using Barbalat's lemma ^[35], $ s_i(t)\in L_2\cap L_{\infty} $ and $ \dot{s}_i(t)\in L_{\infty}, $ it is obvious that $ s_i(t)\to 0 $ as $ t\to\infty $. Hence, there exists that $ e_i^{(j)}(t)\to 0 $ as $ t\to\infty $ for $ i = 1, 2, \cdots, p $ and $ j = 1, 2, \cdots, r_i-1 $.

Now, we can see the singularity problem is avoided effectively by the control law Eq (4.28), which is always well defined. □

4.5.   Procedure of MIMO adaptive FRM controllers

According to the above description on analysis and synthesis in Sections 4.2–4.4, the detailed procedure to design an indirect adaptive FRM controller is summarized for multivariable nonlinear systems. The properties of closed-loop adaptive fuzzy control systems will be further discussed.

Step 1: The necessary offline initial design processes:

● Specify a MIMO plant and its input, output and state variables and the adjusting parameters $ u(t), y(t), x(t), F(t), $ $ G(t), \theta_F, \theta_G $, etc.

● Specify suitable parameters to guarantee the matrix $ \hat{G}(x, \theta_g) $ nonsingular.

● According to the limits of practical variables, determine the design constraints of parameters $ M_x, M_{\theta}, M_u $, etc.

Step 2: Modeling of initial FRM controllers:

● Specify the UOD $ D_x $ for the state vector, construct the fuzzy logical rules of each unknown functions $ f_i $ and $ g_{ij}, i, j = 1, 2, \cdots, p $.

● Design FRM models for all $ f_i $ and $ g_{ij} $ and then combine them into the global FRM models for $ F(x) $ and $ G(x) $, respectively.

● Calculate the maximum values of both $ \mu_{E^{l_1l_2\cdots l_n}} $ and $ \mu_{H^{l_1l_2\cdots l_n}} $ for $ \xi_{f_i}(x) $ and $ \eta_{g_{ij}}(x) $, and then collect them into $ \theta_{f_i}(0) $ and $ \theta_{g_{ij}}(0) $, respectively. Therefore, $ \hat{f}\left(x\; \middle\vert\; \theta_{f_i}\right) $ and $ \hat{g}\left(x\; \middle\vert\; \theta_{g_{ij}}\right) $ are obtained as Eqs (4.14) and (4.15).

● Construct the initial global FRM models $ \hat{F}\left(x\; \middle\vert\; \theta_F\right) $ and $ \hat{G}\left(x\; \middle\vert\; \theta_G\right) $ in Eqs (4.16) and (4.17).

Step 3: Online adaptive control processes:

● Import the adaptation feedback control laws Eqs (4.28) and (4.31) to the plant Eq (4.1).

● Online adjust the matrix parameter vectors $ \theta_F $ and $ \theta_G $ by the adaptive laws until the desired output tracking accuracy is obtained.

In summary, the structure of global FRM models using the proposed MIMO indirect adaptive fuzzy control system is shown in Figure 3. Generally, fuzzy IF-THEN rules in Eqs (4.12) and (4.13) are combined with the initial parameters $ \theta_{f_i}(0) $ and $ \theta_{g_{ij}}(0) $, and then it will be considered as adaptive FRM models in the design procedure for $ \hat{F}\left(x\; \middle\vert\; \theta_F\right) $ and $ \hat{G}\left(x\; \middle\vert\; \theta_G\right) $. Finally, to investigate the performance of the adaptive FRM control systems based on fuzzy STP, the following remarks about the MIMO system analysis is given.

Remark 4.1. The assumptions A1 and A2 and appending control terms $ u_r $ in Eq (4.28) guarantee that Eq (4.26) is always defined well.

Remark 4.2. Theorem 4.1 is the original control objective such that the multiple-variable plant outputs $ y $ and follows the ideal outputs $ y_d $, so the global matrix design of the adaptive FRM system is achieved.

Remark 4.3. In practical systems, there exists constraints for the state and control variables within certain regions. Moreover, it is much more complex for real control problems than the plant in Eqs (4.1)–(4.3), so it is only the first trial to describe the MIMO adaptive FRM fuzzy controller for us based on fuzzy STP operations. There are many works to be done for our research group in the future.

5.   Simulation results

In this section, the tracking control of a two-link rigid robot manipulator moving a horizontal plane ^[34] is employed to test the design of the proposed indirect fuzzy adaptive FRM systems. First, the dynamic equation is as follows:

where

with

In this case, the following parameters are chosen:

Denote

and

and the following matrix model of the robot system is obtained by

According to the specified parameters in Eq (5.1), it is obvious for $ M $ to be definite positive so it is regular, then $ G = M^{-1} $ is definite positive. The control objective is to track the following desired trajectories, respectively, for the output $ y = \left[q_1, q_2\right] $

In this case, the dynamic model of the robot system is only required for simulation purposes. Both $ F(x) $ and $ G(x) $ are supposed to be completely unknown, then two fuzzy systems in the form of Eq (4.12) are used to approximate $ F(x) $, and four to approximate $ G(x) $, respectively.

For state variable

as the inputs of FRM models, the following Gaussian MFs are defined for each state and the corresponding MFs are shown in Figure 3

and

The initial condition of the robot tracking control is set to be

and both initial $ \theta_f(0) $ and $ \theta_g(0) $ are set to be zero. The following parameters are designed for the tests

and $ \delta(0) = 1, \; \; \text{for}\; \; i, j = 1, 2. $ The simulation is shown for tracking results in Figures 4 and 5, respectively.

These simulation results show that both outputs $ y1 $ and $ y2 $ tracked the objective sinusoid curves in five seconds under the control of the proposed FRM-based adaptive controller. At the same time, the control input signals are smooth, as shown in Figure 6, to realize the output tracking control. Hence, the tests on system Eq (5.1) demonstrate the tracking ability of the proposed FRM controller as effective based on STP algorithms in uncertain nonlinear systems.

6.   Conclusions

A global matrix expression of the adaptive fuzzy controller was formulated for MIMO nonlinear systems based on local FRM models and fuzzy STP algorithms in this paper. The MIMO adaptive fuzzy control laws were developed on basic local FRM models with unknown functions, then the tracking performance was guaranteed through the Lyapunov stability analysis. Moreover, global FRM models and uniform bound for all variables were obtained. The simulation results for the two-link rigid robot manipulator show the effective tracking control and the good performance of the adaptive FRM control strategy. In future work, more advanced algorithms related to matrix expression of fuzzy strategies will be applied to MIMO non-linear adaptive systems on the basis of the FRM models and fuzzy STP algorithms.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported in part by the Plan to Introduce High-end Foreign Experts: Research on Resilient Urban Planning Data Model and Development of International Standard (G2022024004L).

Conflict of interest

All authors declare that there are no conflicts of interest in this paper.