Global properties of a delayed SIR epidemic model with multiple parallel infectious stages

1.   Introduction

Avian influenza is an animal infectious disease caused by the transmission of influenza A viruses. Influenza A viruses are divided into subtypes according to two proteins on the surface of the virus: Hemagglutinin (HA) and neuraminidase (NA) ^[1]. Most avian influenza viruses infect only certain species and do not infect humans. However, a few avian influenza viruses have crossed the species barrier to infect humans and even kill them, such as H5N1, H7N1, H7N2, H7N3, H7N7, H9N2 and H7N9. Among them, H5N1 is a highly pathogenic avian influenza virus, which was first detected in human in Hong Kong in 1997. After that, humans infection with avian influenza have occurred from time to time. As of December 2019, the global cumulative number of cases of human infection with H5N1 avian influenza arrives 861, with 455 deaths. Unlike H5N1, H7N9 is classified as a low pathogenicity avian influenza virus ^[2]. In March 2013, there was the first case of human infection with the H7N9 avian influenza virus in Shanghai, China. In the following weeks, this virus spread to several provinces and municipalities in mainland China. As of May 2017, H7N9 has resulted in 1263 human cases in China, of whom 459 died, with a mortality rate of nearly 37%. The frequent outbreak of avian influenza in the world not only brings a serious threat to human health, but also causes psychological panic and huge social impact, and brings a huge blow to the national economy. Therefore, it has been important to understand the dynamical behavior of avian influenza and to predict what may occur. Mathematical modeling has been a useful tool to describe the dynamical behavior of avian influenza and to obtain a better understanding of transmission mechanisms. Recently, many avian influenza models have been built from different perspectives (see ^{[2,3,4,5,6,7,8,9,10,11,12]} and references therein).

As we all know, there exist time delays during the spread of avian influenza, which can be used to describe not only the infection period of avian influenza virus in poultry (human) population, but also the incubation period of avian influenza in poultry (human) population and the immune period of recovered human to avian influenza. Therefore, the time delays should be considered such that the avian influenza models are more realistic. Generally speaking, delayed differential equations exhibit more complex dynamical behavior than differential equations without delay because time delay can make a stable equilibrium position to be unstable ^{[13,14,15,16]}. Consequently, it is of great interest to describe the transmission mechanism of avian influenza by introducing time delay into the models. For example, Liu et al. ^[7] and Kang et al. ^[12] established avian influenza models with different time delays in the poultry and human populations by considering the incubation periods of avian influenza virus and the survival probabilities of infected poultry and humans. By considering the existence of intracellular delay between initial infection of a cell and the release of new virus particles, Samanta ^[17] established a non-autonomous ordinary differential equation with distributed delay to characterize the spread of avian influenza between poultry and humans. These surveys imply that the research of time delay on avian influenza is a meaningful issue and is still open for study.

On the other hand, many existing literatures only focus on the deterministic avian influenza models that do not consider the impact of environmental noise. However, in the real world, the spread of avian influenza is often affected by the variations of environmental factors, such as humidity, temperature and so on ^[18,19]. Due to the fluctuations in the environment, an actual avian influenza system would not remain in a stable state, which would interfere with this stable state by acting directly on the density or indirectly affecting the parameter values. Therefore, it is of great significance to reveal the impact of environmental noise on avian influenza model by using stochastic model, so as to obtain more real benefits and accurately predict the future dynamics of avian influenza. To better understand the transmission dynamics of avian influenza, some authors have introduced stochastic perturbations into the deterministic models ^[20,21,22]. Zhang et al. ^[20] constructed a stochastic avian-human influenza model with logistic growth for avian population, and discussed the dynamical behavior of this model. Further, Zhang et al. ^[21] investigated a stochastic avian-human influenza epidemic model with psychological effect in human population and saturation effect within avian population. On the basis of the deterministic model established by Iwami et al. ^[3], Zhang et al. ^[22] established the corresponding stochastic model by introducing density disturbance. All the papers mentioned above only focused on the extinction and persistence of stochastic avian influenza models. However, to the best of our knowledge, there is no results related to the asymptotic behavior of stochastic avian influenza model around the equilibria of the corresponding deterministic model.

Motivated by the above discussions, in this paper, we investigate the asymptotic behavior of a stochastic delayed avian influenza model with saturated incidence rate. This work differs from existing results ^{[7,12,17,20,21,22]} in that (a) time delays and white noise are taken into account to describe the latency period of avian influenza virus in both poultry and human population and the environmental fluctuations; (b) asymptotic behavior of a stochastic delayed avian influenza model is studied. Overview of the rest of the article is as follows: In section 3, we show that there exists a unique global positive solution of system (2.3) with the given initial value (2.4). In section 4, we prove that the solution of system (2.3) is going around $ E^{0} $ under certain conditions. Further, we derive that the solution of system (2.3) is going around $ E^{*} $ under certain conditions in section 5. In section 6, some numerical examples are introduced to illustrate the effectiveness of theoretic results. Finally, some conclusions are given in section 7.

2.   Model description and formulation

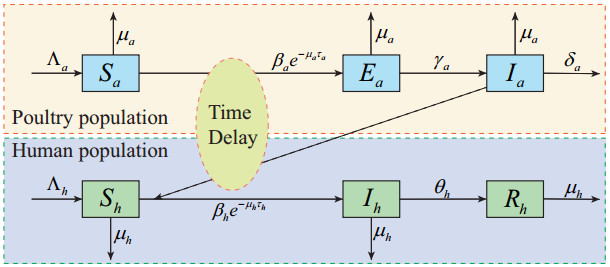
Although the avian influenza virus spreads between wild birds and poultry, and between poultry and humans, we will only consider the transmission dynamics of avian influenza between poultry and humans because poultry is the main source of infection. Moreover, we assume that the virus is not spread between humans and mutate. We denote the total population of poultry and humans at time $ t $ by $ N_{a}(t) $ and $ N_{h}(t) $, respectively. When the susceptible poultry contact with the infected poultry closely, there is usually no quick way to detect whether they are infected or the detection cost is too high, which makes it impossible to distinguish whether the close contacts of poultry are infected with the avian influenza virus. Therefore, the poultry population is divided into three sub-populations depending on the state of the disease: susceptible poultry $ S_{a}(t) $, exposed poultry $ E_{a}(t) $ and infected poultry $ I_{a}(t) $. The total poultry population at time $ t $ is denoted by $ N_{a}(t) = S_{a}(t) + E_{a}(t) + I_{a}(t) $. The human population is divided into three sub-populations, which are susceptible human $ S_{h}(t) $, infected human with avian influenza $ I_{a}(t) $ and recovered human from avian influenza $ R_{h}(t) $. The total population of human at time $ t $ is given by $ N_{h}(t) = S_{h}(t) + I_{h}(t) + R_{h}(t) $.

The reason why we do not consider the exposed class for human population is that the close contacts of human beings are usually isolated and tested to determine whether they are infected with the avian influenza virus. The poultry in $ E_a $ either shows symptoms after incubation period and move to $ I_a $, or always stays in $ E_a $ until natural death. The number of susceptible poultry (human) is increased by new recruitment, but decreases by natural death and infection (moving to class $ I_{a} $ ($ I_{h} $)). The number of infected poultry (human) is increased by the infection of susceptible poultry (human) and reduced through natural and disease-related death. In addition, the number of infected humans is also reduced by recovery from the disease (moving to class $ R_{h} $). Based on the above discussions, we obtain the schematic diagram of our model (see Figure 1).

The corresponding avian influenza model can be represented by the following equations:

All parameters in model (2.1) are assumed non-negative and described in Table 1.

Because the removed human populations $ R_{h}(t) $ has no effect on the dynamics of the first five equations, system (2.1) can be decoupled to the following system:

A realistic avian influenza system would not remain in this stable state due to environmental fluctuations. In this paper, we will reveal how the environmental white noise affects the spread of avian influenza through investigating the dynamics of a stochastic delayed avian influenza model with saturated incidence rate. Taking the same approach as the literatures ^[23,24], we assume that the environmental white noise is directly proportional to the variables $ S_a(t) $, $ E_a(t) $, $ I_a(t) $, $ S_h(t) $ and $ I_h(t) $, respectively. Then, corresponding to system (2.2), the stochastic avian influenza model with time delay is of the following form

in which $ B_{i}(t)\; (i = 1, 2, \cdots, 5) $ are mutually independent standard Brownian motions defined on a complete probability space $ (\Omega, \mathcal{F}, \bf{P}) $ with a filtration$ \{\mathcal{F}_{t}\}_{t \geq 0} $ satisfying the usual conditions (i.e., it is increasing and right continuous while $ \mathcal{F}_{0} $ contains all $ \bf{P} $-null sets), $ \sigma_{i}\; (i = 1, 2, \cdots, 5) $ denote the intensities of the white noises. The initial value of system (2.3) are

where $ \mathcal{C} $ is the Banach space $ \mathcal{C}([-\tau, 0]; \mathbb{R}_+^5) $ of continuous functions mapping the interval $ [-\tau, 0] $ into $ \mathbb{R}_+^5 $, and $ \mathbb{R}_+^5 = \{x = (x_{1}, x_{2}, x_{3}, x_{4}, x_{5}): x_{i} > 0, i = 1, 2, 3, 4, 5\} $. By a biological meaning, we assume that $ \varphi_i(0) > 0\; (i = 1, 2, 3, 4, 5) $.

3.   Existence and uniqueness of the global positive solution

In this section, we prove that the solution of system (2.3) is global and positive for any initial value (2.4).

Theorem 1. For any initial value (2.4), system (2.3) has a unique positive solution $ (S_a(t), E_a(t), I_a(t), S_h(t), I_h(t)) $ on $ t\geq 0 $ and the solution will remain in $ \mathbb{R}_+^5 $ with probability one, in other words, $ (S_a(t), E_a(t), I_a(t), S_h(t), I_h(t))\in \mathbb{R}_+^5 $ for all $ t\geq 0 $ almost surely.

Proof. Since the coefficients of system (2.3) satisfy the local Lipschitz conditions, then for any initial value (2.4), there exists a unique local solution $ (S_a(t), E_a(t), I_a(t), S_h(t), I_h(t)) $ on $ t\in [-\tau, \tau_e) $, where $ \tau_e $ is the explosive time. To show this solution is global, we only need to show that $ \tau_e = \infty $ a.s. To this end, let $ k_0 \geq 1 $ be sufficiently large such that $ (S_a(\theta), E_a(\theta), I_a(\theta), S_h(\theta), I_h(\theta))\; (\theta \in [-\tau, 0]) $ all lie within the interval $ [\frac{1}{k_0}, k_0] $. For each integer $ k\geq k_0 $, define the stopping time as

We set $ \inf \varnothing = \infty $. Obviously, $ \tau_k $ increasing when $ k\rightarrow \infty $. Let $ \tau_\infty = \lim_{k\rightarrow \infty} \tau_k $, where $ \tau_\infty \leq \tau_e $ a.s. If we can verify $ \tau_\infty = \infty $ a.s., then $ \tau_e = \infty $ and $ (S_a(t), E_a(t), I_a(t), S_h(t), I_h(t))\in \mathbb{R}_+^5 $ a.s. for all $ t\geq 0 $. That is to say, to complete the proof we only need to show that $ \tau_\infty = \infty $ a.s. If this assertion is not true, then there is a pair of constants $ T > 0 $ and $ \varepsilon \in (0, 1) $ such that

There exists an integer $ k_1 \geq k_0 $ such that

Define a $ \mathcal{C}^2 $-function $ V $: $ \mathbb{R}_+^5 \rightarrow \mathbb{R}_+ $ by

in which $ a $ and $ b $ are positive constants to be determined later. The nonnegativity of this function can be derived from $ x- 1- \ln x \geq 0 $ for any $ x > 0 $. Applying the Itô's formula to $ V $, we get

where

Choose $ a = \frac{\mu_a e^{\mu_a \tau_a}}{\beta_a} $ and $ b = \frac{\delta_a e^{\mu_h \tau_h}}{\beta_h} $ or $ a = \frac{\delta_a e^{\mu_a \tau_a}}{\beta_a} $ and $ b = \frac{\mu_a e^{\mu_h \tau_h}}{\beta_h} $ such that

Then, we can get

where $ K $ is a positive constant. It thus follows from (3.2) that

Integrating both sides of (3.3) from $ 0 $ to $ \tau_k\wedge T = \min\{\tau_k, T\} $ and then taking the expectation results in

Set $ \Omega_k = \{\tau_k \leq T\} $ for $ k\geq k_1 $, and according to (3.1), we have $ P(\Omega_k) \geq \varepsilon $. For every $ \omega \in \Omega_k $, there exists $ S_a(\tau_k, \omega) $ or $ E_a(\tau_k, \omega) $ or $ I_a(\tau_k, \omega) $ or $ S_h(\tau_k, \omega) $ or $ I_h(\tau_k, \omega) $ equals either $ k $ or $ \frac{1}{k} $. Therefore, $ V(S_a(\tau_k, \omega), E_a(\tau_k, \omega), I_a(\tau_k, \omega), S_h(\tau_k, \omega), I_h(\tau_k, \omega)) $ is no less either $ k-1-\ln k $ or $ \frac{1}{k}- 1- \ln \frac{1}{k} $ or $ k-a-a\ln \frac{k}{a} $ or $ \frac{1}{k}- a+ a\ln ak $ or $ k-b-b\ln \frac{k}{b} $ or $ \frac{1}{k}- b+ b\ln bk $.

Therefore, we have

It follows from (3.4) that

where $ 1_{\Omega_k} $ denotes the indicator function of $ \Omega_k $. Letting $ k\rightarrow \infty $, then

which leads to the contradiction. This completes the proof.

4.   Asymptotic behavior of system (2.3) around the disease-free equilibrium $ E^0 $

In this section, we will investigate the solution of system (2.3) around disease-free equilibrium $ E^0 $ under certain conditions. It is worthwhile to mention that, if $ \mathscr{R}_{0} = \frac{\beta_a \gamma_a\Lambda_a e^{-\mu_a \tau_a}}{\mu_a(\mu_a +\delta_a)(\mu_a +\gamma_a)} < 1 $, the deterministic system (2.2) is globally asymptotically stable around the unique disease-free equilibrium $ E^{0} = (S_{a}^{0}, 0, 0, S_{h}^{0}, 0) = (\frac{\Lambda_a}{\mu_a}, 0, 0, \frac{\Lambda_h}{\mu_h}, 0) $, but $ E^0 $ is not the equilibrium of the stochastic system (2.3). Thus, the result concerning the solution of stochastic system (2.3) around $ E^0 $ is presented by the following theorem.

Theorem 2. Let $ (S_a(t), E_a(t), I_a(t), S_h(t), I_h(t)) $ be the solution of system (2.3) with the initial value (2.4). If $ \mathscr{R}_{0} < 1 $ and the following conditions hold

then,

where

Proof. Since $ (S_a^0, 0, 0, S_h^0, 0) $ is the disease-free equilibrium of system (2.2), then

According to system (2.3), we can obtain that

and

Let $ V_1 = \frac{1}{2} \left(S_a -\frac{\Lambda_a}{\mu_a}\right)^2 $, then applying the Itô's formula to $ V_1 $, together with (4.1), we have

where

Similarly, let $ V_2 = E_a(t+\tau_a)+\frac{\mu_a+\gamma_a}{\gamma_a}I_a(t+\tau_a) + \frac{(\mu_a+\gamma_a)(\mu_a+\delta_a)}{\gamma_a} \int_t^{t+\tau_a} I_a(s)ds $, it follows from (4.2) that

Define $ \bar{V} = e^{-\mu_a \tau_a} V_1 + \frac{\Lambda_a}{\mu_a}V_2 $, then

Integrating both sides of (4.4) from $ 0 $ to $ t $ and taking expectation, we get

Therefore, we can obtain

Similarly, we define

then,

Let $ V_4 = V_3 + \frac{1}{2} (\mu_a + \gamma_a -\sigma_2 ^2)\int_t^{t+\tau_a} E_a^2(s)ds $, we get

Let $ V_5 = \frac{1}{2} I_a^2 $, the derivative of $ V_5 $ can be calculated as

The Young's inequality is used above. Let

which implies that

Integrating both sides of (4.5) from $ 0 $ to $ t $ and then taking expectation yields

Consequently, we can obtain

where $ M_1 $ and $ P_1 $ are defined in Theorem 2. Further, according to system (2.3), we have

and

Let $ V_6 = \frac{1}{2} \left(S_h-\frac{\Lambda_h}{\mu_h}\right)^2 $. Noting (4.6), we have

Let $ V_7 = e^{-\mu_h \tau_h} V_6 + \frac{\Lambda_h}{\mu_h} I_h(t+\tau_h) $, it follows from (4.7) that

Integrating both sides of (4.8) from $ 0 $ to $ t $ and then taking the expectation yields

therefore, we can get

Let $ V_8 = \frac{1}{2} \left[ e^{-\mu_h \tau_h} \left(S_h-\frac{\Lambda_h}{\mu_h}\right) + I_h(t+\tau_h)\right]^2 $, then

Defining

we get

Integrating both sides of (4.9) from $ 0 $ to $ t $ and taking expectation, we obtain

Consequently, we can obtain

where $ P_{2} $ is defined in Theorem 2. This completes the proof.

5.   Asymptotic behavior of system (2.3) around the endemic equilibrium $ E^* $

If $ \mathscr{R}_{0} > 1 $, there exists an endemic equilibrium $ E^* = (S_a^*, E_a^*, I_a^*, S_h^*, I_h^*) $ of system (2.2), but it is not the equilibrium of system (2.3), where $ S_a^* = \frac{\Lambda_a(1+\alpha_1 I_a^*)}{\mu_a(1+\alpha_1 I_a^*)+ \beta_aI_a^*} $, $ E_a^* = \frac{\beta_a \Lambda_a e^{-\mu_a \tau_a}I_a^*}{(\mu_a+\gamma_a)[\mu_a(1+\alpha_1 I_a^*)+ \beta_aI_a^*]} $, $ I_a^* = \frac{\mu_a (\mathscr{R}_{0}-1)}{\alpha_1 \mu_a + \beta_a} $, $ S_h^* = \frac{\Lambda_h(1+\alpha_2I_a^*)}{\mu_h(1+\alpha_2I_a^*)+ \beta_hI_a^*} $, $ E_a^* = \frac{\beta_h e^{-\mu_h \tau_h}S_h^*I_a^*}{(\mu_h+\delta_h+\theta_h)(1+\alpha_2I_a^*)} $. In this section, we show that the solution of system (2.3) is going around $ E^* $ under certain conditions.

Theorem 3. Let $ (S_a(t), E_a(t), I_a(t), S_h(t), I_h(t)) $ be the solution of system (2.3) with initial value (2.4). If $ \mathscr{R}_{0} > 1 $ and the following conditions hold

(i) $ \sigma_1^2 < \mu_a, \sigma_2 ^2 < \frac{1}{2} (\mu_a+\gamma_a), \sigma_3 ^2 < \frac{1}{2} (\mu_a+\delta_a), \sigma_4^2 < \mu_h, \sigma_5 ^2 < \mu_h+\delta_h+\theta_h $;

(ii) $ \max(\sqrt{P_{3}}, \sqrt{P_{4}}, \sqrt{P_{5}}, \sqrt{P_{6}}) < d(E^{*}, E^{0}) $,

then

where

Proof. Since $ (S_a^*, E_a^*, I_a^*, S_h^*, I_h^*) $ is the interior equilibrium of system (2.2), then

Define the Lyapunov function $ W_1 $ as $ W_1 = S_a-S_a^*-S_a^* \ln \frac{S_a}{S_a^*} $, from which we have

where

Similarly, we can define $ W_2 $ as

By using the Itô's formula, the derivative of $ W_2 $ is calculated as follows

Since $ x - 1 - \ln x \geq 0 $ for $ x > 0 $, the following estimate can be obtained

Substituting (5.4) into (5.3), we can get

Choose $ W_3 = W_2 + \frac{\beta_a e^{-\mu_a \tau_a} S_a^*I_a^*}{1+\alpha_1 I_a^*} \int_t^{t+\tau_a} \left(\frac{I_a(s)}{I_a^*} - \ln\frac{I_a(s)}{I_a^*} - 1\right)ds $. Therefore, $ LW_3 $ can be obtained as follows by using (5.5):

Noting that $ x - 1 - \ln x \geq 0 $ holds for $ x > 0 $, we also have

substituting (5.7) into (5.6) and using $ \frac{S_a}{S_a^*} + \frac{S_a^*}{S_a} -2 = \frac{(S_a -S_a^*)^2}{S_aS_a^*} $, we know that

Let $ W_4 = W_1 + \frac{1+\alpha_1 I_a^*}{\beta_a e^{-\mu_a \tau_a} I_a^*} \left(\mu_a + \frac{\beta_a I_a^*}{1+\alpha_1 I_a^*} \right)W_3 $. Applying the Itô's formula, together with (5.2) and (5.8), derives that

Choose Lyapunov function $ W_5 $ as $ W_5 = \frac{(S_a-S_a^*)^2}{2} $, then its derivative is

Let $ \bar{W} = W_5 + \frac{\beta_a S_a^* I_a^*}{\mu_a(1+\alpha_1 I_a^*)}W_4 $, one can derive that

Integrating both sides of (5.10) from $ 0 $ to $ t $ and then taking expectation yields

Then, we can get

where $ P_3 $ is defined in Theorem 3. Defining $ W_6 = \frac{1}{2} \left[ e^{-\mu_a \tau_a}(S_a-S_a^*) + E_a(t+\tau_a) -E_a^* \right]^2 $, the use of Itô's formula yields that

Let $ W_7 = W_6 + \left(\frac{\mu_a+\gamma_a}{2} -\sigma_2 ^2 \right) \int_t^{t+\tau_a}(E_a(s) -E_a^*)^2ds $ and $ W_8 = \frac{1}{2} (I_a -I_a^*)^2 $. We have

and

Let $ \tilde{W} = W_7+ \frac{e^{-\mu_a \tau_a}}{\mu_a - \sigma_1 ^2} \left(\frac{2\mu_a^2 +2\mu_a\gamma_a +\gamma_a^2}{2(\mu_a +\gamma_a)} +\sigma_1 ^2 \right)\bar{W} + \frac{ (\mu_a+\delta_a) (\mu_a+\gamma_a-2\sigma_2 ^2)}{2\gamma_a^2} W_8 $. Making use of (5.10), (5.11) and (5.12) yields that

Integrating both sides of (5.13) from $ 0 $ to $ t $ and then taking expectation yields

Therefore, we can obtain

where $ L_{1}, L_{2} $ have been defined in Theorem 3. Taking $ U_1 = \frac{1}{2}(S_h - S_h^*)^{2} $, we have

Integrating both sides of (5.14) from $ 0 $ to $ t $ and then taking expectation, we get

Therefore, we can obtain

Let $ U_2 = \frac{1}{2}[I_h(t+\tau_{h}) - I_h^*]^{2} $, we have

Let $ \overline{U} = \frac{\beta_h^{2}(I_a^*)^{2}}{2(\mu_h-\sigma_4 ^2)(1+\alpha_2I_a^*)^{2} (\mu_h+\delta_{h} +\theta_{h} -\sigma_5 ^2)}U_{1}+U_{2} $, then

Let $ U_{3} = \frac{\mu_h+\delta_{h}+\theta_{h}-\sigma_5 ^2}{2}\int_t^{t+\tau_{h}} (I_h(s) - I_h^*)^{2} ds $, we obtain

Let $ \widetilde{U} = \overline{U}+U_{3} $, then,

Integrating both sides of (5.15) from $ 0 $ to $ t $ and then taking expectation, we have

Therefore, we can obtain

where $ P_{6} $ has been defined in Theorem 3. The proof is completed.

6.   Numerical simulation

This section is devoted to illustrating the theoretical results by numerical examples. The parameters of system (2.3) are selected as in Table 2, $ \alpha_1 $ and $ \alpha_2 $ are varying parameters that is taken value from $ 0.001 $ to $ 0.1 $, and $ \sigma_1 = 0.01, \, \sigma_2 = \sigma_3 = \sigma_5 = 0.04, \, \sigma_4 = 0.008 $. The initial conditions of system (2.3) are $ S_a(\theta) = 3,000,000, E_a(\theta) = 1,000, I_a(\theta) = 10, S_h(\theta) = 1,000, I_h(\theta) = 5, \, \theta\in[-\tau, 0] $. The Milstein method ^[25] is used to obtain the discrete form of system (2.3) as follows:

where $ \xi_i(k) \sim N(0, 1) (i = 1, \cdots, 5; k = 1, 2, \cdots) $ are independent Gaussian random variables. Initially, we study the effect of $ \mathscr{R}_0 $, which, by Theorems 4.1 and 5.1, can govern the asymptotic behavior.

Example 1 Effect of basic reproduction number $ \mathscr{R}_0 $.

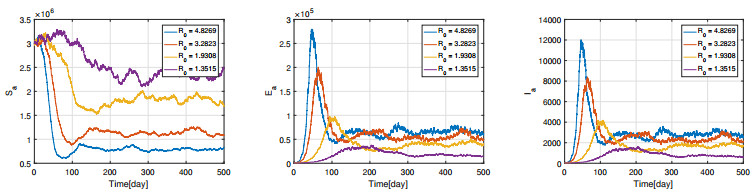
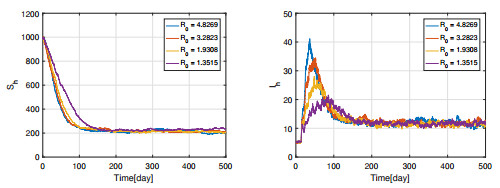
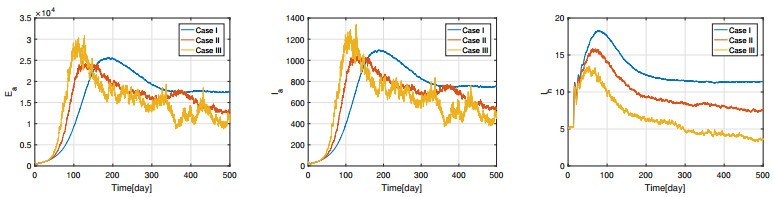
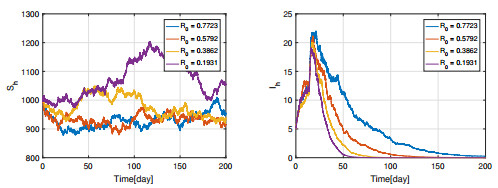
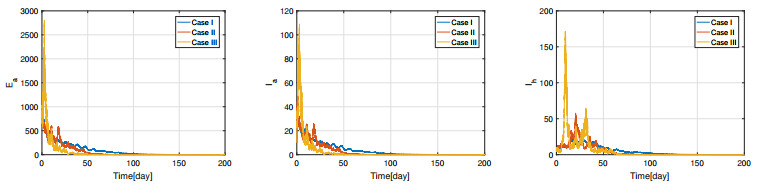
Choose different $ \beta_a $ such that $ \mathscr{R}_0 $ take different values, which are shown in Table 3. Since $ \sigma_1^2 = 10^{-4} < \mu_a = 10^{-2}, \sigma_2^2 = 0.0016 < \frac{1}{2} (\mu_a+\gamma_a) = 0.155, \sigma_3^2 = 0.0016 < \frac{1}{2} (\mu_a+\delta_a) = 5.01, \sigma_4^2 = 0.000064 < \mu_h = 0.0078, \sigma_5^2 = 0.0016 < \mu_h+\delta_h+\theta_h = 0.1978 $, the condition (ⅰ) of Theorem 3 is satisfied. From Table 3, we see that for each $ \mathscr{R}_0 $, the inequality $ P_{m} < d_E $ holds, which means the condition (ⅱ) of Theorem 3 is also satisfied. Thus, all the conclusions of Theorem 3 hold. It follows from Table 3 that the change of $ \mathscr{R}_0 $ can result in different values of $ E^* $, which also illustrate the value of $ E^* $ is related to $ \mathscr{R}_0 $. By the discrete form of system (2.3), the numerical results under different $ \mathscr{R}_0 $ are presented by Figures 2 and 3 when $ \mathscr{R}_0 > 1 $, which show that the solution of system (2.3) goes around the endemic equilibrium $ E^* $. The effectiveness of Theorem 3 is also indicated by these two figures. In addition, we can see from Figures 2 and 3 and Table 3 that the number of infected poultry and humans will reduce with the decrease of $ \mathscr{R}_0 $. On the other hand, in order to explore if the results of Theorem 3 hold, we enhance the intensity of perturbation as $ \sigma = (\sigma_1, \cdots, \sigma_5) = (0.02, 0.08, 0.08, 0.016, 0.08) $ (Case Ⅰ: condition (ⅰ) of Theorem 3 is satisfied but condition (ⅱ) is not satisfied), $ \sigma = (0.06, 0.24, 0.24, 0.048, 0.24) $ (Case Ⅱ: Both conditions (ⅰ) and (ⅱ) are not satisfied) and $ \sigma = (0.10, 0.40, 0.40, 0.080, 0.40) $ (Case Ⅲ: Both conditions (ⅰ) and (ⅱ) are not satisfied). The simulation results are presented in Figure 4, which are obtained by computing the average of 800 simulations. The equilibrium of corresponding deterministic model is $ E^* = (2.3931\times10^{6}, 1.8254\times10^{4}, 0.7812\times10^{3}, 227.3975, 11.5855) $. From Figure 4, we see that the curves will move away from the equilibrium point $ E^* $ with the increasing of intensity of perturbation, which violate the conclusions of Theorem 3.

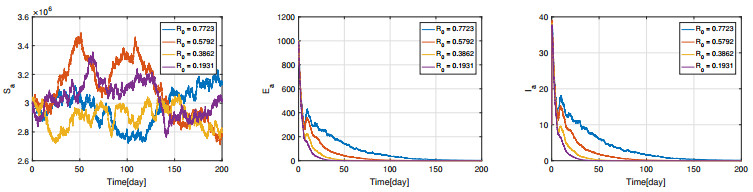
According to the values of $ \sigma_1, \cdots, \sigma_5 $ and the parameters values in Table 2, we easily verify the conditions of Theorem 2 are satisfied. Therefore, from Theorem 2 we know that the solution of system (2.3) will go around the disease-free equilibrium $ E^0 $ when $ \mathscr{R}_0 < 1 $. The numerical simulation results of $ \mathscr{R}_0 $ are presented in Figures 5 and 6. These figures show $ E_a, I_a $ and $ I_h $ all go to zero when $ \mathscr{R}_0 < 1 $, which illustrate the effectiveness of the theoretical results in Theorem 2. Meanwhile, Figures 5 and 6 also show that the rate of $ E_a, I_a $ and $ I_h $ converges to zero is increasing with the decrease of $ \mathscr{R}_0 $. The conditions of Theorem 2 are only a sufficient ones, so we want to know whether the conclusions of Theorem 2 hold when the intensity of perturbation increase such that these conditions are not satisfied. Thus, we choose $ \sigma = (\sigma_1, \cdots, \sigma_5) = (0.02, 0.08, 0.08, 0.016, 0.08) $ (Case I), $ \sigma = (0.06, 0.24, 0.24, 0.048, 0.24) $ (Case II) and $ \sigma = (0.12, 0.48, 0.48, 0.096, 0.48) $ (Case III), and the simulation results are presented in Figure 7. Figure 7 shows $ E_a, I_a $ and $ I_h $ converge to zero for each cases, so the results of Theorem 2 also hold.

Example 2 Effect of time delays $ \tau_a $ and $ \tau_h $.

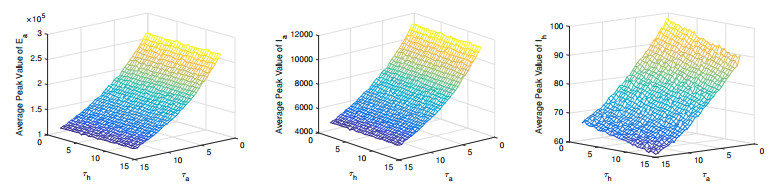
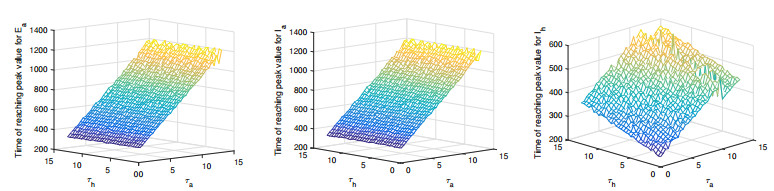
In order to study the effect of time delays, we consider the average peak values of $ E_a $, $ I_a $ and $ I_h $, and the time of reaching average peak values by $ 300 $ simulation runs. The simulation results are shown in Figures 8 and 9. It follows from Figure 8 that the increase of time delay $ \tau_a $ or $ \tau_h $ can reduce the peak value of both infected poultry and human population. Meanwhile, from Figure 9, we know that the large time delay also lead to the delay of reaching peak value. Thus, we may conclude that time delays have significate influence for the spread of avian influenza. According to the practical meaning of $ \tau_a $ and $ \tau_h $, related department can adopt some measures to increase the spread delay to suppress the outbreak of influenza, such as isolation. In addition, the adopting of those control measures will win time for taking drug control.

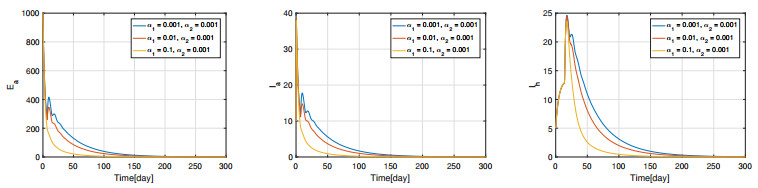
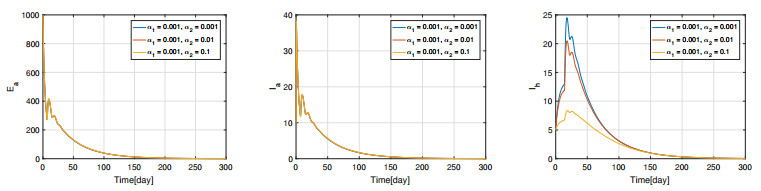
Example 3 Effect of saturation constants $ \alpha_1 $ and $ \alpha_2 $.

According to the analysis of Introduction, the saturation constants $ \alpha_1 $ and $ \alpha_2 $ are important parameters for avian influenza. We thus explore the effects of $ \alpha_1 $ and $ \alpha_2 $ in this example. In order to explore the effect of $ \alpha_1 $ under fixed $ \alpha_2 $, we run 1000 simulations and take their average values. The results are shown in Figure 10. It follows from Figure 10 that $ \alpha_1 $ can influence the rate of convergence to the equilibria of the poultry population, while it can not significantly influence the rate of convergence to the equilibria of the human population. In addition, we study the influence of $ \alpha_2 $ under fixed $ \alpha_1 $. The simulation results are presented in Figure 11, which implies that $ \alpha_2 $ can not change the rate of convergence to the equilibria of the poultry population. Figure 11 also means that $ \alpha_2 $ can not increase the rate of convergence to the equilibria of the human population, but it can evidently reduce the peak value of $ I_h(t) $. In summary, $ \alpha_1 $ and $ \alpha_2 $ have evidently influence to the spreading of avian influenza among both avian and human population.

7.   Concluding remarks

In this paper, we establish a stochastic delayed avian influenza model with saturated incidence rate. To begin with, we investigate the existence and uniqueness of the global positive solution to the system (2.3) with any positive initial value (2.4). Since there is no equilibrium point in the system (2.3) at this time, thus, the asymptotic behaviors of the disease-free equilibrium and the endemic equilibrium are given by constructing some suitable Lyapunov functions and applying the Young's inequality and Hölder's inequality. Theorem 2 shows that if $ \mathscr{R}_0 < 1 $, then the solution of system (2.3) is going around $ E^0 $ while from Theorem 3, we obtain that if $ \mathscr{R}_0 > 1 $, then the solution of system (2.3) is going around $ E^* $. Finally, some numerical examples are given to illustrate the accuracy of the theoretical results.

There are some interesting issues deserve further investigations. On the one hand, we can formulate some more realistic but complex avian influenza models, such as considering the effects of Lévy jumps or impulsive perturbations on system (2.3). On the other hand, the coefficients in our model studied in this paper are all constants. If the coefficients are with Markov switching, how will the properties change? We leave these investigations as our future work.

Acknowledgments

The research was supported by the National Natural Science Foundation of China (11661064), Ningxia Natural Science Foundation Project (2019AAC03069) and the Funds for Improving the International Education Capacity of Ningxia University (030900001921).

Conflict of interest

The authors declare that they have no conflict of interest.