Stability of a delay equation arising from a juvenile-adult model

1.   Introduction

In the case of the species are under the threat of extinction, scientific researches have been focused on evaluating the possibility on the population of the species will grow back to its previous size. Allee effect for social mammals was first introduced by ^[1], but since then the concept has been extended to a wide range of organisms. The Allee effect explains a situation in which low numbers of species are influenced by a positive interaction between population growth rate and size, which raises their probability of extinction. On this subject, a lot of attention has been paid to the corresponding spatial dispersal versions of predator-prey systems with strong Allee effect, and the spatiotemporal pattern formation has been studied in such systems. Under the influence of the Allee effect, the dynamics of the system can significantly change as chaotic patches or traveling population pulses ^[2,3]. Recently, pattern formation of a diffusive predator-prey model under the effect of strong Allee effect ^[4], pattern dynamics in prey-predator system is also focused by ^[5,6]. Most of the current trend of literature leaves the issue of the process of prevention when the population experiences extinction. Petrovskii et al. ^[7] also studied the Allee effect as a possible lagging mechanism between introduction and establishment. They found that, for a particular set of parameters, there are three forms of regimes when the invasive prey affected by the Allee effect. One of them is ‘regimes of anomalous extinction’. As a comparison to this extinction, it is shown in this study that extinction is delayed by a gradient that contributes to the linear term of predator mortality.

It can be mentioned in some studies about population dynamics that highlight the possibility of extinction or invasion of a particular species ^[8,9,10] and/or possible changes in the population structure ^[11,12] were established. With the development of the gradient analysis ^[13,14], spatial patterns have been reported in some literature ^{[15,16,17,18,19,20]}. In another study, this issue is considered by taking the diffusion coefficient as the spatial gradient for the predator-prey system ^[19]. In particular, herbivore dynamics are examined under the effect of gradient ^[20]. Taking the spatial gradient as one of the system parameters, i.e., the rate of growth of the prey, is described by ^[21]. However, the literature covers considerable progress on the issue of the spatial gradient. The effect of the spatial gradient on the system parameters to avoid an approaching extinction is ignored. Consequently, this issue remains somewhat unclear when the environmental conditions are not acceptable for sustainable species. Hence, the species move through space from unsuitable conditions to suitable one to survive. From this point of view, the increase in temperature caused by climate change and therefore the habitat becomes inappropriate for the organisms' survival forces them to migrate and adapt to new environments. This ecological issue constitutes the main purpose of this study.

Species challenge against to get rid of extinction. For this reason, species prefer to adapt instinctively or move to a new habitat to improve resistance against extinction due to their survival instincts. We can safely say that habitat change and beachhead are considered as a response to climate change. The new discovery by Jonkers et al. ^[22] has revealed the results of climate change on the aquamarine life in the oceans. This research has shown that climate change leads to migration of marine zooplankton communities in consequence of 12 years of research by ^[23]. However, we can also give the paper studied by Pecl et al. ^[24] as an evidence. They suggested that the first response of species is to shift their location to climate change to the cooler or warmer locations where the species last their life in a more suitable conditions for preventing extinction.

A large number of theoretical models have been proposed to study the spatial pattern of population dynamics and interactions ^{[4,5,6,25,26,27,28]}. Although considerable progress has been made in understanding the spatial distribution of many species, some of the important issues remain obscure. One of these important issues is the gradient effect on systems' spatial distributions. There are several works in the literature on the gradient effect of spatial patterns. The continuous distribution of species through environmental gradient is described with the development of the gradient analysis ^[13,14]. It is stated that spatially heterogeneous patterning can be described by the spatial gradient response of individuals ^[16,17,18]. Pascual found the spatial gradient to be taken into account both in terms of prey and predator diffusion in ^[19]. At the same rate of diffusion, the distribution of species is concentrated along the spatial gradient ^[29]. In particular, Post ^[20] focuses on the spatial gradient effect on herbivorous population dynamics. Geographical patterns and ecological speciation processes across environmental gradients of spatially structured populations are described in ^[15]. The spatial gradient of the prey growth rate is studied to demonstrate the stability of the system in ^[21]. Apart from the several apparent works, the spatial gradient continues to be literally an issue of vital importance.

The current literature on the gradient impact on system dynamics does not pay enough attention to the event that species face extinction, while environmental conditions for sustainable species survival are not sufficient. For this reason, this work revisits the prey-predator model where prey growth is dampened by the strong Allee effect introduced in ^[7] with the intention of further establishing the species persistence/extinction issue. The present paper extends that study to the case in which the mortality rate of the predator is spatially varying; that is, the mortality rate is given by a spatial function as a response to climate change.

In particular, the biological relevance here is that if individuals threatened by unsuitable environmental conditions are foreseen to result in extinction, whether species continue to diffuse along a spatial gradient in the direction of unsuitable conditions, e.g., more resources, suitable climate conditions, and less predation, etc. Therefore, the focus of this work about concerning this issue, the following scenarios are concentrated: whether the extinction of the species can be prevented or at least postponed to a distant future. In the case of extinction, if it happens, is there any warning before extinction? Obtained numerical results show that when the system is on the verge of extinction the pattern of spatio-temporal oscillations becomes completely regular with fixed period and amplitude. This can serve as an early warning ^[30,31,32].

The issues mentioned above are addressed by mathematical modelling. This begins with the question, even if the decreasing level of predator mortality hampers the growth of prey whether the spatial gradient has the power to prevent extinction. Therefore, the starting point of the predator mortality rate is taken where the system has an extinction without gradient case. Importantly, as an early warning signal, the system produces a regular distribution when the system is near to its extinction point which is why the obtained results are compatible with our previous climate change work performed on the oxygen-plankton model system ^[31,33]. On the other hand, one of the most important stages of species movement is the ‘beachhead’, i.e., the establishment of an invader as a self-sustaining community ^[34]. In this sense, the prey predator system ^[7] is redefined by expanding the system with gradient and beachhead, taking this change in the system as a result of rising temperatures, i.e., climate change.

In brief, in this work a diffusion-reaction model describing predator-prey interactions are studied. Gradient and beachhead are used as precautions when the species faces extinction by adding a spatial gradient to the mortality rate of the predator. Based on extensive numerical simulations and analytical observations, it is revealed that the spatial structure gives some early warning signals, i.e., regular distribution when the predator mortality rate is closer to the extinction point.

In light of the above, the paper is structured as follows. In Section 2, the predator-prey model system is revisited, suggesting that the predator mortality rate decreases linearly. In Section 3, the spatial system is analyzed in one-dimensional and two-dimensional case through comprehensive numerical simulations focused on the system parameter space. The obtained numerical results show that species' extinction is followed by regular pattern formation in the spatial system; see a similar pattern as a response to climate change in ^[31,32,35]. System persistence/extinction map is given in parameter plane $(x_1, \omega)$ for different domains correspond to species' extinction and persistence. In particular, it is established that for the different choices of initial distributions for prey and predator, the spatial distribution of the system does not change and retains its extinction point where the entire system is extinct. The most important observation of this work is that the movement of species as a precaution to change in climate, i.e., addition of a spatial gradient and beachhead, can not stop the extinction. But this movement in space slow down the approaching extinction so that the species can continue to exist for a while. Finally, in the last section, the potential significance of this work is discussed.

2.   Mathematical analysis of the model

We consider one dimension predator prey model, studied earlier in ^[7,36,37,38]:

where $h$ is the densities of prey and $p$ the densities of predator at moment $T$ and position $X$ ^{[39,40,41,42]}. $d_1$ and $d_2$ are the diffusion coefficients and the value of $\kappa$ is the food utilisation. The functions $F(h)$ and $f (h, p)$ describe prey multiplications and predations, respectively. The last term $\mu p$ describes predator mortality. Holling type II functional response ^[7,26,43,44] is used for predator response:

where $A$ is intensity for predation and $b$ is half saturation value. The prey population is assumed to be damped by the Allee effect and parameterized as follows ^[45]:

where $k$ is the carrying capacity, $r$ is the per capita growth rate for the intensity of Allee effect defined by $h_0$. Systems' dynamical structure is studied in detail with the stress of Allee effect in ^[7]. For more detailed explanations on the system parameter, see ^[7]. The system (2.1-2.2) is in a dimensional form. The dimensionless form of parameters is as

Eqs. (2.5 and 2.6) includes five dimensionless parameters instead of nine with the choice

We consider one dimension predator prey model, studied earlier in ^[7,36,38]:

For more details on system parametrizations and its dimensionless version see ^[7].

2.1.   Equilibrium analysis

The nonspatial counterpart of the system becomes:

The steady state of the system (2.5-2.6) is a solution of the following equations:

One of the states is extinction $E_1 = (0, 0)$ is always stable for any values of parameters. Other is semi-trivial equilibrium $E_2 = (\beta, 0)$, $E_3 = (1, 0)$, extinction of predator case. Stability of the predator-free steady state is saddle. For more information on the stability of these boundary states and the phase plane of the system see ^[7]. The other steady state of the system is the coexistence one $E_4 = (u, v)$. The steady state of the coexistence system is:

Jacobian matrix of the system (2.5-2.6) is as follows:

The eigenvalues are the solutions for the characteristic equation for each of the steady states:

where $I$ is the unit matrix and $J_{i}$ is the matrix (2.9) with the components calculated at the steady state ${E_i}$, $i = 1, 2, 3, 4$. For further details on the stability analysis can be found in ^[7]. The system is addressed by numerical simulations with different parameter values and initial conditions, species extinction thresholds with and without spatial gradient is studied.

2.2.   Model in the spatial system

The spatially extended version of the model is as follows:

Here $u$ and $v$ are the densities of prey and predator, respectively, at time $t$ and position $x$. It should be emphasized here that the diffusion coefficients are chosen equal, i.e., $d_1/d_2 = 1$ in order to reduce the number of system parameters. However, it should be clarified that this was not a primary restriction and the specific value $d_1 = d_2$ was chosen. Preliminary numerical simulations for the range of $0.5-2$ for $\epsilon$ have shown that all the obtained regimes still exist ^[7]. Arbitrary choice of the initial conditions is not consistent with the inherent properties of the system ^[46]. So the choice of the system initial conditions should, therefore, correspond to its biological equivalents. In this case, the initial distribution of the species can be represented as a finite support function based on the assumption that foreign species are attacked by an exotic species. The initial conditions, therefore, can be taken into account ^[7]:

where $u_0$, $v_0$ are the initial population densities and $\Delta_u$, $\Delta_v$ correspond the initially invaded domain radius. This type of initial conditions in Eqs. (2.12 and 2.13) also refers to the biological control issue ^[47,48,49]. On the other hand to see the response of spatial distribution to different initial conditions, another type of condition used in our earlier work for the oxygen-plankton system ^[31,33,35] is taken into account. For this case, it is assumed that at the beginning of the spread, the domain already contains both populations at the density level corresponding to stationary state $(\tilde u, \tilde v)$ with the introduction of a linear disruption to the predator distribution. We therefore have the following constant gradient form, i.e.,

where $\tilde u$, $\tilde v$ are the steady states of the system dynamics, given by Eq. (2.15), with $\epsilon = 0.001$ and $x_0 = 200$, i.e., auxiliary parameters ^[50].

To identify the behavior of the system, extensive numerical simulations performed in ^[7] and the systems' parametric dependencies are sketched perfectly. In the light of this work, Eqs. (2.10 and 2.11) is set numerically on the $0 < x < L$ domain by finite difference method using zero–flux boundary conditions. The steps of the numerical mesh are chosen as $\Delta x = 0.5$ and $\Delta t = 0.01$. Since we are mainly interested in spatial gradient effect on system dynamics, we keep the system parameters as in ^[7] (see Figure 5 in ^[7]) to use the bifurcation diagram of the systems shown for $\alpha = 0.5$, $\beta = 0.28$, $\gamma = 7$, $\Delta_u = 5$, $\Delta_v = 3$, $u_0 = 1$, $v_0 = 1$ and $L = 400$.

2.3.   Gradient & ‘beachhead’ as a precaution to extinction

As it is detailed in the introduction, when the surrounding environmental conditions are not favor of species and even also these conditions bring the species to the edge of extinction, species propagate in space to sustain their existence to avoid this environment. In ^[7], the prey-predator system is addressed on the basis that prey development is damped by a strong Allee effect, but with no attention to species persistence/extinction scenario under the effect of a spatial gradient. The rate of zooplankton mortality, i.e., $\delta$, is quantified differently in this study. The mortality rate is specified as a function of space to determine the species precautions for potential unsuitable environmental conditions. Suppose that the species move away to get rid of unsuitable environmental conditions. We then consider $\delta = \delta(x)$, but keep the other parameters unchanged.

Animal movements are affected by some external forces, one of which is the spatial forces, such as the fragmented habitat ^[51], slope ^[52], beachhead ^[34], etc. One of the important stages of the invasion is the ‘beachhead’, i.e., the establishment of an invader as a self-sufficient population. At least these variables should be included in the ‘realistic’ $\delta(x)$ function, but it becomes quite complicated. Since the purpose of this study is to reveal species' precautions, in this case, it is spatial movement, we consider the mortality rate to be a linearly decreasing function, assuming that spatial movement facilitates predator abundance, i.e., mortality rate of predator decrease in space. black The reason behind choosing predator mortality rate to decrease beyond a critical point threaten the system with extinction is that this choice increases the predator size to the point that the prey is pushed below the Allee effect threshold which results in extinction for both prey and predator. Hence the main purpose here is to show the dynamics become persistence under the influence of the spatial gradient in predator mortality rate despite the Allee effect. The possible simplest choice of $\delta$ is given as follows:

Here, $x_1$ is beachhead, $\delta_L$ is predator mortality rate before the spatial movement starts, and the $\omega$ quantifies the slope of the spatial gradient. Here this study aims to understand species' persistence/extinction rather than species' migration in detail, the simplest scenario in this context is to consider spatial gradients considering a decrease in predator mortality in space.

Therefore, we compare two possible approaches. The first is without a spatial gradient scenario, i.e., $(\omega = 0)$. Second is with the case of the spatial gradient, i.e., with the effect of the spatial gradient, the mortality rate decreases $(\omega > 0)$, and taking into account the beachhead as well. In particular, for the initial death rate of the predator, we find $\omega$ from appropriate range corresponding to the phase plane structure in (Figure 14 in ^[7]) and keep the system parameters as in ^[7] to see the species distributions under the effect of this new approach. It should be emphasized here that, contrary to ^[7], $\delta$ is taken as a function of space for the system (2.10-2.11).

To analyze the spatial stability of equilibrium points based on the knowledge of temporal system linearization method is used ^[53].

Theorem 2.1. The trivial equilibrium $E_1$ is stable if $w(x-x_1) < l^2 d_2 + \delta_L$. The semitrivial equilibrium $E_2$ is stable if $d_1 > \tilde{d_1}$, where $\tilde{d_1} = \frac{\gamma \beta (1-\beta)}{l^2}$ and with given condition 2.21. The boundary equilibrium $E_3$ is stable if $d_1 > d_1^{\star}$, where $d_1^{\star} = \frac{\gamma (\beta-1)}{l^2}$ and given stability condition 2.22 is satisfied.

Proof. Let $u = \hat u +M$, $v = \hat v+N$, where $M$ and $N$ are perturbations around an arbitrary equilibrium point $(\hat u, \hat v)$. The linearized form of the system (2.10-2.11) can be given as

where $a_{11} = 2\gamma \hat u-3\gamma {\hat u}^2-\gamma \beta + 2 \gamma \hat u \beta - \frac{\hat v}{(1+\alpha \hat u)^2}$, $a_{12} = -\frac{\hat u}{1+\alpha \hat u}$, $a_{21} = \frac{\hat v}{(1+\alpha \hat u)^2}$, $a_{22} = \frac{\hat u}{1+\alpha \hat u}-\delta$. The eigen function is $\sum_{r = 0}^{\infty} \begin{pmatrix} a_r\\b_r \end{pmatrix}exp(\lambda t + i l x)$ for the wave number $l > 0$ and the growth rate of perturbation $\lambda > 0$, $x$ is the spatial coordinate for reals $a_r, b_r$. General uniform steady state of the spatial system (2.10-2.11) by $(\hat M, \hat N)$, we have the perturbation in the following form,

$\begin{pmatrix} M(t, x)\\ N(t, x) \end{pmatrix} = \begin{pmatrix} \hat M\\ \hat N \end{pmatrix}+\begin{pmatrix} \epsilon_1\\ \epsilon_2 \end{pmatrix} e^{\lambda t +i l x}$

$\epsilon_i$ are assumed to be small enough and the corresponding amplitudes for $i = 1, 2$. Then the problem is reduced to eigenvalue problem in the parameter $\lambda$ for the following matrix at $(\hat M, \hat N)$.

The eigenvalues evaluated at $E_1$ are $-\gamma \beta - l^2 d_1 < 0$ and $-\delta-l^2 d_2$. Since the main point of this work is to reveal the species extinction and persistence issue by taking predator mortality rate as a linear dependence in space, the term $-(\delta_L-\omega (x-x_1))-l^2 d_2$ should be less than zero for stable $E_1$. Hence, $-(\delta_L-\omega (x-x_1))-l^2 d_2 < 0$

It means that if the condition 2.20 is satisfied the system will then collapse and the all species extinct. The eigenvalues evaluated at $E_2$ are $\gamma \beta (1-\beta)-l^2 d_1$ and $\frac{\beta}{1+\alpha \beta}-\delta-l^2 d_2$. This boundary state is spatially stable if $d_1 > \tilde{d_1}$, where $\tilde{d_1} = \frac{\gamma \beta (1-\beta)}{l^2}$ and

is satisfied. The eigenvalues evaluated at $E_3$ are $\gamma \beta-\gamma - l^2 d_1$ and $\frac{1}{1+\alpha}-\delta-l^2 d_2$. This boundary state is spatially stable if $d_1 > d_1^{\star}$, where $d_1^{\star} = \frac{\gamma (\beta-1)}{l^2}$ and with the condition

is satisfied. The coexistence steady state characteristic equation is of the form

where $Q_1 = -a_{11}+l^2(d_1+d_2)$, $Q_2 = a_{21}+l^4(d_1+d_2)-l^2 d_2 a_{11}$. The stability of coexistence state and the sustainability of the species is detailed in numerical simulations. Note that in numerical simulations taking $d_1 = d_2 = 1$ is a technical consequence of being dimensionless form.

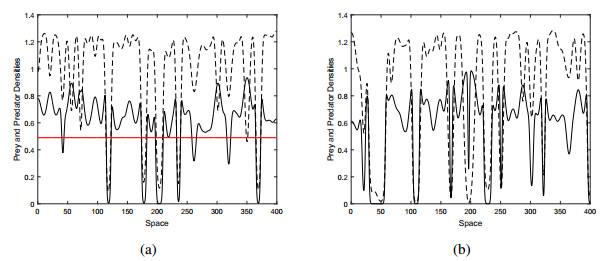
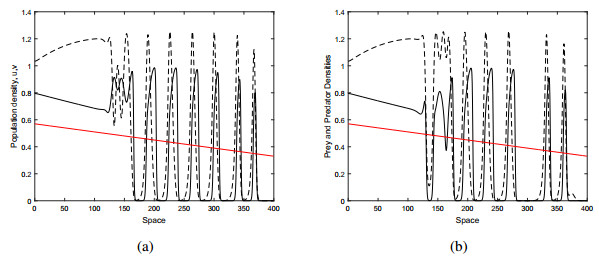
Under the light of above analytical calculations, we start with the response of the systems to different initial conditions. Figure 1a, b show the spatial distributions of predator and prey for the obtained initial conditions given by Eqs. (2.12 and 2.13) and Eq. (2.14), respectively. There is no important qualitative difference between distributions provided by Eqs. (2.12 and 2.13) (shown in Figure 1a) and given by Eq. (2.14) (shown in Figure 1b). It indicates that taking Eqs. (2.12 and 2.13) as shown in Figure 1a and using it as the initial conditions does not allow any qualitative difference to the inherent spatial structures. The following simulations will, therefore, operate with the initial condition provided by Eqs. (2.12 and 2.13). Red solid lines in all numerical simulations show $\delta$ value to see the changes of $\delta$ in space. In general, the red line is shown in the first figures for the same parameter choice.

3.   Numerical simulations

The purpose of this study is to describe the effect of spatial gradient and beachhead on species when the species are faced with unsuitable environmental conditions and these conditions lead to extinction. It is assumed that $\delta$ can change in space with the help of the gradient. Let us begin with the case where $\delta$ is taken from a safe region (i.e., Figure 14 in ^[7]). Since $\delta$ is predator mortality a small quantity of it places a great deal of pressure on its prey. As a consequence, low $\delta$ leads to the extinction of species. That's the point this research has been activated. Therefore, however, the issue is whether the spatial gradient and the beachhead prevent or postpone the eventual extinction even if its population is driven by its predator which is inevitable without a gradient case. For this purpose, the numerical simulations follow the order; first, observing the spatial distribution without a gradient case with the aim of finding the critical value of extinction. Second, beginning from this extinction point and introducing gradient and beachhead to the system to detail species persistence/extinction issue despite the Allee effect. Then some numerical observations on two dimensional space are performed.

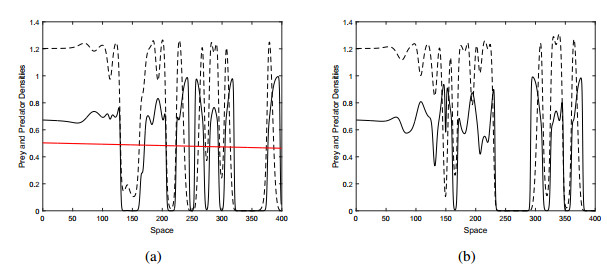
Figure 2 shows the distribution of prey and predator at different times. We note the species invades the whole domain with irregular spatiotemporal oscillations of fixed values of $\delta$. System dynamics is sustainable and extinction is not observed even for longer periods (i.e., $t = 20000$ equivalent simulations are not given for brevity reasons). Note that there is no smooth pattern due to lack of gradient, i.e., $\omega$. Figures 2 and 3 are provided to display the correspondence of the results obtained by a slight decrease in $\delta$, which is detailed and observed in ^[7].

Figure 3 shows snapshots of prey and predator spatial distributions obtained at different times for $\omega = 0.0001$, $\delta_L = 0.49$ and beachhead $x_1 = 133$. For this value of $\delta$, there may be two somewhat different scenarios with invasive species with irregular spatiotemporal oscillations and moving patches (cf. ^[7] how invasive species can be established and general invasive behavior for the corresponding domain). The first scenario is shown in Figure 3a. With a slight slope, i.e., $\omega$, the distributions of the species in $\delta$ do not change at different times. Such irregular patterns are connected to the condition of coexistence (smooth pattern) behind it. The second scenario is shown in Figure 3b, with the same value as $\delta$ but for larger time limits the irregular distribution appears like a series of separate patches. At larger times ($t > 5000$) the system tends to give way to distinctly divided patches but this scenario is not seen here for the sake of brevity.

We now proceed to simulations to obtain an extinction threshold of species without a gradient case. The extinction value is meager in the phase plane map in ^[7], to observe that extensive numerical simulations performed. Note that the obtained numerical simulations indicate that the pattern of distribution when the system approaches its extinction value is regular, i.e., the spatial system gives certain early warning signals for potential extinction. Such findings support the regular patterning of critical transition approaches such as in the oxygen-plankton model ^[31] and in other systems ^{[28,30,54,55,56,57,58]}.

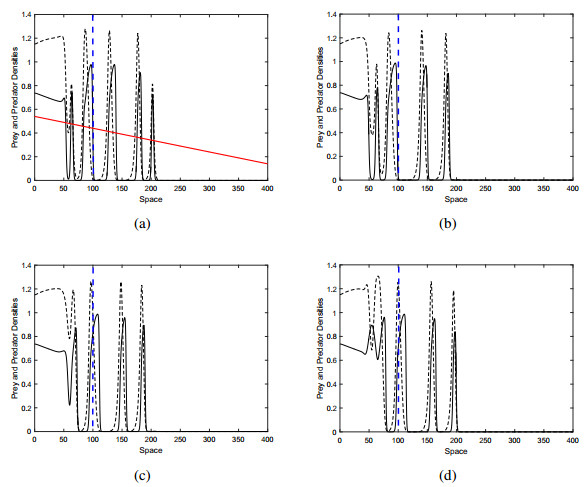
Figure 4a, b show the prey and predator distributions obtained for different values of $\delta$ and Figure 4c is for the power spectrum analysis for the prey distribution of Figure 4b. It is observed that species' extinction happens when the system reaches a critical value of $\delta_{cr} = 0.44$. Therefore the $\delta$ values that are used for Figure 4a, b bring the system close to its extinction value so the system is invaded by regular patterning. Contrary to ^[46], regular oscillations continue for longer periods of time. Figure 4c shows the analysis of the power spectrum as evidence that the system (2.10-2.11) is capable of developing regular spatial patterns. The question here is what is called ‘regular spatial distribution’ is actually regular or irregular. In this case, the analysis of the power spectrum should be taken into account, and the system is accepted as a regular if the analysis of the power spectrum has some leading frequencies. For the regular structure see Figure 4b, some of the leading frequencies are readily distinguishable, see Figure 4c. This regular structure emerges as an early warning signal and says the system is the edge of extinction, see the earlier work on the early warning signal and the regime shift ^[31,56,58]. Note that taking $\delta$ values from a given range of $(0.44, 0.45]$ always results in regular species spatial distributions.

Since the issue of species extinction/persistence is interested, the gradient and the beachhead have been taken into account here. This implies that $\delta_{cr}$ (where the prey and predator species is extinct) is used as a starting point to see whether the gradient and the beachhead can prevent extinction.

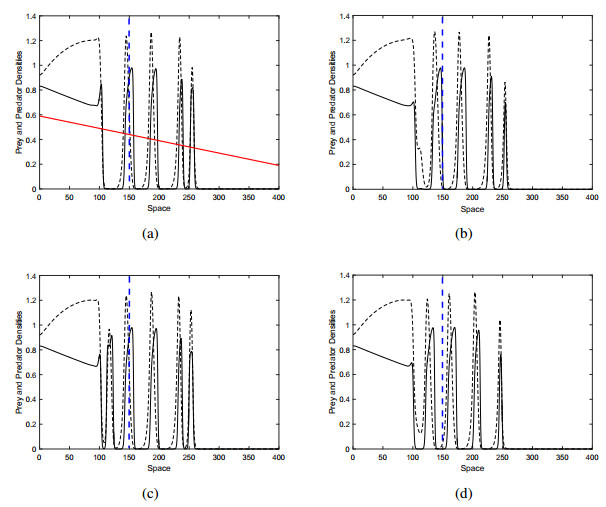
The above results are demonstrated to show the spatial distribution of the system with and without $\omega = 0$ and $x_1$. The following simulations are considered when the system is affected by the gradient of space and the beachhead.

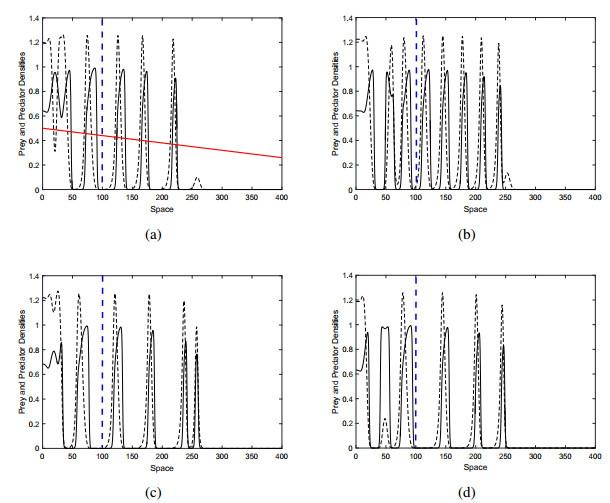
Figure 5 shows the population density snapshots. The vertical blue dashed line indicates the assumed beachhead value. It is important to note here again that, without a spatial gradient, the species is extinct, but for the given parameter $\omega = 0.001$and provided beachhead $x_1 = 100,$ the species propagate through traveling pulses with irregular wavemakers (see system Figure 5 in ^[7]). Traveling pulses die when the system is closer to the critical value of $\delta$. When the traveling pulse reaches this critical point in space (importantly this critical value of $\delta$ is totally different from $\delta_{cr}$, when we call a new settlement of $\delta$ as $\delta_{cr^{\star}}$, it is obvious that $\delta_{cr^{\star}} < \delta_{cr}$, the system results in the first extinction of prey followed by the extinction of predators. Note that, $\delta_{cr^{\star}}$ is to be the place along with the space-axis beyond which neither prey nor predator exists. The system (2.10-2.11) is maintained for a sufficiently long time ($t = 20000$) and the population retains its spatial distributions and does not get extinct. With a decrease in $\omega$ (i.e., $\omega = 0.0006$), in Figure 6 the beachhead stays the same as before (Figure 5, i.e., ($x_1 = 100$)), the region with a smooth spatial distribution disappears and the area is occupied by non-stationary pulses.

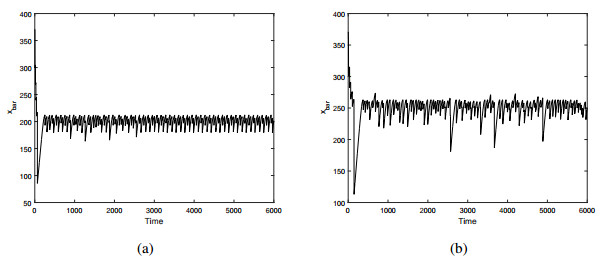
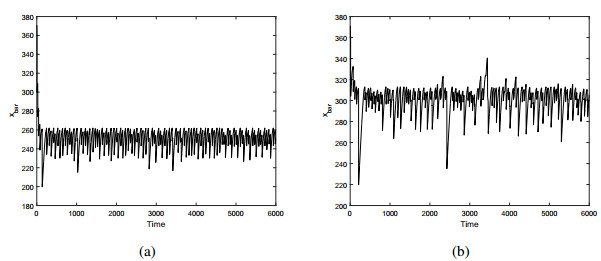
There seems to be a common behavior in all species' spatial distribution that traveling pulses disappear where the system reaches $\delta_{cr^{\star}}$. It may be worth looking at details. It is, therefore, determined to detect the positions of the traveling pulse when it comes to near extinction, i.e., when the prey density is sufficiently small $(u > \epsilon$ where $\epsilon = 0.02)$. The general tendency of predators to extinction is qualitatively close to prey, therefore, we display only distribution of prey to avoid repetition. Figure 7a, b show the extinction position of the traveling pulses in space (i.e., ${x}_{bar}$) for Figure 5 and Figure 6 for $t = 6000$, respectively. As can be easily seen in Figure 7a, the extinction range can be limited to ${x}_{bar} \approx 180$ and ${x}_{bar} \approx 270$. The restriction is clear for $\omega = 0.001$, but there are some lower peaks for $\omega = 0.0006$. It implies that, in some situations, the traveling pulses extinct earlier in space than the general tendency of the system. Interestingly extinction exceeds the value of the beachhead for both slope values so it happens beyond the vertical blue line, i.e., the beachhead.

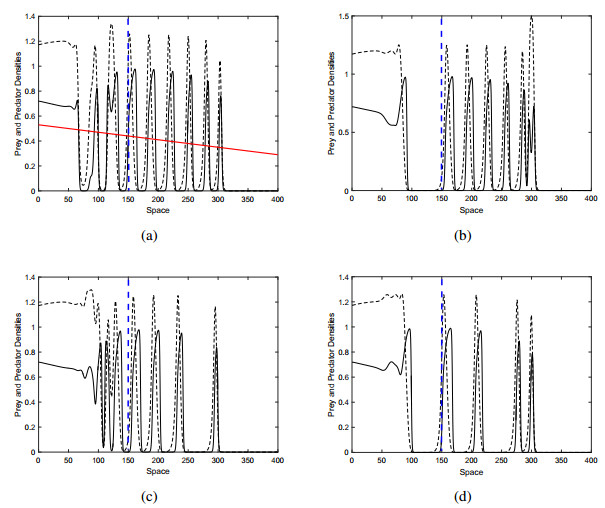
Figure 8 shows the population density snapshots for the given parameter $\omega = 0.001$ and different beachhead from above, i.e., $x_1 = 150$. In Figure 8, traveling pulses are extinct beyond the beachhead and also the scenario is the same more or less. Figure 9 shows snapshots for $\omega = 0.0006$ in the same manner. Figure 10a, b show the extinction position of traveling pulses in space of different values of $\omega$. Once, extinction exceeds the value of the beachhead for both slope values so extinction happens beyond the vertical blue line, i.e., the beachhead. This issue will be discussed in the last section.

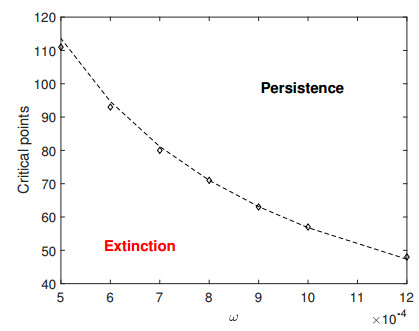
Applying a different spatial gradient with the aid of the slope, i.e., $\omega$, and the beachhead, i.e., $x_1$, an important question emerges as to whether there is any relation between the beachhead and the slope. Figure 11 shows the data point set, where the diamonds represent the extinction position for the corresponding $\omega$ collected as a result of numerous numerical simulations. There is therefore a relationship between the critical point (beachhead) and the spatial gradient defined by simple rational function, i.e., $\frac{1}{\omega ^{\alpha}}$ where $\alpha = 1$. The dashed line in Figure 11 plays a role as a separator of extinction and persistence regions. Thus, the area below the dashed line refers to the species extinction, while above it is the case where the population survives. Therefore, the persistence of the species can be determined by the simultaneous effect of the gradient slope and beachhead. If the slope rises, the extinction region of the species will decline. In this case, even if the beachhead is taken big enough, the species is not extinct.

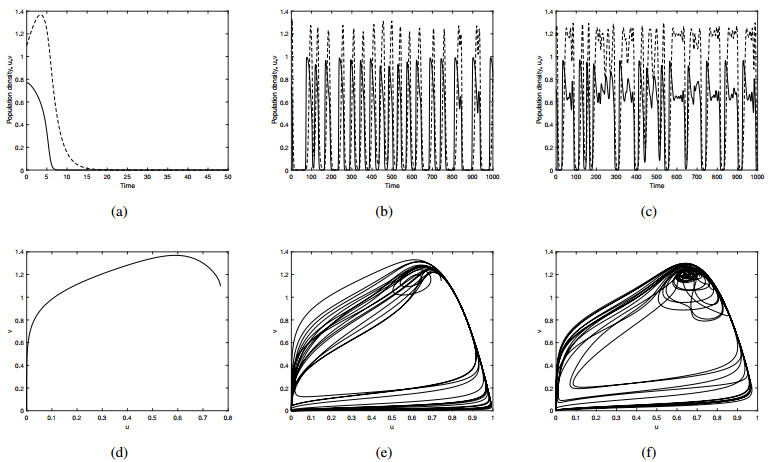
Figure 12 is given to provide more details on temporal variations of population. Figure 12a–c indicate the local dynamics at fixed spatial positions typical for different parameter domains, i.e., extinction and persistence. Figure 12d–f show the phase plane of the local population densities obtained at a fixed position at space $x_1 = 50$, i.e., the system below the dashed line in the extinction region, $x_1 = 94$, i.e., the system on the slightly above extinction threshold. As it is observed in spatial distribution, the temporal distribution at closer to critical point results in regular distribution. Note that for $\omega = 6 \times 10^{-4}$, the threshold value is $x_1 = 93$, see Figure 11 for more detail. $x_1 = 150$, i.e., the system in the persistence region above the dashed line.

Now attempts are being made to create the predator-prey system's spatial dynamics, applied to two spatial dimensions, which are more realistic than its one spatial dimension counterpart. The corresponding two-dimensional simulations coincide with its one-dimensional counterparts, the boundary and the initial conditions are selected accordingly. Therefore, all two dimensional simulations are performed in a rectangular domain: $(x, y) \in [0, L_x] \times [0, L_y]$ at the domain boundaries Neumann boundary conditions are used,

The spatial distribution of prey density is given in a two-dimensional system. Predator density demonstrates qualitatively similar behavior to prey, which is why the distribution of prey is provided only for the sake of brevity. To observe the distribution of prey, different types of initial conditions are used. The first one (see Figure 13) given by Eqs. (3.2 and 3.3) defines spatially homogeneous prey distribution at steady state with constant gradient predator distribution for $\omega = 0.0006$, $\delta_L = 0.44$ and $x_1 = 100$ where $u_0 = v_0 = 1$, $\epsilon_2 = \epsilon_3 = 3.10^{-5}$.

In the latter case, the system's initial distribution is as follows:

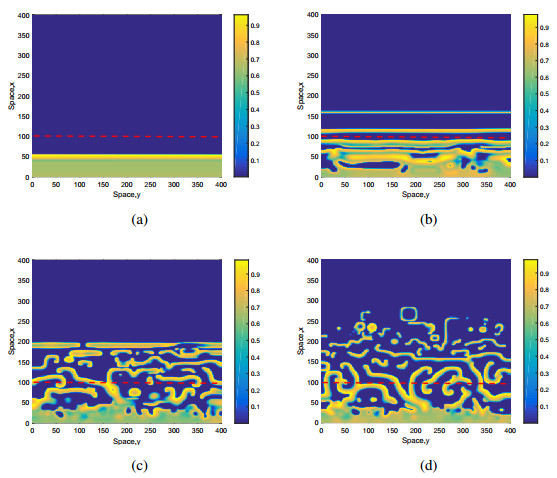
The two-dimensional system dynamics follow more or less the same scenario as the corresponding one-dimensional system. At an early stage (see Figure 13a), a smooth distribution of prey appears. This smooth distribution is followed by stripes corresponding to the traveling pulses in one dimension case, see Figure 13b. Eventually, the stripes are broken and give way to irregular structure in Figure 13c. The irregular structures swell and produce some circular shape and some broken irregular stripes, see Figure 13d. Observed that even for a larger time limit the upper part of the domain is not invaded regardless of the different initial condition, which ensures that the prey distribution stays close to zero.

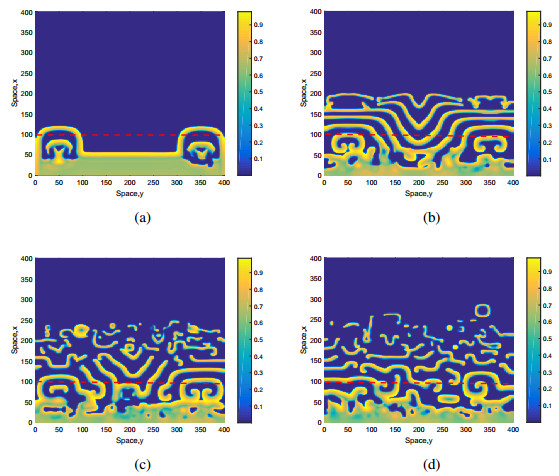
The second one (see Figure 14) given by Eqs. (3.4 and 3.5) describes the spatially homogeneous distribution of prey at its steady state with a constant gradient of predators. $\omega = 0.0006$, $\delta_L = 0.44$ and $x_1 = 100$ with $u_0 = v_0 = 1$, $\epsilon_1 = 2.10^{-7}$, $\epsilon_2 = 3.10^{-5}$, $\epsilon_3 = \epsilon_4 = 6.10^{-5}$. Note that the initial predator mortality rate, i.e., $\delta_L = 0.44$, is based on its one–dimensional case. The only difference between Figure 13 and Figure 14 is the choice of the initial distributions. It can be inferred that there is no qualitative difference between the different initial conditions and the general the tendency of the spread of species. In both cases, the typical sequence of events is the smooth distribution that produces stripes, the stripes are followed by their broken versions and then the domain is invaded by irregular structures, like circular shapes, parts of broken stripes, etc.

It is noticed that the spatial patterns shown in Figures 13 and 14 exist in the parameter range where the species persistence would not be possible in the corresponding one dimensional case (i.e., for $\delta_L = 0.44$). It is, therefore, consistently observed that the dynamics of the two-dimensional system is persistent/sustainable in a broader range ^[35].

4.   Discussion & concluding remarks

In this work a predator-prey reaction diffusion model is studied with an Allee effect on the prey. The model is based on earlier work Petrovskii et al. ^[7], in which the conditions under which the predator-prey system could invade an environment were studied. The present manuscript extends that study to the case in which the mortality rate of the predator is spatially varying; that is, the mortality rate is given in Eq. (2.16) by the function $\delta = \delta_L-\omega (x – x_1)$ where $\delta_L$ is a constant, $\omega$ is the slope, $x$ is distance along the x-axis, and $x_1$ is what is termed the ‘beachhead' that the invading predator-prey system can establish. Therefore, in relation to changing climate, the dynamics of the prey-predator system is assumed to reflect the spatial gradient of predator mortality rate. The objective of this study is to determine the joint effect of the slope of the gradient and the ‘beachhead’, that is, the points along the spatial axis at which the system, despite the Allee effect, can establish a sustainable population as an adaptation mechanism to new environment.

Some interesting results are observed. One is that there is a simple inverse algebraic relationship between the slope of the gradient and critical point. This is found by allowing $\delta_L$ to take the value $0.44$, which is the threshold point for extinction if there is no slope, i.e., $\omega = 0$. Another is that, under circumstances when the system is on the verge of extinction, for example, $\delta_L$ slightly above $0.44$ and $\omega = 0$, the pattern of spatiotemporal oscillations becomes completely regular with a fixed period and amplitude. This can serve as an ‘early warning signals' of changing climate ^[31] that the system is on the verge of extinction if $\delta_L$ decreases further.

Gradient and beachhead are used as a precaution as species face extinction by applying a spatial gradient to the predator mortality rate. This predator prey system has a well-structured parameter plane is labeled in ^[7]. The structure of the system's spatial dynamics with linearly decreasing values of $\delta$ in space is described by comprehensive numerical simulations. The difference of this study from the literature is that the rate of predator mortality changes with space to account for the response to changing climate. It is observed that despite the Allee effect, the species can establish a sustainable population. Such spatial structure provides some early warning signals (i.e., regular distribution) when the rate of predator mortality is closer to the extinction point. As observed in the oxygen-plankton system ^[31,33] when the system is close to extinction, transitions from irregular distribution to regular one which is used for the early warning signal of climate change are also observed for this system.

Note that, the emergence of pulses due to the spatial decrease in $\delta$ corresponds to its non-gradient case phase plane map; see Domain 2 and $2^*$ in Figures 13 and 14 ^[7]. Here, it can be seen that the traveling pulses die when the system becomes closer to the critical value of predator mortality rate, i.e., $\delta$. When the traveling pulse reaches the critical point in time, the species are extinct.

It is observed that the persistence of the species can be interpreted by the slope (steepness) of the spatial gradient and the length of the beachhead. If the slope is raised, the persistence of the system is expanded. In this case, if the beachhead becomes sufficiently large, the species becomes extinct (see the systems' extinction tendency in Figure 11, i.e., a further increase in $\omega$ results in extinction). On the other hand, the gradient addition does not prevent extinction but at least postpones it and allows the species a chance to exist for a while. One of the most interesting results of this work is that the spatial gradient can not prevent the extinction of species, at least for the spatial gradient on prey mortality but it has the capacity to slow down the approaching extinction. Interestingly, when the system reaches its critical value resulting in extinction beyond this value, its spatial distribution becomes regular and compatible with the structure which was obtained in the oxygen-plankton system ^[31].

The one dimension to two dimensions spatially explicit extension is considered. Here, it is shown that the dying traveling pulse in 1-D is represented as broken propagating stripes in 2-D. It should also be emphasized that different choice of initial distributions for both 1-D and 2-D case, spatial system patterns remains qualitatively similar.

In conclusion, the most interesting question here is whether the spatial gradient of different slopes can protect the species from extinction as climate change adversely affects species. This question is verified in this work with extensive numerical simulations, with the choice of large enough $\omega$, and for specific beachhead values, while leaving certain parameters set for convenience. It is observed that, at least for this system (2.10-2.11), a gradient can not stop an inevitable ecological disaster, but has capability to slow it down, which is why the species has a chance to survive for a while.

Acknowledgements

The author is thankful to Sergei Petrovskii (University of Leicester) for his stimulating discussions at the all stages of this study. Useful comments from editor and reviewers are appreciated.

Conflict of interest

The author has no conflict of interest.