The Ecology and Evolutionary Biology of Cancer: A Review of Mathematical Models of Necrosis and Tumor Cell Diversity

1.   Introduction

In general, the definition of a public good is intertwined with the conditions of its existence or production by the Government or Private sector in terms of optimality or efficiency and the matter of who decides for the production of the particular good. Moreover its importance and attributes such as externalities must be examined previously (Samuelson, 1964) as at a latter point from his initial definition (Samuelson, 1954; 1955) he considered public goods to be polar cases of positive externalities (Samuelson and Nordhaus, 2009).

Pigou's definition of externality is the case where "… one person A, in the course of rendering some service, for which payment is made, to a second person B, incidentally also renders services or disservices to other persons C, D and E of such a sort that technical considerations prevent payment being exacted from the benefited parties or compensation being enforced on behalf of the injured parties" (Pigou, 1929) recommending the application of subsidies/taxes to the other persons in order to correct the resource allocation distortion (Pigouvian subsidies ("bounties")/taxes is a form of bilateral taxation) where taxes would be used to finance subsidies in the case of zero administrative costs (Pigou, 1947). There are two types of externalities, technological, where its actions impact on firm B's production function (Scitovsky, 1954), and pecuniary, where actions of firm A involuntarily either raise factors or lower product price for firm B. By following either Pareto optimality arguments (Bator, 1958) or the definition of efficiency set by Holcombe and Sobel (2001) pecuniary externalities are seen to be efficient and no tax/subsidy action need be taken. In a modern setting an externality occurs when some of the costs or the benefits of a good or service are passed onto or "spill over to" someone other than the immediate buyer or seller (McConnell et al., 2012). According to Coase, externalities can be resolved in terms of a rearrangement of legal rights as a result of bargaining (Coase, 1960).

Wicksell in 1896 supported Government ownership of public utilities which would operate at a loss covered by taxation so that their goods or services would be available to a maximum number of individuals, if not all (Wicksell, 1958). In 1924 Sax, based on previous work, defines public goods as "collective needs" that "intend and create conditions of welfare which extend to all members of the community and benefit each alike as if they existed for each alone" which "should be achieved in the greatest measure at the least cost to each" by the Government while "it is the aim of politics to realize an equilibrium between private and collective needs"(Sax, 1887; 1958). Another initial definition of public goods was furnished by Musgrave "the public economy itself will undertake to supply only those goods and services in the production of which it is superior to private enterprise" (Musgrave, 1939) while public goods are those "goods the inherent quality of which requires public production"(Musgrave, 1959). Bowen termed them "social goods" which are indivisible, contrary to private goods, as they become part of the "general environment" and cannot be allocated according to individual demand subject to taste while their total volume is "set by a single (collective or political) decision applicable jointly to all persons " (Bowen, 1943).

The widely accepted definition of a public good is due to Samuelson, that of being a non-excludable and/or (Holcombe, 2000) non-rival good in consumption (Samuelson, 1954; 1955), who studied the authors mentioned above (Samuelson, 1954). This is provided by the Government under a Pareto optimality ensuring condition involving marginal rates of transformation i.e. marginal opportunity costs (Samuelson, 1954) going beyond mere public expenditure as Musgrave pointed out (Musgrave, 1969).

Global Public Goods are defined as "issues that are broadly conceived as important to the international community, that for the most part cannot or will not be adequately addressed by individual countries acting alone and that are defined through a broad international consensus or a legitimate process of decision-making" (International Task Force on Global Public Goods, 2006).

Government provision under the condition of high institutional quality, in terms of bureaucracy among others, is effective, though this does not extend to low income countries (Arora and Chong, 2018). Based on Samuelson's definition, it was shown to hold true at local level that "government provision of public goods need not take a back seat to the private sector" (Tiebout, 1956) and that the revealed preference problem pointed out by Samuelson can be modeled by the government to have zero individual information cost versus an existing cost in collective choice models (Clarke, 1971).

Judging from the classical examples of public goods, e.g. defence or lighthouses, a public good is perceived to take form by some planned process and as a result gains the attribute of a variable in economic theory.

This research paper addresses in a theoretical way the classification as a public good of the entity stemming from Solar Power, as it is not the result of a manufactured process and hence it does not possess in a manifest way the attributes of an economic good. Such an entity may be a public good as " a 'public' good is not necessarily publicly provided. Often, it is provided by no one." (Samuelson and Nordhaus, 2009). To facilitate this, Solar power is defined as a physical entity in a new mathematical way, it is shown that it is an Economic Good and Property Rights and Economic Ownership are shown to exist. Further, its Externalities and Valuation are analysed. To separate it from classical public goods, as it has the additional attribute of reducing pollution relative to other electricity producing fuels, a new definition of a Green Public Good is introduced. In structure it is a superset of the classic definition as it includes a part referring to the climate in the sense of diminishing pollution which is considered to be a negative externality (World Bank Group, 1998).

2.   Determination of the main economic nature of Solar Power

2.1.   Solar Power: physical properties and definition

The irradiance at earth's top atmosphere at zero zenith angle is 1370 W/m2 ± 6 W/m2 (Wald 2018) and the correspondence with irradiance at the earth's surface is as follows:

Table 1.  Irradiance at azimuth angles on the top of the atmosphere and at ground level (Wald, 2018).

Azimuth Angles	0°	30°	60°
Irradiance at atmosphere top	1354	1174	673
Irradiance at ground level	1045	885	464
Clearness Index	0.77	0.76	0.69

---

 | Show Table

DownLoad: CSV

Where the azimuth angle is the angle in the horizontal plane to the horizontal projection of the sun's rays measured from north (Cheng et al., 2019) and the Clearness index is defined as the ratio of the global solar radiation measured at the surface to the extraterrestrial solar radiation (Iqbal, 1983).

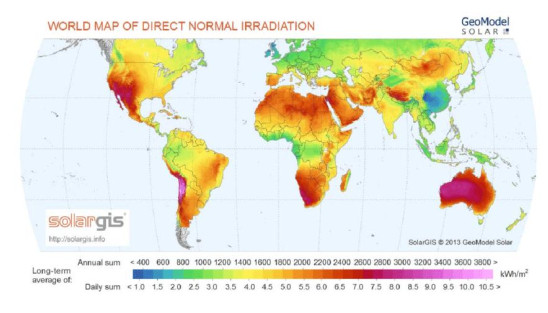
The irradiance distribution per hour (kWh/m²) at ground level is as below:

Figure 1.  World map of direct normal irradiation adapted from (Moghimi, 2017).

DownLoad: Full-Size Img PowerPoint

Where direct normal irradiation occurs with appropriate tilting of the measurement panel.

Carbon intensity for Solar Power in electricity production, which is not due to emissions during electricity production but due to the emissions of the manufacturing of the electricity production over a 25-year emission amortization calculation, denoted by C_a, varies from 20 to 40 gCO₂/kWh in Europe but increases to 80 gCO₂/kWh in China where machinery manufacture is based on coal. Also, the intensity of displaced grid power produced by coal denoted by C_R varies from 900 gCO₂eq/kWh in India to around 500 gCO₂eq/kWh in the UK (Nelson et al., 2014).

As Solar Power electricity production does not produce carbon emissions the total net carbon intensity associated with a kWh production should be related with the displaced quantity's carbon intensity

which is a quantity varying according to national boundaries.

Based on the above the definition of Solar Power is: Solar Power is the radiation in terms of kWh/m² that impacts Earth's surface at clear sky conditions at regions above a prescribed level of daily kWh/m² with carbon intensity CI.

Let $\overset{\vee }{\mathop{W}}\,$ represent a prescribed irradiance level band selected from Figure 2, $\overset{\vee }{\mathop{A}}\,$ an international/national land agglomerate each part with a determining geographic coordinate set and nationality index and $\overset{\vee }{\mathop{CI}}\,$ represent the vector corresponding to the nationality index in $\overset{\vee }{\mathop{A}}\,$. Then we can represent a geographically defined Solar Power "bundle" with a triplet ($\overset{\vee }{\mathop{W}}\,$, $\overset{\vee }{\mathop{A}}\,$, $\overset{\vee }{\mathop{CI}}\,$) where the quantities in the triplet are related. If a particular $\overset{\vee }{\mathop{W}}\,$ is selected then $\overset{\vee }{\mathop{A}}\,$ is determined as well and since $\overset{\vee }{\mathop{CI}}\,$ is a function of $\overset{\vee }{\mathop{A}}\,$ so is $\overset{\vee }{\mathop{CI}}\,$. If $\overset{\vee }{\mathop{A}}\,$ is selected then $\overset{\vee }{\mathop{W}}\,$ and $\overset{\vee }{\mathop{CI}}\,$ are determined. Finally, if $\overset{\vee }{\mathop{CI}}\,$ is selected $\overset{\vee }{\mathop{W}}\,$ and $\overset{\vee }{\mathop{A}}\,$ are determined. This leads to the fact that there exist invertible functions f, g such that

The triplet allows for the creation of the distribution of $\overset{\vee }{\mathop{W}}\,$ over a parcel of transnational land which will include the variation of $\overset{\vee }{\mathop{CI}}\,$ and its full pictorial decomposition is a portion on the map in Figure 2 on the x-y plane while the z axis will depict $\overset{\vee }{\mathop{CI}}\,$

Further, a bundle $\left(\overset{\vee }{\mathop{W}}\, , \overset{\vee }{\mathop{A}}\, , \overset{\vee }{\mathop{CI}}\, \right)$ may be decomposed into sub-bundles

where ${{\overset{\wedge }{\mathop{w}}\, }_{j}}$, ${{\overset{\vee }{\mathop{c\mathit{\iota }}}\, }_{j}}$ are quantities which are associated with ${{\overset{\vee }{\mathop{a}}\, }_{j}}$ and

Due to its nature a bundle is non-transportable.

2.2.   Solar Power as an economic good

In general, there is a growing tendency to stop defining "consumption of nature" as income which led to the implication that it consists of free goods (Tabb, 2007).

Pigou defined economics as "that part of welfare which can be brought directly or indirectly into relation with the measuring rod of money" (Pigou, 1929). According to Lord Robbins economics may be defined as "the science which studies human behaviour as a relationship between ends and scarce means which have alternative uses" (Robbins, 1932).

In the Pigouvian case the Solar Power definition furnished in this paper is clearly a part of welfare as it has at least indirect relation with the "measuring rod of money" since it serves as fuel, a factor of production, for power generation via a variety of photovoltaic processes (Hosenuzzaman et al., 2015) and has macroeconomic effects such as value added, GDP, welfare and employment (IRENA and CEM, 2014).

Lord Robbins' definition is interpreted as being of a spatially global character. As such, the "prescribed level" introduced in the Solar Power definition leads to conditions of scarcity of output in terms of kWh/m² in regions below that level as it is non-transportable and the distribution is globally not isotropic, partly following in spirit the argument presented regarding the definition of water as a good (Perry, et al., 1997). In addition, Solar Power in terms of its nature as irradiance has alternative uses e.g. in agriculture, health, as a source of light etc.

Hence Solar Power fulfils the conditions of an economic good.

2.3.   Property rights and economic ownership associated with Solar Power

Solar Power is not the result of a preplanned economic process, however the moment it begins its existence, according to the definition when it "impacts the Earth's surface", it becomes part of the legal property rights associated with that surface, contrary to the opinion expressed by White (2015), in whatever form they may exist-private, collective, government and open with varying control which may include rights to use and rights to regulate (Starrett, 2003) and if they exist, as an economic good. This economic good is free and clear of every economic dysfunction it may have caused during its descent to the surface, as this descent is by happenstance which cannot be attributed to the property rights owner and as for its existence in this stage, in the immortal words of U.K. Supreme Court Judge Thurlow, "it has no soul to be damned and no body to be kicked" just like a corporation (Poynder, 1844). As it is an economic good it has the character of opportunity in terms of a "course of action that is possible and worth pursuing" (DeBono, 1978) or a "chance to meet an unsatisfied need that is potentially profitable" (Hulbert et al., 1997) more or less in similarity to unprocessed fuel deposits. The distinguishing characteristic of this kind of opportunity is that potentially it exists for a very long period of time, contrary to the bounded time associated with the existence of most opportunities.

On the other hand the economic owner is the person who exercises control over the asset and ultimately benefits from its use (Central Statistical Office of Ireland, 2013), who in this case is the same with the person holding the legal property rights, unless it is otherwise mandated.

2.4.   Externalities and valuation

2.4.1.   Externalities

As Samuelson pointed out in his answer to the pro-cable TV argument (Minasian, 1964), before proceeding to examine whether an action is subject to social or market mechanisms, its "importance and various features such as externalities etc." must be considered, to which we add its total valuation, relegating the final decision to society (Samuelson, 1964).

To be able to consider externalities a production function in which energy carbon equivalence enters must be considered. Such a Cobb-Douglas function is (Zhao, 2011)

where α, β, γ < 1, Y is GDP, A is productivity, K is capital, L is labour, E is energy and ε represents the agammaegate effect of all other variables. Also, a linear relationship is assumed to exist between E and CO₂ (Marvão et al., 2010)

which admits CO₂ as a model state variable if substituted in equation (5).

With this model applied in 53 OECD countries (Zhao, 2011), programmed emission cuts of 50% by 2050 (base year 1990) reduce annual GDP per capita by 0.3% and economic growth is slowed down by 15%. However this is not accurate for emission purposes.

The growth and expansion attained in the past using a Business As Usual (BAU) model without taking into consideration any negative climate impact can be seen in the phase of the "scale effect" of the Environmental Kuznets Curve (EKC) (Grossman, 1995). This is the phase where economic policy disregards any environmental effects in order to maximize growth, including the rate of depletion of natural resources, without setting pre-calculated limits on the size of growth and its duration despite the fact that such limits were shown to exist (Meadows et al., 1972) and this policy is shown to be directly connected with the main components of environmental degradation i.e. pollution and water scarcity (King and Schneider, 1992) and with the corresponding damages caused by degradation. This process, in economic terms, can be considered as a case of over-accumulation of capital and under/zero-investment in climate mitigation leading to market failure caused by inefficient allocation of resources.

Hence, the cumulative effects of "scale effect" policy in terms of excess welfare, GDP, growth impacts, wealth and a general betterment of the main economic variables was attained by creating a surplus which would have not been possible if emission controls were in place at that time. This has the characteristics of debt creation as emission control economic costs were displaced forward in temporal terms, while these costs should have been subtracted from the surplus calculations by a net present value scheme. The emission realization of the debt has currently come close to the point of no return in terms of a threat of "climate bankruptcy" at a global scale as absent climate long term mitigation policies the continued adoption of a BAU model will open the well documented Pandora's Box of calamities whose economic consequences are astronomical and therefore past and current emission economic costs must be repaid in instalments which incurs an economic cost during the repayment period. In the Zhao model initial GDP is assumed to be independent of past economic performance while if the previous analysis was taken into consideration it would be accompanied by the BAU created debt mentioned above. Consequently, the reduction in GDP due to reduced emissions is in a substantial part attributed to the pay-off of accrued previous debts.

Moreover in a recent paper, the main emitters, U.S. and China, were found to have stronger emissions-GDP association during periods of GDP decline than during periods of growth (Doda, 2013).

Further, contrary to Zhao, climate policy will, in general, increase incomes and employment in both the short and long runs as seen in a study applied to 53 countries (Rezai et al., 2017) as well as value added, GDP and welfare in the long term (IRENA and CEM, 2014). In Rezai, Taylor, and Foley (2017) the analysis of the introduction of CO₂ as a state variable is more robust than the one in Zhao (2011) as it is decomposed into production-related emissions G(Y) and mitigation efforts M(m)Y, where m is the share of output employed in mitigation, and the latter is linear in terms of output following the theory developed in Nordhaus and Boyer (2000) and Nordhaus (2008).

In the long term, a permanent decrease of one ton of oil's agammaegate energy consumption reduces annual agammaegate income by €6340 while the same taken in units of electricity production results in an annual reduction of €19,950 (Marvão et al., 2010) which makes displacing of grid power by Solar Power, where that is efficient, a virtual sine qua non.

Therefore, Solar Power is, in terms of the economy, in an important way a short and long term positive or at least neutral externality as it is balanced out by previous BAU debts. Moreover, as it displaces coal produced electricity, the chain of coal-to-electricity machinery manufacturers has to reduce production which in effect makes Solar Power a negative pecuniary externality.

As Solar Power produced electricity is a factor of CO₂ reduction, as equation (2) shows, it is a positive externality to the climate which includes temperature mitigation. Hence Solar Power acts as a "second level" positive externality in many cases in health, agriculture (Schlenker and Roberts, 2009), species extinction e.g. in stopping the reduction of masculinization of certain vertebrates (Valenzuela et al., 2019) etc.

2.4.2.   Valuation

Solar Power has an inherent non-use value, a value existing even if it is not used in electricity production, based on contingency frameworks, as can be seen in various studies, e.g. (K. Arrow et al., 1993). Its non-use value can also be inferred from its role as a "deposit" in the interpretation of Nature as a "Bank of Natural Capital" (Sullivan, 2014) as physically it is a fuel. Moreover, as it is the fuel of Solar Power produced electricity, the Pigou subsidy allotted to electricity producers, as seen below, is embedded in its non-use state.

In examining in-use valuation the social cost of carbon (SC-CO₂) estimates in the U.S., a main emitter, are based on a balanced marginal cost-benefit analysis of emissions reductions and involve the setting of tax and subsidy rates (Kaufman, 2018a; 2018b) part of which goes to electricity producers e.g. in California between February and March 2019 out of a 17 billion USD carbon tax budget 5.8 billion USD went to electricity producers as the State is aiming at carbon neutrality by 2045 (Hamlin, 2019). In France and Portugal electricity producers are subsidized for using renewable energies (Marten and van Dender, 2019). Hence we have a partially Pigouvian bilateral tax scheme as not all taxes are turned into subsidies for the firm A (see Preface). Economic value is defined as "to be the value placed on a good by an individual person and which value can he expressed, at least in principle, in terms of some willingness to pay for the good, or some compensation to forego the good." (Pearce, 1989) and is not always identical to price. The subsidy received allows the electricity producer to assign a value to Solar Power as an unprocessed fuel with low carbon intensity in comparison to coal, without which the subsidy would not had been paid hence the definition part "compensation to forego the good" while, in addition, the value of Solar Power can be reflected by the rent paid out for the surface employed for its collection.

Valuation can also be based on the competitive market pricing of Solar Renewable Energy Certificates (SRECs) which act as carbon offsets due to the fact that Solar Power fuels electricity production with low carbon intensity, else there would be no reason for their existence. The process is a form of Coasian bargaining where commitment to increase the renewable energy share in the firm's consumption, which is offset against their existing cabon emission, can be covered by the purchase of SRECs issued by firms with Solar Power energy surplus instead of actually attaining the Solar Power renewable energy share (Choy and Ho, 2018). The price depends on SREC availability and the levels of Pigouvian tax and of the emission rights scheme (Uimonen, 2001). If the Pigouvian tax is not high enough and the emissions rights scheme is too high, then in a market model consisting of heavy pollution product, a medium pollution product and a zero pollution product the medium pollution product is favored vis-à-vis the other two products, the so called "Grey Paradox" (Coulomb and Henriet, 2018).

An indirect valuation can be based on hedonic models, where a generic type good is characterized by a bundle of its attributes in varying quantities (Epple, 1987). In a study (Smith and Huang, 1995) prospective buyers clearly associate negatively high pollution with real estate values. This can also be seen from the point of view of individual preference where there is a weak complementarity between clean environment and a commodity, in this case real estate, and a Marshallian demand is observed for the clean environment resource and by inference for Solar power (Smith, 1993).

Consequently both non-use and in-use valuations are larger than zero.

3.   Solar Power as a Public Good

3.1.   Redefinition of a Green Public Good

The dominant Samuelson definition (Samuelson, 1954; 1955) must be augmented to accept explicitly goods of the nature of Solar power, which are not the result of a process. To do so we borrow from the public good definition by Kaul and Mendoza (2003) the word "inadvertent". A "relatively positive climate externality" is one caused by the substitution of a good with negative climate externality by one whose negative externality is far less. The definition suggested is : "A Green Public Good, including any whose existence is inadvertent, is a non-excludable and/or non-rival good in consumption with direct or via substitution reduction of negative climate externalities."

It should be noted that under this definition water, which is an economic good (ICWE, 1992), is not a Green Public Good, but water under conditions of sustainability is.

This definition extends the notion of good from that inferred in Samuelson's definition to encompass economic goods such as Solar Power and at the same time limits them to those which either directly or via substitution reduce negative climate externalities. The introduction of this last condition is based upon the premise that negative climate externalities, in particular pollution, reduce welfare as they have economic consequences (OECD, 2016) and should be part of a unified framework, e.g. (Robinson, 1990). In particular a CGE analysis has shown in a quantitative way that air pollution, which includes CO₂ emissions, reduces welfare in Europe (Nam et al., 2010).

The consumer set addressed by the definition is composed by Electric Utility Companies with land rights of the type described in Section 1.3 or their extensions, which includes the ability of setting up a receptor surface by any legal means which may exclude those with these rights in high rise buildings apartments. Consequently they belong to some bundle ($\overset{\vee }{\mathop{W}}\,$, $\overset{\vee }{\mathop{A}}\,$, $\overset{\vee }{\mathop{CI}}\,$) by definition.

Restricting the public good consumer set by classification is theoretically acceptable as one of the classic examples of a public good, the lighthouse, addresses only ships (Arrow, 1969; Samuelson and Nordhaus, 2009). Moreover, as ships are associated with rights as referred to above receiving this warning is inalienably associated with these rights. Although Samuelson assumes that a public good, in this case warning, is distributed in the same quantity to all consumers, a ship moving on the outer edge of the lighthouse's effective radius will receive less warnings than a ship moving closer to the lighthouse as the light is revolving. Hence in reality every lighthouse warning consuming ship will receive at least one warning. Defense, another example of public good (Samuelson, 1954), in the case of an armed asymmetric border dispute is not equally distributed since an increased part of its resources is concentrated on the border which results in the communities near the border receiving a higher benefit than those away from it.

The consumer set definition selected may seem to be narrow but in reality lack of price exclusion from public goods is deemed to be literally impossible (Head, 1962). In terms of individual consumers, as these rights distinguish consumers within any area agglomerate $\overset{\vee }{\mathop{A}}\,$, none is excluded, as the triplet variables may be extended to include him, or enters into rivalry since the marginal cost of adding one more consumer does not reduce the quantity available to others and has zero marginal cost as marginal consumers are known ex ante (Candela and Geloso, 2019). This set may be extended to cover those without any rights if the State extends by fiat conditional free rights to all on vacant land for Solar Power purposes in a non-distortional way, e.g. in Australia 12.5% of the land mass of 7.692 million km² is vacant land. Regarding positive climate externality the bundle ($\overset{\vee }{\mathop{W}}\,$, $\overset{\vee }{\mathop{A}}\,$, $\overset{\vee }{\mathop{CI}}\,$) clearly causes positive climate externality by substitution.

A contrary opinion may be based on the theory of "club goods" these being "goods available for consumption to the whole membership unit of which the reference individual is a member" (Buchanan, 1965) which are in effect excludable, non-rivalrous public goods (Miller, 1990)but as the motivation for joining the club is economic (Buchanan, 1965), whereas here it is automatic, renders the counterargument invalid. (W, A, CI).

3.2.   Samuelson's condition and Pigouvian taxes

3.2.1.   Samuelson's condition

In general there is no Pareto optimal amount of public goods independent of the distribution of private goods except in the case of utility functions that are linear in private goods (Samuelson, 1954; 1955) and more precisely unless the utility function is of the form U(X, Y) = A(Y)X+B(Y) where X is the single private good consumed and Y is the vector of public goods consumed (Bergstrom and Cornes, 1983). Consequently, we must consider consumers with at least one private good.

Consider two Electric Utility companies, 1 and 2, using coal which is a private good, x₀ⁱ, and Solar Power, x₁ⁱ, which is a public good where i = 1, 2. Their utility functions are

which satisfy the Inada conditions (Guasoni and Schachermayer, 2004).

Samuelson assumes that both companies obey the rule "each individual's consumption of such a good (public good) leads to no subtraction of another individual's consumption of that good" and as a result all individuals consume the same quantity of that good (Samuelson, 1954), which is not necessarily the only interpretation of his statement and is quite restrictive as equidistribution is clearly not the only solution and may not be viable. In fact, nominal cost Government Health systems do not dispense their services equally but according to the patient's needs. However, as both firms belong to the same bundle ($\overset{\vee }{\mathop{W}}\,$, $\overset{\vee }{\mathop{A}}\,$, $\overset{\vee }{\mathop{CI}}\,$) and if we consider $\overset{\vee }{\mathop{A}}\,$ to be quite narrow and that all firms share the same solar technology, then this assumption leads to no problem.

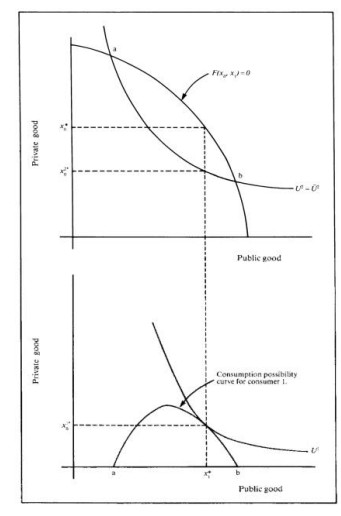
Following Sandmo (2001) and (Samuelson, 1954; 1955) we assume that the production possibility equation is

Figure 3.  Pareto optimality with private good x₀ and public good x₁ adapted from (Sandmo, 2001).

DownLoad: Full-Size Img PowerPoint

In the upper figure there is the production possibility curve from equation (9) and an indifference curve from ${{U}_{2}}\left(x_{0}^{i}, ~x_{1}^{i} \right) = constant$ which intersect at points a and b where both curves hold true. In the lower figure the consumption possibility for firm 1 between points a and b between which both firms consume equal amounts of the public good x₁ while its consumption of good x₀ is determined by the difference in the vertical between the second firm's indifference curve and the consumption possibility curve which leads to the tangency of between the indifference and consumption possibility curves yielding the best allocation which leads to the pairs $\left(x_{0}^{1*}, ~x_{1}^{*} \right)$ and $\left(x_{0}^{2*}, ~x_{1}^{*} \right)$.

The slope of the consumption possibility curve is equal to the difference of the slopes of its constituent curves and therefore MRS¹ = MRT- MRS² where MRS is the Marginal Rate of Substitution and MRT the Marginal Rate of Transformation. Hence

or using the notation in (Samuelson, 1954)

which is Samuelson's condition (Samuelson, 1954). There is no need of lump sum taxation, which is the Achilles' heel of Samuelson's theory, as the cost of x₁ acquisition is covered by the firms.

3.2.2.   Pigouvian taxes

In the case analysed in this paper Pigouvian taxes are used as a "stick and carrot" policy to deter the use of heavy carbon emitters by imposing a carbon tax t on x₀ and subsidizing the public good x₁ by a part of this tax αt where 0 < α < 1. Just by considering the simple case of imposing the carbon tax Sandmo (2001) arrives at the formula

which can be reduced to the Samuelson condition only if t = 0. Hence the imposition of Pigouvian taxation, which is the case in reality, does obey the Samuelson condition making the solution some form of "second best".

4.   Conclusion

Under a new definition Solar power has been defined as the irradiance at the normal on the surface of the Earth and is described by a triplet ($\overset{\vee }{\mathop{W}}\,$, $\overset{\vee }{\mathop{A}}\,$, $\overset{\vee }{\mathop{CI}}\,$) where $\overset{\vee }{\mathop{W}}\,$ represent a prescribed irradiance level band selected from Figure 2, $\overset{\vee }{\mathop{A}}\,$ an international/national land agglomerate each part with a determining geographic coordinate set and nationality index and $\overset{\vee }{\mathop{CI}}\,$ represent the vector corresponding to the nationality index in $\overset{\vee }{\mathop{A}}\,$. It has been shown that under both definitions of Pigou and Robbins it is an economic good and further that it is associated with ownership rights such as private, collective, government and open with varying control which may include rights to use and rights to regulate and that it is subject to economic ownership. Further it has been shown by argumentation that it is in reality a positive externality to the economy if taken into intertemporal and not static consideration besides being a positive externality to the climate. Its valuation both in non-use and in-use has been shown to be larger than zero as it was reviewed using contingency, indirect and direct methods. A Green Public Good has been defined as "A Green Public Good, including any whose existence is inadvertent, is a non-excludable and/or non-rival good in consumption with direct or via substitution reduction of negative climate externalities." and it has been proven that Solar Power is one. The consequences of the definition have been analysed and it has been shown that in no-lump tax situation Samuelson's condition holds true but in the case of Pigouvian taxes it does not.

Conflict of interest

All authors declare no conflicts of interest in this paper.