Two-Species Competition with High Dispersal: The Winning Strategy

1.   Introduction

COVID-19 is an emerging acute infectious disease, which incubation period is 1–14 days, usually 3–7 days. COVID-19 generally have no obvious precursors, the infection will be after the Coronavirus disease early, some patients may also have no obvious symptoms, most common in patients with fever, dry cough, lack of power as the main performance, but beyond that, due to individual differences, the patient also can appear muscle pain, chest tightness, pharyngeal itching, runny nose. The lack of specificity, which can be seen in many diseases and is not unique to COVID-19, makes it difficult for patients to identify infection by symptoms themselves. Some immunity can be acquired after infection or after the cornavirus vaccine, but the duration is unclear.

The establishing and analyzing of mathematical models play an important role in the control and prevention for disease transmissing. McKendrick first proposed the PDE formulation for the age distribution of a population ^[1]. Ever since the research results by Kermack and McKendrick ^[2], Hoppensteadt ^[3], Iannalli ^[4] and Webb ^[5], age structure models have been widely used in the study of transmission dynamics of infectious diseases ^[6,7,8]. Recently, Bentout Soufiane et al. considered an alcoholism model for age structure and investigated the glabal behavior ^[9]. In December 2019, some medical institutions of Wuhan reported some cases of pneumonia of unknown cause. On 11 February 2020, the World Health Organization officially named the pneumonia contracted by the Novel Coronavirus as "COVID-19". Recently many scholars have studied on COVID-19, which all proposed and studied the dynamical model which has helped to control infectious diseases. Glenn Webb proposed a model of a COVID-19 epidemic which is developed to predict the effectiveness of vaccination ^[10]. B. Tang et al. proposed calculation of the basic reproduction number by virtue of mathematical modeling can help decide the potential and severity of an outbreak and provide critical information for identifying the type of disease interventions and intensity ^[11]. J. Jiao et al. presents an SEIR epidemic model with infectivity in incubation period and homestead-isolation on the susceptible ^[12]. Besides, deep learning frameworks ^[13] also can be used for prediction virus spread and a more reliable model incorporating more parameters input into a neural network based virus transmission predictor may be implemented.

McCluskey assumed that infected individuals can develop disease by either of two pathogenic machanism: fast progression or endogenous reactivation ^[14]. Generally, acute infectious diseases develop through four stages, among which the incubation period is very important, which refers to the period from pathogen invasion to the onset of clinical symptoms. Take COVID-19 for example which has a certain incubation period. According to current epidemiological statistics, the incubation period is about 1–14 days. Some patients will show symptoms on the day of infection or one or two days later, while some patients will have a longer incubation period of about two weeks. Consequently, it is necessary to consider the factors of fast and slow progress in infection modeling.

Besides, the treatment of disease is proportional due to medical resources. Capasso and Serill ^[15] introducing saturated incidence in the cholera epidemic model, describes the tingible into infected class average relationship $g(I) = kI/(1+\mu), k, \mu > 0$, which said the disease infection ability, said a crowded or change on the influence of the individual, the increase in the number of infected people, easy to dye more vigilant, lead to easy dyeing behaviour change or when the disease is especially crowded in the environment may be unlimited effective contact.

2.   Materials and methods

Zunyou Wu who is the chief expert of epidemiology at the Chinese Center for Disease Control and Prevention, said there are three possible cases of re-positive symptoms for COVID-19: first, false negative or false positive nucleic acid test; second, the virus is active again; third, reinfection. Zijian Feng who is the deputy director of the Chinese Center for Disease Control and Prevention, said that the re-positive case caused continued transmission is rare and does not play a big role. Recently, some provinces in China have seen new cases of COVID-19 including asymptomatic patients. Therefore an infected individual ows into the exposed class after been treated but not becomes susceptible in our models. Inspired by the above discussions, we consider an SEI epidemic model which introduce the latent age, the nonlinear incidence of reactive unsaturated treatment and the saturation treatment function.

for boundary and initial values conditions

where $S(t), e(t, a)$ and $I(t)$ respectively be the population sizes of susceptible, latent and infective classes. We assume that the population size is changeless. $\beta$ represents susceptible people in contact with an infected person transmit rate, $p$ represents susceptible people contact with an infected person enter slow propagation process called latent stage which denoted by e(t, a) where individuals are infected with disease but are not yet contagious, where $a$ is called the age of latency progression, which is the duration of the incubation period. We denote $E(t) = \int_{0}^{+\infty}e(t, a)da$ as the latent individuals' total density. $1-p$ represents susceptible people and the onset of contact after rapid development for the onset of ratio, $\mu$ and $d$ represent people natural mortality and mortality due to illness. $f(x) = \gamma x/(1+ m x)$ represents the saturation treatment function where the $\gamma$ is cure rate of the disease.

We define $X = R^{+}\times L_{+}^{1}(0, +\infty)\times R^{+}$, equipped with the norm $\|(x_{1}, x_{2}, x_{3})\|_{X} = |x_{1}|+\int_{0}^{\infty}x_{2}(a)da+|x_{3}|$. The initial condition of system ${\rm(2.1)}$ belongs to the positive cone of X, then can be rewritten as $x_{0} = (S_{0}, e_{0}(\cdot), I_{0})\in X$. We can get a continuous semi-flow associated with system ${\rm(2.1)}$, that is, $\Theta:R^{+}\times X\longrightarrow X$ produced be system ${\rm(2.1)}$ adopts the following form, $\Theta(t, x_{0}) = (S(t), e(t, \cdot), I(t)), t\geq 0, x_{0}\in X$, with

For simplicity, let $\varepsilon(s) = u+\alpha(s), \theta = \int_{0}^{\infty}\alpha(a)e^{-\int_{0}^{a}\varepsilon(\tau)d\tau}da, K_{0}(a) = e^{-\int_{0}^{a}\varepsilon(\tau)d\tau}$. The second equation of system ${\rm(2.1)}$ is solved along $t-a = constant$

Let $\Omega = \bigg\{(S(t), e(t, \cdot), I(t))\in X, \ S(t)+\int_{0}^{+\infty}e(t, a)da+I(t)\leq \frac{\Lambda}{\mu}\bigg\}$. The interior of $\Omega$ is $\mathring{\Omega}$. we can easily verify the non-negative and positive invariance set of the system ${\rm(2.1)}$ with the help of article ^[5].

We note that if $R_{0} > 1$, $\Omega$ is the positive invariant set for $\Theta$, and it attracts all solutions of the system ${\rm(2.1)}$ with non-negative initial conditions.

2.1.   Reproduction number

Firstly, there is a disease-free equilibrium point $E_0 = (S_0, 0, 0)$ in the system ${\rm(2.1)}$, where $S_0 = \frac{\Lambda}{\mu}$, and we define the basic reproduction number of the system ${\rm(2.1)}$ as following

and it is easily known that if $R_0 > 1$, system ${\rm(2.1)}$ has an only positive endemic equilibrium point $E_*(S^*, e^*(a), I^*)$, where

Define space

and $X_{0+} = X_{+}\bigcap X_{0}$. Define operator $T:D(T)\subset X\rightarrow X$,

where $D(T) = R\times R \times {0}\times W^{1, 1}((0, +\infty), R)$. Consider nonlinear mapping $F:X_{0}\rightarrow X$, for

define

Therefore systerm ${\rm(2.1)}$ can be rewritten as an abstract Canchy problem

Draw on the results in Magal ^[16] and Magal and Thiemel ^[17], there exists an uniquely deterministic semiflow $\{U(t)\}_{ t\geq0}$ on $X_{0+}$ which is bound dissipative and asymptotically smooth, and $\{U(t)\}_{ t\geq0}$ has a global attractor $T\subset X$ which attracts the bounded sets of $X$.

2.2.   Locally asymptotic stability

Theorem 2.1. If $R_0\leq1$, the disease-free equilibrium $E_0$ is locally asymptotically stable.

Proof. Let $x_1(t) = S(t)-S_0$, $x_2(t) = e(t, a)$, $x_3(t) = I(t)$, linearizing the system ${\rm(2.1)}$ at $E_0$, and considering the exponential solution $x_{1}(t) = x_{1}^{0}e^{\lambda t}, x_{2}(t, a) = x_{2}^{0}e^{\lambda t}, x_{3}(t) = x_{3}^{0}e^{\lambda t}$, we can derive

Integrating the second equation of system ${\rm(2.6)}$ from 0 to $a$, considering the boundary condition, deduces $x^0_2(a) = \big(p\beta S_{0}x^0_3+\gamma x^0_{3}\big)e^{-(\lambda+\mu)a-\int_{0}^{a}\alpha(s)ds}.$ Substituting $x^0_2(a)$ into the fourth equation of system ${\rm(2.6)}$, solving it, we get the characteristic equation

easily know $H'(\lambda) < 0$ which implies that $H'(\lambda)$ is a decreasing function, and

Let $\lambda = x+yi$ is an arbitrary complex root of $H(\lambda) = 0$, then

be equivalent to

And because $0 = -x+\int_{0}^{\infty}\alpha(a)\big(\gamma+p\beta\frac{\Lambda}{\mu}\big)e^{-(\mu+x)a}e^{-\int_{0}^{a}\alpha(\tau)d\tau}cos(ya)da+(1-p)\beta\frac{\Lambda}{\mu}-(d+\mu+\gamma)\leq H(x)$ then $0 = H(\lambda)\leq H(x)$ which stands for $x < \lambda^{*}$, where $\lambda^{*}$ is the unique real root of $H(\lambda) = 0$. Thus if and only if $R_{0} \leq1$, all the roots of system ${\rm(2.6)}$ have negative real part.

Theorem 2.2. If $R_0 > 1$, the unique endemic equilibrium $E_{*}$ is locally asymptotically stable.

Proof. The perturbation variables are as follows

Linearizing system ${\rm(2.1)}$ at $E_{*}$ and assuming the form of solution is as follows

where $y_{1}^{ 0}, y_{2}^{0}(a), y_{3}^{0}$ will be determined. we get

By calculating, we can get the following eqution

where $W(\lambda) = \int_{0}^{\infty}\alpha(a)e^{-(\lambda+\mu)a-\int_{0}^{\infty}\alpha(\tau)d\tau}da$ satisfies the following properties

From the first equation of system ${\rm(2.8)}$ and the Eq ${\rm(2.9)}$, we obtain the following characteristic equation

Note $M$ is the right side of the Eq ${\rm(2.10)}$. Assuming $\lambda > 0$, $M$ satisfies the following inequality

which is equivalent to

where

Since $\lambda > 0$, therefore

Let $A = \frac{(\beta I^*+\mu)(d+\mu)}{(\beta I^*+\mu+1)(\gamma+d+\mu)}$, easily know $A < 1$, i.e. ${R}_0 < 1$ which is contradict with ${R}_0 > 1$. then we can get $\lambda < 0$.

2.3.   Uniform persistence

Theorem 2.3. If $R_0 > 1$, there exists $\varepsilon > 0$, such that for each $\forall\; y\in M_{0}$, $\lim\limits_{t\rightarrow +\infty}inf d(U(t)y, \partial M _{0})\geq \varepsilon$.Furthermore, there exists a compact subset $H_{0}\subset M _{0}$ which is a global attractor for $\{U(t)\}_{t\geq 0}$ in $M_{0}$.

Proof. Define $M_{0} = \{(S, I, 0, e)^{T}\in X_{0+}:T(t) = I+\int_{0}^{\infty}e(a)da > 0\}$, and $\partial M_{0} = X_{0+}\backslash M_{0}$. Firstly, let $(S^{0}, I_{0}, 0, e_{0})\in M_{0}$, we can get $T'(t)\geq -max\{d+\mu, \mu+\alpha_{max}\}T(t),$ where $\alpha_{max} = ess \sup_{a\in(0, \infty)}\alpha(a)$, easily know $U(t)M_{0}\subset M_{0}$. Secondly, if $(S^{0}, I_{0}, 0, e_{0})\in \partial M_{0}$, with the help of system $\rm (2.4)$, we know if $t\geq 0$, we get $I(t) = 0$ and $\int_{0}^{\infty}e(t, a)da\rightarrow0$, for $t\rightarrow +\infty$. Therefore $U(t)\partial M_{0}\subset \partial M_{0}$. Let $(S^{0}, I_{0}, 0, e_{0})\in \partial M_{0}$, we get

Since $S(t)\leq S^{0}$ as $t\rightarrow +\infty$, we get $I(t)\leq \tilde{I}(t), e(t, a)\leq \tilde{e}(t, a)$, where

By the system $\rm (2.4)$, we have

where $K_{0}(a) = e^{-\int_{0}^{a}\varepsilon(\tau)d\tau}$. Substituting system $\rm (2.13)$ into system $\rm (2.12)$, we obtain

where

It's simple to know that if $T_{2} = 0$, we get that system $\rm (2.14)$ has an only solution $\tilde{I}(t) = 0$. From the system $\rm (2.13)$, we can get $\tilde{e}(t, 0) = 0, t\rightarrow +\infty$. Through comparison, we get $(I(t), e(t, a))\rightarrow (0, 0)$ for $t\rightarrow +\infty$.

Since $E_{0} = (S^{0}, 0, 0, 0_{L^{1}})$ is globally asymptotically stable in $\partial M_{0}$, next we only need to proof that $W^{s}(E_{0})\bigcap M_{0} = \Theta$, where $W^{s}(E_{0}) = \{z\in X_{0+}, \lim\limits_{t\rightarrow +\infty}U(t)z = E_{0}\}$. Assume there exists $z\in W^{s}(E_{0})\bigcap M_{0}$, it follows that there exists $t_{0}>0$ such that $I(t_{0})+\int_{0}^{\infty}e(t_{0}, a)da > 0$. Using the method in ^[18], we have $e(t, a)>0$ for $(t, a)\in [0, \infty)\times [0, \infty)$, $I(t)>0$ for $t\geq 0$. By means of the method of Braueretal ^[19], the following function is defined

for $\forall \; a > 0$, $H(a)\geq 0$, and $H(0) = \theta$. Furthermore, for $\forall a\geq 0, H'(a) = -\alpha(a)+\varepsilon(a)H(a).$ Let

which satisfies

If $R_{0} > 1$, there exists $t_{0} > 0$ such that $\Phi(t)\geq\Phi(t_{0})$ for all $t\geq t_{0}$. Since $\Phi(t_{0}) > 0$, this prevents that $(I(t), e(t, a))\rightarrow (0, 0_{L^{1}}, 0_{L^{1}})$, which is contradiction with $S(t)$ converges to $S^{0}$ and $I(t)$ converges to $0$, for $t\rightarrow \infty$. We get the semiflow $\{U(t)\}_{t\geq 0}$ is uniformly persistent with respect to the pair $(\partial M_{0}, M_{0})$. Besides, there exists a compact subset $H_{0}\subset M _{0}$ which is a global attractor for $\{U(t)\}_{t\geq 0}$ in $M_{0}$.

2.4.   Global asymptotic stability

Theorem 2.4. Assume $\alpha(a)$ is an bounded function, if $R_0 < 1$, the infection-free equilibrium $E_{0}$ is globally asymptotically stable. Note $\bar{\alpha} = \lim\limits_{a\in[0, +\infty)}\sup\alpha(a)$.

Proof. Consider systems ${\rm(2.1)}–{\rm(2.4)}$ we get

where $\parallel e\parallel_{L_{1}} = \int_{0}^{+\infty}e_{0}(a)da$. Take the limit of both sides of the inequality (Eq 2.15), since $S\leq\frac{\Lambda}{\mu}$ and $\lim\limits_{t\rightarrow +\infty}e^{-\mu t} = 0$, we get

With the help of Taylor's formula and the third equation of system ${\rm(2.1)}$, we get

By solving inequality (Eq 2.17) and taking the limit of both sides, we can get

Therefore, when $R_0 < 1$, $\lim\limits_{t\rightarrow +\infty}\sup I(t) = 0$. By using inequality (Eq 2.16) and system ${\rm(2.1)}$ respectively, we get $\lim\limits_{t\rightarrow +\infty}\sup e(t, a) = 0$ and $\lim\limits_{t\rightarrow +\infty}\sup S(t) = \frac{\Lambda}{\mu}$. Therefore, if $R_0 < 1$, the disease-free equilibrium point $E_{0}$ is global attraction. Further, with the help of Theorem 2.1, we have the disease-free equilibrium point is global asymptotically stable.

Theorem 2.5. If $R_0 > 1$, the unique endemic equilibrium $E_{*}$ is globally asymptotically stable.

Proof. The Lyapunov functional $\mathbb{V}_*(t)$ is constructed

where

for $W(a) = \int_{a}^{+\infty}\alpha(s)e^{-\int_{a}^{s}(\mu+\alpha(\tau))d\tau}, \; g(x) = -1+x-\ln x$, $\frac{d e^*(a)}{da} = -\varepsilon(a)e^*(a)$. Calculating the derivative of the $\mathbb{V}_*(t)$ along with the solutions of system ${\rm(2.18)}$, yields

if $\frac{I}{I^*} > 1$ and $\frac{S^*}{S} > 1$, or $0 < \frac{I}{I^*} < 1$ and $0 < \frac{S^*}{S} < 1$, we have

Hence,

For $g(x)\geq0, x\in R$, therefore $\frac{dV_*(t)}{dt}\leq 0$ is always true, furthermore the strict equality holds if and only if $S = S^*, \; e(t, a) = e^*(a), \; I = I^*$. Therefore when $R_0 > 1$ the endemic equilibrium $E_{*}$ is globally asymptotically stable.

3.   Simulations and summary of results

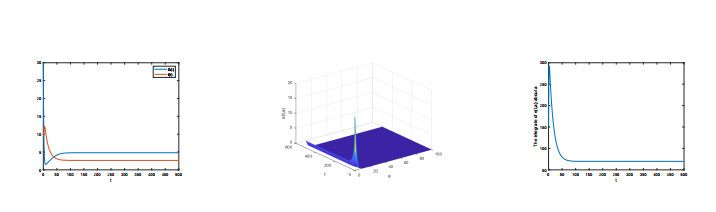
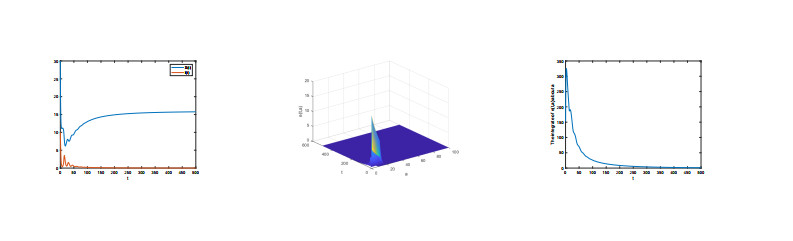
In the work, an age structure epidemic SEI model with fast and slow progression is considered. The basic reproduction number $R_{0}$ is obtained as $R_0 = \frac{p\beta\Lambda\theta+\gamma\mu\theta+(1-p)\beta\Lambda}{(\gamma+d+\mu)\mu}$. We have proved the globally asymptotically stable for disease-free and endemic equilibrium respectively. In the following, we also give some numerical simulations to illustrate the global stability. Let $\Lambda = 1;\beta = 0.055;\gamma = 0.7;\mu = 0.063;d = 0.04;p = 0.8;m = 0.02;S(0) = 30, e(0, a) = 6e^{-0.4a}, I(0) = 10.$ and

In Figure 1, we choose $\tau = 12$, then $R_{0} < 1$, it can be seen that $E_{0}$ is globally asymptotically stable. While in Figure 2, we choose $\tau = 1$, then $R_{0} > 1$, it can be seen that $E^{*}$ is globally asymptotically stable. The figures show the series of $S(t)$ and $I(t)$ which converge to their equilibrium values, in addition the age distribution of $e(t, a)$.

4.   Discussion

COVID-19 has spread rapidly around the world since 2020 with a high fatality rate. Today the epidemic in some countries is still unable to be effectively controlled, and social and economic life has been greatly disrupted. COVID-19 trend prediction has become a major research focus. Current trend prediction methods include epidemic disease prediction model, COVID-19 trend prediction model based on deep learning, etc. These models have effectively assisted medical experts and scientific research institutions to efficiently predict COVID-19. The countermeasures and suggestions for strengthening epidemic prevention and control are put forward, which have a good guiding role for accurate epidemic prevention and control.

The large-scale epidemic of COVID-19 in China has basically ended, but there are still occasional imported cases or local outbreaks caused by cold chain pollution which prevention and control enters a new phase of normalization. Since the outbreak of COVID-19, a large number of researchers have conducted extensive studies on infectious disease dynamics and prevention and control measures through various models and data analysis methods. Many scholars have built traditional dynamics models based on warehouses to explore the development trend of COVID-19 and provide scientific basis for epidemic prevention and control.

5.   Conclusions

According to transmission characteristics of infectious diseases, the paper proposed the methods of fast and slow transmission, which more effectively reveals the transmission mechanism for infectious diseases. The global asymptotic stability of the system has analyzed with the help of the principle of dynamics, and abtained the threshold of infectious disease control. The greater the rate of slow progression of an infectious disease, the fewer the threshold results. The world is now being vaccinated which cannot provide lifelong immunity, but can reduce the mortality of those infected. By vaccinating, the rate of patients entering slow progression increases and the threshold is correspondingly reduced. Therefore, vaccination can effectively control the transmission of Coronavirus.

Acknowledgments

This research is supported by Guizhou Province Science and Technology Support Plan Project ([2020]4Y167), the National Natural Science Foundation of China (N0.12001417), Doctoral Foundation of Guizhou Education University (2018BS001), First-class University Construction Project of Guizhou Education University ([2019]35).

Conflict of interest

The authors declare there is no conflict of interest.