1.
Introduction, motivation, and outline
The study of the relationship between education and labor income has been a central topic in the economic literature, due to the importance of understanding how education impacts income distribution within a society (Becker [1] and Schultz [2]). Education is argued as an investment in human capital that improves individual productivity. Meanwhile, it is also seen as a signaling mechanism to differentiate between various levels of productivity (Spence [3]; Arrow [4]). In Colombia, as in many other countries, there is a growing interest in analyzing how the returns to education vary across different economic sectors and among vulnerable population groups. However, much of this literature has focused on average estimates, without considering the heterogeneity of education returns across the income distribution. In a context like Colombia, characterized by high economic and social inequality, it is crucial to understand how these returns vary among different segments of the population and along the income distribution.
Previous literature has employed various approaches to study education returns. However, quantile and interquantile regression models offer a unique perspective by allowing us to examine how these returns vary across the entire income distribution (Mora [5]). This approach is particularly relevant in a context like Colombia's, where economic and social inequalities are a significant concern. Studies have shown that the benefits of education are not evenly distributed among all individuals, nor are they consistent across all income levels (Castillo et al. [6]). Therefore, it is crucial to understand how these benefits vary for different groups of people and in different parts of the income distribution. Additionally, certain population groups, such as youth and migrants, may face additional challenges in terms of accessing jobs and educational opportunities (García [7]). Herrera et al. [8] analyzed the returns to education, considering the impact of educational mismatches in both formal and informal employment in Colombia. The results show that returns on surplus, required, and deficit years of schooling differ between the two sectors. Additionally, the findings suggest that these returns vary across the wage distribution, with distinct patterns for formal and informal workers. Informal workers, in particular, not only receive lower returns on their education but also face an additional penalty due to educational mismatches, placing them at a greater disadvantage compared to formal workers.
This study aims to fill this gap in the literature by employing quantile and interquantile regression models to analyze returns to education by economic sector in Colombia, with a particular focus on vulnerable populations such as youth and migrants. Unlike traditional methods, these models allow us to examine how the effects of education vary at different points of the income distribution and between these points, providing a more comprehensive view of this relationship than traditional statistical regression approaches. This methodology is particularly relevant in Colombia, where economic and social inequalities are significant concerns, and where the benefits of education are not evenly distributed among all individuals nor consistent across all income levels (Castillo et al. [6]). In a previous article, Tenjo et al. [9] analyzed the evolution of returns to education in Colombia from 1976 to 2014, revealing that overall returns have remained stable, fluctuating between 10.8% and 14.3%, despite significant socio-economic changes. This highlights a stark contrast between pre-university and post-secondary education, with the former experiencing a continuous decline in returns, while the latter has stabilized around 20% since 1995. Additionally, the study points out gender disparities in educational returns and labor market participation. Utilizing household surveys and econometric models, the research corrects for selection bias, emphasizing the need for policies to address the declining returns of pre-university education and the existing gender gaps in the labor market.
Moreover, empirical evidence suggests that certain population groups, such as youth and migrants, face additional challenges in accessing jobs and educational opportunities (García [7]). Therefore, it is crucial to understand how these benefits vary for different groups of people and in different parts of the income distribution, to design more effective and equitable education policies.
Recent developments in understanding the impact of education on earnings have highlighted several scenarios. The basic ordinary least squares (OLS) model traditionally assumes that education affects earnings primarily through factors like years of schooling and qualifications, along with other variables specified by the Mincer model (Mincer [10]). In this framework, the OLS coefficient reflects the overall effect of education on earnings but does not differentiate between two distinct channels: the increase in productivity due to the acquisition of knowledge and skills during schooling (often referred to as the "returns to education") and the wage premium that employers might offer based on educational qualifications, which serves as a signal of potential productivity ("signaling effect").
In the OLS model, both the productivity gains from education and the signaling effect are treated as linear functions of years of schooling and qualifications. However, this approach assumes that these effects are constant across all levels of education and does not account for potential unobserved factors that could influence earnings. Consequently, if no unobserved confounding factors are present, the OLS coefficient represents a combined average of both the "returns to education" (the actual productivity improvement) and the "price of education" (the signaling effect). However, this combined estimate does not allow for a distinction between these two components, which limits our understanding of how education impacts earnings through different mechanisms.
A significant gap in the literature on returns to education in Colombia lies in three key areas. First, while existing studies have largely focused on average returns to education, they have overlooked the critical role of economic sectors in shaping these returns. Different sectors, such as agriculture, manufacturing, and services, exhibit varying wage structures, which can significantly influence the value of education in each sector. Iregui et al. [11] examined wage differentials across various economic sectors in Colombia, highlighting a lack of extensive literature on this topic. The findings indicate significant wage disparities, particularly in sectors such as electricity, gas, water, and mining, which tend to offer higher wages compared to agriculture and related fields. The study also notes that wage dispersion is most pronounced among managerial and professional roles, while minimum wage regulations contribute to lower dispersion in less skilled positions. Urrutia and Ruiz [12], Mesa et al. [13], and Gracia et al. [14] examined wage returns in Colombia through sectoral analysis, focusing on real wages across different economic activities.
Second, most research has traditionally used years of schooling as the main measure of education, rather than considering the possession of academic degrees or credentials. This approach fails to capture the nuanced differences between individuals who, despite having similar years of education, hold different qualifications, such as secondary degrees or postgraduate titles. Addressing these gaps is essential for a more comprehensive understanding of how education translates into income in Colombia's diverse and segmented labor market. For example, Bonilla [15] examined higher education enrollment, focusing on the types of degrees pursued, including academic (4-year) degrees and STEM (Science, Technology, Engineering, and Mathematics) fields.
Third, this article addresses an additional gap in the literature: the differential in returns to education by economic sector. While sectoral wage disparities are explored in some studies, the explicit role of education in generating these differentials remains underexamined. Understanding how education interacts with the specific demands of each sector can provide critical insights into wage formation and labor market inequality. By analyzing the returns to education across various industries, this study offers a nuanced understanding of how academic qualifications translate into wages differently depending on the sector, filling a crucial void in empirical literature.
In this regard, this paper will focus on analyzing education returns using quantile regression, a technique that allows us to examine how economic outcomes vary across different parts of the income distribution. Through this analysis, we can obtain a more comprehensive and accurate picture of the effects of education on income distribution. Additionally, this study aims to address a critical gap in the literature by exploring the differential returns to education by economic sector, highlighting how academic qualifications yield varying wage outcomes depending on the industry. By incorporating sectoral analysis, we can better understand how specific industries, such as finance, manufacturing, and agriculture, shape the economic value of education. Furthermore, this study goes beyond the traditional focus on years of schooling by considering the role of academic degrees, providing a more nuanced view of how educational credentials interact with sector-specific demands to influence wage disparities across the income distribution.
The mean response is the primary focus of standard regression models, while quantile regression describes the quantile for a response conditioned on covariate values. Quantile regression becomes notably more significant when dealing with responses that have an uneven distribution, as in education returns studies. This relevance arises from the inadequacy of the mean to effectively summarize asymmetrically distributed data, as it serves as a poor centrality measure. In such cases, the median offers a more accurate representation of the central trend. Quantile regression emerges as a superior alternative for describing asymmetrically distributed data, encompassing median modeling.
The concept of median regression was introduced by Laplace [16]. However, quantile regression models include median regression as a specific case (50th percentile) and can describe other locations (non-central) of the distribution (such as the 10th, 25th, 75th, and 90th percentiles). Koenker and Bassett [17] introduced quantile regression models, and since then, different versions and applications of these models have been developed. Quantile regression is a statistical technique that allows for a more precise and comprehensive analysis of education returns. Unlike other regression methods, quantile regression enables us to examine how the effects of education vary across the entire income distribution. This is especially important as educational benefits are not distributed evenly among all individuals. By using quantile regression, we can identify not only the average benefits of education but also how these benefits change for different groups of people at different income levels. This information is crucial for understanding economic inequalities and designing more effective and equitable policies in the field of education.
The article contributes to the understanding of the relationship between education (last degree obtained) and wages across different economic sectors (major economic branches) in Colombia. By employing quantile and interquantile regressions on monthly data from Colombia's Great Integrated Household Survey (GEIH) for 2019, it offers a nuanced examination of how the impact of education varies along the income distribution, controlling for variables such as sex, household size, relationship with the household head, marital status, experience, hours worked, and formal sector employment. Additionally, it controls for different vulnerable population groups, such as women, youth, and migrant status, as well as worker qualification and economic sector. This approach provides insights into the differential effects of education on wages, particularly highlighting variations among vulnerable populations. Moreover, by controlling for traditional Mincerian socioeconomic variables, the study offers a comprehensive analysis that sheds light on the unique dynamics within each economic sector. Overall, the research contributes valuable insights into the complex interplay between education, wages, and socioeconomic factors within Colombia's labor market landscape.
The rest of this document proceeds as follows: The theoretical framework and literature review are presented in Section 2, reviewing some labor market and education theories. In Section 3, we describe the methodology, starting with a description of the regression model and its limitations, followed by the methodological framework of quantile regression for parameter estimation, associated inference, goodness of fit, the inverse Mills ratio and its relation to Heckman's two-step method for estimating selection models, the model, and the data used. In Section 4, we present the estimates and results and discuss the implications for both quantile estimation and interquantile differences. Finally, in Section 5, the conclusions of the study and some important points for future studies are presented.
2.
Education and labor market models: A theoretical framework and literature review
Education is a key determinant of individual earnings and plays a crucial role in shaping income inequality. The literature review and theoretical framework section delve into the complex relationship between education and income, highlighting its multifaceted nature and implications for income distribution. Through a comprehensive synthesis of existing research, these sections explore key concepts and theories essential for understanding education's impact on economic outcomes.
Central to this analysis is the human capital theory, initially described by Becker [1] and Schultz [2] and further developed by Becker and Chiswick [18]. This theory posits that education acts as a crucial investment in increasing an individual's human capital, enhancing skills and knowledge, which in turn boosts productivity and potential for higher earnings. This perspective underscores the intrinsic value of education in driving economic prosperity and societal progress. Moreover, the Mincer Equation, introduced by Mincer [10], provides a foundational framework in labor economics, explaining the relationship between educational attainment and income levels. This equation calculates the incremental income increase associated with each additional year of education, encapsulating the average returns to education across various socioeconomic contexts.
Johnson [19] proposed the matching theory, which emphasizes the imbalances generated in the labor market due to biases or asymmetries of information between employers and job seekers. This dynamic implies that both the supply (job seekers) and the demand (companies) acquire information to make decisions regarding hiring and labor conditions. Jovanovic [20] and Stiglitz [21] explored the inefficiencies in labor markets caused by asymmetric information. Jovanovic specifically emphasized the process of job matching, where education serves as a signaling mechanism to reduce information gaps between employers and workers, thereby facilitating more efficient matches and improving productivity. Stiglitz, on the other hand, delved into the broader role of education in correcting market failures by enhancing worker productivity and aligning wages with skills. However, both authors cautioned that these benefits may come with unintended consequences, such as widening income inequality, particularly when access to education is unevenly distributed.
The job competition theory, presented by Thurow [22], highlights that overqualification often arises from labor market mismatches, which occur due to a lack of information about the actual skills and competencies of the workforce. He argued that the job competition model exacerbates this issue, as employers rely heavily on education credentials rather than directly assessing workers' skills. Building on this, Sicherman and Galor [23], as well as Sicherman [24], discussed the phenomenon of educational mismatches as a normal and even functional aspect of the labor market throughout the working life cycle. However, they emphasized that while such mismatches are expected, they must be managed carefully to ensure that workers continue to acquire the necessary skills to remain competitive and productive over time. The efficiency wage theory offers significant insights to provide a solid theoretical explanation for wage differences between sectors after controlling for education and personal characteristics. According to this theory, employers in certain sectors pay higher wages to incentivize productivity, reduce turnover, and mitigate issues like moral hazard and adverse selection. This is particularly relevant in high-risk or high-skill industries such as mining or finance, where retaining a motivated and skilled workforce is critical (Shapiro and Stiglitz [25]). Higher wages in these sectors, therefore, reflect not only worker productivity but also the employers' need to maintain an efficient workforce. This approach aligns with the empirical evidence that sectors like mining or construction often offer higher wages than sectors such as agriculture, even when controlling for education and skills (Caliendo, Cobb-Clark, and Uhlendorff [26]).
Another relevant framework is the rent-sharing hypothesis, which explains how firms in high-profit sectors tend to share a portion of their economic rents with workers in the form of higher wages. This helps to explain wage disparities between industries with differing profit margins, such as mining and agriculture. In industries where firms experience higher profitability, workers may benefit from better wages, despite similar educational backgrounds. Studies such as Card, Devicienti, and Maida [27] demonstrate that workers in high-rent sectors, such as energy or natural resources, are more likely to see wage gains compared to those in less profitable sectors. In addition, job attributes like occupational risk and working conditions also play a role in wage differences, as sectors with higher risks (e.g., mining or construction) often compensate workers for these factors (Lavetti [28]).
Credentialism is a theory advanced by Collins [29], which argues that education primarily functions as a signaling mechanism or credential that facilitates social mobility, rather than directly contributing to productivity. This view suggests that the value of education lies in its ability to distinguish individuals within the labor market, rather than in the skills acquired through formal education. Similarly, Groot and Oosterbeek [30] expand on this by emphasizing that while education serves as a formal qualification, the actual skills and competencies required in most jobs are often acquired through work experience. Wolpin [31] also supports this notion, suggesting that education's role in productivity is limited and that on-the-job training plays a more significant role in developing necessary skills. Thurow [22], meanwhile, posits that education serves as a filter for employers to identify individuals who possess the potential to be productive, rather than directly increasing productivity itself. Thurow's job competition model complements the credentialist view by asserting that employers use education credentials as a proxy for inherent ability and trainability, rather than a direct measure of productivity.
Furthermore, the literature clarifies the convex nature of the relationship between education and income, as elucidated in studies by Bourguignon et al. [32] and Battiston et al. [33]. This convexity underscores a phenomenon in which the marginal returns to education increase as individuals ascend the educational ladder, exacerbating income disparities and contributing to socioeconomic stratification. Additionally, the framework explores the nuanced heterogeneity observed in educational outcomes. Becker and Chiswick [18] highlighted the influence of various individual-level factors, such as familial background, innate abilities, and personal attributes, in modulating the translation of educational credentials into tangible economic gains.
Furthermore, the utility of quantile regression techniques, as expounded upon by Firpo et al. [34], is underscored as an invaluable analytical tool for discerning the differential impact of education across various segments of the income distribution spectrum. By revealing the heterogeneous nature of returns to education, this methodological approach facilitates a granular understanding of income dynamics and its implications for social equity. Lastly, the imperative of elucidating the dynamics of returns to education in informing the formulation of effective education and labor market policies is underscored. Drawing from the seminal work of Acemoglu and Autor [35], the framework accentuates the pivotal role of skills, tasks, and technological advancements in shaping employment patterns and income trajectories, thus underscoring the exigency of evidence-based policy interventions aimed at fostering equitable socioeconomic outcomes. In general terms, the literature on returns to education underscores the multifaceted nature of the relationship between education and earnings. By considering factors such as convexity, heterogeneity, and distributional effects, researchers can provide valuable insights into the mechanisms driving income inequality and inform policy interventions aimed at enhancing human capital development and reducing disparities in earnings.
Now, using the analytical framework proposed by Mincer [10], the theories anticipate a positive correlation between educational levels and wages. However, the underlying transmission mechanism leading to wage increases associated with the ability or skill to achieve labor productivity increments differs. While in the human capital theory education enhances skills, in the signaling theory education facilitates the separation within the group of workers to identify labor productivity. Therefore, even though the evidence suggests a positive increase in wages with increases in educational levels, the theoretical discussion about the main cause of the positive correlation remains open, justifying the relevance of estimating the adjusted Mincer representation to provide new related evidence.
In addition to the above, model identification has improved in recent years. According to the reviewed literature (McGuinness et al. [36], Sachiko Ozawa et al. [37], Peet et al. [38], Vargas-Urrutia [39], Mamun et al. [40], Tenjo et al. [9], Ribero and Meza [41], Forero and Gamboa [42], García-Suaza et al. [43] and Freire and Teijeiro [44]), two identification aspects in estimating an unbiased coefficient of the relationship between educational levels and wages stand out. On the one hand, the presence of selection bias due to the non-randomness of the sample of wages and educational levels, as only individuals participating in the labor market are observed, leads to an overestimated coefficient of the effect of education on wages. On the other hand, the presence of bias due to the endogeneity of wages and educational levels.
The reviewed literature emphasizes the Heckman [45] correction to control for selection bias. This method requires a two-step procedure: in the first step, a Probit model is estimated to predict the probability of being employed, which includes the inactive population; in the second step, the inverse Mills ratio, derived from the first step, is incorporated into the wage equation (typically based on a Mincer representation) to adjust for selection bias. Additionally, the literature highlights the importance of including instrumental variables within a two-stage least squares (2SLS) framework to correct for endogeneity bias in the estimates of the coefficients of interest.
From the perspective of the theoretical validity of education returns in low- and middle-income countries, it is important to note that evidence suggests a greater relevance of factors related to economic development in contrast to the hypothesis of diminishing returns in education returns. In this sense, the limited levels of education coverage and infrastructure in developing countries explain the linear relationship between educational levels and wages. Faced with the low supply of education services and high levels of credit rationing relevant to guarantee access to higher educational levels, the labor market frequently faces a shortage of human talent, pushing wages for educational levels upward. In this way, population growth driving the demand for education faces a limited and costly supply of educational services, increasing the effect of education on wages due to greater growth in the demand for skilled labor relative to the supply of specialized labor (McGuinness et al. [36], Sachiko Ozawa et al. [37], Peet et al. [38]).
In a recent article, Mora et al. [46] analyzed the returns on human capital investments in Colombia from 2016 to 2020, revealing a return rate of 9.7%. This represents a decline of approximately 5 percentage points compared to previous data, indicating a need for renewed focus on human capital investment due to its positive externalities over other investment forms. Therefore, the academic debate on education returns presents a relevant research agenda, particularly for developing countries. Regarding empirical evidence, the linear relationship between education and wages suggested in the reviewed literature implies the importance of education as a factor in economic and human development. Likewise, the lack of theoretical consensus about the transmission mechanism underlying the positive impacts of education on wages through improvements in labor productivity (human capital) and/or separation of workers by capacities and/or credentials (signaling), creating increasing returns in education returns, poses a challenge in identifying the relevant economic theory to understand the functioning of the labor market. Additionally, the methodological approaches implemented in the estimates are also a challenge, which is why in this document we highlight the importance of using quantile and interquantile regression approaches.
3.
Methodology, model, and data
Due to the simplicity of the hypotheses that support it and its ease of calculation, least squares regression is one of the most used methods in econometric estimates. However, the initial hypotheses necessary for its application are frequently not met, especially when dealing with large microeconomic databases from surveys. Common circumstances that give rise to such noncompliance include heteroscedasticity, structural changes, or outliers. One solution to these problems is the quantile regression technique, developed by Koenker and Bassett [17]. It is based on the minimization of absolute deviations weighted with asymmetric weights that are not affected by extreme data points.
3.1. The classic regression model and limitations
The ordinary least squares (OLS) method is the most common way to estimate unknown coefficients in a regression model. This methodology solves an optimization problem by choosing coefficients that minimize the mean square error, which is the sum of the vertical distances between the actual Y values and the predicted Y (ˆY) values at specific data points, taken from all data points. The reason it is the most common method is that minimizing the variance of residuals is equal to minimizing the mean square error. This, combined with each ϵi having a mean of zero, demonstrates that the least squares method gets unbiased and efficient estimators.
Multiple regression aims to build a model predicting Y using the values of different explanatory variables (X_1,X_2,...,X_P) and can be transformed to best fit a p−dimensional hyperplane. Simple linear regression, on the other hand, can be transformed to best fit a straight line, which is useful for predicting the dependent variable given a particular value of X. Simple linear regression occurs when p=1, i.e., only one variable is used to estimate the dependent variable. When we want to examine the relationship between a dependent variable, usually denoted by Y, and one or more independent variables, the model is represented by the following equation:
Here, Y represents the dependent variable, and X1,X2,…,Xp represent the independent variables. The model includes coefficients β0,β1,β2,…,βp, which represent the impact of each independent variable on the dependent variable. The term ε represents the error term, which captures the variability not explained by the independent variables.
This estimation is typically done using various statistical techniques such as ordinary least squares (OLS) regression. Once the model is estimated, we can assess the significance of each coefficient and interpret the results. The coefficients indicate the direction and strength of the relationship between the dependent variable and each independent variable. A positive coefficient suggests a positive relationship, while a negative coefficient suggests a negative relationship. The magnitude of the coefficients provides insights into the relative impact of each independent variable on the dependent variable. Additionally, we can use the estimated model to make predictions. By substituting values of the independent variables into the equation, we can obtain predicted values for the dependent variable. These predicted values can help us understand the expected outcome based on different values of the independent variables.
However, the classic regression model may not be sufficient when it comes to limitations on the normal distribution. The first occurs at the known edge of the design space, where the true relationship is not linear. In this case, the linear approximation may still provide reliable predictions within the design space. However, the usual model fails to adequately represent the effects of different inputs on the output when nonlinearity is present. A nonlinear model takes into account not only the value of a specific variable but also the values of other variables, unlike the partial derivative in the usual regression equation, which quantifies an average effect across all combinations of variables.
Even if nonlinearity does not force observations to lie on or outside the boundaries of the design space, the usual model loses some predictive power. This is because it always follows the derivative of the response surface and does not adapt to the rate of change of the function. In this way, quantile regression provides a robust and flexible alternative to traditional ordinary least squares (OLS) estimation, particularly in cases involving heterogeneity and non-normality in the dependent variable.
One of the main advantages of quantile regression lies in its ability to model and capture the relationship between independent variables and the dependent variable across different parts of the distribution. While OLS focuses solely on the average relationship between variables, quantile regression allows examining how this relationship may vary across different quantiles of the dependent variable's distribution. This is particularly useful when dealing with situations where the relationship between variables may be nonlinear or heterogeneous across different segments of the distribution.
Furthermore, quantile regression is less sensitive to outliers and non-normality in the dependent variable compared to OLS. While OLS may be biased by the presence of extreme observations or non-normal distributions, quantile regression uses quantile estimates that are less sensitive to these irregularities. This allows obtaining more robust and reliable estimates of the effects of independent variables on different parts of the dependent variable's distribution. In Figure 1, each value of Ln(wage), the logarithm of labor income, is plotted against the fraction of the data that have values less than that fraction (left). The diagonal line is a reference line. If Ln(wage) were rectangularly distributed, all the data would be plotted along the line. Since most points are above the reference line, we know that the wage distribution is skewed to the left. This is corroborated by the histogram (right), which shows a left skew.
3.2. The quantile regression model
Quantile regression estimates quantiles of the outcome variable, conditional on the values of the independent variables, with median regression as the default form. Quantile estimation allows us to study different effects across different segments of a population. Koenker and Bassett [10] developed the theory of quantile regression.
Following Wooldridge [47] and Koenker [48], let yi denote a random draw from a population. Then, for 0<τ<1,q(τ) is a τth quantile of the distribution of yi if P(yi≤q(τ))>τ and P(yi≥q(τ))>1−τ. A special case is the median when τ=0.5. For notational convenience, we will write the tau(th) quantile of yi as Quantτ(yi).
Usually, our focus lies in modeling quantiles given a set of covariates xi. In many cases, it is assumed that these quantiles are linear in terms of parameters. Under this linear assumption, we have
where the intercept and slopes depend on τ. To estimate the parameters in a conditional quantile function, it is very helpful to know whether a population quantile solves a population extremum problem. We know that the conditional mean minimizes the expected squared error and the conditional median (when τ=0.5) minimizes the expected absolute error. Generally, if q0(τ) is the τ th quantile of yi, then q0(τ) solves
where 1{·} is the indicator function and is equal to one if the statement in brackets is true and zero otherwise. Then, the objective function to be minimized is
This function is called the asymmetric absolute loss function, the τ-absolute loss function, or sometimes referred to as the check function because it resembles a check mark. The slope of cτ(ϵi) is τ when ϵi>0 and is τ−1 when ϵi<0, but is undefined for ϵi=0.
It follows immediately that a conditional quantile minimizes the asymmetric absolute loss function conditional on xi (when τ=0.5, the median minimizes the absolute error). Therefore, we apply the analogy principle to obtain consistent estimators of the parameters
Under the assumption that θ0(τ)=(α0(τ),β0(τ)')' is the unique minimizer of E[cτ(yi−α−xiβ)] the quantile regression estimator is consistent under very weak regularity conditions. Note that cτ(yi−α−xiβ) is continuous in the parameters because the check function is continuous. However, the check function is not differentiable at zero.
In many applications, the least absolute deviation (LAD) estimator is applied along with OLS, often to supposedly demonstrate the sensitivity of OLS to influential observations. It is recognized that OLS, by minimizing the sum of squared residuals, can be impacted by the presence of extreme observations. Within specific models of data contamination, one can precisely articulate the idea that OLS is non-robust to influential observations, or outliers. Conversely, the LAD estimator (and quantile estimators in general) are considered robust to influential observations. For a formal framework delineating robustness to outlying data, refer to Huber [49]. It is understood that OLS is susceptible to alterations in extreme data points due to the mean's sensitivity to extreme values; whereas LAD is unaffected by changes in extreme data points because the median remains impervious to such variations.
The robustness of the median to extreme value changes is desirable, but it is important not to overlook a significant aspect: often, if not more frequently, our interest lies in the partial effects on the conditional mean. In such cases, it is crucial to acknowledge that least absolute deviations (LAD) regression generally does not consistently estimate parameters in a properly specified conditional mean; only ordinary least squares (OLS) does. Hence, one must exercise caution in attributing differences between LAD and OLS to outliers; there are various other reasons the estimates may significantly diverge. If we define robustness as consistently estimating the parameters of the conditional mean, LAD is not a robust estimator of conditional mean parameters because consistency is maintained only under additional constraints on the conditional distribution. Other so-called robust estimators, where "robust" refers to insensitivity to outliers, are not robust for estimating the conditional mean as they also rely on symmetry for consistency. See Huber [49] and Peracchi [50] for a comprehensive discussion
For asymptotic inference, Buchinsky [51] provided a comprehensive overview of the various methods available for estimating the variance-covariance matrix, considering whether the assumption of independence between regressors and error terms holds or not. These methods include the order statistic estimator, bootstrap estimators, and Kernel estimator, which are valid when the independence condition is met.
Moreover, Buchinsky [52] emphasized that in the presence of indications of heteroscedasticity in the data, the Design matrix bootstrap procedure emerges as the preferred option. Notably, this method is not only considered the most appropriate, alongside the Kernel estimator, in situations where the independence condition is violated, but it also proves to be the most suitable approach even when this condition is met. It is crucial to note that errors estimated through bootstrapping techniques are robust and allow for accurate statistical inference, ensuring the validity of the results obtained.
3.2.1. Pseudo-R2
Finally, as a global measure of model fit, just like in the classic regression model, the R2 value can be calculated. In this case, it is referred to as a pseudo-R2. The pseudo-R2 is calculated as
This is based on the likelihood for a double-exponential distribution eυi|ϵi|, where υi are multipliers
Minimizing the objective function (3) with respect to βτ also minimizes ∑i|ϵi|υi, the sum of weighted least absolute deviations. For example, for the 50th percentile υi=1, for all i, and we have median regression. If we want to estimate the 75th percentile, we weigh the negative residuals by 0.25 and the positive residuals by 0.75. It can be shown that the criterion is minimized when 75% of the residuals are negative.
3.2.2. Interquantile regression
Comparing the coefficients between different quantiles allows us to understand how the relationship between the independent variables and the dependent variable changes across the distribution. If we consider a quantile regression model where the τth quantile is given by
For example, the 90th and 10th quantiles are given by
The difference is then
For these coefficients that are the difference in coefficients of two models in Eq (9), the appropriate standard errors are obtained by bootstrapping.
3.2.3. Inverse Mills ratio
The inverse Mills ratio is commonly used to correct for selection bias, particularly in the two-step Heckman [44] correction model. The process of calculating the inverse Mills ratio involves two main steps:
Step 1: Estimate a Probit model: estimate a selection equation using a Probit model (or sometimes a Logit model). This equation models the probability that an observation is included in the sample (i.e., it is observed in the outcome equation). The Probit equation
where Z = 1 means the observation is included in the sample. Φ() represents the cumulative distribution function (CDF) of that standard normal distribution, and Xβ represents the linear combination of independent variables X and their coefficients β. Predicted values represent the probability of selection for each observation.
Step 2: Calculate the inverse Mills ratio: The inverse Mills ratio is the ratio of the probability density function (PDF) to the cumulative distribution function (CDF) of the standard normal distribution. Mathematically, the inverse Mills ratio
where ϕ(Xβ) is the probability density function (PDF) of the standard normal distribution evaluated at Xβ, and Φ(Xβ) is the cumulative distribution function (CDF) of the standard normal distribution evaluated at Xβ. The inverse Mills ratio is used as an additional regressor in the original equation.
3.2.4. The model and data
Considering the theoretical framework and the literature review, the model specification for analyzing returns to education is grounded in the Mincerian model (Mincer [10]). More precisely, the model to be estimated using quantile regression is as follows:
where Ln (wage) is the logarithm of average monthly labor income. Table 1 presents the variables used and their descriptions. The variables are taken from the Integrated Household Survey (GEIH) of DANE for the year 2019. The formal and young variables are used in the probit model to calculate the inverse mills ratio.
The Great Integrated Household Survey (GEIH) is a survey that requests information about the employment conditions of people (whether they work, what they work, how much they earn, if they have social security in health, or if they are looking for employment), in addition to the general characteristics of the population such as sex, age, marital status, and educational level; information is also collected about their sources of income. The GEIH provides information at the national, urban-rural, regional, and departmental levels, and for each of the departmental capitals.
Table 2 reports summary statistics of the variables used in the estimations and presented in Table 1. The dependent variable, the logarithm of monthly wages [Ln (wage)], has a mean of 13.5021 and a median of 13.6269, indicating a slightly left-skewed distribution. The standard deviation is 0.9644, reflecting some variation in wages, with the minimum value being 3.2189 and the maximum 18.4207. The variable sex, which takes a value of 1 for males and 0 for females, has a mean of 0.5516, indicating that 55% of the sample is male. The number of people in the household (nper) averages 3.9338 with a median of 4, suggesting that most households consist of around four members, though the number ranges from 1 to 28. The migrant variable shows that only 4.11% of the individuals in the sample are migrants.
The variable relationhofh indicates that 54.54% of the individuals are the head of the household. Meanwhile, 60.40% of the sample is either married or in a common-law union, as indicated by the civil status variable. Regarding work experience (p_exp), the average is 19.8673 years, with a large standard deviation of 14.0564 years, reflecting significant variation in experience levels. The variable Academic Degree has a mean value of 2.7539, which suggests that the average level of education lies between secondary education and a technical or technological degree. The average number of hours worked per week (hours worked) is 44.2780, with a wide range extending from 1 to 80 hours, reflecting different working conditions across the sample.
The formal variable indicates that only 38.11% of the workers contribute to social security, suggesting a high rate of informality in the labor market. The young variable shows that 8.49% of the individuals in the sample are young, defined as those between 18 and 28 years of age. The qualification gap variable, with a mean of 0.7832, shows the extent of mismatch between educational qualifications and job requirements, with values ranging from 0 (overqualified) to 2 (underqualified). Finally, the variable economic sector has a mean value of 6.4440, with sectors ranging from 1 (agriculture) to 10 (services), and a median of 6, indicating that a significant portion of individuals work in the middle-tier sectors such as manufacturing, construction, or commerce.
4.
Estimations, results, and discussion
In this section, we present the estimations and results of our empirical analysis on the returns to education. Also, the results are discussed in relation to existing human capital theories and compared with previous empirical findings. Additionally, we explore the policy implications of these findings, particularly in terms of improving access to higher education and addressing inequalities in the distribution of returns to different academic degrees within the labor market.
Table 3 presents the estimated coefficients for each independent variable at different quantiles of the distribution of the logarithm of labor income [Ln (wage)]. For example, the 0.10 quantile represents the lowest 10% of the labor income [Ln (wage)] distribution, while the 0.90 quantile represents the highest 90%. The OLS column presents the results for ordinary least squares estimation, and the LAD median column presents the results for the median. The results for OLS estimation are presented with the aim of comparing them with the estimation at the median (50th percentile). This comparison allows us to analyze the differences in the effects of the explanatory variables across different parts of the income distribution.
Comparing these two estimations enables us to analyze the differences in the effects of the explanatory variables across different parts of the income distribution. First, we observe that the OLS coefficients are higher than those of quantile regression at the median, for most of the coefficients.1 This is evidence that in the median model, the effects are more moderate and consistent across the entire distribution of labor income, and it also highlights the importance of considering the complete income distribution when analyzing the relationship between explanatory variables and the dependent variable.
1 The dependent variable is the logarithm of monthly wages [Ln (wage)], so the interpretation of the coefficients refers to the percentage change in monthly wages when an independent variable changes by one unit, calculated as (eCoef−1)×100%. Many variables are dummy variables, so the interpretation of the coefficients corresponds to the percentage change in wages relative to the reference category.
4.1. Quantile regressions
For the sex variable, there is a significant difference between genders in terms of income. Across all quantiles, the coefficients are positive, indicating that, on average, men tend to earn more than women. For instance, in the 0.10 quantile, the coefficient is 0.1037, suggesting that, on average, men earn approximately 10.93% more than women in this quantile. This difference is magnified in higher quantiles, where the coefficients are larger. For example, in the 0.90 quantile, the coefficient for men is 0.1824, indicating that men earn approximately 20.02% more than women in this quantile. Regarding labor experience (exper), it has a positive impact on income across all quantiles. However, the magnitude of the effect decreases as the quantile increases. The positive coefficient of exper2 (labor experience squared) indicates that the effect of labor experience increases as experience increases, suggesting that the first years of experience have positive returns, given a low level of experience. However, they are not consistent with what would be expected theoretically, and they are also very low.
Concerning the number of people in the household (nper), negative coefficients median and highest quantiles indicate that a higher number of people in the household is associated with lower incomes at all income levels. In quantiles 0.10 and 0.25, the sign is positive in the lowest incomes; this possibly indicates that individuals are more forced to look for a job as the number of people in the household increases. For instance, in the 0.10 quantile, the coefficient is 0.013, suggesting that, on average, each additional person in the household is associated with an increase of 1.3% in labor income, while in the 90th quantile, it is associated with a decrease of 1.27%. Positive coefficients for relationhofh (relationship with the head of the household) across all quantiles suggest that having a closer relationship with the head of the household is associated with higher incomes at all income levels. For example, in the 0.10 quantile, the coefficient is 0.0717, indicating that, on average, having a closer relationship with the head of the household is associated with a 7.44% increase in labor income in this quantile, while in the 0.90 quantile, it is 10.04%. This could be explained as typically the head of the household holds the greatest responsibility in the home. Civil status has positive coefficients in all quantiles except the 0.10 quantile, indicating that being married or in a common-law relationship (for more than two years) is associated with higher incomes. In the 0.10 quantile, married individuals or those in a common-law relationship earn 23.87% less than those with a different marital status, while those in the 0.90 quantile earn 17.07% more.
It is observed that being young has a positive impact on incomes for the lower quantiles (0.10 and 0.25), but this effect diminishes or becomes negative in higher quantiles (0.50, 0.75, and 0.90). For example, in the 0.10 quantile, the coefficient is 0.0280, indicating that young people earn approximately 2.80% more than other groups in this quantile. In the 90th quantile, the coefficient is −0.0325, indicating that young people earn 3.25% less than non-young individuals in this segment of the income distribution. In terms of human capital, when young individuals have high incomes, they are generally more educated (with access to more advanced career opportunities, more academic degrees, or higher levels of qualification) than adults, but they are penalized by experience. A higher number of people in the household tends to be associated with lower incomes across all quantiles.
With respect to vulnerable populations, the coefficients associated with migrant suggest that migrants earn less than nationals across all quantiles. For example, in the 0.10 quantile, the coefficient is −0.3126, indicating that, on average, migrants earn approximately 26.85% less than non-migrants in this quantile, while those in the 0.90 quantile earn 14.03% less.
The results for different levels of academic degrees show what would be expected given the education and years of schooling implied by these titles. For a secondary degree, the positive coefficients for all quantiles suggest that having a secondary degree is associated with higher incomes compared to having no degree. For example, in the 0.10 quantile, the coefficient is 0.2674, indicating that, on average, individuals with a secondary degree earn approximately 30.66% more than those without this degree in this quantile. This difference persists in higher quantiles, although it decreases slightly in the higher quantiles. For the 0.9 quantile, individuals with a secondary degree earn 12.82% more than those without degrees. On the other hand, having a technician or technology degree is associated with higher incomes compared to having no degree. For example, in the 0.10 quantile, the coefficient of 0.4941 indicates that, on average, individuals with a technical or technology degree earn approximately 63.91% more than those without degrees in this quantile. This difference persists and even amplifies in higher quantiles, with individuals in the 0.9 quantile earning 44.17% more than those without degrees. These results can be observed in Figure 2.
The results suggest that having a university degree is associated with higher incomes compared to other degree levels. For example, in the 0.10 quantile, the coefficient is 1.36, indicating that, on average, individuals with a university degree earn approximately 290.95% more than those without degrees in this quantile. This difference persists and is further amplified in higher quantiles, where, for example, in the 0.9 quantile, they earn 100% more than those without degrees in that quantile. The percentages may seem very high at first glance, but if we consider that in Colombia, a person without education (no high school diploma) can earn $1,300,000 pesos in 2023, while a person with a university degree can earn $7,800,000 pesos, this represents a 500% difference.
Finally, having a postgraduate degree implies even higher incomes compared to other educational levels. For example, in the 0.10 quantile, the coefficient is 1.92, indicating that, on average, individuals with a postgraduate degree earn approximately 587% more than those without degrees in this quantile, while in the 0.9 quantile, they earn 513% more. Again, these results can be observed graphically in Figure 2.
Regarding the coefficients measuring qualification gaps, the underqualified are positive compared to qualified, indicating that, on average, individuals in these groups earn more than the qualified. This may seem counterintuitive, but it could be due to various factors such as specific labor demand, work experience, and labor flexibility. In the other hand, the overqualified are negative compared to qualified, indicating that, on average, individuals in these groups earn less than the qualified.
It is possible that, in certain sectors or industries, the specific skills possessed by the underqualified are in high demand, which could increase their incomes compared to the qualified. Additionally, even though they may be overqualified for the job requirements, the qualified individuals may lack the necessary work experience to demand higher salaries. Meanwhile, the underqualified and qualified may have a combination of skills and experience that allows them to obtain better wages. Finally, the underqualified and qualified may be willing to accept a wider range of jobs, allowing them to access better-paying job opportunities compared to the overqualified who may be more selective.
The estimated coefficients by economic sector show that, when comparing each economic sector to agriculture as the baseline, positive coefficients would indicate that individuals working in those sectors earn more on average than those in the agricultural sector. This can be attributed to a variety of factors related to the nature of the industry, labor demand, and working conditions, as some sectors may offer better working conditions, benefits, or advancement opportunities than others. For example, if we consider the Mines and Quarries sector, the positive coefficient of 0.5784 at the median (quantile 0.50) indicates that, on average, individuals working in this sector have significantly higher labor incomes (78.31%) than those in the agricultural sector. This suggests that mining and quarrying-related activities are potentially more lucrative compared to agriculture, as they are often associated with economic activities requiring specialized skills or linked to products with higher market value, as, in Colombia, the oil extraction sector. This difference increases in higher quantiles, reaching 117.44% at the 0.90 quantile.
Sectors such as Financial Establishments or Real Estate Activities may have higher labor demand or are associated with jobs requiring higher levels of education. For example, Financial Establishments at the 0.90 quantile has a coefficient of 0.4633, indicating that individuals in this quantile earn 58.93% more than individuals employed in the agricultural sector. Moreover, sectors such as Elec, gas & water or Services are more oriented toward innovation and technology, which could be reflected in higher salaries for employees working in those areas. For example, workers in the Elec, gas & water sector at the 0.90 quantile have incomes 19.43% higher than those in the agriculture sector, and 29.02% higher in services. On the other hand, if we look at the Commerce, Rest & Hotels sector, which has a positive coefficient of 0.1214, or transport and communications, with a coefficient of 0.0701 at the 0.90 quantile, although still being higher than zero, it is relatively lower compared to other sectors such as Mines and Quarries. This suggests that while workers in this sector may have higher labor incomes than those in agriculture, they are likely not as high as in more specialized or skill-intensive sectors.
Lastly, the Services sector has a positive coefficient of 0.2548 at the 0.90 quantile, indicating that workers in this sector have higher (29.02%) labor incomes on average compared to agriculture. Since the services sector is diverse and can encompass a wide range of industries, this coefficient could reflect variability in labor incomes within the sector, with some subsectors offering higher salaries than others.
These results are consistent with Schultz's theory [2], which suggests that individuals who invest in their human capital through education achieve higher incomes. However, these returns are not homogeneous, as they depend on the type of industry and the demand for skills in each sector. In sectors such as mining, finance, and specialized services, where technical skills and advanced knowledge are highly valued, the returns to education are significantly higher. Workers with university or postgraduate degrees in these sectors earn considerably more than those with lower educational levels. According to Schultz, this occurs because in these sectors, education not only increases worker productivity but also reduces informational asymmetry between employers and employees, as educational qualifications act as a signal of skills and competencies. Conversely, in sectors like agriculture and commerce, where entry barriers are lower and the demand for specialized human capital is reduced, the returns to education are smaller. This reinforces Schultz's idea that investing in education yields higher returns in contexts where advanced skills are essential for improving productivity and generating added value. Individuals with high educational levels in these sectors experience a lower return on their human capital investment, highlighting the importance of aligning educational supply with the demand for skills in the labor market.
Another analysis complements these findings. Figure 3 shows the calculated marginal effects of sectoral returns across different quantiles (Q10, Q25, Q50, Q75, Q90), providing insights into how returns vary both by sector and across different parts of the wage distribution. For example, Sector 2 (Mines and quarries) consistently exhibits the highest marginal effects across all quantiles, with the most pronounced peaks in the Q10 and Q75 quantiles. Sector 1 is agriculture, which shows consistently lower marginal effects across all quantiles.
Across all sectors, as we move from lower to higher quantiles, the marginal effects generally increase, meaning that the wage returns to education or qualifications tend to be higher for those in the upper segments of the income distribution. This trend suggests that higher-income earners in many sectors receive larger proportional gains from education or skills compared to their lower-income counterparts. The graphs highlight significant differences in how sectors reward qualifications across quantiles. For instance, Sectors 2 and 8 offer more substantial marginal returns across multiple quantiles, making them attractive for individuals across the wage distribution. In contrast, Sector 1 appears to offer limited wage growth from additional education or qualifications across all levels of income. The variation in calculated marginal effects across sectors and quantiles indicates that education or qualifications do not yield uniform benefits across sectors or the wage distribution. Sectors with higher marginal effects for upper quantiles, like Sector 8, may contribute to widening wage inequality, as those in higher income brackets benefit disproportionately from additional qualifications. On the other hand, sectors with higher returns in lower quantiles, like Sector 9, suggest that education can serve as a tool for upward mobility for lower-income individuals.
4.2. Interquantile: Coefficients across quantiles
As mentioned earlier, in addition to the previous analyses, an interquantile regression was conducted to examine the differences between quantiles within each group. The differences considered are between (90-Q10), (Q90-Q75), (Q90-Q50), and (Q90-Q25), with the results presented in Table 4, and between (Q75-Q25), (Q50-Q25), and (Q25-Q10), which are shown in Table 5.
In Table 4, regarding the gender variable (sex), the positive coefficients in interquartile comparisons (Q90-Q10, Q75-Q10, Q50-Q10) indicate that, overall, men tend to have higher labor incomes than women across all income levels. This gap tends to be more pronounced in the lower quartiles and diminishes in the upper quartiles.
A higher number of people in the household (nper) is associated with lower labor incomes across all quantile comparisons (Q90-Q10, Q75-Q10, Q50-Q10, and Q25-Q10); the coefficients are negative and statistically significant. For example, in the Q90-Q10 comparison, the coefficient is −0.0258, indicating that larger households are associated with a 2.55 percentual points reduction in wages for high-income earners compared to low-income earners. This suggests that individuals in larger households tend to earn less, and this negative impact on wages is more pronounced among higher earners. The effect diminishes slightly at lower quantiles, but remains statistically significant, indicating that household size consistently exerts a downward pressure on wages across all income levels.
For the migrant status, the coefficients are positive and significant across all quantile comparisons, with the Q90-Q10 coefficient being 0.1613. This indicates that migrants earn 17.51 percentual points more at the 90th quantile compared to the 10th quantile, suggesting that migrants face fewer wage disadvantages at the top of the income distribution. As we move to lower quantiles, the wage advantage for migrants decreases but remains positive. For example, in the Q75-Q10 comparison, the coefficient is 0.1598, and in the Q25-Q10 comparison, it is 0.0648. These findings suggest that migrants are able to overcome some wage penalties at higher income levels, potentially due to access to higher-paying jobs that value their skills and experience more than in lower-paying roles. However, migrants still face wage disadvantages at the lower end of the income distribution, where they may encounter barriers such as discrimination or lack of recognition of their qualifications. This implies that while migrants can improve their wages as they progress in their careers, targeted interventions are needed to reduce wage penalties at the lower end of the income spectrum.
The relationship with the household head (relationhofh) shows a small positive impact in the Q90-Q10 comparison, with a coefficient of 0.0239, suggesting that being the head of the household is associated with 2.43 percentual points increase in wages for higher earners compared to lower earners. However, this effect is not statistically significant in other quantile comparisons, indicating that this relationship does not have a consistent or strong influence on wages across different income levels. The civil status variable, which represents being married or in a free union, shows negative and statistically significant coefficients across all quantile comparisons. In the Q90-Q10 comparison, the coefficient is −0.0564, indicating that the wage premium associated with being married is 5.49 percentual points smaller for high-income earners compared to low-income earners. The effect is even more pronounced in the Q75-Q10 and Q50-Q10 comparisons, with coefficients of −0.0855 and −0.0860, respectively. This suggests that while being married or in a union may offer some wage advantages, these benefits are smaller for higher earners, possibly due to other factors like job type or household responsibilities affecting higher-income individuals differently.
For work experience (exper), the coefficients are negative across all quantile comparisons, indicating that the returns to experience are smaller for high-income earners than for low-income earners. In the Q90-Q10 comparison, the coefficient is −0.0014, meaning that the wage benefit of experience is 0.15 percentual points smaller for those at the top of the income distribution. The effect becomes more pronounced in the Q75-Q10 comparison, where the coefficient is −0.0030, and slightly smaller in the Q50-Q10 comparison (−0.0025). This suggests that while experience contributes to wage growth, its impact diminishes at higher income levels, likely due to diminishing returns as workers accumulate more experience. The insignificant coefficients for the quadratic term (exper²) across all quantiles further confirm that experience has a linear effect on wages across the distribution.
The analysis of educational attainment (Academic degree) reveals important differences in how education impacts wages at different points in the income distribution. For individuals with a secondary degree, the coefficients are consistently negative across all quantile comparisons, though not statistically significant. In the Q90-Q10 comparison, the coefficient is −0.1468, suggesting that having a secondary degree does not significantly improve wages for high-income earners compared to low-income earners. This pattern suggests that secondary education alone does not offer a substantial wage advantage, especially at higher income levels. For those with a technical or technology degree, the results are more positive but still show a diminishing effect at higher income levels. In the Q90-Q10 comparison, the coefficient is −0.1282, indicating that the wage premium for technical or technological degrees is 12.04 percentual points lower for high-income earners compared to low-income earners. This suggests that while these degrees provide wage benefits, they are more pronounced at the lower end of the income distribution.
In contrast, individuals with a university degree experience smaller returns at higher income levels. In the Q90-Q10 comparison, the coefficient is −0.0713, indicating that high earners with a university degree earn 6.89 percentual points less than their counterparts at the lower end of the distribution. This finding suggests that while university education significantly boosts wages, its relative benefit decreases as income increases, likely because high-income earners rely more on other factors, such as work experience or sector-specific skills, to boost their earnings. For those with postgraduate degrees, the Q90-Q10 coefficient is −0.1147, indicating that the wage premium for postgraduate education is 10.84 percentual points smaller for high earners than for low earners. This highlights a diminishing return to advanced education at the top of the wage distribution, suggesting that while postgraduate degrees lead to significant wage gains, the relative advantage decreases as one moves up the income ladder.
The qualification gap variable provides interesting insights into how being underqualified or overqualified affects wages across the distribution. Being underqualified has a positive and statistically significant impact in the Q90-Q10 comparison, with a coefficient of 0.3453, meaning that underqualified individuals earn 41.25 percentual points more in the 90th quantile compared to the 10th quantile. This suggests that underqualified workers are better compensated at higher income levels, likely due to the value of their skills or the specific roles they occupy. Conversely, being overqualified shows a small but negative effect on wages at lower income levels, with the Q50-Q10 coefficient at −0.0263, indicating that overqualified workers earn 2.60 percentual points less in the middle of the distribution compared to the bottom. This suggests that overqualification is more detrimental for lower earners, possibly because they are not fully utilizing their skills in their current roles.
Finally, the economic sector results show substantial wage inequality across sectors. The mining and quarrying sector consistently exhibits large positive coefficients across all quantile comparisons, with a coefficient of 0.4156 in the Q90-Q10 comparison. This indicates that high earners in this sector benefit from a 51.54 percentual points wage premium compared to low earners, reflecting significant wage inequality within the sector. The financial establishments sector also shows positive coefficients, with a Q90-Q10 value of 0.0774, suggesting that wage inequality is present but less pronounced than in mining. On the other hand, sectors such as services and real estate activities exhibit negative coefficients, indicating that wage differentials between high and low earners are smaller in these sectors. For example, in the services sector, the Q90-Q10 coefficient is −0.1117, meaning that top earners in this sector do not experience significantly higher wages compared to lower earners. This implies that sectors like mining and finance contribute more to overall wage inequality, while sectors like services and real estate show more wage equality across the distribution.
The results of the interquartile regression (Q90-25, Q75-Q25, and Q50-Q25), shown in Table 5, show that men consistently earn more than women across all comparisons, with the wage gap widening at higher income levels, indicating that men benefit more from wage premiums in higher-paying jobs. Household size negatively impacts wages, especially for higher earners, while migrants tend to earn more as they move up the wage distribution, with a notable premium for high-income migrants.
Education plays a significant role in wage differences. Secondary education shows little wage improvement across income levels, while technical and technological degrees offer moderate gains, particularly for high earners. University and postgraduate degrees provide strong wage premiums, especially for individuals in the 90th percentile, reinforcing income inequality at the top of the distribution. The wage premium for university education decreases for middle-income earners, suggesting a diminished impact on wages at lower levels.
Industry also influences wage disparities. Workers in mining and finance enjoy substantial wage premiums, especially in the upper-income quantiles, with high earners in mining benefiting disproportionately. Conversely, sectors like services exhibit smaller wage differentials, indicating less income inequality within these industries. Thus, higher education and working in capital-intensive sectors like mining or finance significantly boost wages, particularly for top earners, while gender and household size further contribute to wage inequality. This underscores the importance of both education and industry choice in shaping wage outcomes across the income distribution.
4.3. Implications
The estimations and results reveal substantial differences in wage premiums for individuals with the same educational attainment, depending on the industry in which they are employed. For instance, individuals with a university degree working in sectors such as mining or financial establishments earn significantly more than those with the same degree working in sectors like agriculture or commerce. This disparity highlights the importance of sectoral dynamics and the specific value placed on education and skills in different industries.
The fact that wages can double (over 100%) for the same educational degree depending on the industry can be explained by several factors related to the economic structure, labor demand, and the specific characteristics of different industries, principally industry-specific demand for skills, capital-intensive vs. labor-intensive sectors, productivity differences, bargaining power and unionization, Risk and working conditions, market structure and competition, regional and global factors. For example, different industries place varying levels of importance on specific skills and qualifications, even for the same educational degree. For example, a university degree in engineering may be valued differently in the mining industry versus the education sector. In industries like mining, finance, or technology, highly specialized skills tied to education are in high demand, driving up wages for those with relevant qualifications. Conversely, industries such as retail or hospitality may not require the same level of specialization, which limits wage growth even for highly educated individuals.
Industries that are capital-intensive, such as mining, oil, and technology, often generate higher profits due to the value of their products and services. These industries can afford to pay higher wages, particularly to workers with higher education who are instrumental in managing complex processes and technologies. In contrast, labor-intensive sectors such as agriculture or retail tend to have lower profit margins and are less able to offer high wages, even to workers with the same level of education. As a result, the same degree can command vastly different wages depending on whether the individual works in a capital-intensive or labor-intensive sector.
Also, the productivity of workers often varies significantly across industries, even for workers with the same educational background. In sectors like finance or technology, employees with university or postgraduate degrees may contribute more to the overall productivity and revenue of the firm, which translates into higher wages. In contrast, industries with lower productivity levels may not see the same return on investment from educated workers, leading to lower wage premiums for the same degree.
In some industries, workers have greater bargaining power, either through unions or individual negotiation, which can lead to higher wages for the same level of education. For instance, in sectors like mining or energy, strong unions and collective bargaining agreements often secure higher wages for skilled workers. In contrast, industries like retail or education may have a lower union presence or weaker bargaining power, resulting in lower wages for equally educated individuals.
Certain industries offer higher wages as compensation for more difficult or risky working conditions. For example, workers in industries like mining or construction may receive higher wages to compensate for the physical dangers or harsh environments they face, regardless of their educational level. In contrast, safer and more comfortable working environments, such as those found in office-based sectors like administration or education, may offer lower wages for the same qualifications because the risk premium is absent.
Some industries operate in highly competitive markets with less regulation, which can drive wages down, while others benefit from oligopolistic or monopolistic market structures where firms can afford to pay higher wages. For instance, industries like finance or pharmaceuticals often operate with fewer players and higher profit margins, allowing them to offer more competitive wages to attract highly educated talent. On the other hand, sectors with more competition and lower entry barriers, such as hospitality or retail, may not have the same capacity to offer high wages even to employees with advanced degrees.
Globalization and regional economic development also play a role in how wages differ for the same degree across industries. Industries that are globally competitive, such as technology or finance, often offer higher wages because they need to attract top talent from around the world and have to compete internationally. In contrast, industries that are more localized or regionally focused, like agriculture or public services, may not face the same level of competition for talent and, therefore, offer lower wages.
These industry-specific differences in wage premiums for the same degree have important implications for both individuals and policymakers. For individuals, it underscores the need to consider not only the educational qualifications they obtain but also the industries they choose to enter. For policymakers, it suggests that education and labor policies should focus on guiding students toward high-demand, high-wage industries where their educational qualifications will yield the greatest returns. Additionally, it highlights the importance of addressing wage disparities across sectors through targeted policies aimed at increasing productivity, improving working conditions, and enhancing bargaining power in lower-wage industries.
With respect to the most vulnerable populations in the labor market, we can consider that, for migrants, the wage gaps persist across all quantiles, suggesting that, even with comparable education levels, migrants earn significantly less than non-migrants. This could be attributed to factors such as limited access to networks, lower bargaining power, or discrimination in the labor market. Additionally, migrants may face difficulties in obtaining jobs in industries that offer higher returns to education, such as finance or mining, which exacerbates their wage disadvantage. From a policy perspective, targeted interventions are necessary to facilitate migrants' access to these higher-paying industries, including programs that recognize foreign qualifications and provide job placement support in sectors with higher demand for skilled labor.
Regarding women, the gender wage gap is evident across all industries and educational levels. While women with higher education may have better access to higher-paying jobs, they continue to earn less than their male counterparts in the same industry and with the same qualifications. This suggests that structural barriers, such as gender bias, glass ceilings, and differences in job assignments, persist, limiting women's earning potential. Addressing these inequalities requires policies that promote gender equity in the workplace, such as enforcing equal pay for equal work, improving access to leadership positions for women, and encouraging their participation in high-return sectors like technology, finance, and mining, where the wage premiums for higher education are most substantial.
For young people, the individuals with less experience, the results show that while they may benefit from higher educational attainment, they are often penalized by their lack of experience. In industries where experience is highly valued, such as finance or specialized technical fields, young workers may face difficulties in achieving comparable wage levels to older, more experienced workers, even with similar education levels. This experience gap limits their ability to capitalize on their education early in their careers. To address this, policies that provide early-career support, such as internships, apprenticeships, and mentorship programs in high-return sectors, can help young workers bridge the experience gap and increase their earnings potential.
The interquartile regressions highlight the persistence of gender inequality in high-paying jobs and suggest that policies aimed at reducing the gender wage gap need to focus on improving access to leadership and high-income positions for women. In addition, addressing gender biases in promotions and compensation structures, particularly in high-wage industries, is critical for narrowing the wage gap at the top of the distribution.
The negative coefficients for higher educational degrees, such as university and postgraduate levels, indicate that the returns to education are more substantial for lower earners than for higher earners. This suggests diminishing marginal returns to education as one moves up the income distribution. While education still provides significant wage premiums across all quantiles, these results imply that further investments in education may be more effective in reducing wage inequality if targeted toward lower-income workers. Policies that promote access to higher education for disadvantaged groups or those in lower income brackets could help reduce income disparities. However, for higher earners, other factors, such as work experience, industry, and skill specialization, may play a larger role in wage determination than additional educational attainment.
The significant positive coefficients for sectors like mining and quarries and financial establishments suggest that these industries offer disproportionately higher wage premiums for high earners compared to low earners. This reinforces wage inequality within these sectors, where the gap between top and bottom earners is substantial. Policies that promote broader access to these high-return industries, particularly for lower-income workers, could help mitigate wage disparities. For instance, encouraging education and training programs that focus on skills relevant to these sectors could improve the employability of lower-income individuals in more lucrative industries, thereby reducing income inequality.
Conversely, sectors such as real estate activities and services show smaller or even negative wage differentials between high and low earners. This indicates that wages in these sectors are more evenly distributed, with less of a premium for top earners. While this suggests lower wage inequality within these sectors, it may also reflect limited opportunities for wage growth. Policymakers should consider strategies to increase wage progression in sectors with limited differentiation by promoting skills development, higher education, and career advancement opportunities.
The findings related to migrants and the qualification gap suggest that policies targeting these vulnerable populations could help reduce wage inequality. Migrants appear to fare better at the higher end of the income distribution, indicating that they may face less discrimination or structural barriers in high-paying jobs compared to low-paying jobs. Nonetheless, targeted policies that support migrant integration, especially at lower wage levels, are essential to ensure that all workers can access fair compensation across industries.
For the qualification gap, underqualified workers face less of a penalty at higher wage levels, suggesting that high-earning individuals may be able to compensate for underqualification through experience or specialized skills. Conversely, overqualified workers experience more wage penalties at lower income levels. This suggests that lower earners may be less able to leverage their educational qualifications into higher wages. Addressing this mismatch between education and job requirements, particularly for lower-income workers, is critical. Policies that support continuous skills development, requalification, or job placement programs for overqualified workers could help them fully realize their wage potential.
These findings highlight the need for targeted policy interventions to address wage inequality. Education and training programs should focus on sectors that offer high returns, such as mining, finance, and technology, while also providing support for workers in lower-return sectors. Gender equality initiatives need to emphasize reducing wage gaps at the higher end of the income distribution by addressing barriers to advancement and ensuring equal pay for equal work in high-paying industries.
Additionally, policies should aim to reduce qualification mismatches and support vulnerable groups, such as migrants and overqualified workers, to ensure they can access fair wages throughout the income distribution. Programs that facilitate entry into high-paying sectors, especially for disadvantaged groups, could help close wage gaps and promote more equitable wage growth across industries and education levels.
5.
Conclusions
The relationship between education and labor income has long been a central focus in economic literature, recognized as a key driver of economic development. This study contributes to this body of knowledge by examining how education influences wage outcomes across different sectors and levels of income distribution in Colombia. Building on human capital theory, as outlined by Becker [1], and expanding on the limited use of quantile regression models in Colombia seen in studies by Mora [4], Castillo et al. [5], and García [6], this research employed quantile and interquantile regressions to analyze returns to education by academic degree (Secondary, Technical/Technological, University, and Postgraduate) across economic sectors and vulnerable populations. The results offer a nuanced understanding of how labor incomes differ across income levels, sectors, and population groups, providing critical insights into wage inequality and the role of education.
The quantile regression models revealed significant disparities in returns to education across different income levels. Notably, individuals with postgraduate degrees experienced the greatest increases in their incomes, particularly in the upper quantiles. This finding underscores the outsized impact of higher education on labor incomes, especially in the higher segments of the wage distribution. The implication is clear: education remains a powerful tool for enhancing economic mobility, particularly for those already in higher-paying jobs, further emphasizing the value of advanced degrees in improving economic outcomes.
Significant differences in wage premiums were also observed between academic degree levels. Individuals with university and postgraduate degrees consistently earned more than those with secondary or technical qualifications. Additionally, the results showed that formal employment significantly boosts labor incomes, particularly at the lower end of the wage spectrum, with this effect diminishing in higher wage brackets. These findings point to the need for policies that promote formalization in employment, particularly for lower-income workers, as a means to reduce wage gaps and increase equity in the labor market.
Interquantile regression results provided further insights into the disparities between population groups and sectors. Vulnerable populations, such as migrants and young individuals, faced considerable income disparities between the upper and lower quartiles, highlighting the need for targeted public policies to address these wage gaps and promote equal opportunities. The findings reveal that while education is critical, its impact varies across sectors and demographic groups, requiring tailored interventions to ensure more equitable labor market outcomes.
The interquantile differences in coefficients underscore the growing importance of education at higher wage levels. As individuals move up the income distribution, the wage benefits of having a technical, university, or postgraduate degree become even more pronounced. This suggests that the returns to education, while substantial for all workers, are particularly critical in mitigating wage inequality among higher earners. These dynamics provide a roadmap for policy interventions aimed at promoting inclusive growth by focusing on education, addressing sector-specific wage disparities, and supporting vulnerable populations in achieving equitable labor outcomes.
In analyzing wages by economic sector, the study identified specific industries, such as mining and quarries, that offer higher returns to education, particularly for those in the upper quantiles. This indicates that highly skilled workers with higher education degrees are likely to benefit more from industries that demand specialized skills and have higher productivity levels. Conversely, sectors like agriculture or commerce, where low-skilled work predominates and productivity is lower, offer limited wage premiums even for university graduates. This divergence in sectoral wage returns calls for policies that align educational investment with labor market demands, particularly in high-return industries.
The variation in wage premiums across industries, even for individuals with the same educational level, has critical implications for education and labor policy. For individuals, understanding how industry choice influences the returns to their education can guide more informed career decisions, encouraging students to pursue degrees and skills that are in higher demand in lucrative sectors. For policymakers, these findings highlight the need to support education and training in sectors that offer the highest returns, such as mining, finance, and technology. This approach could enhance the efficiency of educational investments and help reduce income inequality by aligning workforce skills with industry needs.
Overall, this study underscores the central role of education in determining labor incomes in Colombia and highlights the importance of public policies that address wage disparities across sectors and demographic groups. The findings point to the need for targeted interventions aimed at fostering equal opportunities and reducing wage gaps, particularly by promoting education in high-demand sectors and supporting formalization in the labor market.
Looking ahead, future research should delve deeper into the mechanisms driving these income disparities, such as industry-specific demand, labor market structures, and the impact of policy interventions. Furthermore, exploring the effects of macroeconomic trends, technological advancements, and globalization on income inequality across demographic and socioeconomic groups could provide further insights into the evolving nature of wage disparities and inform more effective policy solutions.
Use of Generative-AI tools declaration
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.
Author contributions
Jacobo Campo Robledo: Conceptualization, Methodology, Formal Analysis, Writing– original draft preparation, Writing–review & editing; Cristian Castillo Robayo: Conceptualization, Methodology, Formal Analysis, Writing–original draft preparation, Writing– review & editing; Julimar da Silva Bichara: Conceptualization, Funding Acquisition, Methodology, Formal Analysis, Writing–original draft preparation, Writing– review & editing. All authors have read and agreed to the published version of the manuscript.
Conflict of interest
The authors declare no conflict of interest.
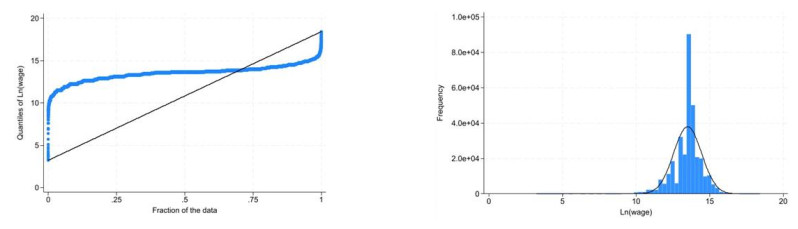









 DownLoad:
DownLoad:





