1.
Introduction
The novel coronavirus, known as Covid-19, has spread worldwide and has caused millions of deaths. The virus causes severe lung complications that may result in breathing difficulties; in some cases, it can cause organ failure or even death of the infected person. The disease is very contagious among humans and spreads through either direct or indirect bodily contact [1]. Coronavirus is usually transmitted through inhalation, exhalation, or coughing of an infected person. Therefore, healthy individuals are always at risk of developing coronavirus disease. The virus has not only affected people's lives, but has also had a significant impact on the economies of underdeveloped and developed countries [2,3]. The incubation period is between 2 to 14 days. People infected with coronavirus can still spread the infection to others, even if they do not experience any symptoms after this period. The majority of coronavirus-infected individuals may experience mild to moderate respiratory symptoms, such as muscle aches, fever, fatigue, cough, severe headaches, diarrhea, vomiting, a runny nose, and a sore throat. Individuals who experience any of these symptoms should immediately seek medical attention. It has been observed that the risk of developing Covid-19 is the greatest in individuals with co-existing conditions such as diabetes, hypertension, immune deficiency, respiratory infection, and being aged over 60 [4]. Having a thorough understanding of the dynamics of the disease can significantly decrease the incidence of infection in society.
Dengue fever is another considerable global public health issue. The disease is spread by Aedes aegypti and Aedes albopictus mosquitoes, which both act as vectors. Dengue fever is caused by four different serotypes. When a person exposed to one serotype recovers, they are immune to that specific serotype; however, they are only partially and temporarily immune to the other three. The severity of dengue fever varies. Throughout the entire life cycle of the dengue fever virus, the mosquito acts as a transmitter (or vector), as well as the main source of infection. Those who contract more severe dengue fever strains typically require hospitalization. Stopping human-vector contact or controlling mosquito vectors are the only ways to either stop or lessen dengue virus transmission [5,6]. The symptoms of dengue infection include fever, rash, nausea, and aches that can last for a week. By better comprehending the dynamics of this fatal disease better, we can lessen its impact on our society.
According to medical sources, the early symptoms of dengue fever and Covid-19 are comparable, which is the premise underlying this co-infection modeling [7]. We aim to evaluate and predict the transmission dynamics of both deadly viruses' propagation to the same person. We believe that the patient had a mild case of Covid-19 infection first, and then contracted dengue fever a week later, while still suffering from the Covid-19 infection. Differentiating between Covid-19 and dengue fever can be challenging since both conditions share similar clinical signs and test findings, including fever, headache, myalgia, and exhaustion [8]. According to clinical evidence, co-infections with Covid-19 and dengue fever are linked to increased morbidity and mortality. Verduyn et al. [7] reported the first case of a co-infection with Covid-19 and dengue fever in a French overseas territory in the Indian Ocean. A thorough analysis of the information on a possible Covid-19 and dengue co-infection in a single person has been published, see [9]. Co-epidemics can place a significant burden on local populations and health systems. Since the symptoms of Covid-19 and dengue are similar, it is possible to misdiagnose one illness as the other, which would reduce the number of co-infections between the two diseases [10,11,12,13]. Cases of co-infection have also been documented in Pakistan. A study revealed that patients with Covid-19 and dengue fever had a higher fatality rate than those with Covid-19 alone [7]. Similar to this, patients with Covid-19 mono-infection display distinct biochemical and hematological markers separate from those with co-infection. For example, those with mono-infection did not experience severe thrombocytopenia, though those with co-infection did. Additionally, co-infected patients have higher concentrations of urea, bilirubin, alanine aminotransferase, creatine phosphokinase, and prothrombin.
Mathematical modeling is a tool that can be used to forecast the evolution of communicable diseases with prevention strategies. In recent years, fractional calculus has been used to solve physical problems that can not be resolved using integer-order differential equations. The fractional-order model is always better for many real-world applications than the corresponding integer-order model. For example, it is not possible to gain a better understanding of the memory effects seen in biological models [14,15,16,17] by utilizing integer-order models. In mathematical models, fractional-order operators can be used to solve differential equations without being limited by an order constraint. This means that fractional models are more resourceful than classic integer-order models, and therefore provide more accurate and precise information about complicated systems. Optimal control problems involving fractional operators are called fractional optimal control problems. Many researchers [17,18,19,20,21] have defined fractional optimal control problems to provide reasonable and effective control strategies to either eradicate or minimize infection or addiction within the human population.
In recent years, many researchers have started to include memory effects in fractional models with various fractional operators to improve epidemiological disease analyses [22,23,24,25]. The most common of these are the Caputo and Riemann-Liouville operators. The basic drawback of these operators is the singularity of the associated kernels. Since it is difficult to resolve many physical systems using singular kernels, non-singular fractional derivatives, such as Caputo-Fabrizo (CF), have been developed and implemented [26,27,28,29]. Despite the non-singular kernel of the CF derivative, it has no memory effects and has an unclear function space [30]. In [31], the authors presented a novel Atangana-Baleanu-Caputo (ABC) fractional derivative operator that made use of a Mittag-Leffler (ML) kernel with a single parameter. The non-local and non-singular behavior of the ML function is its key feature. This feature made the ABC operator the best choice for modeling epidemic diseases. In [32], authors investigated the stability and existence of a unique solution of a random fractional-order system using the global and non-singular kernel of the Atangana-Baleanu derivative in the sense of the Caputo.
Several mathematical models have been built to investigate the dynamics of Covid-19 [33,34,35,36,37,38] and dengue fever [19,39] and to propose methods for disease control. The authors in [40] used different piecewise fractional differential operators to develop a comprehensive nonlinear stochastic model with six cohorts that relied on ordinary differential equations. Their findings revealed a piecewise numerical technique to produce simulation studies for these frameworks. In [41], a novel fractional-order discrete difference Covid-19 model for prevalence and incidence was suggested to advance the field of epidemiological studies. Li et al. [42] established a novel Covid-19 epidemic model to simulate the transmission of a mutated Covid-19 strain (Delta strain) in China with a vaccinated population to develop reasonable and effective plans to restrict the spread of Covid-19.
Meanwhile, researchers also formulated mathematical models to understand the co-dynamics of various infectious diseases [20,43,44,45]. For example, the authors in [43] developed a new mathematical model for dengue and malaria co-infection to better understand the disease dynamics and to create more effective control strategies. However, there are not many articles in the current literature that address Covid-19 and dengue fever co-infection. One notable example can be found in [46], which offers a thorough analysis of Covid-19/dengue co-infection. In this article, the authors developed and analyzed an effective integer-order mathematical model with cost-effectiveness and an optimal control analysis for the co-infection dynamics of Covid-19 and dengue. Various control strategies, such as treatment controls for both Covid-19 and dengue, controls against co-infection with another disease, and controls against incident dengue and Covid-19 infections, were taken into consideration and simulated for the model. Nevertheless, at present, there exists no article that offers a thorough understanding, detailed investigations, and effective control strategies for a fractional model of Covid-19/dengue fever co-infections. To address the gap in the existing literature, we offer a more comprehensive Atangana-Baleanu fractional model for the co-infection of Covid-19 and dengue fever to analyze the dynamics and control of the disease under the memory effect. Another significant contribution made by this article is the implementation of the Toufik-Atangana-type numerical scheme to simulate the state and adjoint equations of the fractional optimal control problem for Covid-19 and dengue co-infection.
In this work, we will formulate a new co-infection model for Covid-19 and dengue fever using the Atangana-Baleanu fractional derivative [47]. The selection of the ABC operator for the proposed model is primarily based on its possession of a non-local and non-singular kernel. Furthermore, when compared to other fractional operators such as Caputo and Caputo-Fabrizo, this operator demonstrates an ability to capture higher susceptibilities while resulting in fewer infections [48]. An essential goal in developing a fractional model for co-infection of Covid-19 and dengue fever is to explore potential control strategies with time-dependent controls and gain insights into the disease's progression within a broader context. To attain our objective, we will first assess the validity of the proposed model. This assessment will involve establishing fundamental properties of the model, including the existence of a unique solution that is both positive and bounded, as well as conducting local and global stability analyses at a disease-free equilibrium point. Furthermore, this article contributes to the advancement of a fractional optimal control problem aimed at determining the optimal vaccination and treatment rates necessary for restricting the spread of Covid-19 and dengue fever infections. The Toufik-Atangana type numerical scheme will be implemented to evaluate the fractional optimal control problem for the co-infection model.
The distribution of the rest of the article is as follows. The co-dynamic fractional model is formulated in Section 2. Section 3 provides a theoretical analysis of the model. This analysis includes the existence and uniqueness of a positive and bounded solution, and a stability analysis at a disease-free equilibrium point with restriction to the reproduction number R0. In Section 4, a finite difference scheme of the Toufik-Atangana type is established for the proposed model and implemented for numerical simulations to see the effect of a fractional order on disease transformation. The model is further updated in Section 5 with time-dependent controls to define an optimal control problem. Then, the Toufik-Atangana numerical system is used to numerically resolve the related optimality conditions arising from Pontryagin's principle to determine the optimal time-dependent vaccination and treatment rates to prevent dengue fever and Covid-19 co-infection. Additionally, Section 5 includes numerical simulations that are performed to support theoretical results. The conclusion with future direction is provided in Section 6.
2.
Formulation of co-infection model
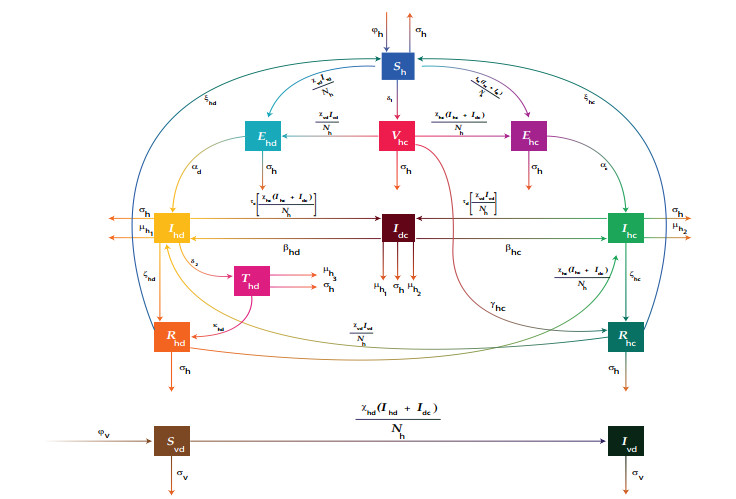
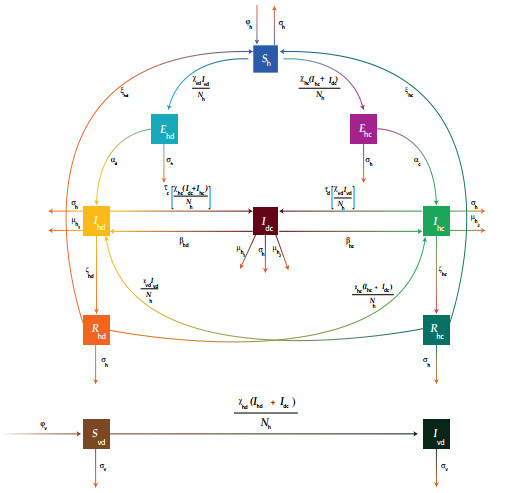
In this section, we develop a fractional mathematical model of Covid-19 and dengue fever co-infection by dividing the total population into two groups, namely the human population denoted by Nh and the vector population (mosquitoes) denoted by Nv. The human population is categorized as susceptible humans Sh, humans exposed to Covid-19 Ehc, humans infected with Covid-19 Ihc, humans recovered from Covid-19 Rhc, humans exposed to dengue fever Ehd, humans infected with dengue fever Ihd, humans recovered from dengue fever Rhd, and humans infected with both Covid-19 and dengue fever Idc. The vector population is subdivided into susceptible vectors Svd and infectious vectors Ivd. The recruitment rate into the human population is denoted by φh and the recruitment rate into the vector population is specified by φv.
Susceptible humans are exposed to Covid-19 at the following rate:
Equivalently, the rate at which susceptible humans are exposed to dengue is as follows:
Moreover, susceptible mosquitoes after interacting with infectious humans are infected at the following rate:
The parameters χhd, χvd, and χhc represent the effective contact rates for the acquisition of dengue fever and Covid-19. Furthermore, we made the following assumptions to build the Covid-19 and dengue fever co-infection model:
● Dengue infections can affect people who have Covid-19 infections, and vice versa;
● Co-infected people can transmit either Covid-19 or dengue fever, but not both at the same time;
● Co-infected people can recover from either Covid-19 or dengue fever, but not both at the same time;
● It is assumed that the transmission rates for those who are only infected and those who are co-infected are the same.
Figure 1 illustrates the transmission dynamics of Covid-19 and dengue fever co-infection. From Figure 1, we establish the Atangana-Baleanu fractional order model to explain the co-dynamics of Covid-19 and dengue fever. The fractional model will allow us to observe the internal memory effects of Covid-19 and dengue fever co-infection.
Thus, the Atangana-Baleanu fractional model describing transmission dynamics of the co-infection is given as follows:
along with the initial conditions:
where the description of parameters with their corresponding numerical values are provided in Table 1, and the Atangana-Baleanu derivative in the Caputo sense is defined as follows.
Definition 2.1. The Atangana-Baleanu fractional derivative of a differentiable function h(t), i.e., h:[a,b]→R of order ρ where ρ ∈(0,1), b>a, is denoted by ABCaDρh(t), where h ∈ H1(a,b) is defined as follows:
where M(ρ) represents the normalization function satisfying M(0) = M(1) = 1. Eρ is known as the Mittag-Leffler(ML) function, which is defined as follows:
The compact form of the model (2.1) is stated as follows:
Since the given system is autonomous, it can be expressed as follows:
where
represents state variables and
is the initial vector.
3.
Theoretical analysis
In the first part of this section, we examine the dynamics of the two sub-models: the Covid-19 sub-model and the dengue fever sub-model. In the second part of this section, the local and global stabilities of the complete co-infected fractional model (2.1) are theoretically discussed at a disease-free equilibrium point.
3.1. Covid-19 sub-model and analysis
First, we consider the Covid-19 sub-model by considering the dengue-associated state variables and the vector-associated variables as zero in (2.1), i.e., we take Ehd=Ihd=Rhd=Idc=Svd=Ivd=0 in (2.1) to obtain the following:
with
where the total population for this sub-model is given as follows:
Differentiating equation (3.2) with respect to time t and then using equations of sub-model (3.1), we obtain the following:
Using Birkhoff and Rota's theorem [49], the differential inequality (3.3) gives us 0<Nh(t)≤φhσh as t→∞.
Thus, the feasible region for sub-model (3.1) can be defined as follows:
which is positively invariant [37,47].
If we put ABC0DαtSh=ABC0DρtEhc=ABC0DρtIhc=ABC0DρtRhc=0, the disease-free equilibrium point of the Covid-19-only fractional model (3.1) is computed to give the following:
Next, we use the next-generation method [50] to compute the reproduction number Roc for the Covid-19 sub-model (3.1). The column matrix of the rate of appearance of new infections, denoted by Fa, and the column matrix of transitional terms, denoted by Va, is presented as follows:
The Jacobian of matrices Fa and Vb at point P∗c are represented as follows:
Then, we compute the spectral radius of the matrix FaV−1a to obtain the following reproduction number:
where γ2=αc, χ1=χhc, K1=αc+σh, K2=ζhc+μh2+σh.
Theorem 3.1. The disease-free equilibrium P∗c of the Covid-19 sub-model is locally asymptotically stable if Roc<1 and it is unstable when Roc>1.
Proof. The Jacobian for the system (3.1) at P∗c is as follows:
where K3=ξhc+σh. Eigenvalues of the Jacobian matrix are computed to give the following: λ1=−σh, λ2=−K3, λ3=−K1, λ4=−K2(1−Roc). Here, λ4 is negative if Roc<1. Thus, the Covid-19 sub-model is locally asymptotically stable if Roc<1 and unstable when Roc>1. □
3.2. Dengue fever sub-model and analysis
Now, we set Ehc, Ihc, Rhc, Idc equal to zero in (2.1) to write the following equations of the dengue fever sub-model:
with
where the total human population in this case will be as follows:
and the total vector population is given as follows:
By differentiation equation (3.5) and then using Eq (3.4a) to (3.4d), we obtain the following inequality:
Similarly, by differentiating equation (3.6) with respect to time and then using Eq (3.4e) and (3.4f), we obtain the following inequality:
Then, the feasible invariant region for the dengue sub-model is defined as follows:
Thus, solutions of the dengue sub-model (3.4) will enter the region Ψd, which is a positively invariant region.
If we put ABC0DαtSh=ABC0DρtEhd=ABC0DρtIhd=ABC0DρtRhd=ABC0DρtSvd=ABC0DρtIvd=0 in (3.4), we obtain the following disease-free equilibrium point for the dengue sub-model:
Next, we compute the reproduction number Rod for the dengue sub-model (3.4). The matrix of the rate of occurrence of new infections and the column matrix of transitional terms, denoted by Fb and Vb, respectively, are given as follows:
The Jacobian of matrices Fb and Vb at point P∗d are respectively given as follows:
Then,
where K4=αd+σh, K5=ζhd+μh1+σh, K8=σv, χ2=χhd, χ3=χvd, γ4=αd.
Theorem 3.2. The disease free equilibrium P∗d of dengue fever is locally asymptotically stable if Rod<1 and it is unstable when Rod>1.
Proof. The Jacobian for system (3.4) at P∗d is as follows:
where K6=ξhd+σh, γ5=ζhd, β2=ξhd, α=σh.
The eigenvalues of this Jacobian matrix are computed to give the following: λ1=−K8, λ2=−K5, λ3=−K4, λ5=−α, λ6=−K6, and
All of the above eigenvalues are negative provided that Rod<1. Thus, the dengue fever sub-model is locally asymptotically stable if Rod<1. The frequency of dengue fever approaches an endemic equilibrium when Rod>1. □
3.3. Co-infection model and analysis
In this section, we first prove that the Covid-19 and dengue co-infection model (2.1) has a unique solution. Second, we establish results for the local stability of the disease-free equilibrium point.
3.3.1. Existence and uniqueness of solutions
To establish the existence and uniqueness of solutions of the co-infected model (2.1), we consider its compact form as given in (2.2), i.e.,
where ϕ denotes a continuous vector that satisfies the Lipschitz condition as follows:
where N>0 is constant. We follow the steps of the proof of Theorem 3.4 described in [45] to establish the existence of a unique solution of (2.2).
Theorem 3.3. If the Lipschitz condition (3.7) and the inequality
are satisfied, then there exists a unique solution to the initial value problem (2.2) for t∈[0,T] in C1∈([0,T],D).
Proof. The application of the Atangana-Balneau fractional integral on both sides of (2.2) will give us the following:
We define the operator Q:C(M,R10)→C(M,R10) by the following:
where M=(0,N). Then, (3.9) can be re-written as follows:
We define the supremum norm on M as follows:
It is obvious that the space C(M,R10) together with the norm ‖.‖M is a Banach space.
Let Y(t)∈C(M,R10) and Z(t,τ)∈C(M2,R) with |Z(t,τ)|M=supt,τ∈M|Z(t,τ)|; then, the following inequality holds:
Consider the following:
Thus,
provided condition (3.8) holds. Thus, the operator Q becomes a contraction, and hence Q has a unique fixed point, which is the solution to the initial value problem (2.2). □
3.3.2. Positively invariant region
The total number of the human population for the complete model (2.1) is as follows:
whereas the total number of the vector population is given as follows:
From Eq (3.10), we have the following:
Now, we incorporate equations of model (2.1) and simplify the resulting equation to obtain the following inequality:
Similarly, from Eq (3.6), we obtain the following inequality:
Thus, the feasible region for the co-infection model (2.1) is defined as follows:
where
and
Following the procedure given in [43,51], it can be proven that the solutions of the co-infection model (2.1) with non-negative initial conditions belong to the feasible region Ψhv for all t≥0. Thus, the region Ψhv is a positively invariant region.
3.3.3. Local stability analysis
We take the infected states Ihc, Ihd, Idc, and Ivd equal to zero and solve the steady state equation of the co-infection model (2.1) to obtain the following disease-free equilibrium (DFE) point:
Here, we used the next-generation matrix approach to determine the relation for the reproduction number Rodc. The matrix of the appearance of new infections and the column matrix of transitional terms in the compartments Ehc, Ihc, Ehd, Ihd, Idc, and Ivd are denoted by Fc and Vc, respectively. These matrices are given as follows:
The Jacobian of the matrices Fc and Vc at DFE point P∗ are computed to give the following matrices:
Then, the spectral radius of the product matrix FcV−1c is computed to give the reproduction number Rodc, i.e.,
Theorem 3.4. The disease free equilibrium P∗ of model (2.1) is locally asymptotically stable if Rodc<1 and it is unstable when Rodc>1.
Proof. The Jacobian of model (2.1) at P∗ is computed to give the following matrix:
where K1=αc+σh, K2=ζhc+μh2+σh, K3=ξhc+σh, K4=αd+σh, K5=ζhd+μh1+σh, K6=ξhd+σh, K7=βhc+βhd+μh1+μh2+σh, K8=σv, χ1=χhc, χ2=χhd, χ3=χvd, γ1=βhc, γ2=αc, γ3=ζhc, γ4=αd, γ5=ζhd, γ6=βhd, β1=ξhc, β2=ξhd, α=σh. The characteristic equation corresponding to the Jacobian matrix is given as follows:
From Eq (3.12), we obtain some of the eigenvalues directly as follows: λ1=−α, λ2=−K3, λ3=−K6, λ4=−K7, λ5=−K8. Additionally, the characteristic equation (3.12) gives us the following two polynomials in λ, i.e.:
where A1=K4+K5+K8, A2=K4K5+K4K8+K5K8, A3=K4K5K8−γ4χ2χ3.
Since all coefficients of Eq (3.13) are positive provided that Rodc<1, by the Routh Hurwitz criterion, the real part of all corresponding eigenvalues are negative. It is obvious that coefficients A1, A2, and A3 of Eq (3.14) are positive; additionally, it can be shown that A1A2>A3. Therefore, by the Routh Hurwitz criterion, the real part of the roots of Eq (3.14) are negative. Thus, the co-infection model (2.1) is locally asymptotically stable if Rodc<1. □
3.3.4. Global stability analysis
Theorem 3.5. The disease-free equilibrium point P∗ of the co-infection model (2.1) is globally asymptotically stable in the region Ψhv when Rodc<1.
Proof. We construct a candidate Lyapunov function G0:Ψhv→R [19,34] at P∗ such that
We apply the Atangana-Baleanu fractional derivative to obtain the following:
We use equations of system (2.1) to replace the fractional derivatives in the above expression:
After re-arranging terms, we obtain the following:
Since ((χhc(Ihc+Idc)Nh)+(χvdIvdNh))S∗h≥0, the above expression can be written as follows:
This implies that ABC0DρtG0≤0. Additionally, we observe that ABC0DρtG0=0 if and only if Sh=S∗h, Ehc=E∗hc, Ihc=I∗hc, Rhc=R∗hc, Ehd=E∗hd, Ihd=I∗hd, Rhd=R∗hd, Idc=I∗dc, Svd=S∗vd, Ivd=I∗vd. Hence, by LaSalle's invariance principle [34,46], the DFE point P∗ is globally asymptotically stable in the region Ψhv. □
The global stability at a disease-free point means that the disease will not persist in the population if a disturbance of any size is introduced into the population.
4.
Numerical discretization and implementation
This section briefly describes the development of a Toufik-Atangana type numerical scheme [52] to approximate the fractional differential equation of type (2.2). We implement this scheme to discretize each equation of the co-infection model (2.1) and simulate the resulting equations for different values of the fractional order ρ to study its impact on the disease dynamics.
We employ the fundamental theorem of fractional calculus to model (2.2) to obtain the following:
In a discrete form, we have the following:
Correspondingly,
Using interpolation of the function ϕ(θ,Y(θ)) over [tp,tp+1], we have the following:
which can be reduced to the following discrete form:
where we have subdivided the time domain [0, Tf] into N subintervals, each of length h=TfN>0 with tq=qh, q=0,1,…N. Equations of model (2.1) will be discretized similarly to (4.2).
4.1. Fractional order effect on disease dynamics
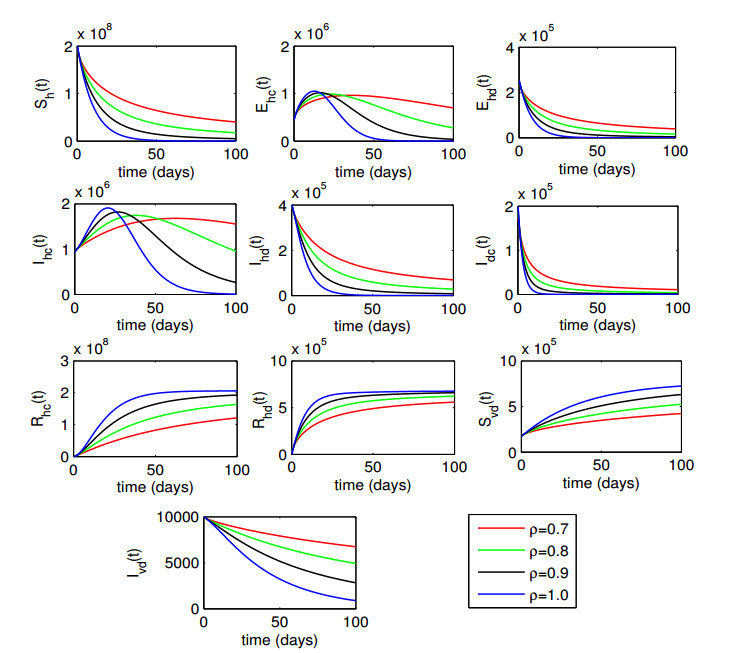
To explore the impact of memory on the disease dynamics, we conducted simulations using continuous equations represented by model (2.1) with the discretization strategy outlined in type (4.2). The simulations for state variables were carried out for ρ=0.7,0.8,0.9,1.0, as shown in Figure 2.
We observe an evident decrease in each of the infectious human populations as the fractional order ρ increases. Interestingly, the population infected with Covid-19 initially rises in the early days of the disease outbreak and subsequently declines steadily as ρ increases. For ρ=1, all three infected human populations move to a disease-free state. Additionally, we notice a decrease in individuals exposed to Covid-19 and dengue fever with an increasing value of fractional order ρ. Ultimately, these populations also reach a disease-free state for ρ=1. This suggests that an increased focus on the past states and interactions within the model has a significant effect on mitigating the spread of infectious diseases among the human population. Moreover, the figure shows a gradual increase in humans recovered from Covid-19 and dengue fever with increasing values of the fractional order ρ. Additionally, the impact of the fractional order on the vector population is observed in this figure. We notice a decrease in the infectious vector population as the fractional order increases. The findings of this analysis emphasize the possibility of including memory effects in epidemic models for more precise forecasts and successful methods in disease prevention and control.
5.
Optimization of co-infection model
In this section, we formulate an optimal control problem to suggest the best vaccination and treatment rates for restricting the spread of Covid-19 and dengue co-infection. To do this, we first update the disease model (2.1) to adjust vaccination and treatment compartments, thus resulting in a system of new coupled fractional order differential equations. We consider the vaccination and treatment rates as control variables and define an objective functional. We will introduce adjoint variables to formulate the Hamiltonian function for developing optimality conditions using Pontryagin's principle [53,54,55]. The optimality conditions will be numerically solved for optimal solutions.
5.1. Optimal control problem and optimality conditions
For optimization, we update the co-infection model (2.1) to adjust the vaccination and treatment compartments, see Figure 3 for a flow diagram of the updated model. We assume that the susceptible humans are vaccinated for Covid-19 at the rate δ1 and may get infected with either dengue fever or Covid-19 after interacting with infectious humans or vectors. Vaccinated individuals may recover at the rate γhc and may die naturally at the rate σh. Additionally, we suppose that the dengue-infected humans are treated at hospitals or homes at the rate δ2 and move to the recovered class at the rate κhd. The humans under treatment may either die naturally or due to the disease at the rates σh or μh3. Thus, as shown in Figure 3, the updated co-infection model describing the flow of disease is mathematically described as follows:
with the following initial conditions:
For the sake of the optimization process, we replace the constant vaccination rate δ1 and the treatment rate δ2 in the updated model (5.1) with time-dependent functions u1(t) and u2(t), and declare them as control variables for the process.
To define a control problem, we consider the following cost functional:
where Ihc(t), Ihd(t), Idc(t), and Ivd(t) are state variables representing infectious classes, Tf is the fixed terminal time, and u1(t),u2(t) are control variables. The non-negative constants b1, b2, b3, and b4 are the weights associated with the infectious classes Ihc(t), Ihd(t), Idc(t), and Ivd(t), respectively. Moreover, 12b5u21(t) and 12b6u22(t) are the cost functions of considered control approaches respectively for vaccination and treatment. The non-negative constants b5 and b6 are the corresponding costs associated with the controls.
Then, the optimal control problem is defined as follows:
where W is the control space, which is defined as follows:
Now, to derive the optimal conditions by Pontryagin's maximum principle, we built the following Hamiltonian for the control problem (5.3):
where B=(Sh,Vhc,Ehc,Ihc,Rhc,Ehd,Ihd,Thd,Rhd,Idc,Svd,Ivd) is a vector of state variables, Ai,i=1,2,....,12 are adjoint variables associated with the state equations of model (5.1), and A∗=(A1,A2,A3,A4,A5,A6,A7,A8,A9,A10,A11,A12) is called the adjoint vector.
Theorem 5.1. Let ˉSh, ˉVhc, ˉEhc, ˉIhc, ˉRhc, ˉEhd, ˉIhd, ˉThd, ˉRhd, ˉIdc, ˉSvd, and ˉIvd be optimal state solutions of model (5.1) associated with optimal control variables u∗1, u∗2 for the optimal control problem (5.3) that minimizes J(Ihc,Ihd,Idc,Ivd,u1,u2) over W. Then, there exists an adjoint system consisting of the following equations:
along with the following transversality conditions:
and we obtain the control set {u∗1,u∗2} characterized by
□
Together, the Hamiltonian (5.4) and the Eq (5.5) lead us to the following system of linear adjoint fractional differential equations:
along with conditions at the terminal time
Equations for the controls u1(t) and u2(t) are obtained by applying the first condition of Pontryagin's principle, i.e.,
Thus, the optimal control characterization for u∗1(t) and u∗2(t) with bounds are given as follows:
The state equations of model (5.1) are simulated by using the Toufik-Atangana type discretizations described in Section 4; for the corresponding adjoint linear equations (5.6), we employ the Toufik-Atangana type discretizations backward in time together with the associated terminal conditions.
5.2. Optimization algorithm
The following algorithm is implemented to solve the optimality conditions for the optimal control problem (5.3).
Here, O is a symbolic representation for each of the control variables, state variables, and adjoint variables, and σ>0 is the tolerance adjusted for accuracy.
5.3. Optimal solutions and discussions
In this section, we will present and discuss the results obtained by resolving the necessary optimality conditions using steps of the above algorithm. The optimality conditions involving state and adjoint equations are discretized using the discretizations developed in Section 4. The cost functional (5.2) is approximated at the discrete points tq=qh, q=0,1,…,N using Simpson's one-by-three rule. Simulation results for optimal control problem (5.3) will be presented for different values of a fractional order (i.e., for ρ=0.7, 0.8, 0.9, 1).
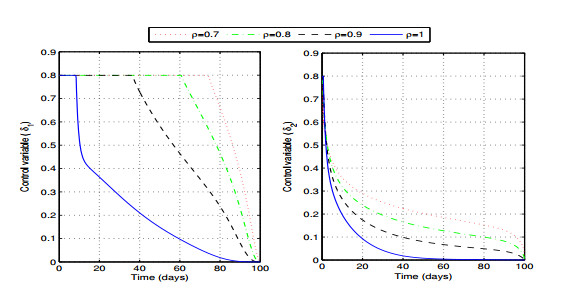
This study aims to determine the best rate of Covid-19 vaccination for susceptible individuals and the most effective treatment rate for dengue-infected individuals to minimize the cost functional, thus optimally restricting the spread of co-infection. Figure 4 shows the plots of the best vaccination and treatment controls that minimize the cost functional (5.2). The optimal curves for time-dependent vaccination rates for different values of the fractional order ρ are shown in the left part of the figure. Notably, early in the disease outbreak, a maximum Covid-19 vaccination to susceptible individuals is crucial. However, this maximum vaccination period diminishes with the increasing fractional order ρ and elapsed time t. The right-hand plot of Figure 4 illustrates the optimal rates for treating dengue-infected individuals. The treatment rates decline over time and with higher fractional order values from ρ=0.7 to ρ=1. By adopting this strategy, the treatment rate approaches zero after the first 50 days for ρ=1, thus suggesting a potential recommendation to alleviate the strain on hospitals.
In Figure 5, we present four sub-graphs of cost functional (5.2) for four different values of fractional order ρ. In each sub-graph, the cost functional reaches its minimum through the application of optimal vaccination and treatment rates. Although the number of solution iterations remains constant across all sub-plots, there is a significant decrease in the cost functional with an increasing fractional order ρ. The most notable reduction in the cost functional is observed when ρ is equal to 1.
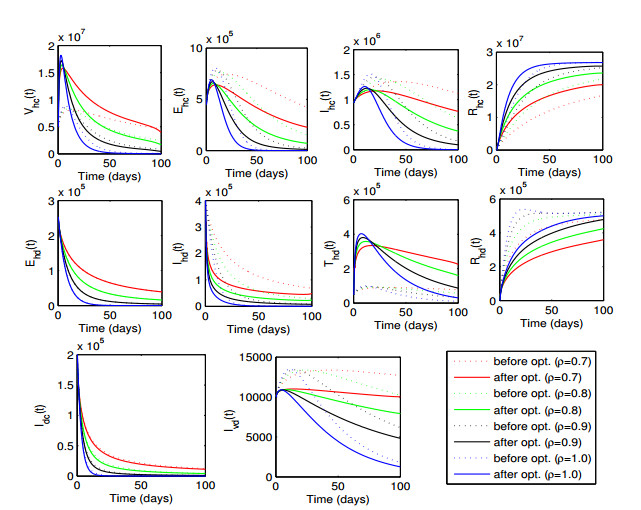
Figure 6 shows the solution trajectories for state variables before and after optimization at the terminal time Tf for different values of fractional order ρ. The dotted lines represent the curves before optimization, whereas the solid lines depict the state variables after optimization. From the figure, we observe a decrease in the number of infectious people affected by Covid-19 and dengue fever after optimization. However, the decrease in the optimal curves for co-infected individuals is relatively small compared to the pre-optimization curves. However in both situations, the curves for co-infected individuals move to a disease-free state for ρ=0.9 and ρ=1. Additionally, we notice a substantial decrease in the optimal curves for the infectious vector population. Furthermore, the optimized curves for infectious humans and vectors exhibit a decline with an increasing fractional order ρ. Similar trends are observed for humans in the exposed class infected with Covid-19, where a more significant reduction in infected individuals is evident after optimization. However, no reduction is observed in exposed humans infected with dengue fever. This may be because the susceptibles have only been vaccinated with the Covid-19 vaccine. However, quarantining dengue-infected humans may help to reduce the number of dengue-infected exposed cases.
The curves for individuals recovered from Covid-19 rise more after optimization, whereas the rise in the curves of dengue-recovered individuals is not greater than the curves before optimization. Nevertheless, the number of recovered individuals in both cases rises as the fractional order increases. Additionally, the figure includes curves for vaccinated and under-treated individuals. It is observed that a higher vaccination rate is initially necessary, but beyond the initial 50 days, the requirement significantly reduces to approach zero for ρ=1. However, the strategy requires the treatment of a greater number of individuals infected with dengue, potentially posing a burden on the healthcare infrastructure.
The simulations indicate that the vaccination of susceptible individuals yields better results in terms of reducing the number of exposed and infected individuals affected with Covid-19, as well as in terms of a rise in the number of recovered individuals. Moreover, the simulations reveal the treatment impact on dengue-infected individuals in terms of a reduction in the number of dengue infections. However, the treatment impact on exposed individuals is negligible. Additionally, it is noticed that these impacts are preserved under different fractional orders.
6.
Conclusions and future directions
In this research, we formulated a new ABC fractional-order model for Covid-19 and dengue co-infection to study the disease dynamics for an optimal control analysis. In the first part of the manuscript, we studied the dynamics of the sub-models, as well as the dynamics of the co-infection model. We proved that there exists a unique solution to the proposed co-infection model that lies in a feasibly invariant region. We demonstrated that at the disease-free equilibrium point, the model satisfies the local stability properties. All of these proofs concluded that the newly constructed co-infection fractional model is well-posed and can be optimally analyzed for disease control.
In the second part of this manuscript, we performed an optimal control analysis to minimize the number of infected humans. For this, we updated the proposed co-infection model to include a vaccination compartment to vaccinate susceptible individuals with the Covid-19 vaccine and a treatment compartment to treat dengue-infected individuals. We considered the vaccination rate of susceptible individuals and the treatment rate of dengue-infected individuals as the control variables. We defined an objective functional and formulated an optimal control problem to determine the best vaccination and treatment rates to minimize the cost functional with a reduction in infectious humans and vectors. We derived the optimality conditions using Pontryagin's principle. The optimality conditions were solved numerically using Toufik-Atangane-type numerical discretizations, both forward and backward in time.
Graphical results for the presented disease control strategy show that 80 percent of the susceptible population needs to be vaccinated with the Covid-19 vaccine in the early days. The span of early days with a maximum vaccination level decreases with an increasing value of the fractional order ρ. Additionally, we observed the impact of the fractional order on optimal treatment rates. For ρ=1, the treatment rate of dengue-infected individuals approached zero after the first 50 days. With both of these strategies, we achieved a reasonable reduction in the number of Covid-19-infected and dengue-infected individuals. However, the reduction in co-infected individuals is negligibly small after optimization. Thus, the graphical results elaborate on the efficacy of the approach to ascertain optimal vaccination and treatment rates for different fractional orders that significantly decrease infections. Moreover, the influence of the memory index on disease transmission and control was explored in this study. We observed a noteworthy decrease in the infectivity with an increase in the fractional order. Therefore, it is clear that, in comparison to the integer-order model, the proposed fractional model provides a more accurate understanding of the disease's behavior.
This theoretical study was conducted to determine effective and feasible control measures to either reduce or eradicate the effect of Covid-19 and dengue co-infection from the population. The findings of this study suggest optimal vaccination and treatment patterns for authorities to follow to minimize the infection rate in the community. Moreover, it is crucial to mention that the investigated fractional disease model provides a more precise understanding of the disease dynamics in contrast to the previously existing integer-order versions. Another distinction of the current research is the implementation of the Toufik-Atangana numerical scheme; for the first time, this numerical scheme was used to solve the fractional optimal control problem defined for Covid-19 and dengue fever co-infection. However, with the proposed control strategies, we do not see a reasonable reduction in the individuals facing both infections at the same time. In the future, we plan to take various non-pharmaceutical control approaches into account to modify the current ABC fractional co-infection model and achieve a more credible and effective optimal control analysis. Additionally, we plan to work on the Covid-19 and dengue fever fuzzy fractional co-infection model to remove the uncertainty of different control strategies with the cost-effective analysis.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in writing the paper. The authors declare that they have only used the Grammarly free AI tool to improve the manuscript's grammar.
Funding
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Project No. GRANT5384].
Data availability statement
All data supporting the findings of this study are available within the paper.
Conflict of interest
This work does not have any conflicts of interest.









 DownLoad:
DownLoad: