Extended MABAC method based on 2-tuple linguistic $T$-spherical fuzzy sets and Heronian mean operators: An application to alternative fuel selection

1.   Introduction

Most physical or chemical phenomena are governed by partial differential equations that describe the evolution of the constituents of the problem under study. If all the parameters of the system are known (the geometry of the domain, the boundary and initial conditions, and the coefficients of the equations), the model to be solved is a direct problem. On the other hand, if certain parameters in the equation are unknown, these parameters can be determined from experimental data or from the values at the final time in an evolution problem. The identification of such a parameter in the partial differential equation represents an inverse problem.

When experimental measurements are made on the boundary to determine a coefficient in a partial differential equation, there is always measurement error, which can mean a very large error in identification. For this reason, most inverse problems are ill-posed (we refer the reader to ^[1], for further details on the results found and the methods developed).

Many papers in this area deal with elliptic problems, see for example ^[2,3,4,5]. On the other hand, the literature on applications governed by elliptic, parabolic and hyperbolic, linear and nonlinear systems is rather limited. Theoretical results for the latter case can be found, for example, in ^[6,7,8].

We are interested in studying the state-constrained optimal control problem of the steady-state Navier-Stokes equations. In this area, several applications have been proposed to solve optimal control problems ^[9,10,11,12]. The elliptic optimization problem was first discussed theoretically by Reyes and R. Griesse ^[13]. Research on numerical methods for optimal control of the Navier-Stokes equations has made significant advancements over the years. The initial approaches for optimal control of the Navier-Stokes equations employed classical optimization methods such as the conjugate gradient method, quasi-Newton method, or augmented Lagrangian method. These methods yielded promising results, but they were often limited by the nonlinearity of the Navier-Stokes equations and the presence of constraints. Then came the domain decomposition methods, which are used to divide the computational domain into smaller subdomains in order to solve the Navier-Stokes equations more efficiently. In the context of optimal control, these methods help reduce the problem size by partitioning the domain into regions that can be solved independently. This facilitates parallel computations and leads to faster results ^[14]. The adjoint-based optimization methods, on the other hand, are commonly used to solve optimal control problems. These methods leverage the principle of dynamic programming by calculating an adjoint variable that provides information about the system's sensitivity with respect to the control. This information is then used to adjust the control optimally. Adjoint-based optimization methods have been successfully applied to the Navier-Stokes equations, enabling the solution of complex optimal control problems ^[15,16]. Also worth mentioning are the methods based on genetic algorithms, which are optimization methods inspired by principles of natural selection. In the context of the Navier-Stokes equations, these methods have been used to solve optimal control problems by generating a population of potential solutions and evolving them over generations. Genetic algorithms have the advantage of being able to explore a larger search space, but they may require a large number of iterations to converge to an optimal solution. It should be noted that the comparison of different approaches will depend on the specific context of the optimal control problem for the Navier-Stokes equations. Each method has its own advantages and limitations, and the choice of method will depend on computational constraints, control objectives and available resources ^[17]. The approach presented in this paper is a powerful technique for solving this and many other such nonlinear problems. We have applied a new method to construct a new family of numerical schemes that convert the inverse problem into a direct problem, which helps us to solve numerical problems easily. We construct an algorithm that can solve this problem. We use spectral methods to find approximate solutions through the preconditioned GMRES method. The stability and convergence of the method are analyzed ^[18,19].

The flow of an in-compressible viscous fluid in a domain $\Omega$ of $\mathbb{R}^2$ is characterized by two variables velocity $\mathbf{u}$ and pressure $p$, given functions $\mathbf{f} = (f_{x}, f_{y})$ in $(\mathbb{L}_{2}({\Omega}))^{2}$ and a control force $\mathbf{g}$ which is the optimization variable.

The problem posed in this paper is to find a solution pair $(\mathbf{u}, \mathbf{g})$ solving the functional $J$ defined by.

where $\mathbf{u}$ is the solution to the problem

where $\mathbf{u}_d$ and $\mathbf{f}$ are the data and $\nu$ is the viscosity. Our work is based on a simple computation of the gradient $J$ which leads to the coupled problem which is the main subject of this study. This paper is organized as follows:

$\bullet$ In Section 2, we introduce the optimal control problem under constraints $(P_{\mathbf{g}})$ ^[20]. We also prove the existence of a global optimal solution for the optimal control problem $(S)$ ^[21].

$\bullet$ In Section 3, after linearization, we study the existence and uniqueness of weak solutions of $(P_{n})$. We prove the convergence of $\mathbf{u}_{n}$ solutions of $(P_{n})$ to the $\mathbf{u}$ solution of $(P_{\mathbf{g}})$. We then derive an optimal system of equations from which the optimal solution can be computed.

$\bullet$ In Section 4, We propose a numerical algorithm for solving coupled systems of equations, where the numerical solution is generated by spectral methods ^[22,23].

2.   Optimal control problem

Let $\Omega$ be a bounded domain of $\mathbb{R}^{2}$ with Lipschitz-continuous boundary $\Gamma$. Additionally, $V = \{ \mathbf{v} \in X, div \; \mathbf{v} = 0 \}$, where $X = H_{0}^{1}(\Omega)^{2} = \{v \in H^{1}(\Omega)^2;\, v|_{\partial \Omega} = 0 \}$.

We set $M = L_{0}^{2}(\Omega) = \left\{v \in L^{2}(\Omega); \, \int_{\Omega} v\, dx = 0\right\}$, $Y = X \times M$ and $W = V \times M$.

Remark 1. The symbol $E \hookrightarrow G$ denotes the continuous and dense embedding of $E$ into $G$.

The symbol $E \rightharpoonup G$ denotes the weak convergence of $E$ to $G$.

The symbol $E \rightarrow G$ denotes the strong convergence of $E$ to $G$.

In this section, we are concerned with the following state-constrained optimal control problem. Find $(\mathbf{u}^{*}, \mathbf{g}^{*}) \in \mathcal{W} \times L^{2}(\Omega)^2$ which solves

where the state $\mathbf{u}$ is sought in the space $\mathcal{W} = H^2(\Omega)^2 \cap V$.

● $\mathbf{C}$ is a closed convex subset of $\mathbf{C}_{0}(\Omega) = \{\omega \in \mathbf{C}(\bar{\Omega}); \, {\omega}_{|\Gamma} = 0 \}$, the space of continuous functions on $\Omega$ vanishing on $\Gamma$.

● $\mathbf{g}$ is a distributed control function.

● The function $\mathbf{u}_d \in L^2(\Omega)^2$ denotes the desired state.

● The parameter $\gamma > 0$ stands for the control cost coefficient.

State constraints are relevant in practical applications to suppress backward flow in channels. Next, we derive necessary optimal conditions for $(S)$.

We have two types of constraint sets $\mathbf{C}$. The first one is

which covers point-wise constraints on each component of the velocity vector field, i.e., $\mathbf{v}(x) \leq y_{b}(x)$ gives $v_{i}(x) \leq y_{b, _{i}}(x)$ for $i = 1, ..., d,$ on a sub-domain $\tilde{\Omega} \subset \Omega$.

The set of feasible solutions is defined as:

The weak formulation of the first and third equations of $(P_{\mathbf{g}})$ is defined as follows Find $\mathbf{\mathbf{u}} \; \in \; V$ knowing that

Before we study the problem of optimal control we start with the following proposition.

Proposition 2. ^[13] Let $\Omega$ be a bounded domain of $\mathbb{R}^2$ of class $C^{2}$ and $\mathbf{f}$ and $\mathbf{\mathbf{g}} \in L^2(\Omega)^2$. Then every solution of $(2.2)$ satisfies $\mathbf{u}\in H^2(\Omega)^{2}$ and $p\in L_0^2(\Omega)\cap H^1(\Omega)$ for the corresponding pressure. Moreover, there exists a constant $c(\nu, \Omega) > 0$ such that

Theorem 3. If $\mathfrak{T}_{ad}$ is non-empty, then there exists a global optimal solution for the optimal control problem $(S)$.

Proof. Since the problem has at least one feasible pair, and J is bounded by zero, we can take the minimization sequence ${(\mathbf{u}_{k}, \mathbf{g}_k)}$ in $\mathfrak{T}_{ad}$. We obtain

which implies that $\{\mathbf{g}_k\}$ is uniformly bounded in $L^{2}(\Omega)^{2}$. Then we may extract a weakly convergent sub-sequence, also denoted by $\{\mathbf{g}_k\}$, such that

Using 2.3, it follows that the sequence $\{\mathbf{u}_k\}$ is also uniformly bounded in $\mathcal{W}$ and, consequently, we may extract a weakly convergent sub-sequence, also denoted by $\{\mathbf{u}_k\}$ such that

In order to proof that $(\mathbf{u}^*, \mathbf{g}^*)$ is a solution of the Navier-Stokes equations, the only problem is to pass to the limit in the nonlinear form $\int_{\Omega} (\mathbf{u}_k.\nabla \mathbf{u}_k)\; \mathbf{v} \; dx$. Due to the compact embedding $\mathcal{W}\hookrightarrow V$ and the continuity of $\int_{\Omega} (\mathbf{u}_k.\nabla \mathbf{u}_k)\; \mathbf{v} \; dx$, it follows that

Consequently, taking into account the linearity and continuity of all terms involved, the limit ${(\mathbf{u}^{*}, \mathbf{g}^{*})}$ satisfies the state equations.

Since $\mathcal{C}$ is convex and closed, it is weakly closed, so $\mathbf{u}_{k} \rightharpoonup \mathbf{u}^{*}$ in $\mathcal{W}$ and the embedding $H^2(\Omega) \cap (H_{0}^1(\Omega)) \hookrightarrow \mathcal{C}_{0}(\Omega)$ implies that $\mathbf{u}^{*} \in \mathcal{C}$. Taking into consideration that $J(\mathbf{g})$ is weakly lower semi-continuous, the result follows via ^[13]. □

3.   The linearized problems

3.1.   Linearization

To solve $(P_g)$, we construct a sequence of linear problems. Starting from an arbitrary $\mathbf{u}^{0} \in X$, we consider the iterative scheme

3.2.   The convergence

The variational formulation of ($P_{n}$) is

Find $(\mathbf{u}^{n}, p^{n})$ $\in$ $Y$ such that

The bilinear forms $a_0$, $a_{n}$ and $b$ are given by $\forall p \in M$ and $\mathbf{v} \in X$

with $\; \mathbf{f} \in H^{-1}(\Omega)$.

Using Green's Theorem and $div \; \mathbf{v} = 0$, we have $b(p, \mathbf{v}) = 0$. Then, we associate with the problem $(PV_{n})$, the following problem

For each $n$ and for $\mathbf{f}, \mathbf{g}^{n} \in L_2(\Omega)^{2}$, the problem $(PV_{n})$ has a unique solution $\mathbf{u}^{n} \in V$ ^[13].

The sequence $(\mathbf{u}^{n})_{n \in \mathbb{N}}$ satisfies the following inequality:

Using the continuity of the linear form $L(.)$ and Schwarz's inequality, we obtain the following inequality

which implies that the sequence $(\mathbf{u}_{n})_{n \in \mathbb{N}}$ is bounded in $X = (H_{0}^{1}(\Omega))^{2}$. Hence, there is a subsequence that converges weakly to $\phi$ in $X$ on the one hand. However, on the other hand, it converges strongly in $L^{2}(\Omega)^{2}$.

Lemma 4. If $\mathbf{u}^{0} \in H^{2}(\Omega)^{2} \cap H_{0}^{1}(\Omega)^{2}$, $\mathbf{f} \in L_{2}(\Omega)^{2}$, and $\mathbf{g}^{n} \in L_2 (\Omega)^{2}$, then

Proof. If $\mathbf{u}^{0} \in H^{2}(\Omega)^{2} \cap H_{0}^{1}(\Omega)^{2}$, $\mathbf{f} \in L_{2}(\Omega)^{2}$ and $\mathbf{g}^{n} \in L_2 (\Omega)^{2}$, then a regularity theorem gives: $\mathbf{u}^{n}$ and $\phi$ are in $H^{2}(\Omega)^{2} \cap H_{0}^{1}(\Omega)^{2}.$ Furthermore,

with

and

and

Using $(3.3)$ we obtain

Then we increase the regularity of $\mathbf{u}$ using the method of singular perturbation, we conclude via ^[11] that $\mathbf{u}^{n}$ is bounded in $H_0^{2}(\Omega)$, then we extract a sequence still denoted by $\mathbf{u}^{n}$, which converges weakly to $\mathbf{u}$ in $H_0^{2}(\Omega)$ since the injection of $H_0^{2}(\Omega)$ into $H_0^{1}(\Omega)$ is compact, there is a subsequence still denoted by $\mathbf{u}^{n}$ which converges strongly to $\mathbf{u}$ in $H_0^{1}(\Omega)$, we prove via ^[11]

□

We need this result.

Lemma 5. 1) $\lim_{{n \rightarrow \infty}} a_0(\mathbf{u}^{n}, \mathbf{v}) = a_0(\phi , \mathbf{v}).$

2) $\lim_{{n \rightarrow \infty}} a_{n}(\mathbf{u}^{n}, \mathbf{v}) = a_{\infty}(\phi , \mathbf{v}) = \int_{\Omega} (\phi \cdot \nabla) \phi \cdot \mathbf{v} \, dx.$

Proof. On the one hand, we have,

Using Lemma 4, we obtain the result.

2) On the other hand, we have

Setting

By using the continuity of the bi-linear form $a_{n}(\mathbf{u}^{n}, \mathbf{v})$, it gives the following

□

Theorem 6. The sequence $\left(\mathbf{u}^{n}\right)_{n\in\mathbb{N} }$ of solutions of problem $(\mathcal{P}_{n})$ converges to the solution $\Phi$ of problem $(P_{\mathbf{g}})$.

Proof. It follows from Lemma $5$ that

The problem ($\mathcal{P}V_{n}$) gives

and we have $\frac{\gamma}{2} \|\mathbf{g}^{n}\|^{2} \leq J(\mathbf{v}^{n}, \mathbf{g}^{n}) < \infty,$ which implies that $\mathbf{g}^{n}$ is uniformly bounded in $(L^{2}(\Omega))^{2}$. Hence, we can extract a weakly convergent sub-sequence, denoted by $\mathbf{g}^{n}$, such that $\mathbf{g}^{n} \rightharpoonup \breve{\mathbf{g}} \in (L^{2}(\Omega))^{2}$.

Then, using Lemma 5, we obtain

Here we used Rham's Theorem. Let $\Omega$ be a bounded regular domain of $\mathbb{R}^{2}$ and $\mathcal{L}$ be a continuous linear form on $H_{0}^{1}(\Omega)^{2}$, then the linear form $\mathcal{L}$ vanishes on $V$ if and only if there exists a unique function $\varphi \in L^{2}(\Omega)/\mathbb{R}$ such that

Now let $\mathcal{L}(\mathbf{v}) = a_0(\phi , \mathbf{v}) + a_{\infty}(\phi , \mathbf{v}) - \langle \mathbf{f}+\breve{\mathbf{g}}, \mathbf{v} \rangle$, therefore the form $\mathcal{L}(\mathbf{v}) = 0$ for all $\mathbf{v} \in V$, then Rham' theorem implies the existence of a unique function $p \in \mathrm{L}^{2}(\Omega)/\mathbb{R}$ such that

which gives

then in $\mathcal{D}'(\Omega)$:

Since $\phi \in V$ and $(\phi , \breve{\mathbf{g}})$ satisfies Eqs $(1)$ and $(2)$ of $(P_{\mathbf{g}})$, we conclude that $\phi$ is a solution of $(P_{\mathbf{g}})$ and the result follows.

□

3.3.   Coupled problem and variational formulation

Consider the problem $(S_n)$, defined as follows

where we define the functional

The set of admissible solutions is defined as follows:

The method to calculate the gradient is defined by

By linearity, $\mathbf{u}^{n}(\mathbf{g}^{n}+\varepsilon \mathbf{w}) = \mathbf{u}^{n}(\mathbf{g}^{n})\mathbf{+}\varepsilon \tilde{\mathbf{ u}^{n}}(\mathbf{w})$ with

Otherwise, $\tilde{\mathbf{u}}^{n}(\mathbf{w}) = ((\mathbf{u}^{n}$ $(\mathbf{g}^{n}))^{'}, \mathbf{w}).$

As $J(\mathbf{g}^{n})$ is quadratic, we obtain

To simplify the expression of the gradient, we use the following system where $p$ is defined as the unique solution in $H_{0}^{1}(\Omega)$

Multiplying the first equation of (3.17) by $p^{n}$ and the first equation of (3.18) by $\tilde{\mathbf{u}}^{n}(\mathbf{w})$ and integrate by parts, we obtain

As

Indeed

Hence,

Consequently

So $J$'$(\mathbf{g}) = p^{n}+c\mathbf{g}^{n} = 0$, implies $p^{n} = -c\mathbf{g}^{n}$ and $\Delta p^{n} = -c\Delta \mathbf{g}^{n}$, we then obtain the two systems defined as follows

We now consider the variational formulation related to both problems (3.19) and (3.20).

Find $(\mathbf{u}^{n}, q^{n}, \mathbf{g}^{n}, \eta^{n})$ in $V\times M \times V \times M$ such as:

where $\langle\; \; \rangle_{\Omega}$ represents the duality product between $H^{-1}(\Omega)$ and $H_{0}^{1}(\Omega)$. The following result is a consequence of the density of $D(\Omega)$ in $L^{2}(\Omega)$ and $H_{0}^{1}(\Omega)$.

Proposition 7. The problem S is equivalent to the problem (3.21) in the sense that for all triples $(\mathbf{u}, p, \mathbf{g})$ in $H_{0}^{1}(\Omega)^{2}\times L_{0}^{2}(\Omega)\times L^{2}(\Omega)^{2}$ is a solution of the system $(S)$ in the distribution sense if and only if it is a solution of the problem (3.21).

3.4.   Spectral discretization of the problem

We are now interested in the discretization of problem $(PV_{n})$ in the case where $\Omega = ]-1, 1[^{2}.$

In dimension $d = 2$, for any integers $n, m \geq 0$, we define $\mathbb {P}_{l, m} (\Omega)$ as the the space of polynomials on $\mathbb {R}$.

We denote by $\mathbb {P}_{l, m} (\Omega)$ the space of the restrictions of functions on $\Omega$ of the set $\mathbb {P}_ {l, m}$ of degree $\leq l$ respectively $x$ and $\leq m$ $y$ respectively.

In dimension $d = 2$, denoting by $\mathbb{P}_{N}(\Omega)$ the space of restrictions to $]-1\; \; 1[^{2}$ of polynomials with degree $\leq N$. The space $\mathbb{P}_{N}^{0}(\Omega)$ which approximates $H_{0}^{1}(\Omega)$ is the space of polynomials of $\mathbb{P}_{N}(\Omega)$ vanishing at $\mp 1$.

Setting $\xi _{0} = -1$ and $\xi _{N} = 1$, we introduce the $N-1$ nodes $\xi _{j}$, $1\leq j\leq N-1$, and the $N+1$ weights $\rho _{j}$, $0\leq j\leq N$, of the Gauss-Lobatto quadrature formula. We recall that the following equality holds

We also recall (^[24], form. (13.20)) the following property, which is useful in what follows.

Relying on this formula, we introduce the discrete product, defined for continuous functions $u$ and $v$ by

It follows from $(3.23)$ that this is a scalar product on $\mathbb{P}_{N}(\Omega)$.

Finally, let $\mathcal{I}_{N}$ denote the Lagrange interpolation operator at the nodes $\xi _{i}, 0\leq i\leq N$, with values in $\mathbb{P}_{N}(\Omega)$.

3.4.1.   Discrete spaces

To approximate $L_{0}^{2}(\Omega)$, we consider the space

The space that approximates $H_{0}^{1}(\Omega)$ is

We now assume that the functions $f$ and $g_{n}$ are continuous on $\overline{\Omega }$. Thus, the discrete problem is constructed from $(PV_{n})$ by using the Galerkin method combined with numerical integration and is defined as follows

Find $(\mathbf{u}^{n}_{N}, p^{n}_{N}) \in \mathbb{X}_{N} \times \mathbb{M}_{N}$ such that

where $\mathbf{ f}_{N} = \mathcal{I}_{N} f.$

The existence and uniqueness of the solution $(\mathbf{u}^{n}_{N}, p^{n}_{N})$ is proved in ^[25], see also Brezzi approach and Rappaz Raviart for more details ^[26]. Thus, the discrete problem deduced from (3.21) is

$\mbox{Find} \quad (\mathbf{u}^{n}_{N}, q^{n}_{N}, \mathbf{g}^{n}_{N}, \eta^{n}_{N}) \in \mathbb{X}_{N}\times\mathbb{M}_{N}\times\mathbb{X}_{N}\times\mathbb{M}_{N}\nonumber \; \mbox{such as}$

where $\mathcal{I}_{N}\mathbf{u}_{d} = \mathbf{u}_{dN}$.

Proposition 8. The problem (3.27) has a unique solution $(\mathbf{u}^{n}_{N}, q^{n}_{N}, \mathbf{g}^{n}_{N}, \eta^{n}_{N})$ in $\mathbb{X}_{N}\times\mathbb{M}_{N}\times\mathbb{X}_{N}\times\mathbb{M}_{N}$.

4.   Numerical results

In this part, we will implement some tests illustrating the effectiveness of the proposed algorithm. We choose MATLAB as the programming tool for the numerical simulations.

The matrix system deduced from (3.21) and (3.27) has the following form

Which can be represented as follows

Therefore we obtain a linear system with the form $\mathbf{EX = F}$, where $\mathbf{E}$ is a non-symmetric invertible matrix. This linear system is solved by a preconditioned GMRES method. To simplify we assume that $c = \nu = 1$. In the first and second tests the pair $(\mathbf{u}_{d}, p)$ is a solution of problem $P_{g}$ with $g = 0$$.$ Theoretically, the solution $\mathbf{u}$ must be equal to $\mathbf{u}_{d}$ and $\mathbf{g}$ must be zero in this case. Moreover, this case is among the rare cases where the pair $(\mathbf{u}, \mathbf{g})$ can be provided and $J(\mathbf{g})$ must be zero.

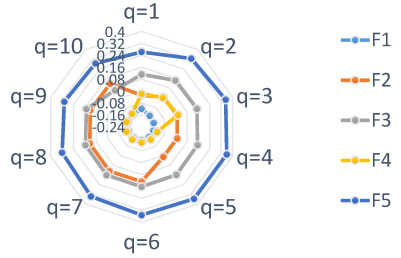
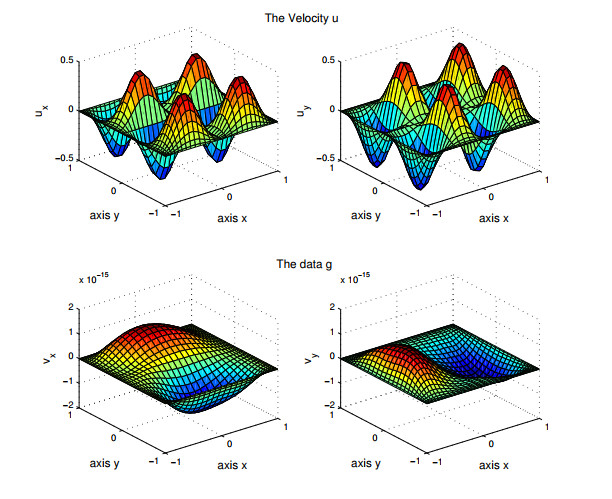
First test: Let $\mathbf{u}_{d} = \left(\begin{array}{c} 0.5\sin (\pi x)^{2}sin(2\pi y) \\ -0.5\sin (2\pi x)sin(\pi y)^{2} \end{array} \right)$, an analytic function which vanishes on the edge $\partial \Omega$ and $p = x+y$. In Figure 1, we present the graphs of the solutions $\mathbf{u}$ and $\mathbf{g}$ for $N = 32$. Note that $J(\mathbf{g})$ reaches $10^{-12\text{ }}$ when $N = 15$ ($N$ is the a number of nodes in the spectral discretization of the problem).

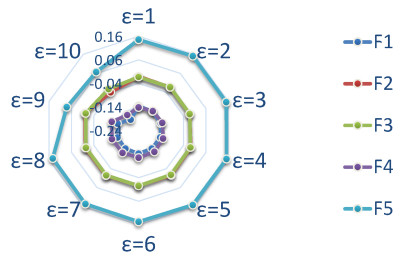
Second test: We now choose $\mathbf{u}_{d} = \left(\begin{array}{c} y(1-x^{2})^{\frac{7}{2}}(1-y^{2})^{\frac{5}{2}} \\ -x(1-x^{2})^{\frac{5}{2}}(1-y^{2})^{\frac{7}{2}} \end{array} \right)$, a singular function that vanishes on the edge $\partial \Omega$ and $p = y.\cos (\pi x)$. In Figure 2, we present the graphs of solutions $\mathbf{u}$ and $\mathbf{g}$ (for N = 32). In Table 1, we illustrate the variation of $J(\mathbf{g})$ with respect to the value of $N$.

In both validation tests, $\mathbf{u}$ converges to $\mathbf{u}_{d}$ and $\mathbf{g}$ converges to $\mathbf{0}$.

The convergence of $J(\mathbf{g})$ is perfectly shown in the first case because of the choice of the function $\mathbf{u}_{d}$ which is an analytic function. However in the second case $\mathbf{u} _{d}$ is a singular function. In this case, $J(\mathbf{g})$ reached a good convergence for $N = 40.$

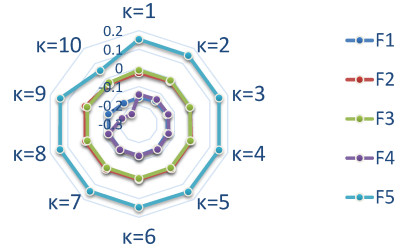
In the third test, the solution $(\mathbf{u, g})$ is unknown. We solve the problem (3.27) with $\mathbf{u}_{d} = \left(\begin{array}{c} y\left(1-x^{2}\right) ^{2}\left(1-y^{2}\right) \\ -x\left(1-x^{2}\right) \left(1-y^{2}\right) ^{2} \end{array} \right)$ and $\mathbf{f} = \left(f_{x}, f_{y}\right)$ where $f_{x} = f_{y} = 10^{3}xy^{2}$.

Figure 3 presents the solutions $\mathbf{u}$ and $\mathbf{g}$. In Table 2, we give the approximate values of $J(\mathbf{g})$ as a function of the parameter $N$. This case shows that the algorithm converges. Without knowing the real solution, we note that $J(\mathbf{g})$ converges to a particular number every time $N$ increases.

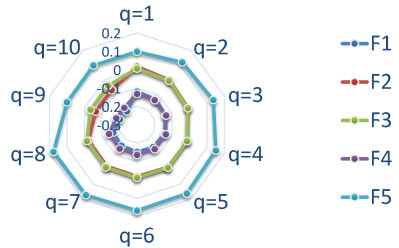
To better estimate this convergence, Figure 4 presents the difference between two successive values of $J(\mathbf{g})$ in the function of the average of two associated values of $N$.

5.   Conclusions

The aim of this paper is to develop a numerical method that solves an optimal control problem by transforming it into a coupled problem. We have tried to simplify the theoretical part as much as possible, and we have even preferred not to add the part related to the discretization of the method since it risks becoming too long. We have considered two examples to illustrate the efficiency of the proposed algorithm. The results given show a good convergence of the algorithm, in particular, a high degree of convergence of $J(\mathbf{g})$ (thanks to the spectral method, which is known for its precision) as a function of the variation of N. We can also use this method for other types of similar nonlinear problems. However, it should be noted that one must always be careful when linearizing the nonlinear term, for example, in our case, if we take the term $(\mathbf{u}^{n+1}.\nabla \mathbf{u}^n)$ un instead of $(\mathbf{u}^n.\nabla) \mathbf{u}^n$ or $(\mathbf{u}^n.\nabla) \mathbf{u}^{n+1}$, the algorithm does not converge.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

We would like to thank you for following the instructions above very closely in advance. It will definitely save us lot of time and expedite the process of your paper's publication.

Conflict of interest

The authors declare no conflict of interest.