A new three-term conjugate gradient algorithm with modified gradient-differences for solving unconstrained optimization problems

1.   Introduction

Although the majority of human papillomavirus (HPV) infections are transient and thus are relatively harmless, persistent infection with certain high-risk HPV genotypes can cause cervical precursor lesions and cervical carcinoma ^[1,2]. Cervical cancer is the most common malignancy reported among women in developing countries and is a leading cause of cancer deaths worldwide, with an estimated 233,000 deaths in 2000 ^[3]. By 2002, the number of women dying from cervical cancer had risen to 274,000 ^[4,5,6]. Nearly, all cervical cancers are attributable to genital infection with HPV ^[7,8]. Up to 70% of women in the general population will acquire genital HPV infection during their lifetime ^[9]. Most HPV related infections are cleared by treatment or natural healing of the host, while some are persistent and may develop into cervical cancer ^[10,11]. The progression from persistent infection to cervical cancer typically needs a period of 20 years or longer ^[12,13]. Fortunately, therapeutic HPV vaccines have made progress in clinical trials after long-term exploration and development. These vaccines include DNA vaccines, RNA replicon vaccines, peptide vaccines, vector vaccines, cell vaccines, and protein vaccines ^[14,15].

Mathematical models have been established to understand the dynamics of HPV related disease. In the modeling, some important variables specific for infectious disease are developed. For example, a variable representing how often an infectious individual contacts with a susceptible individual in a unit time is defined as the contact rate. The probability of each contact is set as $\beta$, indicating the ability of an infectious person to infect others (susceptible persons) in unit time. Considering that there are other members (e.g., immune persons $R\left( t \right)$), and that the number of members infected by one infected person in a unit time is limited, let $N\left( t \right) = S\left( t \right) + I\left( t \right) + R\left( t \right)$, where the total population $N\left( t \right)$ is divided into three epidemiological states: $S\left( t \right)$ is size of the susceptible population at time $t$ and $I\left( t \right)$ is size of the infected population at time $t$. This generates a formula for the incidence rate: the standard incidence rate $\frac{{\beta S\left( t \right)I\left( t \right)}}{{N\left( t \right)}}$ represents the newly infected individuals infected by infectious individuals in unit time at time $t$. Based on these studies, A Omame et al ^[16] formulated a mathematical model to investigate the impact of treatment and vaccination on HPV transmission dynamics. Elamin H and Elbasha et al ^[17] developed a nonlinear, deterministic and age-structured mathematical model. In the same year, Elamin H and Elbasha ^[18] studied the dynamic behaviors of a two-sex, deterministic model for assessing the potential impact of a prophylactic HPV vaccine with several properties. Mo’tassem and S Robert ^[19] developed an age-dependent two-sex mathematical model to describe the HPV vaccination program for a vaccine targeting HPV types 16 and 18 in both childhood and adult stages.

With the development of the mathematical model used to explain the spread of infectious diseases, optimization strategies are introduced into the model. Eihab B M et al ^[20] studied an optimal control model governed by a system of delay differential equations. The optimal vaccination strategy for a constrained time-varying SEIR (Susceptible, Exposed, Infected and Recovered) epidemic model was solved ^[21]. T K Kar and AshimBatabyal ^[22] formulated a nonlinear mathematical SIR epidemic model with a vaccination program. Yang and Tang et al ^[23] studied a mathematical model to explore the impact of vaccination and treatment on the transmission dynamics of tuberculosis (TB).

The purpose of this study was to incorporate both therapeutic HPV vaccines and partial immunity compartments based on the present models to investigate how they influence dynamic behavior and to further examine the optimal treatment control measures to minimize the number of asymptomatic patients and treatment costs. We formulate a mathematical model for HPV transmission, and the existence and stability of the equilibria are discussed. In the next section, we present a sensitivity analysis of the model through Partial Rank Correlation Coefficients to identify the key factors in the model. After that, we use optimal control and theory to minimize the number of asymptomatic patients and treatment costs; we also carry out some numerical simulations to highlight the effect of optimal treatment control on the model. Finally, we give concluding remarks.

2.   A HPV model with treatment

2.1.   Model formulation

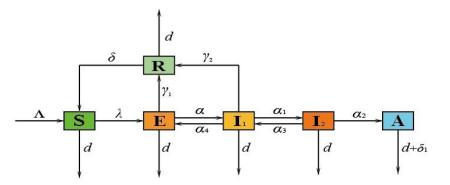
Since persistent infection with high-risk HPV genotypes is the main cause of precursor cervical lesions and cervical carcinoma ^[24], we divided a cohort into three groups, namely, asymptomatic infectious individuals $\left( E \right)$, symptomatic infectious females or males$\left( {{I_1}} \right)$, and individuals with persistent HPV infection $\left( {{I_2}} \right)$. The persistently infected individuals who have not been treated will develop cervical cancer $\left( A \right)$ after a period of time. Moreover, we consider that $E$, ${I_1}$, ${I_2}$ can be cured and become recovered $\left( R \right)$, thus gaining permanent or temporary immunity, which is less reported in previous studies (Table 1). Our assumptions for the dynamic transmission of HPV are demonstrated in Figure 1.

The total human population at time $t$, denoted by $N\left( t \right)$, is subdivided into 6 mutually exclusive compartments of $S$, $E$, ${I_1}$, ${I_2}$, $A$, $R$. Thus

Combining all the aforementioned definitions and assumptions, it follows that the model for the transmission dynamics of HPV in a population is given by the following system of nonlinear differential equations:

where

2.2.   Positivity and boundedness of solutions

Here, we shall show the positivity and boundedness of the population.

Lemma 1. ^[25] Assume that $x(t)$ satisfies $x(0)>0$ and $a>0$, $b>0$, $\frac{{dx}}{{dt}} \le b - ax$, then

.

Theorem 1. Let $S\left( 0 \right) \geqslant 0$, $E\left( 0 \right) \geqslant 0$, ${I_1}\left( 0 \right) \geqslant 0$, ${I_2}\left( 0 \right) \geqslant 0$, $A\left( 0 \right) \geqslant 0$, $R\left( 0 \right) \geqslant 0$, then the solutions $S\left( t \right)$, $E\left( t \right)$, ${I_1}\left( t \right)$, ${I_2}\left( t \right)$, $A\left( t \right)$, $R\left( t \right)$ are positive for all $t > 0$.

Proof It follows from the first equation of the system (2.2) that

which can be re-written as

hence

so that

Similarly, it can be shown that $E\left( t \right) \geqslant 0$, ${I_1}\left( t \right) \geqslant 0$, ${I_2}\left( t \right) \geqslant 0$, $A\left( t \right) \geqslant 0$, $R\left( t \right) \geqslant 0$.

Theorem 2. The region $\Omega$ is positively invariant for model (2.2) with initial conditions in $R_ + ^6$.

Proof Adding all the equations in the differential equation system (2.2) gives

by using Lemma 1, one could easily obtain that

when $t \to \infty$, we have

Let

the region $\Omega$ is positively invariant.

In this region, the model can be considered as been epidemiologically and mathematically well-posed ^[26]. Thus, each solution of the basic model (2.2) with initial conditions in $\Omega$ remains in $\Omega$ for all $t > 0$.

2.3.   Stability analysis

The model (2.2) has a disease-free equilibrium (DFE), given by

Let $X = \left( {E, A, {I_2}, {I_1}, S, R} \right)$, using the notation ^[27], the model consists of nonnegative initial conditions together with the following system of equations:

where

and ${a_1} = \alpha + {\gamma _1} + d$, ${a_2} = {\alpha _1} + {\alpha _4} + {\gamma _2} + d$, ${a_3} = {\alpha _3} + {\alpha _2} + d$, ${a_4} = {\delta _1} + d$, ${a_5} = d + \delta$. It is obvious that

the matrices $F$ and $V$, for the new infection terms and the remaining transfer terms, are, respectively, given by

and

we can get

Consequently, we have the following conclusions

Theorem 3. The DFE of the model (2.2) is globally asymptotically stable if ${R_0} < 1$.

Proof Model (2.2) can be rewritten as

where $F$ and $V$ is given by (2.6), and from ^[28], we have

when $t \to \infty$, $S \to \frac{\Lambda }{d}$, $\left( {E, A, {I_2}, {I_1}} \right) \to \left( {0, 0, 0, 0} \right)$, that is, $\left( {S, R, E, A, {I_2}, {I_1}} \right) \to {x_0}$ if $t \to \infty$. Further, $F$ is nonnegative, $V$ is a nonsingular matrix and all eigenvalues of ${J_4}$ have positive real part. According to ^[27], all eigenvalues of $F - V$ have negative real part. Therefore, the DFE of the model (2.2) is globally asymptotically stable if ${R_0} < 1$.

2.4.   Non-existence of limit cycles

Theorem 4. In the first quadrant, there is no limit cycle in system (2.2).

Proof We consider the Dulac function as $B\left( {S,E} \right) = \frac{1}{{SE}}$, now we have

therefore, by the Dulac–Bendixson theorem ^[29], there is no periodic orbit for the system (2.2).

2.5.   Existence of forward bifurcation

The epidemiological implications of backward bifurcation are that the effective disease control is only feasible if the basic reproduction number is reduced to values below another subthreshold less than unity ^[28]. Compared with backward bifurcation, the epidemiological significance of forward bifurcation means that the disease will disappear as long as the basic reproduction number is less than unity. Clearly, this phenomenon has important public health implications. Next, we analyze the existence and properties of bifurcation of the model.

Let

${D_1} = \frac{{{a_2}{a_3} - {\alpha _1}{\alpha _3}}}{{\alpha {\alpha _1}}} > 0$, ${D_2} = \frac{{{a_3}}}{{{\alpha _1}}}$, ${D_3}{\rm{ = }}\frac{{{\alpha _2}}}{{{a_4}}}$, ${D_4} = \frac{{{\gamma _1}\left( {{a_2}{a_3} - {\alpha _1}{\alpha _3}} \right) + {\gamma _2}\alpha {a_3}}}{{\alpha {\alpha _1}{a_5}}}$,

${D_5} = {\beta _1}{D_1} + {\beta _2}{D_2} + {D_3}$, ${D_6} = 1 + {D_1} + {D_2} + {D_3} + {D_4}$,

Setting the right-hand sides of model (2.2) to zero (at steady state) give by ${E_*} = \left( {{S_*}, {E_*}, {I_{1*}}, {I_{2*}}, {A_*}, {R_*}} \right)$, where

${S_*} = \frac{{\Lambda {R_0}{D_7}\left( {{R_0} - 1} \right)}}{{{D_5}\left( {{R_0} - 1} \right) + d{D_6}{R_0} - \delta {R_0}\left( {{R_0} - 1} \right){D_4}}}$, ${E_*} = \frac{{\Lambda {R_0}{D_1}\left( {{R_0} - 1} \right)}}{{{D_5}\left( {{R_0} - 1} \right) + d{D_6}{R_0} - \delta {R_0}\left( {{R_0} - 1} \right){D_4}}}$,

${I_{1*}} = \frac{{\Lambda {R_0}{D_2}\left( {{R_0} - 1} \right)}}{{{D_5}\left( {{R_0} - 1} \right) + d{D_6}{R_0} - \delta {R_0}\left( {{R_0} - 1} \right){D_4}}}$, ${I_{2*}} = \frac{{\Lambda {R_0}\left( {{R_0} - 1} \right)}}{{{D_5}\left( {{R_0} - 1} \right) + d{D_6}{R_0} - \delta {R_0}\left( {{R_0} - 1} \right){D_4}}}$,

${A_*} = \frac{{\Lambda {R_0}{D_3}\left( {{R_0} - 1} \right)}}{{{D_5}\left( {{R_0} - 1} \right) + d{D_6}{R_0} - \delta {R_0}\left( {{R_0} - 1} \right){D_4}}}$, ${R_*} = \frac{{\Lambda {R_0}{D_4}\left( {{R_0} - 1} \right)}}{{{D_5}\left( {{R_0} - 1} \right) + d{D_6}{R_0} - \delta {R_0}\left( {{R_0} - 1} \right){D_4}}}$.

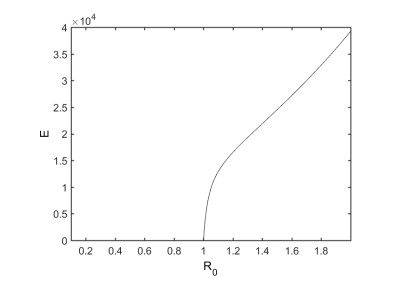
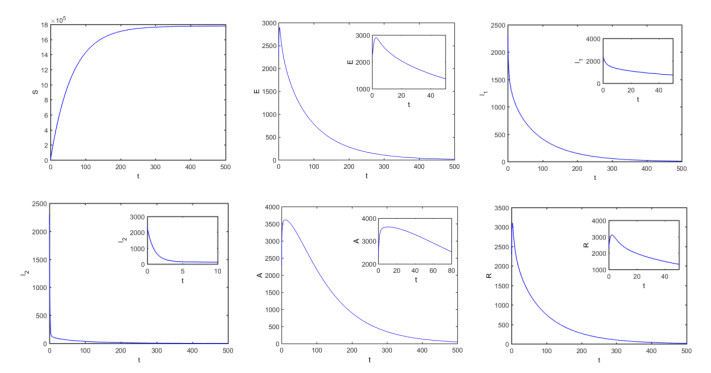
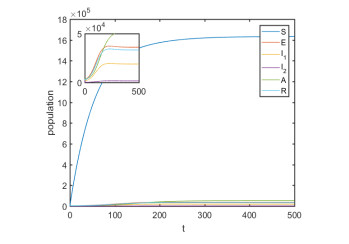
It is instructive to characterize the type of bifurcation the model (2.2) may undergo, and we demonstrate the results in Appendix A. This phenomenon is illustrated by simulating model (2.2) with the set of parameter values listed in Table 2. The associated forward bifurcation diagram, depicted in Figure 2, shows that the model has a disease-free equilibrium (corresponding to ${R_0} < 1$) (Figure 3) and an endemic equilibria (corresponding to ${R_0} > 1$) (Figure 4).

3.   Efficacy of interventions and sensitivity analysis

3.1.   Efficacy of interventions

We used the parameter values given in Table 2 (unless otherwise stated) for our numerical simulations and changed the key parameter values to observe the corresponding effects on the disease outbreak.

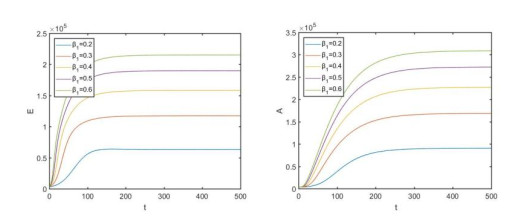
To investigate the effect of contact rate on disease infection, we varied ${\beta _1}$, as shown in Figure 5. The figure shows that as the contact rate of $E\left( t \right)$ with $S\left( t \right)$ increases, the number of infected individuals increases, and consequently, the increased contact rate will result in an increase in the disease outbreak.

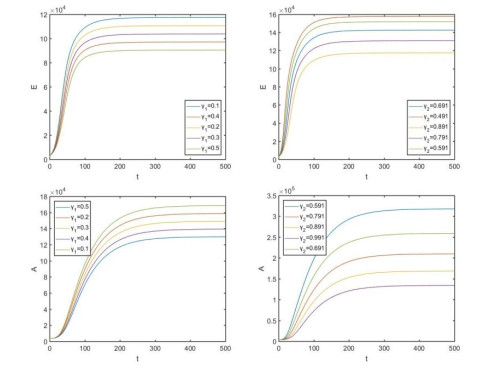
To examine the effect of treatment rate on disease infection, we plotted Figure 6. It demonstrates that increasing the parameter ${\gamma _1}$ and ${\gamma _2}$ decreases the endemic levels of asymptomatic patients and cancer-infected individuals. In particular, if we increased treatment rate ${\gamma _1}$ by $400\%$, the population of the asymptomatic patients and cancer-infected individuals would be decreased by $23\%$, and treatment rate ${\gamma _2}$ would be increased by $68\%$. Finally, the endemic levels of the cancer-infected individuals population would be decreased by $58\%$. Moreover, increasing treatment rate ${\gamma _2}$ by $81\%$would decrease the population of asymptomatic patients by $25\%$.

3.2.   Sensitivity analysis of parameters in R₀

Latin hypercube sampling (LHS) is one of the Monte Carlo (MC) sampling methods that was first proposed by Mckay ^[34] in 1979. The advantage of LHS sampling is that the number of iterations is less than in other methods of random sampling, and the clustering phenomenon of sampling is avoided ^[35].

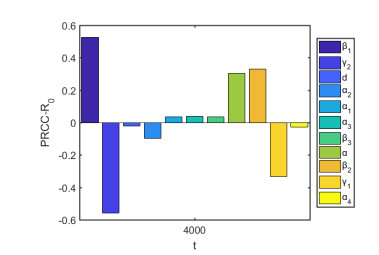
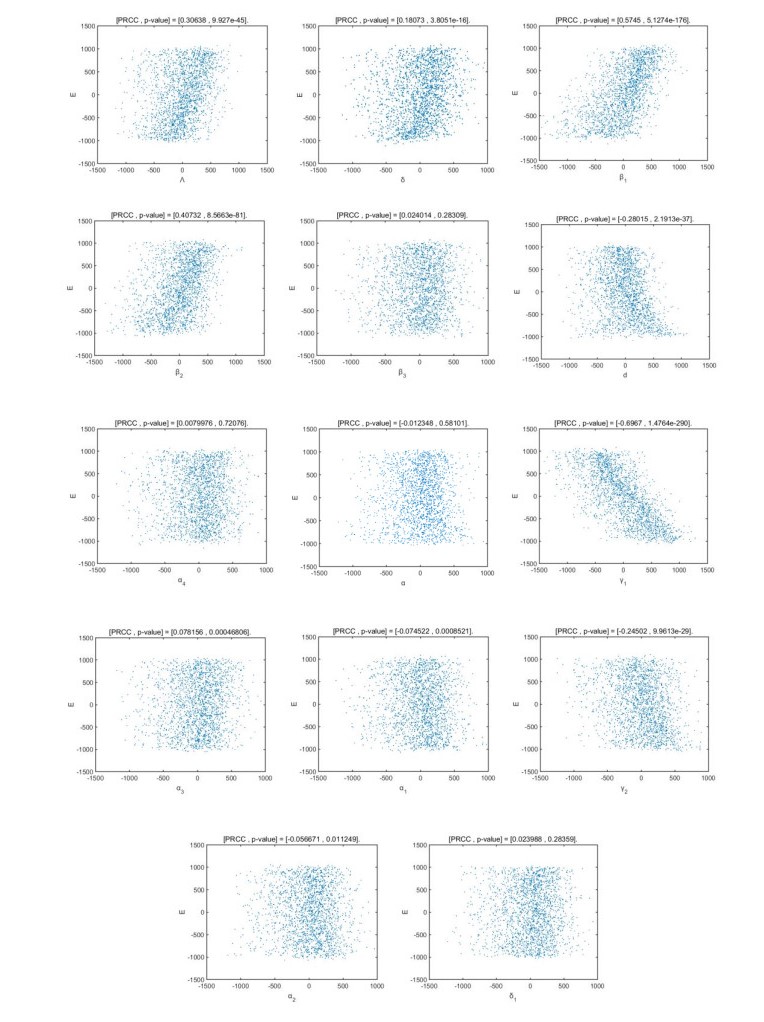
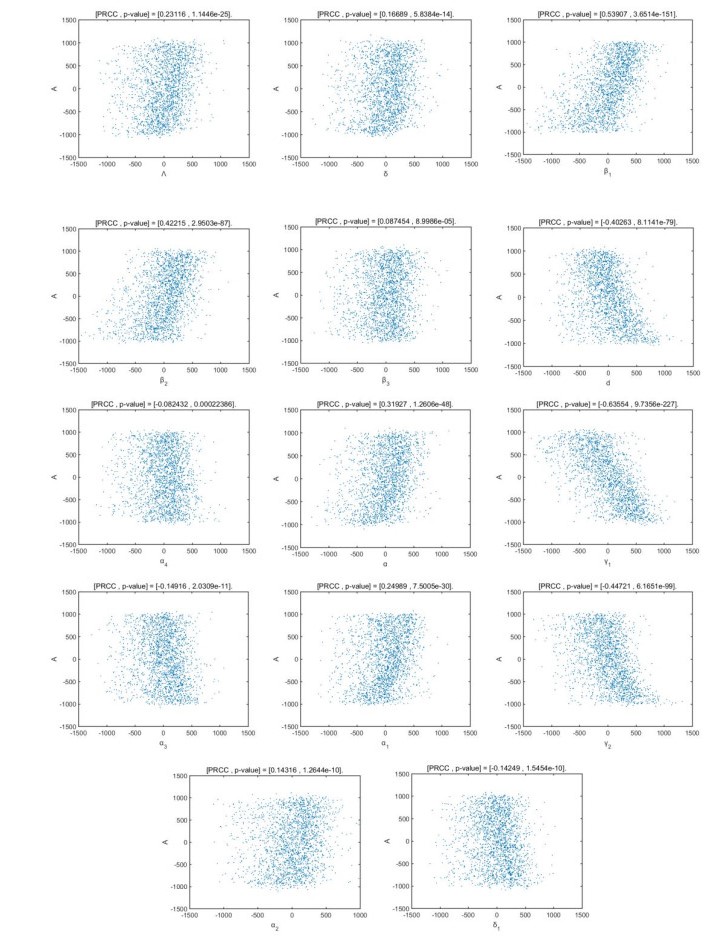
Model (2.2) has 14 parameters. In order to identify the factors associated with a given intervention that most strongly affect the spread of a new infection, following ^[36] we performed Latin Hypercube Sampling on the parameters that appear in ${R_0}$. For the parameters in Eq. (2.7), Partial Rank Correlation Coefficients (PRCC) were calculated, and a total of 1000 simulations per LHS run were carried out. We chose a uniform distribution as the prior distribution when performing parameter sampling; the parameters of the model were set as input variables, and ${R_0}$ as the output variable. If the absolute value of the PRCC is larger, the influence of the parameter in ${R_0}$ is greater. It is assumed that if the $p$ value is greater than 0.05, the parameter is not significant for ${R_0}$.

Table 3 lists the PRCC values of the estimated parameters associated with ${R_0}$. The values reflect the correlation between the parameters ${\beta _1}$, ${\gamma _2}$, $d$, ${\alpha _2}$, ${\alpha _1}$, ${\alpha _3}$, ${\beta _3}$, $\alpha$, ${\beta _2}$, ${\gamma _1}$, ${\alpha _4}$ and ${R_0}$. From Table 3 and Figure 7, ${\beta _1}$, ${\alpha _1}$, ${\alpha _3}$, ${\beta _3}$, $\alpha$, ${\beta _2}$ are positively correlated with ${R_0}$, while ${\gamma _2}$, $d$, ${\alpha _2}$, ${\gamma _1}$, ${\alpha _4}$ are negatively correlated with ${R_0}$. Among the parameters, the positive influence of ${\beta _1}$ and ${\beta _2}$ on ${R_0}$ is most obvious, that is, as ${\beta _1}$ and ${\beta _2}$ increase, the values of ${R_0}$ increase rapidly, and more individuals will become infected. When symptomatic infectious individuals are continue to be infected and suffer from cancer, not only will the treatment be more difficult, the value of ${R_0}$ will also increase. This indicates that the rate of progression to the symptomatic stage for individuals has a greater positive impact on ${R_0}$. In addition, ${\gamma _2}$ and ${\gamma _1}$ have the greatest negative impact on ${R_0}$, indicating that the value of ${R_0}$ will decrease if the individuals with HPV symptoms or infectious individuals with no symptoms can be treated. Moreover, we can obtain that $\left| {PRCC\left( {{\gamma _2}} \right)} \right| > \left| {PRCC({\beta _1})} \right| > \left| {PRCC({\gamma _1})} \right| > \left| {PRCC\left( {{\beta _2}} \right)} \right| > \left| {PRCC\left( \alpha \right)} \right|$, namely, ${\gamma _2}$, ${\beta _1}$, ${\gamma _1}$, ${\beta _2}$, $\alpha$, play the most important roles in determining ${R_0}$.

3.3.   Sensitivity analysis of parameters in infectious variables

Time-varying sensitivity explains the influence of parameters on state variables when they change with time ^[35], thereby evaluating the influence and dependence of parameters on state variables in dynamic models. Given the different outbreak time periods of various diseases, one should pay attention to the effect of time period. For example, after being infected with HPV, the clinical manifestations are diverse, and individuals can even be asymptomatic. Therefore, the entire time period of disease prevention, outbreak, infection, and treatment should be considered.

Based on the pathogenesis of HPV, this section considers the sensitivity analysis of parameters in state variables from two aspects, namely, a continuous period of time and a single point in time.

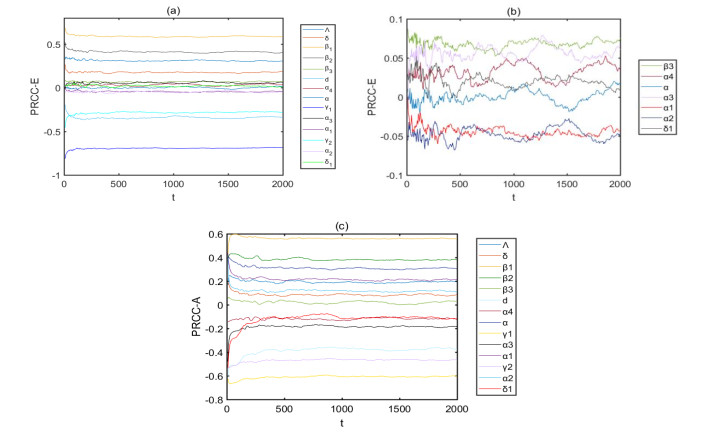
The sensitivity analysis of parameters in $E\left( t \right)$ and $A\left( t \right)$ in continuous time period is shown in Figure 8, we set parameters are input variables, $E\left( t \right)$ and $A\left( t \right)$ are output variables, the number of samples $N = 2000$.

In Figure 8, we show that the sensitivity of parameters in the early stages of disease outbreak changes significantly, especially before $t = 500$. As can be seen from Figure 8(a), the influence of ${\gamma _2}$, ${\gamma _1}$, ${\beta _1}$, ${\beta _2}$, $d$ and $\alpha$ has obvious changes, where the PRCC values of ${\gamma _2}$ and ${\gamma _1}$ decrease significantly with time, indicating that with the outbreak of disease, people have a certain understanding on the way of disease infection and have made great progress in the treatment. As the time increases, the treatment method quickly forms a treatment system, and it is difficult to progress within a short period of time, meaning that when $t > 500$, the influence of ${\gamma _2}$ and ${\gamma _1}$ is lessened. The PRCC values of $\alpha$ have positive and negative fluctuations over time, indicating that in addition to the factors for abandoning treatment due to economic or social discrimination, it is also affected by the use of condoms and other protective measures. There are obvious changes illustrated in Figure 8(c), when $t < 500$, the influence of the transmission coefficients and the disease-induced mortality ${\delta _1}$ gradually increase, while due to the improvement of medical intervention, the PRCC values of ${\alpha _3}$, ${\alpha _1}$ and ${\alpha _2}$ decrease.

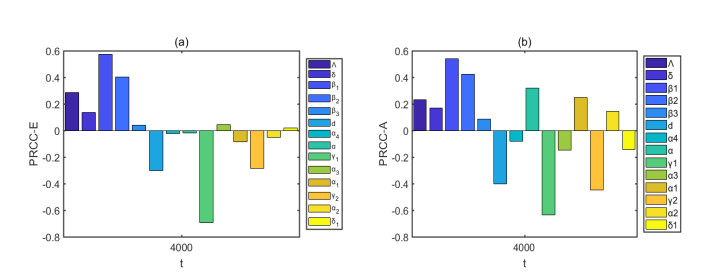
The influence of different parameters on state variables is also different at a certain time ^[37], so the influence of parameters on state variables at $t = 4000$ is studied, and the numerical simulation results can be seen in Table 4, Table 5, Figure 9, Figure 10, and Figure 11.

Figure 9 (a) and Table 4 shows that${\beta _1}$, ${\beta _2}$ and $E\left( t \right)$ are positively correlated, namely, the increase of ${\beta _1}$, ${\beta _2}$ will lead to the increase of $E\left( t \right)$; while ${\gamma _1}$, ${\gamma _2}$ and $E\left( t \right)$ have a significant negative correlation. Moreover, from Figure 10, we can get that the monotonicity of parameters ${\gamma _2}$, ${\beta _1}$, ${\beta _2}$, $\Lambda$ and $d$ is most significant, in other words, $E\left( t \right)$ is mainly affected by these parameters at this time.

From Figure 11 and Table 5, the monotonicity of parameter ${\beta _1}$, ${\beta _2}$, ${\gamma _1}$, ${\gamma _2}$, $d$, ${\alpha _1}$ and $\alpha$ is obvious, from Figure 9 (b), ${\beta _1}$, ${\beta _2}$, $\alpha$, ${\alpha _1}$ has a positive correlation with $A\left( t \right)$, while ${\gamma _1}$, ${\gamma _2}$, $d$ has a negative correlation with $A\left( t \right)$, which means that at this time, with the increase of ${\beta _1}$, ${\beta _2}$, $\alpha$, ${\alpha _1}$, the number of $A\left( t \right)$ will increase, but when ${\gamma _1}$, ${\gamma _2}$, $d$ increases, the number of $A\left( t \right)$ will decrease.

4.   Optimal control of the extended model

The spread of infectious diseases can be controlled through reasonable treatment ^[16]. In this section, the optimal treatment problem will be addressed within the framework of the optimal control problem for constraints ^[21].

4.1.   Formulation of the optimal treatment problem

We recorded ${\gamma _1}$ as $u$, and indicated the rate of people receiving treatment in $E\left( t \right)$. Then an additional variable $V\left( t \right)$ was introduced:

where the value of $V\left( t \right)$ at the initial time was set to $0$. According to the actual situation, the treatment capacity of a city or a country is limited, and the number of people who can be treated is limited as well ^[38], so the following formula can be established as

where ${\Omega _1}\left( t \right)$ is the time-dependent upper limit of the number of people that can be treated at each time instant. In addition, state restrictions can be introduced to keep the asymptomatic patients population at a low level, according to ^[39] we proposed the following constraints

where ${E_{\max }}$ is the upper limit of $E\left( t \right)$.

Let $x = {\left[ {S, E, {I_1}, {I_2}, A, R} \right]^T}$, and the treatment rate $u\left( t \right)$, was taken as the control variable. As to the cost function, the state variables and control variables are quadratic functions, which consider both the treatment rate and the number of asymptomatic patients. Based on the above description, the optimal treatment strategy can be formulated as the following problems with inequality constraints and free terminal state:

where ${t_f} \in {R^ + }$ is the terminal time; ${A_1} \in {R^ + }$ is the weight coefficient of $E\left( t \right)$.

4.2.   Analysis of optimal controls

The optimal control of the problem (P) is expressed as ${u_*}$. Next, we use the maximum principle of Pontryagin ^[21] to derive the optimal system for problem (P). Prior to this, we converted the inequality constraints in the problem (P) into equality constraints with some non-negative parameter parameters ${\eta _i}\left( {i = 1, 2, 3, 4} \right)$:

and we denoted $\eta = {\left[ {{\eta _1}, {\eta _2}, {\eta _3}, {\eta _4}} \right]^T}$. Therefore, the Hamilton function of the problem (P) was obtained as follows

where $\varphi = {\left[ {{\varphi _S}, {\varphi _E}, {\varphi _{{I_{}}}}, {\varphi _{{I_2}}}, {\varphi _A}, {\varphi _R}} \right]^T}$ are costate variables, $\mu = {\left[ {{\mu _1}, {\mu _2}, {\mu _3}, {\mu _4}} \right]^T}$ are non-negative penalty multipliers.

By using Pontryagin’s maximum principle, the first-order necessary conditions can be obtained. The optimality conditions with respect to state, costate and parametric variables generate a two-point boundary value problem coupled with a nonlinear complementarity problem ^[21] as follow:

and $\eta \geqslant 0$, $\mu \geqslant 0$, ${\eta ^T}\mu = 0$.

Consider the optimality conditions with respect to the control variable

and from Eq. (4.8), the adjoint system can be derived as follow:

with the transversality conditions

From (4.4) we had $0 \leqslant u \leqslant {u_{\max }}$ and $u \leqslant \frac{{{\Omega _1}}}{E}$, in other words, $0 \leqslant u \leqslant \left\{ {{u_{\max }}, \frac{{{\Omega _1}}}{E}} \right\}$ is required to be satisfied. Let ${u_{\max }} = 1$ and ${\Omega _1} < {E_{\max }}$. Hence, $\frac{{{\Omega _1}}}{E} < {u_{\max }}$ always establishes.

By solving (4.9), we got

We considered the case of $\frac{{{\Omega _1}}}{E} > {u_{\max }}$, under this assumption, ${u_*} < \frac{{{\Omega _1}}}{{{E_*}}}$ always establishes, therefore, ${\mu _4} = 0$. Next, to determine the explicit expression of optimal control without ${\mu _1}$ and ${\mu _2}$, we considered the following three assumptions:

(1) On the set $\left\{ {\left. t \right|0 < {u_*} < {u_{\max }}} \right\}$, we had ${\mu _1} = {\mu _2} = 0$, hence, ${u_*} = \frac{{\left( {{\varphi _E} - {\varphi _R}} \right)E}}{2}$.

(2) On the set $\left\{ {\left. t \right|{u_*} = 0} \right\}$, we had ${\mu _2} = 0$, therefore, $0 = {u_*} = \frac{{\left( {{\varphi _E} - {\varphi _R}} \right)E + {\mu _1}}}{2}$, and ${\mu _1} \geqslant 0$, it is determined that $\left( {{\varphi _E} - {\varphi _R}} \right)E \leqslant 0$.

(3) On the set $\left\{ {\left. t \right|{u_*} = {u_{\max }}} \right\}$, we had ${\mu _1} = 0$, hence, ${u_*} = {u_{\max }} = \frac{{\left( {{\varphi _E} - {\varphi _R}} \right)E - {\mu _2}}}{2}$, and ${\mu _2} \geqslant 0$, it is determined that $\frac{{\left( {{\varphi _E} - {\varphi _R}} \right)E}}{2} \geqslant {u_{\max }}$.

Combining the above three cases, the optimal control ${u_*}$ is characterized as

Using the similar arguments, we can characterize the optimal control ${u_*}$ under the condition where $\frac{{{\Omega _1}}}{E} \leqslant {u_{\max }}$ as

from the above discussions, an analytical expression of the optimal treatment rate is derived

4.3.   Numerical simulations

In this section, the symplectic pseudospectral method (SPM) developed in ^[40,41] is used to conduct numerical simulation. It owns structure-preserving property since the inherent Hamiltonian structure of optimal control problems is utilized. The local pseudospectral discretization scheme and the successive convexification technique are incorporated to make the algorithm fast and accurate. On one hand, the SPM can precisely quantify the energy variation for mechanical systems in optimal control and is thus widely used in vehicle trajectory planning ^[42,43,44]. On the other hand, it has sound stability for optimal control problems with long time span, which makes it an attractive method to solve policy-making problems for biological system ^[21].

When using the SPM in this section, the whole time span is divided into 10 regular sub-intervals and a 10-order approximation polynomial is used in each sub-interval. The parameters for the optimal control problem is set as Table 2 (unless otherwise stated in Table 6).

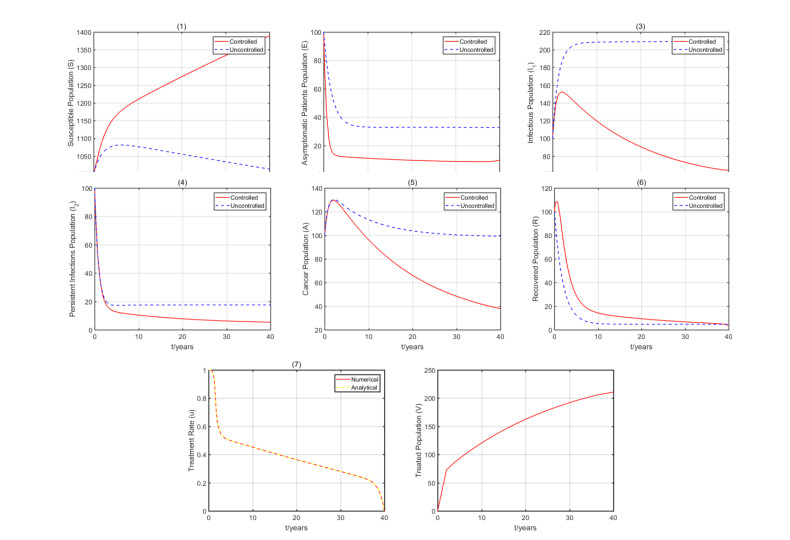
The controlled solution is shown in Figure 12 along with the uncontrolled solution. It can be seen that the treatment strategy is effective, ${I_1}$ and $A$ decreases rapidly and almost reaches zero at $t = 40$, and the values of $E$ and ${I_2}$ are also significantly reduced compared to before the addition of the treatment strategy. In addition, the values of $S$ and $R$ increased at the initial stage, and the effect before adding the treatment strategy is very obvious compared with the effect after the addition.

In the controlled case, the control variable $u\left( t \right)$ is continuously reduced and reaches zero at the terminal. It can be seen from Figure 12(7) that the numerical solution of the control variable is in good agreement with the analytical solution given in (4.12), which verifies the characteristics of the optimal control.

5.   Conclusion

For humans and some social animals, the standard incidence rate is more realistic than the bilinear incidence rate, so we used the standard incidence rate to indicate the ability of an infected person to infect others. Moreover, we assumed that the patients with persistent infection of HPV could be controlled and that mild infection could be cured, thus, those who are cured or have self-healed will gain immunity. Next, we established the model and analyzed its properties. It can be seen from the analysis results that controlling the value of the parameter in ${R_0}$, making ${R_0}$ less than 1, the disease will be die out, and when ${R_0}$ greater than 1, the infection will experience an outbreak and form an endemic disease. The sensitivity analysis of the parameters in ${R_0}$ and state variables illustrates that the value of ${R_0}$ can be reduced or increased more efficiently, and the results can be used to control the spread of HPV. In the last section, the treatment rate is selected as the control variable, and the optimal treatment strategy is analyzed theoretically and simulated numerically. The results show that the appropriate treatment strategy can efficiently reduce the spread of the disease.

Acknowledgments

This work was supported by the Fundamental Research Funds for the Central Universities (31920200037; 31920200070), the National Natural Science Foundation of China (31560127), the Program for Yong Talent of State Ethnic Affairs Commission of China (No. [2014]121), and Gansu Provincial First-class Discipline Program of Northwest Minzu University (No. 11080305).

Conflict of interest

The authors declare that no conflict of interest.