Semi-$(E, F)$-convexity in complex programming problems

Abbreviations: ${A}_{*}$: permeability component; ${\beta }_{0}$: the strength magnetic field; ${\beta }_{1}$: The ratio of nanolayer thickness to Particle radius; ${\sigma }_{el}$: electrical conductivity; p: pressure; $\widehat{T}$: fluids temperature; ${k}_{s1}$: thermals conductivity of first Particle; ${k}_{s2}$: thermals conductivity of second Particle; ${k}_{bf}$: thermals conductivity of base fluids; ${k}_{nf}$: thermals conductivity of the nanofluid; ${k}_{nfl}$: thermals conductivity of the Nanofluid with effect of nanolayer; ${k}_{hnf}$: thermals conductivity of the Hybrid nanofluid; ${k}_{hnfl}$: effective nanolayer thermal conductivity of hybrid nanofluid; ${k}_{pe}$: equivalent thermals conductivity of equivalent Particle; ${k}_{pe1}$: equivalent thermals conductivity of first equivalent Particle; ${k}_{pe2}$: equivalent thermals conductivity of second equivalent Particle; S: shape factor; ${\sigma }_{hnf}$: thermals conductivity of the hybrid nanofluid; ${\sigma }_{s1}$: thermals conductivity of first nanoparticle; ${\sigma }_{s2}$: thermals conductivity of second nanoparticle; ${\rho }_{s1}:$ density of the first nanoparticle; ${\rho }_{s2}:$ density of the second nanoparticle; ${c}_{p}:$ Specifics heats at constant pressures; ${\left({c}_{p}\right)}_{nf}:$ Specifics heats for the Nanofluid; ${M}_{*}$: the magnetic parameter; ${S}_{c}$: Schmidt number; ${R}_{e}:$ the permeability Reynolds number; ${P}_{r}:$ the Prandtl number; ${\mu }_{hnf}:$ the viscosity of the hybrid nanofluid; ${\rho }_{hnf}$: the density of the hybrid nanofluid; ${\alpha }_{hnf}$: the thermal diffusivity of hybrid nanofluid; ${\upsilon }_{hnf}:$ the kinematic viscosity of hybrid nanofluid; HNF: hybrid nanofluid; ENTC: effective nanolayer thermal conductivity; NENTC: non-effective nanolayer thermal conductivity; SFC: Skin friction coefficients; MNC: Matrix nanocomposite; ${\alpha }_{*}:$ the wall expansion ratio; $\eta :$ scaled boundary layer coordinate; $\theta :$ self-similar temperature; $\mu :$ dynamic viscosity; $\upsilon :$ kinematic viscosity; $\rho :$ density; ${\varphi }_{s1}$: first nanoparticle volume fraction; ${\varphi }_{s2}$: second nanoparticle volume fraction; nf: nanofluid; hnf: hybrid nanofluid; hnfl: effective hybrid nanofluid; s1: first nanoparticle; s2: second nanoparticle

1.   Introduction

Polytetrafluoroethylene (PTFE) is an excellent claimant in extensive applications, such as mechanical systems, biomaterials, chemical, and electrical, because of its low frictional coefficient and dielectric constant, few moistures absorption, chemical inertness, and excellent thermal stability ^[1]. Plunkett ^[2] initially described PTFE, which has remarkable physical properties in addition to the highly fluorinated saturated organic compounds. Polymer matrix nanocomposites (PMNC) is the material which composes of polymeric matrix distributed in silica, CNT, or organic substances. The distribution and reinforcement of matrix material particles at the nano-scale lead to a significant improvement in the mechanical properties of the produced composite. PMNC is appreciative in transportation, aircraft, defensive weapons etc. The most widely used reinforcement in PMNC is CNT due to their remarkable mechanical and electrical properties ^[3]. Chen et al. ^[4] have examined the behavior of CNT-filled composites of PTFE. Lin et al. ^[5] have investigated the Functionalization of Polymeric Carbon Nanocomposites from CNT with polymer matrix.

Yu et al. ^[6] demonstrated that liquid molecules near particle surfaces form layered structures and behave like solids. Despite the fact that the related layer of fluid molecules at the interface is only a few nanometers thick, it may play a significant role in heat transmission from concrete to a surrounding fluid. As a result, the theoretical investigation by Yu and Choi ^[7] suggested that the nanolayer which exists between the base fluid and NPs is a key factor. Xue ^[8] suggested a thermal conductivity (TC) model based on the theory of Maxwell and theory of the average polarization. An elliptical interfacial layer was examined Yu and Choi ^[9]. However, with the various sorts and forms of particles, it is not clear what his model's depolarization factor would be. Furthermore, it is complicated to determine the TC of complex NPs (NPs with an interfacial layer). The experimental data is matched with the expected TC values by using a thicker interfacial layer thickness (h = 03nm), which cannot be accurate for smaller particles. The influence of nanolayer near the particles to the Maxwell equation for the effective TC of solid–fluid interruption. The TC of the nanolayer was assumed to be similar as that of the particles in their model. This is impracticable due to the fact that interfacial layer is formed via way of means of fluid molecules surrounding the particle surface, and the awareness of these adsorbed molecules with inside the interfacial layer is smaller than that of the solid particle. As a result, the interfacial layer's TC should be smaller than that of solid particles but greater than that of liquid.

Permeable co-axial disks have remarkable applications in the fields of biomechanics, the processes of crystal growth, oceanography, mass and heat transfer, lubricants, viscometer, rotating machineries, and storage devices for computers. Several researchers have focused on issues with disks with various wall conditions. As an example, the impact of shape and size on the dispersion of metallic/ceramic matrix nanocomposite material in magnetized hybrid nanofluids flow via permeable coaxial disks was examined by Qureshi et al. ^[10]. Abdelmalek et al. ^[11] investigated the effects of several magnetized hybrid nanoparticles on the fluid flow between two orthogonal spinning disks. Banchok et al. ^[12] investigated heat transfers in nanofluid flow over a rotating porous disk. The Heat and Mass Transfer Analysis of Unsteady Non-Newtonian Fluid Flow between Porous Surfaces in the Presence of Magnetic Nanoparticles was investigated by Qureshi et al. ^[13]. By using the Darcy-Forchheimer relation, Bilal et al. ^[14] investigated the mathematical analysis of hybridized ferromagnetic nanofluid with the induction of copper oxide nanoparticles in permeable surfaces.

The flow behavior of a moving conducting fluid is described by magnetohydrodynamics, which polarizes it. Magnetic field effects are studied in industrial operations such as fuel manufacturing, electrical generators, crystal fabrication, nuclear power plants, and aerodynamics, among others. Elfven et al. ^[15] established the field of magnetohydrodynamics. Aly et al. ^[16] presented a numerical study of a hybrid magnetic nanomaterial in a stretching medium that is permeable. The MHD nanofluids natural convection in an insertion below have an effect on thermal radiation usage of the controlled volume-based finite element approach, as well as the form factor of NPs using the Duan Rach Approach was investigated by Chamkha et al. ^[17]. For turbine cooling applications, Dogonchi and Ganji ^[18] have explored the equations for the transfer of heat in an axisymmetric channel with permeable walls for a non-Newtonian fluid flow. Krishna ^[19] has analyzed the heat transfer of aluminium oxide and copper nanofluids flowing through a stretched porous surface in a steady MHD flow. Devi and Devi ^[20] investigated the magnetohydrodynamics flow of copper-alumina/H₂O hybrid nanofluids computationally. Krishna et al. ^[21] have recently investigated the radiative MHD Casson hybrid nanofluids flow across an immense exponentially improved perpendicular permeable surface. Abbas et al. ^[22] investigated heat transfer in MHD hybrid nanofluid flow across a nonlinear stretched curved surface with thermal slip. Upreti et al. ^[23] investigated the entropy generation and unstable squeezing flow of MHD hybrid nanofluids within parallel plates. Heat transfer in three-dimensional hybrid nanofluids flow due to convective surface and base fluids was investigated by Upreti et al. ^[24]. Abbas et al. ^[25] investigated the techniques of data collection of Cu−Al₂O₃/H₂O flow over a vertical wedge in water. Nadeem et al. ^[26] investigated the flow of a nanomaterial with a base viscoelastic MHD micropolar fluid over a stretched surface. Anwar et al. ^[27] investigated the computational analysis of induced MHD nonlinear stretching sheet flow. MHD hybrid nanofluid flow investigated by many researchers ^{[28,29,30,31,32,33,34]}.

The above mentioned literature revealed to the authors that no research has been done on the dispersion of polymer/CNT matrix nanocomposite material through permeable surfaces subject to magnetized hybrid nanofluids flow with the influence of morphological nanolayer. Further, in the present study, we examined numerically the prominence of the permeability function consisting of the permeable Reynold number associated with the expansion/contraction ratio. The governing equations are transformed into dimensionless ordinary differential equations (ODEs) via similarity variable transformation technique. The Runge-Kutta and shooting procedures are implemented to achieve the solution of ODEs. Variations in skin friction coefficient and Nusselt number at the lower and upper walls of disks, as well as heat transfer rate measurements are computed using important engineering physical factors. A comparison table and graph of effective nanolayer thermal conductivity and non-effective nanolayer thermal conductivity are presented.

2.   Mathematical modeling

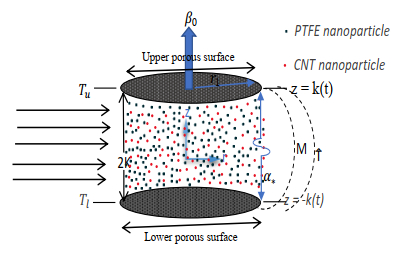
Flows between two disks have many important applications in the fields of biomechanics, the processes of crystal growth, oceanography, mass and heat transfer, lubricants, viscometer, rotating machineries, and storage devices for computers. The disks in thrust bearings are separated through a lubricant pumped via disks. Furthermore, in modern lubrication technology fluids with polymer additives have been used as enhanced lubricating oils. In this problem, we assume the laminar, viscous, incompressible, unsteady, 2D flow of hybrid nanofluid (HNF) containing PTFE-SWCNT/H₂O between two porous disks which are orthogonally moving in the presence of an external magnetic field utilized in the z-direction. $2{\mathrm{r}}_{1}$ is the diameter of the boundary disks. $2\mathrm{k}\left(\mathrm{t}\right)$ is the distance between the disks. The disks move uniformly at a time-dependent rate $\mathrm{k}\mathrm{\text{'}}\left(\mathrm{t}\right)$ down or up and have the same permeability. The physical model uses a cylindrical coordinate system (r, θ, z) velocity $\widehat{\mathrm{u}}$ in the line of r and velocity $\widehat{\mathrm{w}}$ in the line of z, but velocity v̂ disappears. The ${\mathrm{T}}_{\mathrm{l}}$ represents the temperature at the lower disk and ${\mathrm{T}}_{\mathrm{u}}$ represents the temperature at the upper disk shown in Figure 1. The thermophysical properties of nanoparticles and bases fluids are mentioned in the Tables 1 and 2. The governing equations are as follows ^[35]:

where ${\mathrm{\rho }}_{\mathrm{h}\mathrm{n}\mathrm{f}}$ is the density of HNF, ${\mathrm{\beta }}_{0}$ is magnetic field strength, ${\mathrm{\sigma }}_{\mathrm{h}\mathrm{n}\mathrm{f}}$ is the electrically conductivity of hybrid nanofluid, T̂ is the temperature, $\mathrm{P}$ is the pressure, ${\left(\mathrm{\rho }{\mathrm{C}}_{\mathrm{p}}\right)}_{\mathrm{h}\mathrm{n}\mathrm{f}}$ is the heat capacitance of HNF, ${\mathrm{K}}_{\mathrm{h}\mathrm{n}\mathrm{f}\mathrm{l}}$ is the ENTC and ${\mathrm{\mu }}_{\mathrm{h}\mathrm{n}\mathrm{f}}$ is the viscosity of HNF. Which are given in Table 1.

In Table 1, ${\varphi }_{s1}$ and ${\varphi }_{s2}$ shows volume fraction, ${\rho }_{f}$ is the base fluid density, ${\rho }_{s1}$ and ${\rho }_{s2}$ is the solid NP density, ${\left(\rho {C}_{p}\right)}_{s1}$ and ${\left(\rho {C}_{p}\right)}_{s1}$ is the thermal capacitance of solid NP, the thermal capacitance for base fluid is represented as ${\left(\rho {C}_{p}\right)}_{f}$, ${k}_{hnfl}$ is the ENTC of HNF, ${k}_{f}$ and ${k}_{bf}$ represent base fluid TC, ${k}_{nfl}$ is the nanofluids TC with the effect of nanolayer, ${k}_{pe1}\; and \;{k}_{pe2}$ is equivalent TC of the equivalent solid NP, the ratio of the nanolayer thickness to the radius of NP is ${\beta }_{1}=\frac{h}{r}$, ${\lambda }_{1}=\frac{{k}_{layers}}{{k}_{s1}}$ is the ratio of TC of nanolayer to TC of the first particle, $\lambda =\frac{{k}_{layers}}{{k}_{s2}}$ is the ratio of ENTC to TC of the second particle, ${k}_{s1}\;and\;{k}_{s2}$ is TC of the first particle and second particle respectively, The particle radius is r, and the thickness of the nanolayer is h, ${\sigma }_{hnf}$ is the electrical conductivity of hybrid nanofluid, ${\sigma }_{nf}$ is the electrical conductivity of nanofluid, ${\sigma }_{s1}$ and ${\sigma }_{s2}$ are the electrical conductivity of first and second nanoparticles, respectively, ${\sigma }_{bf}$ is the electrical conductivity of base fluid.

Table 2, ${C}_{P}$ shows Specifics heats at constant pressures, $\rho$ is the density, and $K$ is the thermal capacitance of base fluid and solid NP.

The upper boundary and lower boundary have the following boundary conditions:

where ${\mathrm{A}}_{\mathrm{*}}$ is denote the permeability and the prime denotes the time derivative w.r.t t.

The similarity variables listed below are used as:

First of all the continuity equation is satisfied by the similarity variables stated in Eq (6). Furthermore, the similarity variables are used in the governing equations to acquire Eqs (7) and (8):

where ${\mathrm{\alpha }}_{\mathrm{h}\mathrm{n}\mathrm{f}}$ is the thermal diffusivity of HNF and ${\mathrm{\alpha }}_{\mathrm{h}\mathrm{n}\mathrm{f}}=\frac{{\mathrm{K}}_{\mathrm{h}\mathrm{n}\mathrm{f}\mathrm{l}}}{{\left(\mathrm{\rho }{\mathrm{C}}_{\mathrm{p}}\right)}_{\mathrm{h}\mathrm{n}\mathrm{f}}}$, ${\mathrm{\upsilon }}_{\mathrm{h}\mathrm{n}\mathrm{f}}$ is the kinematics viscosity of the HNF and ${\mathrm{\upsilon }}_{\mathrm{h}\mathrm{n}\mathrm{f}}=\frac{{\mathrm{\mu }}_{\mathrm{h}\mathrm{n}\mathrm{f}}}{{\mathrm{\rho }}_{\mathrm{h}\mathrm{n}\mathrm{f}}}$, ${\left(\mathrm{\rho }{\mathrm{C}}_{\mathrm{p}}\right)}_{\mathrm{h}\mathrm{n}\mathrm{f}}$ is the heat capacitance of HNF, the viscosity of HNF is ${\mathrm{\mu }}_{\mathrm{h}\mathrm{n}\mathrm{f}}$, the density of HNF is ${\mathrm{\rho }}_{\mathrm{h}\mathrm{n}\mathrm{f}}$.

Associated boundary conditions are

here ${\mathrm{R}}_{\mathrm{e}}=\frac{{\mathrm{A}}_{\mathrm{*}}\mathrm{k}\mathrm{k}\mathrm{\text{'}}\left(\mathrm{t}\right)}{2{\mathrm{\upsilon }}_{\mathrm{f}}}$ is absorptivity Reynold number, here ${\mathrm{A}}_{\mathrm{*}}$ is the permeability, and is defined as the function of Reynold number and wall expansion ratio, and mathematically defined as ${\mathrm{A}}_{\mathrm{*}}={\mathrm{A}}_{\mathrm{*}}\left({\mathrm{\alpha }}_{\mathrm{*}}, {\mathrm{R}}_{\mathrm{e}}\right)=\frac{{\mathrm{R}}_{\mathrm{e}}}{2{\mathrm{\alpha }}_{\mathrm{*}}}$, ${\mathrm{\alpha }}_{\mathrm{*}}=\frac{\mathrm{k}\mathrm{k}\mathrm{\text{'}}\left(\mathrm{t}\right)}{{\mathrm{\upsilon }}_{\mathrm{f}}}$ is the ratio of wall expansion, and ${\mathrm{M}}_{\mathrm{*}}=\frac{{\mathrm{\sigma }}_{}{\mathrm{\beta }}_{0}^{2}{\mathrm{k}}^{2}}{{\mathrm{\mu }}_{\mathrm{f}}}$ is the magnetic parameter.

Finally, we set $\mathrm{F}=\mathrm{f}{\mathrm{R}}_{\mathrm{e}}$ and by following Majdalani et al. ^[36]. When $\mathrm{\alpha }$ is constant, $\mathrm{f}=\mathrm{f}\left(\mathrm{\eta }\right)$ and $\mathrm{\theta }=\mathrm{\theta }\left(\mathrm{\eta }\right)$, which leads to ${\mathrm{\theta }}_{\mathrm{t}}=0$ and ${\mathrm{f}}_{\mathrm{\eta }\mathrm{\eta }\mathrm{t}}=0$. Thus, we have

At lower and upper wall of channel boundary condition are

2.1.   Quantities of engineering interest

Nusselt number and SFC at both permeable walls are computed coefficients that are of engineering interest are computed in this section.

2.1.1.   Skin friction coefficients (SFC)

The SFC of the upper and lower disk represents as ${\mathrm{C}}_{\mathrm{f}1}$ and ${\mathrm{C}}_{\mathrm{f}-1}$ and expressed as in ^[10],

where ${\mathrm{R}}_{\mathrm{e}}$ denote the Reynold number and ${\mathrm{\varsigma }}_{\mathrm{z}\mathrm{r}}$ denote the shear stress at the bottom and upper disks in the radial direction, respectively,

2.1.2.   Nusselt number

The heat transfer rate (Nusselt number) calculations at the bottom and upper disks are given as ${\mathrm{N}}_{\mathrm{u}}{\mathrm{ǀ}}_{\mathrm{\eta }=-1}$ and ${\mathrm{N}}_{\mathrm{u}}{\mathrm{ǀ}}_{\mathrm{\eta }=1}$, respectively ^[10]

here ${\mathrm{s}}_{\mathrm{z}}$ is the heat flux, which is following as,

3.   Modeling of effective nanolayer thermal conductivity

Thermophysical properties like density, viscosity, heat capacitance, and TC of base liquids are changed due to the mixing of NPs and distinguishing the efficacy of NPs on thermo-physical properties of resulting nanofluids. Gupta et al. ^[39] give a detailed investigation of the thermophysical characteristics of nanofluids. TC is a key thermophysical feature of nanofluids, according to a comprehensive examination of their thermophysical properties. Over the years, numerous investigations on the TC of nanofluids have been done. Yang et al. ^[40] have submitted a report on the effect of critical factors on the TC of nanofluids. Until now, several researchers have attempted to calculate the TC of nanofluids using various methods to provide a comprehensive correlation to compute this in nanofluids. Maxwell ^[41] established the first correlation to calculate the TC of nanofluids in 1881. This relationship is accurate for globe-shaped NP and small amounts of NP. Later, in 1962, Hamilton and Crosser (H-C) ^[42] established the Maxwell correlation, which included the effect of morphology on nanofluids TC. Subsequently, a research study by Jiang et al. ^[43] found that i = 1.550 was more suitable for CNT nanofluids.

The three models in Table 3 of TC failed to predict the high TC of nanofluids. The reason for this is that these TC models ignore the effect of nanolayer and particle radius. Murshed et al. ^[44] proposed a TC model in which the nanolayer is assumed as a separate component when calculating the effective TC of nano-fluids in 2007. Below is a representation of a nanoparticle with a nanolayer in the base fluid.

In the above Table 3, ${k}_{bf}$ denotes the TC of the base fluid, ${\mathrm{k}}_{\mathrm{s}}$ denotes the TC of NP, and ${\mathrm{k}}_{\mathrm{n}\mathrm{f}}$ denotes the TC of nanofluid, $\mathrm{S}=\frac{3}{{\left(\mathrm{\varpi }\right)}^{\mathrm{i}}}$ where$\mathrm{\varpi }$ is sphericalness, $\mathrm{\varpi }=1.00$ for spherical NP, and $\mathrm{\varpi }=0.50$ for cylindrical NP, and the variable "i" is experimental. In the actual H-C correlation, I = 1 is used.

The model of effective TC is given below, for nanofluids,

where ${\mathrm{k}}_{\mathrm{n}\mathrm{f}\mathrm{l}}$ is the TC of nanofluids with the effect of nanolayer, ${\mathrm{k}}_{\mathrm{p}\mathrm{e}}$is equivalent TC of the equivalent particles, where $\mathrm{\lambda }=\frac{{\mathrm{k}}_{\mathrm{l}}}{{\mathrm{k}}_{\mathrm{s}}}$ is the ratio of nanolayer TC to TC of particle, the ratio of the thickness of nanolayer to the radius of NP is ${\mathrm{\beta }}_{1}=\frac{\mathrm{h}}{\mathrm{r}}$.

The effective TC correlation is shown below, for HNF,

where ${\mathrm{k}}_{\mathrm{p}\mathrm{e}1}\; \mathrm{a}\mathrm{n}\mathrm{d}\; {\mathrm{k}}_{\mathrm{p}\mathrm{e}2}$ are equivalent TC of the equivalent first particle and second particle respectively, and defined as

where ${\mathrm{\lambda }}_{1}=\frac{{\mathrm{k}}_{\mathrm{l}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{s}}}{{\mathrm{k}}_{\mathrm{s}1}}$ is the ratio of nanolayer TC to TC of the first particle, $\mathrm{\lambda }=\frac{{\mathrm{k}}_{\mathrm{l}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{s}}}{{\mathrm{k}}_{\mathrm{s}2}}$ is the ratio of nanolayer TC to TC of the second particle, ${\mathrm{k}}_{\mathrm{s}1}\; \mathrm{a}\mathrm{n}\mathrm{d}\; {\mathrm{k}}_{\mathrm{s}2}$ is TC of the first particle and second particle respectively.

4.   Numerical method procedure

Because the system of ODE$\mathrm{\text{'}}$s is manipulated in Eqs (10) and (11) are complex and involve boundary value conditions, the numerical solution is obtained rather than using analytical methods. The shooting technique is used in conjunction with the RK method for numerical computations. The Runge–Kutta method is a preferable alternative since it requires less computing, is more stable, and produces accurate results in less time. The rapidity (computational cost) and additivity of this technique to the IVP are its main advantages. Finding the IVP (initial value problem) using an appropriate shooting approach is massively successful because of the importance of IVPs in real-world/practical applications. The missing beginning condition at the Interval's start point is assumed in a shooting method, and the DE (differential equation) is then numerically integrated as an IVP. The accuracy of the missing initial condition is determined by comparing the computed value of the dependent variable at the terminal point with its given value here. If there is a difference, the process is repeated with a new value. This method is repeated until the calculated and given conditions are in agreement. Table 4 shows how our numerical results converge as the step size gets reduced for this purpose, providing us confidence in our computing technique. Our boundary conditions satisfy accurate and symmetric shear stress results at the lower wall as well.

A massive representation of a non-linear coupled system of ODE$\mathrm{\text{'}}$s with coefficients that have matrix composite material and HNF properties.

Where, we let the following expressions as:

By putting the values of ${\mathrm{G}}_{1}$, ${\mathrm{G}}_{2}$, ${\mathrm{G}}_{3}$, ${\mathrm{G}}_{4}$, and ${\mathrm{G}}_{5}$ in Eqs (21) and (22), the final Equations are:

For the determination of solving the existing flow model, we used the RK technique with the addition of shooting methods. The following substitution is required to begin the process:

First, in Eqs (22) and (23), change the model in the following pattern:

The following system is obtained by using the substitution contained in Eq (24):

Consequently, the initial condition is:

Mathematical techniques and an appropriate initial condition are now used to solve the aforementioned system. Runge-Kutta and the well-known accurate "shooting method" have been considered in this case. This approach is suitable for dealing with dimensionless ODEs. First, we create the initial condition by applying the shooting procedure in a way that satisfies boundary criteria and yields the necessary level of efficiency and accuracy.

5.   Results and discussion

This section explains the influence of flow on concerning equations and physical parameters like expansion/contraction ratio parameter "${\mathrm{\alpha }}_{\mathrm{*}}$", suction/injection permeable Reynold number "${\mathrm{R}}_{\mathrm{e}}$", NTP (nanolayer thickness of particles) "h", the radius of particles "r", shape size factor "S", the magnetic parameter "${\mathrm{M}}_{\mathrm{*}}$", volume friction parameters "${\mathrm{\varphi }}_{\mathrm{s}1}$ and ${\mathrm{\varphi }}_{\mathrm{s}2}$", Prandtl number "${\mathrm{P}}_{\mathrm{r}}$", on velocity and temperature profile are explained through Figures 3–10. The default values of involve parameters are: for $\mathrm{h}=0.4, \; \; \; \; \mathrm{r}=0.8, {\mathrm{\varphi }}_{\mathrm{s}1}={\mathrm{\varphi }}_{\mathrm{s}2}=0.02, {\mathrm{R}}_{\mathrm{e}}=-2.5, {\mathrm{P}}_{\mathrm{r}}=6.2, {\mathrm{M}}_{\mathrm{*}}=1 \; \mathrm{a}\mathrm{n}\mathrm{d}\;{\mathrm{\alpha }}_{\mathrm{*}}=3$. In addition, engineering quantities such as shear stress coefficients at the upper and lower disks, as well as heat fluxes, are estimated numerically against the variables involved. Table 5 shows the comparison result of effective nanolayer thermal conductivity (ENTC) and non-effective nanolayer thermal conductivity (NENTC). It is observed that the enhancement in h, increases the ENTC, and has no effect on NENTC. The reason is that the NENTC does not include the influence of the nanolayer thickness of the particle. The nanolayer thickness and radius of particle have opposite behavior on ENTC. The increment in volume fraction increases the ENTC and NENTC are noticed. For all three cases of shape size factor (sphere, cylindrical, laminar) the highest values of ENTC and NENTC are achieved for aspherical shape. Table 6 represents the variation in SFC and Nusselt numbers for suction and injection cases at the lower disks. For suction ${\mathrm{R}}_{\mathrm{e}} < 0$ case, suction occurs when inertia is less than viscosity, it is observed the increment in NTP increases the Nusselt number. The NTP and radius of particles have opposite behavior on the Nusselt number. For all three cases of shape size factor (sphere, cylindrical, laminar) the highest value of Nusselt number is achieved for aspherical shape. It is also obtrusive that the amount of SFC and Nusselt number rises with the volume fraction and magnetic parameter. it is noticed that as the value of ${\mathrm{\alpha }}_{\mathrm{*}}$ changes from negative to positive the SFC and Nusselt numbers decreased. The Prandtl number and radius of particles have the same behavior as the Nusselt number. The reason is that the Prandtl number is the product of diffusive momentum to the inverse of thermal diffusivity, so increasing the ${\mathrm{P}}_{\mathrm{r}}$ momentum increases diffusivity, which decreases the coefficient of heat flux. For injection ${\mathrm{R}}_{\mathrm{e}} > 0$ cases, injection occurs when inertia is greater than viscosity, it is observed that the effect of NTP, radius of particles, shape size factor, volume fraction, expansion/contraction ratio parameter, and magnetic parameter have the same nature in both suction /injection case on SFC and Nusselt number. The Prandtl number has opposite behavior in both suction /injection cases on SFC and Nusselt number, therefore as the increment in Prandtl number increases the Nusselt number.

Table 7 demonstrates the variation in SFC and Nusselt numbers for expansion and contraction cases at the lower disk. For contraction ${\mathrm{\alpha }}_{\mathrm{*}} < 0$ cases, contraction occurs when viscosity is enhanced, it is observed the increment in NTP increases the Nusselt number. The NTP and radius of particles have opposite natures on Nusselt number that is the Nusselt number is decrease as the increase in radius of particles. It is also evident that the amount of SFC and Nusselt number rises with volume fraction and magnetic parameter. For all three cases of shape size factor (sphere, cylindrical, laminar) the highest value of Nusselt number is achieved for aspherical shape. It is noticed that the value of ${\mathrm{R}}_{\mathrm{e}}$ changes from negative to positive the increase the SFC and decrease the Nusselt number. It is observed that the NTP and Prandtl number have opposite in nature to the Nusselt number. For expansion ${\mathrm{\alpha }}_{\mathrm{*}} > 0$ cases, expansion occurs when viscosity decreases, it is observed that the effect of NTP, radius of particles, shape size factor, volume fraction, magnetic parameter, and Prandtl number have the same nature in both contraction /expansion cases on SFC and Nusselt number. The ${\mathrm{R}}_{\mathrm{e}}$ have opposite behavior in both contraction /expansion cases on SFC and Nusselt numbers. Table 4 states the numerical stability of the results for$\mathrm{f}\; (-1), \; \mathrm{f}\; \mathrm{\text{'}}\; (-1), \; \mathrm{a}\mathrm{n}\mathrm{d}\; \mathrm{f}\; \mathrm{\text{'}}\mathrm{\text{'}}\; (-1)$ at various values of$\mathrm{\eta }$. Table 8 demonstrates the comparison result of the Nusselt number for the suction case via bvp4c method and shooting method. An excellent comparison between two numerical techniques is obtained which certifies the present finding validity. Table 9 shows the comparison results of the heat transfer rate of the present work with already published results of Kashif et al. ^[35]. An astonishing relationship has been accomplished which certifies the validity of present results.

Figure 2 shows a comparison graph of ENTC and NENTC we observed that ENTC is able to determine the high TC of nanofluids as compared to NENTC of hybrid nanofluids. The reason is that NENTC does not include the influence of the radius of particles and nanolayer thickness. Figures 3 and 4 are established to signify the consequences of expansion/contraction parameter on radial and axial velocity field for fixed values $\mathrm{h}=0.4, \; \; \; \; \mathrm{r}=0.8, {\mathrm{\varphi }}_{\mathrm{s}1}={\mathrm{\varphi }}_{\mathrm{s}2}=0.02, {\mathrm{R}}_{\mathrm{e}}=-2.5, {\mathrm{P}}_{\mathrm{r}}=6.2, {\mathrm{M}}_{\mathrm{*}}=1.$ It is observed that ${\mathrm{\alpha }}_{\mathrm{*}}$ changes from contraction to expansion axial velocity increases, whereas the increment in radial velocity in the region between the disks and decrement near the disk.

Figure 5 elaborates on the thermal phenomenon against the Prandtl number. If the value of ${\mathrm{P}}_{\mathrm{r}}$ is decreased, then the maximum temperature profile achieved for ${\mathrm{P}}_{\mathrm{r}}$= 3 at the lower disk and for ${\mathrm{P}}_{\mathrm{r}}$ = 6.2 for an upper disk. The reason is that the Prandtl number is the product of diffusive momentum to the inverse of thermal diffusivity, so increasing the ${\mathrm{P}}_{\mathrm{r}}$ momentum increases diffusivity, which decreases the coefficient of heat flux. Figure 6 is plotted to show the behavior of the magnetic parameters onto the radial velocity profile. It is observed that by increasing the magnetic parameter radial velocity component decreases. This is because by enhancing the magnetic value, Lorentz forces are produced, decreasing the axial momentum of fluid particles. We can conclude from this argument that the transverse application magnetic field normalizes fluid velocity. The magnetic effect causes the particles within the fluid to vibrate, which is governed by the Lorentz force.

Figure 7 is sketched to illustrate the impact of volume fraction on axial profile. It is examined that as the volume fraction value is increasing the axial component of velocity rises. Figure 8 represents that when disks are expanding, and fluid is sucked if the NTP is increased then the temperature profile increase at the upper disk and decreased at the lower disk.

The contour of variable M's influence on radial velocity is shown in Figure 9. In Figure 9, contour lines depicting variants on the radial velocity are sketched, showing the optimal change in velocity against edges and zero change at the Centre. The variation of temperature against (M) is depicted in Figure 10 by contour lines. Contour lines are shown to be roughly fat around the problem's midpoint, with a minimal decreasing pattern along the problem's perimeter.

6.   Conclusions

The impact of nanolayer on TC of HNF flow with the influence of shape and size via porous surfaces is presented in this paper. Polymeric and CNT nanocomposite properties are combined with hybrid nanofluids. In terms of SFC and Nusselt numbers, numerical and graphical results are achieved. The contour graph of temperature and velocity profiles is drawn in this paper.

● effective nanolayer thermal conductivity indicates better results as compared to non-effective nanolayer thermal conductivity

● the NTP (h) has a significant effect on ENTC and the heat transfer rate of hybrid nanofluids

● the Nusselt number is increase with increment in values of NTP, volume fraction, and magnetic field parameter but decreases with the increase in radius of particles, S, ${\mathrm{\alpha }}_{\bf{*}}$, ${\mathrm{P}}_{\mathrm{r}}$ for suction case

● SFC rises with the increase in volume fraction, and magnetic field parameter and decreases against the value of ${\mathrm{\alpha }}_{\bf{*}}$ for suction case

● the Nusselt number is rise with increment in values of NTP, volume fraction, magnetic field parameter, ${\mathrm{P}}_{\mathrm{r}}$ but decrease with the increase in radius of particles, S, ${\mathrm{R}}_{\mathrm{e}}$ for contraction

● SFC increases with the increase in ${\mathrm{R}}_{\mathrm{e}}$, volume fraction, and magnetic field parameter for contraction

● the contrary effect of ${\mathrm{R}}_{\mathrm{e}}$ in expansion case as compared contraction case to except NTP, S, r is seen. The effect of NTP, S, and r on Nusselt number and SFC are the same in both cases.

This work has been done for Newtonian hybrid nanofluid. In the future similar work can be done for non-Newtonian hybrid nanofluid and second-grade hybrid nanofluid.

Acknowledgments

This research received funding support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation, (grant number B05F650018).

Conflict of interest

The authors declare no conflict of interest.