Numerical solution of stochastic and fractional competition model in Caputo derivative using Newton method

1.   Introduction

The problems arising in science and engineering have been successfully modeled through the mathematical models tools ^[1,2,3,4,5]. Besides this, the application of mathematical models to the social sciences and other financial areas are getting attention these days from researchers around the world. In the country's economic growth, the role of the banks is considered to be a backbone. Strong banking policy and its benefits to the citizens play an important role in the overall development of the country, the bank's related terms and explanations can be found in ^[6]. The banking sector may be Islamic or conventional or maybe both of these. The banks that follow the rule of syriah law or conventionally are defined as per the rule Act No. 10 of 1998. The activities of rural and commercial banks in Indonesia are observed and documented that commercial banks have more business activates than the former ^[7,8]. Further, in Indonesia, it is reported that commercial banks are more than the rural, but the products of both the banks are consider to be the same ^[9]. Although, the commercial banks are greater but the rural are still improving their business activities to attract customers. Due to the improvements in their business products, the rural banks may have competition with commercial banks.

If the rural banks continue their efforts to improve their products, then definitely there may have close competition in Indonesia. This competition can be effectively studied through evolutionary differential equations known as the Lotka Volterra system ^[10]. The researchers utilized the Lotka Volterra equations in order to study the competition in many real-word problems, see ^{[11,12,13,14,15,16,17,18]}. For an instant, one of the applications of the Korean mobile company data through the competition system is explored in ^[11]. The competition system as a technological substitution, see ^[12], modeling the policy and their implications to the Korean stock market ^[13], dynamics estimations of the market exhibition, see ^[14], competition dynamics in the operating system market, see ^[15], and the analysis of the banking dynamics system, see ^[16]. Moreover, some recent works regarding this, can be seen in ^{[17,18,19,20]}.

In the above-mentioned studies, it is worthy to mention that the Lotka Volterra system was used to obtain the dynamics of different problems with the integer-order study, except ^{[17,18,19,20]}. From the last years, it is observed that fractional calculus plays a vital role in the dynamic modeling of such practical problems. One of the reasons is considered to be the memory and the heredity properties. The model of real-life problems is often nonlinear and the crossover behavior makes it difficult to solve it exactly. The model formulated in fractional derivatives has many advantages, such as the data fitting, the memory index, the heredity properties, and the cross-over behavior. The dynamics of the model with fractional order derivatives and its applications to the real-life problems can be seen in ^{[21,22,26,27,28,29,30,31]}. For example, the competition among rural and commercial banks through fractional derivatives is discussed in ^[21]. The dynamics of TB using the fractional-order derivative are explored in ^[22]. An introduction to fractional derivative, fractional differential equations, and its numerical solution is discussed in ^[26]. A fractional lotka Volterra mathematical model and its analysis are studied in ^[27]. The Hepatitis E model in fractional Caputo Fabrizio derivative is explored in ^[28]. A fractional-order TB model with relapse is considered in ^[29]. The authors in ^[30] considered the HIV infection model using two-sex populations. The RLC circuit model using the fractional derivative and its numerical investigations is considered in ^[31]. The authors used the concept of fractional derivatives to study different problems, see for example, the training model for football movement trajectory ^[32], the educational reforms through fractional differential equations ^[33], a fractional model for the sugar ^[34], a fractional model for the impact of financial repression ^[35], and the university education model using fractional differential equations and its numerical solution ^[36]. Some more mathematical model formulated in fractional derivatives and their applications to COVID-19 infection is explored in ^[37,38,40], where the authors studied a mathematical model for COVID-19 with isolation class ^[37], COVID-19 with stochastic perturbation ^[38], COVID-19 model with control in fractional environment ^[39] and the COVID-19 model with crowding effect in ^[40]. Application of fractional derivative to Hepatitis B ^[41,42], and COVID-19 ^[43]. The fractional-order model to study the leakage delay ^[44], the fractional-order with neural networks using multi-delays ^[45], bifurcation analysis in a fractional-order ^[46], a delayed BAM fractional-order system ^[47], fractional-order model with control ^[48], and fractional-order neural networks with mixed delays ^[49]. It is important that real-life problems with realistic data, give more accurate information about that particular phenomena than the assumed data, such useful results can be seen in ^{[19,20,21,22]}, where a particular focus is given to show the data fitting to the system of equations. The works mentioned above, have been solved numerically by using the novel numerical technique.

The goal of this work is to study the competition of the banking data between two banks in Indonesia with real statistical data through a fractional model. The fractional derivative considered in this work is the Caputo derivative. For the numerical solution of the fractional model, we use the recently developed new numerical method using the approach of Newton polynomial. This novel technique was introduced recently in literature to get the numerical solution of fractional ordinary differential equations, that has been used for many scientific problems, see ^[23,24,25]. For example, the authors introduced this technique for the solution of the COVID-19 model in fractional derivative in Atangana-Baleanu derivative ^[23]. The HIV dynamics and its mathematical analysis through a fractional model with real cases using this new approach is considered by the authors in ^[24]. The application of this new method to groundwater flow is considered by the authors in ^[25]. This novel technique is more accurate and reasonable than the other technique available in the literature for the factional models. The proposed technique will show how the data fits well with the consideration of the specific fractional orders. The rest of the results in this paper are as follows: The model and their descriptions are shown in Section 2. The related definition and the integral are shown in Section 3. The solution of the model numerically by giving the algorithm is shown in Section 4. Section 5 explain the numerical investigations of the model while Sections 6 and 7 respectively show the formulation of the stochastic problem and the summary of the results.

2.   Concepts related to fractional operator

We provide here the related concepts for Caputo derivative ^[59].

Definition 1. ^[59] Suppose $g: \mathbb{R}^+\rightarrow \mathbb{R}$ and $\rho \in (m-1, m)$, $j\in \mathbb{K}$. Then, the representation of Caputo derivative with order $\rho$ for a function $g$ can be defined by the way below,

Definition 2. ^[59] The integral for the above is given by the following,

3.   Mathematical model

The competition among the commercial and rural banks can be described here through the useful mathematical model called the Lotka-Volterra system. The Lotka-Volterra system has two equations, which were designed to have competition among two species for food etc. This competition model has been used effectively in many studies by the authors for real statistical data and found it interesting. So, on the basis of the competition model, it aims to describe the two equations by commercial and rural banks dynamics. At any time $t$, the dynamics of commercial banks is shown by $x(t)$ while the rural banks dynamics is given by $y(t)$, with the assumptions of maximum profit having both the banks. Further, the banking limited funds behave logistically their growths. So, with this hypothesis, the dynamical analysis of the competition model among the two banks system is shown by,

the initial conditions to the (3.1) are $x(0) = {x}_0\geq 0$, and $y(0) = {y}_0\geq 0$. The parameters $\alpha_i$ for $i = 1, 2$ describe the growth factor respectively for commercial and rural banks and so is positive. The others parameters $K_i$ for $i = 1, 2$ that define the maximum profit gained respectively, by the commercial and the rural banks. The coefficients $\psi_i$ for $i = 1, 2$ are used as a competition parameter respectively for commercial and rural banks. So, it is obvious from this discussion that these parameters are positive.

3.1.   A fractional Caputo model

We use the model presented above (3.2) and apply the Caputo derivative to generalize it. With this generalization, the model (3.2) takes the following fractional form below:

where $\rho\in(0, 1)$ that defines the fractional order is considered in Caputo sense.

3.2.   Equilibria and their stability

The equilibrium points for the considered model (3.2) can be obtained by the following way,

The condition (3.3), gives the following:

Solving the equations in (3.4), we have:

Consider the aforementioned equilibrium points, we discuss its stability results for the system (3.2) below: Initially, we find the Jacobian matrix of the system (3.2) given by the following:

We consider now the stability at the above fixed points. First, we consider $E_0 = (0, 0)$. At this equilibrium point, we get the eigenvalues $\alpha _1, \alpha _2$ which are positive, and so at this point the system is not stable. At $E_1$, we have the eigenvalues, $-\alpha _2, \alpha _1-K_2 \psi _1$, where the second one can be negative if $\alpha _1 < K_2 \psi _1$, and the equilibrium point of the system will be stable. The equilibrium point $E_2$ gives the eigenvalues, $-\alpha _1, \alpha _2-K_1 \psi _2$. If the second one becomes negative, then the proposed model will be locally asymptotically stable. For the last equilibrium point, which is feasible, and their stability is shown below by having the characteristics polynomial:

where

The coefficients $\varpi_1$ and $\varpi_2$ can be positive if $\left(\alpha _1-K_2 \psi _1\right) > 0$, $\left(\alpha _2-K_1 \psi _2\right) > 0$ and $\alpha _1 \alpha _2-K_1 K_2 \psi _1 \psi _2 > 0$. If these conditions hold then the system will be locally asymptotically stable.

3.3.   Existence and uniqueness

Consider the system (3.2), we write for simplicity the model (3.2),

We define the following norm,

where $D = [0, T]$. We assume to show that $x(t)$ and $y(t)$ are bounded in $[0, T]$, therefore, $\forall t\in [0, T]$ there exists $\lambda_1$ and $\lambda_2$ such that $||x||_{\infty} < \lambda_1$ and $||y||_{\infty} < \lambda_2$. We first show that $f_1$ and $f_2$ are bounded

Similarly, we can show

Therefore, if $x$ and $y$ are bounded then there exists $M_1$ and $M_2$ such that

On the other hand if $\forall t\in [0, T]$, $|f_1(x, y, t)| < M_1$ and $|f_2(x, y, t)| < M_2$, then $||x||_{\infty} < \infty$ and $||y||_{\infty} < \infty$.

Proof. Assuming that $f_1$ and $f_2$ are bounded, then

Then without loss of generality, we present for $x(t)$

Therefore,

Similarly, we can show

To prove that our system admits a unique solution, we need to show that

● $\forall t\in [0, T]$, $f_1$ and $f_2$ satisfy the following condition, $|f_1(x, y, t)|^2 < \beta_1(1+|x|^2)$, $|f_2(x, y, t)|^2 < \beta_2(1+|y|^2)$,

● $\forall t\in [0, T]$, $f_1$ and $f_2$ satisfy the Lipschitz condition $|f_1(x_1, y, t)-f_1(x_2, y, t)|^2 < \overline{\beta_1}|x_1-x_2|^2$, $|f_2(x, y_1, t)-f_2(x, y_2, t)|^2 < \overline{\beta_2}|y_1-y_2|^2$.

Without loss of generality, we show he proof for $f_1$,

where $\overline{\beta_1} = \Big(\alpha^2_1+2\alpha^2_1\Big(\frac{2\lambda^2_1}{K^2_1}\Big)+\psi^2_1\lambda^2_2\Big)$. On the other hand

where $\beta_1 = \Big(3\alpha^2_1+\frac{3\alpha^2_1}{K^2_1}\lambda^2_1+3\psi^2_1\lambda^2_2\Big)$. Therefore, the system (3.2) has a unique system of solution.

4.   Solution procedure with Caputo fractional derivative

This section presents a new discretization for the Caputo derivative through Newton polynomial, which was established recently in ^[60]. We explain below briefly the procedure by considering a general fractional differential equation in the form given by:

where $D^{\rho}_{ t}$ shows the Caputo derivative and the $f$ is the nonlinear function. To present a numerical solution procedure to get the solution of fractional differential equation using Newton descritization, we have to rewrite the problems is as follows:

At $t_{n+1} = (n+1)\Delta t$, the following can be written,

Also, we can write

We now using the Newton approach to approximate the $f(\tau, z(\tau))$ which is inside the integral, and has the following

Substitution of the result (4.5) into (4.4), the following is obtained,

Re-arranging Eq (4.6), leads to the following,

So, we have

We simplify the integrals in Eq (4.8) below,

the following formula is obtained after inserting the above solution into Eq (4.9), the following is presented,

The procedure explained above to obtained the graphical results for the model of competition system will be used in next section.

5.   Numerical results

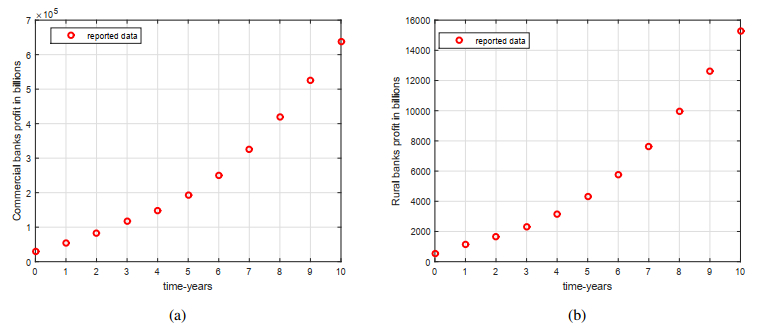
The efficient numerical algorithm described above is considered to obtain the numerical solution of the fractional model in Caputo derivative. We used the real statistical data to investigate the model parameters for the competition between the two banking systems in Indonesia for the given years 2004–2014. Using the statistical data and the parameters obtained that is considered are below: $\psi_1 = 2.90\times10^{-10}$, $\psi_2 = 3.9\times10^{-8}$, $K_1 = 669318.198$, $K_2 = 17540.6219$, $\alpha_1 = 0.6$, and $\alpha_2 = 0.58$. These parameters are also the same estimations presented in the work published in ^[51]. Using these parameters values, we presented the graphical results. The real data of commercial and rural banks in cumulative form is shown in Figure 1. The comparison of real data with the model is shown in Figure 2 when $\rho = 1$. Figures 3 and 4 are plotted in order to show model fitting with real data for the arbitrary order $\rho = 0.9, 0.8, 0.7$. It is observed from the results depicted in Figures 3 and 4, that decreasing the fractional-order $\rho$, we see the good agreement of the data versus model fitting. The future predictions of the real statistical data are depicted in Figure 5. It is observed a good fitting for a long time of the model versus real data. Further, we provided by choosing many values of the arbitrary order and show the results in Figure 6. We also utilized the approach of the FDE12 (predictor-corrector PECE method for fractional differential equations) to solve the present model and compare the result with the Newton polynomials method used in this work. We used the method given in ^[57,58] to obtain the graphical results for the fractional-order model 3.2 using the FDE12 and the Newton polynomial method with the same parameter and initial conditions, with the step size $h = 0.01$. The results are shown in Figure 7. We show them in graphics legends, the Newton method by "present method" while the PECE method is by FDE12. One can observe that both the methods give the same results for the integer and fractional order value $\rho = 0.96$.

6.   A stochastic competition model

This section studies the model in stochastic version. There are many stochastic models in literature which study different physical problems, some are listed here ^{[52,53,54,55,56]}. The model (3.1) is extended to the stochastic version given by

where $\sigma_1$ and $\sigma_2$ are the real constants that represent the intensity of the stochastic differential equations, where $W(t)$ refereed to be the stochastic Brownian motion. Keeping in view the model (3.1), we use it for simulation purposes and check whether the data fit well to the stochastic model. In this regard, we keep the same numerical values as we used for the fractional case model (3.2). The simulation of the model (6.1) with data is given in Figure 8. We can see that the model (6.1) also behaves well with the real data. Figure 9 shows the model behavior for a large time level.

7.   Conclusions

We obtained some new findings regarding the competition system for the real data of the two banks in Indonesia through a fractional model with Caputo derivative through new numerical solution. Initially, we presented the model in ordinary derivative and then applied the Caputo derivative to the model for its generalization. The generalized model is then used to present a novel numerical procedure for their numerical solution. The real statistical data obtained from ^[50] for the year 2004–2014 are utilized and obtained various graphical results. The realistic parameters are fitted for the model of two different data sets which provide a reasonable fitting to the model. For comparison purposes, we considered also the FDE12 method and presented the results. We found that both the methods provide the same results and it can be used confidently for other physical or social problems. The suggested graphical results were tested in order to find the best fractional-order values for which the data provide good fitting is $\rho = 0.7$. While using the stochastic version of the model, we observed that the data provide reasonable fitting to the model. The stochastic version for some different values of the intensities parameters has been shown. It is obvious that the real data fitting provides useful information for the phenomenon's future prediction, where some policy and rule can be designed to obtain the future goals. Thus, we hope that these new results for the competition model for the bank data with the real statistical data will bring new information for the banking and finance sector.

Acknowledgments

This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant No. (D-743-135-1443). The authors, therefore, gratefully acknowledge DSR technical and financial support.

Conflict of interest

No conflict of interests exists regarding the publication of this work.