A new fixed-time stability criterion for fractional-order systems

1.   Introduction

Stability analysis is one of the fundamental issues in control theory. There are several important concepts to describe the dynamic behaviors of the control system, such as asymptotic stability, finite-time stability, fixed-time stability, and so on. From the practical perspective, convergence time of system trajectories is an important performance specification. We usually require that the designed controller ensures finite-time convergence of the closed-loop system trajectories. However, asymptotic stability of a control system implies that the closed-loop system trajectories converge to an equilibrium state over the infinite time, which restricts its application in engineering. Finite-time stability can guarantee the finite-time convergence, but the settling time strongly depends on the initial conditions. To overcome this drawback, fixed-time stability was introduced in ^[1] where the settling time does not depend on the initial conditions. In recent years, fixed-time stability, stabilization and synchronization of control systems have been the subjects of in-depth research, e.g., see ^{[2,3,4,5,6,7,8]}.

Since the geometric and physical interpretations of fractional-order derivatives were given in ^[9], researchers found that fractional-order systems can more accurately model large amounts of practical systems. At present, some of traditional integer-order systems describing physical, biological and chemical phenomena have been successfully extended to fractional-order ones and many meaningful results are established, see for example ^{[10,11,12,13,14]} and the references therein. Over the last decade, the problems of finite-time stability of fractional-order systems, especially for fractional-order neural networks, have attracted considerable attention of scholars ^{[15,16,17,18,19,20]}. Due to a lack of theoretical framework related to fixed-time stability of fractional-order systems, researchers usually adopt the method of fixed-time stability of integer-order systems to deal with that of fractional-order systems ^{[21,22,23,24,25,26,27]}. It should be pointed out that the above method requires us to construct a special Lyapunov function including fractional-order derivative and integral terms. On the other hand, for the integer-order control systems, the setting time of fixed-time stability only depends on the parameters of controller. However, intuitively, setting time of fractional-order control systems should be related to the order of the fractional-order derivative. Motivated by the above arguments, we will establish a new fixed-time stability theorem. The advantage of this result is that, when discussing the fixed-time stability of fractional-order systems, we can construct a more general Lyapunov functions instead of a special one. Also, the setting time depends on the order of the fractional-order derivative.

2.   Problem statement and preliminaries

Consider the following fractional-order system:

where $_{t_0}D_{t}^{\alpha}$ denotes Riemann-Liouville fractional derivative of order $\alpha$, $0 < \alpha < 1$, $x(t)\in \mathbb{R}^{n}$ is state vector, and $f(t, x(t)):\mathbb{R}_{+}\times \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ is a smooth enough function. The initial condition to (2.1) is defined as $_a I_{t}^{1-\alpha}x(t)|_{t = 0}\triangleq x_{0}$. We assume that the solutions $x(t)$ of system (2.1) exist on $[0, +\infty)$ and the origin is an equilibrium of system (2.1).

The aim of this work is to develop a fixed-time stability theorem for the fractional-order system (2.1). To achieve this goal, we first introduce the following definition, lemma and property which will be useful in the sequel.

Definition 1. (Modified Riemann-Liouville derivative ^[28]) Let $f(t)$ denote a continuous function. Then, its fractional derivative of order $\alpha$ can be defined by the expression

Proposition 1. ^[29]Assume that $x(t)$ is both differentiable and $\alpha$-differentiable, then $_{0}D_{t}^{\alpha}f(x(t)) = (1-\alpha)!x^{\alpha-1}D_{x}^{\alpha}f(x)D_{t}^{\alpha}x(t)$.

Lemma 1. ^[30]Let $f:[a, b]\rightarrow \mathbb{R}$ be a continuous function and set $\alpha > 0$. Then

for $f \in C([a, b])$.

Lemma 2. ^[31]Let $z_{1}, z_{2}, \cdots, z_{n} > 0$, $0 < l\leq1$ and $r > 1$, then the following two inequalities hold

3.   Main results

3.1.   Fixed-time stability of fractional-order systems

Theorem 1. Suppose there exists a positive definite function $V(t, x(t))\triangleq V(t)$, such that

with $\lambda_{1} > 0$, $\lambda_{2} > 0$, $1 < \gamma < \alpha+1$ and $\alpha-1 < \beta < \alpha$. Then the origin of system (2.1) is fixed-time stable for any initial conditions, and the settling time is estimated by

Proof: Due to $1 < \gamma < \alpha+1$, we have $-\alpha < 1-\gamma < 0$, which leads to $\Gamma(1-\gamma) < 0$. It follows from (3.1) that the following two inequalities hold simultaneously

The corresponding comparison systems are respectively defined as

By virtue of the Property 1, we get

Thus, the first comparison system in (3.4) can be rewritten as

Taking Riemann-Liouville fractional integration for (3.6) from $0$ to $t$ and considering Lemma 1, we have

Further, it follows from (3.7) that

Note that $\lambda_{1} > 0$, $\Gamma(1+\alpha) > 0$ and $\gamma-\alpha > 0$. The right-hand side of Eq (3.8) is a monotone decreasing function with respect to $t$. When $\nu(0) > 1$, there exists a moment $T^{*}_{1}$ such that $\nu(T^{*}_{1}) = 1$. Next, let us estimate $T^{*}_{1}$. Considering (3.8) and the fact

we can choose $T^{*}_{1} = \left(\frac{\nu^{\gamma-\alpha}(0)-1}{\frac{\lambda_{1}}{\Gamma(1+\alpha)}\nu^{\gamma-\alpha}(0)}\right)^{\frac{1}{\alpha}}$. In order to estimate the setting time, we choose $T_{1} = \left(\frac{\Gamma(1+\alpha)}{\lambda_{1}}\right)^{\frac{1}{\alpha}}$. It should be pointed out that $T_{1} > T^{*}_{1}$ due to the fact $\frac{\nu^{\gamma-\alpha}(0)-1}{\nu^{\gamma-\alpha}(0)} < 1$.

For the second comparison system in (3.4), following a procedure similar to (3.5) and (3.6) yields

Taking Riemann-Liouville integration for (3.10) from $T^{*}_{1}$ to $t$, one has

which implies

Denote $T_{2} = \left(\frac{\Gamma(1+\alpha)}{\lambda_{2}}\right)^{\frac{1}{\alpha}}$. It follows from (3.12) that $\nu(t) = 0$ when $t = T^{*}_{1}+T_{2}$. We claim that $\nu(t)\equiv 0$ when $t\geq T^{*}_{1}+T_{2}$. Otherwise, with the increasing of $t$, $\nu(t)$ becomes negative, which contradicts the positive definiteness of $\nu(t)$. From the previous discussion, the setting time can be estimated by $T = T_{1}+T_{2}$, which implies $\nu(t) = 0, \forall t\geq T$. By invoking the comparison principle for fractional-order systems ^[32], it can be derived that $V(t)\leq \nu(t)$ when $V(0)\leq \nu(0)$. Thus, $V(t) = 0, \forall t\geq T$. Taking into account the positive definiteness of $V(t)$, one has $x(t) = 0, \forall t\geq T$. Therefore, the system (2.1) is fixed-time stable, and the settling time is estimated by (3.2).

3.2.   Application to fixed-time synchronization of fractional-order neural networks

Consider the following neural networks:

where Eq (3.13) is the master system and Eq (3.14) is the corresponding response system; $\delta_{i} > 0$ is the rate of neuron self-inhibition, $p_{ij}$ denotes connection weight, $I_{i}$ is external input, $u_{i}(t)$ is control input; $f_{j}(\cdot)$ expresses the activation function which satisfies Lipschitz condition: $\big|f_{j}(\upsilon)-f_{j}(\varsigma)\big|\leq l_{j}|\upsilon-\varsigma|, \; \; \; l_j > 0$. We define the synchronization errors as: $e_{i}(t) = y_{i}(t)-x_{i}(t)$. The error systems can be described by:

In this work, we design the following controller:

where $k_{1i} > 0$, $k_{2i} > 0$ and $k_{3i} > 0$.

Theorem 2. If $3-2\alpha < \xi < 3$, $0 < \zeta < 2\alpha-1$ and $k_{1i}\geq-\delta_i+\frac{|p_{ij}|l_{j}+|p_{ji}|l_{i}}{2}$, $k_{2i} > 0$, $k_{3i} > 0$, then the master system (3.13) and the response system (3.14) can achieve fixed-time synchronization under controller (3.16). Furthermore, the setting time is estimated by

where $\varrho = \frac{\Gamma(2-\alpha)\Gamma(3)}{\Gamma(3-\alpha)} > 0$, $k_{2} = \min_{i}\{k_{2i}\}$ and $k_{3} = \min_{i}\{k_{3i}\}$.

Proof: Consider the Lyapunov function: $V(e(t)) = \sum_{i = 1}^{n}e^{2}_{i}(t)$. Considering the Property 1 and taking derivative for $V(e(t))$, we have

Recalling that $3-2\alpha < \xi < 3$, $0 < \zeta < 2\alpha-1$ and $0 < \alpha < 1$, we have $1 < \frac{\xi+1}{2}$ and $0 < \frac{\zeta+1}{2} < \alpha < 1$. It follows from Lemma 2 that

Note that $k_{1i}\geq-\delta_i+\frac{|p_{ij}|l_{j}+|p_{ji}|l_{i}}{2}$. Substituting (3.19) into (3.18) yields

Comparing (3.20) with (3.1), we have $\lambda_{1} = -\frac{\varrho k_{2}\Gamma(2-\alpha)\Gamma\left(\frac{3-\xi}{2}\right)n^{\frac{1-\xi}{2}}}{\Gamma\left(\frac{3-\xi}{2}-\alpha\right)}$ and $\lambda_{2} = \frac{\varrho k_{3}\Gamma(2-\alpha)\Gamma\left(\frac{3-\zeta}{2}\right)}{\Gamma\left(\frac{3-\zeta}{2}-\alpha\right)}$ by letting $\frac{\xi+1}{2} = 1-\alpha+\gamma$ and $\frac{\zeta+1}{2} = 1-\alpha+\beta$, respectively. According to Theorem 1, we conclude that the error systems (3.15) is fixed-time stable within the setting time (3.17), i.e., the master system (3.13) and the response system (3.14) can achieve fixed-time synchronization under the controller (3.16).

4.   Numerical simulation

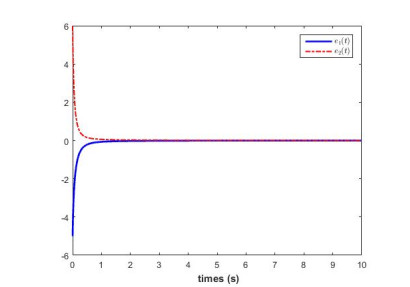
Example 1. Consider the master system (3.13) and the response system (3.14). We choose $\alpha = 0.9$, $\delta_{1} = 0.9$, $\delta_{2} = 1.1$, $p_{11} = 2$, $p_{12} = -0.1$, $p_{21} = -5$, $p_{22} = 4.5$, $I_{1} = \text{5sin}(\pi t)$ and $I_2 = \text{5cos}(\pi t)$. The activation functions are assumed to be $f_{j}(x_{j}(t)) = \frac{1}{2}(|x_{j}(t)+1|-|x_{j}(t)-1|)$, $j = 1, 2$. From the activation functions, we can choose $l_{1} = l_{2} = 1$. The parameters in (3.16) are selected as $k_{11} = 5$, $k_{12} = 7.5$, $k_{21} = k_{22} = 1$, $k_{31} = k_{32} = 1$, $\xi = 2$ and $\zeta = 0.5$. It can be verified that the previous parameters satisfy the given conditions in theorem 2. By using these parameters, the setting time is $T = 1.9438$. When we take $\alpha = 0.75$, the setting time is $T = 3.4590$. For the purpose of the simulation, we assume the initial conditions $x(0) = [5\; -6]^{T}$, $y(0) = [0\; 0]^{T}$. The error systems trajectories of systems (3.15) are shown in Figures 1 and 2, which indicate that synchronization can be reached within fixed time. On the other hand, Figures 1 and 2 show the order $\alpha$ of systems will effect the setting time, and the setting time will increase as the decrease of order $\alpha$.

5.   Conclusions

The fixed-time stability of fractional-order systems has been discussed in this paper. A new fixed-time stability theorem for fractional-order systems has been established. Based on the developed theorem, we discussed the problem of fixed-time synchronization of fractional-order neural networks. Numerical simulation verifies the correctness of our results.

Conflict of interest

The authors declare that they have no competing interests concerning the publication of this article.