$S$-asymptotically $\omega$-periodic dynamics in a fractional-order dual inertial neural networks with time-varying lags

1.   Introduction

Since artificial neural networks own tremendous applications and potentials in a wide range of areas, numerous academics have pay close attention to neural network models and its applications in the last few decades, such as secure communication ^[1,2], signal processing ^[3], wireless sensor ^[4], system identification ^[5], image encryption ^[6] and so on. It is worth noting that a majority of neural network models are described by first-order differential equations, until Babcock and Westervelt ^[7] introduced inertia term in neural network and discussed stability, chaos and bifurcation of electronic inertial neural network, that the inertia term is defined by a second-order derivative term. In recent years, many literatures learned integer-order inertial neural networks, especially inertial neural networks with time delays, and numerous interesting conclusions are acquired, such as, stability ^[8,9], glaobal exponential stability ^[10,11], Mittag-Leffler stability ^[12], anti-periodicity ^[13], periodicity ^[14], synchronization ^[15,16] and so on. In addition, making use of the topological degree theory, Zheng ^[17] researched the global exponential stability of the equilibrium point for inertial neural networks with reaction-diffusion terms and distributed delays. In ^[18], the authors considered the stability and stabilization of a class of inertial memristive neural networks with discrete and unbounded distributed delays. They transformed the model into first order differential equations by means of an appropriate variable substitution method, and derived some novel conditions ensuring the global stability and stabilization of the model. Tang and Jian ^[19] studied the exponential convergence of impulsive inertial complex-valued neural networks with time-varying delays by constructing proper Lyapunov–Krasovskii function and using inequality techniques. In ^[20], Rakkiyappan et al. presented the stability and synchronization of memristive inertial neural networks with time delays according to Halanay inequality and matrix measure. Kong et al. ^[21] built delay-dependent Lyapunov function rather than taking reduced-order transformation and investigated the global exponential stability of periodic solutions for inertial neural networks with time delays by Cauchy–Schwarz inequality and continuation theorem.

Fractional-order calculus ^[22,23] is an extension of integer-order calculus and fractional-order denotes the number of derivative and integral is arbitrary order, which largely overcomes the weakness of the integer-order calculus and has great practical significance. Furthermore, fractional-order calculus can better describe the dynamical behaviors of neural networks than integer-order calculus. Therefore, in the past few years, many literatures have researched the dynamical behaviors of fractional-order neural networks and they have achieved a lot of results, e.g., asymptotical stability ^{[24,25,26,27]}, Mittag-Leffler stability ^[28,29], synchronization ^[30,31] and so on. Remarkably, few papers researched fractional-order neural networks with an inertial term. Inertial term is very helpful in characterizing dynamical behaviors of neural networks, thus it is of great importance to regard inertial term in neural networks. Fractional-order inertial neural networks are obviously distinct from the present fractional-order neural networks and few papers consider this type neural networks in the past years. For example, by the composition properties of Riemann-Liouville fractional-order derivative and adequate feedback control, Gu et al. ^[32] considered global synchronization of Riemann-Liouville fractional-order inertial neural networks with time invariable delays. Zhang et al. ^[33] discussed the synchronization of a Riemann–Liouville-type fractional inertial neural network with two inertial terms by constructing Lyapunov functions. Nevertheless, to our knowledge, so far few papers focus on fractional-order inertial neural networks in the sense of Caputo ^[34], because it is extremely difficult to manage the fractional-order derivatives with two different states. With the above analysis, this paper investigates the global asymptotical stability of $S$-asymptotically $\omega$-periodic oscillation for fractional-order dual inertial neural networks (FODINNs) with time-varying lags.

In practical applications, periodic motion is an interesting and significant dynamical property for the models in engineering, since many biological and cognitive activities (e.g., heartbeat, locomotion, memorization, etc) regularly repeat. Meanwhile, human brain is often in periodic oscillation, thus it is worth studying periodic motion of the models for finding the working principle of human brain. Yet, fractional-order models can not generate nonconstant periodic oscillation ^[35,36]. Owing to this, many scholars devoted to the study of $S$-asymptotically periodic solution for fractional-order models in recent years, see ^[37,38]. Therefore, this article considers the $S$-asymptotically periodic oscillation and stability for FODINNs (2.1). To date, almost no paper focuses on the periodic dynamics of FODINNs.

The main contributions of this paper lie in the following aspects: $(1)$ Based on the composition properties of Caputo fractional-order derivative, two important lemmas on calculation of Caputo fractional-order derivative are deduced; $(2)$ Novel and concise conditions are derived for the existence, uniqueness and global asymptotical stability of $S$-asymptotically periodic oscillation for FODINNs (2.1); (3) The influences of time lags on dynamic behaviors of FODINNs (2.1) are discussed; (4) The acquired results in this paper can complement the corresponding works in literatures ^{[9,12,14,24,27,28,30,39,40]}.

The framework of this paper is organized as follows. In Section $2$, some required definitions, properties and lemmas are presented. In Section $3$, the existence and uniqueness of $S$-asymptotical $\omega$-periodic oscillation of FODINNs (2.1) are gained by the contraction mapping principle. In Section $4$, global asymptotical stability of FODINNs (2.1) is deduced in accordance with comparison principle and stability criteria for delayed Caputo fractional-order differential equations. In Section $5$, two numerical examples are given to illustrate the validness of the obtained conclusions. The conclusions and the future works are described in Section $6$.

Notations: $\mathbb{N}$ represents the set of positive integers; $\mathbb{R}^{2n}$ represents the $2n$-dimensional real vector space; $\mathbb{R}^+ = (0, +\infty)$; $\mathbb{C}$ represents the set of complex numbers and $C^{2n}(J, \mathbb{R}^{2n})$ represents the space composing of $2n$-order continuous differentiable functions from $J$ to $\mathbb{R}^{2n}$.

2.   Caputo derivative, Mittag-Leffler function and Model description

2.1.   Caputo derivative

Definition 2.1. (^[41]) The $\alpha$-order Caputo fractional derivative of $f\in C^{n}([t_0, +\infty), \mathbb{R})$ is given by

where $t > t_0$ and the Gamma function $\Gamma(\cdot)$ is defined by $\Gamma(z) = \int_0^{\infty}s^{z-1}e^{-s}\mathrm{d}s\, (z > 0)$.

Lemma 2.1. (^[41]) $^c\!D_{t_0}^{\alpha}[ax(t)+by(t)] = a{^c\!D}_{t_0}^{\alpha}x(t)+b{^c\!D}_{t_0}^{\alpha}y(t),$ where $x(t), y(t)\in C^{n}([t_0, +\infty), \mathbb{R})$, $0 < n-1 < \alpha < n, \, n\in\mathbb{N}$.

Property 2.1. (^[42]) $^c\!D_{t_0}^{\alpha}{^c\!D}_{t_0}^{\beta}x(t) = {^c\!D}_{t_0}^{\alpha+\beta}x(t)$, where $x(t)\in C^{1}([t_0, +\infty), \mathbb{R})$, $\alpha, \beta\in\mathbb{R}^+$, $\alpha+\beta\leq 1$.

Property 2.2. (^[42]) Suppose that $x(t)\in C^m([t_0, +\infty), \mathbb{R})$, then

where $t\geq t_0$, $\alpha = \sum\limits_{i = 1}^n\alpha_i$, $\alpha_i\in(0, 1]$, $m-1 < \alpha\leq m\in \mathbb{N}$ and it has $i_k < n$ such that $\sum\limits_{j = 1}^{i_k}\alpha_j = k$, $k = 1, 2, \ldots, m-1$.

Lemma 2.2. If $x(t)\in C^2([t_0, +\infty), \mathbb{R})$, then ${^c\!D}_{t_0}^{\alpha-\beta}{^c\!D}_{t_0}^{\beta}x(t) = {^c\!D}_{t_0}^{\alpha}x(t)$, where $1 < \alpha\leq 2$, $0 < \beta\leq 1$.

Proof. From Property 2.1 and Property 2.2, it yields

The proof is end.

2.2.   Mittag-Leffler function

The one-parameter and two-parameter Mittag-Leffler functions ^[41] are defined by

In particular, $(1)$ $\mathbb{E}_1(z) = e^z$; $(2)$ $\mathbb{E}_{\alpha, 1}(z) = \mathbb{E}_{\alpha}(z)$; $(3)$ $\mathbb{E}_{1, 2}(z) = \frac{e^z-1}{z}$.

Lemma 2.3. (^[41]) $\frac{\mathrm{d}}{\mathrm{d} z}\big[z^{\alpha}\mathbb{E}_{\alpha, \alpha+1}(\lambda z^\alpha)\big] = z^{\alpha-1}\mathbb{E}_{\alpha, \alpha}(\lambda z^\alpha)$, where $\alpha, \lambda, z\in\mathbb{C}$.

Lemma 2.4. (^[35]) If $\lambda > 0$ and $\alpha\in(0, 1]$, then $\lim\limits_{t\rightarrow \infty}t^\alpha \mathbb{E}_{\alpha, \alpha+1}(-\lambda t^\alpha) = \frac{1}{\lambda }$ and $t^\alpha \mathbb{E}_{\alpha, \alpha+1}(-\lambda t^\alpha)\leq\frac{1}{\lambda }$ for $t\geq0$.

Lemma 2.5. (^[35,36]) If $a, \lambda > 0$ and $\alpha\in(0, 1]$, then

2.3.   Model description

In this paper, we investigate the global asymptotical stability of $S$-asymptotically $\omega$-periodic oscillation for fractional-order dual inertial neural networks (FODINNs) with time-varying lags in the form of

with initial conditions

where $^c\!D_0^{\alpha}$, $^c\!D_0^{\beta}$ and $^c\!D_0^{\gamma}$ are the Caputo derivative of orders $1 < \alpha\leq2$, $0 < \beta\leq1$ and $\gamma = \alpha-\beta$, respectively; $x_i(t)\in\mathbb{R}$ is the state of $i$th neuron at time $t$; $n$ is the amount of units in the neural network; $a_i(t) > 0$ is variable coefficient and $b_{i}(t) > 0$ is damping coefficient; $c_{ij}(t)$ represents the synaptic connection weight of the unit $j$ to the unit $i$ at time $t$; $d_{ij}(t)$ denotes the synaptic connection weight of the unit $j$ to the unit $i$ at time $t-\tau_j(t)$; $f_j(x_j(t))$ is the output of $j$th neuron at time $t$; $g_j(x_j(t-\tau_j(t)))$ is the output of $j$th neuron at time $t-\tau_j(t)$; $I_i(t)$ represents the external input at time $t$; $\tau_j(t)$ is time variable delay at time $t\geq0$; $\varphi_i(s)$ and $\psi_i(s)$ are bounded and continuous functions; $\xi_i > 1$ is a constant, $i, j = 1, 2, \ldots, n$.

Let $y_i(t) = {^{c}\!D}_{0}^{\beta}x_i(t)+\xi_ix_i(t)$, it gets from Lemmas 2.1 and 2.2 that

where $t > 0$ and $i = 1, 2, \ldots, n$.

Substituting (2.2) into Eq (2.1), then Eq (2.1) can be described by

Let $SAP_\omega(\mathbb{R}^{2n}) = \Big\{(x, y)^T\in C([0, +\infty), \mathbb{R}^{2 n}):$ $x = (x_1, x_2, \ldots, x_n)^T$, $y = (y_1, y_2, \ldots, y_n)^T$, $x_i$ and $y_i$ are $S$-asymptotically $\omega$-periodic functions with initial conditions $\varphi_i(s)$ and $\psi_i(s)+\xi_i\varphi_i(s)$, $s\in[-\tau, 0]$, $i = 1, 2, \ldots, n \Big\}$. $SAP_\omega(\mathbb{R}^{2n})$ is a Banach space with norm $\|x\|_\infty = \sup\limits_{t\geq0}\max\limits_{1\leq i\leq n}\{|x_i(t)|, |y_i(t)|\}$.

Equation $(2.3)$ can be converted to

where $A$ is undetermined constant. From Eq $(2.4)$, for any $\phi = (\phi_1^x, \ldots, \phi_n^x, \phi_1^y, \ldots, \phi_n^y)^T \in SAP_\omega(\mathbb{R}^{2n})$, it obtains

Define operator $T: \phi\rightarrow x^{\phi}$, $\forall \phi = (\phi_1^x, \ldots, \phi_n^x, \phi_1^y, \ldots, \phi_n^y)^T\in SAP_\omega(\mathbb{R}^{2n})$ as

where

If $T$ has a unique fixed point $\phi^*\in SAP_\omega(\mathbb{R}^{2n})$, then $\phi^* = T\phi^* = x^{\phi^*}$ is a unique $S$-asymptotically $\omega$-periodic oscillation of FODINNs $(2.1)$.

Remark 2.1. If $\alpha\rightarrow \beta$, then Eq $(2.1)$ is turned into the typical fractional-order neural networks as follows:

where

$t > 0$ and $i, j = 1, 2, \ldots, n$. Numerous dynamical properties of Eq $(2.7)$ were discussed in literatures ^{[24,27,39,40]}, e.g., finite-time stability, global asymptotical $\omega$-periodicity and Mittag-Leffler stability, etc. Apparently, the discussed models in this article extends the models in literatures ^{[24,27,39,40]}.

Remark 2.2. If $\alpha = 2$ and $\beta = 1$ in Eq $(2.1)$, then it is shifted to the classical integer-order inertial neural networks ^{[43,44,45,46,47]} described by

In allusion to Eq $(2.8)$, the Volterra integral expression with the exponential function kernel is given by

By employing Eq (2.9), the periodic dynamics of Eq $(2.8)$ had been studied in literatures ^[43,44]. So our works in this paper supplement the works in literatures ^[43,44].

3.   $S$-asymptotical $\omega$-periodicity

Define $\bar{f} = \sup\limits_{t\geq t_0}|f(t)|$ and $\underline{f} = \inf\limits_{t\geq t_0}|f(t)|$ for a bounded function $f\in C([t_0, +\infty), \mathbb{R})$, $\|x\| = \max\limits_{1\leq i\leq n}|x_i|$ for $\forall x = (x_1, x_2, \ldots, x_n)^T\in\mathbb{R}^n$.

Definition 3.1. (^[38]) If for any $x = (x_1, x_2, \ldots, x_n)^T\in C([t_0, +\infty), \mathbb{R}^n)$, it has $\omega > 0$ ensure that $\lim\limits_{t\rightarrow +\infty}\|x(t+\omega)-x(t)\| = \lim\limits_{t\rightarrow +\infty}\max\limits_{1\leq i\leq n}|x_i(t+\omega)-x_i(t)| = 0$, then $x$ is $S$-asymptotically $\omega$-periodic.

Assume the conditions below in FODINNs $(2.1)$ are fulfilled.

$(H_{1})$ $a_{i}(t) > 0$, $b_{i}(t) > 0$, $c_{ij}(t)$, $d_{ij}(t)$ and $I_i(t)$ are $S$-asymptotically $\omega$-periodic functions; $\tau_j(t)$ is $\omega$-periodic function, $\forall t\geq0$, $i, j = 1, 2, \ldots, n$.

$(H_{2})$ There exist two numbers $L_j^f > 0$ and $L_j^g > 0$ such that

$(H_{3})$ $\xi_i > 1$ and $\underline{b}_{i} > \xi_i\bar{a}_{i}+ \sum\limits_{j = 1}^n\bar{c}_{ij}L_j^f+ \sum\limits_{j = 1}^n\bar{d}_{ij}L_j^g$, $i, j = 1, 2, \ldots, n$.

By $(H_3)$, it has $A > \bar{b}_i$ satisfying the following inequality:

Theorem 3.1. If $(H_1)$–$(H_3)$ hold, then FODINNs $(2.1)$ exists a unique $S$-asymptotical periodic oscillation.

Proof. Let $T: SAP_\omega(\mathbb{R}^{2 n})\rightarrow C([0, +\infty), \mathbb{R}^{2n})$ be defined as that in Eq $(2.5)$.

To begin with, it shows that $T: SAP_\omega(\mathbb{R}^{2n})\rightarrow SAP_\omega(\mathbb{R}^{2n})$. For $\forall\phi = (\phi_1^x, \ldots, \phi_n^x, \phi_1^y, \ldots, \phi_n^y)^T\in SAP_\omega(\mathbb{R}^{2n})$, $\forall\epsilon > 0$, there exists $t_1 > 0$ resulting

Because of $\varphi$ is asymptotically periodic, so $\|\varphi\|_{\infty} < +\infty$.

For $t > 0$, from the first equation of Eq $(2.6)$, it gets

Hence, for $t > 0$, it yields

where

According to Lemma 2.5, for $\epsilon > 0$, it has $t_2 > t_1$ such that

If $t\geq0$, then $\mathbb{E}_{\beta, \beta}[-\xi_i t^\beta]\geq0$, together with Lemma 2.3 it obtains

where $\forall t > t_1$, $i = 1, 2, \ldots, n.$ By means of Lemmas 2.4 and 2.5, there exists $t_3 > t_2$ ensuring

Similarly, it has $t_4 > t_3$ such that

From $(3.2)$–$(3.4)$, there exists a positive number $M_{i1}$ large enough satisfying

On the other hand, for $t > 0$, by the second equation of Eq $(2.6)$, it obtains

which obtains

where

Based on Lemma 2.5, for $\epsilon > 0$, it has $t_5 > t_4$ ensuring

Obviously, when $t\geq0$, $\mathbb{E}_{\alpha-\beta, \alpha-\beta}[-A t^{\alpha-\beta}]\geq0$ and applying Lemma 2.3, it acquires

where $\forall t > t_1$, $i = 1, 2, \ldots, n.$ From Lemmas 2.4 and 2.5, it has $t_6 > t_5$ such that

In the same way, there exists $t_7 > t_6$ such that

By means of $(3.6)$–$(3.13)$, there exists a $M_{i2} > 0$ large enough such that

Combining $(3.5)$ and $(3.14)$, it implies that $\|(T\phi)(t+\omega)-(T\phi)(t)\|_{\infty} < \min\limits_{1\leq i\leq n}\{M_{i1}, M_{i2}\}\epsilon$, therefore $T\varphi\in SAP_\omega(\mathbb{R}^{2n})$.

Then, we will show that $T$ is contractive mapping. For $\Phi, \Psi\in SAP_\omega(\mathbb{R}^{2n})$, applying Lemma 2.4, from the first equation of Eq $(2.6)$, it achieves

based on $(H_{3})$, it deduces

Similarly,

by (3.1), it gains

From (3.16) and (3.18), it deduces

which induces $T$ is contractive mapping. Hence, $T$ has a unique fixed point $\varphi^* = T\varphi^*$ and $\varphi^*\in SAP_\omega(\mathbb{R}^{2n})$ is a unique $S$-asymptotical periodic oscillation of FODINNs $(2.1)$. The proof is end.

Remark 3.1. It is well known that one of the most important dynamical property in neural networks is periodic oscillations and many physiological activities such as heartbeat, memorization, respiration are repetitive. Hence, it is necessary to take period into account. Over the past few years, some academics have researched the periodic solutions of integer-order INNs ^{[43,44,45,46,47]} and fractional-order neural networks ^{[26,39,40,48]}. However, to the best of our knowledge, for asymptotically periodic oscillations of FODINNs, almost no scholars concentrate on it. Therefore, the work in this paper fills the gap in this regard and has great significance.

Remark 3.2. Obviously, Lemmas 2.4 and 2.5 hold under the condition of $0 < \alpha\leq 1$. However, if $\alpha > 1$, it is difficult to confirm the boundedness and asymptotic properties of Mittag-Leffler functions. Hence, let $\alpha > 1$, it is not sure Lemmas 2.4 and 2.5 hold and this issue will be considered in the future work.

Remark 3.3. In ^[12], the author researched the asymptotical $\omega$-periodicity of Riemann-Liouville fraction-order inertia neural networks under the condition of $\sup_{t\geq 0}\int_0^t(t-s)^{q-1}|I_i(s+\omega)-I_i(s)| < +\infty$, which is very strict. Whereas, in this paper we don't need the above-mentioned condition hold, which sorts of extend the results of ^[12].

4.   Global asymptotical stability

Let

Lemma 4.1. (^[49]) Assume that $x\in C^{1}([t_0, +\infty), \mathbb{R})$, then $^c\!D_{t_0}^{\alpha}x^2(t)\leq 2x(t)\, ^c\!D_{t_0}^\alpha x(t)$, $\forall t\in[t_0, +\infty)$, $0 < \alpha\leq 1$.

Definition 4.1. (^[41]) The Laplace transform for $f(t)$ is defined by

Lemma 4.2. (^[41]) Suppose that $F(s)$ is the Laplace transform of $f(t)\in C^{n}([0, +\infty), \mathbb{R})$, it gets

$(1)$ $L\big\{{^cD_0^{\alpha}f(t)}; s\big\} = s^\alpha F(s)-\sum\limits_{k = 0}^{n-1}s^{\alpha-k-1}f^{(k)}(0)$, $0 < n-1 < \alpha\leq n$, $n\in\mathbb{N}$, $t\geq0$, $s\in\mathbb{C}$.

$(2)$ $\lim\limits_{t\rightarrow +\infty}f(t) = \lim\limits_{s\rightarrow0}sF(s)$.

Lemma 4.3. Assume that nonnegative functions $u_i, v_i\in C\left([0, +\infty), \mathbb{R}\right)$. Considering the fractional-order differential inequalities below

and the following fractional-order differential system

where $\sigma_j(t)$ is defined as in $(4.1)$, $i, j = 1, 2, \ldots, 2n$. If $a_i > 0$, $b_i > 0$ and $c_i > 0$, then $u_i(t)\leq v_i(t)$, $\forall t\geq0$, $i = 1, 2, \ldots, 2n$.

Proof. Based on Eq $(4.2)$, considering the following fractional-order system:

where $m_i(t)$ is nonnegative continuous function in $[0, +\infty)$, $i = 1, 2, \ldots, 2n$. By Theorem 3.25 in literature ^[41] and similar to the proof of Theorem 3.1 in literature ^[35], it easily verifies that

From Eq $(4.3)$, it has

Next, we will prove $u_i(t)\leq v_i(t)$ via proof by contradiction. Since $u_i$ and $v_i$ are continuous, it must exist $t_0\in(0, +\infty)$ and $i_0\in\{1, 2, \ldots, 2n\}$ such that $u_{i_0}(t_0) > v_{i_0}(t_0)$, and $u_i(t)\leq v_i(t)$ for $t\in[0, t_0)$ and $i\in\{1, 2, \ldots, 2n\}$. By $(4.4)$ and $(4.5)$, it yields

and

According to $(4.6)$ and $(4.7)$, it has

This is a contradiction. So $u_i(t)\leq v_i(t)$ for $t\geq 0$, $i = 1, 2, \ldots, 2n$. The proof is end.

Define $a_i^0 = \sup_{t\geq 0}|\xi_ia_i(t)-b_i(t)|$, $L^f = \max\limits_{1\leq j\leq n} L_j^f$, $L^g = \max\limits_{1\leq j\leq n} L_j^g$, $\bar{c}_{i*} = \max\limits_{1\leq j\leq n} \bar{c}_{ij}$ and $\bar{d}_{i*} = \max\limits_{1\leq j\leq n} \bar{d}_{ij}$, $i = 1, 2, \ldots, n$.

Theorem 4.1. Suppose that $(H_2)$ and the following condition hold.

$(H_{4})$ $\inf_{s\geq0}a_i(s) > 0$, $\xi_{i} > 1$, $\min\limits_{1\leq i\leq 2n}m_i > \sum\limits_{i = 1}^{2n}\tilde{m}_i+ \max\limits_{1\leq i\leq 2n}\sum\limits_{j = 1}^{2n}\frac{M_j}{1-\dot{\sigma}_i^+}$, where $\dot{\sigma}_j^+ = \sup\limits_{t\geq 0}\dot{\sigma}_j(t) < 1$,

Then FODINNs $(2.1)$ is globally asymptotically stable.

Proof. Let $(x, y)^T = (x_1, \ldots, x_n, y_1, \ldots, y_n)^T$ and $(\tilde{x}, \tilde{y})^T = (\tilde{x}_1, \ldots, \tilde{x}_n, \tilde{y}_1, \ldots, \tilde{y}_n)^T$ be two solutions of Eq $(2.3)$. Let $u_i = x_i-\tilde{x}_i$, $v_i = y_i-\tilde{y}_i$ and $z = (z_1, \ldots, z_{2n})^T$, where $z_i = u_i^2$, $z_{n+i} = v_i^2$, $i = 1, 2, \ldots, n$.

From the first equation of Eq (2.3), it obtains

which yields from Lemma 4.1 that

which deduces

where $t > 0$, $i = 1, 2, \ldots, n$.

It gets from the second equation of Eq (2.3) that

which derives from Lemma 4.1 that

where $t > 0$, $i = 1, 2, \ldots, n$. By $(4.10)$, it acquires

where $t > 0$, $i = 1, 2, \ldots, n$. Summarizing (4.9) and (4.11) leads to

Next, considering the following equations:

If $\mu_j(t)$ is the inverse function of $t-\sigma_j(t)$, then $\mu_j(t-\sigma_j(t)) = t$, $j = 1, 2, \ldots, 2n$. Set $Q_i(s)\geq0$ is the Laplace transform of $q_i(t)\geq0$, $i = 1, 2, \ldots, 2n$. Referring to Eq $(4.13)$ and Lemma 4.2, it acquires

Let $Q = \sum\limits_{i = 1}^{2n}Q_i$, $\bar{\alpha} = \max\{\beta, \alpha-\beta\}$ and $\underline{\alpha} = \min\{\beta, \alpha-\beta\}$. It gains

thus

By Lemma 4.2, it derives $\lim\limits_{t\rightarrow +\infty}q_i(t)\leq\lim\limits_{s\rightarrow 0^+}sQ(s) = 0$, $i = 1, 2, \ldots, 2n$. It indicates from Lemma 4.3 that $\lim\limits_{t\rightarrow +\infty}|z_i(t)|\leq \lim\limits_{t\rightarrow +\infty}q_i(t) = 0$, which gains the global asymptotical stability of FODINNs (2.1). The proof is end.

From Theorem 3.1 and Theorem 4.1, it deduces

Theorem 4.2. Suppose that $(H_1)$–$(H_4)$ are fulfilled, then FODINNs $(2.1)$ exists a unique $S$-asymptotical $\omega$-periodic oscillation, which is globally asymptotically stable.

Remark 4.1. Apparently, the time-varying lags have no influence on $S$-asymptotical $\omega$-periodic oscillation for FODINNs $(2.1)$, but can affect the global asymptotical stability for FODINNs $(2.1)$.

Remark 4.2. In recent years, numerous articles were devoted to the studies of stability and periodicity of integer-order inertial neural networks ^{[8,12,14,16,43,44,45,46,47]}, and few papers studied asymptotical stability ^[26,27], Mittag-Leffler stability ^[28,29] and periodicity ^[39,40] of FODINNs. To the best of our knowledge, up to now, only ^[32,33,34] studied global synchronization of FOINNS and other dynamics (e.g., asymptotical stability) of FODINNs have not been considered in the past years. Therefore, the works of this section fill this gap and lay the groundwork for future development in studying other dynamics of FOINNS.

Remark 4.3. If $\alpha_i\equiv\alpha$ and $\sigma_i(t)\equiv0(i = 1, 2, \ldots, 2n)$, then inequality $(4.12)$ is turned into $^c\!D^{\alpha}_0Z(t)\leq-kZ(t)$, where $Z(t) = \sum\limits_{i = 1}^{2n}z_i(t)$, $k = m- \sum\limits_{i = 1}^{2n}\tilde{m}_i-\sum\limits_{i = 1}^{2n}M_i$, $m = \min\limits_{1\leq i\leq 2n}m_i$, $t > 0$. Therefore, $Z(t)\leq Z(0)\mathbb{E}_{\alpha}(-k t^{\alpha})$, $t > 0$. If $k > 0$, then FODINNs (2.1) is global Mittag-Leffler stability.

Remark 4.4. Based on Lemma 4.1, the global asymptotical stability of FODINNs (2.1) is gained. Assume that $\alpha > 1$, it is worth to study that whether the stability of FODINNs (2.1) holds, this is an interesting topic and deserves to further research.

Remark 4.5. In this section, the global asymptotical stability for FODINNs $(2.1)$ is investigated, ^[12] researched the Mittag-Leffler stability for fractional-order inertial neural networks with time-delays. Moreover, the fractional order in ^[12] is even number, comparatively speaking, the results of this article are more general.

5.   Numerical examples

Example 5.1. Considering FODINNs with periodic coefficients as follows:

where $\alpha = 1.8$, $\beta = 0.8$, $a_i(t) = 3+0.005\sin t$, $b_i(t) = 13+0.02\cos t$, $\tau_j(t) = 1+0.01\sin t$, $I_i(t) = 1+\cos t$, $\xi_i = 4$, $f_j(x_j) = g_j(x_j) = \frac{0.05x_j^2}{1+x_j^2}$,

$i, j = 1, 2$. Obviously, $L_j^f = L_j^g = 0.1$,

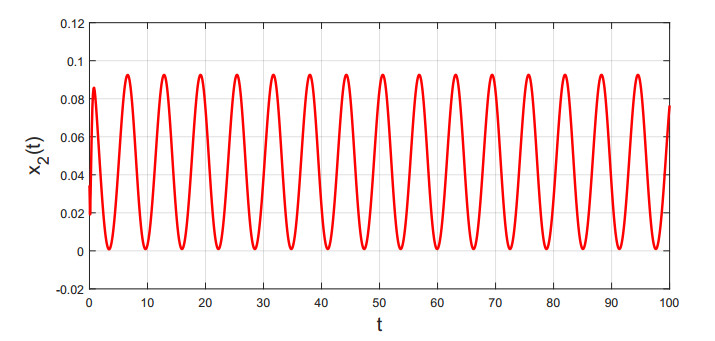
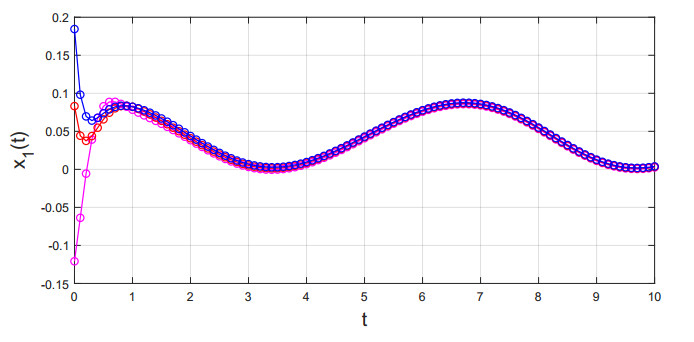
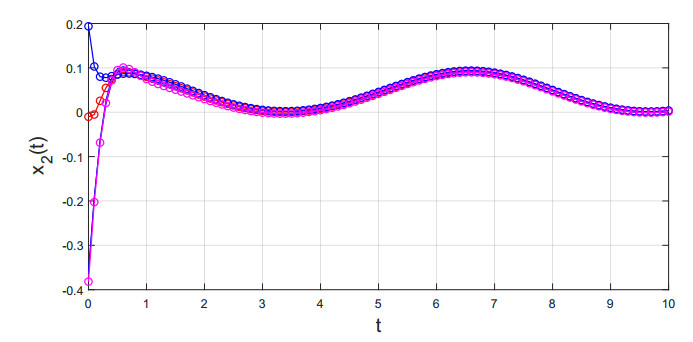
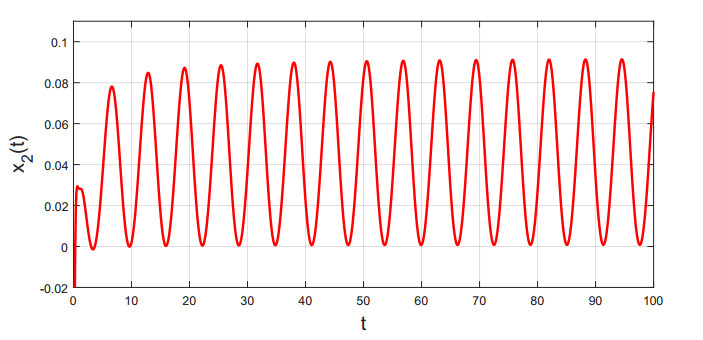
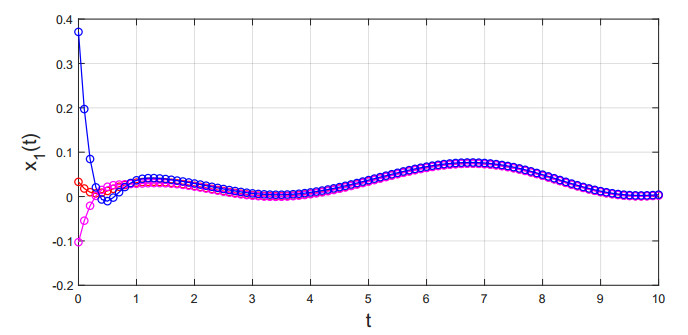
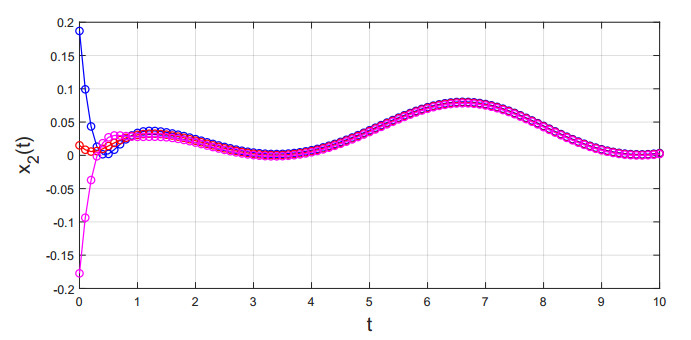
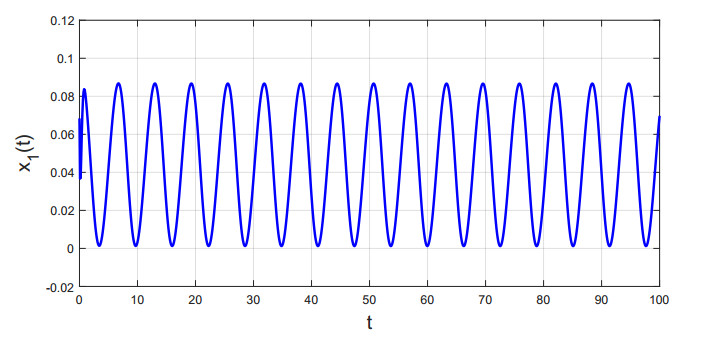
Thus, conditions $(H_1)$–$(H_3)$ are validated. By Theorem 3.1, the existence and uniqueness of $S$-asymptotical $2\pi$-periodic oscillation for system (5.1) are obtained, see Figures 1 and 2.

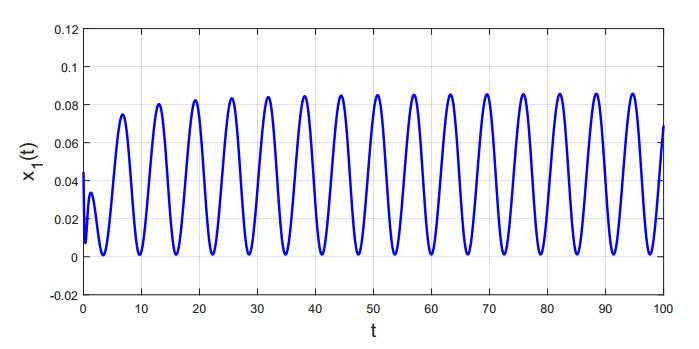
Besides, $m_i = 4.76172$, $\tilde{m}_i = 1.12828$, $M_i = 1$, $\dot{\sigma}_j^+ = 0.01$, $\sum\limits_{j = 1}^{2}\frac{M_j}{1-\dot{\sigma}_i^+} = 2.0202$, $i = 1, 2$, i.e., condition $(H_4)$ in Theorem 4.1 holds. By Theorem 4.1, system (5.1) is globally asymptotically stable, see Figures 3 and 4.

Example 5.2. Considering the following FODINNs with asymptotic periods:

where $\alpha = 1.8$, $\beta = 0.8$, $a_i(t) = \frac{t}{1+t}(3+0.005\sin t)$, $b_i(t) = 13+0.02\cos t$, $\tau_j(t) = 1+0.01\sin t$, $I_i(t) = \frac{t}{1+t}(1+\cos t)$, $\xi_i = 4$, $f_j(x_j) = g_j(x_j) = \frac{0.05x_j^2}{1+x_j^2}$,

It is easy to get that

Therefore, $(H_1)$–$(H_3)$ in Theorem 3.1 are fulfilled. By Theorem 3.1, system (5.2) owns a unique $S$-asymptotical periodic oscillation, see Figures 5 and 6.

On the other hand, $m_i = 4.76172$, $\tilde{m}_i = 1.12828$, $M_i = 1$, $\dot{\sigma}_j^+ = 0.01$, $\sum\limits_{j = 1}^{2}\frac{M_j}{1-\dot{\sigma}_i^+} = 2.0202$, $i = 1, 2$, which implies that condition $(H_4)$ in Theorem 4.1 holds. Therefore, by Theorem 4.1, system (5.1) is globally asymptotically stable, see Figures 7 and 8.

6.   Conclusions and future works

This paper research a class of Caputo fractional-order inertial neural networks with time variable delays and some interesting results for FODINNs are achieved as follows. By the features of Mittag-Leffler functions and contraction mapping theorem, the existence and uniqueness of $S$-asymptotically $\omega$-periodic oscillation for FODINNs $(2.1)$ have been discussed. Based on the comparison theorem and stability criteria of delayed fractional-order differential equations, global asymptotical stability of $S$-asymptotically $\omega$-periodic oscillation for FODINNs $(2.1)$ has been addressed.

In the future, there are several issues that deserve further consideration, which are listed as follows:

(1) It is essential to focus on whether the paper's work can be extended to the models with other fractional orders, e.g., $\alpha > 2$ and $1 < \beta\leq 2$.

(2) The methods in this paper can be used to study other FODINNs, e.g., BAM FODINNs, memristive FODINNs, Cohen–Grossberg FODINNs, etc.

(3) Other dynamics of FODINNs are also need to be considered, e.g., almost periodicity and synchronization, etc.

(4) Other neural networks can be considered by using the method in this paper, e.g., fractional-order quaternion-valued neural networks ^[50,51], fractional-order multi-dimension-valued fuzzy neural networks ^[52], fractional-order multi-dimension-valued BAM neural networks ^[53], fractional-order multi-dimension-valued memristive neural networks ^[54].

Acknowledgments

This work is supported by National Natural Science Foundation of China under Grants 11961078.

Conflict of interest

The authors declare that they have no conflict of interest.