A parametric approach of partial eigenstructure assignment for high-order linear systems via proportional plus derivative state feedback

1.   Introduction

In practical engineering application field, many controlled objects have natural second-order forms. Generally speaking, we analyze and design the control system under the second-order model, but when some conditions in practical applications are harsh or changed, or the model can not be simplified, it is more in line with the objective reality that the controlled object is equivalent to a high-order model. Therefore, the research on the control strategy of high-order systems is very significant and has attracted much attention recently ^[1,2,3]. Moreover, high-order systems are widely used in real life, including multi-body system control ^[4], large-scale flexible space structure controlled fluid mechanics ^[5], damping gyroscope system ^[6], robot control design ^[7], and other applications ^[8,9,10].

Eigenstructure assignment is a major and significant subject in the research of control system strategy. Compared with pole assignment, eigenstructure assignment can accurately grasp the comprehensive performance of the system, such as the system stability and the response speed of the system to instructions ^[11,12]. Hence, the research on eigenstructure assignment problem has always been the focus of many scholars. At present, pieces of literature concentrates on the second-order dynamic systems, and many effective results have been achieved in ^{[13,14,15,16]}. However, the above literature are all about the second-order systems, the research on high-order systems are less. In ^[17,18,19], Duan et al. have established a complete set of parametric methods for eigenstructure assignment. Meanwhile, the robust eigenstructure assignment of high-order and descriptor high-order systems is established in ^[20]. Besides, based on the eigenstructure assignment theory, Gu et al. established parametric control methods for quasi-linear high-order and descriptor high-order systems in ^[21,22,23].

In the eigenstructure assignment problem, we usually assign all the eigenvalues and the corresponding eigenvectors of the original system, which is also called "entire eigenstructure assignment". However, in most cases, only a small number of eigenstructures do not meet the requirements of the system. In this paper, we define this small number of eigenstructures as "unsatisfactory eigenstructures". Therefore, a natural idea is to replace the unsatisfactory eigenstructures while leaving the satisfactory ones in the open-loop system. It has many applications in real life. For example, in vibration systems, in order to eliminate the influence of unsatisfactory eigenvalues on the system such as resonance, we need to reassign those unsatisfactory part, while leaving the rest part unchanged in the original system ^[24]. This gives birth to the issue of partial eigenstructure assignment (PESA). In the author's work, the problem of PESA for high-order linear time-invariant (LTI) systems is well considered. In our article, this problem is closely related to the solutions of Sylvester matrix equations, and its generalized versions have been recently utilized in applied linear algebra and is proved to be very practical in the areas related to this topic ^[25,26].

As a result of the sophisticated characteristic of the high-order systems, the problem of PESA has not been paid attention until recent years, and the current related achievements are few. Therefore, we mainly list the latest research results on PESA in recent years. Yu proposed two orthogonal relations to transform the PESA problem of second-order LTI systems into solving an "entire eigenstructure assignment" problem with a low-order system in ^[27] and utilized gradient-based method to minimize norms. Meanwhile, the state observer is innovatively added to estimate the system state for the PESA problem by Silva et al. in power system ^[28]. Combined with parametric method, the observed states are directly used as inputs to the controller. Recently, a new type of PESA algorithm aiming to a class of undamped vibration systems was proposed by Ouyang et al. They used state feedback and static output feedback control law to modify the mass and stiffness matrices to preserve the partial eigenstruture. The main advantages of the above method is numerically stable and allow the relative matrices (input and output matrices) to be given beforehand ^[29,30]. Finally, for the high-order system studied in this paper, Zhang employed the differential equation algorithm to solve this kind of problem. Under this circumstances, it does not reduce the order of the system like the traditional method, but directly acts on the high-order system, which realizes the no spill-over property of the system and reduces the computational load ^[31].

In general, the references and methods discussed above are very diverse, but they have some common limitations. For example, the expression results lack of degrees of freedom and the design process is complicated. Based on the above consideration, a parametric approach for proportional plus derivative (PD) state feedback to a type of high-order LTI systems based on the solution of a class of high-order generalized Sylvester equation (HGSE) is proposed in ^[35,36,38]. In ^[39,40], they have done preliminary research on the parametric method of this issue. Compared with the different given methods in ^{[24,32,33,34]}, the core superiority of the parametric approach is that it provides all analytical solutions, which are expressed by a group of parameters. Furthermore, the desired closed-loop system and eigenstructure can be obtained by changing and choosing these kinds of arbitrary parameters.

The main contribution of this work is reflected on the following two aspects. On the one hand, the unsatisfactory eigenstructure is replaced by the expected eigenstructure, and the complete parametric expression is directly established in the framework of the high-order system. On the other hand, the degrees of design freedom in arbitrary parameter matrix $Z$ is fully utilized to achieve additional system design requirements such as robustness.

The structure of this paper is organized as follows. Section 2 formulates the PESA problem and gives some lemmas and preliminaries. Section 3 puts forward a solution to PESA problem by utilizing the degrees of freedom in arbitrary parameters and discusses the different expressions of the parametric solution in different forms of the matrix $\Lambda$. Section 4 summarizes the previous content and proposes a specific algorithm to solve this problem. Section 5 illustrates two examples to demonstrate the availability of the proposed method. Finally, Section 6 concludes the results of this paper.

Notation. We present some notation that will be used throughout this paper. $\mathbb{R}^{n}$ represents set of all real vectors of dimension $n$. $\mathbb{C}^{n}$ represents set of all complex vectors of dimension $n$. $\mathbb{R}^{n\times m}$ denotes set of all real matrices of dimension $n\times m$. $\mathbb{R}^{n\times m}\left[s\right]$ denotes set of all polynomial matrices of dimension $n\times m$ with real coefficients. $I_n$ denotes the identity matrix with $n$ dimensions. $\mathrm{rank}\; A$ and $\mathrm{det}\; A$ represent the rank and determinant of the matrix $A$, respectively. $\mathrm{deg}\; A(s)$ denotes the degree $n$ of polynomial matrix $A(s) = A_0+sA_1+\cdots+s^nA_n$. $\mathrm{diag}\left\lbrace s_1, s_2, \cdots, s_{n_u}\right\rbrace$ indicates the diagonal matrix with diagonal elements $s_i$, $i = 1, 2, \dots, n_u$.

2.   Problem formulation

Consider a type of the dynamic high-order LTI systems

where $q\in \mathbb{R}^{n}$, and $u\in \mathbb{R}^{r}$ are the state vector and the control input vector, respectively; $A_{i}\in \mathbb{R}^{n\times n}, i = 0, 1, \dots, m$, are the coefficient matrices of the system, and $B_i\in \mathbb{R}^{n\times r}$ are the input matrices of the system. When $B_i = 0, i = 1, 2, \dots, m$, and $B_0$ is substituted by $B$, then the above system can be simplified as

which is encountered more often than Eq (2.1) in many practical applications. Therefore, we mainly discuss this kind of system in our paper.

Assumption 1. $\mathrm{det}\; A_{m} \neq 0$.

Assumption 2. $\mathrm{rank}\; B = r {\leq n}$.

Assumption 3. $\mathrm{rank}\left[\begin{array}{cc} \sum_{i = 0}^{m}s^{i}A_i & B \end{array}\right] = n, \forall s\in \mathbb{C}.$

Based on the above assumptions, let

then the system (2.2) can be rewritten in the following first-order space form

where

For the high-order linear system (2.2), the following PD feedback control law is proposed

where $F_{i}\in \mathbb{R}^{r\times n}, i = 0, 1, \dots, m-1$, are the PD feedback gain matrices which need to design in the next section. Then the closed-loop system can be transformed into the following form

where

The above system can be rewritten in the following first-order form

with

where

According to linear system theory, the stability and performance of system (2.8) depends on the closed-loop matrix $A_{ec}$.

To introduce the problem of PESA, we firstly express the Jordan matrix $A_e$ of the open-loop system as follows

with

and

with

In this paper, matrices $\Lambda_{0}$ and $\Lambda_{u}$ represent satisfactory and unsatisfactory eigenstructures, respectively, that is to say, $\Lambda_{0}$ contains $n_s$ stable eigenvalues while the matrix $\Lambda_{u}$ has $n_u$ unstable eigenvalues. Meanwhile, $p^{0}_{i}, p^{u}_{i}$ represent the order of the Jordan block corresponding to satisfactory and unsatisfactory eigenvalues among $s^{0}_i$ and $s^{u}_i$.

With the above description, we similarly partition the right eigenvector matrix $V_r$ of $A_e$ into two parts

where $V_0\in\mathbb{C}^{mn\times n_s}$, $V_u\in\mathbb{C}^{mn\times n_u}$ are both full-column matrices satisfying

In this paper, we focus on keeping the satisfactory eigenstructure $\Lambda_{0}$ as well its corresponding right eigenvector matrix $V_0$ in the open-loop system. Conversely, the unsatisfactory part $\Lambda_{u}$ and $V_u$ will be altered by the matrix $\Lambda\in\mathbb{C}^{n_u\times n_u}$ and a full-column matrix $V_{al}\in\mathbb{C}^{mn\times n_u}$. Specifically, by introducing a proper controller in (2.5), we let the reassigned part of the matrix $A_{ec}$ be similar to an arbitrary constant matrix $\Lambda\in\mathbb{C}^{n_u\times n_u}$ with desired eigenstructure.

Denote the Jordan matrix $\Lambda$ as

with

and

where $p_{i}, i = 1, 2, \dots, n_u$ represent the order of the Jordan block corresponding to the eigenvalues $s_i, i = 1, 2, \dots, n_u$ which can be selected arbitrarily.

2.1.   The right eigenvector matrix of altered part in closed-loop system

Let the matrix $V_{al}$ be the substitution matrix of the matrix $V_{u}$ in right eigenvector matrix. For the right eigenvector matrix of the altered part in closed-loop system, we introduce the following lemma.

Lemma 1. Let the matrix $A_{ec}$ be given in Eq (2.9). There exists the following matrix $V_{al}$

satisfying

if and only if

and

Then, the matrix $V_{al}$ can be written in the following form

Proof. since

and

For convenience, let $V_{1} = V$. Thus, combine Eqs (2.23), (2.24) with $A^{d}_{i}$ in (2.10), Eqs (2.20) and (2.21) naturally hold. Then, taking Eq (2.21) into (2.18), Eq (2.22) can be easily deduced. The proof is finished.

2.2.   Problem statement

Based on the above preparation, we propose the problem statement of partial eigenstructure assignment in high-order LTI systems via PD feedback.

Problem 1 (PESAH). Given a type of high-order LTI systems (2.2) satisfying Assumptions 1-2, the satisfactory eigenstructure $\{ \Lambda_{0}$, $V_{0}\}$ as described previously satisfying Eq (2.14), and a constant matrix $\Lambda\in \mathbb{C}^{n_u\times n_u}$ in Eqs (2.15)-(2.17) with desired eigenstructure. Find all the PD feedback gain matrices $F_{i}\in \mathbb{R}^{r\times n}, i = 0, 1, \dots, m-1$, and the right full-column rank eigenvector matrix $V_{al}\in \mathbb{C}^{mn\times n_{u}}$ to be altered such that

3.   Solutions to Problem 1 (PESAH)

In this paper, the key of solving Problem 1 (PESAH) is to transform it into solving a kind of high-order generalized Sylvester equation (HGSE), and the specific transformation process will be given in the following section.

Based on the above viewpoints, we propose the following HGSE

where $A_{i}$, $\Lambda$ and $B$ are the given matrices, while $V$ and $W$ are unknown matrices to be determined.

Remark 1. In fact, introducing a set of right coprime polynomials is a necessary procedure before solving the Sylvester Eq (3.1). Thus, there exists a pair of right coprime polynomial matrices $N(s)\in \mathbb{R}^{n\times r}$, $D(s)\in \mathbb{R}^{r\times r}$, satisfying the following Right coprime factorization (RCF)

with

Denote $N(s) = \left[n_{ij}(s)\right] _{n \times r}$, $D(s) = \left[d_{ij}(s)\right] _{r \times r}$, and $\mu = \max\{\mathrm{deg}(d_{ij}(s)), i = 1, 2, \dots, n, j = 1, 2, \dots, r\}$. Then matrices $N(s), D(s)$ can be written in the following form

For the solution to HGSE (3.1), we introduce the following lemma.

Lemma 2. ^[37,38] Let $\Lambda\in \mathbb{C}^{n_u\times n_u}$ be given in Eqs (2.15)-(2.17) and Assumptions 1-2 hold. Furthermore, let $N(s)\in \mathbb{R}^{n\times r}$ and $D(s)\in \mathbb{R}^{r\times r}$ be a pair of polynomial matrices satisfying the RCF (3.2) and have the form of Eq (3.4). Then, a general solution to HGSE (3.1) is given by

where $Z \in \mathbb{R}^{r \times n_u}$ is an arbitrary parameter matrix.

3.1.   $\Lambda$ is an arbitrary matrix

With the above preparations, we propose the following theorem to solve Problem 1 (PESAH).

Theorem 3.1. Let $N(s)$ and $D(s)$ be a pair of right polynomial matrices satisfying RCF (3.2), then

1. Problem 1 (PESAH) has a solution if and only if there exists a group of arbitrary parameter matrix $Z \in \mathbb{R}^{r \times n_u}$ satisfying the following constraint

Constraint. $\mathrm{det}\; V_{ec}(Z) \neq 0$,

where

with the matrix $V$ in $V_{al}$ can be given by

and $V_{al}$ in Eq (2.22) can be written as

2. When the above Constraint 1 is met, the PD feedback gain matrix $F$ in Eq (2.5) is solved by

where

Proof. This proof is carried out in two steps.

Step 1. Obtain the parametric forms of matrices $V_{al}, W$.

Firstly, consider Eq (2.25), the eigenstructure assignment for unsatisfactory part can be written as

This process has been shown in Eqs (2.18)-(2.22).

Secondly, substituting $A^{c}_i$ in (2.7) into (2.20), we can obtain

Let

then Eq (3.12) can be transformed into the HGSE in Eq (3.1)

By using Lemma 2, we can obtain the matrix $W$ in Eq (3.10). Besides, owing to the results in Eqs (3.5) and (2.22), the matrix $V_{al}$ can be written in the form of Eq (3.8). Thus, we complete the proof of the first step.

Step 2. Derive the parametric solutions of the PD feedback gain matrix $F$.

Combining Eqs (2.9), (2.10), (2.14) and (2.25), we can easily obtain

Due to the Assumption 2, $B_e$ is a full rank matrix, the above formula is equivalent to

Thus, according to Eqs (3.13) and (3.16)

and the Constraint 1 ensures the following equation holds

Therefore, we prove the Eq (3.9), the proof of this step has been completed.

With the above two steps, we finish the whole proof.

3.2.   $\Lambda$ is a diagonal matrix

Normally, we choose the matrix $\Lambda$ as a diagonal form since it is often encountered in many practical applications. Besides, it can reduce the complexity of calculation and simplify the expression, which means

where $s_{i}\in \mathbb{C}^{-}, i = 1, 2, \dots, n_u$, are a set of self-conjugate complex poles to be determined.

In this form, we propose the following theorem regarding to Problem 1 (PESAH).

Theorem 3.2. Let $N(s)$ and $D(s)$ be a pair of right polynomial matrices satisfying RCF (3.2), then

1. Problem 1 (PESAH) has a solution if and only if there exists a group of arbitrary parameter vectors $z_{i}\in \mathbb{C}^{r}, i = 1, 2, \dots, n_u$, satisfying the following constraints, then the matrices $V, W, V_{al}$ have the following form

and

where

with

satisfying the following constraints

Constraint. $\mathrm{det}\; V_{ec}(z_i, i = 1, 2, \dots, n_u)\neq 0$.

Constraint. $z_{i} = \bar{{z}}_{j}$ if $s_{i} = \bar{{s}}_{j}, i, j = 1, 2, \dots, n_u$.

2. When the above conditions are satisfied, the coefficient matrices of PD feedback controller (2.5) can be obtained as Eq (3.9), and matrices $V, W$ given by Eq (3.5) and $V_{al}$ in Eq (3.8) can be parametrized by columns as Eqs (3.20)-(3.24), and $z_i\in \mathbb{C}^{r}$ are a group of parameter vectors satisfying Constraints 2-3.

Proof. When the matrix $\Lambda$ is chosen to be a diagonal form, $V$ in Eq (3.7) and $W$ in Eq (3.10) can be written in Eqs (3.20) and (3.21) (see ^[36]). Now we only need to prove Eqs (3.22) and (3.23).

According to Eqs (2.24) and (3.20), the $i$-th column of the matrix $V_{al}$ can be written as

Obviously, Eq (3.23) holds. The proof is completed.

4.   A general step for solving Problem 1 (PESAH)

Based on the discussion and proof of the above results, we give the following steps to solve Problem 1 (PESAH).

Step 1. Partition the right eigenvector matrix $V_r$ of the open-loop matrix $A_e$ into two parts satisfying Eq (2.14).

Step 2. Choose a Hurwitz matrix $\Lambda$ with desired eigenstructure.

Step 3. Solve a pair of polynomial matrices $N(s)$ and $D(s)$ according to the RCF (3.2).

Step 4. Find a group of parameters $z_{i}, i = 1, 2, \dots, n_u$, satisfying the Constraints 2-3.

Step 5. Compute the matrices $V, W, V_{al}$ according to Eqs (3.5) and (3.8) or (3.20)-(3.23) based on the chosen parameters in Step 4.

Step 6. Obtain the PD feedback gain matrix $F$ through Eq (3.9) based on the solutions in Step 5.

Remark 2. In practical systems, the robustness of the system needs to be considered due to the existence of disturbances. There are arbitrary parameters in the parametric design method proposed in this paper, so these arbitrary parameters can be utilized to optimize the performance index of robustness to achieve the purpose of anti-interference. Therefore, we can optimize the following index

as small as possible ^[17].

Noteworthy, the index $J$ is closely related to the arbitrary parameter $Z$. Therefore, the desired index can be optimized by selecting appropriate parameter matrix $Z$ or parameter vectors $z_i, i = 1, 2, \dots, n_u$.

5.   Two illustrative examples

5.1.   A numerical example

5.1.1.   System description

Consider a third-order system in the form of Eq (2.2) in ^[18], which the coefficient matrices are shown as follows

For the system, it can be easily compute that

Therefore, Assumptions 1-3 hold. Meanwhile, it is easy to obtain the open-loop system eigenvalues as

We can see that the eigenvalues $\{0.329544, 1.000000, 0.544587+0.897497\mathrm{i}, 0.544587-0.897497\mathrm{i}\}$ are unstable eigenvalues. Therefore, we need to replace the above unstable eigenvalues and the related eigenvector matrices while others unchanged.

In this situation, we design the following PD feedback control law

and choose the diagonal matrix with expected eigenvalues

The matrix $V_{0}$ in Eq (2.14) can be obtained as

where

A pair of polynomial matrices $N(s), D(s)$ satisfying RCF (3.2) can be easily obtained as

where $d(s) = -8s^9-8s^8+4s^7-4s^6+s^5-3s^4+14s^3+2s^2+4s-2$.

We specially choose the parameters as

based on Eqs (3.20)-(3.24), we obtain the following particular solution

Then, based on Eqs (3.6) and (3.9), the PD feedback gain matrices can be obtained as

With the above controller, the closed-loop system in Eq (2.6) can be given by

and the closed-loop eigenvalues are assigned to

5.1.2.   Simulation results

Choose the initial value as follows

then the simulation results are shown in the following figures.

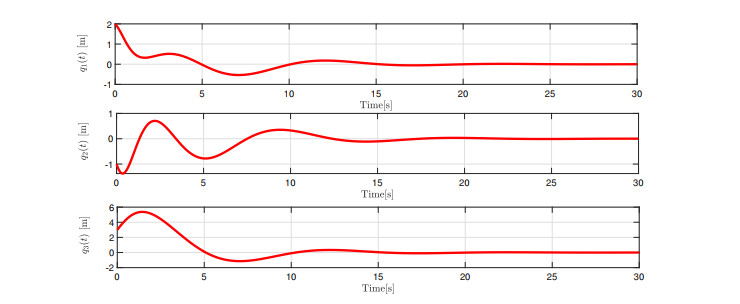
It is obvious to see that the final high-order closed-loop system achieves the desired eigenstructure. At the same time, it can be seen from the simulation diagrams that the final states of the closed-loop system tend to be zero in a very short time, which means that the closed-loop system is eventually stable. The above process reflects the feasibility of the parametric method proposed in this paper.

5.2.   Three-axis dynamic flight motion simulator system

5.2.1.   System description

Consider a three-axis dynamic flight motion simulator system shown in Figure 5, which possesses a linearized model in the form of ^[41]

where

The state vector $q$ and the control input vector $u$ can be written as

with the variables $\alpha$, $\beta$, $\gamma$, $u_{1}$, $u_{2}$, $u_{3}$ respectively represent the angles of three directions and the voltage inputs along the three axises.

For the particular experimental system, the values of these parameters are given by

thus yields

For this system, it can be easily obtain the eigenvalues of the open-loop system are

We assign eigenvalues $\{0, 0, 0, -0.000310, -13.652856\}$ to $s_{1} = -110$, $s_{2} = \bar{s}_3 = -30+25\mathrm{i}$, $s_{4} = \bar{s}_5 = -50+25\mathrm{i}$, respectively, while keeping the rest of eigenvalues unchanged in the open-loop system. In order to achieve the above objectives, we design the following PD feedback control law

Choose the diagonal matrix with expected eigenvalues

and the matrix $V_{0}$ can be easily obtained as

with

With the coefficient matrices $A_i, i = 0, 1, \dots, 3$, we have

and

Therefore, Assumptions 1-3 hold. Meanwhile, noted that the matrix $B = I_{3\times 3}$, a pair of $N(s)$ and $D(s)$ satisfying RCF (3.2) can be easily obtained as

5.2.2.   Non-optimized solution

Simply choose the parameters as follows

based on Eqs (3.20)-(3.24), we obtain the following particular solution

Then, based on Eqs (3.6) and (3.9), the PD feedback gain matrices can be obtained as

Denote the non-optimized index as $J_u$. In this situation, it can be calculated that the index $J_u = 2.4\times 10^{10}$.

With the above controller, the closed-loop system can be given by

and the closed-loop eigenvalues are assigned to

5.2.3.   Optimized solution

Consider the optimized index in Remark 2. Choose the initial value in Eq (5.3), the optimized parameters can be obtained by using the fminsearch function in MATLAB Optimization Toolbox$\circledR$

yields the following optimized solution

In this situation, we obtain the optimized feedback gain matrices

Denote the optimized index as $J_o$. On this condition, it can be calculated that the index $J_o = 3.8\times 10^{7}$.

With the above controller, the closed-loop system can be given by

where

and the closed-loop eigenvalues are assigned to

It can be seen that through the above optimization process, we have

Obviously, $J_o < J_u$, which illustrates that the robustness of the system is improved effectively by fully utilizing the degrees of freedom in the solution. In order to illustrate the effectiveness of optimization more intuitively, simulation and comparison will be given in next subsection.

5.3.   Simulation and comparison

To test the effectiveness of the proposed approach, we give the following simulation between non-optimized solution, optimized solution and open-loop system.

Choose the initial value as follows

then the simulation results are shown in the following Figures.

5.4.   Simulation analysis

The analysis of simulation can be described from the following three aspects. Firstly, from Figures 7-10, we can clearly see that some unstable states in original open-loop system finally tend to be stable while the rest of the stable states are still stable after PESA (in Figures 11-15), which illustrates that the parametric approach we utilize is effective. Secondly, from the above figures, the optimized solutions obviously reduce the amplitude of oscillation and have faster convergence time while the non-optimized solutions have no such benefits. This indicates that the closed-loop eigenvalues in optimized solution are less sensitive than non-optimized solution when encountered external disturbance ($J_o < J_u$). Finally, from Figure 6, it can be seen that the optimized solution control inputs are less than non-optimized solution, which means that the optimized solution lead to better control performance and cost less energy. To sum up, on the premise of ensuring the stability of the closed-loop system, the unsatisfactory eigenstructures in the open-loop system are reassigned into the closed-loop system with desired eigenstructure.

Through above example, it can be seen that only a subset of eigenstructures need to be assigned into the closed-loop system, which is more often encountered in many practical applications. Under this circumstances, the design of the controller can be simplified and becomes more economical and efficient compared to "entire eigenstructure assignment".

Remark 3. In this paper, the parameter selection is arbitrary. The parameter selection needs to satisfy only a few simple constraints. In fact, it is almost possible to find parameter matrix $Z$ or vectors $z_i$ to meet the Constraints 1-3 in state feedback. To simplify the calculation process, we just choose several groups of simple arbitrary parameters and meanwhile verify all the constraints are satisfied. From this point of view, we can argue that the choice of free parameters is valid.

Remark 4. In previous problem of PESA in high-order systems ^[24,41], the design process of the controller is complicated and the expression results lack of degrees of freedom. However, through the deduction in our paper, the core advantage of the parametric approach is very simple and neat, and the degrees of freedom can be well increased by the arbitrary parameter matrix $Z$, which can be utilized to improve the additional performance of the system and will play an important role in the optimization of system performances ^[17,23,39]. In this paper, we just give a simple example to show that the desired control objectives (robust index in Remark 2) can be achieved by selecting different arbitrary parameter $Z$, which reflects the convenience and feasibility of the parameterization approach.

Remark 5. To solve Problem 1 (PESAH), the choice of controller has a crucial influence on the final control result. The state feedback is a common control strategy in most research. In high-order system, displacement, velocity and acceleration sensors can be utilized to achieve real-time measurement of system state. Although the parametric method of this paper solves this problem well, it also has some limitations. For example, in many practical applications, the state of the system is not accessible. Therefore, a natural idea is to deal with it through static output feedback or adding dynamic compensator, which is a direction and will be fully considered in our future research.

6.   Conclusions

In this paper, a fully parametric method inspired by the HGSE for partial eigenstructure assignment in high-order systems is proposed. Firstly, by partitioning the open-loop system into the altered part and the unchanged part, a general parametric expression of PD feedback controller concerning the matrices $\Lambda$ and $Z$ with the desired eigenstructure is established. In the meanwhile, through drawing into a group of arbitrary parameters providing all the degrees of freedom, the optimization problem of the system is taken into consideration and well met the design requirements of the system. Finally, a numerical example and a practical example with simulation results prove the feasibility and effectiveness of the parametric method.

Acknowledgments

We sincerely thank the Editor-in-Chief and the anonymous reviewers for their helpful comments and suggestions which have helped to improve the quality of this paper. This work was supported in part by the Major Program of National Natural Science Foundation of China (grant numbers 61690210, 61690212).

Conflict of interest

All authors declare no conflict of interest in this paper.