Synchronizations of fuzzy cellular neural networks with proportional time-delay

1.   Introduction

The chaotic systems have become interesting topic among the researchers, scientists and engineers during last few years. In dynamical system, chaotic character is introduced by highly sensitivity to its initial conditions with variations of parameters. Chua and Yang ^[1] have first introduced cellular neural networks (CNNs). At that time basic CNN was structured in three types, first one is the traditional CNN ^[1] and it explains analogical computational network along with analog weights, states, inputs and outputs. Second one is CNN with delay term ^[2], which is slightly different from traditional CNN consists of delayed weights with inputs, outputs states and analogue weights and last one is the CNN in discrete-time ^[3] which includes analog weights, inputs, digital outputs and states. Due to immense applications in the areas of image processing, classification of patterns, quadratic optimization, associative memories, those have been broadly introduced by the researchers. Yang and Yang ^[4] have studied forward FCNNs, which link fuzzy logic into CNN and maintain all aspects and local connectedness among cells. So far, some different types of synchronization schemes on fuzzy neural networks and also control of the same networks have been introduced, viz., finite-time synchronization, adaptive control, lag and exponential lag synchronization, etc. ^[5,6,7]. Duan et al.^[8] have considered discontinuous activation functions to show synchronization in finite-time of time-delayed FCNNs and Tang et al.^[9] have also studied non-chattering quantized controllers for finite-time cluster synchronization of FCNNs. Abdurahman et al.^[10] have shown synchronization in finite-time for FCNNs which include the time-varying delay terms, using finite-time stability theory. Mani et al.^[11] have considered the adaptive control of fuzzy chaotic CNNs in fractional order and also showed its applications in image encryption. Based on the Lyapunov method and graph theory, the finite-time synchronization criteria have been obtained for FCNNs with stochastic perturbations and mixed delays by constructing appropriate state feedback controllers in ^[12]. The FCNN has fuzzy logic between its templates of input and output. It has potential applications in pattern recognition and image processing. Therefore, it is very important to analyze dynamical behaviors, stability analysis and synchronization of FCNNs in the aspects of theoretical and application points of view. The study of dynamical behavior of synchronization of FCNNs is also important. In the last few years, in the area of the neural network and other applied dynamical systems, many researchers have studied the stability problems ^{[13,14,15,16,17,18,19,20]}.

The stability analysis for a neural network is also employed in synchronization problems. So the synchronization problems of neural networks are often changed to a the stability problem of a error system, which is obtained from master and response systems. Synchronization of the neural networks model is addressed to the synchronization of the master-response chaotic systems having different initial values and it was first investigated by Pecora and Carroll ^[21]. In the literature review, it is found that a few researchers have studied stability and synchronization analyses for some different problems, viz. ^{[22,23,24,25,26,27,28]}. The synchronization problems of the neural networks mainly include finite-time, fixed-time and asymptotic synchronizations. The asymptotically synchronization is different from the FFTS because asymptotic synchronization does not give us the time interval or fixed time for synchronization while the FFTS is achieved after a fixed time or a finite-time interval between the master-response systems. The asymptotic synchronization is another area of research interest in which the synchronization error asymptotically vanishes under limiting conditions. Although it is not a realistic as machines and human beings having a limited life span. The limitations of asymptotic stabilization overcome by finite time protocol. The article ^[29] shows various parameters are appeared during control methods. Finite-time synchronization is studied during last few years by the researchers ^[30,31]. Applications in wireless sensor networks and secure communication have been studied using finite-time synchronization communication. If we compare asymptotic synchronization and finite-time synchronization, then the later can be realized at a particular moment and hence may be controlled. The fixed-time method is first studied by Polyakov ^[32] in which he has stabilized the systems in the finite-time considering that the settling time does not depend on initial values of the systems. This is a better method compared to other finite time methods. Some notable fixed time control works are investigated by the researchers from time to time like ^[33,34,35] by using neural networks as well as complex networks. The finite-time synchronization is introduced using finite-time stability analysis by Kamenkov ^[36]. It is seen from the definition, fixed-time stability analysis is the particular case of finite-time stability analysis and in both stability analyses, the trajectories will converge over a finite-time interval. In the finite-time stability the convergence time or settling time of the trajectories depends on the initial conditions of the model and in fixed-time stability analysis, the settling time of the trajectories has a uniform upper bound for all initial conditions within the domain which is not dependent on the initial conditions. This is the main difference between finite time and fixed time stability analyses. In these types of synchronization control problems and the estimation of time are the key features for the stability analyses. From the literature review, so many practical systems are formed such as power systems, traffic signals ^[37,38]. These problems are controlled using fixed-time interval. The initial conditions are rarely be given for many real practical problems. Polyakov ^[39] has studied the finite-time stability by using nonlinear feedback design of linear control system. In this point of view, the fixed-time synchronization (FTS) has more advantages compared to finite-time synchronization because FTS has nothing to do with initial conditions of error systems. Many synchronization problems have been done by the researchers on finite-time synchronization of FCNNs. But the study on FTS is few ^[40]. By designing state feedback controller and discontinuous activation function, the fixed time synchronization problem for FCNNs with time-varying delay have been discussed in ^[41]. Under the differential inclusion theory and discontinuous state feedback control technique, Sun and Liu ^[42] have investigated the fixed-time synchronization of fractional-order memristor-based FCNNs with time-varying delays by defining appropriate Laypunov functional. By constructing delay dependent controllers with or without fuzzy terms and using matrix analysis method, fixed time synchronization criteria have been discussed for delayed markovian jump FCNNs in the presence of stochastic disturbance in ^[43]. To study the significance of the control and synchronization in delayed FCNNs, Ding and Han ^[44] have studied synchronization on delayed FCNNs by using adaptive control method with unknown parameters, in which control functions are designed using Lyapunov-Lasall principle and some other synchronization conditions. The global exponential synchronization on delayed FCNNs using Lyapunov-like stability theory with some other criteria has been studied by Feng et al.^[45]. From literature review it is confirmed that the researchers were only focused on synchronization problems of FCNNs with time-varying delay corresponding to finite-time problems ^{[46,47,48,49,50,51]}. The study on FTS is still in a primal stage. In the year 2015, Polyakov et al.^[52] have studied the FFT stability of robust stabilization of nonlinear systems using the new nonlinear control laws and implicit lyapunov function. Wan et al.^[53] have investigated the robust FTS for CGNNs by using Lyapunov stability theory, Liu and Chen ^[54] have also introduced the finite-time cluster and fixed-time cluster synchronizations in presence or absence of pinning control law.

Based on the above analysis, the authors have motivated to study FFTS of FCNNs with interaction and proportional delay terms. In real-time, the interactions ^[55,56] of two networks are diverted through the nonlinear signals, mutual connections, or by the hub nodes. The proportional delay ^[57,58,59] has wide existence in the real-world such as routing decision and web quality of service ^[60]. The dynamical nature of the neural networks include proportional delays term have been introduced by the researchers and most of the works concerning synchronizations of neural networks include proportional delays term are asymptotic. This implies synchronization of neural networks is achieved when time becomes large. In this article a drive has been taken to study FFTS in which the error model of networks will be convergent in an estimated time domain. The main contributions of this article are summarized as:

(1) Almost all works in references ^[61,62] are related to study on FNNs assuming that the continuous activation functions are time varying-delays or smooth, and Lipschitz continuous. In this article, the main focus is given on the study of synchronization of FCNNs with continuous activation function having interaction and proportional delay terms.

(2) Simple controller is designed for FFTS of considered FCNN models by using some new algebraic criteria and some sufficient conditions which confirm that the both master and response systems can be synchronized in finite and fixed time, and also it gives a range of domain of time for FFTS.

(3) In this article, the settling time can easily be estimated. The settling time of the fixed-time synchronization is bounded for any initial states. Furthermore, as compared to the classical results, our proposed estimation bound of the settling time is more effective and accurate.

(4) Two examples are considered to show the effectiveness, reliability and the accuracy of the proposed numerical scheme of FFTS.

The organization of the article is as follows. Some preliminaries in which system description, some definitions, lemmas, assumptions, and problem formulation are introduced in section 2. Two control laws for the FFTS are designed in the section 3. Two examples have been taken to validate, the reliability, effectiveness and efficiency of the results given in section 4. The overall conclusions of the article are discussed in the section 5.

2.   Some preliminaries and system description

2.1.   Preliminaries

Notations

In this section the symbols $\bigvee$ and $\bigwedge$ are used to denote the fuzzy OR operation and fuzzy AND operation respectively. p is used for positive integer, $||{.}||$ denotes the vector norm and $||{.}||_{p}$ is the representation of p-norm. $C([-\tau, 0], R^{n})$ is taken in Banach space, where $\tau$ stands for delay term in time. $f_{j}(.)$ and $h_{j}(.)$ are taken as activation function and interaction function between two neurons, respectively.

Suppose $p\geq 1$ be a positive integer and $R^{n}$ is the real column vectors of n-dimensional space and $z = (z_{1}, z_{2}, ..., z_{n})^{T}$, then $||{z}||$ represents vector norm and is defined as

Lemma 2.1. ^[10] Assume $z$ and $w$ are two state variables, then we have following inequalities as

Lemma 2.2. Suppose $0 < s < 1$ and $c, d \; \in R$, then the following condition

is satisfied.

Lemma 2.3. Consider $n\in N$ and $0 < i < j$, $i, j\in R$, then the following condition holds

2.2.   Systems' description

Let us consider n-dimensional FCNNs with interaction and proportional delay terms as drive system given by

with initial conditions $z_{i}(s) = \psi_{i}(s), \; s\in [-\tau, 0],$ where $i\in I \triangleq \{1, 2, ..., n\}$, $z_{i}(t)$ represents the $i$-th unit state variable at time $t$. $a_{ij}$ and $b_{ij}$ represent the elements of feedback templates, $c_{i}$ denotes the passive decay rate of the $i\rm{th}$ unit state, $q_{ij}$ is taken for the feed-forward template and $\alpha_{ij}$ and $\beta_{ij}$ respectively represent fuzzy feedback templates of MIN and MAX, $T_{ij}$ and $S_{ij}$ respectively denote fuzzy feed-forward templates of MIN and MAX. $v_{i}$ and $I_{i}$ represent input of neuron and bias of neuron at $i$-th iteration respectively. The proportional delay term is $r\in(0, 1)$ and $rt = t-(1-r)t$, with $\tau(t) = (1-r)t$ is a continuous time varying function which satisfies $(1-r)t\to +\infty$ as $t\to +\infty$. $d_{ij}$, $\bar{d_{ij}}$ denote the interaction structures. $f_{j}$ and $h_{j}$ are the activation and interaction functions between the networks, respectively, $\epsilon$ is outer interaction strength. Here $\psi(s) = (\psi_{1}(s), \psi_{2}(s), ..., \psi_{n}(s))^{T}\in C([-\tau, 0], R^{n})$ represents the Banach space of all continous functions with p-norm defined as

where $p > 0$ is an even integer.

Now, we consider the following assumptions as $\boldsymbol{(H_{1})}$ $\exists$ real constants $\underline{L}_{i}$, $\underline{N}_{i}$ and positive real numbers $\overline{L}_{i}$, $\overline{N}_{i}$ such that

$\boldsymbol{(H_{2})}$ The neuron activation function $f_{i}$ and interaction function $h_{i}$ are bounded then $\exists$ $L_{i} > 0$ and $N_{i} > 0$ for each i, such that

Let the response system is

where $w_{i}(s) = \xi_{i}(s), \; s\in [-\tau, 0], \xi_{i}(s)\in C([-\tau, 0], R)$ is the initial conditions and $u_{i}(t)$ is the coupling control.

Let us consider $z_{i}(t), w_{i}(t)$ are state variables of the systems (2.1) and (2.2), and $\psi_{i}, \xi_{i}$ are initial conditions respectively. Assuming that $e_{i}(t) = w_{i}(t)-z_{i}(t)$, $i\in I$ and $f_{j}(e_{j}(t)) = f_{j}(w_{j}(t))-f_{j}(z_{j}(t))$, we get the error system as

Definition 2.1. ^[10] The systems (2.1) and (2.2) are synchronized in a finite time after appropriate design of the controller $u_{i}(t)$, if $\exists$ a constant $T > 0$ s.t.

$\lim_{t\to T}|z_{i}(t)-w_{i}(t)| = 0$

and $|z_{i}(t)-w_{i}(t)| = 0\; \; for\; \; t > T, i\in I.$

Definition 2.2. ^[63] The considered system (2.1) achieves FTS with response system (2.2) if $\exists$ a settling time function $T(e_{0}(\theta))$ and a fixed time $T_{max}$ such that

where $||{.}||$ represents the Euclidean norm.

Definition 2.3. ^[64] If f(t) is differentiable on R, then the upper Dini derivative of $|f(t)|$ is given by $D^{+}(|f(t)|)$ = $\dot{(f(t))}sgn(f(t))$ for $f(t)\neq 0$.

Lemma 2.4. ^[10] Suppose $V_{1}(t)$ is a continuous and positive-definite function, then it satisfies

where $0\leq \mu < 1, \beta\geq 0$ are constants.

Then, for given $t_{0},$ the following inequalities hold for $V_{1}(t)$.

and

with $T$ is given by

Remark. In the view of Lemma 2.4, the system (2.3) is fixed-time stable at origin and the settling time is obtained as

3.   Main results

3.1.   Finite-time synchronization

Suppose that the activation functions $f_{i}$ are bounded, then we define the control law in the following form as

where $e_{i}(t) = z_{i}(t)-w_{i}(t)$, with $\eta_{i}, k$ are the parameters.

Theorem 3.1. Assuming $H_{1}$ and $H_{2}$ are satisfied, then the drive system (2.1) will be finite-time synchronized with response system (2.2) with the help of controller (3.1) if the conditions $\eta_{i}\geq -c_{i}+\lambda_{i}+w_{i}+v_{i}$ and $\rho_{i}-\sigma_{i}\leq 0$ are satisfied,

where $w_{i} = \frac{1}{p}\sum_{j = 1, j\neq i}^{n}\sum_{i = 1}^{p-1}|a_{ij}|^{p\gamma_{lij}}L_{j}^{p\delta_{lij}}+\frac{1}{p}\sum_{j = 1, j\neq i}^{n}|a_{ji}|^{p\gamma_{pij}}L_{i}^{p\delta_{pij}}$

and $v_{i} = \frac{\epsilon}{p}\sum_{j = 1, j\neq i}^{n}\sum_{i = 1}^{p-1}|d_{ij}|^{p\gamma_{lij}}N_{j}^{p\delta_{lij}}+\frac{\epsilon}{p}\sum_{j = 1, j\neq i}^{n}|d_{ji}|^{p\gamma_{pij}}N_{i}^{p\delta_{pij}}$.

Proof. Let the Lyapunov functional is

In view of (2.3), calculating the upper right-hand Dini derivative of Eq (3.2), we have

From $H_{1}, H_{2}$ and Lemma 2.1, we obtain

where $L_{j}$ = $max\{|\underline{L}_{j}|, |\overline{L}_{j}|\}$, $N_{j}$ = $max\{|\underline{N}_{j}|, |\overline{N}_{j}|\}$, then from Eqs (3.3) and (3.4), we get

where $\lambda_{i}$ is given by

and $\mu_{ij} = |b_{ij}|+|\alpha_{ij}|+|\beta_{ij}|$ and $q = p+\theta-1 > 0$. Assume that $\gamma_{lij}, \delta_{lij} \geq 0$ are real numbers and satisfy $\sum_{l = 1}^{p}\gamma_{lij} = 1, \sum_{l = 1}^{p}\delta_{lij} = 1$. Then applying the condition $pc_{1}c_{2}...c_{p}\leq c_{1}^{p}+c_{2}^{p}+...+c_{p}^{p}$, where $c_{i} > 0$ for $i = 1, 2, ..., p$, we get

with

$w_{i} = \frac{1}{p}\sum_{j = 1, j\neq i}^{n}\sum_{l = 1}^{p-1}|a_{ij}|^{p\gamma_{lij}}L_{j}^{p\delta_{lij}}+\frac{1}{p}\sum_{j = 1, j\neq i}^{n}|a_{ji}|^{p\gamma_{pij}}L_{i}^{p\delta_{pji}}$.

Similarly,

with

$v_{i} = \frac{\epsilon}{ p}\sum_{j = 1, j\neq i}^{n}\sum_{l = 1}^{p-1}|d_{ij}|^{p\gamma_{lij}}N_{j}^{p\delta_{lij}}+\frac{\epsilon}{ p}\sum_{j = 1, j\neq i}^{n}|d_{ji}|^{p\gamma_{pij}}N_{i}^{p\delta_{pji}}$,

$\rho_{i} = \sum_{j = 1}^{n}\mu_{ij}M_{j}, i\in{I}$.

Using Eqs (3.6) and (3.7) in Eq (3.5), we get

Choosing $\eta_{i}$ such that $\eta_{i}\geq -c_{i}+\lambda_{i}+w_{i}+v_{i}$ and $(\rho_{i}-\sigma_{i})\leq 0$, we get using Lemma 2.3,

Hence from Lemma 2.4, the systems (2.1) and (2.2) will be synchronized in the finite-time $T_{1} = \frac{V_{1}^{\frac{1-\theta}{p}}(0)}{k(1-\theta)}$. Also the control law (3.1) and the system (2.3) will converge to zero within time $T_{1}$.

Note. If $p = 2, \gamma_{lij} = \delta_{lij} = \frac{1}{2}$ for $l = 1, 2$, then

$\bar{w_{i}} = \sum_{j = 1, j\neq i}^{n}\frac{(|a_{ij}|L_{j}+|a_{ji}|L_{i})}{2}$, $\bar{\rho_{i}} = \sum_{j = 1}^{n}M_{j}(|b_{ij}|+|\alpha_{ij}|+|\beta_{ij}|), i\in$ I.

3.2.   Fixed-time synchronization

Let us define controller as

where $\sigma_{i}, \eta_{i}$, $i = 1, 2, ...n.$ and $k$ are parameters.

Theorem 3.2. If we consider $H_{1}$ and $H_{2}$ hold, then systems $(2.1)$ and $(2.2)$ will be synchronized in the fixed time with the help of controller $(3.8)$.

The settling time $T_{max}$ is estimated as

Proof. Assume that Lyapunov function as

In view of (2.3), calculating the upper right-hand Dini derivative of $V_{1}(t)$, we get

Using Lemma 2.1 and Assumptions $H_{1}$ and $H_{2}$, we obtain

where $L_{j}$ = $max\{|\underline{L}_{j}|, |\overline{L}_{j}|\}$, $N_{j}$ = $max\{|\underline{N}_{j}|, |\overline{N}_{j}|\}$.

Thus from Eqs (3.9) and (3.10), we get

Similarly, by Theorem 3.1, we obtain

Choosing $\eta_{i}$ and $\sigma_{i}$ such that $\eta_{i}\geq -c_{i}+\lambda_{i}+w_{i}+v_{i}$ and $\rho_{i}-\sigma_{i}\leq 0$ and using Lemma 2.3, we get

where $q = p+\theta-1$, From the Lemma 2.4, we say that error system (2.3) is fixed-time stabled at origin. Then fixed-time synchronization is achieved between the considered systems (2.1) and (2.2).

By Lemma 2.4, we can estimate the settling time as

Remark. Since the controllers (3.1) and (3.8) contain the discontinuous sgn function, as a hard switcher, it may be caused to undesirable chattering. In order to avoid the chattering, the sgn function is replaced by a continuous tanh function to remove discontinuity. For examples, the control laws (3.1) and (3.8) can be modified as follows

where $\xi_{i}, \kappa_{i} > 0$ and $i\in I$.

4.   Numerical simulation and discussions

In this section two numerical examples are considered to demonstrate the effectiveness and efficiency of our proposed synchronization scheme.

Example 4.1. Suppose that following FCNN with interaction and proportional delay terms as drive system. Then for n = 2,

where $f_{j}(x_{j}) = tanh(x_{j})$ and $h_{j}(x_{j}) = sin(x_{j})$. $c_{i}, a_{ij}, b_{ij}, \alpha_{ij}, \beta_{ij}$ and $d_{ij}$ are the parameters of the system which are taken as $c_{1} = 1.5, c_{2} = 0.5, a_{11} = 1.4, a_{12} = -0.8, a_{21} = 1.8, a_{22} = 2, b_{11} = -1, b_{12} = 0.2, b_{21} = -0.5, b_{22} = 0.5, \alpha_{11} = 1.2, \alpha_{12} = -0.2, \alpha_{21} = 1.8, \alpha_{22} = -0.4, \beta_{11} = 0.4, \beta_{12} = -1.2, \beta_{21} = 1.5, \beta_{22} = -0.2, d_{11} = 0.5, d_{12} = 0, d_{21} = 0, d_{22} = 0.5, r = 0.7, \tau(t) = 0.3exp(t)$ and $I_{1} = 0, I_{2} = 0$, $\epsilon = 0.5.$

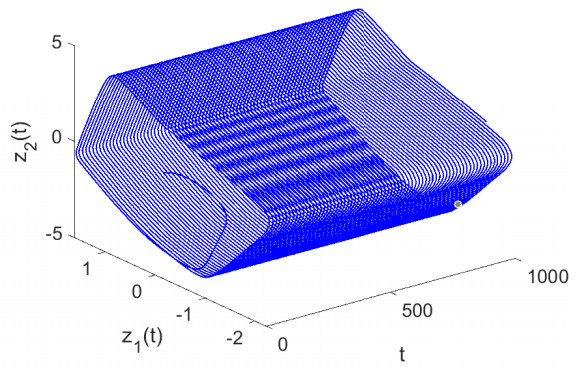
The 3-D plot of the trajectories $z_{1}(t)$ and $z_{2}(t)$ with time t of the system (4.1) is depicted through Figure 1 with initial values as $z_{1}(s) = -0.50, z_{2}(s) = 0.75, w_{1}(s) = -0.25, w_{2}(s) = 0.25$ for $s\in[-0.3, 1]$.

The corresponding response system is taken as

where $c_{i}, a_{ij}, b_{ij}, d_{ij}, \alpha_{ij}, \beta_{ij}, f_{j}, h_{j}, r$ and $I_{i}$ are similar to the system (4.2), and $u_{i}(t)$ is the controller which is given as

where $e_{i}(t) = w_{i}(t)-z_{i}(t)$.

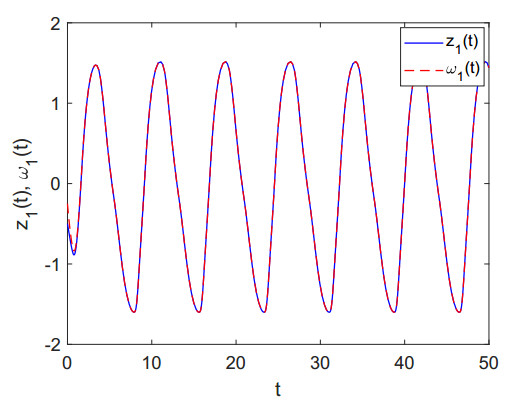
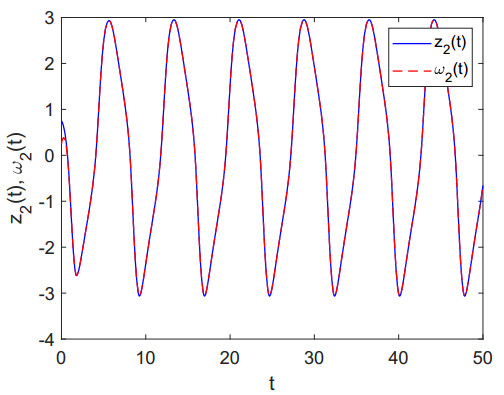
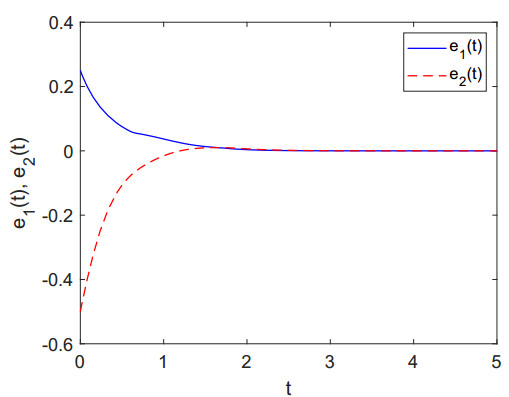
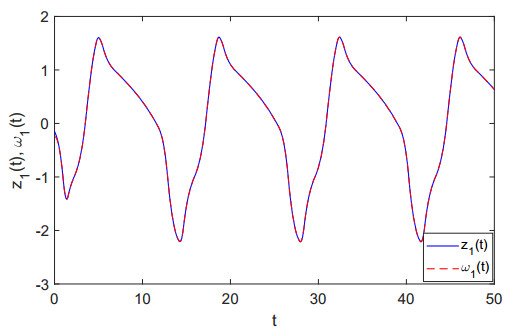
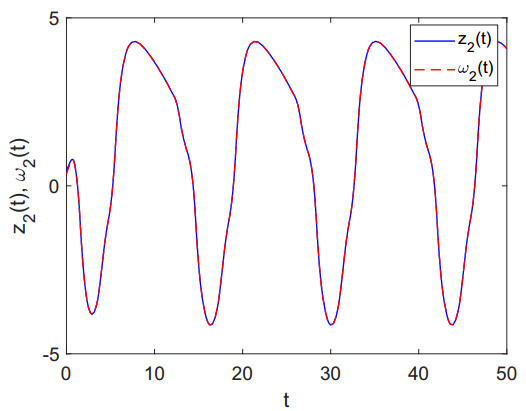
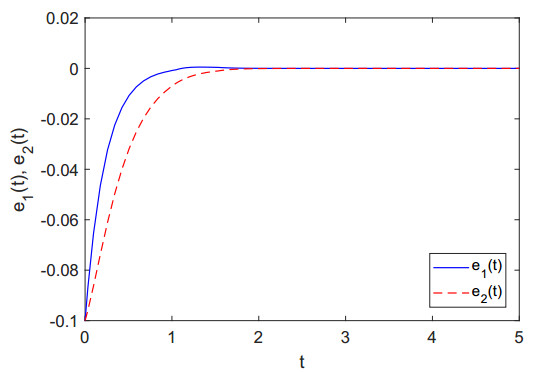
For $\underline{L}_{i} = 0, \overline{L}_{i} = M_{i} = 1$, $N_{i} = 1$, $i = 1, 2$, the assumptions $(H_{1})$ and $(H_{2})$ hold. After choosing the values $p = 2$, $\theta = 0.6$ and k = 3, we have $L_{1} = L_{2} = 1, \lambda_{1} = 1.4, \lambda_{2} = 2, \bar{w_{1}} = \bar{w_{2}} = 1.30, \bar{\rho_{1}} = 4.2, \bar{\rho_{2}} = 4.9, \bar{v_{1}} = \bar{v_{1}} = 0$. Considering $\eta_{1} = 1.50$, $\eta_{2} = 3$, $\sigma_{1} = 4.2$, $\sigma_{2} = 4.9,$ all the conditions of Theorem 3.1 hold. Therefore, in view of the Theorem 3.1, the considered systems (4.1) and (4.2) will be synchronized in a finite time with the help of the defined controllers given in Eq (4.3). Figures 2 and 3 show the synchronizations between the systems (4.1) and (4.2). The synchronizations of errors between systems (4.1) and (4.2) are depicted through Figure 4 for the earlier considered initial values.

Example 4.2. Let us consider following FCNN with interaction and proportional delay terms for fixed time synchronization as a drive system as

where $h_{j}(x_{j}) = sin(x_{j})$ and $f_{i}(x) = (|x+1|-|x-1|)/2, i = 1, 2$. Now the values of the parameters of the system (4.4) are taken as $c_{1} = 1.2, c_{2} = 1, a_{12} = -0.5, a_{11} = 1.5, a_{21} = 1.8, a_{22} = 2.1, b_{12} = 0.2, b_{11} = -1, b_{21} = -0.5, b_{22} = 0.5, \alpha_{12} = -0.1, \alpha_{11} = 1.5, \alpha_{22} = -0.4, \alpha_{21} = -0.5, \beta_{11} = 0.5, \beta_{12} = -1.1, \beta_{21} = 1.5, \beta_{22} = -0.1, d_{12} = 0, d_{11} = 0.4, d_{22} = 0.4, d_{21} = 0, r = 0.2, \tau(t) = 0.8exp(t)$ and $I_{1} = 0.1, I_{2} = 0.2, \epsilon = 0.5.$

Figure 5 depicts the 3-D plot of the trajectories $z_{1}(t)$ and $z_{2}(t)$ at time t of the system (4.4) with initial values as $z_{1}(s) = -0.15, z_{2}(s) = 0.45, w_{1}(s) = -0.25, w_{2}(s) = 0.35$ for $s\in[-0.5, 1]$.

The corresponding response system is considered as

where $c_{i}, a_{ij}, b_{ij}, d_{ij}, \alpha_{ij}, \beta_{ij}, f_{j}, h_{j}, r$ and $I_{i}$ are the same parameters as considered in system (4.4), and $u_{i}(t)$ is the controller designed as

where $e_{i}(t) = w_{i}(t)-z_{i}(t)$.

For $\underline{L}_{i} = 0, \; \overline{L}_{i} = M_{i} = 1$, $N_{i} = 1$, $i = 1, 2$, Assumptions $(H_{1})$ and $(H_{2})$ hold. Choosing the values $p = 2$, $\theta = 0.3$ and k = 3, we have $L_{1} = L_{2} = 1, \lambda_{1} = 1.5, \lambda_{2} = 2.1, \bar{w} = \bar{w} = 1.15, \bar{\rho_{1}} = 4.4, \bar{\rho_{2}} = 4.6, \bar{v_{1}} = \bar{v_{1}} = 0$. After considering $\eta_{1} = 1.60, \eta_{2} = 2.50, \sigma_{1} = 4.4, \sigma_{2} = 4.6,$ all conditions of Theorem 1 hold. So in view of the Theorem 1, the systems (4.4) and (4.5) will be synchronized with the help of the controllers (4.6). Figures 6 and 7 show the fixed time synchronizations between systems (4.4) and (4.5). The synchronizations of the errors between systems (4.4) and (4.5) are shown through Figure 8.

Here the settling time is $T_{max} = 0.4761$. In order to show the estimation bound of the settling time in more effective and more accurate ways a comparison is executed with the results given in ^[42].

As far as we know, there is no research on the finite and fixed-time synchronization for FCNNs model with interaction and proportional delays. Here it is mentioned that interaction functions are bounded and delays are proportional, which are more general than the bounded delays. Here, some special types of controller are taken to achieve finite and fixed-time synchronizations. The method used in this article provides a useful approach to study the problems on the finite and fixed time synchronizations of other fuzzy neural networks with interaction term and proportional delays.

5.   Conclusions

In the present endeavor, finite and fixed-time synchronizations (FFTS) of FCNNs are discussed under the impact of proportional delays and interaction terms. Based on Lyapunov stability technique, finite-time and fixed-time convergence theory and some other criteria along with Lyapunov functional, the FFTS is achieved. The controllers have been designed in a simple way to achieve the said synchronizations for FCNNs. In the case of finite-time synchronization of FCNNs, the upper bound of the settling time can be estimated which depends on initial conditions, whereas in FTS of FCNNs, the settling time does not depend on initial conditions. Two numerical examples are taken to verify the correctness of the mathematical results. Consequently, the obtained results on FCNN models with interaction and proportional delay terms are first of its kind and also convenient as compared to the previous available results of the FTS obtained by ^{[8,9,10,31,34,35,61,63]}. Our future work will be focused on quasi-synchronization problem of FCNNs with interaction terms. Also the FFTS of impulsive FCNNs with mixed delay and interaction terms will be considered in near future.

6.   Acknowledgement

The authors are extending their heartfell thanks to the revered reviewers for their valuable comments towards upgradation of the article. The second author S.Das acknowledges the project grant provided by the SERB, Government of India under the MATRICS scheme (File no: MTR/2020/000053).

Conflict of interest

The authors declare that they have no conflict of interest.