In this paper, we discuss the existence and uniqueness of solutions for a new kind of Langevin equation involving Riemann-Liouville as well as Caputo fractional derivatives, and variable coefficient, supplemented with nonlocal-terminal fractional integro-differential conditions. The proposed study is based on modern tools of functional analysis. We also extend our discussion to the associated inclusions problem. For the applicability of the obtained results, several examples are constructed. Some interesting observations are also presented.
1.
Introduction
Optimization techniques have much importance and popularity in real life while solving optimization problems. A variety of mathematical models exists while dealing with real-life scenarios of different problems. Hence, the mathematical models contain some specific objective function(s) along with a set of well-defined constraint(s) subject to which the problems are to be optimized (either maximized or minimized). Thus, a mathematical programming problem having multiple conflicting objectives under a set of mixed constraints is termed as a multiobjective programming problem (MOPP). In real life, the different fields of optimization such as transportation problem, inventory control, assignment problems, portfolio optimization, supplier selection, manufacturing system, supply chain management, engineering problems, etc. contain more than one conflicting objectives (either minimization or maximization) and take the form of MOPP. While dealing with multiple objectives, it is not always possible to obtain a single solution that optimizes each objective efficiently. However, a compromise solution is possible that satisfies each objective simultaneously. Therefore the concept of compromise solution is an important aspect and leads in search of the global optimality criterion. In the past few decades, a tremendous amount of research has been presented in the context of multiobjective optimization techniques.
Initially, the fuzzy set (FS) was investigated by [35], which contains the degree of belongingness (membership functions) for the element into the feasible solution set. Based on FS, [39] presented the fuzzy programming approach (FPA) for MOPP in which membership functions represent the marginal evaluation of each objective. In FPA, the decision-makers satisfaction level is achieved by maximizing the membership function of each objective. Later on, the extensions of FPA such fuzzy interval programming, fuzzy stochastic programming, fuzzy goal programming, etc. have been presented and successfully applied to solve the MOPP according to the nature of the problem and appropriate requirement of the techniques.
In some cases, only the membership function may not be the best representative of the degree of belongingness of an element into the feasible solution set. However, the degree of non-belongingness would be better to represent the hesitation aspects of an element into the feasible solution set. As a result, intuitionistic fuzzy set (IFS) was presented by [11], which is the generalization and extension of the FS. The IFS deals with both the degree of belongingness and non-belongingness of the element into the feasible solution simultaneously. Based on the IFS, P. P. Angelov [10] suggested the intuitionistic fuzzy programming approach (IFPA) to solve the MOPP in which the marginal evaluation of each objective function is determined by the membership as well as non-membership functions. In IFPA, the satisfaction level of the decision-maker is achieved by maximizing the membership and minimizing the non-membership functions of each objective simultaneously. Afterward, the extended version of IFPA, such as intuitionistic fuzzy stochastic programming, intuitionistic fuzzy goal programming, etc. have been developed and applied to various decision-making problems.
Further extension of FS and IFS has been presented because indeterminacy degree also exist in decision-making processes. To cope with the degree of indeterminacy/neutrality, F. Smarandache [32] proposed the neutrosophic set (NS). The NS considers three different membership functions namely; the truth (degree of belongingness), indeterminacy (degree of belongingness up to some extent) and a falsity (degree of non-belongingness) membership functions for the element into a feasible solution set. Recently, many authors have used the concept of NS such as [2,4,5,26] while making the optimal decisions. An indeterminacy degree are the areas of ignorance of propositions' points between the truth and a falsity degree. It means that the indeterminacy degrees are independent and can be optimized simultaneously. For example, if we collect some information from scholars regarding a journal and the possibility that the journal is good is 0.7, the journal is not good is 0.6, and do not know about the journal is 0.3. Then, this kind of linguistic vagueness or impreciseness are beyond the scope of FS and IFS and consequently beyond FPA and IFPA to decision making process respectively. Therefore, it is worth to incorporate the indeterminacy degree while dealing with MOPP.
A continuous effort is being made by many researchers or practitioners to obtain the best possible solution of multiobjective linear programming problems (MOLPPs). A large part of the literature is full of fuzzy-based optimization techniques for MOLPPs. In the past few years, the generalized concept of a fuzzy set is utilized to solve the MOLPPs. An intuitionistic fuzzy-based optimization method is also implemented by many researchers and gained a wide range of applicability and acceptability while optimizing the MOLPPs. However, the existing approaches have some limitations and can be overcome by applying the proposed neutrosophic optimization technique. The following are some essential points that ensure a remarkable contribution to the domain of multiobjective optimization techniques.
● An indeterminacy degree is the region of ignorance of propositions' values between the truth and falsity degrees. This aspect can only be managed with the neutrosophic optimization method.
● The existing methods of solving MOLPPs [19,28,36] considered only the membership function whereas [22,30,31] included the membership as well as non-membership degrees of each objective function. They do not cover the indeterminacy degree while making decisions. We have successfully cope with the concept of neutrality and hence suggested indeterminacy degree along with membership and non-membership degrees simultaneously.
● The methods of handling MOLPPs [13,17] only take care of the degree of belongingness among the parameters and do not consider the degree of non-belongingness. Therefore, this study captured the concepts of belongingness and non-belongingness degrees among the parameters and dealt with the hesitation aspects.
● The presented approach by [18] is applicable only for single-objective problems. Hence the addressed method can be easily applied to MOLPPs with different types of membership functions.
● The study presented by [30,36] does not permit the versatility of vagueness degree (shape parameters) in indeterminacy degrees, but while applying exponential-type membership function under neutrosophic environment, it can be availed.
The rest of the paper has been summarized as follows: In Section 2, related research work have been discussed whereas Section 3 represents the preliminary concepts regarding intuitionistic fuzzy and neutrosophic sets. The Section 4 represents modeling of IFMOLPPs. The proposed neutrosophic optimization technique is presented in Section 5, whereas in Section 6, numerical illustration, and comparative study with other existing approaches is depicted to verify the performance of the propounded solution method. Finally, concluding remarks and future research direction is presented in Section 7.
2.
Literature review
Literature suggests lots of research has been carried out to solve the multiobjective programming problems using fuzzy, intuitionistic fuzzy, and neutrosophic programming approaches. [20] presented a satisfying solution approach for multiple objectives, which comprise the more critical objective attainting the higher satisfying degree. A modified method based on the fuzzy ranking function is suggested by [33] and the crisp model so obtained. An uncertain goal programming approach was proposed by [21] for the solution of uncertain MOPP. P. Singh, et al. [28] discussed an efficient method that carries the quality of three different approaches, namely, fuzzy programming, goal programming, and interactive programming. Furthermore, the developed algorithm is applied to the multiobjective transportation problem. The MOPP under uncertainty was addressed by [38] and named as an uncertain multiobjective programming problem. The knowledge of efficiency concepts with different forms, such as expected-value, proper expected value, and their relationships with each other, have been established under the uncertain environment. A multiobjective fractional programming problem was presented by [14], and a novel linearization strategic technique has been developed to solve the problem. J. Dong, et al. [16] also suggested a new approach based on ranking function and TOPSIS to solve the MOPP under uncertainty. A new approach is proposed by [17] to solve the fully fuzzy MOPP under fuzzy parameters that reduces the computational complexity of the problem. A solution approach is also discussed by [13] to solve the fully fuzzy multiobjective linear programming problem under fuzzy trapezoidal parameters. S. L. Tilahu [34] developed a feasibility reduction approach for hierarchical decision-making in MOPP, and the preference free method (ideal point method) is applied to solve it.
The intuitionistic fuzzy goal programming approach is discussed by [25] that has taken the advantages of intuitionistic fuzzy set, goal programming, and interactive procedures, to solve the MOPP. A. K. Nishad, et al. [23] addressed an intuitionistic fuzzy goal programming to solve the MOPP under imprecise objectives and constraints and; implemented to solve the agricultural production management system. D. Rani, et al. [24] also suggested an algorithm to solve MOPP under an intuitionistic fuzzy environment. The proposed approach has been compared with other existing approaches. S. K. Singh, et al. [30] also addressed intuitionistic fuzzy MOPP under triangular intuitionistic fuzzy parameters and mixed constraints and; solved the MOPP using different membership functions. V. Singh, et al. [31] presented the modeling and optimization framework for MOPP under an intuitionistic fuzzy environment with an optimistic and pessimistic point of view. S. K. Singh, et al. [29] solved the multi-objective mixed integer programming problem under intuitionistic fuzzy environment and implemented on the supply chain planning problem. Recently, A. A. H. Ahmadini, et al. [9] investigateed a novel preference scheme for multiobjective goal programming problems under different sorts of membership functions.
Based on neutrosophic set theory, F. Ahmad, et al. [6] addressed a modified neutrosophic optimization algorithm for supply chain management in an uncertain situation. S. Zeng, et al. [37] presented multi-criteria supplier selection framework bassed on the neutrosophic fuzzy data set. Recently, many authors have contributed to the application of neutrosophic optimizaation theory in various real-life problems. F. Ahmad [8] discussed the supplier selection problem under Type-2 fuzzy parameters and solved using the interactive neutrosophic programming approach. A. Y. Adhami, et al. [1] also proposed a novel Pythagorean-hesitant fuzzy optimization technique and applied it to solve the transportation problem. F. Ahmad, et al. [7] performed a study on Energy-Food-Water security nexus management and applied the neutrosophic programming approach to solve the propounded model. Hence, the proposed neutrosophic approach emphasizes indeterminacy and truth and falsity degrees while making the decisions. It also generalizes the fuzzy and intuitionistic fuzzy-based approaches under different types of membership functions such as linear, exponential, and hyperbolic membership functions.
3.
Preliminary concepts
In this section, we have discussed some basic concepts related to intuitionistic fuzzy and neutrosophic sets.
Definition 1. [11] (Intuitionistic Fuzzy Set) Consider a universal discourse W; then an intuitionistic fuzzy set (IFS) ˜Y in W is depicted by the ordered triplets as follows:
where μ˜Y(w):W→[0,1] denotes the membership function and ν˜Y(w):W→[0,1] denotes the non-membership function of the element w into the set ˜Y, respectively, with the conditions 0≤μ˜Y(w)+ν˜Y(w)≤1.
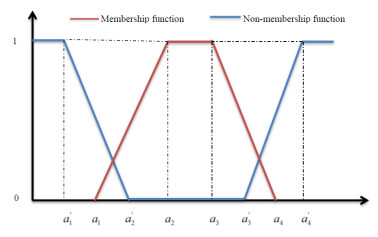
Definition 2. [30] (Trapeziodal intuitionistic fuzzy number) An intuitionistic fuzzy number ˜Y is said to be trapeziodal intuitionistic fuzzy number (TrIFN) if the membership function μ˜Y(w) and non-membership function ν˜Y(w) is given by
where a′1≤a1≤a′2≤a2≤a3≤a′3≤a4≤a′4 and is represented by ˜Y={(a1,a2,a3,a4;μ˜Y);(a′1,a′2,a′3,a′4;ν˜Y)}.
Remark 1. If a′2=a2=a3=a′3 then TrIFN ˜Y=a′1≤a1≤a′2≤a2≤a3≤a′3≤a4≤a′4 is reduced into triangular intuitionistic fuzzy number (TIFN). (see Figure 1)
Definition 3. [22] A TrIFN ˜Y={(a1,a2,a3,a4;μ˜Y);(a′1,a′2,a′3,a′4;ν˜Y)} is said to be a non-negative TrIFN if and only iff a′1≥0.
Definition 4. [22] Arithmetic operations on TrIFNs.
Assume that ˜A={(a1,a2,a3,a4);(a′1,a′2,a′3,a′4)} and ˜B={(b1,b2,b3,b4);(b′1,b′2,b′3,b′4)} be two TrIFNs. Then
Definition 5. [22] (Accuracy function) The accuracy function ϕ for TrIFN ˜A={(a1,a2,a3,a4);(a′1,a′2,a′3,a′4)} can be represented as follows:
Theorem 1. Suppose that ˜A and ˜B be two TrIFNs. Then the accuracy function ϕ:IF(R)→R is a linear function i.e., ϕ(˜A+˜B)=ϕ(˜A)+pϕ(˜B) for all p∈R.
Proof: Let us consider that ˜A={(a1,a2,a3,a4);(a′1,a′2,a′3,a′4)} and ˜B={(b1,b2,b3,b4);(b′1,b′2,b′3,b′4)} be two TrIFNs. Then, based on the nature of p, two different cases will arise:
Case I: when p≥0, then
Therefore,
Case II: when p<0, then
Such that,
In each case, we have proved that ϕ(˜A+˜B)=ϕ(˜A)+pϕ(˜B). Thus accuracy function ϕ is linear.
Definition 6. [2] (Neutrosophic Set (NS)) Suppose that X be a universal discourse such that x∈X. A neutrosophic set A in X can be stated by three membership functions namely, truth μA(x), indeterminacy λA(x) and a falsity νA(x), which can be represented by the following expressions:
where μA(x),λA(x) and νA(x) are real standard or non-standard subsets belong to ]0−,1+[, also given as, μA(x):X→]0−,1+[, λA(x):X→]0−,1+[, and νA(x):X→]0−,1+[. There is no restriction on the sum of μA(x),λA(x) and νA(x), so we have,
Definition 7. [2] Suppose that X be a universe of discourse. A single valued neutrosophic set A can be represented as follows:
where μA(x),λA(x) and νA(x)∈[0,1] and 0≤μA(x)+λA(x)+νA(x)≤3 for each x∈X.
Definition 8. [5] Consider that there be two different single valued neutrosophic sets W and Y. The union of W and Y also results in a single valued neutrosophic set Z, i.e., Z=(W∪Y), whose truth μZ(x), indeterminacy λZ(x) and falsity νZ(x) membership functions can be represented as follows:
μZ(x)=max(μW(x),μY(x))
λZ(x)=max(λW(x),λY(x))
νZ(x)=min(νW(x),νY(x)) for each x∈X.
Definition 9. [5] Consider that there be two different single valued neutrosophic sets W and Y. The intersection of W and Y also results in a single valued neutrosophic set Z, i.e., Z=(W∩Y), whose truth μZ(x), indeterminacy λZ(x) and falsity νZ(x) membership functions can be represented as follows:
μZ(x)=min(μW(x),μY(x))
λZ(x)=min(λW(x),λY(x))
νZ(x)=max(νW(x),νY(x)) for each x∈X.
4.
Intuitionistic fuzzy multiobjective linear programming problem
Most often, real-life problems exhibits optimization of more than one objectives at a time. The most promising solution set that satisfies each objective efficiently is termed as the best compromise solution. Hence the conventional form of multiobjective linear programming problem (MOLPP) with k objectives is given as follows (4.1):
where Ok(x)=∑Kk=1ckjxj,∀k=1,2,⋯,K is the k-th objective function and is linear in nature, bi,∀i=1,2,⋯,I and; xj,∀j=1,2,⋯,J are the right hand sides and a set of decision variables, respectively.
Definition 10. Assume that G be the set of feasible solution for (4.1). Then a point x∗ is said to be an efficient or Pareto optimal solution of (4.1) if and only if there does not exist any x∈G such that, Ok(x∗)≥Ok(x),∀k and Ok(x∗)>Ok(x) for all at least one k.
Definition 11. A point x∗∈G is said to be weak Pareto optimal solution for (4.1) if and only if there does not exist any x∈G such that, Ok(x∗)≥Ok(x),∀k=1,2,⋯,K.
In MOLPP (4.1), if all the parameters are intuitionistic fuzzy number then it is termed as intuitionistic fuzzy multiobjective linear programming problem (IFMOLPP). It is assumed that all the parameters present in problem (4.2) is trapeziodal intuitionistic fuzzy number. Thus the mathematical formulation of IFMOLPP can be stated as follows (4.2):
where ˜OIFk(x)=∑Kk=1(˜ckj)IFxj,∀k=1,2,⋯,K is the k-th objective function with trapeziodal intuitionistic fuzzy parameters.
With the aid of accuracy function (Theorem 1) which is linear, the IFMOLPP (4.2) can be converted into the following deterministic MOLPP (4.3):
where O′k(x)=ϕ(˜OIFk(x))=∑Kk=1ϕ((˜ckj)IF)xj,∀k=1,2,⋯,K; b′i=ϕ(˜bIFi) and a′ij=ϕ(˜aIFij), for all i=1,2,⋯,I,j=1,2,⋯,J are the crisp version of all the objective functions and parameters.
Theorem 2. An efficient solution for deterministic MOLPP (4.3) is also an efficient solution for IFMOLPP (4.2).
Proof: Assume that X=(x1,x2,⋯,xn) be an efficient solution of problem (4.3). Then X is feasible for problem (4.3), it means that the following condition will hold:
Since it has been proved that ϕ is linear (Theorem 1), then we have
Consequently, we have
Hence, X is a feasible solution for problem (4.2).
Moreover, since X is an efficient solution for problem (4.3), there does not exist any X∗=(x∗1,x∗2,⋯,x∗n) such that Ok(X∗)≤Ok(X)∀k=1,2,⋯,K and Ok(X∗)<Ok(X) for at least one k. Thus we have no X∗ such that Min∑Kk=1ϕ((˜ckj)IF)xj≤Min∑Kk=1ϕ((˜ckj)IF)x∗j∀k=1,2,⋯,K and Min∑Kk=1ϕ((˜ckj)IF)xj<Min∑Kk=1ϕ((˜ckj)IF)x∗j for at least one k.
Since ϕ is a linear function (Theorem 1), we have no X∗ such that Min∑Kk=1ϕ((˜ckj)IF)xj≤Min∑Kk=1ϕ((˜ckj)IF)x∗j∀k=1,2,⋯,K and Min∑Kk=1ϕ((˜ckj)IF)xj<Min∑Kk=1ϕ((˜ckj)IF)x∗j for at least one k.
Thus X is efficient solution for problem (4.2).
Consider a single-objective intuitionistic fuzzy linear programming problem (SOIFLPP) as given in problem (4.4):
Using the accuracy function which is linear in nature, SOIFLPP (4.4) can be converted into the following deterministic single-objective linear programming problem (SOLPP) (4.5):
Theorem 3. An optimal solution for the deterministic SOLPP (4.5) is also an optimal solution for SOIFLPP (4.4).
Proof. Same as Proof 2.
Hence the optimal solution for an IFLPP can be easilly transformed into deterministic LPP with the aid of accuracy function. Now, we will proceed towards the solution procedures of the MOLPP (4.3) under neutrosophic environment.
5.
Proposed neutrosophic fuzzy optimization technique
Many multiobjective optimization techniques are popular among researchers. Based on the fuzzy set, different fuzzy optimization method came into existence. In the fuzzy programming approach, the marginal evaluation of each objective function is depicted by only the membership functions and can be achieved by maximizing it. The extension of the fuzzy optimization method is presented by introducing intuitionistic fuzzy optimization techniques. It is comparatively more advanced than the fuzzy technique because the marginal evaluation of each objective function is depicted by the membership and non-membership functions, which can be achieved by maximizing the membership and minimizing the non-membership functions, respectively. The real-life complexity most often creates the indeterminacy situation while making optimal decisions. Apart from the acceptance and rejection degrees in the decision-making process, the indeterminacy degree also has much importance. Thus to cover the indeterminacy degree of the element into the feasible solution set, F. Smarandache [32] investigated a neutrosophic set. The name "neutrosophic" is the advance combination of two explicit terms, namely; "neutre" extracted from French means, neutral, and "sophia" adopted from Greek means, skill/wisdom, that unanimously provide the definition "knowledge of neutrality degree" (see [2,32]). The NS considers three sorts of membership functions, such as truth (degree of belongingness), indeterminacy (degree of belongingness up to some extent), and a falsity (degree of non-belongingness) degrees into the feasible solution set. The idea of independent indetermincy degree differs the NS with all the uncertain decision sets such as FS and IFS. The updated literature work solely highlights that many practitioners or researchers have taken the deep interest in the neutrosophic research field (see, [3,4,5,26]). The NS research domain would get exposure in the future and assist in dealing with indeterminacy in the decision-making process. This study also fetches the novel ideas of neutrosophic optimization techniques based on the NS. The marginal evaluation of each objective function is quantified by the truth, indeterminacy, and falsity membership functions under the neutrosophic decision set. Thus the NS plays a vital role while optimizing the multiobjective optimization problems by incorporating, executing, and implementing the indeterminacy degrees.
R. E. Bellman, et al. [12] first propounded the idea of a fuzzy decision set. After that, it is widely adopted by many researchers. The fuzzy decision concept comprises fuzzy decision (D), fuzzy goal (G), and fuzzy constraints (C), respectively. Here we recall the most extensively used fuzzy decision set with the aid of following mathematical expressions:
Consequently, we also depict the neutrosophic decision set DN, which contemplate over neutrosophic objectives and constraints as follows:
where
where μD(x),λD(x) and νD(x) are the truth, indeterminacy and a falsity membership functions of neutrosophic decision set DN respectively.
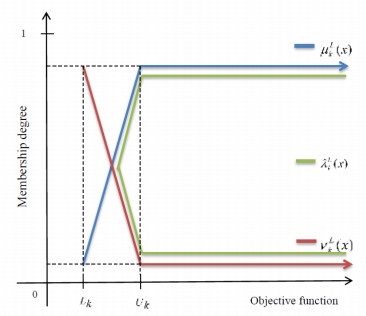
In order to depict the different membership functions for MOLPP (4.3), the minimum and maximum values of each objective functions have been represented by Lk and Uk and; can be obtained as follows:
The bounds for k-th objective function under the neutrosophic environment can be obtained as follows:
where sk and tk∈(0,1) are predetermined real numbers prescribed by decision-makers.
5.1. Various membership functions
In MOPPs, the marginal evaluation of each objective function is depicted by its respective membership functions. In general, the most extensive and widely used membership function is a linear one due to its simple structure and more accessible implications. The linear-type membership function contemplates over the constant marginal rate of satisfaction or dissatisfaction degrees towards an objective. Most commonly, the marginal evaluations have been evaluated by using linear membership function to obtain the objective. However, it may be possible to represent each objective's aspiration level with the aid of non-linear membership function. The flexible behavior of non-linear membership also functions well enough to determine the marginal evaluation of objectives satisfaction degree. It also depends on some parameters' value, which is well enough to efficiently execute the DM(s) strategy. An exponential membership reflects the situation when the decision-maker is worse off concerning an objective and chooses a higher marginal rate of satisfaction. Thus by preferring an exponential membership function, the decision-maker can also reduce duality gaps by selecting appropriate shape parameters involved in the development of membership function. A hyperbolic membership function shows the flexible characteristic behavior for the objective function. The hyperbolic membership function shows the convexity behavior over a portion of the objective and reveals concavity characteristic features for the remaining portion. A worse-off situation of the decision concerning a goal is depicted by the convex portion of the hyperbolic membership function, and the decision-maker intends to gain a higher marginal rate of satisfaction level. Despite this, a better-off condition of the decision concerning a goal is depicted by the concave portion of the hyperbolic membership function, and the decision-maker intends to gain a lower marginal rate of satisfaction level concerning that goal. Therefore, to deal with the IFMOLPPs, one can apply linear, exponential, or hyperbolic membership functions, depending upon the choice of decision-maker.
Thus the linear, exponential, and hyperbolic membership functions are constructed under the neutrosophic environment. Each of them is defined for the truth, indeterminacy, and a falsity membership function, which seems to be more realistic.
5.1.1. Linear-type membership functions approach (LTMFA)
The linear-type truth μLk(Ok(x)), indeterminacy λLk(Ok(x)) and a falsity νLk(Ok(x)) membership functions under neutrosophic environment can be furnished as follows:
In the above case, L(.)k≠U(.)k for all k objective function. If for any membership L(.)k=U(.)k, then the value of these membership will be equal to 1 (see Figure 2).
Using the concept of [12], we maximize the objective function to reach the optimal solution of each objectives. The mathematical expression for objective function is defined as follows:
Also, assume that μLk(Ok(x))≥α, λLk(Ok(x))≤β and νLk(Ok(x))≤γ, for all k.
Using auxiliary parameters α,β and γ, the problem (5.8) can be transformed into the following problem (5.9):
Remark 2. The ultimate aim of problem (5.9) (LTMFA) manifests the maximization of minimum possibility level (truth) to accept the best possible solution and; minimization of maximum possibility level (indeterminacy) and (a falsity) to reject the worst possible solution by considering all the objective functions at a time. It means that we try to determine a solution in such a way that it maximizes the minimum truth degree (acceptance) and minimize the maximum indeterminacy (rejection upto some extent) and a falsity (rejection) degrees by taking all objectives simultaneously, to attain the optimal compromise solution.
Theorem 4. A unique optimal solution of problem (5.9) (LTMFA) is also an efficient solution for the problem (4.3).
Proof: Suppose that (ˉx,ˉα,ˉβ,ˉγ) be a unique optimal solution of problem (5.9) (LTMFA). Then, (ˉα−ˉβ−ˉγ)>(α−β−γ) for any (x,α,β,γ) feasible to the problem (5.9) (LTMFA). On the contrary, assume that (ˉx,ˉα,ˉβ,ˉγ) is not an efficient solution of the problem (4.3). For that, there exists x∗(x∗≠ˉx) feasible to problem (4.3), such that Ok(x∗)≤Ok(ˉx) for all k=1,2,⋯,K and Ok(x∗)<Ok(ˉx) for at least one k.
Therefore, we have Ok(x∗)−LkUk−Lk≤Ok(ˉx)−LkUk−Lk for all k=1,2,⋯,K and Ok(x∗)−LkUk−Lk<Ok(ˉx)−LkUk−Lk for at least one k.
Hence, maxk(Ok(x∗)−LkUk−Lk)≤(<)maxk(Ok(ˉx)−LkUk−Lk).
Suppose that γ∗=maxk(Uk−Ok(x∗)Uk−Lk), then γ∗≤(<)ˉγ.
Also, consider that β∗=maxk(Uk−Ok(x∗)Uk−Lk), then β∗≤(<)ˉβ.
In the same manner, we have Uk−Ok(x∗)Uk−Lk≥Uk−Ok(ˉx)Uk−Lk for all k=1,2,⋯,K and Uk−Ok(x∗)Uk−Lk>Uk−Ok(ˉx)Uk−Lk for at least one k.
Thus, mink(Uk−Ok(x∗)Uk−Lk)≥(>)mink(Uk−Ok(ˉx)Uk−Lk).
Assume that α∗=mink(Uk−Ok(x∗)Uk−Lk), this gives (ˉα−ˉβ−ˉγ)<(α∗−β∗−γ∗) which means that the solution is not unique optimal. Thus, we have arrived at a contradiction with the fact that (ˉx,ˉα,ˉβ,ˉγ) is the unique optimal solution of (LTMFA). Therefore, it is also an efficient solution of the problem (5.9). This completes the proof of Theorem 4.
5.1.2. Exponential-type membership functions approach (ETMFA)
The exponential-type truth μEk(Ok(x)), indeterminacy λEk(Ok(x)) and a falsity νEk(Ok(x)) membership functions under neutrosophic environment can be stated as follows:
where d is the measures of vagueness degree (shape parameter) and assigned by the decision-makers.
Followed by problem (5.8), we assume that μEk(Ok(x))≥α, λEk(Ok(x))≤β and νEk(Ok(x))≤γ, for all k. Using auxiliary parameters α,β and γ, the problem (5.8) can be converted into the following problem (5.13):
Remark 3. If d→0, then the exponential-type membership functions will be reduced into linear-type membership functions.
Theorem 5. A unique optimal solution of problem (5.13) (ETMFA) is also an efficient solution for the problem (4.3).
Proof. This will be proved by arriving at a contradiction.
Suppose that (ˉx,ˉα,ˉβ,ˉγ) be a unique optimal solution of problem (5.13) (ETMFA) which is not an efficient solution for the problem (4.3). Then, there exists x∗(x∗≠ˉx) feasible to problem (4.3), such that Ok(x∗)≤Ok(ˉx) for all k=1,2,⋯,K and Ok(x∗)<Ok(ˉx) for at least one k.
Consequently, we have Ok(x∗)−LkUk−Lk≤Ok(ˉx)−LkUk−Lk for all k=1,2,⋯,K and Ok(x∗)−LkUk−Lk<Ok(ˉx)−LkUk−Lk for at least one k.
Hence, we have
e−d(Ok(x∗)−LkUk−Lk)−e−d1−e−d≥e−d(Ok(ˉx)−LkUk−Lk)−e−d1−e−d for all k=1,2,⋯,K and
e−d(Ok(x∗)−LkUk−Lk)−e−d1−e−d>e−d(Ok(ˉx)−LkUk−Lk)−e−d1−e−d for at least one k.
Thus, mink(e−d(Ok(x∗)−LkUk−Lk)−e−d1−e−d)≥(>)mink(e−d(Ok(ˉx)−LkUk−Lk)−e−d1−e−d).
If α∗=mink(e−d(Ok(x∗)−LkUk−Lk)−e−d1−e−d), then α∗≥(>)ˉα.
Similarly, we have Uk−Ok(x∗)Uk−Lk≥Uk−Ok(ˉx)Uk−Lk for all k=1,2,⋯,K and Uk−Ok(x∗)Uk−Lk>Uk−Ok(ˉx)Uk−Lk for at least one k.
Consequently, it gives
e−d(Uk−Ok(x∗)Uk−Lk)−e−d1−e−d≤e−d(Uk−Ok(ˉx)Uk−Lk)−e−d1−e−d for all k=1,2,⋯,K and
e−d(Uk−Ok(x∗)Uk−Lk)−e−d1−e−d<e−d(Uk−Ok(ˉx)Uk−Lk)−e−d1−e−d for at least one k.
Hence, maxk(e−d(Uk−Ok(x∗)Uk−Lk)−e−d1−e−d)≤(<)maxk(e−d(Uk−Ok(ˉx)Uk−Lk)−e−d1−e−d).
Assuming β∗=maxk(e−d(Uk−Ok(x∗)Uk−Lk)−e−d1−e−d), we have β∗≤(<)ˉβ.
Again, by considering γ∗=maxk(e−d(Uk−Ok(x∗)Uk−Lk)−e−d1−e−d), we get γ∗≤(<)ˉγ.
This gives (ˉα−ˉβ−ˉγ)<(α∗−β∗−γ∗), that contradicts the fact that (ˉx,ˉα,ˉβ,ˉγ) is the unique optimal solution of the problem (5.13) (ETMFA). Hence, the Theorem 5 is proved.
5.1.3. Hyperbolic-type membership functions approach (HTMFA)
The hyperbolic-type truth μHk(Ok(x)), indeterminacy λHk(Ok(x)) and a falsity νHk(Ok(x)) membership functions under neutrosophic environment can be depicted as follows:
where θk=6Uk−Lk,∀k=1,2,…,K.
Moving with the same procedure upto problem (5.8), we suppose that μHk(Ok(x))≥α, λHk(Ok(x))≤β and νHk(Ok(x))≤γ, for all k. Using auxiliary parameters α,β and γ, the problem (5.8) can be transformed into the following problem (5.17):
Equivalently, we have problem (5.18) as follows:
Theorem 6. A unique optimal solution of problem (5.18) (HTMFA) is also an efficient solution for the problem (4.3).
Proof. Let us consider that (ˉx,ˉα,ˉβ,ˉγ) be a unique optimal solution of problem (5.18) (HTMFA), but not an efficient solution for the problem (4.3). This gives, there exists x∗(x∗≠ˉx) feasible to problem (4.3), such that Ok(x∗)≤Ok(ˉx) for all k=1,2,⋯,K and Ok(x∗)<Ok(ˉx) for at least one k.
Simultaneously, tanh(θk(Uk+Lk2−Ok(x∗)))≥tanh(θk(Uk+Lk2−Ok(ˉx))) for all k=1,2,⋯,K and tanh(θk(Uk+Lk2−Ok(x∗)))>tanh(θk(Uk+Lk2−Ok(ˉx))) for at least one k.
Furthermore, it gives,
mink(tanh(θk(Uk+Lk2−Ok(x∗))))≥(>)mink(tanh(θk(Uk+Lk2−Ok(ˉx)))).
If α∗=mink(12tanh(θk(Uk+Lk2−Ok(x∗)))+12), then α∗≥(>)ˉα.
Similarly, we have β∗=maxk(12tanh(θk(Ok(x∗)−Uk+Lk2))+12), then β∗≤(<)ˉβ
and γ∗=mink(12tanh(θk(Ok(x∗)−Uk+Lk2))+12), then γ∗≥(>)ˉγ.
Thus, we get (ˉα−ˉβ−ˉγ)<(α∗−β∗−γ∗). This arises a contradiction with the fact that (ˉα−ˉβ−ˉγ) is the unique optimal solution of the problem (5.18) (HTMFA). Hence, the Theorem 6 is proved.
5.2. Proposed solution algorithm
The step-wise solution algorithm is summarized as follows:
Step-1. Formulate the IFMOLPP as given in problem (4.2).
Step-2. Using accuracy function, obtain the crisp version of IFMOLPP as given in problem (4.3).
Step-3. Solve each objective function individually and determine the upper and lower bound by using Eq (5.1).
Step-4. With the aid of Uk and Lk, calculate the upper and lower bound for truth, indeterminacy and a falsity membership under neutrosophic envirnment as given in Eqs (5.2)–(5.4).
Step-5. Elicit the different-types of membership functions under neutrosophic environment by using Eqs (5.5–5.7), (5.10–5.12) and (5.14–5.16) according to decision-makers' preference respectively.
Step-6. Develop the neutrosophic optimization models such as (LTMFA) or (ETMFA) or (HTMFA) under the given set of well-defined constraints.
Step-7. Solve the neutrosophic MOPPs (5.9), (5.13) and (5.18) to determine the optimal compromise outcomes by applying the appropriate methods or different optimization software packages.
6.
Numerical illustrations
Following numerical examples are solved using different methods by many researchers. All the crisp MOLPPs are coded in AMPL language and solved with help of solver Kintro 10.3.0 via NEOS server version 5.0 on-line facility executed by Wisconsin Institutes for Discovery at the University of Wisconsin in Madison for solving optimization problems, see [15,27].
Example 1. [30] This numerical example assumes that the trapezoidal intuitionistic fuzzy number represents all the parameters. Thus the mathematical formulation of the problem can be stated as follows:
The intuitionistic fuzzy parameters related to Example 1 are furnished in Table 1. Using the accuracy function (Definition 5), the crisp version of the Problem (6.1) can be depicted as follows:
● Using the LTMFA (5.9), Problem (6.2) will be equivalent to the following (6.3):
● Using the ETMFA (5.13), Problem (6.2) will be equivalent to the following (6.4):
● Using the HTMFA (5.18), Problem (6.2) will be equivalent to the following (6.5):
On solving the neutrosophic optimization model (6.3), (6.4) and (6.5), the solution results are summarized in Table 2. It is clear that the objective values are quite better than [30] method for all the membership functions. Also, the proposed neutrosophic's performance measures of various membership functions can be depicted as Hyperbolic>Exponential>Linear. Since [30] did not use the Exponential membership functions; therefore, it is unjustifiable to perform comparisons among the membership function. However, our proposed method's maximum attaintment of acceptance degree is better achieved and reveals its superiority over [30] method.
Example 2. [22] Consider the following numerical illustration.
The intuitionistic fuzzy parameters related to Example 2 are summarized in Table 3. On solving each objective individually (Example 2), we get the upper and lower bounds U1=8631.25,U2=3163.75,L1=7981.25 and L2=2923.75 for the first and second objective functions respectively. On implementing the neutrosophic MOPPs (5.9), (5.13) and (5.18), the solution results are summarized in Table 4. For this example, the objective values are quite better than [22] method for all the membership functions. The performance measures of the proposed neutrosophic of various membership functions can be depicted as Hyperbolic>Exponential>Linear. Thus, the proposed neutrosophic optimization technique outperforms [22] method for all the membership functions. However, the maximum attaintment of acceptance degree is better achieved by our proposed technique that shows the most promising method over [22] method.
Example 3. [22] Let us consider the following numerical example.
The intuitionistic fuzzy parameters related to Example 3 are summarized in Table 5. On solving each objective individually (Example 3), we get the upper and lower bounds U1=428.25,U2=531.75,L1=378.00 and L2=484.12 for the first and second objective functions respectively. By applying the neutrosophic MOPPs (5.9), (5.13) and (5.18), the solution results are summarized in Table 6. On solving the final neutrosophic optimization model, the obtained objective values are more promising than [22] method for all the membership functions. The working efficiency of the proposed neutrosophic method under various membership functions can be depicted as Hyperbolic >Exponential>Linear. Thus, the proposed neutrosophic technique is the most prominent method compared to [22] method under all the membership functions. Moreover, the maximum attaintment of acceptance degree is better achieved by our proposed technique that can be a preferable method over [22] method.
7.
Conclusions
In this paper, an effective modeling and optimization framework for the IFMOLPP is presented under neutrosophic fuzzy uncertainty. The proposed optimization technique has been designed under the neutrosophic environment, consisting of independent indeterminacy degree in decision-making processes. The satisfactory degree of decision-maker is always maximized in different forms to achieve the best possible compromise solution of each objective function. We have also developed a variety of membership functions to determine the best possible optimal solution. The use of linear, exponential, and hyperbolic membership functions more flexible and realistic in decision-making processes due to the indeterminacy degree while obtaining the optimal compromise solution. The proposed models are implemented on three different existing numerical examples, and a comparative study is done. The solution results obtained by our proposed neutrosophic optimization technique outperforms as compared to others for all the discussed numerical examples. An ample opportunity to select the different solution results is also depicted by incorporating various sorts of membership functions under the neutrosophic environment. In the case of exponential-type membership function, a set of different optimal solution results can be generated by tuning the shape parameters.
Several advantages can be availed by applying the proposed approach efficiently in both numerical problems as well as real-life applications.
● The proposed neutrosophic optimization techniques deal with the indeterminacy degree, which is the area of ignorance of propositions' values between the acceptance and rejection degrees.
● The proposed multiobjective modeling approach deals with the intuitionistic fuzzy parameters, which involves membership as well as non-membership functions and are more realistic as compared to fuzzy parameters.
● Different sorts of membership functions under the neutrosophic environment provide an opportunity to select the desired membership functions according to decision-makers' choices.
● The shape parameter (d) in exponential-type membership functions depicts the degree of uncertainty at a different level and provides more flexibility in decision-making processes.
● An ample scope for generating a variety of compromise solution sets by tuning the parameters in indeterminacy degrees is also a benchmarking advantage of the proposed approach.
● It can be easily implemented on different real-life problems such as transportation, supplier selection, supply chain, manufacturing, inventory control, assignment problems, etc.
The propounded study has some limitations that can be addressed in future research. Various metaheuristic approaches may be applied to solve the proposed neutrosophic model as a future research scope. The discussed models can be applied to various real-life applications such as transportation problems, supplier selection problems, inventory control, portfolio optimization, etc.
Acknowledgments
All authors are very thankful to the Editor-in-Chief, anonymous Guest Editor, and potential reviewers for providing in-depth comments and suggestions that improved the readability and clarity of the manuscript. The first author is very thankful to Jazan University for providing the online access of various paid journals.
Conflict of interest
All authors declare no conflict of interest.









 DownLoad:
DownLoad: