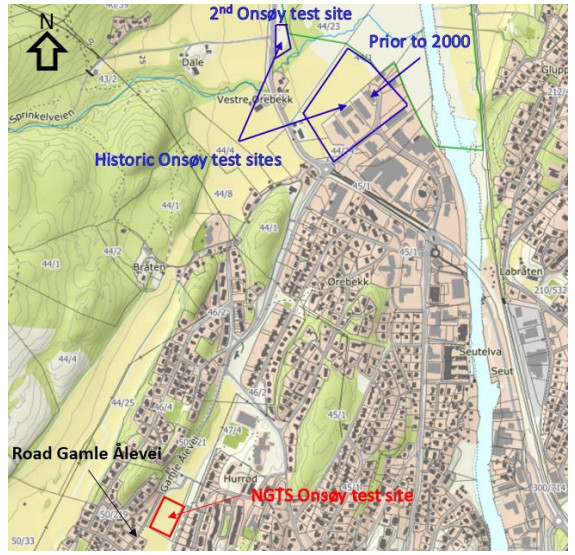
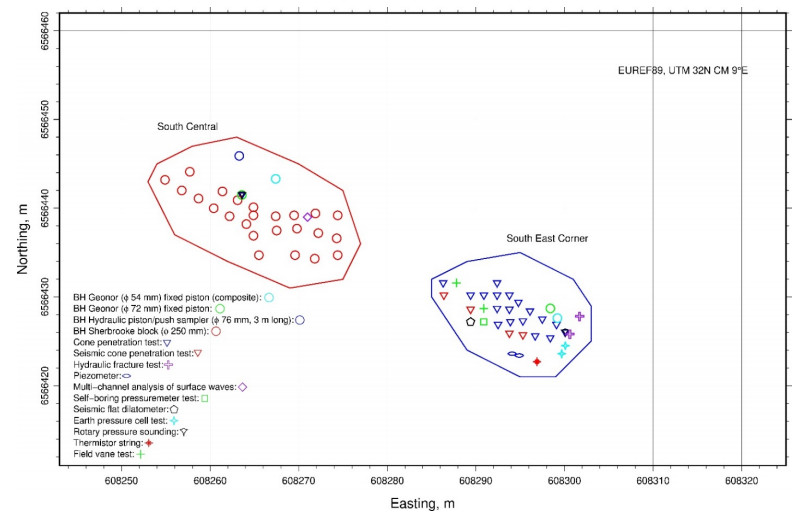
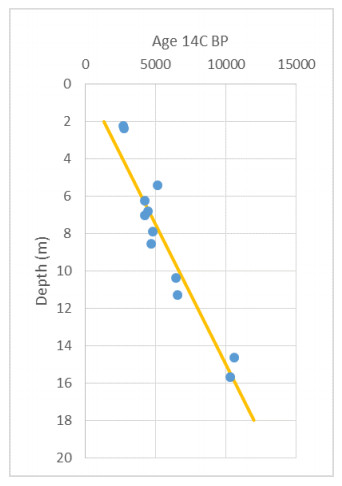
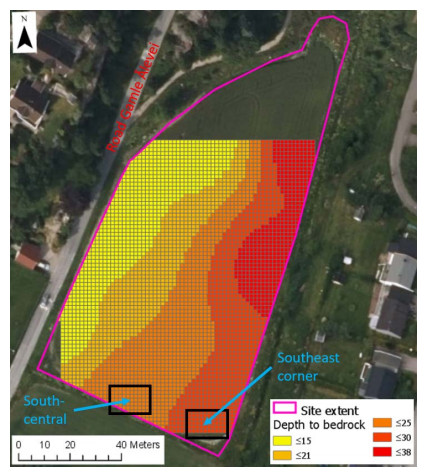
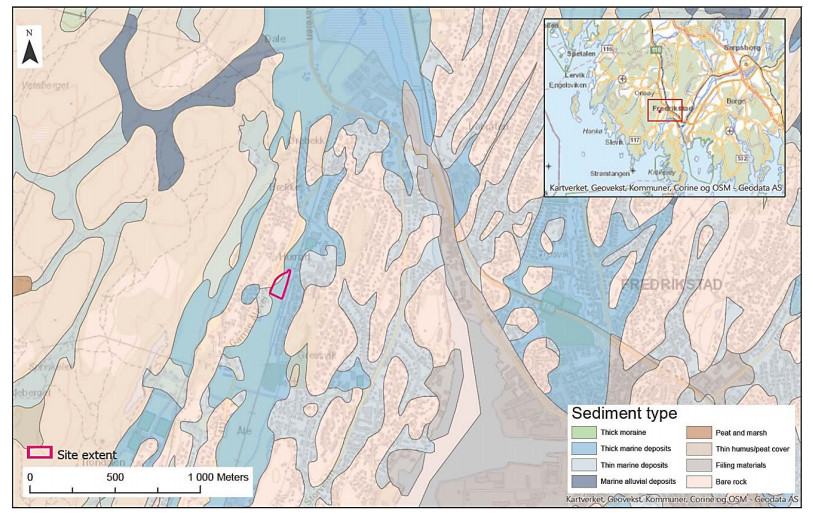
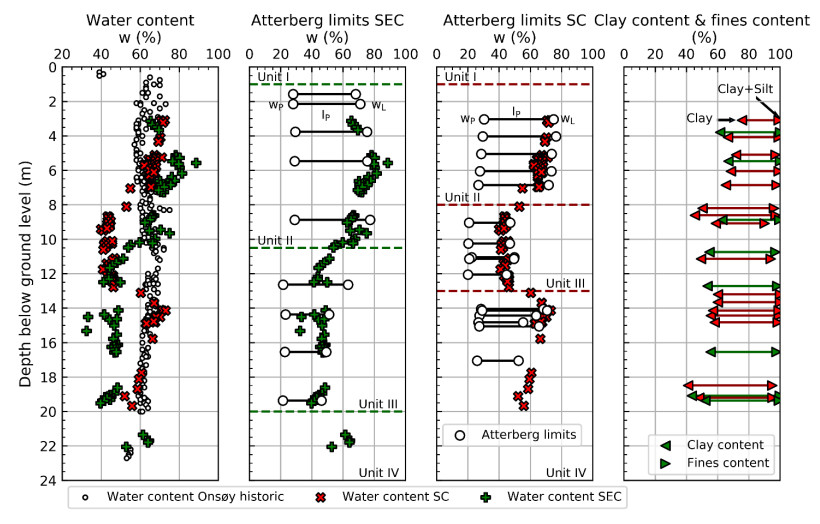
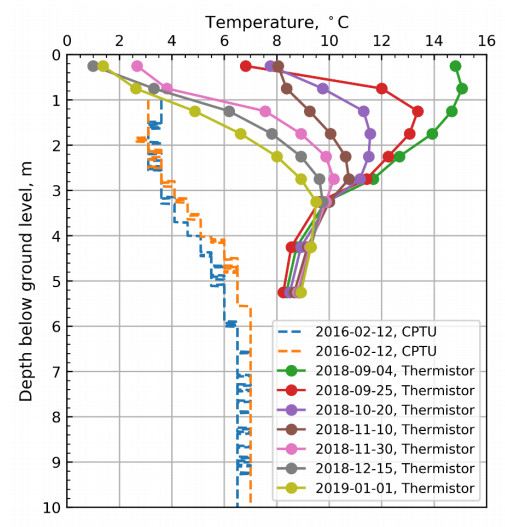
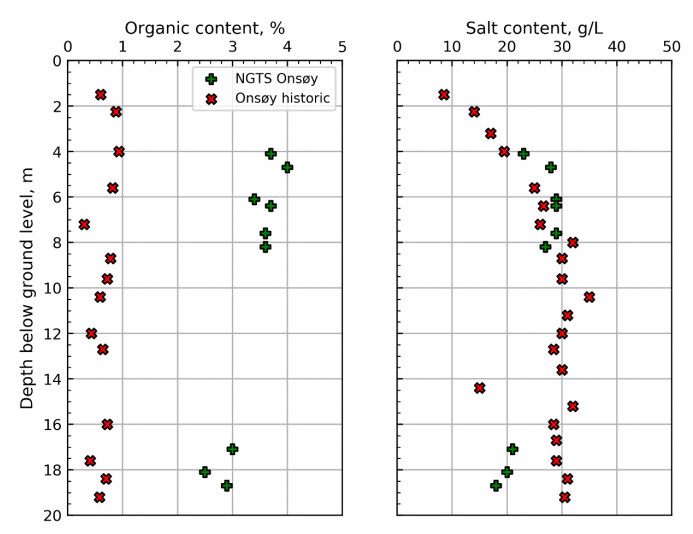
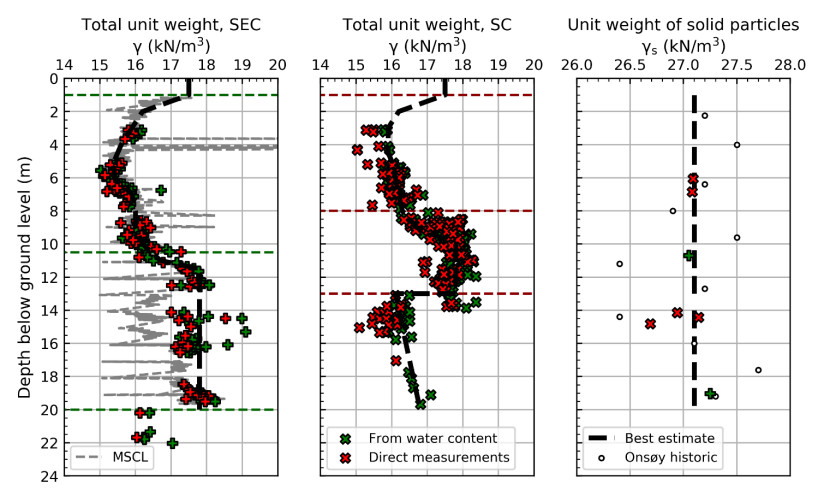
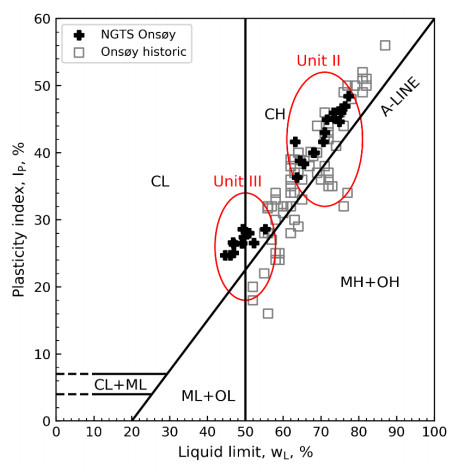
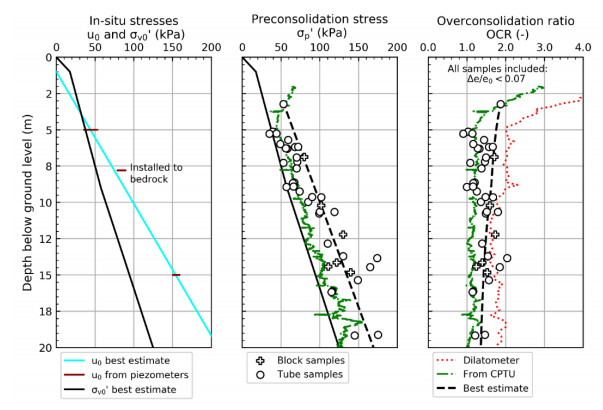
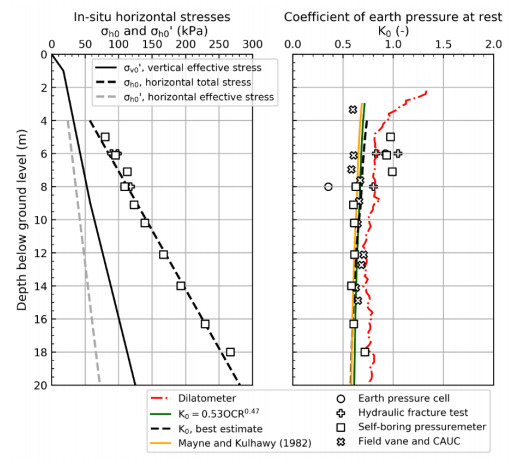
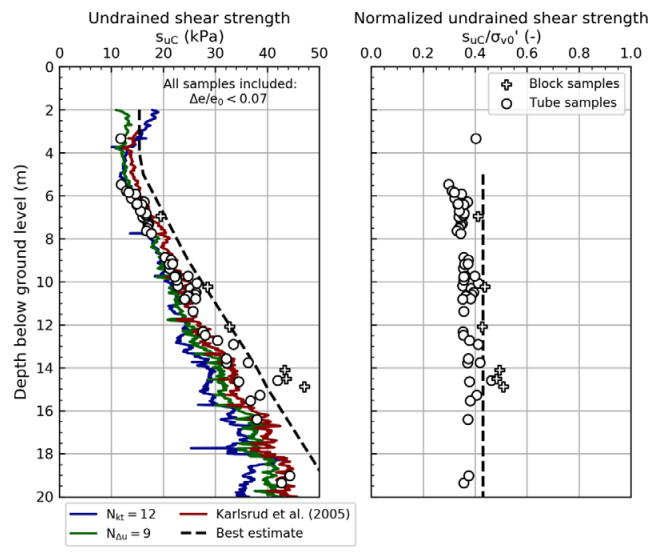
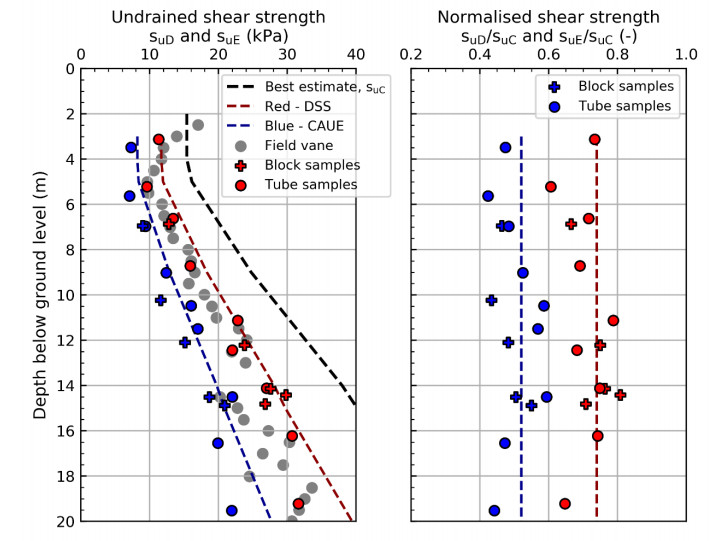
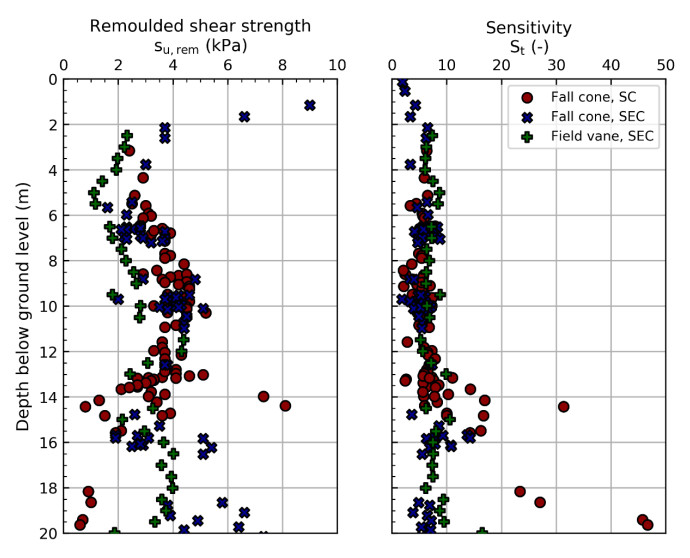
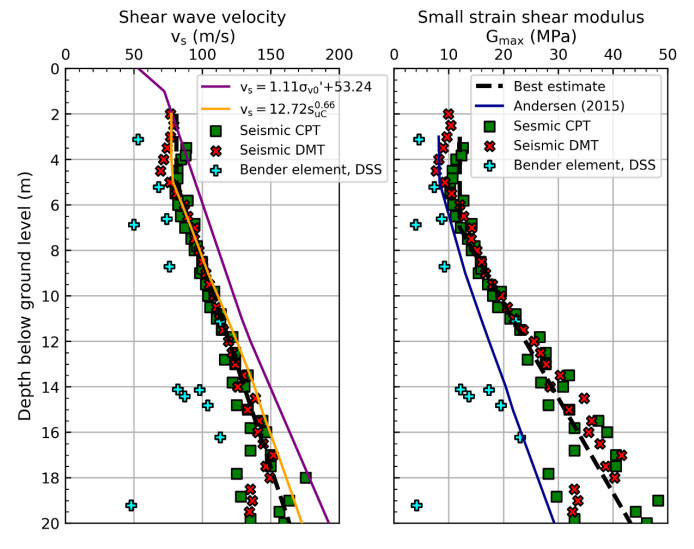
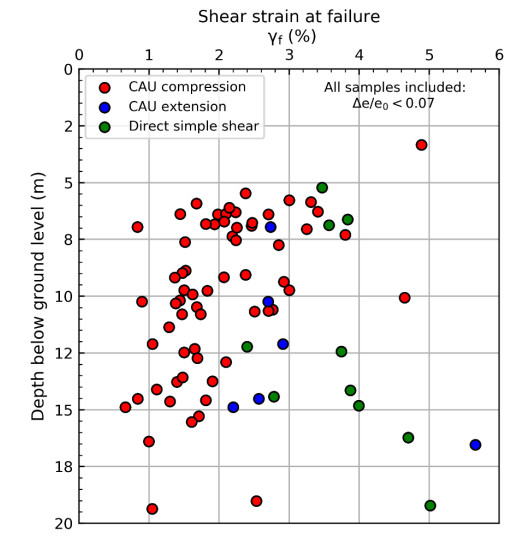
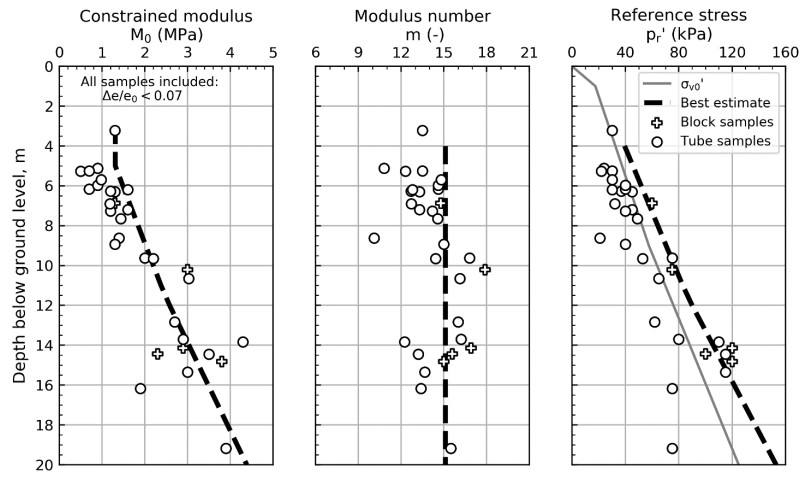
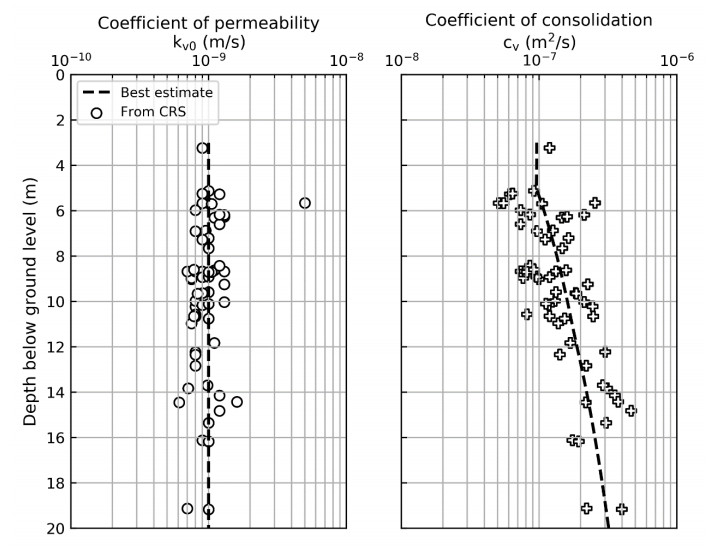
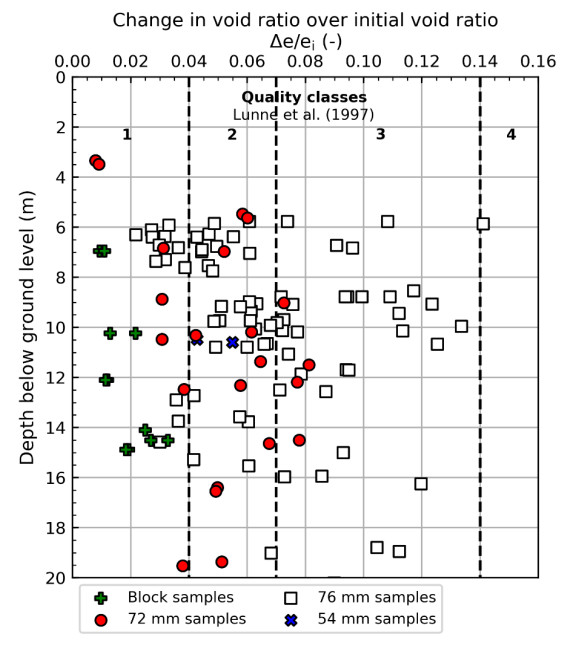
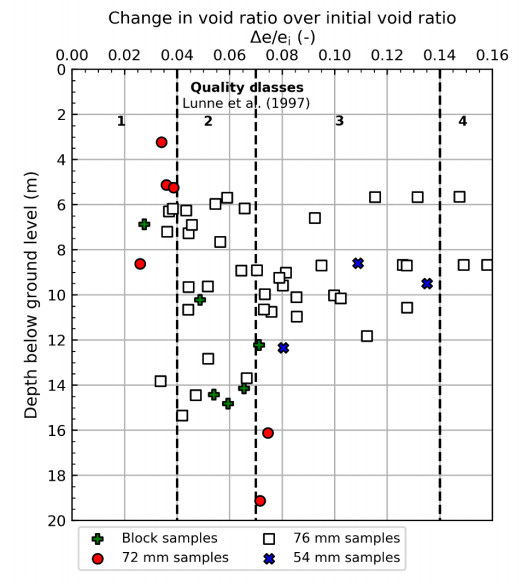
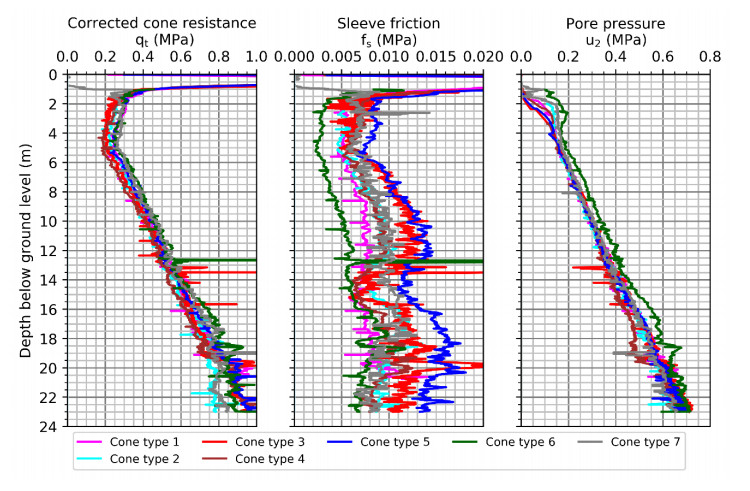
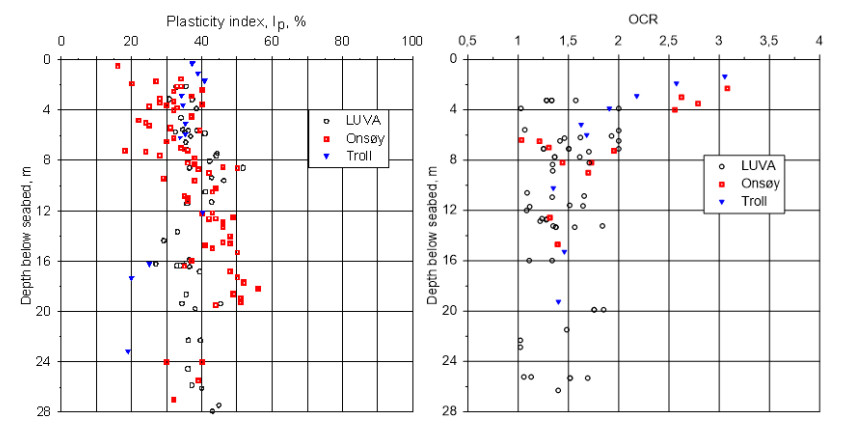
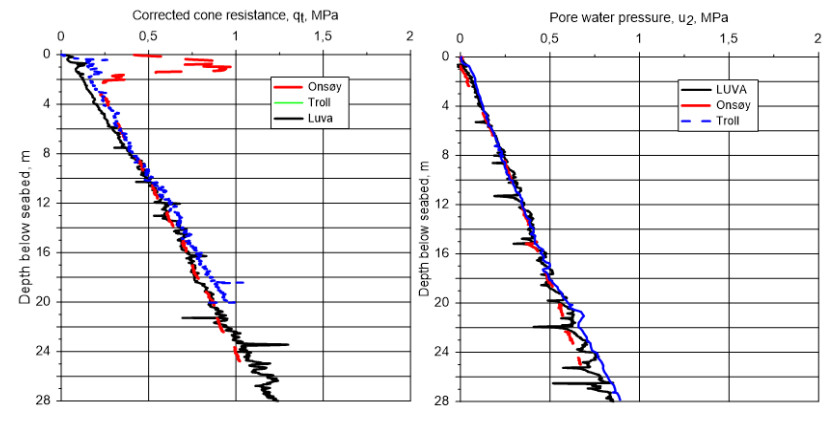
In the 1960s, NGI investigated numerous potential research sites and established the first Onsøy soft clay site in 1968. In 2016, the NGTS project established five research sites, one of which is the NGTS Onsøy soft clay site. The purpose of this paper is to provide a reference for further in-situ and laboratory testing at the site and easy access to high-quality soil investigation data. The paper interprets the soil conditions providing engineering soil properties, comments on data reliability and quality, and correlations between different soil parameters where appropriate. The lightly overconsolidated soft clay site has been characterized based on extensive in-situ and laboratory testing. In-situ methods include electrical resistivity tomography, multichannel analysis of surface waves, total soundings, rotary pressure soundings, cone penetration testing with and without seismic and electrical resistivity measurements, dilatometer with seismic measurements, self-boring pressuremeter, electric piezometers, thermistor string, hydraulic fracture testing and earth pressure cells. Soil samples were obtained using Sherbrook block sampler, Geonor ϕ 72 mm piston sampler, Geonor ϕ 54 mm composite piston sampler and hydraulic piston and push samplers with liners. Laboratory tests include multi-sensor core logging, index testing, cyclic and monotonic, consolidated and unconsolidated triaxial tests, bender element tests, oedometer tests with constant rate of strain and incremental loading and direct simple shear tests.
1.
Introduction
Animal gaits are a rhythmic behavior controlled by central pattern generator (CPG), which generates rhythmic signals to the muscle groups of animals, controls their own rhythmic movements, and produces various gaits in animal locomotion. From a biological perspective, CPG is a distributed vibration network composed of neurons in the central nervous system of animals. Human beings get inspiration from the organizational structure, movement mechanism, and behavior of biological bodies, and constantly learn and imitate the characteristics and functions of certain organisms, thereby improving their adaptability to nature and making contributions to the development of science and technology. Therefore, biologists and mathematicians have established some CPG biological and mathematical models by imitating the neural network patterns of animal CPG. Golubitsky et al. [1] has investigated a composition pattern of CPG neurons in quadrupedal gaits and obtained a new primary gait ''jump''. The animal gait network proposed by Buono et al. [2] can generate six primary gaits: walk, trot, pace, bound, pronk, and jump. Furthermore, based on the primary gait, the phase patterns of transverse gallop and rotary gallop in quadruped secondary gait were provided [3]. The present authors have studied CPG neural network models for the primary gait of quadrupeds [4,5].
Animal gait CPG neural networks have wide applications. Inspired by animal movements, in the gait planning of biomimetic robots, a CPG model is set for the robot system by imitating the CPG network of animals in nature. By utilizing the coupling between oscillators in the CPG model, periodic oscillation signals are generated to achieve stable rhythmic gait behavior of the robot. For instance, the CPG network can be used to construct gait networks for hexapod robots gait networks [6,7] and quadruped robots gait networks [8,9,10]. In article [11], a method for designing a robot system controller was proposed using a CPG control network, and in article [12], the robot gait was produced based on animal gait. In [13], a CPG animation model was constructed using the CPG network system.
In quadruped mammals, goats have smaller bodies and stronger bones in their limbs, and their hindlimbs are stronger than their forelimbs specifically. Goats have a brisk and agile gait when walking, and they can walk freely, flexibly, and quickly on the ground, slopes, steep walls and uneven surfaces. Moreover, they can also walk long distances and have good road adaptability and obstacle crossing ability. Goats are less restricted by the environment and, therefore, goat gaits have certain research value. In literature [14], the author used goats as the research object and conducted kinematic analysis on the multimode gait of goats on conventional and unconventional roads. In work [15], the author analyzed the gait of goats from the perspective of structural bionics. At present, there is little research on mathematical models of goat gaits to our knowledge. In this paper, we deal with this problem and propose the CPG neural network models of goat gaits from a mathematical perspective. We study the following model given in [5]
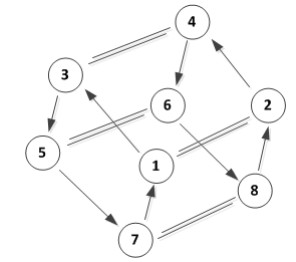
where a,b,c,d are constants and τ≥0 is the time delay. The state variable (x1(t),x2(t),⋯,x8(t)) is the output signal from the CPG to the legs, where x1(t) and x7(t) are the output signals to the left hind leg, x3(t) and x5(t) are the output signals to the left fore leg, x2(t) and x8(t) are the output signals to the right hind leg, and x4(t) and x6(t) are the output signals to the right fore leg. The network diagram of system (1.1) is shown in Figure 1.
In reference [5], the authors give the conditions (H1):|c|>|a+b+d|if(a+b)d>0, (H2):|c|>|a+b−d|if(a+b)d<0, and critical values τkj(j=1,2,3,4,5,6,7,8) (see Table 1 in [5]) for the Hopf bifurcations of the model (1.1) at the zero equilibrium.
The main objective of this paper is to provide further the bifurcation direction and stability conditions of the bifurcating periodic solutions of the model (1.1). Based on the model (1.1), the CPG neural network models of goat gaits are given by using the parameter inversion algorithm.
2.
Normal form for Hopf bifurcation
In this section, we use the method in reference [16] to calculate the normal forms of Hopf bifurcations on the center manifold of the Eq (1.1) at the zero equilibrium. Normalizing the delay τ by the time-scaling t↦tτ, Eq (1.1) can be rewritten as a functional differential equation in C=C([−1,0],R8),
Denoting U=(u1,u2,u3,u4,u5,u6,u7,u8)T, Ut=U(t+θ),Ut∈C, where θ∈[−1,0]. Let τ=τ02j+μ(j=1,2,3,4), for μ is a bifurcation parameter, then Eq (2.1) can further be written as the following form:
where
and
where φ=(φ1,φ2,φ3,φ4,φ5,φ6,φ7,φ8)T∈C. By the Riesz representation theorem, there is η(θ,μ), such that L(μ)φ=∫0−1dη(θ,μ)φ(θ), and we select η(θ,μ)=(τ02j+μ)(Aδ(θ)+Bδ(θ+1)), where
The Taylor expansion of F(Ut,μ) is denoted as
with
Expanding space C to BC={φ:[−1,0]→C8|φ is continuous on [-1, 0) and limθ→0−φ(θ)∈C8}. The element of BC can be expressed as υ=φ+X0ν,φ∈C,ν∈C8, and
with I as the identity matrix.
For ϕ∈C1=C1([−1,0],C8), we define
For ψ∈C1∗=C1([−1,0],C8∗), the adjoint operator of A0 is
and a bilinear inner product is the following:
Let Φ(θ) and Ψ(s) be the eigenvectors corresponding to the eigenvalues iωjτ02j and −iωjτ02j, respectively. Note that Φ(θ)=(ϕ(θ),ˉϕ(θ)), Ψ(s)=(ˉψ(s),ψ(s))T with ˙Φ=Φ(θ)J,˙Ψ(s)=−JΨ(s),<Ψ(s),Φ(θ)>=I, and J=diag(iωjτ02j,−iωjτ02j). It can be easily calculated from (2.3) and (2.4) that
Hence, we obtain D=18(−1+ceiωjτ02j) from <ϕ(s),ϕ(θ)>=1.
Let P be a vector space expanded by ϕ(θ) and ˉϕ(θ), P∗ be a vector space expanded by ϕ(s) and ˉϕ(s), then C can be decomposed as C=P⊕Q, where Q={ϕ∈C:<ψ,ϕ>=0,∀ψ∈P∗}. Define mapping Π:BC→P as Π(φ+X0ν)=Φ[(ψ,ϕ)+ψ(0)ν] and Q1=kerπ⋂C1.
Using the decomposition of U=Φx+y with x=(x1,x2)T,y=(y1,y2,y3,y4,y5,y6,y7,y8)T, system (2.1) can be decomposed as
We have the Taylor expansion as follows:
where
Normal form of Eq (2.7) on the center manifold at the origin is given by
where
After calculating, we obtain
where a1=8D(−a−b−d+ceiωjτ02j).
In the following, we can compute the cubic terms 13!g13(x,0,μ) as
with
Since f12(x,0,0)=(0,0)T,f12(x,y,0)=(0,0)T, we obtain U12(x,0)=(0,0)T,(Dyf12)(x,0,0)=(0,0)T,
thus
where a2=−8τ02jD(−b+ceiωiτ02j−d).
Then, the normal form (2.8) can be written as
By transforming the variables x1=w1+iw2, x2=w1−iw2 and w1=rcosξ, w2=rsinξ, Eq (2.9) can be written as
where k1=Re(a1),k2=Re(a2).
According to [16], we obtain the following results.
Theorem 2.1 When k2≠0, then
1) If k2<0, then the bifurcation periodic solutions of system (1.1) near τ02j(j=1,2,3,4) are stable; if k2>0, then the bifurcation periodic solutions of system (1.1) are unstable.
2) If k1k2<0, then Hopf bifurcations are supercritical; if k1k2>0, then Hopf bifurcations are subcritical.
3.
Numerical simulations
In this section, we will provide two numerical examples to validate our theoretical analysis.
Example 1. We consider system (1.1) with a=−4.5,b=1,c=6.5,d=−2, which satisfies the conditions (H1). Using the algorithm in [5], we obtain ω2=7.4772,ω3=6.325,τ04=0.2861,τ06=0.2852. From ω2=7.4772,τ04=0.2861, we get k1=Re(a1)=0.4179>0, k2=Re(a2)=−0.2349<0,k1k2=−0.0982<0. According to Theorem 2.1, the bifurcation periodic solution of system (1.1) is stable and supercritical at τ=0.4>τ04=0.2861, as shown in Figure 2. This periodic solution corresponds to the walking gait of quadrupeds.
From ω3=6.325,τ06=0.2852, we know that k1=Re(a1)=0.6486,k2=Re(a2)=−0.2544<0,k1k2=−0.1650<0. According to Theorem 2.1, the bifurcation periodic solution of system (1.1) is stable and supercritical at τ=0.4>τ06=0.2852 (see Figure 3), and this periodic solution corresponds to the trotting gait of quadrupeds.
Example 2. In system (1.1), we select parameters a=−3,b=0.1,c=4,d=1, which satisfies (H2). By calculation, it is obtained that w1=3.5119,τ02=0.5869,k1=Re(a1)=0.5957>0, k2=Re(a2)=−0.5951<0,k1k2=−0.3545<0. From Theorem 2.1, the bifurcation periodic solution of system (1.1) is stable and supercritical at τ=0.7>τ02=0.5869, as shown in Figure 4. This periodic solution corresponds to the pacing gait of quadrupeds.
4.
Goat gait model
In this section. we employ model (1.1) as the inversion model, and use the trust region algorithm [17] to give the goat's diagonal trotting model on flat ground and the walking gait model on the ground with a slope of 18 degrees.
4.1. Gait model for goat diagonal trotting on flat ground
By analyzing the spatiotemporal characteristic diagram of the goat's diagonal trot gait (Figure 3.2(b) in [14]), we obtain that the two legs on the diagonal of the goat are mostly in a supported or airborne state when trotting diagonally on flat ground, and the four legs airborne and single legs support the states only account for a small part of the whole gait cycle and can be ignored. So, we assume that the support state and airborne state of the two legs on the diagonal each account for half of the whole cycle. In the diagonal trotting joint angle change curve of goats (Figures 3 and 4 in [14]), an average of 20 points are extracted from the pastern joint angles and wrist joint angles curves of the two front legs, as well as the toe joint angle and tarsal joint angle curves of the two hind legs, respectively (within one cycle). Next, we translate these points to the vicinity of the origin and convert them into radians as the true values ˆxi(tl)(i=1,2,⋯,8;l=1,2,⋯,20) of CPG oscillators of the corresponding legs of goats. Finally, we averagely select 20 values of periodic solutions x1(t) to x8(t) within one cycle of model (1.1)(a=−2,b=1,d=−2,τ=0.25) as the theoretical values xi(tl,c)(i=1,2,⋯,8;l=1,2,⋯,20) of CPG oscillators, respectively. Using the trust region algorithm [17], the parameter c=6.4300 is obtained, as shown in Table 1. The error in Table 1 is f=128∑i=120∑l=1(ˆxi(tl)−xi(tl,c))2.
Next, in order to better describe the effect of the simulation, we calculated the synchronization error between the theoretical value and the real value. That is, we calculated the point-by-point difference between the 20 pairs of theoretical values and true values of the corresponding joint angles of each leg, as shown in Figures 5 and 6.
As can be seen from Figures 5 and 6, the synchronization error ranges of the pastern joint angle and wrist joint angle of the front leg are [-0.5, 0.6] and [-0.85, 0.08], and the synchronization error ranges of the toe joint angle and the tarsal joint angle of the back leg are [-0.4, 0.95] and [-0.6, 0.95].
For parameters a=−2,b=1,c=6.4300,d=−2,τ=0.25, the critical value τ06=0.2227 of trotting gait and k1=Re(a1)=1>0,k2=Re(a2)=−0.2227<0,k1k2=−0.2227<0 are calculated. According to Theorem 2.1, the bifurcation periodic solution of system (1.1) is stable and supercritical at τ=0.25>τ06=0.2227 (see Figure 7).
Therefore, the model (1.1) (a=−2,b=1,c=6.4300,d=−2,τ=0.25) provides a reference model for the goat's diagonal trot gait on flat ground.
4.2. Gait model of goats walking on an 18 degree slope
According to the analysis of the spatiotemporal state diagram of each leg of a goat walking on an 18 degree slope (Figures 3–8 in [15]), it is found that during one gait cycle, each leg of the goat takes turns to be suspended while the other three legs are in a supported state, and they took almost the same amount of time. Assuming that within a gait cycle, each leg of the goat is in a suspended state while the other three legs are in a supported state for the same amount of time.
Similar to Section 4.1, we take 20 data from the joint angle curve of each leg in the Figures 3–9 [15] (the curve of the wrist joint angle α of each leg and the curve of the angle β between the thighs of each leg and the forward direction) as the true values ˆxi(tl)(i=1,2,⋯,8;l=1,2,⋯,20) of CPG oscillators, then we select 20 values (within one cycle) from the periodic solutions x1(t) to x8(t) of the model (1.1)(a=−2,b=1,c=6.5,d=−2) as the theoretical values xi(tl,τ)(i=1,2,⋯,8;l=1,2,⋯,20) of CPG oscillators, and the parameter τ=0.2450 is obtained by the trust region algorithm, as shown in Table 2. The precision ε in Table 2 is the degree of accuracy that the gradient of the objective function f=128∑i=120∑l=1(ˆxi(tl)−xi(tl,τ))2 needs to achieve when the objective function f reaches its optimal solution in the trust region algorithm. Similar to Section 4.1, synchronization error diagrams between theoretical values and true values are shown in Figures 8 and 9.
From the two figures, we see that the synchronization error ranges of the wrist angle of left hind leg, right hind leg, left front leg, and right front leg are [-1.2, 1.2], [-0.9, 0.95], [-1.2, 0.9], and [-0.9, 1.45]. The synchronization error ranges of the angle between the forward direction of thigh movement and the left hind leg, right hind leg, left front leg, and right front leg are, respectively, [-0.95, 0.9], [-1.45, 0.6], [-1.3, 1.5], and [-1.6, -0.6].
For parameters a=−2,b=1,c=6.5,d=−2, the critical values τ04=0.2048 of the walking gait and k1=Re(a1)=0.8232>0,k2=Re(a2)=−0.1867<0,k1k2=−0.1537<0 are calculated. According to Theorem 2.1, the bifurcation periodic solution of system (1.1) is stable and supercritical at τ=0.2450>τ04=0.2048, as shown in Figure 10.
Figure 10 indicates that the periodic solution obtained by the system (1.1) corresponds to a stable walking gait when the parameters a=−2,b=1,c=6.5,d=−2,τ=0.2450. Therefore, model (1.1)(a=−2,b=1,c=6.5,d=−2) provides a reference model for the CPG walking gait model of goats walking uphill on an 18 degree slope when the time delay parameter τ=0.2450.
5.
Conclusions
We employed the normal form theory according to Faria and Magalh˜aes to derive the normal form for Hopf bifurcation of a quadruped gait CPG model on the center manifold, and the bifurcation direction and stability of bifurcating periodic solution at the origin are analyzed. The quadruped gait CPG model was used as an inversion model, and goat gait models were constructed using the trust region inversion algorithm. The feasibility of using the CPG model as a goat gait model was verified through simulations.
The neural network model presented in this article can predict the goat gait to contribute to artificial intelligence. The weakness of this paper is that the synchronization errors of some points are slightly larger when using our mathematical model to simulate goat gait, especially walking gait. We will modify this model further in the future.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This research is supported by the Fundamental Research Funds for the Central Universities, (No.2572022DJ08).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: