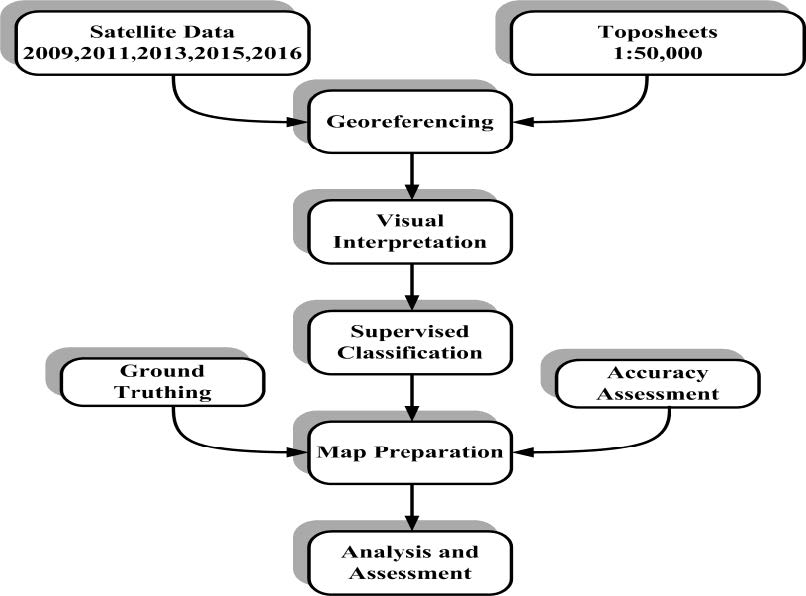
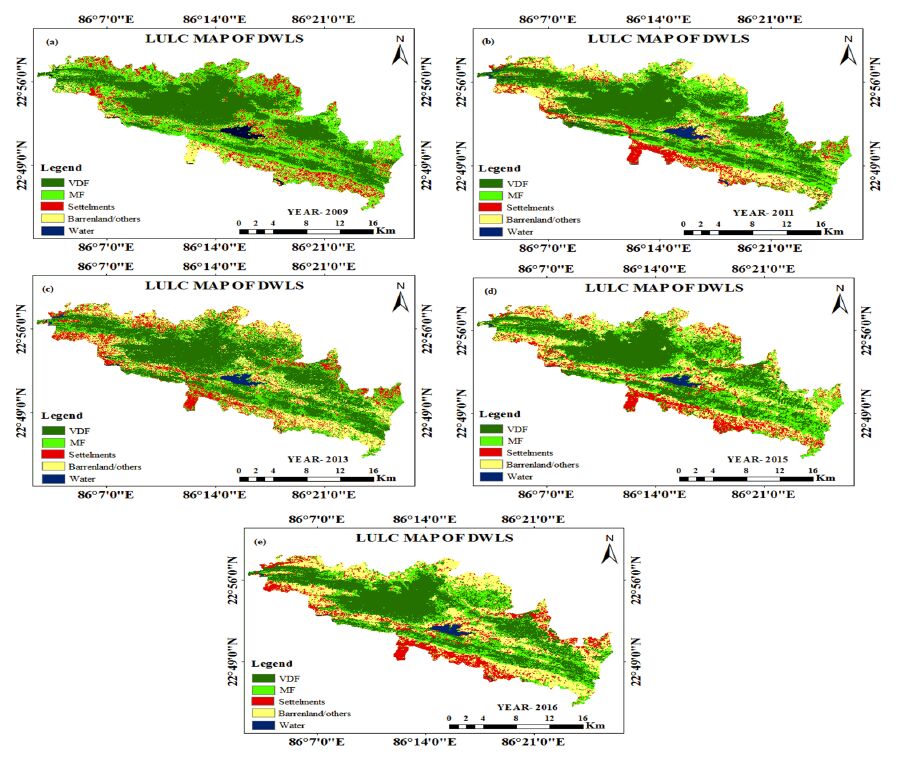
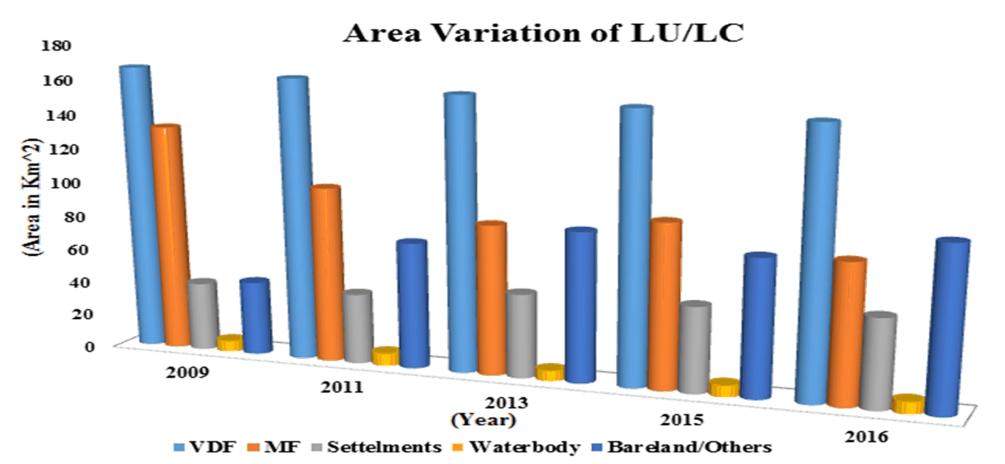
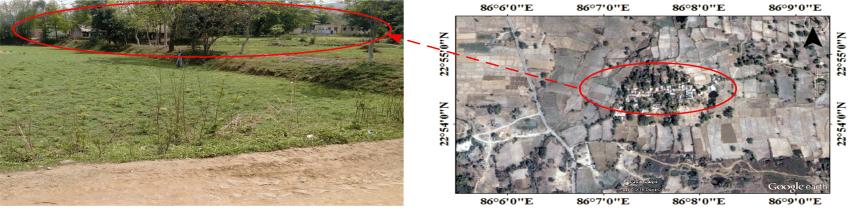
Geo-informatics technology has dynamic role in mapping, monitoring and management of forest resources. The transformation of forest cover and its analysis on the earth’s surface are essential for understanding the associations and interactions between natural phenomena and living organism, especially human. Also deforestation is a major reason for global warming and one of the origin keys for the enhancement of greenhouse effect and climate change. The present study is grounded on the 3S technology in assessment of LU/LC changes within the forest cover area in Dalma Wildlife Sanctuary (DWLS) Jamshedpur-Jharkhand, India. The movement of forest-cover variation over the years 2009, 2011, 2013, 2015 and 2016 is precisely studied using high resolution Satellite Data (SD). It is noted that, due to shifting cultivation, forest fire, and conversion of forest cover into crop land/bare land and settlement encroachments in forest region by villagers are rapidly increasing; as a result deforestation is taking place. It is predicted that the study would demonstrate the effectiveness of 3S technology in forest renovation, planning and management.
1.
Introduction
First we give the definitions of generalized fractional integral operators which are special cases of the unified integral operators defined in (1.9), (1.10).
Definition 1.1. [1] Let f:[a,b]→R be an integrable function. Also let g be an increasing and positive function on (a,b], having a continuous derivative g′ on (a,b). The left-sided and right-sided fractional integrals of a function f with respect to another function g on [a,b] of order μ where ℜ(μ)>0 are defined by:
where Γ(.) is the gamma function.
Definition 1.2. [2] Let f:[a,b]→R be an integrable function. Also let g be an increasing and positive function on (a,b], having a continuous derivative g′ on (a,b). The left-sided and right-sided fractional integrals of a function f with respect to another function g on [a,b] of order μ where ℜ(μ),k>0 are defined by:
where Γk(.) is defined as follows [3]:
A fractional integral operator containing an extended generalized Mittag-Leffler function in its kernel is defined as follows:
Definition 1.3. [4] Let ω,μ,α,l,γ,c∈C, ℜ(μ),ℜ(α),ℜ(l)>0, ℜ(c)>ℜ(γ)>0 with p≥0, δ>0 and 0<k≤δ+ℜ(μ). Let f∈L1[a,b] and x∈[a,b]. Then the generalized fractional integral operators ϵγ,δ,k,cμ,α,l,ω,a+f and ϵγ,δ,k,cμ,α,l,ω,b−f are defined by:
where
is the extended generalized Mittag-Leffler function and (c)nk is the Pochhammer symbol defined by (c)nk=Γ(c+nk)Γ(c).
Recently, a unified integral operator is defined as follows:
Definition 1.4. [5] Let f,g:[a,b]⟶R, 0<a<b, be the functions such that f be positive and f∈L1[a,b], and g be differentiable and strictly increasing. Also let ϕx be an increasing function on [a,∞) and α,l,γ,c ∈ C, p,μ,δ ≥ 0 and 0<k≤δ+μ. Then for x∈[a,b] the left and right integral operators are defined by
where the involved kernel is defined by
For suitable settings of functions ϕ, g and certain values of parameters included in Mittag-Leffler function, several recently defined known fractional and conformable fractional integrals studied in [6,7,8,9,10,1,11,12,13,14,15,16,17] can be reproduced, see [18,Remarks 6&7].
The aim of this study is to derive the bounds of all aforementioned integral operators in a unified form for (s,m)-convex functions. These bounds will hold particularly for m-convex, s-convex and convex functions and for almost all fractional and conformable integrals defined in [6,7,8,9,10,1,11,12,13,14,15,16,17].
Definition 1.5. [19] A function f:[0,b]→R,b>0 is said to be (s,m)-convex, where (s,m)∈[0,1]2 if
holds for all x,y∈[0,b]andt∈[0,1].
Remark 1. 1. If we take (s,m) = (1,m), then (1.12) gives the definition of m-convex function.
2. If we take (s,m) = (1,1), then (1.12) gives the definition of convex function.
3. If we take (s,m) = (1,0), then (1.12) gives the definition of star-shaped function.
2.
Properties of the kernel Kyx(Eγ,δ,k,cμ,α,l,g;ϕ)
P1: Let g and ϕx be increasing functions. Then for x<t<y, x,y∈[a,b] the kernel Kyx(Eγ,δ,k,cμ,α,l,g;ϕ) satisfies the following inequality:
This can be obtained from the following two straightforward inequalities:
The reverse of inequality (1.9) holds when g and ϕx are decreasing.
P2: Let g and ϕx be increasing functions. If ϕ(0)=ϕ′(0)=0, then for x,y∈[a,b],x<y,
Kxy(Eγ,δ,k,cμ,α,l,g;ϕ)≥0.
P3: For p,q∈R,
Kxy(Eγ,δ,k,cμ,α,l,g;pϕ1+qϕ2)=pKxy(Eγ,δ,k,cμ,α,l,g;ϕ1)+qKxy(Eγ,δ,k,cμ,α,l,g;ϕ2).
The upcoming section contains the results which deal with the bounds of several integral operators in a compact form by utilizing (s,m)-convex functions. A version of the Hadamard inequality in a compact form is presented, also a modulus inequality is given for differentiable function f such that |f′| is (s,m)-convex function.
3.
Main results
In this section first we will state the main results. The following result provides upper bound of unified integral operators.
Theorem 3.1. Let f:[a,b]⟶R, 0≤a<b be a positive integrable (s,m)-convex function, m∈(0,1]. Let g:[a,b]⟶R be differentiable and strictly increasing function, also let ϕx be an increasing function on [a,b]. If α,β,l,γ,c∈C, p,μ≥0,δ≥0 and 0<k≤δ+μ, then for x∈(a,b) the following inequality holds for unified integral operators:
Lemma 3.2. [20] Let f:[0,∞]⟶R, be an (s,m)-convex function, m∈(0,1]. If f(x)=f(a+b−xm), then the following inequality holds:
The following result provides generalized Hadamard inequality for (s,m)-convex functions.
Theorem 3.3. Under the assumptions of Theorem 3.1, in addition if f(x)=f(a+b−xm), m∈(0,1], then the following inequality holds:
Theorem 3.4. Let f:[a,b]⟶R, 0≤a<b be a differentiable function. If |f′| is (s,m)-convex, m∈(0,1] and g:[a,b]⟶R be differentiable and strictly increasing function, also let ϕx be an increasing function on [a,b]. If α,β,l,γ,c∈C, p,μ≥0, δ≥0 and 0<k≤δ+μ, then for x∈(a,b) we have
where
4.
Proofs of main results
In this section we give the proves of the results stated in aforementioned section.
Proof of Theorem 3.1. By (P1), the following inequalities hold:
For (s,m)-convex function the following inequalities hold:
From (4.1) and (4.3), the following integral inequality holds true:
Further the aforementioned inequality takes the form which involves Riemann-Liouville fractional integrals in the right hand side, provides the upper bound of unified left sided integral operator (1.1) as follows:
On the other hand from (4.2) and (4.4), the following integral inequality holds true:
Further the aforementioned inequality takes the form which involves Riemann-Liouville fractional integrals in the right hand side, provides the upper bound of unified right sided integral operator (1.2) as follows:
By adding (4.6) and (4.8), (3.1) can be obtained.
Remark 2. (ⅰ) If we consider (s,m) = (1, 1) in (3.1), [18,Theorem 1] is obtained.
(ⅱ) If we consider p=ω=0 in (3.1), [20,Theorem 1] is obtained.
(ⅲ) If we consider ϕ(t)=Γ(α)tα, p=ω=0 and (s,m) = (1, 1) in (3.1), [21,Theorem 1] is obtained.
(ⅳ) If we consider α=β in the result of (ⅲ), then [21,Corollary 1] is obtained.
(ⅴ) If we consider ϕ(t)=tα, g(x)=x and m=1 in (3.1), then [22,Theorem 2.1] is obtained.
(ⅵ) If we consider α=β in the result of (v), then [22,Corollary 2.1] is obtained.
(ⅶ) If we consider ϕ(t)=Γ(α)tαkkΓk(α), (s,m) = (1, 1), g(x)=x and p=ω=0 in (3.1), then [23,Theorem 1] can be obtained.
(ⅷ) If we consider α=β in the result of (ⅶ), then [23,Corollary 1] can be obtained.
(ⅸ) If we consider ϕ(t)=Γ(α)tα, g(x)=x and p=ω=0 and (s,m) = (1, 1) in (3.1), then [24,Theorem 1] is obtained.
(ⅹ) If we consider α=β in the result of (ⅸ), then [24,Corollary 1] can be obtained.
(ⅹⅰ) If we consider α=β=1 and x=a or x=b in the result of (x), then [24,Corollary 2] can be obtained.
(ⅹⅱ) If we consider α=β=1 and x=a+b2 in the result of (ⅹ), then [24,Corollary 3] can be obtained.
Proof of Theorem 3.3. By (P1), the following inequalities hold:
For (s,m)-convex function f, the following inequality holds:
From (4.9) and (4.11), the following integral inequality holds true:
Further the aforementioned inequality takes the form which involves Riemann-Liouville fractional integrals in the right hand side, provides the upper bound of unified right sided integral operator (1.1) as follows:
On the other hand from (4.9) and (4.11), the following inequality holds which involves Riemann-Liouville fractional integrals on the right hand side and estimates of the integral operator (1.2):
By adding (4.12) and (4.13), following inequality can be obtained:
Multiplying both sides of (3.2) by Kax(Eγ,δ,k,cμ,α,l,g;ϕ)g′(x), and integrating over [a,b] we have
From Definition 1.4, the following inequality is obtained:
Similarly multiplying both sides of (3.2) by Kxb(Eγ,δ,k,cμ,β,l,g;ϕ)g′(x), and integrating over [a,b] we have
By adding (4.15) and (4.16) the following inequality is obtained:
Using (4.14) and (4.17), inequality (3.3) can be obtained, this completes the proof.
Remark 3. (ⅰ) If we consider (s,m) = (1, 1) in (3.3), [18,Theorem 2] is obtained.
(ⅱ) If we consider p=ω=0 in (3.3), [20,Theorem 3] is obtained.
(ⅲ) If we consider ϕ(t)=Γ(α)tα+1, p=ω=0 and (s,m) = (1, 1) in (3.3), [21,Theorem 3] is obtained.
(ⅳ) If we consider α=β in the result of (iii), then [21,Corollary 3] is obtained.
(ⅴ) If we consider ϕ(t)=tα+1, g(x)=x and m=1 in (3.3), then [22,Theorem 2.4] is obtained.
(ⅵ) If we consider α=β in the result of (v), then [22,Corollary 2.6] is obtained.
(ⅶ) If we consider ϕ(t)=Γ(α)tαk+1, (s,m) = (1, 1), g(x)=x and p=ω=0 in (3.3), then [23,Theorem 3] can be obtained.
(ⅷ) If we consider α=β in the result of (ⅶ), then [23,Corollary 6] can be obtained.
(ⅸ) If we consider ϕ(t)=Γ(α)tα+1, p=ω=0, (s,m)=1 and g(x)=x in (3.3), [24,Theorem 3] can be obtained.
(ⅹ) If we consider α=β in the result of (ⅸ), [24,Corrolary 6] can be obtained.
Proof of Theorem 3.4. For (s,m)-convex function the following inequalities hold:
From (4.1) and (4.18), the following inequality is obtained:
Similarly, from (4.2) and (4.19), the following inequality is obtained:
By adding (4.20) and (4.21), inequality (3.4) can be achieved.
Remark 4. (ⅰ) If we consider (s,m) = (1, 1) in (3.4), then [18,Theorem 3] is obtained.
(ⅱ) If we consider p=ω=0 in (3.4), then [20,Theorem 2] is obtained.
(ⅲ) If we consider ϕ(t)=Γ(α)tα+1, p=ω=0 and (s,m) = (1, 1) in (3.4), then [21,Theorem 2] is obtained.
(ⅳ) If we consider α=β in the result of (iii), then [21,Corollary 2] is obtained.
(ⅴ) If we consider ϕ(t)=tα, g(x)=x and m=1 in (3.4), then [22,Theorem 2.3] is obtained.
(ⅵ) If we consider α=β in the result of (v), then [22,Corollary 2.5] is obtained.
(ⅶ) If we consider ϕ(t)=Γ(α)tαk+1, (s,m) = (1, 1), g(x)=x and p=ω=0 in (3.4), then [23,Theorem 2] can be obtained.
(ⅷ) If we consider α=β in the result of (ⅶ), then [23,Corollary 4] can be obtained.
(ⅸ) If we consider α=β=k=1 and x=a+b2, in the result of (ⅷ), then [23,Corollary 5] can be obtained.
(ⅹ) If we consider ϕ(t)=Γ(α)tα+1, g(x)=x and p=ω=0 and (s,m) = (1, 1) in (3.4), then [24,Theorem 2] is obtained.
(ⅹⅰ) If we consider α=β in the result of (x), then [24,Corollary 5] can be obtained.
5.
Boundedness and continuity
In this section, we have established boundedness and continuity of unified integral operators for m-convex and convex functions.
Theorem 5.1. Under the assumptions of Theorem 1, the following inequality holds for m-convex functions:
Proof. If we put s=1 in (4.5), we have
Further from simplification of (5.2), the following inequality holds:
Similarly from (4.8), the following inequality holds:
From (5.3) and (5.4), (5.1) can be obtained.
Theorem 5.2. With assumptions of Theorem 4, if f∈L∞[a,b], then unified integral operators for m-convex functions are bounded and continuous.
Proof. From (5.3) we have
which further gives
where K=(g(b)−g(a))(m+1)Kab(Eγ,δ,k,cμ,α,l,g;ϕ).
Similarly, from (5.4) the following inequality holds:
Hence the boundedness is followed, further from linearity the continuity of (1.9) and (1.10) is obtained.
Corollary 1. If we take m=1 in Theorem 5, then unified integral operators for convex functions are bounded and continuous and following inequalities hold:
where K=2(g(b)−g(a))Kab(Eγ,δ,k,cμ,α,l,g;ϕ).
6.
Conclusions
This paper has explored bounds of a unified integral operator for (s,m)-convex functions. These bounds are obtained in a compact form which have further interesting consequences with respect to fractional and conformable integrals for convex, m-convex and s-convex functions. Furthermore by applying Theorems 3.1, 3.3 and 3.4 several associated results can be derived for different kinds of fractional integral operators of convex, m-convex and s-convex functions.
Acknowledgments
This work was sponsored in part by Social Science Planning Fund of Liaoning Province of China(L15AJL001, L16BJY011, L18AJY001), Scientific Research Fund of The Educational Department of Liaoning Province(2017LNZD07, 2016FRZD03), Scientific Research Fund of University of science and technology Liaoning(2016RC01, 2016FR01)
Conflict of interest
The authors declare that no competing interests exist.













 DownLoad:
DownLoad: