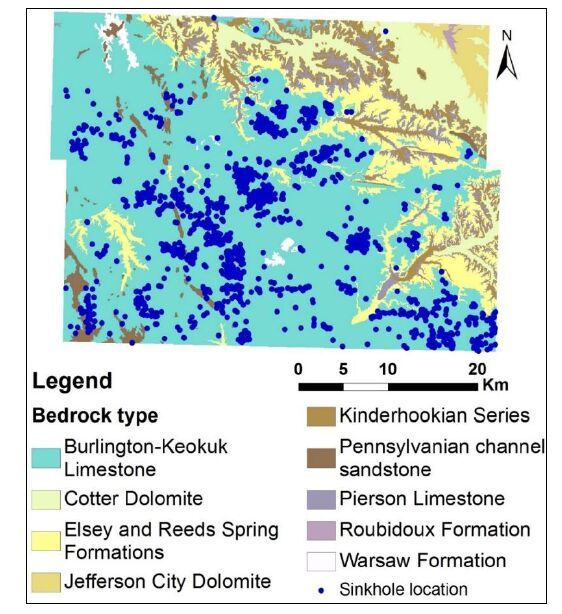
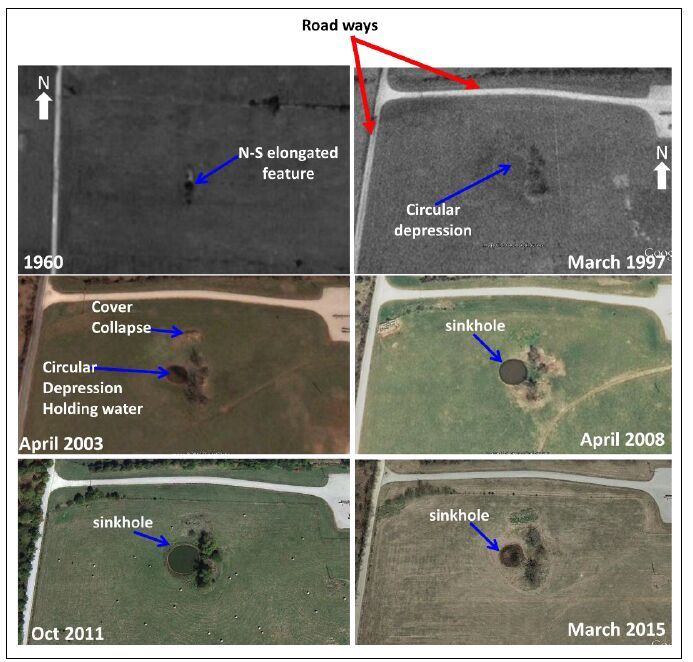
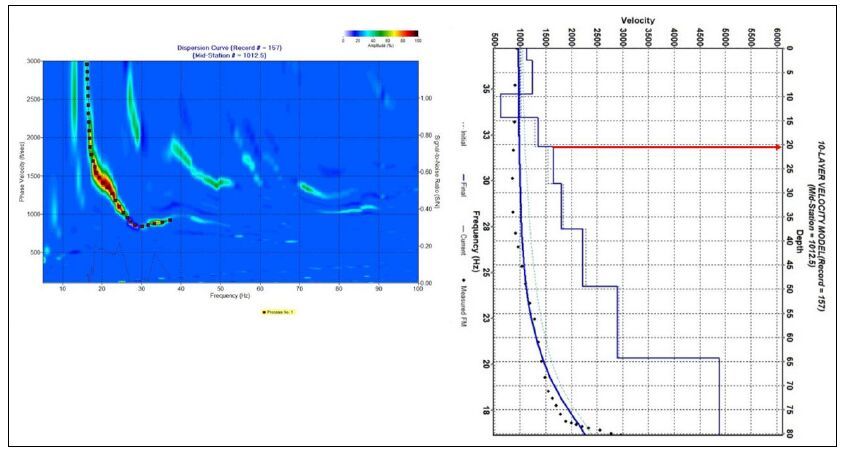
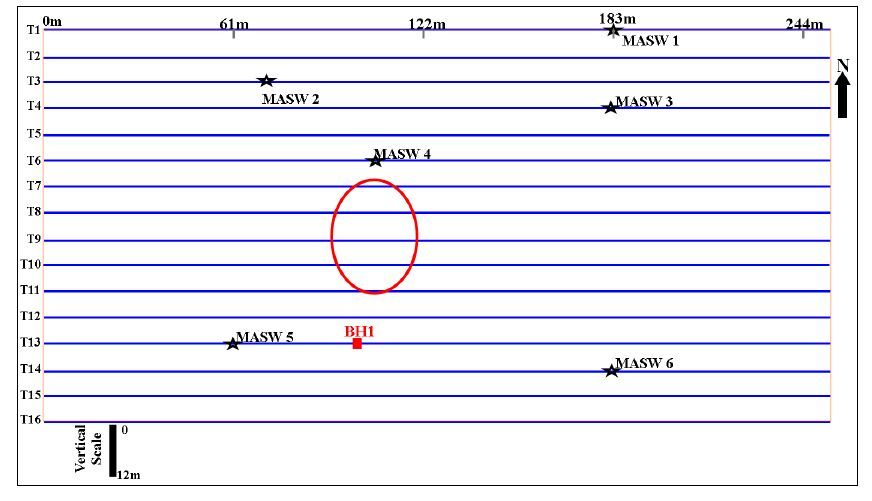
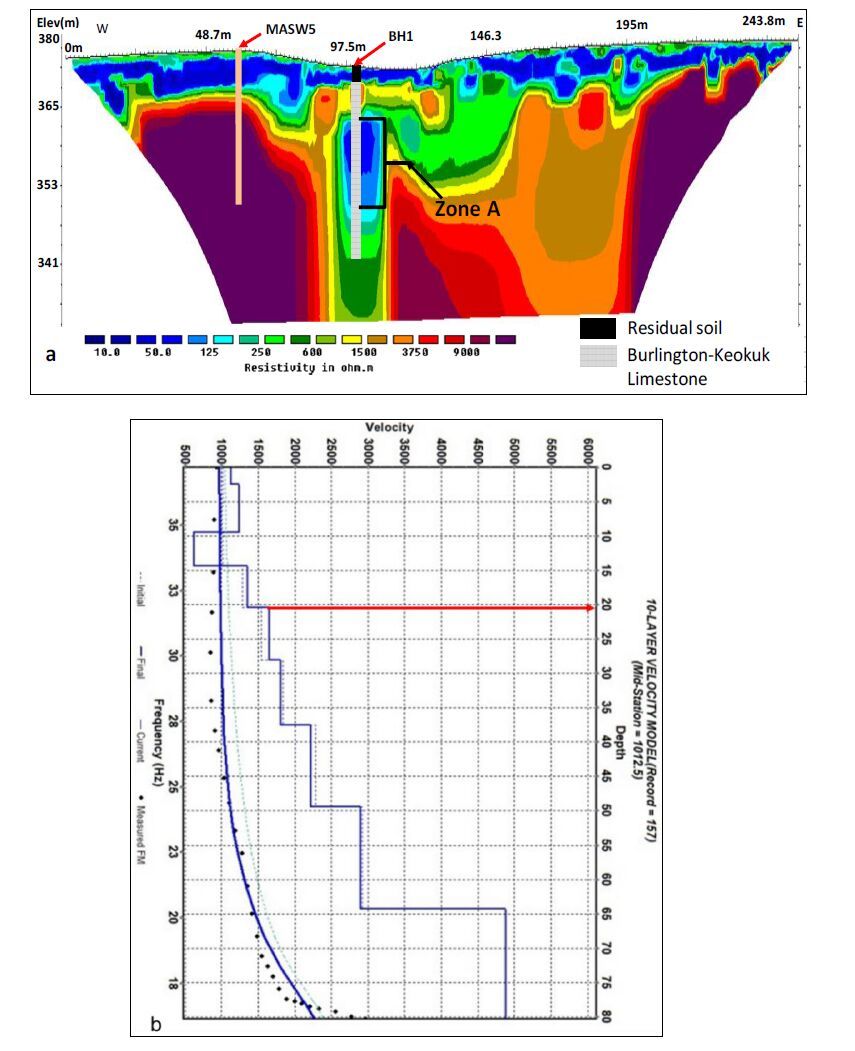
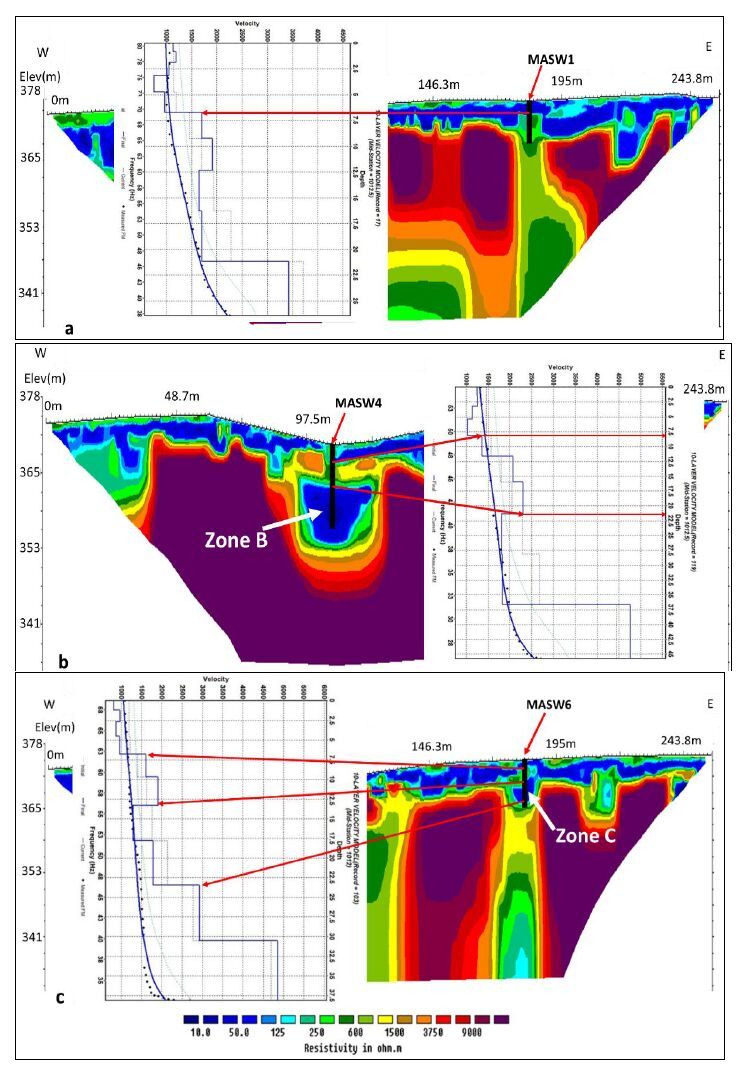
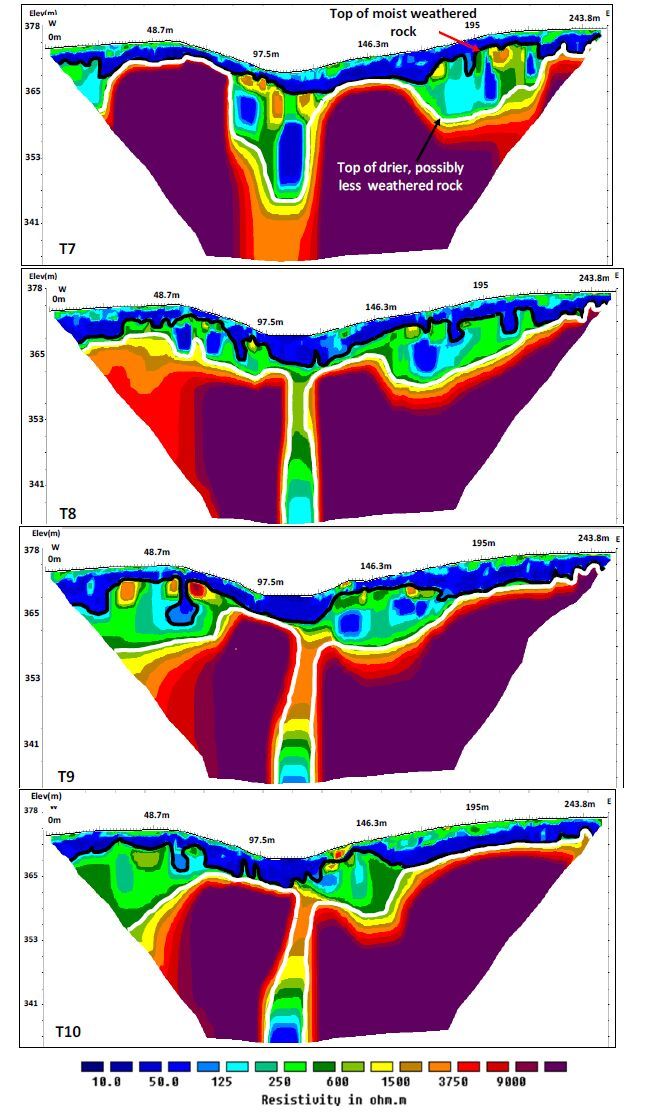
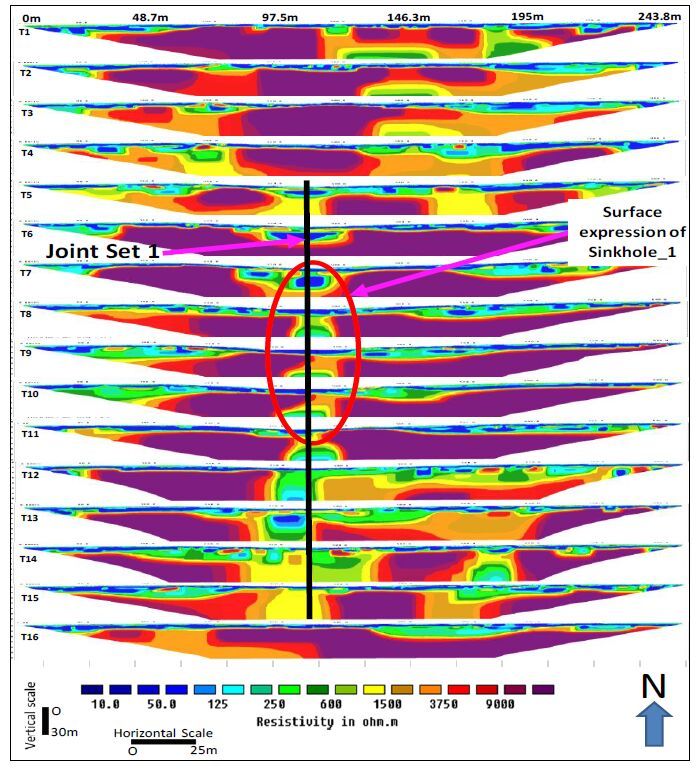
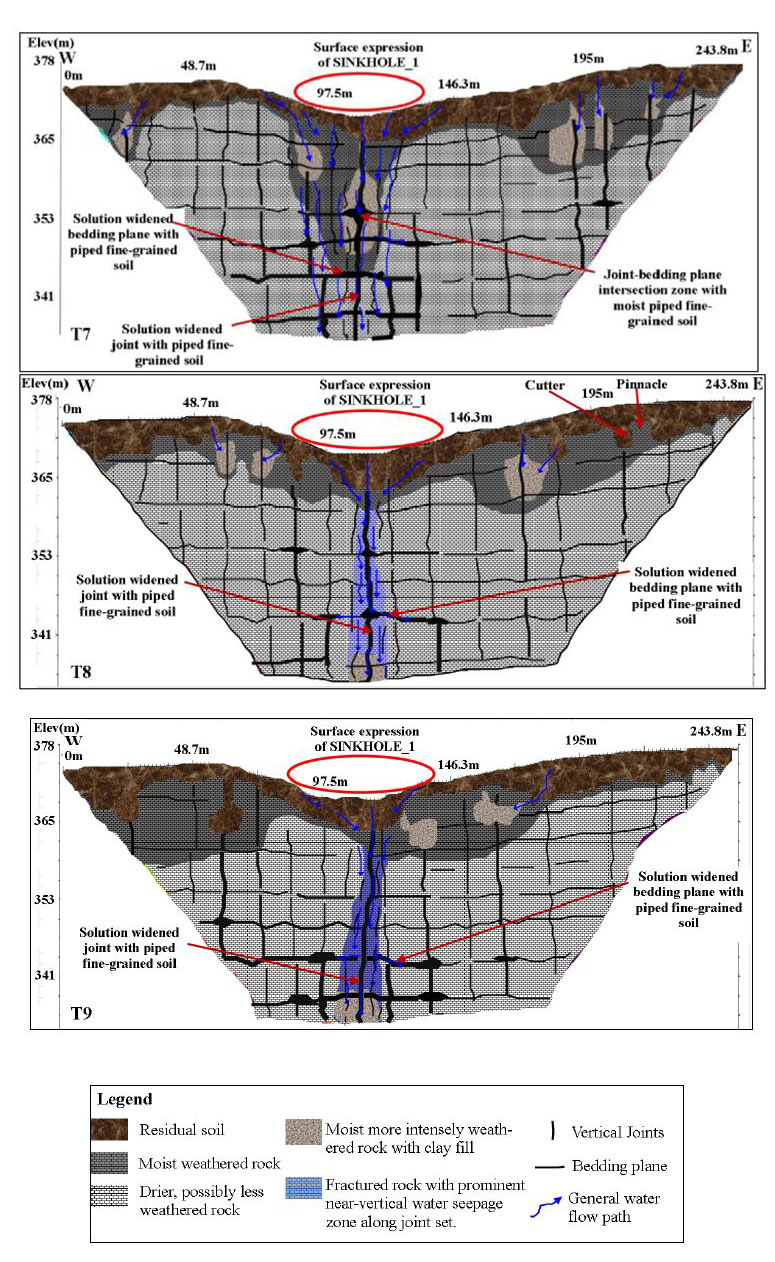
Investigating sinkhole morphology and formation mechanisms is key to understanding their long term impact and susceptibility to development, and aids in the design of effective mitigation measures. In this study, ERT (electrical resistivity tomography), MASW (multichannel analysis of surface waves) and borehole data were used to image the subsurface morphology of an active sinkhole in Greene County, Missouri. The study reveals that the sinkhole developed along a natural surface drainage pathway above a pervasively fractured limestone. The subsurface image of the sinkhole depicts a zone of near-vertical water seepage and soil piping. Based on the nature of the overburden material, and the morphology and current/past surface expression of the sinkhole, it is concluded that the sinkhole is predominantly a cover subsidence type of sinkhole. However, it is possible that minor cover collapse occurred locally and in an area slightly to the north of the current active sinkhole.
1.
Introduction
A semiring is an algebra with two associative binary operations +,⋅, in which + is commutative and ⋅ distributive over + from the left and right. Such an algebra is a common generalization of both rings and distributive lattices. It has broad applications in information science and theoretical computer science (see [5,6]). In this paper, we shall investigate some small-order semirings which will play a crucial role in subsequent follows.
The semiring A with addition and multiplication table (see [12])
The semiring B with addition and multiplication table (see [4])
Eight 2-element semirings with addition and multiplication table (see [2])
For any semiring S, we denote by S0 the semiring obtained from S by adding an extra element 0 and where a=0+a=a+0,0=0a=a0 for every a∈S. For any semiring S, S∗ will denote the (multiplicative) left-right dual of S. In 2005, Pastijn et al. [4,9,10] studied the semiring variety generated by B0 and (B0)∗ (Denoted by Sr(2,1)). They showed that the lattice of subvarieties of this variety is distributive and contains 78 varieties precisely. Moreover, each of these is finitely based. In 2016, Ren et al. [12,13] studied the variety generated by B0,(B0)∗ and A0 (Denoted by Sr(3,1)). They showed that the lattice of subvarieties of this variety is distributive and contains 179 varieties precisely. Moreover, each of these is finitely based. From [4,10], we have HSP(L2,R2,M2,D2)⫋HSP(B0,(B0)∗). So
In 2016, Shao and Ren [15] studied the variety HSP(L2,R2,M2,D2,Z2,W2) (Denoted by S6). They showed that the lattice of subvarieties of this variety is distributive and contains 64 varieties precisely. Moreover, each of these is finitely based. Recently, Ren and Zeng [14] studied the variety generated by B0,(B0)∗,N2,T2. They proved that the lattice of subvarieties of this variety is a distributive lattice of order 312 and that each of its subvarieties is finitely based. In [16], Wang, Wang and Li studied the variety generated by B0,(B0)∗,A0,N2,T2. They proved that the lattice of subvarieties of this variety is a distributive lattice of order 716 and that each of its subvarieties is finitely based. It is easy to check
So semiring variety HSP(B0,(B0)∗,A0,N2,T2) is a proper subvariety of the semiring variety HSP(B0,(B0)∗,A0,N2,T2,Z2,W2). The main purpose of this paper is to study the variety HSP(B0,(B0)∗, A0,N2,T2,Z2,W2). We show that the lattice of subvarieties of this variety is a distributive lattice of order 2327. Moreover, we show this variety is hereditarily finitely based.
2.
Preliminaries
By a variety we mean a class of algebras of the same type that is closed under subalgebras, homomorphic images and direct products (see [11]). Let W be a variety, let L(W) denote the lattice of subvarieties of W and let IdW(X) denote the set of all identities defining W. If W can be defined by finitely many identities, then we say that W is finitely based (see [14]). In other words, W is said to be finitely based if there exists a finite subset Σ of IdW(X) such that for any p≈q∈IdW(X), p≈q can be derived from Σ, i.e., Σ⊢p≈q. Otherwise, we say that W is nonfinitely based. Recall that W is said to be hereditarily finitely based if all members of L(W) are finitely based. If a variety W is finitely based and L(W) is a finite lattice, then W is hereditarily finitely based (see [14]).
A semiring is called an additively idempotent semiring (ai-semiring for short) if its additive reduct is a semilattice, i.e., a commutative idempotent semigroup. It is also called a semilattice-ordered semigroup (see [3,8,12]). The variety of all semirings (resp. all ai-semirings) is denoted by SR (resp. AI). Let X denote a fixed countably infinite set of variables and X+ the free semigroup on X (see [8]). A semiring identity (SR-identity for short) is an expression of the form u≈v, where u and v are terms with u=u1+⋯+uk, v=v1+⋯+vℓ, where ui,vj∈X+. Let k_ denote the set {1,2,…,k} for a positive integer k, Σ be a set of identities which include the identities determining AI (Each identity in Σ is called an AI-identity) and u≈v be an AI-identity. It is easy to check that the ai-semiring variety defined by u≈v coincides with the ai-semiring variety defined by the identities u≈u+vj,v≈v+ui,i∈k_,j∈ℓ_. Thus, in order to show that u≈v is derivable from Σ, we only need to show that u≈u+vj,v≈v+ui,i∈k_,j∈ℓ_ can be derived from Σ (see [9]).
To solve the word problem for the variety HSP(B0,(B0)∗,A0,N2,T2,Z2,W2), the following notions and notations are needed. Let q be an element of X+. Then
● the head of q, denoted by h(q), is the first variable occurring in q;
● the tail of q, denoted by t(q), is the last variable occurring in q;
● the content of q, denoted by c(q), is the set of variables occurring in q;
● the length of q, denoted by |q|, is the number of variables occurring in q counting multiplicities;
● the initial part of q, denoted by i(q), is the word obtained from q by retaining only the first occurrence of each variable;
● the final part of q, denoted by f(q), is the word obtained from q by retaining only the last occurrence of each variable;
● r(q) denotes set {x∈X|the number of occurrences of x in q is odd}.
By [13,Lemma 1.2], Sr(3,1) satisfies the identity p≈q if and only if (i(p),f(p),r(p))=(i(q),f(q), r(q)). This result will be used later without any further notice. The basis for each one of N2,T2,Z2,W2 can be found from [2] (See Table 1).
By [15,Lemma 1.1] and the Table 1, we have
Lemma 2.1. Let u≈v be a nontrivial SR-identity, where u=u1+u2+⋯+um, v=v1+v2+⋯+vn, ui,vj∈X+, i∈m_,j∈n_. Then
(i) N2⊨u≈vifandonlyif{ui∈u||ui|=1}={vi∈v||vi|=1};
(ii) T2⊨u≈vifandonlyif{ui∈u||ui|≥2}≠ϕ,{vi∈v||vi|≥2}≠ϕ;
(iii) Z2⊨u≈vifandonlyif(∀x∈X)u≠x,v≠x;
(iv) W2⊨u≈vifandonlyifm=n=1,c(u1)=c(v1)orm,n≥2.
Suppose that u=u1+⋯+um,ui∈X+,i∈m_. Let 1 be a symbol which is not in X and Y an arbitrary subset of ⋃i=mi=1c(u1). For any ui in u, if c(ui)⊆Y, put hY(ui)=1. Otherwise, we shall denote by hY(ui) the first variable occurring in the word obtained from ui by deleting all variables in Y. The set {hY(ui)|ui∈u} is written HY(u). Dually, we have the notations tY(ui) and TY(ui). In particular, if Y=∅, then hY(ui)=h(ui) and tY(ui)=t(ui). Moreover, if c(ui)∩Y≠∅ for every ui in u, then we write DY(u)=∅. Otherwise, DY(u) is the sum of all terms ui in u such that c(ui)∩Y=∅. By [13,Lemma 2.3 and 2.11] and [4,Lemma 2.4 and its dual,Lemma 2.5 and 2.6], we have
Lemma 2.2. Let u≈u+q be an AI-identity, where u=u1+⋯+um,ui,q∈X+,i∈m_. If u≈u+q holds in Sr(3,1), then
(i) for every Z⊆⋃i=mi=1c(ui)∖c(q), there exists p1 in X+ with r(p1)=r(q) and c(q)⊆c(p1)⊆⋃i=ki=1c(ui) such that DZ(u)≈DZ(u)+p1 holds in Sr(3,1), where DZ(u)=u1+⋯+uk.
(ii) for every Y⊆Z=⋃i=mi=1c(ui)∖c(q), HY(DZ(u))=HY(DZ(u)+p1) and TY(DZ(u))=TY(DZ(u)+p1).
Throughout this paper, u(3.1),(3.2),⋯≈v denotes the identity u≈v can be derived from the identities (3.1),(3.2),⋯ and the identities determining SR. For other notations and terminology used in this paper, the reader is referred to [1,4,7,13,15].
3.
Equational basis of HSP(B0,(B0)∗,A0,N2,T2,Z2,W2)
In this section, we shall show that the variety HSP(B0,(B0)∗,A0,N2,T2,Z2,W2) is finitely based. Indeed, we have
Theorem 3.1. The semiring variety HSP(B0,(B0)∗,A0,N2,T2,Z2,W2) is determined by (3.1)–(3.12),
Proof. From [13] and Lemma 2.1, we know that both Sr(3,1) and HSP(N2,T2,Z2,W2) satisfy identities (3.1)–(3.12) and so does HSP(B0,(B0)∗,A0,N2,T2,Z2,W2).
Next, we shall show that every identity that holds in HSP(B0,(B0)∗,A0,N2,T2,Z2,W2) can be derived from (3.1)–(3.12) and the identities determining SR. Let u≈v be such an identity, where u=u1+u2+⋯+um, v=v1+v2+⋯+vn, ui,vj∈X+, 1≤i≤m,1≤j≤n. By Lemma 2.1 (ⅳ), we only need to consider the following two cases:
Case 1. m=n=1 and c(u1)=c(v1). From Sr(3,1),T2,Z2⊨u1≈v1, it follows that (i(u1),f(u1),r(u1))=(i(v1),f(v1),r(v1)), |u1|≥2 and |v1|≥2. Hence u1(3.1)∼(3.6)≈v1.
Case 2. m,n≥2. It is easy to verify that u≈v and the identity (3.12) imply the identities u≈u+vj, v≈v+ui for all i,j such that 1≤i≤m,1≤j≤n. Conversely, the latter m+n identities imply u≈u+v≈v. Thus, to show that u≈v is derivable from (3.1)–(3.12) and the identities determining SR, we need only show that the simpler identities u≈u+vj, v≈v+ui for all i,j such that 1≤i≤m,1≤j≤n. Hence we need to consider the following two cases:
Case 2.1. u≈u+q, where |q|=1. Since N2⊨u≈u+q, there exists us=q. Thus u+q≈u′+us+q≈u′+us+us(3.12)≈u′+us≈u.
Case 2.2. u≈u+q, where |q|≥2. Since u≈u+q holds in T2, it follows from Lemma 2.1 (ⅱ) that there exists ui in u such that ui>1. Put Z=(⋃i=mi=1c(ui))∖c(q). Assume that DZ(u)=u1+⋯+uk. Then ⋃i=ki=1c(ui)=c(q). By Lemma 2.2 (ⅰ), there exists p1∈X+ such that r(p1)=r(q) and c(q)⊆c(p1)⊆⋃i=ki=1c(ui). Moreover,
Write p=p31u21u22⋯u2k. Thus c(p)=c(q), r(p)=r(q) and we have derived the identity
Due to |p|>1, it follows that (3.4) implies the identity
Suppose that i(q)=x1x2⋯xℓ. We shall show by induction on j that for every 1≤j≤ℓ, u≈u+x21x22⋯x2ℓp is derivable from (3.1)–(3.11) and the identities defining SR.
From Lemma 2.1 (ⅱ), there exists ui1 in DZ(u) with c(ui1)⊆c(q) such that h(ui1)=h(q)=x1. Furthermore,
Therefore
Assume that for some 1<j≤ℓ,
is derivable from (3.1–3.12) and the identities defining SR. By Lemma 2.1 (ⅱ), there exists ui in DZ(u) with c(ui)⊆c(q) such that ui=ui1xjui2 and c(ui1)⊆{x1,x2,…,xj−1}. It follows that
Consequently
Moreover, we have
Hence u≈u+x21x22⋯x2j−1x2jp. Using induction we have
Dually,
Thus
It follows that u≈u+q.
4.
The lattice L(HSP(B0,(B0)∗,A0,N2,T2,Z2,W2))
In this section we characterize the lattice L(HSP(B0,(B0)∗,A0,N2,T2,Z2,W2)). Throughout this section, t(x1,…,xn) denotes the term t which contains no other variables than x1,…,xn (but not necessarily all of them). Let S∈HSP(B0,(B0)∗,A0,N2,T2,Z2,W2) and let E+(S) denote the set {a∈S|a+a=a}, where any element of E+(S) is said to be an additive idempotent of (S,+). Notice that HSP(B0,(B0)∗,A0,N2,T2,Z2,W2) satisfies the identities
By (4.1) and (4.2), it is easy to verify that E+(S)={a+a|a∈S} forms a subsemiring of S. To characterize the lattice L(HSP(B0,(B0)∗,A0,N2,T2,Z2,W2)), we need to consider the following mapping
It is easy to prove that φ(W)={E+(S)|S∈W} for each member W of L(HSP(B0,(B0)∗,A0,N2,T2, Z2,W2)). If W is the subvariety of HSP(B0,(B0)∗,A0,N2,T2) determined by the identities
then ˆW denotes the subvariety of HSP(B0,(B0)∗,A0,N2,T2,Z2,W2) determined by the identities
Lemma 4.1. [16] The ai-semiring variety HSP(B0,(B0)∗,A0,N2,T2) is determined by the identities (3.1)–(3.11) and L(HSP(B0,(B0)∗,A0,N2,T2)) is a distributive lattice of order 716.
Lemma 4.2. Let W be a member of L(HSP(B0,(B0)∗,A0,N2,T2)). Then, ˆW=W∨HSP(Z2,W2).
Proof. Since W satisfies the identities (4.4), it follows that W is a subvariety of ˆW. Both Z2 and W2 are members of ˆW and so W∨HSP(Z2,W2)⊆ˆW. To show the converse inclusion, it suffices to show that every identity that is satisfied by W∨HSP(Z2,W2) can be derived by the identities holding in HSP(B0,(B0)∗,A0,N2,T2,Z2,W2) and
if W is the subvariety of L(HSP(B0,(B0)∗,A0,N2,T2)) determined by ui(xi1,…,xin)≈vi(xi1,…,xin), i∈k_. Let u≈v be such an identity, where u=u1+u2+⋯+um,v=v1+v2+⋯+vn,ui,vj∈X+,1≤i≤m,1≤j≤n. By Lemma 2.1 (8), we only need to consider the following two cases.
Case 1. m,n≥2. By identity (3.12), HSP(B0,(B0)∗,A0,N2,T2,Z2,W2) satisfies the identities
Since u≈v holds in HSP(B0,(B0)∗,A0,N2,T2), we have that it is derivable from the collection Σ of ui≈vi,i∈k_ and the identities determining HSP(B0,(B0)∗,A0,N2,T2). From [1,Exercise Ⅱ.14.11], it follows that there exist t1,t2,…,tℓ∈Pf(X+) such that
● t1=u,tℓ=v;
● For any i=1,2,…,ℓ−1, there exist pi,qi,ri∈Pf(X+) (where pi, qi and ri may be empty words), a semiring substitution φi and an identity u′i≈v′i∈Σ such that
Let Σ′ denote the set {u+u≈v+v|u≈v∈Σ}. For any i=1,2,…,ℓ−1, we shall show that ti+ti≈ti+1+ti+1 is derivable from Σ′ and the identities holding in HSP(B0,(B0)∗,A0,N2,T2,Z2,W2). Indeed, we have
Further,
This implies the identity
We now have
Case 2. m=n=1 and c(u)=c(v). Since Z2⊨u1≈v1, u1≠x,v1≠x, for every x∈X. Since u1≈v1 holds in HSP(B0,(B0)∗,A0,N2,T2), we have that it is derivable from the collection Σ of ui≈vi,i∈k_ and the identities defining HSP(B0,(B0)∗,A0,N2,T2). From [1,Exercise Ⅱ.14.11], it follows that there exist t1,t2,…,tℓ∈Pf(X+) such that
● t1=u1,tℓ=v1;
● For any i=1,2,…,ℓ−1, there exist pi,qi∈Pf(X+) (where pi and qi may be empty words), a semiring substitution φi and an identity u′i≈v′i∈Σ (where u′i and v′i are words) such that
By Lemma 4.1, we have that u1≈v1 can be derived from (3.1)–(3.6), so, by Theorem 3.1, it can be derived from monomial identities holding in HSP(B0,(B0)∗,A0,N2,T2,Z2,W2). This completes the proof.
Lemma 4.3. The following equality holds
There are 716 intervals in L(HSP(B0,(B0)∗,A0,N2,T2,Z2,W2)), and each interval is a congruence class of the kernel of the complete epimorphism φ in (4.3).
Proof. Firstly, we shall show that equality (4.9) holds. It is easy to see that
So it suffices to show that
for each member W of L(HSP(B0,(B0)∗,A0,N2,T2)). If W1 is a member of [W,ˆW], then it is routine to verify that W⊆{E+(S)|S∈W1}⊆W. This implies that {E+(S)|S∈W1}=W and so φ(W1)=W. Hence, W1 is a member of φ−1(W) and so [W,ˆW]⊆φ−1(W). Conversely, if W1 is a member of φ−1(W), then W=φ(W1)={E+(S)|S∈W1} and so φ−1(W)⊆[W,ˆW]. This shows that (4.9) holds.
From Lemma 4.1, we know that L(HSP(B0,(B0)∗,A0,N2,T2)) is a lattice of order 716. So there are 716 intervals in L(HSP(B0,(B0)∗,A0,N2,T2,Z2,W2)). Next, we show that φ a complete epimorphism. On one hand, it is easy to see that φ is a complete ∧-epimorphism. On the other hand, let (Wi)i∈I be a family of members of L(HSP(B0,(B0)∗,A0,N2,T2,Z2, W2)). Then, by (4.3), we have that φ(Wi)⊆Wi⊆^φ(Wi) for each i∈I. Further,
This implies that φ(⋁i∈IWi)=⋁i∈Iφ(Wi). Thus, φ is a complete ∨-homomorphism and so φ is a complete ∨-epimorphism. By (4.10), we deduce that each interval in (4.3) is a congruence class of the kernel of the complete epimorphism φ.
In order to characterize the lattice L(HSP(B0,(B0)∗,A0,N2,T2,Z2,W2)), by Lemma 4.3, we only need to describe the interval [W,ˆW] for each member W of L(HSP(B0, (B0)∗,A0,N2,T2)). Next, we have
Lemma 4.4. Let W be a member of L(HSP(B0,(B0)∗,A0,N2,T2)). Then, W∨HSP(Z2) is the subvariety of ˆW determined by the identity
Proof. It is easy to see that both, W and HSP(Z2) satisfy the identity (4.11) and so does W∨HSP(Z2). In the following we prove that every identity that is satisfied by W∨HSP(Z2) is derivable from (4.11) and the identities holding in ˆW. Let u≈v be such an identity, where u=u1+u2+⋯+um,v=v1+v2+⋯+vn,ui,vj∈X+,1≤i≤m,1≤j≤n. We only need to consider the following cases.
Case 1. m=n=1. Since Z2 satisfies u1≈v1, it follows that |u1|≠1 and |v1|≠1. By Lemma 4.2, ˆW satisfies the identity u31+u31≈v31+v31. Hence u1(3.4)≈u31(4.11)≈u31+u31≈v31+v31(4.11)≈v31(3.4)≈v1.
Case 2. m=1, n≥2. Since Z2 satisfies u1≈v, it follows that |u1|≠1. By Lemma 4.2, ˆW satisfies the identity u31+u31≈v+v. Hence u1(3.4)≈u31(4.11)≈u31+u31≈v+v(3.11)≈v.
Case 3. m≥2, n=1. Similar to Case 2.
Case 4. m,n≥2. By Lemma 4.2, ˆW satisfies the identity u+u≈v+v. Hence u(3.11)≈u+u≈v+v(3.11)≈v.
Lemma 4.5. Let W be a member of L(Sr(3,1)). Then W∨HSP(W2) is the subvariety of ˆW determined by the identities
Proof. It is easy to see that both, W and HSP(W2) satisfy the identity (4.12) and so does W∨HSP(W2). So it suffices to show that every identity that is satisfied by W∨HSP(W2) is derivable from (4.12) and the identities holding in ˆW. Let u≈v be such an identity, where u=u1+u2+⋯+um,v=v1+v2+⋯+vn,ui,vj∈X+,1≤i≤m,1≤j≤n. By Lemma 4.2, ˆW satisfies the identity u3≈v3. Hence, u(4.12)≈u3≈v3(4.12)≈v.
Lemma 4.6. Let W be a member of L(HSP(B0,(B0)∗,A0,N2,T2)). Then the interval [W,ˆW] of L(HSP(B0,(B0)∗,A0,N2,T2,Z2,W2)) is given in Figure 1.
Proof. Suppose that W1 is a member of [W,ˆW] such that W1≠ˆW and W1≠W. Then, there exists a nontrivial identity u≈v holding in W1 such that it is not satisfied by ˆW. Also, we have that W1 does not satisfy the identity x+x≈x. By Lemma 4.2, we only need to consider the following two cases.
Case 1. HSP(Z2)⊨u≈v,HSP(W2)⊭u≈v. Then, u≈v satisfies one of the following three cases:
● m=n=1, c(u1)≠c(v1), |u1|≠1 and |v1|≠1;
● m=1,n>1 and |u1|≠1;
● m>1,n=1 and |v1|≠1.
It is easy to see that, in each of the above cases, u≈v can imply the identity x3≈x3+x3. By Lemma 4.4, we have that W1 is a subvariety of W∨HSP(Z2). On the other hand, since W1⊨x3≈x3+x3 and W1⊭x+x≈x, it follows that Z2 is a member of W1 and so W∨HSP(Z2) is a subvariety of W1. Thus, W1=W∨HSP(Z2).
Case 2. HSP(Z2)⊭u≈v,HSP(W2)⊨u≈v. Then, u≈v satisfies one of the following two cases:
● m=n=1, c(u1)=c(v1) and |u1|=1;
● m=n=1, c(u1)=c(v1) and |v1|=1.
If N2,T2∉W, then, in each of the above cases, u≈v can imply the identity x≈x3. By Lemma 4.5, W1 is a subvariety of W∨HSP(W2). On the other hand, since W1⊨x≈x3 and W1⊭x≈x+x, it follows that W2 is a member of W1 and so W∨HSP(W2) is a subvariety of W1. Thus, W1=W∨HSP(W2).
If N2∈W, then, by Lemma 2.1 (ⅰ), |u1|=|v1|=1, a contradiction. Thus, V1=ˆV.
If T2∈W, then, by Lemma 2.1 (ⅱ), |u1|≥2,|v1|≥2, a contradiction. Thus, V1=ˆV.
By Lemma 4.3 and 4.6, we can show that the lattice L(HSP(B0,(B0)∗,A0,N2,T2,Z2, W2)) of subvarieties of the variety HSP(B0,(B0)∗,A0,N2,T2,Z2,W2) contains 2327 elements. In fact, we have
Theorem 4.7. L(HSP(B0,(B0)∗,A0,N2,T2,Z2,W2)) is a distributive lattice of order 2327.
Proof. We recall from [16] that Sr(3,1)∨T2 [Sr(3,1)∨N2] contains 358 subvarieties since Sr(3,1) contains 179 subvarieties. By Lemma 4.3 and 4.6, we can show that L(HSP(B0,(B0)∗,A0,N2,T2,Z2, W2)) has exactly 2327 (where 2327=179×4+358×3×2−179×3) elements. Suppose that W1,W2 and W3 are members of L(HSP(B0,(B0)∗,A0, N2,T2,Z2,W2)) such that W1∨W2=W1∨W3 and W1∧W2=W1∧W3. Then, by Lemma 4.3
and
Since L(HSP(B0,(B0)∗,A0,N2,T2) is distributive, it follows that φ(W2)=φ(W3). Write W for φ(W2). Then both W2,W3 are members of [W,ˆW]. Suppose that W2≠W3. Then, by Lemma 4.6, W1∨W2=W1∨W3 and W1∧W2=W1∧W3 can not hold at the same time. This implies that W2=W3.
By Theorem 4.1, 4.7 and [14,Corollary 1.2], we now immediately deduce
Corollary 4.8. HSP(B0,(B0)∗,A0,N2,T2,Z2,W2) is hereditarily finitely based.
5.
Conclusions
This article considers a semiring variety generated by B0,(B0)∗,A0,N2,T2,Z2,W2. The finite basis problem for semirings is an interesting developing topic, with plenty of evidence of a high level of complexity along the lines of the more well-developed area of semigroup varieties. This article is primarily a contribution toward the property of being hereditarily finite based, meaning that all subvarieties are finitely based. This property is of course useful because it guarantees the finite basis property of a large number of examples.
Acknowledgments
This work was supported by the Natural Science Foundation of Chongqing (cstc2019jcyj-msxmX0156, cstc2020jcyj-msxmX0272, cstc2021jcyj-msxmX0436), the Scientific and Technological Research Program of Chongqing Municipal Education Commission (KJQN202001107, KJQN202101130) and the Scientific Research Starting Foundation of Chongqing University of Technology (2019ZD68).
Conflict of interest
The authors declare that they do not have any conflict of interests regarding this paper.









 DownLoad:
DownLoad: