1.
Introduction
The vibration of membranes plays a significant role in analysis of wave mechanics in two dimensions and wave propagation, bio-engineering etc. Membranes create main components in acoustics and music such as components of microphones, speakers and related devices [1]. To investigate design of hearing aids, the knowledge of large membrane vibration [2] is vital. In bio-engineering, several human tissues are anticipated as membranes. The vibrational features of eardrum is valuable to understand hearing. The equation of vibration is used to designate vibration of membranes [3]. The integer order vibration equation [4] is,
where ω(r,t) signifies probability density function of particle [5] at time t at a position r while c is the wave velocity of vibrations.
Fractional order derivatives offer a superb mechanism for describing hereditary and memory related properties of various real-life processes and materials [6]. The analysis of fractional differential equations (FDE) [7,8,9,10] in Mathematical Physics, vibration, oscillation, signal processing [11], visco-elasticity [12], chemical engineering [13], seismic wave propagation [14], modelling of diseases [15] etc. is a growing field of interest for researchers. In literature, there exist operational matrix method [3], decomposition method [4], homotopy perturbation scheme [5], variational iteration technique [16] etc. to solve vibration equation.
Homotopy analysis method (HAM) offers an easier way to confirm convergence of solution. HAM was introduced by Liao [17] for solving differential equations. El-Tavil and Huseen [18,19] proposed q-homotopy analysis technique (q-HAM) by generalization of HAM. But these methods have limitations like massive computation with more time consumption. So, they necessitate to be linked with a transform operator. Hybrid methods using integral transforms [20,21] are useful to treasure some solution of nonlinear FDE. Homotopy analysis Laplace transform method (HATM) is a united form of HAM and the transform of Laplace. In [1], Srivastava et al. used HATM and Laplace decomposition technique to solve vibration equation of arbitrary order. The reliability of solution procedure of a nonlinear equation is an important characteristic than modeling dimensions of equations [22,23,24].
Sumudu transform has an interesting advantage of the ‘unity’ feature over Laplace transform. It leads combinations into permutations hence it is useful in discrete systems. The function along with its Sumudu transform possess identical Taylor coefficients other than factor n. Sumudu transform is used due to its strong properties to get solution of many problems [25,26]. Watugala [27,28] proposed Sumudu transform and Asiru [29] proved its properties. Weerakoon [30,31] discussed its applications in finding solution to wave equation with variable coefficients.
Homotopy analysis Sumudu transform method (HASTM) is a graceful merger of HAM and Sumudu transform. The benefit is its power of embracing two robust computational schemes for tackling FDE. The projected approaches can reduce time and computation work as compared to existing schemes simultaneously preserving result efficiency. Singh et al. [32] used HASTM to solve fractional Drinfeld-Sokolov-Wilson equation. The q-homotopy analysis Sumudu transform method (q-HASTM) is an improvement of q∈[0,1] in HASTM to parameter q∈[0,1n],n≥1 The existence of (1n)m in solution helps in converging quickly.
Our aim is to investigate the fractional model of vibration Equation (1) and get its numerical solution by q-HASTM. The paper is presented as follows. Section 1 is introductory. In section 2, basic results of derivative in Caputo sense, Sumudu transform and its properties are provided. In section 3, mathematical model of time dependent vibration equation of fractional order is discussed along with its necessity and our motivation in finding its solution. In section 4, basic idea of q-HASTM is provided. In section 5, its implementation on fractional vibration equation is shown with convergence analysis. In section 6, we conduct numerical experiments by taking various initial conditions. In section 7, numerical results are discussed using figures and tables while in section 8, we summarize conclusion.
2.
Preliminaries
Definition 2.1. [33] A real function h(χ), χ>0 is said to be in spaces
a. Cζ,ζ∈R if there exists a real number q (>ζ), s.t. h(χ)=χqh1(χ),h1(χ)∈C[0,∞). Clearly,
Cζ⊂Cγ if γ≤ζ.
b. Cmζ,m∈N∪{0} if h(m)∈Cζ.
Definition 2.2. [33] Fractional derivative in Caputo sense [34] of h(t),h(t)∈Cm−1,m∈N∪{0} is:
a.[35] Iζth(x,t)=1Γζ∫t0(t−s)ζ−1h(x,s)ds;ζ,t>0.
b.[35] DvτV(x,τ)=Im−vτ∂mV(x,τ)∂τm,m−1<v≤m
c.[35] DζtIζth(t)=h(t),m−1<ζ≤m,m∈N.
d.[35] IζtDζth(t)=h(t)−∑m−1k=1h(k)(0+)tkk!,m−1<ζ≤m,m∈N.
e.[35] Iβtα=Γ(α+1)Γ(β+α+1)tβ+α.
Definition 2.3. [36] Sumudu transform on domain of functions:
is in the form of S[h(p)]=∫∞0h(wp)e−pdp,w∈(−s1,s2).
Definition 2.4. [36] Sumudu transform for arbitrary order derivative in Caputo sense is:
3.
Mathematical model of time dependent vibration equation of fractional order
Many physical quantities are concerned with the past so to understand their physical models better by inducing the effects of memory, fractional models of such systems get more importance [3]. The FDE accomplish the systems with memory effect. The non-local property is the main benefit of working with FDE in physical models. It signifies that future system state is dependent on former states also. Thus, the models having fractional order derivatives adhere to reality. The integer order model suggested in [4] was found unable to possess memory effect in vibrational motion, so to include these effects, the integer order model is generalized to model of arbitrary order by converting derivative of integer order to fractional order in Caputo sense. The differential equation of arbitrary order [1,5,6,16] for vibration model is given as,
with initial settings:
Caputo’s derivative is suitable for differentiable functions [34] and permits conditions to comprise in modelling a problem. The general response expression contains a parameter that states the arbitrary order of the derivative. It can be varied to get different responses [6]. In case α=2 Eq. (2) reduces to integer order Eq. (1).
It is also observed that the total hierarchy of moments Mk=⟨rk(t)⟩ possess similar time dependence as arbitrary Brownian motion in spite of little difference in their statistical features. In [6], power law decay of solution is found with α in disparity to exponential decay perceived in arbitrary Brownian motion. The time fractional equations depict the particle motion with memory in time. Time fractional derivative proposes inflection of memory. It is obvious that vibrational motion is affected by memory in time. It scripts suitability of fractional modeling for this system. So, the comprehensive study of Eq. (2) to find the numerical solution of this mathematical model is very important. It motivated us to solve Eq. (2) by an efficient and novel numerical scheme q-HASTM.
4.
Basic idea of the proposed method q-HASTM
Consider a general fractional order non-linear partial differential equation of the form:
where Pα signifies the general fractional linear and nonlinear partial differential operator, u(x,t) is an unknown function of independent variables x and t Linear terms of Pα are decomposed to Dα+R where Dα is linear operator of the highest order. (Dαu)(t) is Caputo fractional derivative of u(x,t). R is remains of the linear operator. Eq. (4) may be written as,
where Nu shows non-linear terms.
Applying Sumudu transform [37] in Eq. (5), we get,
Here, S is Sumudu transform operator.
Using property [37] of Sumudu transform, we find,
We state nonlinear operator as,
Here,
q∈[0,1n];n≥1 is an embedding parameter. ξ(x,t;q) is a real valued function of x,q and t
Homotopy is constructed as:
Here, H≠0,ℏ≠0.H is auxiliary function and ℏ is auxiliary parameter. u0(x,t) is an initial guess of u(x,t) and ξ(x,t;q) is unknown function.
By choosing q=0 and 1n;n≥1 in Eq. (9), we get,
As q surges from 0 to 1n,n≥1,ξ(x,t;q) varies from u0(x,t) to u(x,t).
Expanding ξ(x,t;q) in Taylor’s series about q, we get,
where,
If u0(x,t), auxiliary linear operator, ℏ and H(x,t) are suitably selected, series (11) converge at q=1n. Then, we find,
Express vectors as,
Differentiating with regard to q, Eq. (9) m times then dividing by m! and taking q=0, we find deformation equation of m order :
Taking inverse Sumudu transform in Eq. (15),
Here,
Hence, the q-HASTM solution is offered as,
5.
Implementation of q-HASTM on vibration equation of fractional order
We take the fractional order vibration model discussed in section 3 as,
with initial settings,
Applying Sumudu transform, we attain,
Nonlinear operator is
The homotopy is,
For q=0,ξ(r,t;0)=w0(r,t),
and, q=1n′ξ(r,t;1n)=w(r,t).
As discussed in Section 4, the q-HASTM solution will be obtained as,
Theorem[25]. If there exists χ (a constant) as 0<χ<1 such that,
∥ζp+1(r,t)∥≤χ∥ζp(r,t)∥ for all p and
if truncated series ∑kp=0ζp(r,t) is taken as estimated solution ζ(r,t), maximum absolute truncation error is
Proof. We have,
that proves the theorem.
6.
Numerical experiments
In this section, applicability of q-HASTM is illustrated via some test examples.
Test Example 1. Taking initial condition w(r, 0) = r2+ctr in Eq. (2) and using Sumudu transform, we get,
Nonlinear operator is,
Deformation equation for H(r,t)=1 is,
where, æm(→wm−1)=S[wm−1]−(1−kmn)(r2u+cru2)u−uα[S{c2(∂2wm−1∂r2+1r∂wm−1∂r)}].
Taking inverse Sumudu transform in Eq. (24), we get,
Simplification gives,
and so on.
Hence, subsequent iterations wm(r,t),m≥3 can be computed using Maple software package.
The solution is
Test Example 2. Taking w(r, 0) = r+c t r in Eq. (2) and using Sumudu transform, we get,
Also, N[ φ (r,t;q)]=S[ φ (r,t;q)]−(1−kmn)(ru+cru2)u−u α [S{c2(∂2 φ (r,t;q)∂r2+1r∂ φ (r,t;q)∂r)}].
Deformation equation for H(r,t)=1 is,
where, æm(→wm−1)=S[wm−1]−(1−kmn)(r+ucr)−uα[S{c2(∂2wm−1∂r2+1r∂wm−1∂r)}].
Taking inverse Sumudu transform in Eq. (27), we get,
Simplification yields,
and so on.
Hence, subsequent iterations wm(r,t),m≥3 can be found.
The solution is,
Test Example 3. Taking w(r,0)=√r+ct√r in Eq. (2) and using Sumudu transform, we get,
Deformation equation for H(r,t)=1 is,
where, æm(→wm−1)=S[wm−1]−(1−kmn)(√r+cu√r)−uα[S{c2(∂2wm−1∂r2+1r∂wm−1∂r)}].
Taking inverse Sumudu transform in Eq. (30), we get,
Simplification yields:
and so on.
Hence, subsequent iterations wm(r,t),m≥3 can be found.
The solution is,
w(r,t)=w0(r,t)+∑∞m=1wm(r,t)(1n)m.
7.
Results and discussion
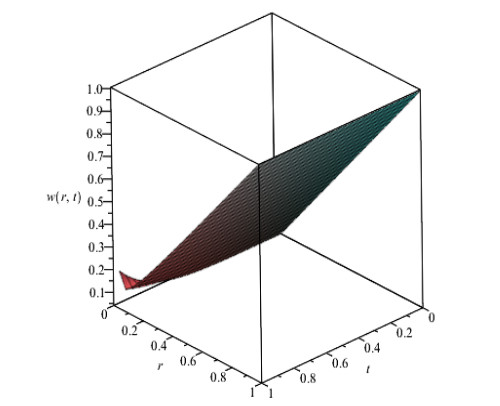
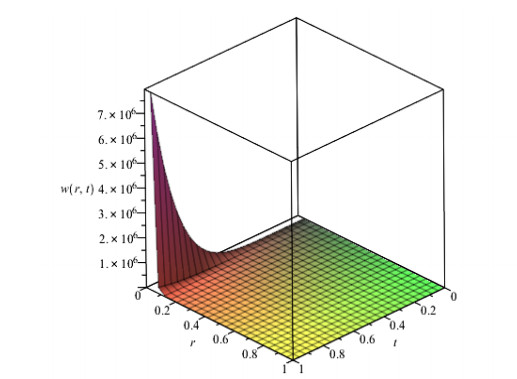
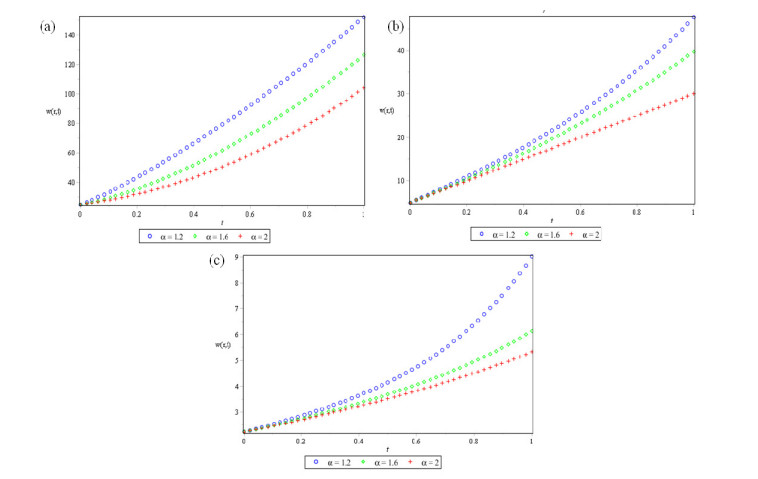
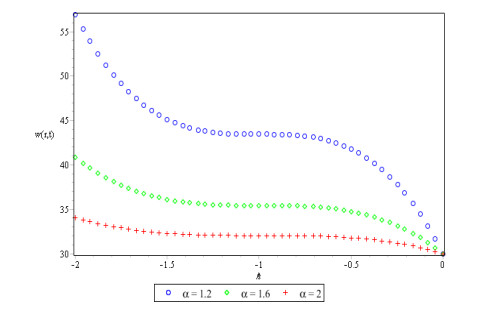
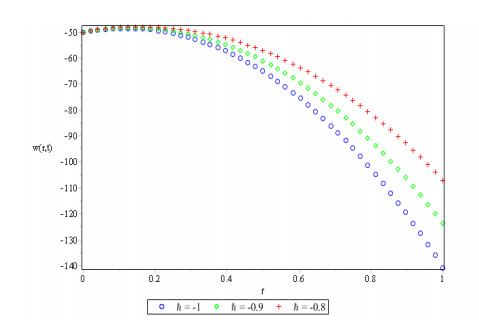
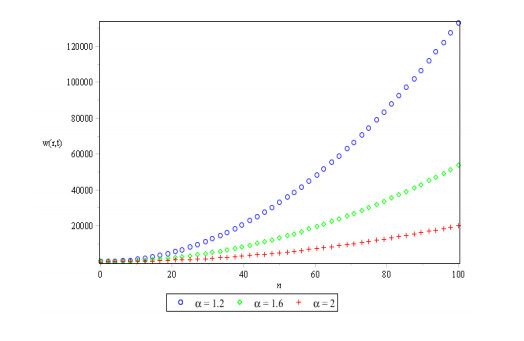
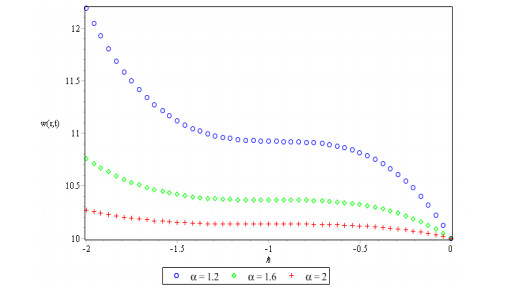
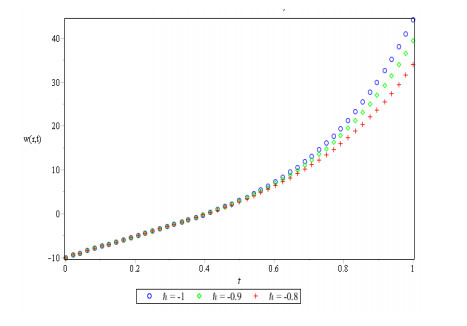
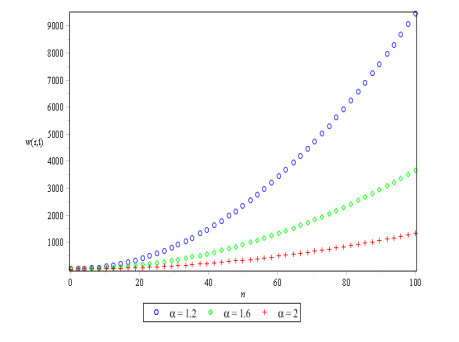
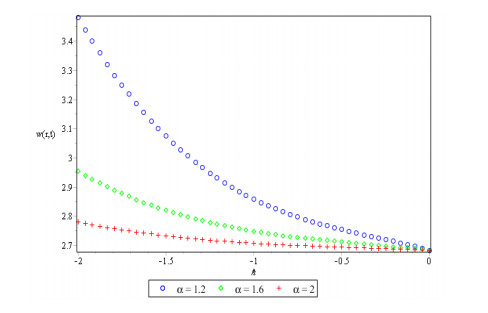
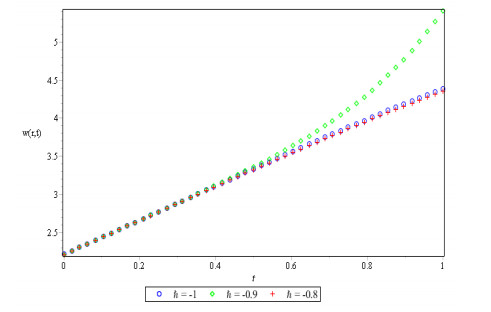
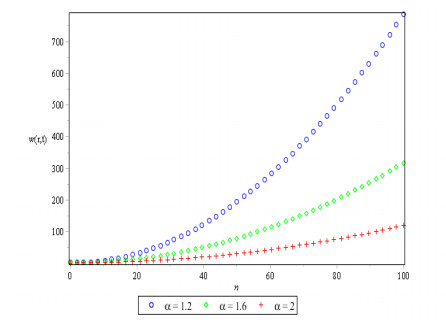
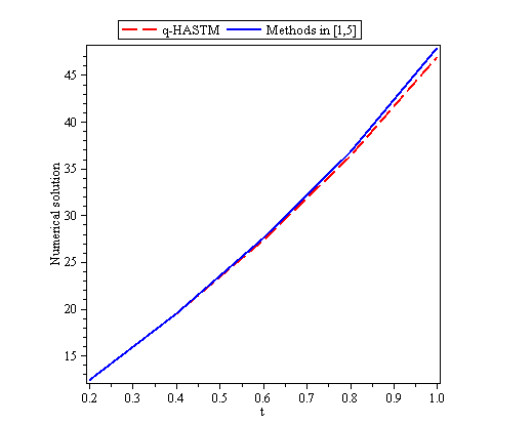
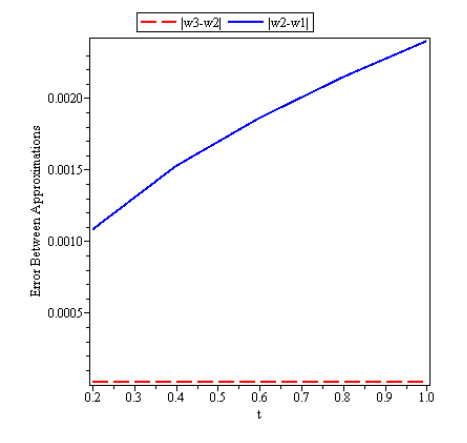
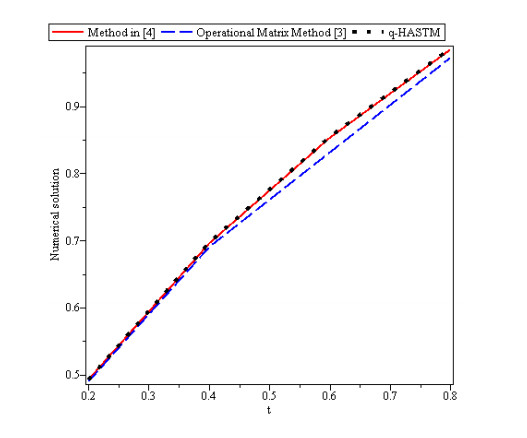
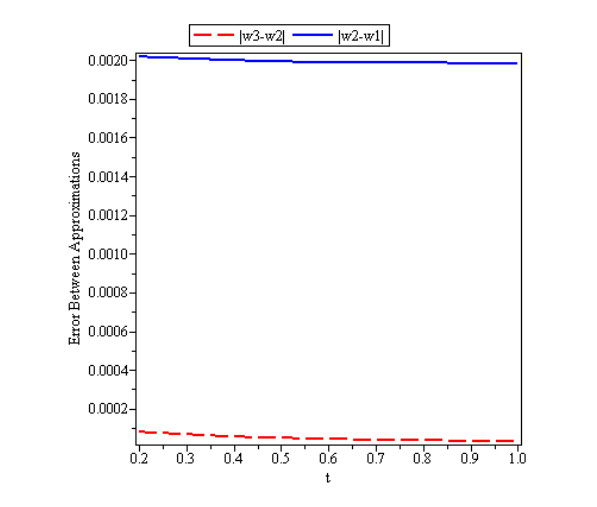
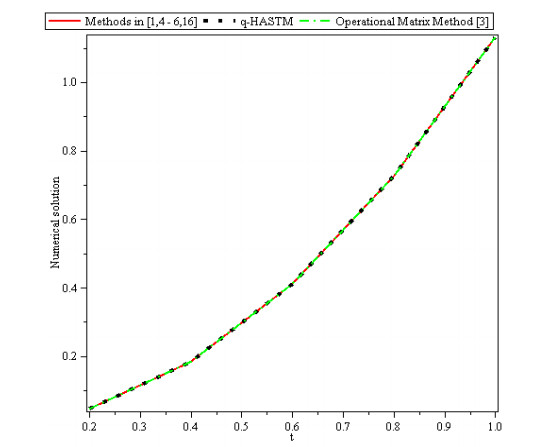
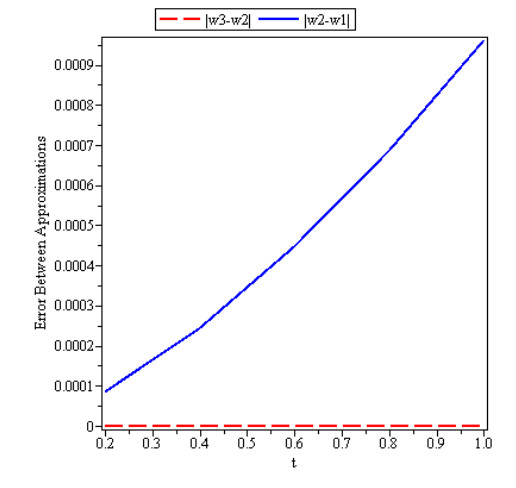
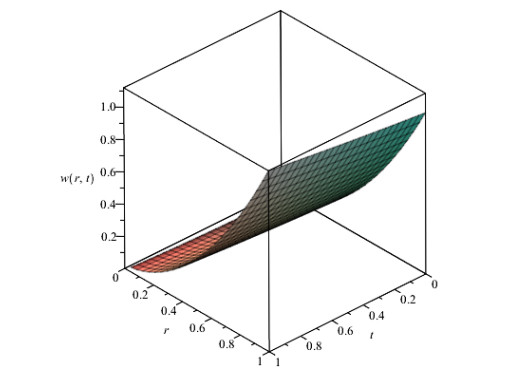
Figures 1, 2 and 3 show behavior of numerical solution of time fractional vibration Eq. (2) acquired at by using q-HASTM for examples 1, 2 and 3 respectively. They have been drawn for to show the nature of the unknown exact solution of the vibration model. Figure 4 shows the plots of solution of Eq. (2) by q-HASTM at taking for examples 1, 2 and 3 respectively. They reveal that increases with increasing t but decreases as arbitrary order increases. This is in total agreement with the point discussed in section 3. In Figures 5, 8 and 11, behaviour of solution Vs. ħ at distinct is shown. In Figures 6, 9 and 12, behaviour of Vs. t at diverse values of are carried out for for examples 1, 2, 3 similarly. Distinct ħ are taken to make residual error small and guarantee solution convergence. In Figures 7, 10 and 13, plots of Vs. n at different values of for are shown for examples 1, 2 and 3 respectively. We notice that by increasing n, increases slowly but decreases with increasing order The legitimacy of solution in convergence region is seen through and -curves. Figure 14 illustrates the comparison of numerical solution obtained by q-HASTM and methods in [1,5] at for example 2. Figure 15 depicts the absolute error between successive approximations at in example 2. It is clear from Figure 15 that there is a sharp decrease in the error between approximations in example 2 which confirms that the obtained solution in example 2 is convergent. Figure 16 shows the comparison of numerical solution by q-HASTM and methods in [3,4] at for example 3. Figure 17 illustrates the absolute error between successive approximations at in example 3. It is clear from Figure 17 that there is a sharp decrease in the error between approximations in example 2 which again confirms that the obtained solution in example 3 is convergent. Figure 18 shows the comparison of solution by q-HASTM and methods in [1,3,4,5,6,16] at for example 1. Figure 19 depicts the absolute error between successive approximations at in example 1 which clearly indicates that the obtained solution in example 1 is convergent. Also, the tabular comparison of results with published work are performed in Tables 1, 3 and 5 at distinct values of order . Tables 2, 4 and 6 show that error between successive approximations is negligible and becomes zero as iterations increase. Hence, it is concluded that the q-HASTM work also for those physical models which have derivatives of arbitrary order and have no exact solution.
8.
Conclusion
In this investigation, q-HASTM is effectively applied to solve the time fractional vibration equation. The outcomes show that the derived results are trustworthy. The simulations shown confirm great accuracy of gained results. It is found that this scheme is capable of diminishing the calculation size. The q-HASTM has parameters that manage solution convergence. It is exciting to observe that the q-HAM works efficiently when coupled with Sumudu transform due to its ‘unity’ feature. Also, the nonlinear term can easily be handled via Sumudu transform. Hence, it is concluded that this scheme is accurate, systematic, logical, easy to use and attractive. It can be applied to study a wide variety of arbitrary order models of physical, biological, medical and social importance.
Conflict of interest
Authors declare that there is no conflict of interest in this paper.









 DownLoad:
DownLoad: