1. Introduction
Longevity is a physiological process depending more than 90% on the genotype and is a species-specific characteristic [1]. Throughout an organism’s life, the efficiency of various physiological processes progressively declines with advancing age [2,3]. The ageing process is irreversible and progressive.
Currently, the most implicated factors correlated with longevity in vertebrate animals and mammals at the cellular level are the rate of mitochondrial ROS production (mROS) [4,5,6,7] and the degree of fatty acid unsaturation of tissue cellular membranes, including the mitochondrial ones [8,9,10].The progressive dysregulation of homeostatic mechanisms associated with aging is thought to be due to an accumulation of oxidative molecular damage [11,12] based on oxygen toxicity [12,13]. Molecular oxygen (O2) can generate partially reduced molecules such as superoxide anion (O2−∙), hydrogen peroxide (H2O2) and the hydroxyl radical (OH.), which represent the incomplete reduction of oxygen due to the acquisition of one, two or three electrons, respectively [14]. These products of partial oxygen reduction are highly reactive and in the absence of an adequate protective system, can cause damage to biological structures. ROS can cause structural and functional damage to lipids, proteins and DNA [15]. The increase in ROS production has been considered a significant factor for the development of the aging process because ROS contribute heavily to cellular oxidative stress associated with aging [16] and age-related diseases [17]. Oxidative DNA damage has been proposed as a major cause of the physiological changes associated with aging and degenerative diseases related. Other potential effects exerted by ROS include decreased mitochondrial function, reduced muscle contractile force, and loss of muscle mass [18]. The primary system which protects against ROS is made up mainly of superoxide dismutase (SOD, the enzyme that catalyzes the dismutation of superoxide radicals), catalase (which converts H2O2 to H2O and O2, ) and glutathione peroxidase (that can metabolize H2O2 and lipid peroxides). The secondary defence system is provided by vitamins E, C, beta-carotenes, as well as glutathione, urates, bilirubin and others, which all have scavenging properties against an overproduction of ROS [3,19]. It worth noting that ROS are also implicated in various important biochemical processes finalized to healthy maintenance such as the mitochondriogenesis [20], they also have functional roles in innate and adaptive immunity, and in initiating secondary signal transduction processes [21,22]. Potential interventions to promote longevity are related to molecular processes that underlie biological aging [23]. Understanding the basic mechanisms of biological aging can help to establish strategies to slow this process, delay age-associated diseases and active appropriate treatments.
The main objective of this review is to discuss the biological mechanisms affecting ROS production, given that these reactive species are involved in both pathological and physiological processes. Both these processes can be exploited in efforts to extend lifespan.
2. The determinants of longevity
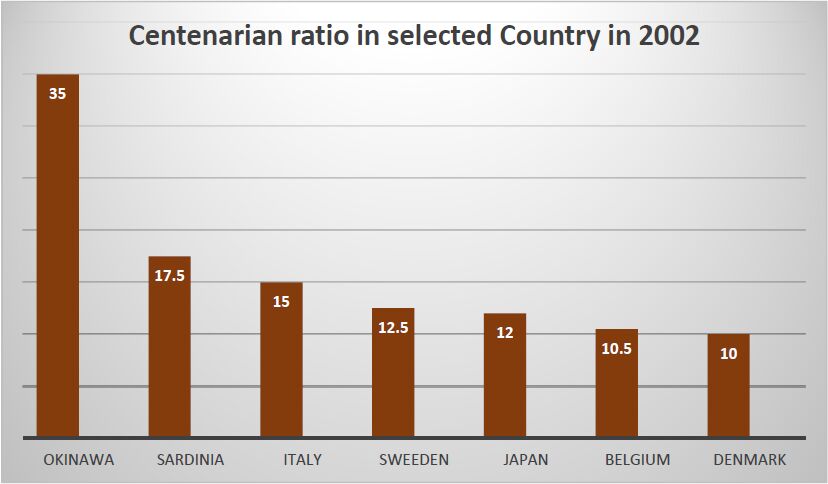
Longevity is one of the fascinating topics of research for human biologists. It has been suggested that people who live longer, such as centenarians, possess genes that protect from aging and diseases [24]. Subjects with exceptionally long life experience the onset of major chronic diseases very late, usually after the age of eighty [25]. Many genes are involved in the maintenance of a healthy status. The Okinawa Centenarian Study represents a rare phenotype among the industrialized countries, with an incidence of centenarians people of 40-50 per 100, 000 persons which are double on Sardinia people and more than three times that of Americans (see Figure 1). Mitochondrial gene variants are the most important genetic factor correlated with longer survival. Mitochondrial DNA (mtDNA) mutates up to 20 times on nuclear DNA, and this mutation accumulates with age [26]. The alteration at mtDNA is responsible for many clinical disorders of the cardiovascular and central nervous system [27] and are correlated with the aging process [28]. In centenarian Japanese, it was found that longevity was correlated with mitochondrial genotype [29]. Based on this concept, ROS-lowering interventions have been proposed to extend lifespan in humans. Various studies conducted on animals have shown that peroxidation of membrane lipids was negatively correlated with longevity. Comparative studies in mammals and birds have shown the existence of a negative correlation between the peroxidation index and a species’longevity in the phospholipids of skeletal muscle and liver mitochondria [30].
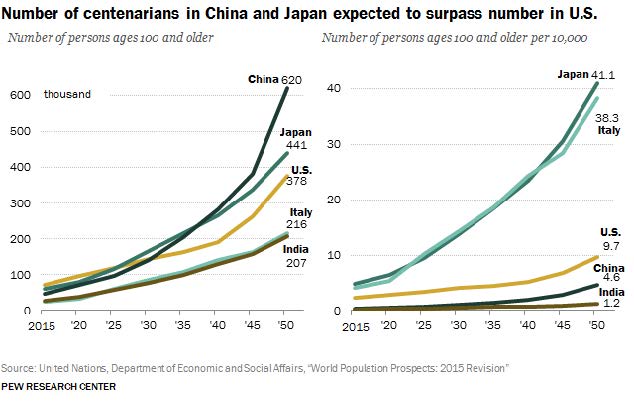
Munro et al. [31] reported that the longest living metazoan species, the Arctica Islandica mud clam, has a maximum longevity of 507 years, remarkable in comparison with other bivalve molluscs, which are characterized by a great difference in longevity (28, 37, 92, and 106 years). Analyzing the composition of phospholipids from the mitochondrial membranes, the authors found that the mitochondrial membrane plays a fundamental role in determining longevity; the peroxidation of membrane lipids was negatively correlated to the longevity, as observed in metazoan Artica Islandica. Oxidative damage in mitochondrial DNA is low in long-lived animals [32]. The degree of unsaturation of membrane fatty acids decreases as longevity increases in the mammalian heart [8]. However, cells are a complex system, and the global cellular oxidative stress depends on the equilibrium of ROS production and ROS elimination. The general balance can contribute to cell survival or death. Nevertheless, due to the complexity of human biology, including genetics, lifestyle and socio-cultural systems, the causes of longevity cannot be extrapolated by lower organisms. The expected longevity in the year 2050 it will be ten times higher more than in the year 2015, particularly in Japan, Italy, and the US (see Figure 2). These data can sustain the importance of lifestyle modifications to improve longevity.
3. The role of mitochondria and ROS in aging
ROS are thought to be the most important factor in determining biochemical and physical changes during the senescence process. Mitochondria, through the respiratory chain, are the major producers of ROS and its components are thus exposed to the hazards of ROS. Evidence suggests, however, that even ROS produced outside the mitochondrion may damage mitochondrial components [33,34], thus impairing mitochondrial functionality. Decreased mitochondrial functionality has been observed in senescence [35], and this decline could be due to different oxidative damages of the cellular constituents. The impairment of mitochondrial components results in a decrease in the electron transfer rate associated with increased ROS production, leading to a vicious circle of increased oxidative stress and oxidative damage. The mitochondrial theory of aging, a variant of the free radical theory of aging (FRTA), proposes that accumulation of damage to mitochondria and mitochondrial DNA (mtDNA) leads to aging of humans and animals. It has been supported by the observation that mitochondrial function declines and mtDNA mutation increase in tissue cells in an age-dependent manner, particularly in tissues with great demand for energy. mtDNA mutations underlie different human pathologies. However, it is possible to distinguish two different groups: primary mitochondrial diseases (PMDs) that are caused by mtDNA defects and secondary mitochondrial diseases (SMDs) caused by defects of nuclear genes encoding mitochondrial proteins (mtDNA encodes only 13 mitochondrial proteins). In both cases, mitochondrial diseases (MDs) have been associated with different deficiencies in mitochondrial function [36]. Despite the suggestion that mitochondria-derived oxidative stress impacts many disease states and aging, the molecular mechanism of aging is still vigorously debated. One of the latest discussions involves the recent observation about the association of respiratory complexes in the form of super-complexes which control ROS generation by the respiratory chain [37].
4. Mitochondrial hormesis
Mitochondrial hormesis, also called mitohormesis, is a positive action induced on mitochondria in response to a mild stress; the same stress, at a higher intensity, would be detrimental to the cell or organism [38]. There is constant renew of mitochondria through a turnover including mitochondria biogenesis and degradation (autophagy), in a process that promotes the maintenance of healthy mitochondria. In healthy cells, autophagy is essential to remove the damaged or aged mitochondria [39]. The exposure of mitochondria to a low dose of a stressor (such as exercise) [40,41,42] triggers an adaptive response inducing biogenesis. At the mitochondrial level, it has been observed that ROS, produced at modest levels by this organelle, can act as second messengers and can trigger mitochondriogenesis [43]. In the contest of mitochondrial hormesis increased ROS formation within the mitochondria evokes an adaptive response that culminates in subsequently increased stress resistance assumed to ultimately cause a long-term reduction in oxidative stress [44,45]. This idea questions the FTRA and rather suggests that ROS act as essential signalling molecules promote metabolic health and longevity. Various transcription factors are involved in the mitohormesis process, including nuclear respiratory factors (NRF-1/NRF-2), the mitochondrial transcription factor A (Tfam), the estrogen receptor α (ERα) and β (ERβ) [46], the transcription factor (PPARγ) and coactivator-1α (PGC-1α) [47]. PGC-1α, a principal co-regulator of mitochondrial biogenesis, metabolism and antioxidant defences [48], activates the silent information regulator-1 and-3 (SIRT1 and SIRT3). SIRT1 mediates the transcription of nuclear and mitochondrial genes encoding for proteins promoting mitochondria proliferation, oxidative phosphorylation, and energy production [49]. Overexpression of SIRT3 or PGC-1α in myotubes decreases basal ROS levels and stimulates mitochondrial biogenesis [50]. The alteration in mitochondrial biogenesis is responsible for damage to skeletal and heart tissue leading to compromised function depending on impaired AMPK-PGC-1α signalling [51]. Adiponectin has potent cardioprotective effects regulating cardiac mitochondrial function by activating the AMPK pathway, improving PGC-1α activity, thereby increasing mitochondrial biogenesis, and attenuating mitochondrial disorders [51]. Interestingly, Yan et al. [50] showed that dysfunction at the mitochondrial level is the first event responsible for and anticipating diseases. PGC-1α is related to the estrogen receptor-α (ER-α) and stimulates the expression of Mfn2 (Mitofusin 2, a mitochondrial membrane protein) [52]. Stimulation of Mfn2 increases oxygen consumption, glucose oxidation, and the expression of oxidative phosphorylation proteins [53]. These studies show that several physiological stimuli such as caloric restriction and exercise activate the mitochondrial adaptation regulating PGC-1α, ER-α, and Mfn2 expression. Healthy mitochondria are essential generators of cellular energy, but in aging people, they become bio-energetically inefficient and are sources of increased ROS formation. Adequate intake of nutrients or certain drugs can maintain mitochondrial homeostasis which represents important preventive and therapeutic approach for age-related chronic diseases [54]. A recent study has found that oxidative stress in pre-diabetics compromised testicular mitochondrial function by repressing the PGC-1α/Sirt3 axis and mDNA copy number, thus declining the respiratory capacity [55]. This study gave new insights into testicular bioenergetics, showing a decreased testicular antioxidant capacity and increased lipid and protein oxidation.
5. Hormonal control of mitochondrial genome
There is an age-related decline in serum levels of testosterone in men [56] and estradiol in menopausal women [57]. The reduction in circulating sex steroids is an important occurrence in the aging process; these hormones influence nuclear and mitochondrial gene transcription to adapt the cell to the changes of energy demands [58]. Testosterone administration combined with low-intensity exercise improved muscle mass and strength in old mice. This effect was correlated with the action of testosterone on mitochondrial biogenesis and with an increase in mitochondrial fusion, fission and reduced oxidative stress [59]. Testosterone deprivation in gonadectomized male rats caused a significant reduction in proteins (NADPH dehydrogenase subunit 1, subunit 4, cytochrome b, and cytochrome c oxidase subunit 1 and subunit 3) in the hippocampus and increased gene expression of PGC-1α. Testosterone administration recovered the expression of the mitochondrial gene and transcriptional co-activators in the brain at the level of the hippocampus [60]. In vivo studies with ovariectomized Wistar rats, the estradiol administration up-regulated the markers of mitochondrial biogenesis and function in skeletal muscle, whereas testosterone showed no effect.
Adiponectin receptor-1 expression was increased by estradiol treatment, both in vivo and in-vitro, but testosterone decreased it [61]. Estradiol and testosterone have an opposite effect on mitochondrial biogenesis and adiponectin levels [62]. Adiponectin increases skeletal muscle mitochondrial biogenesis by suppressing mitogen-activated protein kinase phosphatase-1 [63]. A sexual dimorphism in skeletal muscle mitochondrial function has been previously reported and showed that estradiol is the main effector, enhancing mitochondrial function and reducing oxidative stress. Moreover, there is a link between mitochondrial function and adiponectin expression in skeletal muscle, which could be modulated by sex hormones. Thyroid hormones are also involved in mitochondrial function. A deregulation of the direct triiodothyronine mitochondrial pathway could be one of the parameters involved in the occurrence of sarcopenia, and over-expression of the triiodothyronine receptor determined muscle loss in old mice [64]. Insulin resistance reduces the expression of nuclear-encoded genes involved in mitochondrial oxidative metabolism in skeletal muscle in women with polycystic ovary syndrome [65] and type-2 diabetes [66]. Insulin is also a major regulating factor of mitochondrial oxidative phosphorylation in human skeletal muscle [67]. Defects in oxidative phosphorylation genes and individual transcription co-factors in insulin-sensitive tissues may play an important role in the development of type 2 diabetes and the insulin-resistant state [66]. The co-existence of insulin resistance directly or indirectly related to a reduced mitochondrial function remains to be elucidated. Muscle mitochondrial dysfunction in type 2 diabetes seems to be a functional defect consequent to impaired response to insulin and not intrinsic of the mitochondria [68].
6. The relationship between ROS and diseases
There are many clinical situations related to mitochondrial malfunction and oxidative stress. Mitochondrial dysfunctions due to oxidative stress are involved in the pathophysiology of ischemic heart diseases [69] and they are the prime source of neurodegenerative diseases and myopathies [70,71]. Mitochondria biogenesis plays a central role in neural development, survival, activity, connectivity and plasticity [72]. Alterations at the mtDNA are involved in the pathogenesis and progression of myoclonic epilepsy and ragged red fibres syndrome [73] and skeletal muscle and heart diseases [74,75]. Cardiac dysfunction induced by an excess of ROS production, most likely involves abnormalities in calcium homeostasis [76]. ROS facilitates normal cardiac function through the activation of ryanodine receptor 1 (RyR1) receptor inducing Ca2+ release. However, a high level of ROS production can lead to RyR1 malfunction and aberrant calcium release with consequent contractile dysfunction, arrhythmia, and myopathy [77]. High levels of ROS can determine alteration of cellular homeostasis or defective repair of ROS-induced damage characterized by both neurodegeneration and bone marrow failure as well as cancer [78]. ROS overproduction is also induced mitochondrial dysfunction in the testes, easily targeting spermatozoa DNA and decreasing sperm quality. Rato et al. [79] demonstrated that high-energy diets had detrimental effects on testicular metabolism and sperm production, amplifying subfertility [80]. In pre-diabetic subjects, reduced testicular antioxidant capacity has been observed due to compromised testicular mitochondrial function by repressing the PGC-1α/SIRT3 axis and mtDNA copy number [55]. Oxidative stress activates a signalling pathway as an adaptive response triggered by mitochondrial dysfunction and enables the communication between mitochondria and the nucleus [81]. The mitochondrial loss of function in the elderly could be a consequence and not the cause of the aging process. The severely depressed mitochondrial function due to ubiquinone suppression (involved in mitochondrial electron transport), a membrane antioxidant depletion in the heart, does not acutely impair organ function. However, severe disease phenotypes and shortened lifespan are reversible upon partial restoration of ubiquinone levels and mitochondrial function. This observation strongly suggests that the irreversible degenerative phenotypes characterizing the aging process are not secondarily caused by the gradual mitochondrial dysfunction [82], but that the damage at the mitochondrial level could be a consequence of aging.
7. Muscle exercise and ROS
ROS production from contracting skeletal muscles is known to affect both muscle adaption and function [83,84] and only when generated in excess amounts they contribute to oxidative stress. ROS play a fundamental role in the regulation of skeletal muscle function [84,85] and are involved in the process of muscle fatigue and the dysfunction of various chronic diseases [86]. On the other hand, ROS are useful in facilitating muscle adaptation after stressors such as physical exercise. ROS may mediate the adaptive responses by facilitating glucose uptake or inducing mitochondrial biogenesis [87,88]. ROS can trigger the pathways that result in skeletal muscle remodeling and protein synthesis, encouraging the adaptation of skeletal muscle in response to increased muscular activity [89,90]. ROS are also necessary for remodelling of skeletal muscle after strenuous exercise [91,92]. There is also evidence that ROS are involved in skeletal muscle damage and dysfunction after intense or unaccustomed exercise [93]. The exercise of extreme duration or intensity generates a much higher ROS level that overwhelms the reserves of cellular antioxidants, thus causing tissue damage and altering proteins, lipids, and the DNA repair system. The increase in ROS levels during high-intensity exercise has been proposed to be the major cause of muscle fatigue [94,95]. Kuwahara et al. [94] showed in the skeletal muscle of a genetically modified mice-model, that exercise leads to increased oxidative damage and reduced ATP content in the skeletal muscle tissue, but reported that antioxidant deficiency was not responsible for skeletal muscle atrophy [94,95,96]. These results indicate that oxidative stress generated in mitochondria plays a pivotal role in the progression of exercise intolerance, but not a causal one in age-related muscle atrophy. Moderate exercise determined moderate oxidative stress-induced damage in the same way as exhaustive exercise did, and up-regulated the expression of antioxidant defence systems [97]. The chronic contractile activity of skeletal muscle induces an increase in mitochondria located in proximity to the sarcolemma and mitochondria interspersed between the myofibrils [98]. Acute and chronic exercise attenuates these deficits, restoring mitochondrial turnover and promoting a healthier mitochondrial pool that leads to the preservation of muscle function [99]. Exercise activates key stress signals that positively impact major transcriptional pathways that transcribe genes involved in skeletal muscle mitochondrial biogenesis, fusion, and metabolism. The positive effect of exercise is not limited to younger, healthy adults, but also benefits the elderly and patients with chronic disease [100,101]. By increasing physical capacity with training, the antioxidant function is improved, and ROS production is decreased. A significant correlation between antioxidant capacity and maximal aerobic capacity (VO2 max) has been found [102a>]. In master swimmers, six weeks of high-intensity discontinuous training improved VO2 max (12%), antioxidant activity (+13%) and significantly decreased baseline ROS production (−20%). The study showed that exercise training determines a higher level of antioxidant capacity compared to that in untrained subjects. Vezzali et al. [103] reported that high-intensity discontinuous and continuous moderate-intensity training-induced similar beneficial effects in master runners, reducing the levels of oxidative stress biomarkers in plasma and urine. High-intensity interval training seems to be the most effective training modality to induce significant increases in skeletal muscle oxidative capacity similar to traditional endurance training [104,105]. Conversely, extended periods of skeletal muscle inactivity determine a redox imbalance that probably causes muscle fibers atrophy and a decrease in muscle force production. Skeletal muscle disuse determines an increased ROS production which significantly contributes to muscle atrophy [106]. ROS production plays a key signaling role in immobilization-induced limb muscle atrophy by triggering catabolic signals that contribute to disuse muscle atrophy [107,108]. That is a consequence of activation of the proteolytic pathways leading to muscle atrophy [109,110]. Interestingly, the muscle response to inactivity or exercise is mediated by NF-κB (a redox protein complex that controls transcription of DNA, cytokine production, and cell survival), that regulate as many as 150 genes [111]. In muscle atrophy following denervation and consequent muscle disuse, the loss of mitochondrial content and increased apoptosis signals are prevalently due to increased ROS production [112]. During periods of prolonged disuse, such as bed rest or in hind-limb unloading, oxidative stress increases and activates the proteolytic pathways leading to muscle atrophy [109,110]. Following surgical denervation, ROS production increases dramatically with a greater loss of muscle mass [113]. Apoptosis has been implicated as a mechanism of muscle loss in normal aging and may occurs in a cell through either the caspase-mediated extrinsic or intrinsic pathways that activate the effector apoptotic caspases [114]. The intrinsic apoptotic pathway is mitochondria-dependent and converge at the mitochondrial level in response to different stress conditions [115]. Caspases are central to the mechanism of apoptosis [116] and Caspase 2 and JNK-mediated intrinsic pathway signalling is one of the mechanisms involved in the age-related increase in muscle cell apoptosis [117]. Oxidative stress activates caspase-3 in muscle fibres in vitro and in vivo [118,119] and contributes to muscle protein degradation and fibre atrophy [120]. The inhibition of caspase-3 activity suppresses the proteolysis process in diabetes-mediated cachexia myofiber atrophy [121]. In conclusion, exercise is the only known strategy for improving skeletal muscle mitochondrial function, combating sarcopenia and improving health. Understanding the molecular basis of how physical exercise influences mitochondria in older muscle will improve exercise protocols to maximize beneficial effects in the elderly [122]. However, the reports described above support the hypothesis that ROS could be important signalling molecules that contribute to muscle function.
8. Effect of nutrition on ROS production
Recent advances in the understanding of the genetic basis of lifespan control in yeast, invertebrates, and mammals have been paralleled by increasing evidence that caloric restriction (CR) is the most important non-genetic intervention that robustly extends lifespan in mammals [123] and probably also in humans [124]. The underlying molecular mechanisms of how nutrition can extend lifespan remain largely unknown [125,126]. CR was believed to extend lifespan and reduce age-related diseases in multiple species [125]. While it is known that chronic CR attenuates the increase in age-associated ROS production [127,128], reduces lipid peroxidation [129] and limits oxidative damage in mitochondrial and nuclear DNA [130], it is still a matter of debate whether it is capable of increasing life expectancy. The efficacy of CR has been related to the reduction of caloric intake [131], although similar results have been obtained by the restriction of dietary methionine [132]. In rodents, several studies have demonstrated that the maximum lifespan-extending effect was achieved by a reduction of 40-45% CR while a stronger CR was detrimental [113]. Colman et al. [134] demonstrated that moderate CR in rhesus monkeys lowered the incidence of aging-related deaths (50% of control fed animals survived as compared with 80% of the CR animals). Specifically, CR reduced the incidence of diabetes, cancer, cardiovascular disease, and brain atrophy and attenuated cellular redox stress. The lower rate of mitochondrial H2O2 production [135,136], increased the glutathione GSH/GSSG ratios in mitochondrial and tissue homogenates and enhances the redox potential [137,138,139]. In humans, CR is thought to extend lifespan through different mechanisms, the first of which is by inducing metabolic changes correlated with an improved insulin activity [136]. Fasting insulin level and body temperature are decreased by prolonged CR in humans and represent biomarkers of longevity [140]. Carotid artery intima-media thickness was approximately reduced by 40% in the CR group compared to controls, showing a powerful protective effect against atherosclerosis [141]. Among the mechanisms which favourite longevity should be considered the slowing of growth, the reduction of body fat, immunologic and hormonal changes, enhanced capacity to repair the tissues, changes in gene expression. Furthermore, enhanced autophagy and apoptosis, alterations in IGF/insulin/TOR signalling, hormesis, activation of sirtuins, decrease in body temperature, reduction of metabolic rate, and attenuation of ROS are also determinant factors [125,133,142,143,144,145,146].
9. The risk of undernutrition
Severe undernutrition is a risk factor for mortality. Weight loss can be detrimental to health in patients who are at normal weight. The risk of mortality due to cardiovascular events is equivalent in both underweight and overweight [147,148]. The body mass index (BMI) is of utmost importance in longevity determination. There is an association between extremes in BMI and increased early mortality in the general population. Romero-Corral et al. [149] studied the correlation between BMI and mortality; an increase in mortality rate was observed at lower and higher BMI values. However, many studies and meta-analyses have demonstrated that although obesity is a cardiovascular disease risk factor, there is an“obesity paradox, ”in that overweight and mildly obese patients have a better prognosis than do their leaner counterparts with the same cardiovascular-disease [150,151]. One of the most important physiological aspects to explain the obesity paradox is the reduced muscle mass in underweight patients. A low BMI is predominantly due to low free fat mass, and these patients show lower exercise capacity [152]. Free fat mass correlated with muscle strength is a positive prognostic and protective factor for health [153] and cardio-respiratory fitness for the general population [154] and thus free fat mass can be considered a predictor of exercise capacity and health. Low nutrition influences loss of muscle mass [155] and exercise capacity [156]. Severe CR, as observed in anorexic patients, determined in leukocytes a significant reduction in mitochondrial mass and impairment in mitochondrial function with consequent increased ROS production [157]. Although the mechanisms that determine lifespan in humans are presently poorly understood, it is possible to say that free fat mass and exercise capacity play a fundamental role. Future research concerning mitochondrial dysfunction and oxidative stress under different nutritional and hormonal conditions is necessary to prevent and treat chronic diseases.
10. Caloric excess
Over-nutrition, with the consequent increment of body fat, predisposes to metabolic disorders including insulin resistance, type 2 diabetes, and cardiovascular complications, which together form the metabolic syndrome [158]. Increased body fat deposition, particularly visceral body fat, represents a marker of oxidative stress [159,160]. Oxidative stress is associated with systemic inflammation, endothelial cell proliferation, apoptosis, and increasing risk factors for endothelial dysfunction [161]. Endothelium dysfunction has been associated with several vascular diseases [162]. Bioavailable nitric oxide (NO) production is diminished in dysfunctional endothelium, and this increases vasoconstriction [163]. Adipokines, such as leptin and adiponectin, are involved in the regulation of appetite, energy expenditure, inflammatory response, immunity, cardiovascular function, and reproduction [164]. Leptin, a hormone secreted by adipocytes, regulates energy intake by suppressing food intake and increasing energy expenditure [165], thereby maintaining body weight and fertility [166]. Mutations in leptin or leptin receptor gene lead to severe obesity [167]. Leptin is elevated in obese individuals, and an adverse effect of leptin include oxidative stress [168] mediated by activation of NADPH oxidase [169]. This physiological link may explain the relationship between obesity, oxidative stress and inflammation. Systemic inflammation, diminished the ability to respond to stressors and weakened regenerative capacity are all associated with sarcopenia [170]. Restoring oxidative balance may prevent or delay the onset of sarcopenia. Obesity and a high-fat diet have shown to increase mitochondrial hydrogen peroxide release [171]. In fatty hepatocytes of obese mice, mitochondrial ROS generation is increased by 200% while the activity of detoxifying enzymes is reduced [172]. In humans, a high fat diet increases ROS emission by mitochondria and reduces insulin sensitivity [171]. Abdul-Ghani et al. [173] found that mitochondrial ROS production was not increased in skeletal muscle, in obese insulin-resistant participants, and type-2 diabetes patients. These data do not support the role for increased ROS production in the pathogenesis of insulin resistance. The higher mitochondrial ROS release in type-2 diabetes patients [173] can be explained by a lower in vivo mitochondrial function in type-2 diabetes patients [174,175]. The decrease in mitochondrial ROS production observed by Abdul-Ghani et al. [173] probably reflects the reduced rate of mitochondrial ATP synthesis associated with increased insulin resistance and decreased insulin-stimulated glucose disposal. ROS production capacity measured in vivo in obese and type-2 diabetic participants was not increased. The relationship between ROS enhancement and insulin resistance is complex and not completely understood [176]. Mitochondrial production of ROS may play an important role in determining skeletal muscle insulin sensitivity. Experimental evidence has shown that chronic ROS production has an inhibitory effect on insulin signalling [177], and mitochondrial dysfunction may be a central cause of insulin resistance [178]. Loh et al. [176] demonstrated that increased ROS levels could enhance insulin signalling in vitro and in vivo, reducing insulin resistance. Mitochondrial biogenesis and the response to acute exercise are lower in insulin-resistant non-diabetic participants than in lean control participants [179]. Improving insulin sensitivity through an aerobic exercise in type-2-diabetes patients [180,181] leads to concomitant improvement in vivo mitochondrial function [182]. Hence mitochondrial efficiency can be restored [183]. No low intrinsic mitochondrial activity or low oxidative capacity in insulin resistance in obese type-2 diabetic patients has been observed [184].
11. Nutritional prevention
Macronutrients, carbohydrates, lipids and proteins, provide the bulk of energy requirement for the organism; however, only glucose can be metabolized in the absence of oxygen. ATP generation using fatty acids and amino acids requires mitochondrial oxidative phosphorylation and therefore oxygen. Little investigation has been devoted to the effect of restriction of single macronutrients compared to general CR. The restriction of lipid uptake in mice without CR had no influence on lifespan [185]. The reduction of protein intake results in life extension in mice [186], while essential amino acid supplementation, especially methionine, abolished the lifespan extension effect of CR in flies [187,188]. Other studies showed that amino acid supplementation increased the chronological lifespan of Saccharomyces cerevisiae, and branched-chain amino acids have been shown to extend chronological lifespan in yeast [189]. Methionine restricted diet exerts anti-aging properties and improves mitochondrial biogenesis and aerobic capacity [190,191]. A high protein diet results in increased lipid peroxidation and reduced superoxide dismutase activity [192]. The restriction of dietary glucose in eukaryotic organisms and rodents reduces mortality and extended lifespan, but by an amount that is unrelated to the calorie content of the food [193]. A glucose-free diet does not extend lifespan in rats that show cardio-toxicity, due to increased vacuolization of cardiac myocytes free of both glycogen and lipids [194]. A prolonged high-fat diet induced high ROS formation and vascular cell adhesion molecule (VCAM)-1 expression (indicative of a pro-inflammatory MV phenotype) in primary rat cardiac endothelial cells in vitro [195]. A high-fat diet also results in both a decrease in the mitochondrial quinone pool and a profound modification in mitochondrial lipid composition. These changes appear to play a key role in the resulting inhibition of fatty acid oxidation and mitochondrial oxidative phosphorylation associated with increased mitochondrial ROS production. The mitochondrial quinone pool could have prospects as a crucial event, potentially leading to interesting therapeutic perspectives [196]. The excess in fat and calorie intake in combination with mitochondrial ROS production accelerates steatohepatitis and liver fibrosis in aged animals [197]. A high-fat diet can induce testicular metabolic alterations due to mitochondrial dysfunction, which is closely related to ROS overproduction and oxidative stress. Infertility is a consequence because ROS easily target spermatozoa DNA and lipids, contributing to decreased sperm quality [79].
12. Effect of polyphenols
In Mediterranean countries, the main dietary sources of polyphenols are coffee and fruit, but particularly olive oil and olives [198]. Virgin olive oil exerts an anti-inflammatory effect on the cardiovascular system since it down-regulates cellular and circulating inflammatory biomarkers related to atherogenesis [199]. The increase in polyphenol intake is associated with decreased inflammatory biomarkers, suggesting a dose-dependent anti-inflammatory effect of polyphenols. High polyphenol intake improves cardiovascular risk factors, and the lipid profile [200]. A high intake of total polyphenols, total flavonoids (specifically flavanones and dihydroflavonols), and stilbenes is associated with a reduced risk of diabetes in elderly persons at high risk of cardiovascular disease [198]. Resveratrol, a polyphenol contained in red wine, reduces oxidative stress in skeletal muscle [201] However, resveratrol is ineffective in attenuating sarcopenia [202].
Gordon et al. [203] showed that resveratrol administration (100 mg/kg body mass) in male mice with Duchenne muscular dystrophy improved muscle function without changing oxidative capacity. Similar results were obtained in a mouse model [204]. Tamaki et al. [205] found that resveratrol improved systemic oxidative and nitrosative stress at the gingival tissue and alveolar bone. In a recent review, De Oliveira et al. [206] demonstrated that resveratrol had promising effects on mitochondria in different experimental models. Other reports evidenced the detrimental effects induced by resveratrol on mitochondria [207], so that further clinical studies are needed to establish its potential therapeutic effect, bearing in mind that this molecule is rapidly metabolized in a conjugated form [208]. Curcumin is a major bioactive polyphenol that has been used widely as a spice, food additive and herbal medicine in Asia. Although curcumin directly acts as an antioxidant, its lifespan-prolonging effects seem to be dependent mainly on its indirect antioxidant action (induction of antioxidant proteins) or interference with cellular signalling [209]. However, in spite of a plethora of studies, the answer to the question of whether exogenous antioxidants can prolong life is far from being clear. Results of studies on the supplementation of model organisms with antioxidants are divergent.
13. Vitamin C and E
Isolated vitamin C and E, which have an antioxidant effect because they are capable of scavenging free radicals, are among the most commonly used vitamins for health and muscle damage recovery [210].Vitamin E antioxidant function is strongly supported by regeneration promoted by vitamin C.
Recent studies have demonstrated that antioxidant supplementation may interfere with exercise-induced cell signalling in skeletal muscle fibres [211], and a reduction in cell signalling could reduce or potentially block the adaptations to training [212]. In the skeletal muscle of exercise-trained and sedentary rats, the effects of long-term antioxidant supplementation with vitamin E and alpha-lipoic acid suppressed skeletal muscle mitochondrial biogenesis, regardless of the training status [213]. Gomez-Cabrera et al. [214] found that the administration of high doses of vitamin C in humans and animals affected the adaptation to endurance exercise training. The endurance performance increased significantly more in animals treated with the placebo compared with animals treated with vitamin C. Furthermore, the markers for mitochondrial biogenesis (PGC-1α) increased only in animals treated with the placebo. In humans, Morrison et al. [215] in a double-blinded, placebo-controlled randomized control trial conducted in healthy young males, found that supplementation with vitamin C and E significantly attenuated increased skeletal muscle superoxide dismutase (SOD) activity and mitochondrial transcription factor A. The skeletal muscle oxidative stress were not reduced. Paulsen et al. [216] reported that supplementation with high doses of vitamin C and E blunted the training-induced increase in mitochondrial COX4 protein content. Some of the endurance training-induced adaptations in human skeletal muscles were reduced, and the VO2 max had not increased. Furthermore, several prospective clinical studies were unable to show that supplementation with antioxidants had some health-beneficial effects in humans [217,218,219]. Other reports even suggest that antioxidants may promote cancer growth and increase overall mortality [220,221,222].
14. Conclusions
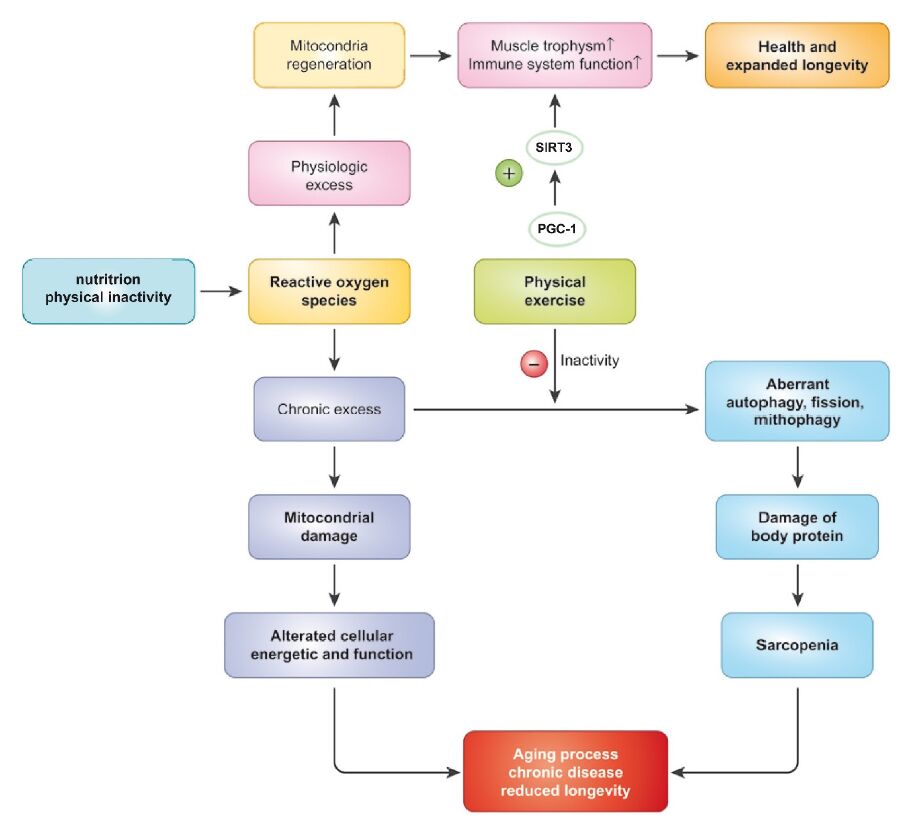
An excess ROS production has been largely accepted to be responsible for ageing process and for promoting chronic diseases, cardiovascular mortality [223] and bone marrow mesenchymal stem cells apoptosis [224]. However, ROS also play an important role as secondary messengers, mediating numerous cellular functions in stem cells such as self-renewal, proliferation, and differentiation, and thus improving health conditions [225]. Therefore ROS production has a dual effect depending on the level and duration of the stress induced. A physiological effect of ROS contributes to expanding longevity by activating the redox-sensitive signalling pathways related to longevity, while a chronic excess activates aging processes and reduces longevity (Figure 3). The study in Okinawans showed the benefits of prolonged CR, and posits that it might contribute to longevity [226]. The specific diet of this population is characterized by being vegetarian 90% [227]. Particular attention should be given to avoiding the risks related to excessive CR and undernutrition. Muscle exercise is the most important stimulator of physiological ROS production [228], as it activates PGC-1α, the most effective stimulator of mitochondriogenesis and gene transcription in liver, heart and skeletal muscle [229]. Activation of PGC-1α can prevent mitochondrial dysfunction for treating neurodegenerative diseases [230] and pathologies, such as diabetes, muscular dystrophies, neurodegenerative diseases or cancer [231]. Finally, sex hormones that decrease with advancing age are responsible for increased mitochondrial dysfunction. Longevity is the expression of an integrated biologic system including nutrition, physical exercise and hormonal equilibrium, which determine physiological ROS production, the messenger of vital utility released from the mitochondria to regulate cell longevity.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: