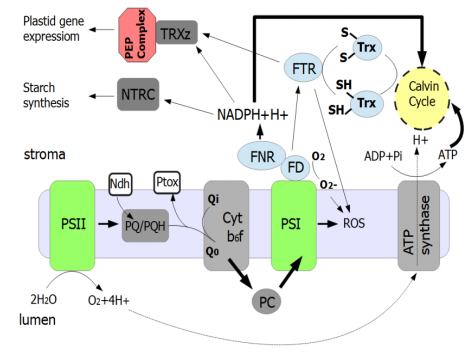
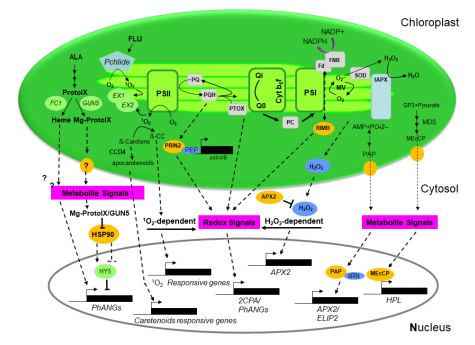
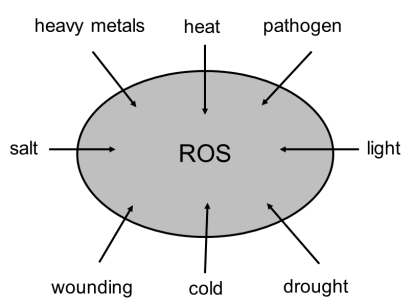
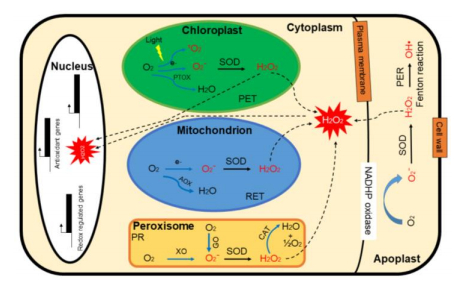
In plants, different stimuli, both internal and external, activate production of reactive oxygen species (ROS). Photosynthesis is considered as high rate redox-metabolic process with rapid transients including light/photon capture, electron fluxes, and redox potentials that can generate ROS; thus, regulatory systems are required to minimize ROS production. Despite their potential for causing harmful oxidations, it is now accepted that redox homeostasis mechanisms that maintain the intracellular reducing environment make it possible to use ROS as powerful signaling molecules within and between cells. Redox and ROS information from the chloroplasts is a fine-tuning mechanism both inside the chloroplast and as retrograde signal to the cytosol and nucleus to control processes such as gene expression/transcription and translation. Wide repertoires of downstream target genes expression (activation/repression) is regulated by transcription factors. In many cases, transcription factors function through various mechanisms that affect their subcellular localization and or activity. Some post-translational modifications (PTMs) known to regulate the functional state of transcription factors are phosphorylation, acetylation, and SUMOylation, ubiquitylation and disulfide formation. Recently, oxPTMs, targeted in redox proteomics, can provide the bases to study redox regulation of low abundant nuclear proteins. This review summarizes the recent advances on how cellular redox status can regulate transcription factor activity, the implications of this regulation for plant growth and development, and by which plants respond to environmental/abiotic stresses.
1.
Introduction
The dynamics of network flows is usually modelled by systems of Partial Differential Equations (briefly PDEs), most of time balance laws. The dynamics is defined on a topological graph with evolution on arcs given by system of PDEs, while additional conditions must be assigned at network nodes, e.g. conservation of mass and momentum. There is a large literature devoted to these problems and we refer to [5] for a extensive survey and for additional references.
In particular, here we focus on water flows on a oriented network of open canals and the model given by Saint-Venant or shallow water equations. The latter form a non linear system of balance laws composed by a mass and momentum balance laws. In water management problems, these equations are often used as a fundamental tool to describe the dynamics of canals and rivers, see [1] and papers in same volume, and various control techniques were proposed, see [2,3,17,15,19,23,26] and references therein. Moreover, the need of dynamic models in water management is well documented, see [25]. The shallow water system is hyperbolic (except when water mass vanishes) and has two genuinely nonlinear characteristic fields. Moreover, it exhibits two regimes: fluvial or sub-critical, when one eigenvalue is negative and one positive, and torrential or super-critical, when both eigenvalues are positive. This is captured by the so called Froude number, see (1). For a complete description of the physics of the problem one needs to supply the equations with conditions at nodes, which represent junctions. The junction conditions are originally derived by engineers in the modeling of the dynamic of canals and rivers. The first and most natural condition is the conservation of water mass which is expressed as the equality between the sum of fluxes from the incoming canals and that from outgoing ones. One single condition is not sufficient to isolate a unique solution, thus different additional condition were proposed in the literature. Physical reasons motivate different choices of conditions, among which the equality of water levels, of energy levels and conservation of energy. For the assessment of coupling conditions on canals networks and for more details on the existence of solutions in the case of subcritical flows, we refer the reader to [9,18,16,20,14,22,24]. For discussion on supercritical flow regimes, we refer the reader to [18] and references there in.
Then, to construct solutions one may resort to the concept of Riemann solver at a junction, see [13]. A Riemann solver at a junction is a map assigning solutions to initial data which are constant on each arc. Alternatively one may assign boundary conditions on each arc, but, due to the nonlinearity of equations, one has to make sure that boundary values are attained. This amounts to look for solutions with waves having negative speed on incoming channels and positive on outgoing ones: in other words waves do not enter the junction. A Riemann solver with such characteristics is called consistent, see also [12].
In this paper we are interested in transitions between different flow regimes, when the transition occurs at a junction of a canals network. We assume to have incoming canals which end at the junction and outgoing canals which start at the junction. Thus we formulate a left-half Riemann problem for incoming canals and a right-half Riemann problem for outgoing canals to define the region of admissible states such that waves do not propagate into the junction. This corresponds to identify the regions where Riemann solvers can take values in order to be consistent. Such regions are enclosed by the Lax curves (and inverted Lax curves) and the regime change curves. To help the geometric intuition, we developed pictures showing such curves and the regions they enclose.
The definitions described above and given in Section 4, are the necessary basis for an analysis on a complex network. Due to the complexity of the problem, we consider as case study the specific case of two identical canals interconnected at a junction (simple junction). We start focusing on conservation of water through the junction and equal height as coupling conditions. It is typically expected the downstream flow to be more regular, thus we consider three cases: fluvial to fluvial, torrential to fluvial and torrential to torrential. In the fluvial to fluvial case there exists a unique solution. However such solution may be different than the solution to the same Riemann problem inside a canal (without the junction) and may exhibit the appearance of a torrential regime. The torrential to fluvial case is more delicate to examine. Three different cases may happen: the solution propagates the fluvial regime upstream, the solution propagates the torrential regime downstream or no solution exits. Finally, in the torrential to torrential case, if the solution exists then it is torrential.
To illustrate the achieved results we perform simulations using a Runge-Kutta Discontinuous Galerkin scheme [6]. The RKDG method is an efficient, effective and compact numerical approach for simulations of water flow in open canals. Specifically, it is a high-order scheme and compact in the sense that the solution on one computational cell depends only on direct neighboring cells via numerical fluxes, thus allowing for easy handling the numerical boundary condition at junctions. In the first example we show a simulation where an upstream torrential regime is formed starting from special fluvial to fluvial conditions. The second example shows how a torrential regime may propagate downstream.
We conclude by discussing the possible solutions if the water height condition is replaced by the equal energy condition.
The paper is organized as follows: in Section 2, we present the model starting from the one-dimensional shallow water equations. In Section 3, we give useful notations and preliminary results that allow to determine the admissible states for the half-Riemann problems discussed in the following Section 4. In Section 5 we study possible solutions at a simple junction for different flow regimes and different junction conditions. Finally, in Section 6 we illustrate the results of the previous section with a couple of numerical tests.
2.
Flow classification and governing equations
The most common and interesting method of classifying open-channel flows is by dimensionless Froude number, which for a rectangular or very wide channel is given by the formula:
where v is the average velocity and h is the water depth. The three flow regimes are:
● Fr<1 subcritical flow or fluvial regime;
● Fr=1 critical flow;
● Fr>1 supercritical flow or torrential regime.
The Froude-number denominator (gh)1/2 is the speed of an infinitesimal shallow-water surface wave. As in gas dynamics, a channel flow can accelerate from subcritical to critical to supercritical flow and then return to subcritical flow through a shock called a hydraulic jump, see [11] and references there in.
We are interested in the transition between different flow regimes when it occurs at a junction of a canals network. On each canal the dynamics of water flow is described by the following system of one-dimensional shallow water equations
The quantity q=hv is often called discharge in shallow water theory, since it measures the rate of water past a point. We write the system as:
where
For smooth solutions, these equations can be rewritten in quasi-linear form
where the Jacobian matrix f′(u) is given by
The eigenvalues of f′(u) are
with corresponding eigenvectors
The shallow water equations are strictly hyperbolic away from h=0 and both 1-th and 2-th fields are genuinely nonlinear (∇λj(u)⋅rj(u)≠0, j=1,2). Note that λ1 and λ2 can be of either sign, depending on the magnitude of v relative to √gh, so depending on the Froude number.
Solutions to systems of conservation laws are usually constructed via Glimm scheme of wave-front tracking [10,21]. The latter is based on the solution to Rieman problems:
Here u(x,0)=(h(x,0),q(x,0)) and ul=(hl,ql) and ur=(hr,qr). The solution always consists of two waves, each of which is a shock or rarefaction, thus we first describe these waves.
(R) Centered Rarefaction Waves. Assume u+ lies on the positive i-rarefaction curve through u−, then we get
where, for the 1-family
for ξ∈[v+−√h−,v−+2√h−), and for the second family
for ξ∈[λ2(u−),∞).
(S) Shocks. Assume that the state u+ is connected to the right of u− by an i-shock, then calling λ=λi(u+,u−) the Rankine-Hugoniot speed of the shock, the function
provides a piecewise constant solution to the Riemann problem. For strictly hyperbolic systems, where the eigenvalues are distinct, we have that
3.
The geometry of Lax and regime change curves
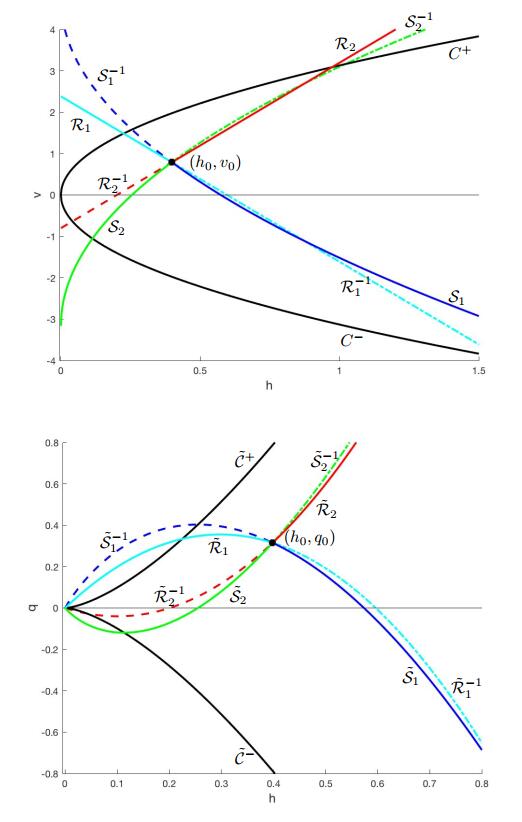
To determine a solution for problems on a network, we need to analyze in detail the shape of shocks and rarefaction curves and, more generally, of Lax curves (which are formed by joining shocks and rarefaction ones, see [4]). We start fixing notations and illustrating the shapes of curves.
For a given point (h0,v0), we use the following notations for shocks and rarefaction curves:
Moreover, we define the inverse curves:
Similarly, we set:
We will also consider the regime transition curves: the 1-critical curve is given by
and the 2-critical curve by
In Figure 1 we illustrate the shape of these curves.
To construct a solution to a Riemann problem (ul,ur), we define the Lax curves. Given a left state ul=(hl,ql) the Lax curve is given by:
For the right state ur=(hr,qr), we define the inverse Lax curve:
Remark 1. The Riemann problem for shallow water equations 2 with left state ul and right state ur has a unique solution if and only if the Lax curves ϕl(h) and ϕr(h) have a unique intersection. In that case, the intersection will be called the middle state um. As shown in Figure 2, the function v=ϕl(h) is strictly decreasing, unbounded and starting at the point vl+2√ghl and, v=ϕr(h) is strictly increasing, unbounded, with minimum vr−2√ghr. Thus, the Riemann problem for shallow water has a unique solution in the region where
When working with (h,q) variables we use the following notations for Lax curves and regime transition curves:
Moreover, for a given value (hi,vi) (or (hi,qi)) we set
3.0.1. The Lax curve ˜ϕl(h)
In this subsection we study in detail the properties of the function q=˜ϕl(h). For a given left state ul=(hl,ql),
with
By computing its first and second derivatives,
and
we can conclude that ˜ϕl∈C2(]0,+∞[). Specifically, in ]0,+∞[ ˜ϕ′′l<0, ˜ϕ′l(h) is strictly decreasing and ˜ϕl is a strictly concave function. As
we investigate two different cases:
Case 1. If vl≤−2√ghl, ˜ϕl is a strictly negative decreasing concave function and specifically ˜ϕl(h)<˜C−(h) for h>0. Therefore, in this case ˜ϕl never intersects the critical curves ˜C+ and ˜C−.
Case 2. If vl>−2√ghl, the function ˜ϕl admits a maximum point hmaxl, so it is increasing in (0,hmaxl) an decreasing in (hmaxl,+∞). In this case the function ˜ϕl intersects the two critical curves ˜C+ and ˜C−. The intersection points vary with the choice of the left state ul, see Figure 3. To compute this points, we distinguish the following subcases: ul is such that −2≤Fl≤1 or such that Fl>1.
Case 2.1. For −2<Fl≤1, it is the rarefaction portion of ˜ϕl to intersect the 1-critical curve ˜C+ at u+l,R=(h+l,R,˜C+(h+l,R)) with
and we have that the maximum point hmaxl is such that ˜ϕl(hmaxl)≡˜C+(hmaxl), i.e. hmaxl≡h+l,R. In the special case Fl=1 we get hmaxl≡hl. Moreover,
Notice that for −2<Fl≤−1 the rarefaction portion of ˜ϕl intersects ˜C− at u−l,R=(h−l,R,˜C−(h−l,R)) with
while for −1<Fl≤1, the shock portion of ˜ϕl intersects ˜C− at u−l,S=(h−l,S,˜C−(h−l,S)) with h−l,S given by the following condition:
Case 2.2. For Fl>1, the maximum value of ˜ϕl is reached by the shock portion and so hmaxl>hl. The shock portion intercepts the critical curve ˜C+ at u+l,S=(h+l,S,˜C+(h+l,S)) with
and the curve ˜C− at u−l,S defined in 21.
Notice that for h≥hl the equation
has two solutions:
Moreover, for Fl>1, we have h∗l>h+l, where the height h+l=(q2l/g)13 is given by the intersection between ˜C+ and the horizontal line q=ql. That is:
Indeed, using the relation q2l=gh3lF2l, if Fl>1 then 2F43l−F23l−1>0. So, for (hl,ql) supercritical, the point (h∗l,ql) is subcritical, i.e. |F∗l|<1.
3.0.2. The Lax curve ˜ϕr(h)
Here we study the properties of the function ˜ϕr(h), given by:
By straightforward computations we get its derivatives:
Then, ˜ϕr(h)∈C2(]0,+∞[) and in ]0,+∞[ ˜ϕ′′l>0, ˜ϕ′l(h) is strictly increasing and ˜ϕl is a strictly convex function. As
we investigate two different cases:
Case 1. If vr≥2√ghr, ˜ϕr is a strictly positive increasing convex function and specifically ˜ϕr(h)>˜C+(h), for h>0. Therefore, ˜ϕr never intersects the critical curves ˜C+ and ˜C−.
Case 2. If vr<2√ghl, the function ˜ϕr admits a minimum point hminr. In this case the function ˜ϕr intersects the two critical curves ˜C+ and ˜C−. As done before we distinguish two subcases:
Case 2.1. For −1<Fr≤2, the rarefaction portion of ˜ϕr intersects the 2-critical curve ˜C− at u−r,R=(h−r,R,˜C−(h−r,R)), with
and we have that the minimum point hminr is such that ˜ϕr(hminr)≡˜C−(hminr), i.e. hminr≡h−r,R. In the special case Fr=1 we get hminr≡hr. Moreover,
For 1<Fr≤2 the rarefaction portion of ˜ϕr intersects ˜C+ at u+r,R=(h+r,R,˜C+(h+r,R)), with
while for −1<Fr≤1, the shock portion of ˜ϕr intersects ˜C+ at u+r,S=(h+r,S,˜C+(h+r,S)), with h+r,S such that
Case 2.2. For Fr<−1, the minimum value of ˜ϕr is reached by the shock portion and so hminr>hr. The shock portion intercepts the critical curves ˜C− at u−r,S=(h−r,S,˜C−(h−r,S)), with
and curve ˜C+ at u+r,S given by 26.
Notice that the equation
has two solutions:
Moreover, for Fr<−1 we have h∗r>h−r=(q2r/g)13, where the height h−r is given by the intersection between ˜C− and the horizontal line q=qr. So, for (hr,qr) supercritical, the point (h∗r,qr) is subcritical.
4.
The half Riemann problems
4.1. Left-half Riemann problem
[The case of an incoming canal] We fix a left state and we look for the right states attainable by waves of non-positive speed.
Fix ul=(hl,ql), we look for the set N(ul) of points ˆu=(ˆh,ˆq) such that the solution to the Riemann problem
contains only waves with non-positive speed. We distinguish three cases:
● Case A: the left state ul is such that |˜Fl|<1;
● Case B: the left state ul is such that ˜Fl>1;
● Case C: the left state ul is such that ˜Fl<−1.
4.1.1. Case A
For this case we refer to Figure 4.We identify the set NA(ul) as the union of three regions IA1, IA2 and IA3 defined in the plane (h,q). The first region is identified by all points that belong to the curve ˜ϕl(h) such that ˜C−(h)≤˜ϕl(h)≤˜C+(h), i.e.
where the points h+l,R and h−l,S are given in 19 and 21 respectively. The second region is defined as follows
The last region IA3 is defined by the set of all possible right states ˆu that can be connected by a 2-shock with non-positive speed to an intermediate state um lying on ˜ϕl(h) curve such that |˜Fm|≤1 and
To define this region, we have to look for values q=hS2(hm,vm;h) as h<hm such that q≥qm. That is,
This inequality is verified for −1≤Fm<0 and for all h≤h∗m with h∗m given by
We obtain (see Figure 4),
4.1.2. Case B
For this case we refer to Figure 5. It is always possible to connect the left value ul to a value u∗l by a 1-shock with zero speed (vertical shock). Specifically, we set h∗l>hl such that q∗l=ql, i.e.
as previously computed in 23. Moreover, as previously observed at the end of subsection 3.0.1 the value (h∗l,ql) falls in the subcritical region, then
where NA(ul) falls under the previous Case A.
4.1.3. Case C
For this case we refer to Figure 6. We have that: if Fl≤−2 then
otherwise if −2<Fl<1 the intersection point u−l,R between hR1(hl,vl;h) and ˜C−(h) given in 20 is different from zero and defines the admissible region
4.2. Right-half Riemann problem
[The case of an outgoing canal] We fix a right state and we look for the left states attainable by waves of non-negative speed. For sake of space the figures illustrating these cases will be postponed to the Appendix.
Fix ur=(hr,qr), we look for the set P(ur) of points ˜u=(˜h,˜q) such that the solution to the Riemann problem
contains only waves with non-negative speed. As in the previous case we identify three cases:
● Case A: the right value ur is such that |˜Fr|<1.
● Case B: the right value ur is such that ˜Fr>1
● Case C: the right value ur is such that ˜Fr<−1.
4.2.1. Case A
For this case we refer to Figure 12 in the Appendix. We identify the set PA(ur) as the union of three regions OA1, OA2 and OA3 defined in the plane (h,q). The first region is defined by all points that belong to the curve ˜ϕr(h) such that ˜C−(h)≤˜ϕr(h)≤˜C+(h), i.e.
where the points h−r,R and h+r,S are given in 24 and 26 respectively.
The second region is such that
The third region is defined by the set of all possible left states ˜u that can be connected by a 1-shock with non-negative speed to a middle state um lying on ˜ϕr(h) curve such that |˜Fm|≤1 and
To define this region we have to look for values q=hS−11(hm,vm;h) for h<hm such that qm≥q. Then, following the same reasoning done for the left-half Riemann problem we get
4.2.2. Case B
For this case we refer to Figure 13 in the Appendix. If F≥2 then
otherwise, if 1≤F<2 the intersection point u+r,R between R−12(ur;h) and C+(h), given in 24 is different from zero and defines the admissible region
4.2.3. Case C
For this case we refer to Figure 14 in the Appendix. It is always possible to connect the right value ur to a value u∗r by a 2-shock with zero speed (vertical shock). Specifically, we set h∗r>hr such that q∗r=qr, i.e.
as done in 27. Moreover, as previously observed at the end of subsection 3.0.2, the point (h∗r,qr) is subcritical and then
where PA(u∗r) falls under the previous Case A.
5.
A simple junction
We consider here as case study a fictitious network formed by two canals intersecting at one single point, which artificially represents the junction. The junction is straight and separates two equal canals, one is the continuation of the other. This simple scenario appears to be like considering a problem for one straight canal, but by adding a fictitious junction we mimic a network and we provide the first analysis necessary for addressing more complicated networks for which the solution strongly depends on the given assumptions at the junction.
We name the canals such that 1 is the incoming canal and 2 is the outgoing ones. We indicate by ub=(hb,vbhb)=(hb,qb) the traces at the junction. The flow is given by the one-dimensional shallow-water equations 2 in each canal coupled with special conditions at the junction. Our aim is to define and solve Riemann problems at the junction.
A Riemann Problem at a junction is a Cauchy Problem with initial data which are constant on each canal incident at the junction. So, assuming constant initial conditions u01, u02 on canal 1 and 2 respectively, the Riemann solution consists of intermediate states ub1 and ub2 such that ub1∈N(u01) and ub2∈P(u02) and verifying given coupling conditions. Here, we are interested in evaluating possible solutions for different types of initial data belonging to different flow regimes. We start assuming, as junction conditions, the conservation of mass
and equal heights
In the following we study the boundary solution ub at the junction in the following interesting cases: A→A, the water flow is fluvial in both incoming and outgoing canals around the junction; B→A, the water flow is torrential with positive velocity in the incoming canal while it is fluvial in the outgoing one; B→B, the water flow is torrential with positive velocity in both incoming and outgoing canals.
Case A→A (Fluvial → Fluvial). Here we assume to have a left state ul and a right state ur such that |Fl|<1 and |Fr|<1. The solution at the junction consists of two waves separated by intermediate states ub1 and ub2 such that
with hb1,hb2>0.
Proposition 1. Under the subcritical condition on ul and ur, the system 42 admits a unique solution.
Proof. We distinguish two cases:
Case 1. The two curves ˜ϕl and ˜ϕr intersect inside the subcritical region (Figure 7). In this case the solution is trivially the intersection point.
Case 2. The two curves ˜ϕl and ˜ϕr do not intersect inside the subcritical region. If hr<hl (specifically h+r,S<h+l,R, see Figure 8) then the only point that verifies the junction conditions 42 is the critical point u+l,R given in 19, thus
If hr>hl (specifically h−r,R>h−l,S, see Figure 9) the only point that verifies the junction conditions 42 is the critical point u−r,R given in 24, then
Remark 2. Notice that the proposed procedure may give a solution which is different from the classical solution of the Riemann problem on a single channel, given by the intersection point of ϕl and ϕr curves, see Remark 1.
Case B→A (Torrential → Fluvial). Here we assume to have a left state ul and a right state ur with Fl>1 and |Fr|<1. The solution at the junction consists of two waves separated by intermediate states ub1 and ub2 such that
with hb1,hb2>0. Next Proposition provides the results about solutions, while the illustrating figures are postponed to the Appendix.
Proposition 2. System 45 admits a solution if the two regions NB and PA intersect in the subcritical set {(h,q):h>0, ˜C−(h)≤q≤˜C+(h)} or if ul∈PA(ur).
Proof. We distinguish two cases:
Case 1. The two curves hS1(h∗l,v∗l;h) and ˜ϕr(h) intersect inside the subcritical region (Figure 15 of the Appendix). If ul∉PA(ur) the solution is trivially the intersection point. On the contrary, if ul∈PA(ur) we have two possible solutions: the intersection point inside the subcritical region or the starting supercritical value ul. So, we may obtain both fluvial or torrential regime. Coherently with the solution that would be obtained in a single channel we choose the fluvial regime assigning as solution the intersection point inside the subcritical region.
Case 2. The two curves hS1(h∗l,v∗l;h) and ˜ϕr(h) do not intersect inside the subcritical region. We distinguish the two subcases shown in Figure 16 and in Figure 17 of the Appendix.
Case 2.1. Referring to Figure 16, the point ul may fall or not in the PB(ur) region. If ul∈PA(ur) the only possible solution is ul self and ub1=ub2=ul; if on the contrary ul∉PA(ur), system 45 does not admit a solution.
Case 2.2. Referring Figure 17, if ul∉PA(ur) the only possible solution is the critical point u−r,R defined in 24, then ub1=ub2=u−r,R; If ul∈PA(ur), both ul self and the critical point u−r,R are admissible solutions. Coherently with the solution obtained in the previous subcase, we select again ul as solution and we assign ub1=ub2=ul. So, the torrential regime propagates on the outgoing canal.
Case B→B (Torrential → Torrential). As shown in Figure 18 of the Appendix, the two admissible regions NB and PB may have empty intersection. So, in this case there exists a solution at the junction which verifies the conditions of conservation of the mass and of equal heights, if and only if ul∈PB(ur), i.e. ub1=ub2=ul.
5.1. Other possible conditions at the junction
Assuming different conditions at the junction give rise to new possible solutions. In canals network problems, it is usual to couple the conservation of the mass with the conservation of energy at the junctions. The specific energy E is a useful parameter in channel flow and it is defined as
For a given flow rate, there are usually two states possible for the same specific energy. Studying E as a function of h for constant q, there is a minimum value of E at a certain value of h called the critical depth,
Critical depth hc corresponds to some critical channel velocity vc defined by Fc=1. For E<Emin solution does not exists, and thus such a flow is impossible physically. For E>Emin solutions are possible: large depth with |F|<1 subcritical flow, and small depth with |F|>1 supercritical flow.
In our case, assuming equal energy at the junction gives
Moreover, assuming qb1=qb2=qb to be constant (and known) we get from 48
where F1=v1/√gh1 and where we used the following relations
Then, we have two possible solution for the heights values at the junction:
or
So, for hb1≠hb2 we get new possible solutions at the junction with (hb1,qb) subcritical and (hb2,qb) supercritical or vice-versa. Specifically, case Torrential→Fluvial and case Torrential→Torrential may admit solution even if their admissible regions have empty intersection in the subcritical set.
Remark 3. In the case of a simple junction, the natural assumption (consistent with the dynamic of shallow-water equations) should be to assume the conservation of the momentum. With our notation, the relation 49 or 48 sholud be replaced by the following:
By the same reasoning used before in the case of the conservation of energy, from 51 we get
Then, we have again two possible relations for the heights values at the junction:
or
So again, for hb1≠hb2 we get new possible solutions at the junction. Case Torrential→ Fluvial and case Torrential→Torrential may have solution and specifically we have that in Figure 16, points (h∗l,ql) and (hl,ql) verify 53 (see 23) and if ul∈PA(ur) they are candidate to be the new solution. Even in the case described in Figure 18, if ul∈PB(ur) the points (h∗l,ql) and (hl,ql) are the solution at the junction.
Let us conclude observing that for appropriate values of (hl,ql), for Torrential→ Fluvial we would get the same solution considering our simple network as a simple canal, i.e. a stationary shock called hydraulic jump characterized indeed by the conservation of the momentum in the transition from a supercritical to subcritical flow [11].
6.
Numerical tests
In this Section we illustrate the results of Section 5 by means of numerical simulations. We first give a sketch of the adopted numerical procedure and then we focus on two numerical tests which illustrate the regime transitions from fluvial to torrential and viceversa. The latter depend on well chosen initial conditions for Riemann problems at the junction.
We consider again a network formed by two canals intersecting at one single point, which represents the junction. Following [6], we use a high order Runge-Kutta Discontinuous Galerkin scheme to numerically solve system 3 on both canals 1 and 2:
The 1D domain of each canal is discretized into cells Cm=[xm−12,xm+12], with xm=(xm−12+xm+12)/2, m=1,…,M, being M the total number of computational cells. The DG method for 3 is formulated by multiplying the equation system by some test functions w, integrating over each computational cell, and performing integration by parts. Specifically, we seek the approximation U=(u1,u2) with ui∈WΔx={w:w|Cm∈Pk(Cm),m=1,…,M}, i=1,2, where Pk(Cm) is the space of polynomials of degree at most k on cell Cm, such that ∀ w∈WΔx
Terms w±m+12 denote left and right limits of the function values and the numerical fluxes ˆfm±12=f(U−m±12,U+m±12) are approximate Riemann solvers. In our simulations, we use the Lax-Friedrich flux. For implementation, each component of the approximate solution U, e.g. u1, on mesh Cm is expressed as
where {ψlm(x)}kl=0 is the set of basis functions of Pk(Cm). Specifically, we choose the Legendre polynomials as local orthogonal basis of Pk(Cm) and take the test function w(x) in eq. 55 exactly as the set of basis functions ψlm(x), l=0⋯k, assuming the polynomial degree k=2. The equation system 55 can then be evolved in time via the method of lines approach by a TVD RK method. More implementation details for RKDG methods can be found in the original paper [7] and the review article [8].
Once the numerical procedure on both canals has been settled, the two systems in 55 have to be coupled with boundary conditions. At the junction the boundary values is settled as follows: at each time step and at each RK stage via the method-of-line approach, we set as left state in 42 (or 45) the approximate solution from canal 1 at the left limit of the junction, i.e.
with [xM−12,xM+12] being the right-most cell in the 1D discretization of the incoming canal 1, and as right state in 42 (or 45) the approximate solution from canal 2 at the right limit of the junction, i.e.
with [x12,x32] being the left-most cell in the 1D discretization of the outgoing canal 2. With this two values, we compute the intermediate states ub1 and ub2 by solving 42 (or 45) and, preserving the mass we directly assign the numerical fluxes at the junction as
Finally, in our simulations we assume Neumann boundary conditions at the free extremity of the channels.
Applying this numerical procedure, in Figure 10 and 11 we give two examples which illustrate the solution that is obtained in the regime transitions from fluvial to torrential and viceversa. In Figure 10, we assume to have a starting configuration given by the following subcritical constant states: ul=(0.25,0.025) on canal 1 (left) and ur=(2.5,0.25) on canal 2 (right). We are in the situation showed in Figure 9 and the boundary value at the junction is defined by the critical value u−rR≈(1.088,−3.55). The solution is a backward water movement along canal 1 with a torrential regime. In Figure 11, we assume as initial state on canal 1 the supercritical constant value ul=(0.2,3) and on canal 2 the subcritical constant value ur=(1.8,4). We are in the configuration given in Figure 16 and the boundary value at the junction is defined by the starting point ul. The solution is a forward movement with positive velocity, so the torrential regime propagates on canal 2.
7.
Conclusions
This paper deals with open canal networks. The interest stems out of applications such as irrigation channels water management. We base our investigations on the well-known Saint-Venant or shallow water equations. Two regimes exist for this hyperbolic system of balance laws: the fluvial, corresponding to eigenvalues with different sign, and the torrential, corresponding to both positive eigenvalues. Most authors focused the attention on designing and analysing network dynamics for the fluvial regime, while here we extend the theory to include regime transitions. After analyzing the Lax curves for incoming and outgoing canals, we provide admissibility conditions for Riemann solvers, describing solutions for constant initial data on each canal. Such analysis allows to define uniquely dynamics according to a set of conditions at junctions, such as conservation of mass, equal water height or equal energy. More precisely, the simple case of one incoming and outgoing canal is treated showing that, already in this simple example, regimes transitions appear naturally at junctions. Our analysis is then visualized by numerical simulations based on Runge-Kutta Discontinuous Galerkin methods.
Acknowledgments
M. Briani is a member of the INdAM Research group GNCS.
Appendix
Here we collect additional figures illustrating attainable regions for half-riemann problems and solutions for a simple channel. Figures 12-14 refer to the right-half Riemann problem described in Section 4.2. They show the regions of admissible states such that waves on the outgoing canals do not propagate into the junction, given a right state ur such that |˜Fr|<1, ˜Fr>1 and ˜Fr<−1 respectively.
Figures 15-18 refer to Section 5 in which we study the possible solutions at a simple junction for different flow regimes, assuming the conservation of mass and equal heights at the junction. Specifically, Figures 15-17 illustrate the possible configurations and their associated solution that may occur during the transition from torrential to fluvial regime. The last Figure 18 shows instead the only possible configuration that admits a solution for the torrential flow regime.









 DownLoad:
DownLoad: