Distributed model predictive control of irrigation canals

1.   Introduction

In nature, there are many predator-prey relationships among various organisms, and this is also the reason for the balance of nature. This relationship has gone through a long process of natural evolution. Predators and prey have formed various adaptations of predation and anti-predation in structure, physiology, habits and lifestyle, forming a certain balanced relationship. In 2012, Choh et al. ^[1] found a phenomenon in an experiment that there is a role reversal (anti-predator behavior) between predators and prey. When the prey species were threatened, in order to survive and reproduce, they will fight back, and even kill the predators' juveniles. In 2013, Hoover et al. ^[2] revealed that fathead minnows exhibit typical anti-predator behavior; as a response to the predator scent signatures and chemical alarm cues, they will go into shelters and decrease activity. In 2015, O'Connor et al. ^[3] revealed that stimulated by the predators, cichlid fish species spend less time exploring and more time searching for cover and congregating with other similar species to avoid being attacked by predators. In addition, researchers have revealed that in the presence of predation hazards, many species such as the three-spined stickleback ^[4], monkey goby ^[5], red tilefish ^[6] and other species will exhibit anti-predator behavior.

To characterize the anti-predator behavior of prey species and analyze its impact on the dynamics of the system, many scholars have introduced the anti-predator effect into the predator-prey model ^{[7,8,9,10,11,12]}; among others, Tang and Xiao ^[7] revealed that the predator will go extinct as a consequence of the anti-predator behavior, which means that anti-predator behavior can aid prey species in resisting predator aggressiveness. Sun et at. ^[8] introduced a kind of anti-predator behavior, which occurs only when the prey group size is larger than a threshold. Mortoja et al. ^[9] introduced anti-predator behavior into a stage-structure model, and, through numerical simulations, they found that the anti-predator factor may change the system's stability. Prasad ^[10] analyzed an additional food provided predator-prey system with anti-predator behaviour in prey. Sirisubtawee et al. ^[11] introduced anti-predator behavior into an impulsive Holling type IV predator-prey model, and discussed the complex dynamics such as the periodic solution of the impulsive model. Tian and Gao ^[12] presented a predator-prey model with an anti-predation effect and prey-dependent threshold control and analyzed the dynamics of the proposed model.

On the other hand, fishing activities are carried out for both commercial and livelihood needs. However, it is worth pointing out that overfishing will always lead to depletion of fishery resources. Therefore, rational management of fishery resources is necessary from the perspective of renewable resources protection, and appropriate fishing levels can not only protect fishery resources, but also maximize profits. Fishing activities can be carried out in different manners, which include continuous form ^[13,14,15], semi-continuous form ^[16], periodic form ^[17,18] and state-dependent form ^[19,20,21]. Fishing activity is a typical human activity and it is usually determined by the density of the fish population. State-dependent harvesting strategy takes the current state of the species into consideration and avoid the adverse impacts on the sustainability of the species. There are many cases of human intervention in real world problems, which often occur at state-dependent times or involve state-dependent thresholds. For such situations, state-dependent strategies are usually used to model this phenomena or problems, and the corresponding system can be described by impulsive semi-dynamical systems (ISDSs) ^{[22,23,24,25]}. In the past two decades, many scholars have applied the theory and method of impulsive semi-dynamic system into different subjects and scientific problems, such as pest control ^{[26,27,28,29,30]}, disease control ^[31,32], process of sugar manufacturing ^[33], prey-predator system ^{[34,35,36,37,38]}, competitive system ^[39] and other subjects ^[40,41]. Predator-prey systems based on state feedback control had received much attentions, the corresponding models can be divided into predator-dependent ^[19,20], prey-dependent ^{[42,43,44,45]}, ratio-dependent ^[46,47] and prey-predator hybrid-dependent ^[21,48,49]. In natural systems, predators and prey are mixed, so it is impossible to determine the exact number of the two species, but their proportions are usually kept constant. Based on this consideration, a weight capture strategy was introduced into a fishery model ^[21], where fishing activity is permitted when the weighted sum of both species populations reaches a threshold. In the current work, we present a predator-prey model with anti-predator behavior and analyze how anti-predator behavior affects system dynamics. Then, following application of the weight capture strategy to the system, we analyze the complex dynamics induced by a discontinuous weighted fishing strategy. In addition, in order to obtain the optimal fishing strategy that maximizes economic profits, we discuss the problem of fishing process optimization.

The article structure is as follows. In Section 2, we propose a predator-prey model for fisheries with anti-predator behavior and construct a capture model based on weighted fishing strategies, followed by presenting some basic knowledge. In the next section, we first investigate the effects of anti-predator behavior on system dynamics, and then discuss the complex dynamics of the system induced by a weighted fishing strategy. In addition, in order to maximize the economic profit, we carried out the study of the optimization of the fishing process. In Section 4, we discuss the numerical simulations performed to verify the theoretical results obtained in the previous section. In the last section, we present a summary and discussion.

2.   Mathematical model and basic knowledge

Let $x$ denote the prey density and $y$ denote the predator density. Then the classical predator-prey model can be expressed as follows:

where, $B(x)$ describes the prey growth rate, $D(x)$ represents the functional response, $s$ represents the predator mortality rate and $\mu$ denotes the conversion rate from prey to predator. In this study, the logistic type growth rate and Holling-II type functional response are considered, i.e., $B(x) = rx(1-x/K)$ and $D(x) = bx/(1+h_{1}x)$.

When the prey species shows anti-predator behavior, let $p$ characterize the anti-predator rate of the prey; the term $-pxy$ is added to the change rate of predators. Then, Model (2.1) takes the form

where $r$ describes the intrinsic growth rate, $K$ represents the environmental capacity, $b$ denotes the predation rate, $h_1$ is the saturation constant, $h = h_{1}+bh_2$ and $h_2$ describes the conversion saturation constant. Considering the biological significance of the model, the study is regionally limited in $\Omega_{0} = \{(x, y)|0\leq x\leq K, \; y\geq 0\}$.

For both commercial and livelihood needs, fishing activities are carried out when the fish populations satisfy certain conditions. Let $w$ denote the proportion of prey species, $(1-w)$ be the proportion of a predator population, $H$ denote the threshold of the weighted sum of both species populations, $E$ represent the capture strength and $q_i$ ($i = 1, 2$) denotes the capture rate. Besides, in order to prevent the extinction of predators caused by anti-predator behavior, a quantity of predator pups, denoted by $\tau$, is released into the system. Based on the above capture strategies, the predator-prey model guided by the weighted fishing strategy is as follows:

where $\tau$ satisfies that $\tau < \min\{\tau_1, \tau_2\}$, and

The research objective of this paper is to analyze how anti-predator behavior affects the dynamics of System (2.2), and also to discuss the complex dynamics of the Model (2.3) induced by a weighted fishing strategy. Besides, to obtain an optimal capture strategy that maximizes the economic profit, we discuss the problem of fishing process optimization.

We present some basic concepts and results of an ISDS for convenience, and the readers are referred to the literature ^{[21,23,25,29,30,45]}.

Let us consider a planar impulsive model with following threshold

where $f_i$, $I_i$ and $\chi$ are differentiable with respect to $x$ and $y$. Let $\Omega$ represent the domain of solutions and $\pi = (\pi_1, \pi_2):$ $\Omega\times R\rightarrow \Omega$ characterize the solution map of the corresponding continuous system; define $\mathcal{M}\triangleq\{(x, y)\in \Omega|\chi(x, y) = 0\}$ and $I = (I_1, I_2)$: $\mathcal{M}\rightarrow \mathcal{N} = I(\mathcal{M})$. Then we call the system constituted by (2.4) as an ISDS, which is denoted by $(\Omega, \pi; I, \mathcal{M})$. For any point $S_0\in \mathcal{N}$, the solution of $(\Omega, \pi; I, \mathcal{M})$ from $S_0$ is denoted by $\mathbf{z}(t) = (x(t), y(t))'$, i.e. $\mathbf{z}(0) = \mathbf{z}_0\triangleq S_0$. The orbit is denoted by $\gamma_{S_0}(\mathbf{z})\triangleq\{\mathbf{z}(t)|t\geq 0, \mathbf{z}(0) = S_0\}$. If $\gamma_{S_0}(\mathbf{z})\cap \mathcal{M}\neq \emptyset$, the trajectory $\mathbf{z}(t)$ will reach the pulse set $\mathcal{M}$ many times due to the pulse action; the set of the time is denoted by $\Sigma\triangleq\{t_k|k = 1, 2, \cdots\}$, i.e. $\mathbf{z}^{-}_k = \mathbf{z}(t_k)\in \mathcal{M}$ and $\mathbf{z}_k = I(\mathbf{z}^{-}_k)\in \mathcal{N}$.

Definition 2.1 (Periodic solution ^{[21,23,29,30,45]}) The solution $\tilde{\mathbf{z}}(t)$ with $\tilde{\mathbf{z}}_0\in \mathcal{N}$ is said to be periodic if there exists $n \geqslant 1$ satisfying $\tilde{\mathbf{z}}_{n} = \tilde{\mathbf{z}}_{0}$. Denote $m\triangleq\min\{k|1\leq k\leq n, \tilde{\mathbf{z}}_{k} = \tilde{\mathbf{z}}_{0}\}$; then, $\tilde{\mathbf{z}}(t)$ is called an order-$m$ periodic solution with period $T = t_{m}$.

Definition 2.2 (Oorbitally asymptotically stable ^{[21,23,29,30,45]}). For the periodic solution $\tilde{\mathbf{z}}(t)$, if for an arbitrary $\epsilon > 0$, there is a neighborhood $U_{\delta}$ of $\mathbf{\tilde{z}}$, for any $\mathbf{z}\in U_{\delta}$, there exists a re-parameterized function $\hat{t}(t)$ and $|\mathbf{z}(t)-\mathbf{\tilde{z}}(\hat{t}(t))| < \epsilon$ for all $t\geq t_0$; then, $\gamma(\mathbf{\tilde{z}})$ is called orbitally asymptotically stable.

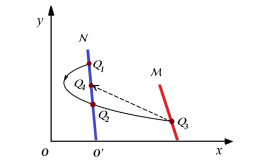
Definition 2.3 (Successor function ^[23,29,30]). Let us assume that $\mathcal{M}$ and $\mathcal{N}$ in $(\mathbb{R}^2_{+}, \pi, \mathbb{R}_{+}; \mathcal{M}, I)$ are two disjoint lines. Denote $\mathcal{N}\cap x\mbox{-axis} = \{O'\}$. For a given $Q_1\in \mathcal{N}$, denote $\gamma_{Q_1}(\mathbf{z})\cap \mathcal{M} = \{Q_3\}$, $\gamma_{Q_1}({\mathbf{z}})\cap \mathcal{N} = \{Q_2\}$ and $Q_4 = I(Q_3)$, as illustrated in Figure 1. Then the type-I successor function ${{f}}^{\text{I}}_{\text{sor}}$ is defined by ${{f}}^{\text{I}}_{\text{sor}}(Q_2) = d(Q_4, O')-d(Q_2, O')$, and the type-II successor function ${{f}}^{\text{II}}_{\text{sor}}$ is defined by ${{f}}^{\text{II}}_{\text{sor}}(Q_1) = d(Q_4, O')-d(Q_1, O')$.

Figure 1.  Schematic diagram of successor function.

DownLoad: Full-Size Img PowerPoint

Lemma 2.1 (Stability criterion ^{[21,23,29,30,45]}). The order-$m$ periodic solution $\mathbf{z}(t) = (\xi(t), \eta(t))'$ with the period $T$ is said to be orbitally asymptotically stable if $\vert \mu_m \vert < 1$ holds, where

with

$f_1^+ = f_1(\xi (\tau_j^ +), \eta (\tau_j^ +))$, $f_2^+ = f_2(\xi (\tau_j^+), \eta (\tau_j^+))$ and $f_1$, $f_2$, $\frac{\partial {I_1} }{\partial x}$, $\frac{\partial {I_1} }{\partial y}$, $\frac{\partial {I_2} }{\partial x}$, $\frac{\partial {I_2} }{\partial y}$, $\frac{\partial \chi }{\partial x}$ and $\frac{\partial \chi }{\partial y}$ are calculated at $(\xi(\tau_j), \eta(\tau_j))$.

3.   Dynamical analysis of Systems (2.2) and (2.3)

This section focuses on analyzing the dynamics of the free system (2.2) and the capture system (2.3), respectively. Since, in the case of $\mu b \leqslant sh$, there is $\text{d}y/\text{d}t < 0$, i.e., the predator species will eventually become extinct. Therefore, from the perspective of ecological diversity, it is assumed that $\mu b > sh$.

3.1.   Dynamics of System (2.2)

For System (2.2), we mainly discuss the existence and stability of equilibria. For convenience, denote

and $y^{p}_{i} = F(x^{p}_{i})$, $i = 1, 2$.

Define

Let $\overline{p}\in (0, p_1)$ satisfy $g(\overline{p}) = 0$. Since the dynamic behavior of System (2.2) are related to the parameters $p$ and $K$, we divide the analysis into the following three cases:

($A1$): $0\leq p\leq p_1, x^{p}_{1} < K\leq x^{p}_{2}$;

($A2$): $0 < p < p_1, K > x^{p}_{2}$;

($A3$): $p > p_1$.

Further, ($A1$) is divided into five subcases:

($A1$-1): $0\leq p\leq \overline{p}$, $x^{p}_{1} < K\leq 2x^{p}_{1}+1/h_1$;

($A1$-2): $0\leq p\leq \overline{p}$, $2x^{p}_{1}+1/h_1 < K\leq x^{p}_{2}$;

($A1$-3): $\overline{p} < p < p_1$, $x^{p}_1 < K\leq x^{p}_2$;

($A1$-4): $p = p_1$, $x^{p}_{1} < K\leq x^{p}_{2}$

and ($A2$) is divided into three subcases:

($A2$-1): $\overline{p} < p < p_1$, $x^{p}_2 < K < 2x^{p}_{1}+1/h_1$;

($A2$-2): $0\leq p < p_1$, $K > \underline{K}\triangleq \max\{2x^{p}_{1}+1/h_1, x^{p}_2\}$.

3.1.1.   Existence of equilibria

In System (2.2), $E_O(0, 0)$ and $E_K(K, 0)$ always exist.

Theorem 3.1. In System (2.2), if Case ($A1$) holds, there exists a unique positive equilibrium $E_1$; if Case ($A2$) holds, there exists two positive equilibria $E_1$ and $E_2$; for Case ($A3$), the positive equilibrium does not exist.

Proof of Theorem 3.1. Define $Q_0(x) = (1+hx)Q(x)$. Then, System (2.2) has a positive equilibrium if and only if the equation $Q_0(x) = 0$ has a positive root less than $K$. Since $Q_0(x) = 0$ does not have a positive root when $p > p_1$, the positive equilibrium does not exist for Case ($A3$). While, for $0\leq p\leq p_1$, we have the following cases:

Case I: $p = 0$. Then $Q_0(x) = 0$ has a unique positive root $x = x^{0}_{1}$. Let $y^{0}_{1} = F(x^{0}_{1})$. Then $E_{1}(x^{0}_{1}, y^{0}_{1})$ is a positive equilibrium if $K > x^{0}_{1}$;

Case II: $0 < p < p_{1}$. In this case, $Q_0(x) = 0$ has two positive roots $x = x^{p}_{1}$ and $x = x^{p}_{2}$. Let $y^{p}_{i} = F(x^{p}_{i}), i = 1, 2$. When $x^{p}_{1} < K \leqslant x^{p}_{2}$, $E_{1}(x^{p}_{1}, y^{p}_{1})$ is a unique positive equilibrium. When $K > x^{p}_{2}$, $E_{1}(x^{p}_{1}, y^{p}_{1})$ and $E_{2}(x^{p}_{2}, y^{p}_{2})$ are two positive equilibria.

Case III: $p = p_{1}$. In this case, $Q_0(x) = 0$ has two identical positive roots $x_{E_{1}} = x^{p_1}_1$. Let $y^{p_1}_{1} = F(x^{p_1}_{1})$. If $K > x^{p_1}_{1}$, then $E_{1}(x_{E_{1}}, y_{E_{1}})$ is a unique positive equilibrium.

3.1.2.   Stability of equilibria

For any equilibrium $\overline{E}(\overline{x}, \overline{y})$, the Jacobian matrix is

The corresponding characteristic equation is

where

Theorem 3.2. $E_O(0, 0)$ is a saddle point and unstable. $E_K(K, 0)$ is a saddle point for Cases ($A1$-1)–($A1$-3), and it is locally asymptotically stable for Cases ($A1$-4), ($A2$) and ($A3$). $E_1(x^{p}_1, y^{p}_1)$ is locally asymptotically stable for Cases ($A1$-1), ($A1$-3) and ($A2$-1), and unstable for Cases ($A1$-2), ($A1$-4) and ($A2$-2). $E_2$ is a saddle point and unstable for Case ($A2$).

Proof of Theorem 3.2. Since $q_{E_{O}} = -rs < 0$, $E_O$ is a saddle point. Given that $q_{E_{K}} = -rQ(K)$, and for Cases ($A1\mbox{-}1$)–($A1\mbox{-}3$), $Q(K) > 0$; then, $E_K$ is a saddle point. For Case ($A1$-4), ($A2$) and ($A3$), $Q(K) < 0$ and $p_{E_{K}} = Q(K)-r < 0$; then, $E_K$ is locally asymptotically stable. When $K = x^{p}_{2}$, there is $Q(K) = 0$; in this case, $E_K$ is a saddle-node.

For $\overline{E}(\overline{x}, \overline{y})$, we have

For Cases ($A1$-1), ($A1$-3) and ($A2$-1), there exist $q_{E_1} > 0$ and $p_{E_{1}} < 0$ due to $Q_{0}'(x^{p}_{1}) > 0$ and $K < 2x^{p}_{1}+1/h_1$, which implies that $E_{1}(x^{p}_{1}, y^{p}_{1})$ is locally asymptotically stable; for Cases ($A1$-2) and ($A2$-2), there is $p_{E_{1}} > 0$; then, $E_{1}(x^{p}_{1}, y^{p}_{1})$ is unstable. For Case ($A1$-2), there is $\dot{y}\leq 0$ and $\dot{y} = 0$ if and only if $x = x^{p}_1$, so $E_1$ is unstable. For Case ($A1$-2), a limit cycle $\Gamma_{LC}$ exists around $E_1$. Since $Q_{0}'(x^{p}_{2}) < 0$ for Case ($A2$), i.e., $q_{E_2} < 0$, $E_{2}(x^{p}_{2}, y^{p}_{2})$ is a saddle point and unstable.

3.2.   Dynamics of the capture system (2.3)

For System (2.3), there are

and we denote $k_\mathcal{M}\triangleq -w/(1-w)$ and $K_\mathcal{N}\triangleq k_\mathcal{M}(1-q_2E)/(1-q_1E)$.

3.2.1.   Periodic solution for $\tau=0$

In this case, the system (2.2) has a subsystem (3.1) since $y\equiv 0$ if $y_0 = 0$

where $w > 0$ and $x_H\triangleq Hw^{-1}$.

Denote $\overline{\xi}_0 = (1-q_1E)x_H$ and

then, a periodic solution exists in the subsystem (3.1):

Define

Theorem 3.3. For the case $w > 0$ and $\tau = 0$, if $H < wK$, there exists a periodic solution $\mathbf{z} = (\overline{\xi}(t), 0)$ in System (2.3), and it is orbitally asymptotically stable when $R_0 < 1$.

Proof of Theorem 3.3. The proof can be seen as Theorem 2 in ^[21,45]; therefore, it is omitted here.

3.2.2.   Periodic solution for $\tau > 0$

The intersection point of $\mathcal{N}$ with the $x$-axis is denoted as $G(x_G, y_G)$. For $0 < \sigma < \tau$, select a point $Q\in \mathcal{N}\cap U(G, \sigma)$, where the trajectory $\mathbf{z}(t)$ with $\mathbf{z}(0) = Q$ intersects $\mathcal{M}$ at $Q^{-}$, and denote $Q^{+}$ as the phase point of $Q^{-}$ after the pulse.

The trajectory of System (2.2) tangent to $\mathcal{N}$ is denoted by $\hat{\mathbf{z}}(t)$, and the tangent point is denoted by $A(x_A, y_A)$, i.e. $\text{d}\hat{y}/\text{d}\hat{x}|_{A} = k_\mathcal{N}$. If $\gamma_A(\hat{\mathbf{z}})\cap \mathcal{M}\neq \emptyset$, let $A^{-}$ be the first intersection point, and $A^{+}$ be the phase point of $A^{-}$ after the pulse. If $\gamma_A(\hat{\mathbf{z}})\cap \mathcal{M} = \emptyset$ or $\gamma_{A'}(\hat{\mathbf{z}})\cap \mathcal{M} = \{A^{-}\}$ for some $A'(\neq A)\in \mathcal{N}$, then let $\tilde{\mathbf{z}}(t)$ be the trajectory tangent to $\mathcal{M}$, and the tangent point is denoted by $F$, i.e. $\text{d}\tilde{y}/\text{d}\tilde{x}\mid_{F} = k_\mathcal{M}$. Moreover, let $R_1(x_{R_{1}}, y_{R_{1}})\in \mathcal{N}$ and $R_2(x_{R_{2}}, y_{R_{2}})\in \mathcal{N}$ with $y_{R_{2}} < y_{R_{1}}$ such that $\gamma_{R_i}(\hat{\mathbf{z}})\cap \mathcal{M} = \{F\}$ $(i = 1, 2)$. For Case ($A1$-2), if $\Gamma_{LC}\cap \mathcal{M}\neq \emptyset$, then denote $\Gamma_{LC}\cap \mathcal{M} = \{M_1, M_2\}$ with $y_{M_2} < y_{M_1}$. Similarly, if $\Gamma_{LC}\cap \mathcal{N}\neq \emptyset$, then denote $\Gamma_{LC}\cap\mathcal{N} = \{N_1, N_2\}$ with $y_{N_2} < y_{N_1}$.

Define $H_i\triangleq wx^{p}_{i}+(1-w)y^{p}_{i}$ ($i = 1, 2$) and

For Cases ($A1$) and ($A3$), we have

Theorem 3.4. For System (2.3), there exists an order-1 periodic solution for $w > 0$ and $H\leq \overline{H}^{p}_K$ in any case of ($A1$-1), ($A1$-3), ($A1$-4) and ($A3$). Moreover, for the case ($A1$-1) (or ($A1$-3)) and $H > \overline{H}^{p}_{K}$, an order-1 periodic solution exists if $x_{R_2}\leq (1-q_1E)x_{F}$. For the case ($A1$-2), an order-1 periodic solution exists for $w > 0$ and $H\leq H_1$; while, for $H_1 < H\leq \overline{H}^{p}_K$, an order-1 periodic solution exists if $x_{N_2}\leq (1-q_1E)x_{M_2}$.

Proof of Theorem 3.4. In any case of ($A1$-1) or ($A1$-3) or ($A1$-4) or ($A3$), for $w > 0$ and $H\leq \overline{H}^{p}_K$, any trajectory starting from $\mathcal{N}$ will intersect $\mathcal{M}$, as illustrated in Figure 1. For the point $A$, if $y_{A^{+}} = y_{A}$, then the orbit $\gamma_A(\mathbf{z})$ forms an order-1 periodic solution. Otherwise,

i) In the case of $y_{A^{+}} < y_{A}$, we have $f^{\text{I}}_{\text{sor}}(A) = d_{A^{+}G}-d_{AG} < 0$. Since $f^{\text{I}}_{\text{sor}}(Q) = d_{Q^{+}G}-d_{QG} > 0$, then $\exists S \in \overline{A Q}$ such that $f^{\text{I}}_{\text{sor }}(S) = 0$, which means that the orbit $\gamma_S(\mathbf{z})$ forms an order-1 periodic solution, as illustrated in Figure 2 (a);

Figure 2.  Schematic diagram of trajectory change in System (2.3) for Case ($A1$-1) (or ($A1$-3)) and $H < H^{p}_{K}$: (a) $y_{A^{+}} < y_{A}$; (b) $y_{A^{+}} > y_{A}$.

DownLoad: Full-Size Img PowerPoint

ii) In the case of $y_{A^{+}} > y_{A}$, we have $f^{\text{I}}_{\text{sor}}(A) = d_{A^{+}G}-d_{AG} > 0$. The orbit $\gamma_{A^+}(\mathbf{z})$ intersects $\mathcal{M}$ at $A^{+-}$, and then it is pulsed to the point $A^{++}$. Since $y_{A^-} > y_{A^{+-}}$ and $y_{A^{+}} > y_{A^{++}}$, we have $f^{\text{II}}_{\text{sor}}(A^+) = d_{A^{++}G}-d_{A^+G} < 0$. Next, according to the continuity of the solution, for $\epsilon = d_{AA^{+}}/2$, we can select a point $H\in \mathcal{N}\cap U(A, \epsilon)$, and there is $d_{H^{-}A^{-}} < \epsilon$. Then, by the impulse effects, there is $d_{H^{+}A^{+}}\leq \max\{1-q_1E, 1-q_2E\}\epsilon < \epsilon$. Thus

The continuity of $f^{\text{II}}_{{\text{sor}}}$ implies that there exists $S \in \overline{HA^+}$ such that $f^{\text{II}}_{{\text{sor}}}(S) = 0$, as illustrated in Figure 2(b).

Moreover, for Case ($A1$-1) (or ($A1$-3)) and $H > \overline{H}^{p}_w$, if $x_{R_2}\leq (1-q_2E)x_{F}$, then $f^{\text{I}}_{\text{sor}}(R_2) = d_{F^{+}G}-d_{R_2G}\leq 0$. Similar to Case I), there exists an order-1 periodic solution in system (2.3). While, for ($A1$-2), we can adopt a proof similar to ($A1$-1); hence, it is omitted.

For Case ($A2$), two positive equilibria $E_1$ and $E_2$ exist simultaneously in System (2.2), where $E_2$ is a saddle point, $E_K$ is locally asymptotically stable. Define

For Case ($A2$-1), $E_1$ is locally asymptotically stable. For Case ($A2$-2), $E_1$ is unstable. Moreover, there exists $\overline{K} > \underline{K}$ and System (2.2) has a limit cycle $\Gamma_{LC}$ for $\underline{K} < K < \overline{K}$. In this case, let $\overline{H}\triangleq\max\{H|\Gamma_{LC}\cap \mathcal{M}\neq \emptyset\}$. For $H_{1} < H\leq \overline{H}$, denote $\Gamma_{LC}\cap \mathcal{M} = \{D_1, D_2\}$ with $y_{D_1}\leq y_{D_2}$. Similarly, if $\Gamma_{LC}\cap \mathcal{N}\neq \emptyset$, denote $\Gamma_{LC}\cap \mathcal{N} = \{B_1, B_2\}$ with $y_{B_1}\leq y_{B_2}$. For $K\geq \overline{K}$, $E_K$ is globally asymptotically stable.

Since $E_2$ is a saddle point, let $\Gamma_{\text{sm}}$ and $\Gamma_{\text{usm}}$ respectively represent the stable and unstable manifolds that pass through $E_2$ below the isoline $\dot{x} = 0$. For $H_1 < H\leq H_2$, denote $\Gamma_{\text{sm}}\cap \mathcal{M} = \{D\}$. If $\Gamma_{\text{sm}}\cap \mathcal{N}\neq \emptyset$, then denote $B$ as the intersection point with a smaller $y$ label. Otherwise, let $B$ be a point on $\mathcal{N}$ with $y_{B} = (1-q_2E)y_{D}+\tau$. For $H_2 < H\leq wK$, denote $\Gamma_{\text{usm}}\cap \mathcal{M} = \{D\}$, and $\Gamma_{\text{sm}}\cap\mathcal{N} = \{B\}$.

Theorem 3.5. For Case ($A2$), there exists an order-1 periodic solution in System (2.3) if one of the conditions holds: 1) $0 < w\leq w_1^*$ and $H\leq wK$; 2) $w_1^* < w\leq 1$ and $H\leq H_1$; 3) $w_1^* < w\leq w_2^*$, $H_1 < H\leq wK$ and $y_{B_1}\geq (1-q_2E)y_{D_1}+\tau$; 4) $w_2^* < w\leq 1$, $H_2 < H\leq wK$ and $y_{B}\geq (1-q_2E)y_{D}+\tau$.

Proof of Theorem 3.5. It can be easily verified that for any case of 1) $0 < w\leq w^*$ and $H\leq wK$ or 2) $w^* < w\leq 1$ and $H\leq H_1$, any trajectory starting from $\mathcal{N}$ will intersect $\mathcal{M}$; then, using a proof similar to Theorem 3.4, we can prove that there exists an order-1 periodic solution. While, for 3), $w_1^* < w\leq w_2^*$ and $H_1 < H\leq H_2$, if $y_{B_1}\geq (1-q_2E)y_{D_1}+\tau$, any trajectory starting from $\overline{B_2G}\subset \mathcal{N}$ will intersects $\mathcal{M}$; similarly, we can prove that there exists an order-1 periodic solution. Case 4) is similar to Case 3) and thereby omitted.

Let $\tilde{\mathbf{z}} = (\tilde{\xi}(t), \tilde{\eta}(t))$, $0 \leq t \leq T$ be the order-1 P.S.. Denote $\xi_{1} = \tilde{\xi}(T), \eta_{1} = \tilde{\eta}(T), \xi_{0} = \left(1-q_{1} E\right) \xi_{1}$, $\eta_{0} = \left(1-q_{2} E\right) \eta_{1}+\tau$, $f^{0}_{1} = f_1(\xi_{0}, \eta_{0}), f^{1}_{1} = f_1(\xi_{1}, \eta_{1}), f^{0}_{2} = f_2(\xi_{0}, \eta_{0})$ and $f^{1}_{2} = f_2(\xi_{1}, \eta_{1})$. Then, we have the following theorem.

Theorem 3.6. The order-1 periodic solution $\tilde{\mathbf{z}} = (\tilde{\xi}(t), \tilde{\eta}(t))$ is orbitally asymptotically stable if

Proof of Theorem 3.6. From Model (2.3), we have

Then we have

In addition,

Thus,

Therefore, $\left|\mu_{1}\right| < 1$ if and only if (3.4) holds; then, by Lemma 2.1, the order-1 periodic solution $\tilde{\mathbf{z}} = (\tilde{\xi}(t), \tilde{\eta}(t))$ is orbitally asymptotically stable.

Theorem 3.7. For the case ($A1$-1) (or ($A1$-3)) and $H\leq \overline{H}^{p}_{K}$, the order-1 periodic solution $\mathbf{z} = (\tilde{\xi}(t), \tilde{\eta}(t))$ is orbitally asymptotically stable and globally attractive if $y_{A^+} < y_A$.

Proof of Theorem 3.7. According to Theorems 4 and 5, when $H\leq \overline{H}^{p}_{K}$, there exists an order-1 P.S. in system (2.3). If $y_{A^+} < y_A$, then $L\in \overline{AQ}$, which means that for any $S\in N$, $f^{\text{I}}_{\text{sor}}(S) < 0$ with $y_S > y_L$, $f^{\text{I}}_{\text{sor}}(S) > 0$ with $y_S < y_L$ and $f^{\text{I}}_{\text{sor}}(S) = 0$ if and only if $S = L$. Thus, for any $S_0^{+}\in \overline{AL} \subset N$, there exists a sequence $\{S_k^{+}\}(k = 0, 1, 2, \cdots)$ satisfying $y_{S_{k+1}^{+}} = y_{S_{k}^{+}}+f^{\text{I}}_{\text{sor}}(S_{k}^{+})$. If $S_{0}^{+}\in \overline{AL}$, $\{S_k^{+}\}$ is monotonically decreasing. Moreover, $y_L$ is the lower limit. If $S_{0}^{+}\in \overline{LQ}$, $\{S_k^{+}\}$ is monotonically increasing, and $y_L$ is the upper limit. Thus $y_{S_{k}^{+}}\rightarrow y_{S'}(k\rightarrow \infty)$. Therefore,

Moreover $f^{\text{I}}_{\text{sor}}(S) = 0$; then, we have $S' = S$, and the orbit from any point $S_0^{+}\subset \mathcal{N}$ will approach $\mathbf{z} = (\tilde{\xi}(t), \tilde{\eta}(t))$, which means that $\mathbf{z} = (\tilde{\xi}(t), \tilde{\eta}(t))$ is globally attractive.

Next, we discuss the order-2 periodic solution. For a given point $S(x_S, y_S)$ on $N$ with $0\leq y_S\leq \overline{y}\triangleq (1-q_2E)H/(1- w)+\tau$, when $y_S\leq y_A$, there is $\psi_N(y_S) = (1-q_2E)\pi(S, T_S)+\tau$. While for $y_S > y_A$, there exists a unique $S'\in N$ with $y_{S'}\in (0, y_A)$ and $\hat{T_z}$ such that $y_{S'} = \pi(S, \hat{T_S})$. Then $\psi_N(y_S) = (1-q_2E)\pi(S, T_{S'})+\tau$. For the above summary, there is

Property 3.1. For Case ($A1$) and $H\leq \overline{H}^{p}_{K}$, the Poincaré map $\psi_N$ defined by (3.5) has the following characteristics: 1) $\psi_N$ is continuous on $[0, \overline{y}]$. Moreover, $\psi_N$ increases and then decreases, and it reaches a maximum at $y = y_A$; 2) $\psi_N$ is continuously differentiable on $[y_A, \overline{y}]$.

For Case ($A1$) and $H\leq H^{p}_{K}$, if $\psi_N(y_A) < y_A$, the order-1 periodic solution of System (2.3) is orbitally asymptotically stable and globally attractive (Theorem 3.7); in this case, there does not exist an order-$n$ $(n\geq 2)$ periodic solution. For the case $\psi_N(y_A) > y_A$, there exists a unique $y_{L_{2}}\in[y_A, \psi_N(y_A)]$ such that $\psi_N(y_{L_{2}}) = y_{L_{2}}$. Let $y_{L_{1}}\in[0, y_A]$ such that $\psi_N(y_{L_{1}}) = y_{L_{2}}$. Then $\psi_N^{2}(y_{L_{1}}) = \psi_N(y_{L_{2}}) = y_{L_2}$. Meanwhile, let $y_{N_{1}}\in[0, y_A]$ and $y_{N_{2}}\in[y_{L_2}, \overline{y}]$ such that $\psi_N(y_{N_{1}}) = \psi_N(y_{N_{2}}) = y_{A}.$

Theorem 3.8. For $w > 0$, $H\leq \overline{H}^{p}_{K}$ and $\psi_N(y_A) > y_A$, if i) $\psi_N^{2}(y_A) < y_{A}$ or ii) $\psi_N^{2}(y_A) > y_{A}$ and $\mu_{1} > 1$ holds, then there exists an order-2 periodic solution in System (2.3).

Proof of Theorem 3.8. Because $\psi_{N}\left(y_{N_{1}}\right) = \psi_{N}\left(y_{N_{2}}\right) = y_{A}$, obviously, $\psi_{N}^{2}\left(y_{1}\right) = \psi_{N}^{2}\left(y_{2}\right) = \psi_{N}\left(y_{A}\right)$. Then, $\psi_{N}^{2}$ is increasing on $\left[0, y_{N_{1}}\right]$ and $\left[y_{A}, y_{N_{2}}\right]$ and $\psi_{N}^{2}$ is decreasing on $\left[y_{N_{1}}, y_{A}\right]$ and $\left[y_{N_{2}}, \overline{y}\right]$. Since $\psi_{N}^{2}\left(y_{N_{1}}\right) = \psi_{N}\left(y_{A}\right) > y_{A} > y_{N_{1}}$, there is $\psi_{N}^{2}(y_{N_{1}}) > y_{N_{1}}$.

i) If $\psi_{N}^{2}\left(y_{A}\right) < y_{A}$, then there is $\psi_{N}\left(y_{A}\right) > y_{N_{2}}$. As $\psi_{N}\left(y_{A}\right) = \psi_{N}^{2}\left(y_{N_{2}}\right)$, there is $\psi_{N}^{2}\left(y_{N_{2}}\right) > y_{N_{2}}$, which also implies that $\psi_{N}^{2}\left(\psi_{N}\left(y_{A}\right)\right) < \psi_{N}\left(y_{A}\right)$. Thus there exist $y_{M_{1}} \in\left[y_{N_{1}}, y_{A}\right]$ and $y_{M_{2}} \in\left[y_{N_{2}}, \psi_{N}\left(y_{A}\right)\right]$ such that $\psi_{N}^{2}\left(y_{M_{1}}\right) = y_{M_{1}}, \psi_{N}^{2}\left(y_{M_{2}}\right) = y_{M_{2}}$. And there is $\psi_{N}\left(y_{M_{2}}\right) = y_{M_{1}}, \psi_{N}\left(y_{M_{1}}\right) = y_{M_{2}}$.

ii) If $\psi_{N}^{2}\left(y_{A}\right) > y_{A}$, there is $\psi_{N}\left(y_{A}\right) < y_{N_{2}}$, i.e. $\psi_{N}^{2}\left(y_{N_{2}}\right) < y_{N_{2}}$. For any $y \in\left[y_{A}, \psi_{N}\left(y_{A}\right)\right]$, we have $y_{A} < \psi_{N}(y) < \psi_{N}\left(y_{A}\right)$. Next, it discusses the property of $\psi_{N}$ on $\left[y_{A}, \psi_{N}\left(y_{A}\right)\right]$. Let $y_{0} = y_{A}$; then, $y_{1} = \psi_{N}\left(y_{0}\right) = \psi_{N}\left(y_{A}\right) > y_{0}, y_{2} = \psi_{N}\left(y_{1}\right) = \psi_{N}^{2}\left(y_{0}\right) > y_{0}$ and $y_{3} = \psi_{N}\left(y_{2}\right) < \psi_{N}\left(y_{0}\right) = y_{1}$. A sequence $\left\{y_{n}\right\}$ is obtained under $\psi_{N}$, where $y_{0} < y_{2} < y_{4} < \cdots < y_{L_{2}} < \cdots < y_{5} < y_{3} < y_{1}.$ Denote $y_{M_{1}} = \lim\limits_{n \rightarrow \infty} y_{2 n}$ and $y_{M_{1}} = \lim\limits_{n \rightarrow \infty} y_{2 n+1}$. It is obvious that $y_{M_{1}} \leq y_{L_{2}} \leq y_{M_{2}}$. Since $\mu_{1} > 1$, $y_{M_{1}} < y_{L_{2}} < y_{M_{2}}$. Besides $\psi_{N}\left(y_{M_{2}}\right) = y_{M_{1}} and \psi_{N}\left(y_{M_{1}}\right) = y_{M_{2}}$, so $\mu_{2} < 1$, i.e., the order-2 periodic solution is orbitally asymptotically stable.

3.3.   Fishing process optimization

In order to realize the sustainability of fishery resources and maximize economic benefits, it is necessary to consider the problem of harvest optimization. In Model (2.3), let $H = wl+(1-w)ml$, where $m\triangleq y^{p}_1/x^{p}_1$, and the weight $w$ and harvest density $l$ are the decision variables. Besides, we assume that $E$ and $\tau$ are also linearly dependent on the decision variables $w$ and $l$, i.e.

where $l_1$ and $l_2$ are, respectively, the lower and upper limits of the harvest level, $E_{\min}$ and $E_{\max}$ respectively represent the minimum and maximum harvest effort and $\tau_{1}$ and $\tau_{2}$ respectively represent the minimum and maximum quantities of released predator populations. Let $c_1$ be the unit sale revenue of prey species, $c_2$ represent that of predator species, $c_3$ denote the unit price of harvesting and $c_4$ be the feeding predator unit cost. In general, $c_3$ and $c_4$ are fixed, and $c_1/c_2$ varies with season and market demand; also, denote $\sigma\triangleq c_{2}/c_{1}$. Therefore, the total revenue can be expressed as $H_{benefit}(w, l) = c_1q_1E(l)\xi(T(w, l))+c_2q_2 E(l)\eta(T(w, l))-c_3 E(l)-c_4 T(l)$. The objective is to find the maximum of $P_{benefit}(w, l)$, which can be described as follows:

The optimal control level $l^*$, $w^{*}$ can be obtained by solving the optimization model (3.7). Accordingly, it is possible to determine the release amount $\tau^{*} = \tau(l^{*}, w^{*})$, the optimal capture effort $E^{*} = E(l^{*}, w^{*})$, and the optimal capture period $T^{*} = T(l^{*}, w^{*})$.

4.   Computer simulation verification

We will verify the main results through numerical simulations. For System (2.2), we set the model parameters as follows $r = 2$, $b = 20\% = 0.2$, $\mu = 10\% = 0.1$, $h_1 = 0.01$, $h_2 = 0.3$, $s = 14\% = 0.14$. Then there is $p_1 = 0.0018$.

4.1.   Theory verification

4.1.1.   Verification of Theorem 3.1 and Theorem 3.2

First, for K = 100, how the anti-predator rate $p$ affects the dynamics of the system (2.2) is presented in Figure 3. When $p = 0.0015$, two positive equilibria exist in the system; when $p = 0.0018$, a unique positive equilibrium exists; and, when $p = 0.02$, there is no positive equilibrium. It is clear that the anti-predator factor has a certain effect on the number of equilibria; with the increase of the anti-predator factor, the number of positive equilibria gradually decreases.

Figure 3.  Effect of anti-predator rate $p$ on the dynamics of the system (2.2).

DownLoad: Full-Size Img PowerPoint

Next, for $p = 0.0015$, how the environmental capacity $K$ affects the dynamics of the system (2.2) is shown in Figure 4. For $K = 100$, $E_1$ is locally asymptotically stable, and for $K = 150$, $E_1$ is unstable; and, a limit cycle exists surrounding $E_1$; while, for $K = 200$, $E_K$ is globally asymptotically stable.

Figure 4.  Effect of environmental capacity $K$ on the dynamics of the system (2.2).

DownLoad: Full-Size Img PowerPoint

Next, we will verify the main results by changing the capture level $H$. The control parameters were set as $w = 0.2$, $\tau = 0.5$, $E = 1$, $q_1 = 0.5$ and $q_2 = 0.2$.

4.1.2.   Verification of Theorem 3.4

Case I: $H\leq \min\{H_1, wK\}$ Here we consider three subcases:

i) $p = 0$ and $K = 100$. Then a unique positive equilibrium $E_{1}(13.73, 9.81)$ exists in System (2.2). Since $H_1 = 10.5944$, for $H = 10$, there exists an order-1 periodic solution; its period is about $T = 0.74$, as shown in Figure 5-4.

Figure 5.  Diagram of trajectory tendency of the system (2.3) and presentation of the order-1 periodic solution with $H\leq \min\{H_1, wK\}$ for different $p$ and $K$ in case ($A1$).

DownLoad: Full-Size Img PowerPoint

ii) $p = 0.0015$ and $K = 50$. Then at the positive equilibrium $E_{1}(21.8584, 6.8586)$, there is $H_1 = 9.86$. For $H = 9 < H_1$, there exists an order-1 periodic solution; its period is about $T = 1.35$, as illustrated in Figure 5-5.

iii) $p = 0.0018$ and $K = 100$. Then at the equilibrium $E_{1}(33.33, 8.89)$, there is $H_1 = 13.78$. For $H = 13 < H_1 = 13.78$, an order-1 periodic solution with the period $T = 0.84$ exists, as depicted in Figure 5-6.

Case II: $H_{1} < H < H_{2}$ In this case, the order-1 periodic solution exists conditionally. For $p = 0$, $K = 100$ and $H = 13$, since $x_{R_2}\geq (1-q_1E)x_{F}$ holds for a given $q_1$, $q_2$ and $\tau$ (Figure 6-1), an order-1 periodic solution exists (Figure 6-4); its period is about $T = 0.96$. It should be pointed out that the inequality is dependent on the values of $q_1$, $q_2$ and $\tau$; once the inequality is reversed, all trajectories will go forward to $E_1$ after several pulses. For $p = 0.0015$, $K = 50$ and $H = 10$, System (2.3) also has an order-1 periodic solution with the period $T = 2.37$ (Figure 6-5) since $x_{R_2}\geq (1-q_1E)x_{F}$ holds (Figure 6-2). For $p = 0.0018$, $K = 100$ and $H = 16$, since $x_{B}\geq (1-q_1E)x_{D}$ holds for a given $q_1$, $q_2$ and $\tau$ (Figure 6-3), an order-1 periodic solution exists (Figure 6-6); its period is about $T = 1.144$.

Figure 6.  Diagram of trajectory tendency and order-1 periodic solution of system (2.3) with $H_{1} < H < H_{2}$ for different values of $p$ and $K$ in Case $A1$.

DownLoad: Full-Size Img PowerPoint

4.1.3.   Verification of Theorem 3.5

For Case $A2$, we assume that $p = 0.0015$; then, $x^{p}_1 = 21.86$, $x^{p}_2 = 61$ and $\underline{K} = 143.7$. Diagrams of the trajectory tendency of the System (2.3) for different values of $K$ and $H$ are illustrated in Figure 7.

Figure 7.  Diagram of the trajectory tendency of the System (2.3) for different values of $K$ in Case $A2$: 1) $H < H_1$; 2) $H_1 < H < H_2;\; 3) H_2 < H < wK$.

DownLoad: Full-Size Img PowerPoint

For $K = 100$, $E_1(21.86, 9.52)$ is locally asymptotically stable. Since $H_1 = 12$, $H_2 = 17.2$ and $wK = 20$, for $H = 11$, the order-1 periodic solution exists unconditionally (Figure 7-1); for $H = 14$ and $H = 18$, when $y_{B}\geq (1-q_2E)y_{D}+\tau$ holds, the existence of the order-1 periodic solution is guaranteed (Figure 7-4 and Figure 7-7). For $K = 150 > \underline{K}$, $E_1(21.86, 10.4)$ is unstable and a limit cycle exists. In this case, $H_1 = 12.6$, $H_2 = 19.8$ and $wK = 30$. Similarly, for $H = 12$, the order-1 periodic solution exists unconditionally (Figure 7-2)), while for $H = 17$ and $H = 22$, when $y_{B}\geq (1-q_2E)y_{D}+\tau$ holds, the existence of the order-1 periodic solution is guaranteed (Figure 7-5 and Figure 7-8). For $K = 200 > \overline{K}$, $E_1(21.86, 10.4)$ is unstable and $E_K$ is globally asymptotically stable. In this case, $H_1 = 13.1$, $H_2 = 21$ and $wK = 40$. Similarly, for $H = 13$, the order-1 periodic solution exists unconditionally (Figure 7-3); while, for $H = 19$ and $H = 25$, when $y_{B}\geq (1-q_2E)y_{D}+\tau$ holds, the existence of the order-1 periodic solution is guaranteed (Figure 7-6 and Figure 7-9).

4.1.4.   Verification of Theorem 3.8

For Case ($A2$), when $\underline{K} < K < \overline{K}$, $E_1$ is unstable and a limit cycle $\Gamma_{LC}$ exists. For $H_1 < H\leq \overline{H}$ and a smaller $\tau$ with $y_{B}\geq (1-q_2E)y_{D}+\tau$, there exists an order-1 periodic solution (Theorem 3.5, Figure 7-5). Notice that $y_{B}\geq (1-q_2E)y_{D}+\tau$ is just a sufficient condition to ensure that there is a periodic solution. In fact, as long as $y_{B_1}\geq (1-q_2E)y_{D_1}+\tau$, for example, $\tau = 1.74$, the order-1 periodic solution will exist (Figure 8-1) for $p = 0.0015$, $K = 150$ and $H = 15$. For a bigger $\tau$, for example, $\tau = 2.1$ and $\tau = 2.2$, there may also exist an order-1 periodic solution (Figure 8-2, 8-3), but existence is not guaranteed. From Figure 8-2, it is observed that even if an order-1 periodic solution exists, its shape has changed. Figure 8-3 presents an order-2 periodic solution. The existence of an order-2 periodic solution implies the existence of an order-1 periodic solution, but in this case, the order-1 periodic solution is unstable.

Figure 8.  Presentation of the order-1 periodic solution for $p = 0.0015$, $K = 150$, $H = 15$ and different values of $\tau$ in Case $A2$.

DownLoad: Full-Size Img PowerPoint

The dynamics of System (2.3) depends on the control parameters $w$, $q_1$ and $q_2$. Next, we consider another set of control parameters: $w = 0.6$, $q_1 = 0.6$ and $q_2 = 0.4$. For $p = 0$ and $K = 150$, there is $K > \underline{K} = 127$; then, $E_K$ is unstable, $E_{1}(13.72, 10.33)$ is unstable and a limit cycle exists. We have $H = 18.55 > H_{1} = 12.37$. Presentation of the order-$m$ periodic solution of System (2.3) for $p = 0$, $K = 150$, $H = 18.55$ and different values of $\tau$ is shown in Figure 9. For $\tau = 4.1$, System (2.3) has an order-2 periodic solution, as depicted in Figure 9-1. In this case, the order-1 periodic solution exists but is unstable. For $\tau = 4$, there exists an order-3 periodic solution (Figure 9-2) and for $\tau = 3.95$, System (2.3) has an order-4 periodic solution (Figure 9-3). The existence of an order-$m$ periodic solution ($m\geq 3$) would also lead System (2.3) to chaos ^[42,50].

Figure 9.  Presentation of the order-$m$ periodic solution ($m = 2, 3, 4$) for $p = 0$, $K = 150$, $H = 18.55$ and different values of $\tau$ in case $A2$.

DownLoad: Full-Size Img PowerPoint

4.2.   Numerical optimization

Let $K = 100$, $E_1 = 40\%$, $E_2 = 100\%$, $\tau_{1} = 0.5$ and $\tau_{2} = 2$, and the other model parameters are the same as in the above simulations. Here, we consider two scenarios: 1) without anti-predator behavior, i.e., $p = 0$; 2) with anti-predator behavior, i.e., $p = 0.0015$. Besides, it is assumed that $l_1 = 20\%x_{E_1}$, $l_2 = 90\%x_{E_1}$, $c_1 = 5$, $c_3 = 30$ and $c_4 = 5$. For $p = 0$ and $\sigma = 20, \; 30$, the dependence of $T$ and $P_{benefit}$ on $w$ and $l$ are presented in Figure 10. When $\sigma = 20$, the unit benefit $P_{benefit}$ achieves its maximum at $w^* = 0.1$ and $l^* = 0.69x_{E_1}$. When $\sigma = 30$, $P_{benifit}$ achieves its maximum at $w^* = 1$ and $l^* = 0.34x_{E_1}$.

Figure 10.  Dependence of $T$ and $P_{benefit}$ on $w$ and $l$ for $p = 0$ and $K = 100$.

DownLoad: Full-Size Img PowerPoint

For $p = 0.0015$, $E_K$ is locally asymptotically stable. It is assumed that $0.1\leq w\leq 1$. For $\sigma = 20, \; 30$, the dependence of $T$ and $P_{benefit}$ on $w$ and $l$ are presented in Figure 11. For $\sigma = 20$, the unit benefit $P_{benefit}$ achieves its maximum at $w^* = 0.1$ and $l^* = 0.69x_{E_1}$. For $\sigma = 30$, $P_{benifit}$ achieves its maximum at $w^* = 1$ and $l^* = 0.34x_{E_1}$.

Figure 11.  Dependence of $T$ and $P_{benefit}$ on $w$ and $l$ for $p = 0.0015$ and $K = 100$.

DownLoad: Full-Size Img PowerPoint

5.   Summary and discussion

This work presented a fishery predator-prey model with anti-predator behavior and analyzed the dynamics of the model in detail. Besides, it introduced a weighted fishing strategy into the system and established a fishery capture model (2.2). It analyzed the dynamics of the model and showed that the anti-predation intensity affects the number of equilibria, that is, with the increase of anti-predation intensity, the number of equilibria will decrease (Figure 3). Moreover, it showed that, for a fixed anti-predator factor, the carrying capacity $K$ has certain impact on the stability of the equilibria (Figure 4).

It also discussed the dynamic behavior of the capture model (2.3) according to different levels of anti-predation factors. The results showed that an order-1 periodic solution always exists when $H\leq H_{1}$, no matter how strong the anti-predator factor (Figure 5 and Figure 7). For $H_1 < H\leq H_2$, there is a constraint that ensures the existence of an order-1 periodic solution (Figure 6 and Figure 7). Moreover, for $0\leq p < p_1$ and $\underline{K} < K < \overline{K}$, System (2.3) presents an order-$m$ periodic solution ($m \geq 2$) for certain values of $\tau$ (Figure 8 and Figure 9). However, it is difficult and challenging to prove the existence of an order-$m$ periodic solution $(m > 2)$, which will be our next study.

In the numerical optimization, it was shown that the benefits from fishing processes are dependent on the unit sales price of prey and predators, as well as on the harvest unit cost. For given values of $c_1, c_3$ and $c_4$, the unit benefit may achieve the maximum at different pairs of $(l^*, w^*)$ for different values of $\sigma$ (Figure 10 and Figure 11). This also indicates that we can determine the optimal capture strategy ($E^*$, $\tau^*$ and $T^*$) based on the selling prices of predators and prey, and then carry out fishing activities.

Funding

The research was supported by the Fundamental Research Funds for the Central Universities (No. DUT21LAB125).

Data availability statement

The data used to support the findings of this study are available from the corresponding author upon request.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.