1.
Introduction
Like many other developing countries, Turkey has been passing through an extensive trade liberalization from the beginning of the 1980s. It operates many liberalized economic reforms aiming to integrate into the world economy. However, these adjustment attempts have not solved many economic problems and create new challenges in terms of foreign dependency on domestic production, persistent trade deficits even in the economic growth environment after the 2000s.
As regards to liberalization process, using the import tariff rates as an instrument of adjusting to the world economy is crucial. Erero et al. (2014) state that compares to lowering non-tariff barriers, it would be much easier for countries to cut tariffs and duties. On the other hand, governments benefit from tariff rates in order to raise tax revenues and to protect domestic producers against their foreign competitors. While many of the relevant literature on the issue focus on the positive effects of tariff reduction in terms of improvements in productivity, income and employment levels, some other studies found negative adjustments in households' income. For that matter, this paper seeks to add to efforts aimed at analyzing the impacts of import tariff reductions on sectoral production while giving a locus of international trade.
The economic impacts of various policy changes on sectoral production have been analyzed through the computable general equilibrium (CGE) modeling. CGE models provide a framework that enables to reveal the direct and indirect impacts of a specific economic policy in a multi-sectoral manner. Thanks to computational advances and increasing standardization in the modeling practices, CGE modeling has been used widely in economic policy studies.
The aim of this paper is to test the effects of tariff rate changes on some crucial economic indicators and to present a case for existing literature from a developing economies perspective. The main contributions of this paper are twofold: To best of our knowledge this paper is the unique and the most updated attempt that examine the effects of tariff changes in Turkey employing multi-sectoral CGE modeling. Our second contribution to literature is the construction of the most updated Social Accounting Matrix of 2012 in Turkey which is compatible to test the changes in the tariff rates.
The paper is structured as follows. Section 2 provides an overview of the related literature of the import tariff reductions emphasizing on the CGE modeling approaches. Section 3 is on the structure of the CGE modeling. It presents the simultaneous equations that are solved in the modeling process and examines economic policy scenarios. Finally, paper finishes with the evaluations of the modeling findings and discusses the economic policy alternatives for the Turkish economy.
2.
Background and literature
As trade deficit is accepted as one of the main reasons of macroeconomic vulnerability; volumes of exports and imports are crucial concerns for economists. On the other hand, the volume of trade is also affected by the macroeconomic situation as well. For that reason, looking over the global economic performance will be helpful in order to examine the trade dynamics, thoroughly. Lower volumes of trade are recorded worldwide especially in recent years due to low economic growth rates. Accordingly, the world economy as a whole grew in 2015 at a rate of 2.4% which is lower than the expected rate of 3% (IMF World Economic Outlook, April 2016). Deceleration of growth in China and some other developing economies, the decline in the prices of oil and other commodities, and geopolitical developments were among the main reasons for the low economic growth. World Trade Organization (WTO) has also recorded a shrinkage of 15% in world trade volume in 2015.
Similarly, in Turkey, the total trade volume of 403 billion USD in 2013 declined to 341 billion USD in 2016 (TURKSTAT). Most of the decrease in total trade in Turkey has aroused from the shrinkage in the value of imports caused by the decrease in the prices of oil and metals. Because of foreign dependency on oil and some other raw materials, changes in prices of these primary goods create severe effects on the trade performance in Turkey.
The literature regarding benefits of trade goes back to the theory of absolute advantage which is developed first by Adam Smith in his famous work of The Wealth of Nations published in 1776. Later Ricardo (1951) extended the theory of comparative advantages in which he suggests that all countries benefit from international trade even if one of them has an absolute advantage in all goods. On the other hand, the neoclassical theory of Solow (1956) and Swan (1956) suggests that trade liberalization will improve per capita income but not the long-run growth rate. Finally, endogenous growth models (e.g., Romer, 1986) which employ technical progress and positive externalities endogenously can explain the long-term economic growth effects of trade liberalization.
Aghion and Howitt (2009) listed several channels on why trade should increase productivity and income. In the first place, trade openness increases the scale of production and so the scope for learning-by-doing externalities (Grossman and Helpman, 1995; Young, 1991). They also state that this market size effect is more important in small economies. Besides, trade serves to economic growth as increasing competition between foreign and domestic producers enhance productivity. It also stimulates knowledge spillovers especially from more advanced to less advanced economies. Araujo and Flaig (2016) also explain why barriers to international trade limit potential growth via several channels. Accordingly, trade barriers lead domestic firms to have lower incentives to innovate, and they seek efficiency by shielding them from international competition. Additionally, as import tariffs increase the cost of intermediate inputs and capital goods, the competitiveness of the domestic producers' weakens. On the other hand, there are also some arguments that defend trade protectionism. These arguments generally based on the importance of satisfying adequate national defense, the infant industry argument and the diversification argument. National defense argument is criticized as it ignores the possibility of purchases from friendly countries during the emergences (Caughlin et al., 1988). Thereby, we focus on the last two arguments. Infant industry argument goes back to List (1841) and it states that infant industries may be suffer from comparative advantage because of foreign firms. Therefore, domestic firms have to be protected in order to make them grow and benefit from the economies of scale. Otherwise, local firms may not be able to compete against foreign firms and will be pulled out of the market. Diversification argument states that trade protectionism contributes to the diversification of the domestic economy and the export, and thereby support economic growth and decrease the vulnerability in export income.
There is a vast literature about the economic impacts of trade liberalization, and they focus on different economic facts. However, two of the among facts are more common: poverty (e.g., Chitiga and Mabugu, 2005; Khan, 2005; Raihan, 2010; Mohammed, 2016) and income distribution (e.g., Siddiqui et al., 1999; Siddiqui and Iqbal, 2001). It is also worth to note that there are different indicators for measuring trade liberalization, but we refer only to studies which handle import tariff reductions. Of the studies which have dealt with poverty; Chitiga and Mabugu (2005) make a contribution to literature by directly connecting trade and external policies to poverty within the same framework and applying this approach to Zimbabwe. After the simulation of the removal of import tariffs, they observe that poverty is falling for all income groups, but poor households get the least benefits. In a later study Khan (2005) reaches contradicting results. Accordingly, he finds that tariff reduction has a nonlinear impact on poverty in South Asia, especially in India, Pakistan, and Bangladesh. However, it is observed that the tariff reduction will ultimately benefit the poor. Raihan (2010) confirms the finding of Khan (2005) for Bangladesh. He examines the welfare and poverty effects of trade liberalization with a scenario of trade liberalization simulated where zero tariffs on all imports. As a conclusion, he finds that resources are reallocated towards the more efficient and expanding sectors and create poverty reduction in the long run.
Mohammed (2016) pays attention to compensating the loss in government revenue arising from tariff reduction by applying different taxes. He tests the effects of reducing tariffs in Algeria by using a CGE model based on the stylized model of Lofgren (2000). In three simulation scenarios, they quantify the effects of the reduction in import tariffs in different proportions. In the fourth simulation, the loss in revenue due to the elimination of tariff compensated through increasing corporate and income tax rate. He observes that reduction in tariff can increase domestic production, promote exports and raise employment level. He also advises compensating the fall in government revenue by reducing net subsidies or increasing income tax progressively.
Of the studies which have dealt with income distribution, Siddiqui et al. (1999) test the effects of tariff reforms in Pakistan with a particular focus on the effect of changes in relative prices. A scenario of reduction in tariff rate on industrial imports is simulated, and the results show that the income of each household group declines. The reduction in the income of the poorest group is found to be largest. Therefore, the paper suggests that income distribution is worsening after trade reform. Siddiqui and Iqbal (2001) focus on functional income distribution in Pakistan in later work. The same baseline scenario is simulated, and they show that percentage share of labor in GDP has increased while of capital has declined. There are also some studies that analyze the effects of tariff reduction on some other economic variables. For example, Erero et al. (2014) test the effects of tariff reductions in the Democratic Republic of Congo (DRC) through a CGE analysis. They also contribute to the literature by differentiating between the formal and informal sectors. Their results show that tariff reduction increases employment and output in the formal sector, however, it is not valid for the informal economy. Similarly, Araujo and Flaig (2016) analyze the effects of different policy reforms in order to strengthen Brazil's integration into global trade, one of which is characterized as a reduction in import tariffs. They find that all simulation scenarios towards liberalizing trade would raise agammaegate production, employment, investment as well as households' income and consumption. They also observe an expansion in exports after liberalization policies with the largest effects occurring in manufacturing sectors. Studies that focus on the effects of tariff changes on specific goods such as sugar (e.g. Cororaton, 2013; Pudjiastuti et.al., 2013) or wheat (e.g. Elsheikh et.al., 2015) are also available.
Some previous studies handle foreign trade for Turkey depending on CGE (e.g., Dervis and Robinson, 1978; Yeldan, 1987; Harrison et.al., 1997; Diao et.al., 1998). However, Dervis and Robinson (1978) and Yeldan (1987) focus on the effects of different trade policy packages such as devaluation and export-promotion programs. Harrison et al. (1997) analyze the impact of the Customs Union between Turkey and the European Union, as well. On the other hand, Diao et al. (1998) test the impacts of the elimination of import tariff on the economy. Their results indicate that elimination of import tariff would cause a drastic dynamic adjustment in investment but a smooth adjustment in consumption. They also observe a fall in household income arising from the reduction in wage and capital rental rates.
In sum, studies that examine the effects of the changes of trade reforms based on a general equilibrium framework for Turkey are very rare. And, to best of our knowledge, our study is the first that analyze the effects of the changes in import tariffs on sectoral production in Turkey with the CGE modeling.
3.
The CGE modeling
Following the relevant literature on the issue, this paper utilizes open economy CGE modeling to search for the effects of import tariff reduction on the sectoral production in Turkey. CGE models rely on solving the simultaneous equations that represent functional and behavioral relations of economic units. Thanks to improvements in mathematical computation, CGE modeling has been used widely in economic policy issues empirically. Since it allows to analyze mutually dependent relations among the different productive sectors and economic units with demand-supply equilibrium, it is possible to see the direct and indirect effects of the specific economic policy changes.
Besides increasing easiness in mathematical computation, analytically CGE modeling has achieved a point of standardization in terms of the determination of behavioral equations, assumptions regarding production technologies and approaches to international trade. In that matter, mathematical formulations of our study rely on these standard modeling approaches (e.g., Hosoe et al., 2010; Lofgren et al., 2002). In pursuing the CGE modeling, firstly, simultaneous equations are determined. Determining equations involves choosing variables and parameters that are thought to be relevant for the economy through evaluations of both theoretical and empirical works on the issue. The second step is to calculate parameters for a benchmark equilibrium of the economy namely, model calibration. To do this, we constitute a Social Accounting Matrix (SAM) of 2012 for Turkey which is based on gathering the most recent updated Input-Output table of 2012 from TURKSTAT. We also benefit from evaluations of the previous constructed SAM's for Turkey (e.g., Erten, 2009; Telli, 2004), together with different data sources concerning the household consumption, government budgeting and investment. Finally, the scenario analyses are applied to the model using the calibrated parameters. By simulating the model, we establish two scenarios implementing the import tariff rate reductions in Scenario 1 and the import tariff expansions in Scenario 2. In the following sections, after the structure of the CGE modeling is presented the findings of the model simulations will be evaluated.
3.1. The Structure of CGE modeling
We construct our CGE model1 as a set of nonlinear simultaneous equations followed by Hosoe et al. (2010) and Lofgren et al. (2002). It has the multi-sectoral open economy framework. The sectors that our model covers are the following: agriculture, mining, industry, energy, construction, and services. The sectors agammaegated from the 2012 Turkish Input-Output table which has 64 sectoral subdivisions. Sectoral agammaegations are compatible with the statistical classification of economic activities in the European Community, NACE Rev 2. and the Statistical Classification of Products by Activity in the European Economic Community, CPA-2008. On the other hand, economic institutions and units encompass households, enterprises, social security institution, government and the rest of the world. The model assumes the Walrasian supply and demand equilibrium for each economic unit's expenditures and income. The CGE model consists of four equation blocks. These are production, demand, external blocks and equations that represents market clearing conditions. (For the description of the variables, parameters and their abbreviations see Appendix A).
1 See Dervis, De Melo and Robinson (1989), Devarajan and Robinson (2002) and Miller and Blair (2009) for detailed information about the sectoral linkages and the advantages of CGE models.
3.1.1. Production
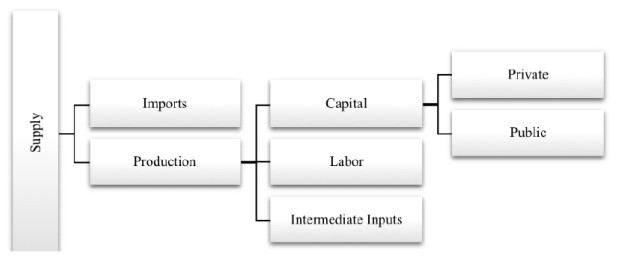
The production block is designed as the combination of linked production functions as shown in Figure 1. Our model modifies the standard approach to CGE modeling through the treatment of capital input. In the model, we assume a constant elasticity of transformation (CET) function for the composite capital input. This type of specification is thought to be more informative on the relations of the public and private capital.
The composite good on sectoral basis is a combination of domestic commodities and imports depending on the usual Armington (1969) function under the assumption of imperfect substitutability. Domestic producers who aim to maximize their profits subject to imperfect transformability, decide to export or to sell domestically. So, the composite good is a CET agammaegation of exports and domestically consumed goods.
Production block includes equations related to domestic production and the substitution between imports and domestic goods. The model assumes that value added is produced by using the labor, the private and the public capital in two stages. In the first stage, private (CPj) and public (CGj) capital are combined in CET production function, and a composite capital input (Cj) is created (Equation (4)). The treatment of capital as such is to capture the relevant division of labor between the public and the private capital in Turkey recently. Then, this composite capital input together with the labor input (Lj) demand is used under a Cobb-Douglas type production function to produce the composite factor (Yj) (Equation 1). For the production of the gross domestic output, the model covers another stage which uses the intermediate inputs (Xi, j). In the third stage, the intermediate inputs are blended with the composite factor produced in the second stage (Equation 7–8). Since the initial formulation of the gross domestic product is Leontief in essence, the kinks in the isoquants add difficulties in numerical computations. In order to overcome it, by following Hosoe et al. (2010), we employ Equation 9 which reflects the zero-profit condition and replace with the Leontief production function. Accordingly, the value of the gross domestic output is equal to the sum of the value of the composite factor and intermediate inputs (Equations 9).
3.1.1.1. Domestic production
Labor demand:
Price of the labor:
Composite capital input:
Private capital demand:
Public capital demand:
Intermediate input:
Production:
Price of the domestic product:
3.1.1.2. Substitution between imports and domestic goods
Our model is an open economy CGE model which includes behavioral equations of imports and exports. Since we employ Armington type production function for the imported goods and the domestic goods, the production block includes equations that display the substitution between imports and domestic good. The model utilizes the Armington assumption which considers imperfect substitutability between imports and domestic goods. A Constant Elasticity of Substitution (CES) function in Equation 10 captures the Armington assumption on the imports and the domestic good. Equation 11 and 12 show the demand for the imported (Mi) and the domestic (Di) goods, respectively. Within this process, an Armington composite good (Qi) is produced and then consumed as the intermediate goods by the firms, used as the final consumption by the households and government or it is invested.
Composite good:
Imported good:
Domestic good:
3.1.2. Demand
Demand section of the CGE model includes the behavioral equations of the private sector (including both households and enterprises), the government expenditures, and the investment demand.
3.1.2.1. Private sector
In the private sector section, consumption demand (XPi) is obtained through utility maximization subject to the net income (Equation 13). Net income of the private sector is the leftover after the subtraction of the private savings (SP), income taxes (Td), transfers of enterprises to the abroad (FFTRE) and to the government (FTRG) including corporation tax from private sector income (HI) Income of private sector is determined as the sum of the value of factor endowments of both the capital and the labor, the government transfers to the households (GTRHH), the government transfers to the enterprises (GTREE), the monetary transfers to the households from enterprises (EETRH), workers' foreign exchange earnings (FFTRH), and foreign exchange earnings of the enterprises (FFTRF) (Equation 14–15).
Household consumption:
Income:
Private Savings:
3.1.2.2. Government
Government finances its expenditures (XGi) with the tax revenues as well as other sources of public income. Equation 16–17 show how government gets the income tax (Td), the import tariff tax (Tmi) and the other indirect tax (Tzj) revenues. Addition to these revenues, government income, includes the corporation taxes and public factor income (FTRG) and the net unilateral transfers to the government from the abroad (FFTRG) (Equation 20). Government expenditures consist of the purchases of goods and services, the public foreign debt payments (FGDI), the transfer payments to the social security system (GTRSS), households (GTRHH) and enterprises (GTREE) (Equation 19).
CGE model explicitly incorporates the social security system into government behavior. The government transfers to the social security system imply payments to compensate income-expenditure deficits within the social security system. While revenues come from premiums obtained from both employers (SSPWT) and employees (SSPET) as a fraction of the value of the factors of production, expenditures (SSPP) are the payments done through the social security system such as pensions, medication expenses, etc. (Equation 21–23).
Income taxes:
Other indirect taxes:
Import tariff:
Consumption:
Income:
Transfers to social security system:
Employers' premium:
Employees' premium:
Government Savings:
3.1.2.2. Investment
Investment𝑠 (XVi) proportional to the total savings. The total savings are the sum of the private (SP), public (SG) savings and exchange rate adjusted foreign savings (ξSF) (Equation 25). The foreign savings measure the differences between inflow funds to the home country and outflow funds to trading partners and are merely equal to the trade deficit (Equation 31).
Total investment:
3.1.3. External demand
3.1.3.1. Transformation between exports and domestic goods
For the external demand, the CGE model assumes the imperfect substitution between the exports and the domestic good. In order to grasp this substitutability, the model specifies CET function which considers the transformation of exports and domestic goods into gross domestic output (Zi) as a composite good. Producers sells some of this output in the international markets, and the other part is traded in the domestic markets (Equation 26). Maximization of the gross domestic output subject to profits of the firms engaged in this transformation yields the export demand (Ei) and the supply of the domestic good (Di).
Gross domestic output:
Exports:
Domestic good:
3.1.3.2. Export and import prices and the balances of payment constraint
The determination of transformation of the gross domestic output into the export and supply of the domestic good as well as of the substitution between imports and the domestic output requires distinguishing the export prices (PEi) and the import prices (PMi) with respect to the world prices. On that issue, we assume a small country open economy in the model. This assumption implies that the economy at hand is so small that it cannot have significant effects on world export and import prices. In that respect, model accepts the world export (PWei) and import (PWmi) prices in terms of the domestic currency as given (Equation 29–30).
Export prices:
Import prices:
The balance of payment:
3.1.4. The market clearing conditons
The last step for CGE modeling is to set the market clearing conditions in the fourth equation block. It includes the equations of supply and demand in both commodity, labor and capital markets. Previously mentioned Armington composite good is equal to the sum of consumption of households, government, consumption of intermediate goods and investment goods (Equation 32). For the production factors market, Equation 33 and 34 indicates that initial factor endowments must be equal to the factor demand. In other words, labor and capital demand meet the supply of private and public capital.
Goods market equilibrium:
Labor market equilibrium:
Capital market equilibrium:
The simultaneous equations the structure of which explained above are solved through the General Algebraic Modelling System (GAMS) software in order to obtain the parameters of the benchmark equilibrium. We carry out the scenario analysis by using these parameters and utilize the social accounting matrix (SAM) for Turkey in 2012 for the calibration of the parameters in the benchmark equilibrium. Model parameters are generally set endogenously in a manner that assures the reference benchmark equilibrium solution accurately reproduces the values in the SAM. Remaining parameters are set as exogenous since they are not calibrated from the observed data. Table A.2 presents the calibrated parameters with their definitions. The following lines evaluate the findings of the import tariff policy scenario analysis from the CGE modeling simulations.
4.
Results and discussion
4.2. The import tariff rate policy scenario results
This paper identifies two different scenarios to investigate the impacts of the changes in the import tariff rates on sectoral production. Scenario 1 focus only on the tariff rate reductions. It tries to get the sectoral production changes after the tariff rate reductions compared to the base case scenario in which the benchmark equilibrium parameters are calibrated. For that purpose; we apply 40%, 60%, 80%, and full tariff rate reductions (zero tariff rate) to the model. Scenario 2 aims to test the effects of the increase in import tariff rates and for that purpose we apply 40%, 60%, 80% and 100% tariff rate increase.
4.2.1. Scenario 1: The import tariff rate reduction
Table 1 shows the percentage changes in the sectoral production, imports, exports, trade deficits, and employment after tariff rate reductions. According to Scenario 1, all import tariff rate reductions decrease domestic production in the model. After imposing a zero tariff rate, total domestic production drops down by 0.06%. Among other economic sectors, the highest decrease is in mining with a decrease of 3.01%. Services and agriculture follow the mining with 0.28% and 0.05% declines, respectively. This finding is crucial as the mining sector constitutes one of the largest parts of the total imports as we mentioned in Section 2. It is also true that other sectors which have a significant share in the gross domestic product such as agriculture and services will decrease their domestic production in response to the tariff rate reductions.
Composite good in the models refers to the transformation of imports and domestic production to the supply of goods. Since the increase in total imports compensate declines in total domestic production, the total supply increase after each tariff reduction. Compared to the base case scenario, reducing tariff rates increases the total imports. Even though some sectors such as the agriculture, energy, and the services decrease their imports in response to the tariff reductions, in other productive sectors namely, the mining, and the industry there were increases in the imports. If full tariff rate reduction were implemented, the imports would decline by 0.77% in the agriculture, 9.73% in the energy, and 9.55% in the service sectors. Due to import expansion the total supply increase by 0.09% after implementing a zero tariff rate.
Similar to the changes in the imported goods, the tariff rate reductions increase the total exports as well. When import tariffs are set to zero, the total exports are expected to increase by 0.45%. The highest export expansions would be observed in the energy sector by 12.27%. While in the energy sector which includes electricity and gas there are increase in exports, the mining sector would experience declines in exports. If we put mining and energy together to search the effects of tariff rates on the energy-related production broadly, it can be argued that the positive impacts of tariff rate on energy production are limited. In other words, given the domestic production declines, tariff rate reductions would not be likely to make desired positive impacts on Turkey's energy production in general.
In the light of previous discussions on the export and the imports, simulation results on the trade deficits indicate that tariff rate reductions have no positive effects of reducing the trade deficits in productive sectors except the agriculture and energy. Respective tariff rate reductions resulted in an increase in total trade deficits by 4.89% and 10.90%. Even the service sector in which Turkey traditionally achieves the trade surpluses get expansions in the trade deficits. Among these sectors the trade deficit expansions in the industry are notable. The full tariff rate reduction expands trade deficits by 264.59%.
According to the model simulation, the three sectors-agriculture, mining, and industry have considerable adverse employment effects, while in other sectors grows in terms of employment, agriculture, mining, and industry has negative growth rates of employment by 0.01%, 4.21%, and 0.23%, respectively.
In general, simulation results indicate that tariff rate reductions lead to domestic production declines together with increases in total imports in most of the sectors. Even though the intermediate price falls and increases in domestic production might be expected after the tariff reform, increasing foreign competition transforms total supply from domestic to imports. At the same time, we have an increase in exports. However, this increase does not compensate for the reduction in domestic production and trade deficits since the import contents of exports are traditionally higher in Turkey.
4.2.2. Scenario 1: The import tariff rate reduction
We observe the decrease in domestic production and an increase in trade deficits after the trade reform of tariff rate reduction. Therefore, in the next scenario, we test the effects of tariff rate increases. The simulation results for related variables are presented in Table 2. The total domestic production increases are 0.02%, 0.03%, 0.04%, and 0.05% for the respective tariff rate increases and we observe an increase in production of productive sectors except industry, energy, and construction. Among all the production sectors, the highest increase in production are in the mining sector. The services and agricultural sectors follow the mining sector. When the tariff rate is doubled, the production in the mining sector, services sector, and the agricultural sector expanded by 2.84%, 0.15%, and 0.09%, respectively.
Compared to the base case scenario, increasing tariff rates decreases the level of imports. When the tariff rate is doubled, imports of mining and industry by 1.97% and 1.36%. Total import also decreases by 0.12% in the same baseline scenario.
The increase in the import tariff rates pushes down the level of exports in all sectors except mining and industry. Increase in exports in mining and industry are by 7.88% and 1.32%, respectively. On the other hand, the reduction in exports is the fact in other sectors, and the level of total exports also declines at a rate of 0.14% in the scenario of doubling import tariffs. These findings associate with the considerable trade deficit improvements among the productive sectors except agriculture and energy. The full tariff rate expansion increases trade deficits in agriculture and energy sectors by 4.73% and 10.87%, respectively.
In the model, after doubling tariff rates, we have positive employment effects in the energy, construction and services while model indicates negative impacts on agriculture, mining, and industry. The highest decrease in employment are observed in the mining sector. The decline in the employment rate is 4.21%.
In addition to these simulations we run Hicksian equiavalent variation, as follows.
Equivalent Variation:
EV is the difference between the minimum expenditure with after tariff reform utility and existing tariff rate utility. ep(pq0,UU0) indicates the minimum expenditure level pq0Xp given utility level under the price vector (pq0) valid before tariff rate increase. Then, ep(pq0,UU1) is the minimum expenditure level after tariff rate utility under the price vectors before tariff rate increases. The positive difference between these minimum expenditures imply a welfare gains from tariff rate reform. After applying this measure to the model, we found welfare gains. Note here that EV is related to different utility levels-assuming a Cobb-Douglas type utility function in the model-compared to different consumption (Xp) levels increasing imports has also positive impacts on welfare gains.
5.
Conclusion
After the 1980s many developing countries, generally adopt trade liberalization policies. To liberalize trade decreasing the import tariff rates has been widely used. However, theoretical literature presents no consensus about the economic effects of decreasing tariff barriers. To this aim, we try to analyze the effects of the changes in import tariffs on the economy for Turkey.
Turkey has a deficiency in obtaining government budget long term data arising from the change in budgeting technique in 2012, and this led the findings of empirical studies based on time series data to become more unreliable. For that reason, we choose to build our framework on a general equilibrium basis. Doing so, we also can overcome "all else equal" assumption of partial equilibrium analysis. We construct our model as a simultaneous equations system and use GAMS software in order to employ CGE methodology. We test the effects of the decrease and the increase in the import tariff rates by applying two different scenarios. In the first scenario, we decrease the import tariff rate by 40%, 60%, 80% and 100%, respectively. Our results suggest that this simulation cause domestic production to decrease. The level of trade deficit, which is already one of the major economic problems of Turkey, does not decreases after the policy reform. From that point forth, in the next scenario, we increase the import tariff rate by 40%, 60%, 80% and 100%. In line with our findings in the first scenario, we observe an increase in the domestic production with improvements in trade deficits and employment. One might expect increase in domestic production due to declines intermediate prices after reducing tariffs. However, domestic firms may not be able to compete with the foreign firms which generally benefit from the economies of scale. This situation is especially common in the developing countries such as Turkey and consistent with the previous works of List (1841) and Caughlin et al. (1988).
We find that the most significant change in the production will arise in the mining and services sectors, which together with constitute the most substantial part of the total GDP in Turkey. We also observe that the highest decrease in the level of trade deficit arises in the industry sector which constitutes the most substantial part of total imports in Turkey. Therefore, economic policies aiming to establish a level of import substitution seems to be more favorable in Turkey. Arguably, tariff-distorted effects were small in Turkey. These findings could also be helpful to provide additional insights to the discussions on the determination of trade policies of the developing world.
Conflict of interest
All authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad:


