A generalization on derivations of Lie algebras

1.   Introduction

The study of the dynamical behavior of dynamical systems is attracting a lot of research efforts from various fields. The existence of chaos is an interesting phenomenon associated with a nonlinear dynamical system. Various dynamics, the existence of chaos, control, and synchronization have been studied on a large number of dynamical systems. A dynamical system involving fractional time derivatives instead of integer order time derivatives is known as a fractional dynamical system ^{[1,2,3,4,5,6]}. The fractional-order system is a generalization of an integer order system. It has been extensively applied for the modeling of many real problems appearing in Viscoelastic systems ^[7], distributed-order dynamical systems ^[8], hydroturbine-governing systems ^[9], glucose-insulin regulatory systems ^[10] and so on.

Stability, control and synchronization are three important concepts to investigate in chaotic fractional dynamical systems. In recent years, several methods of chaos synchronization have been proposed in the literature for fractional-order chaotic systems. For example, ^[11] investigated optimal synchronization of chaotic fractional systems. They used finite time synchronization for an optimal control problem. The authors ^[12] applied function cascade synchronization for the fractional-order chaotic systems. Mahmoud et al. ^[13] presented the idea of complex modified projective phase synchronization of the nonlinear chaotic system with complex variables. Aghababa ^[14] proposed a sliding mode technique for the goal of finite-time chaos control and synchronization of fractional-order nonautonomous chaotic systems. The adaptive fuzzy control scheme, sliding-mode control, linear, nonlinear, active, feedback, and adaptive control methods have been applied for the global stability and synchronization of chaotic fractional systems ^{[15,16,17,18,19]}.

Estimation of ultimate bound sets (UBSs) and global exponential attractive sets (GEAS) is an important topic in dynamical systems that is applied to the study of chaos control, chaos synchronization, Hausdorff dimension, and numerical search of hidden attractors ^{[20,21,22,23,24]}. In fact, if one can calculate an ultimate bound set (UBS) or globally attractive set (GAS) for a system, then the system cannot have chaotic attractors, equilibrium points, periodic solutions, quasi-periodic solutions, etc. outside the GAS ^[25,26]. This is very important for engineering applications, since it is very difficult to predict the existence of hidden attractors. Therefore, how to get the GASs of a chaotic dynamical system is particularly significant both for theoretical research and practical applications. In 1987, Leonov published the initial results of the global UBS for the Lorenz model ^[27,28,29]. After that, Swinnerton-Dyer ^[30] showed that the Lyapunov function can be used to study the bounds of the states of the Lorenz equations. This idea was developed by many researchers, and they were able to compute the GAS and PIS for different chaotic systems by constructing a family of generalized Lyapunov functions including general Lorenz system ^[31], complex Lorenz ^[32], financial risk ^[33], chaotic dynamical finance model ^[34], etc.

Motivated by the above discussion, in this article, a five-dimensional fractional-order chaotic complex system is proposed. By means of theoretical analysis and numerical simulation, some basic dynamical properties, such as phase portraits, bifurcation diagram, Lyapunov exponents and chaos diagram of the presented system are studied with varying the fractional derivative orders. An interesting point that we investigated for this system is that varying the fractional-order parameter ($\alpha$) causes the transition of the system from a chaotic state to a steady state. The UBS and GAS for the chaotic fractional systems have been estimated so far in two papers by Jian et al. ^[35,36]. Also, Jian et al. investigated the global Mittag-Leffler boundedness for fractional-order neural networks ^[37,38]. To the best of our knowledge, the GAS and the PIS for the fractional chaotic complex system have not been investigated. As an innovation, in addition to proving the global boundness of the proposed system, we calculate a family of GASs. In fact, by changing system parameters and other conditions, we can create a variety of attractive sets. The boundaries calculated for the complex chaotic system in this paper can be used for the purpose of global chaos synchronization via linear feedback controls.

This article is organized in the following sections. Section 2 presents the chaotic complex system with the fractional-order derivative. In Section 3, we will study the Mittag-Leffler GASs of the fractional chaotic complex system. Section 4 discusses the global synchronization of two fractional chaotic systems. Conclusions are drawn in Section 5.

2.   System description

In this section, we introduce a complex chaotic system with Caputo's fractional derivative. Some dynamical properties of the fractional order system, including equilibrium points, bifurcation diagrams, Lyapunov exponent spectra (LEs), and the largest Lyapunov exponent (LLE), will be presented.

2.1.   The integer-order chaotic complex system

The complex chaotic system can be represented as follows ^[39,40]:

where $z_1$ and $z_2$ are complex variables, $z_1 = x_1 + jx_2, z_2 = x_3 + jx_4, z_3 = x_5, j = \sqrt{-1}, \overline{z_1}$ and $\overline{z_2}$ are the conjugates of $z_1$ and $z_2.$ The imaginary part and the real part of the complex system (2.1) are separated, which can be expressed as follows :

The authors ^[26,39,40] derived some properties of system (2.2), including Lyapunov exponents, chaotic attractor, and ultimate bound estimation.

2.2.   The fractional-order chaotic complex system

The definitions of the Caputo integral and derivative are expressed in the following.

Definition 2.1. The fractional integral function $\mathfrak{X}(t)$, is

where $\Gamma(.)$ is the Gamma function:

Definition 2.2. The Caputo fractional-order derivative of function $\mathfrak{X}\in C^n([t_0, +\infty), \mathbb{R})$ is

Definition 2.3. The Mittag-Leffler function $E_{p, q}(.)$ with two parameters is defined as

where $p > 0, q > 0,$ and $m$ is a complex number. Obviously,

Here, we consider the five-dimensional fractional-order system

where $\sigma, \beta,$ and $r$ are parameters to be varied, and $\alpha \in (0, 1]$ is the derivative order.

The equilibrium points of the system (2.7) can be found by solving the equations

After solving this equation, one can get the equilibrium points as

where,

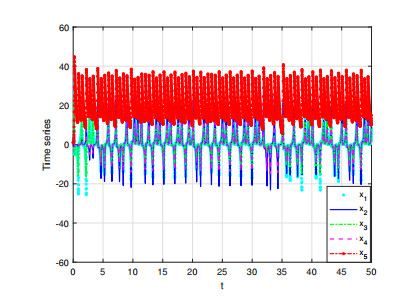
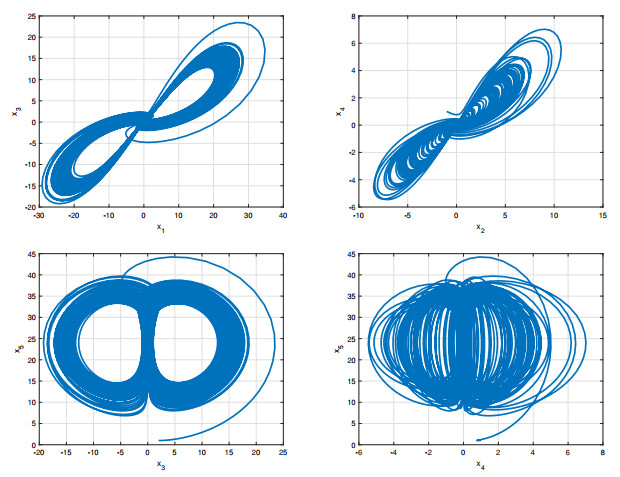
When the parameters are chosen as $\sigma = 35, \; \beta = \frac{8}{3}, \; r = 25$ and $\alpha = 0.98$, the system (2.7) is chaotic, as depicted in Figures 1 and 2.

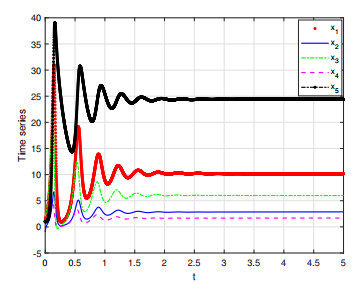
For the fractional-order system (2.7) with $\sigma = 35, \beta = \frac{8}{3}, r = 25$ and $\alpha = 0.9$ in Figures 3 and 4, chaos is suppressed, which means the system is controlled.

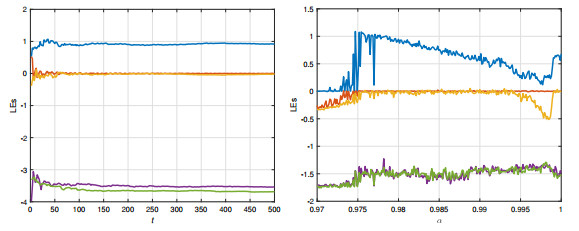
For the values of the parameters $\sigma = 35, \beta = \frac{8}{3},$ and $r = 25$, Lyapunov exponents are shown in Figure 5. The values of Lyapunov exponents at the $500$th second are $L_1 = 0. 92$, $L_2 = 0.0007$, $L_3 = -0.0194$, $L_3 = -0.0194$, $L_4 = -3.5401$, $L_5 = -3.6868.$

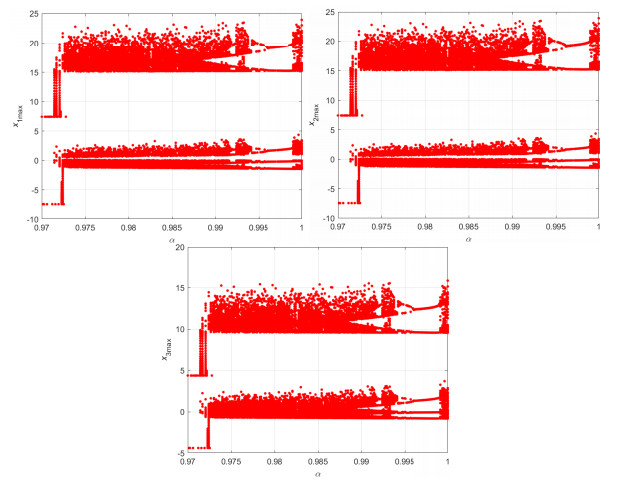
By means of the bifurcation diagrams, Lyapunov exponent spectra (LEs) and the largest Lyapunov exponent (LLE), the dynamical properties of system (2.7) are studied. The bifurcation diagrams of the system with varying derivative orders are plotted, and the results are shown in Figure 6, where $\sigma = 35, \beta = \frac{8}{3},$ and $r = 25$. In Figure 6 derivative order $\alpha$ varies from $0.97$ to $1$ with step size of $0.005$. When $\alpha < 0.972,$ the system converges to a fixed point, where the LLE of the system is zero or negative. There is a periodic window when $\alpha \in(0.9941, 0.9992)$. From Figure 6, it is clearly shown that the fractional-order complex system (2.7) is chaotic over most of the scope $\alpha \in(0.97, 1)$, where the LLE of the system is positive.

The derivative orders can change the bifurcation types and dynamics of the system. Indeed, the derivative order is a bifurcation of the fractional-order chaotic complex system.

3.   Mittag-Leffler GAS estimation of the fractional chaotic complex system

In this section, we will calculate the Mittag-Leffler GASs for the fractional-order of complex chaotic system (2.7). Let consider the following fractional-order system:

where $\mathfrak{X} \in \mathbb{R}^n$, $f:\mathbb{R}^n\rightarrow \mathbb{R}^n$ is sufficiently smooth, and $\mathfrak{X}(t, t_0, \mathfrak{X}_0)$ is the solution.

Definition 3.1. ^[35] For a given Lyapunov function $\mathcal{V}_{\lambda}(t) = \mathcal{V}_{\lambda}(\mathfrak{X}(t))$ with $\lambda > 0$, if there exist constants $\mathcal{L}_{\lambda} > 0$ and $r_{\lambda} > 0 \mbox{ for all } \mathfrak{X}_0 \in \mathbb{R}^n$ such that

for $\mathcal{V}_{\lambda}(\mathfrak{X}) > \mathcal{L}_{\lambda}$, then $\mathcal{U}_{\lambda} = \{\mathfrak{X}|\mathcal{V}_{\lambda}(\mathfrak{X}(t)) \leq \mathcal{L}_{\lambda}\}$ is said to be the Mittag-Leffler GAS of system (3.1). If for any $\mathfrak{X}_0 \in \mathcal{U}_{\lambda}$ and any $t > t_0, \ \mathfrak{X}(t, t_0, \mathfrak{X}_0) \in \mathcal{U}_{\lambda}$, then $\mathcal{U}_{\lambda}$ is said to be a Mittag-Leffler PISs, where $\mathfrak{X} = \mathfrak{X}(t), \mathfrak{X}_0 = \mathfrak{X}(t_0).$

Lemma 3.1. ^[36] If $\mathfrak{X}(t) \in \mathbb{R}$ is a continuous and differentiable function, then

Lemma 3.2. ^[36] For $\alpha \in (0, 1)$ and constant $\kappa\in \mathbb{R}$, if a continuous function $\mathfrak{X}(t)$ meets

then

The following theorem investigated the Mittag-Leffler GASs and the Mittag-Leffler PISs of the system (2.7):

Theorem 3.1. Let $\beta > 0, \sigma > 0$ and $r > 0.$ Define

Then, $\mathcal{U}_{\lambda, \mu}$ is the ultimate bound and positively invariant set of system (2.7), where

and $\eta = min\{1, \sigma, \beta \} > 0.$

Proof. Define the following generalized positively definite and radically unbounded Lyapunov function

where $\lambda > 0, \; \mu > 0.$

Computing the fractional derivative of $V_{\lambda, \mu}$ along the trajectory of system (2.7) and using Lemma 3.1, we have

where,

It is obvious that $F(X)\leq \sup\limits_{X \in \mathbb{R}^5} F(X) = l_{\lambda, \mu} = \frac{\beta((\sigma+r) \lambda+r \mu)^2}{2\mu}.$ From there we have

i.e.,

Based on Lemma 3.2, one can obtain

Based on Definition 3.1, from (3.12) we conclude that the ellipsoid $\mathcal{U}_{\lambda, \mu}$ for $\beta > 0, \sigma > 0$ and $r > 0$ is a Mittag-Leffler GAS and Mittag-Leffler PIS for the system (2.7). This completes the proof.

By changing the values of $\lambda$ and $\mu$, we can achieve different bounded sets. An interesting property about the the fractional-order parameter is that the change of $\alpha$ leads to a change in the behavior of the dynamical system from a chaotic state to a steady state.

(i) If we take $\lambda = 1, \mu = 1,$ then

is the Mittag-Leffler GAS of system (2.7).

When $\sigma = 35, b = \frac{8}{3},$ and $r = 25,$ we have

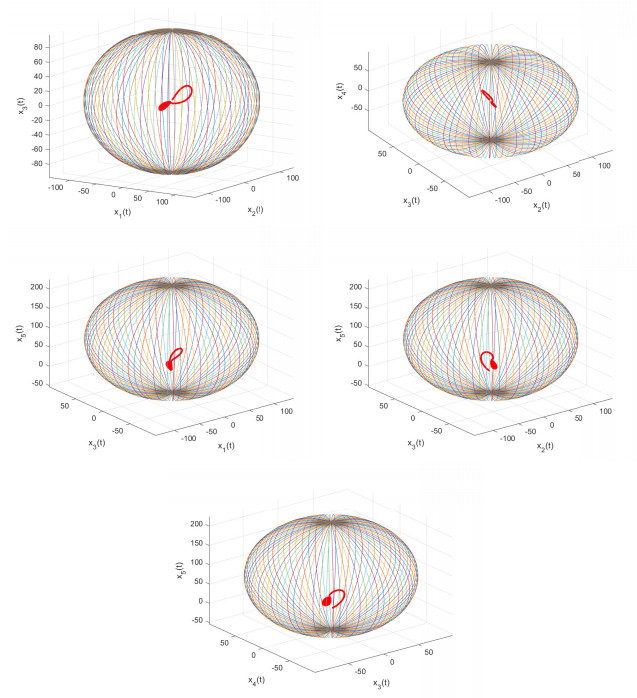
Figure 7 shows the chaotic attractors and the Mittag-Leffler GASs of the system (2.7) in the different spaces defined by $\mathcal{U}_{1, 1},$ for $\sigma = 35, \beta = \frac{8}{3}, r = 25,$ and $\alpha = 0.98$. Considering the value of $\alpha = 0.95,$ the solutions of (2.7) change from chaotic to steady-state. In this case, we found that chaos does not exist in the nonlinear fractional-order model. The phase portraits and Mittag-Leffler GAS of system (2.7) are shown through Figure 8.

(ii) Let us take $\lambda = 1, \mu = 2,$ and then we get that the set

is the Mittag-Leffler GAS of system (2.7).

When $\sigma = 35, b = \frac{8}{3},$ and $r = 25,$ we have

Figure 9 shows the phase portraits and the Mittag-Leffler GAS of system (2.7) in the different spaces defined by $\mathcal{U}_{1, 2}.$

(iii) Let us take $\lambda = 2, \mu = 1,$ and then we get that the set

is the Mittag-Leffler GAS of system (2.7).

When $\sigma = 35, b = \frac{8}{3}, r = 25,$ and $\alpha = 0.98,$ we have

4.   Global synchronization via linear feedback

In this section, we study the global synchronization of the complex chaotic system via linear feedback control. Let us state the following two lemmas which are used to prove synchronization in the presented system.

Lemma 4.1. ^[32] For any $\epsilon > 0, \mathfrak{a} \in \mathbb{R}, \mathfrak{b} \in \mathbb{R},$ the inequality $2\mathfrak{a}\mathfrak{b} \leq \epsilon \mathfrak{a}^2 +\frac{1}{\epsilon} \mathfrak{b}^2$ holds.

Lemma 4.2. ^[32] For $k > 0, \mathfrak{a} \in \mathbb{R}$ and $\mathfrak{b} \in \mathbb{R},$ the inequality $-k \mathfrak{a}^2 + \mathfrak{a}\mathfrak{b} \leq -\frac{1}{2} k \mathfrak{a}^2 +\frac{1}{2k} \mathfrak{b}^2$ holds.

Let system (2.7) be the drive system with the response system

where $y_1, y_2, \cdots, y_5$ are state variables and $u_1, u_2, \cdots, u_5$ are controllers to be designed so as to achieve global chaos synchronization between systems (4.1) and (2.7). From (3.6) in Theorem 3.1, we have

Therefore, we can get the maximum boundness of states as the following:

where $\theta = \frac{(\sigma+r)\lambda +r \mu}{\mu}.$ Then, we have the following theorem.

Theorem 4.1. The global synchronization between the drive system (2.7) and response system (4.1) will occur via the control laws

where

$k_3 > \frac{\sigma+2r+M_5}{2 \epsilon}+\frac{M_1}{2}-2, \; \; \; k_4 > \frac{\sigma+2r+M_5}{2 \epsilon}+\frac{M_2}{2}-2, \; \; \; 0 < \epsilon < \frac{\sigma}{\sigma+2 r+M_5+\theta}.$\\

Proof. Let the state errors be $e_i = y_i-x_i, i = 1, 2, \cdots, 5.$ By subtracting (2.7) from (4.1), we obtain the error dynamical system:

Let $V(e) = \frac{1}{2}e_1^2+\frac{1}{2} e_2^2+ e_3^2+e_4^2+\frac{1}{2}e_5^2$. Based on Lemma 3.1, the fractional-order derivative of $V$ along the system (4.3) is

From Lemmas 4.1 and 4.2, we have

Then,

Set

Then, $D_t^\alpha V(e) \leq -\eta V,$ where $\eta = \min\{\eta_1, \eta_2, \eta_3, \eta_4, \eta_5\}.$ By Lemma 3.2, one can obtain $V (t)\leq V(0) E_{\alpha}(-\eta t^{\alpha}), \; t\geq 0$; and thus the error system (4.3) is global stable at $e = 0,$ implying the global Mittag-Leffler synchronization of trajectories in fractional-order systems (2.7) and (4.1) by control laws (4.2).

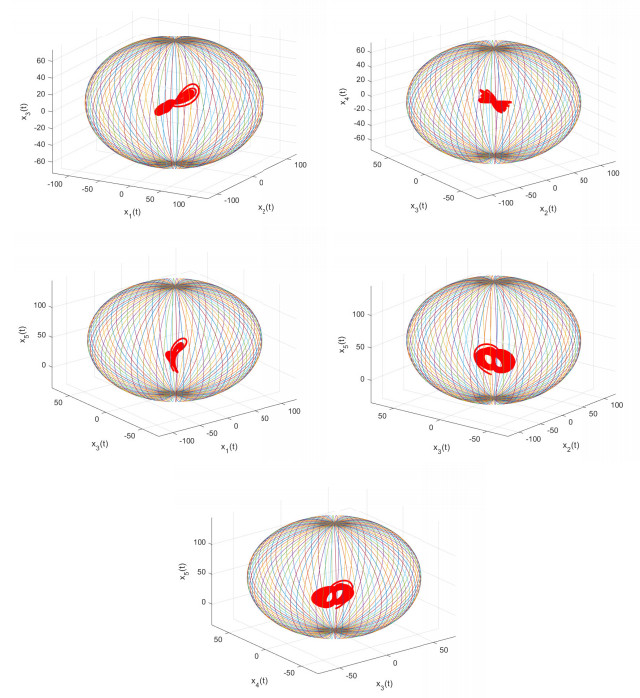
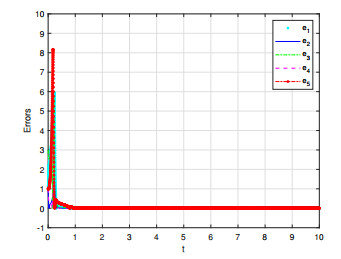
To check the correctness of the presented theory for synchronization, we used simulation using MATLAB version 2021. The parameters of both systems are taken as $\sigma = 35, \beta = \frac{8}{3}, r = 43,$ and $\alpha = 0.98$. The initial values of the master and slave systems are $(1, -1, 2, 1, 1)$ and $(0, 0.1, -1, 0, 0).$ Controllers (4.2) with $k_3 = 150$, (4.2) and $k_4 = 160$, are chosen, and then response system (4.1) synchronizes with drive system (2.7), as shown in Figures 10. Figure 11, shows synchronization errors between systems (2.7) and (4.1). From these figures, it is evident that the response trajectories fully converge to the drive, and the synchronization errors $e_i = y_i - x_i$ for $i = 1, 2, 3, 4, 5$ converge to zero.

5.   Conclusions

In this paper, we introduced the fractional-order chaotic complex system. Using the Lyapunov function and fractional-order derivative, the Mittag-Leffler GASs and Mittag-Leffler PISs for this system are obtained. Furthermore, we investigated some dynamical properties of the system, including phase portraits, bifurcation diagrams, and the Lyapunov exponents. Finally, based on the Lyapunov theory, we designed a linear feedback control to synchronize the two chaotic complex systems. Simulation results are given to show the validity of the proposed schemes.

Acknowledgments

This work was supported by the National Science and Technology Council of Republic of China under contract NSTC 111-2622-B-214-001.

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of this article.