Traveling waves for a nonlocal dispersal SIR model equipped delay and generalized incidence

1.   Introduction

Time-fractional partial differential equations (TFPDEs) have attracted considerable attention due to their ability to model memory and nonlocal properties. It has been established that TFPDEs are crucial mathematical and physical models for describing a wide range of anomalous phenomena and complex systems in the fields of natural science and engineering ^[1,2,3,4,5]. Successful applications of TFPDEs include signal processing ^[6], Powell-Eyring fluid ^[7], fluid mechanics ^[8,9], and robotics ^[10]. The multi-term TFPDEs have been found useful in describing many complex natural phenomena, such as magnetic resonance imaging (MRI) ^[11], viscoelastic mechanical models ^[12], and oxygen delivery through capillaries to a tissue (see ^[13] and the references therein). The multi-term time-fractional mixed sub-diffusion and diffusion wave equations belong to an important class of multi-term TFPDEs that have three major subclasses: the time-fractional sub-diffusion equations (TFSDEs), whose fractional order belongs to $(0, 1)$; the time fractional diffusion-wave equations (TFDWEs), whose fractional order belongs to $(1, 2)$; and TFDEs whose fractional order belongs to $(0, 2).$ Some researchers studied the analytical solutions of these equations, such as the authors of ^[14] who studied the solution of multi-term TFDWEs using the method of separation of variables. In ^[15], the authors used the Laguerre polynomials for obtaining the approximate solution of 1D TFDWE. The authors of ^[16] obtained the analytic solution of the multi-term space-time fractional advection-diffusion equation using a method based on spectral representation of fractional Laplacian operator. In most cases, the analytical solution of the these equations is provided in terms of special functions such as the multivariate Mittag-Leffler function and the Fox H-function ^[17,18], which are very complex and challenging to evaluate. Therefore, to solve these equations, numerical methods would be preferable, particularly in situations where analytical solutions are not present. Various numerical schemes have been developed to solve TFPDEs. Liu et al.^[19] developed a first-order finite difference approach with stability constraints for both time and spatial derivatives. The multi-term time-fractional mixed sub-diffusion with a variable coefficient was introduced by Zhao ^[20] using the finite element method. The solution of the wave-diffusion equation based on the Legendre spectral method and finite difference method for discretization of space and time derivatives was established in ^[21]. Shen and Gu ^[22] developed two novel finite difference schemes for 2D time fractional mixed diffusion and wave-diffusion equations. Agrawal ^[23] utilized the Laplace transform and finite sine transform for obtaining the solution of the wave-diffusion equation. In ^[24], the authors coupled spatial extrapolation method with the Crank-Nicholson method to obtain the solution to the fractional diffusion problem. In ^[25], a fully discrete spectral method was employed for the solution of a novel multi-term time-fractional mixed diffusion and diffusion-wave equation. The mesh-less method based on radial basis function was employed by ^[26] for the approximate solution of multi-term time-fractional mixed sub-diffusion. In ^[27], the authors coupled the dual reciprocity method and the improved singular boundary method for multi-term fractional wave-diffusion equations. Ye et al. ^[28] solved the 2D and 3D multi-term time-space fractional diffusion equations via a series expansion. Li et al.^[29] analyzed the temporal asymptotic behavior with well-posedness for the solution of the multi-term time-fractional diffusion equation. The authors of ^[30] employed the spectral method for the numerical solution of the two-dimensional multi-term time-fractional mixed sub-diffusion. Sun ^[31] examined the simultaneous inversion of the potential term and the fractional orders in a multi-term time-fractional diffusion equation. Spectral methods are among the most popular techniques for discretizing spatial variables in partial differential equations, which have the reputation of producing extremely accurate approximations of sufficiently smooth solutions ^[32,33]. Over time, spectral methods have been widely used in many fields, such as quantum mechanics ^[34], fluid dynamics ^[35], weather forecasting ^[36], and heat conduction ^[37], due to their high-order accuracy. These techniques haven't, however, been applied to many problems where the finite-difference and finite-element approaches are still frequently used because of some disadvantages. One disadvantage is that using spectral methods to discretize partial differential equations results in the solution of large systems of linear or nonlinear equations that require full matrices. On the other hand, finite-difference and finite-element approaches produce sparse matrices, which can be handled by suitable techniques to significantly reduce the computational complexity. Another drawback of spectral methods is that they face difficulties for problems defined on complex geometries. Although, some authors have attempted to use spectral methods in complex geometries^[38,39]. In this work, our aim is to obtain the approximate solution of the multi-term time-fractional mixed sub-diffusion using the pseudospectral method in space coupled with the Laplace transform in time. The pseudospectral method is an easy method to implement and offers low computational cost with high accuracy. Also, it has been proven that for time discretization, the Laplace transform is suitable for solving various initial and boundary value problems and can be utilized as an alternative to the classical time stepping techniques ^[40]. In finite difference time stepping techniques, the accuracy can be obtained for extremely short time steps, which results in high computational cost and crucial stability constraints. A large number of valuable works are available in the literature, which couples Laplace transform in time with another method in space (see ^[41,42] and references therein). In this article, we consider a two-dimensional multi-term time-fractional mixed sub-diffusion and diffusion-wave equation of the following form ^[43]:

with boundary conditions

and initial condition

where $\mathcal{G}(\mathit{\boldsymbol{\bar{\xi}}}, t), \; g_{1}(\mathit{\boldsymbol{\bar{\xi}}}), \; g_{2}(\mathit{\boldsymbol{\bar{\xi}}}), \; h(\mathit{\boldsymbol{\bar{\xi}}}, t)$ are given continuous functions, $\varrho_{1, k} > 0, \varrho_{3, r} > 0, \; \varrho_{l} > 0,$ $l = 2, 4, 5, 6,$ the coefficients are not simultaneously equal to zero, $1 < \alpha_{1} < \alpha_{2} < ... < \alpha_{p} < 2, \; 0 < \beta_{1} < \beta_{2} < ... < \beta_{q} < 1, \; 0 < \gamma < 1,$ $\mathit{\boldsymbol{\bar{\xi}}} = (\xi, \zeta), \; D_{t} = \frac{\partial}{\partial t}, \; \Delta = \frac{\partial^{2}}{\partial \xi^{2}}+ \frac{\partial^{2}}{\partial \zeta^{2}}, \; \; \mathit{\boldsymbol{\mathcal{L}}}_{\mathcal{B}}$ is the boundary operator, $\Gamma \subset \mathbb{R}^{2}$ is the domain, $\partial \Gamma$ is its boundary, and $\frac{\partial^{\alpha}u(\mathit{\boldsymbol{\bar{\xi}}}, t)}{\partial t^{\alpha}},$ $\frac{\partial^{\beta}u(\mathit{\boldsymbol{\bar{\xi}}}, t)}{\partial t^{\beta}}$, and $\frac{\partial^{\gamma}u(\mathit{\boldsymbol{\bar{\xi}}}, t)}{\partial t^{\gamma}}$ are fractional derivatives in Caputo's sense, defined as in ^[44].

In literature, there are many physical processes whose characteristics cannot be described by utilizing the time fractional sub-diffusion equations or the time fractional wave diffusion equation independently. In order to avoid such limitations, the multi-term time-fractional mixed sub-diffusion can be utilized as an effective mathematical model ^[43]. These models are particularly beneficial at representing anomalous diffusion processes and capturing the properties of media, including power-law frequency dependence ^[30]. Additionally, they are proficient in the modeling of various types of viscoelastic damping, modeling the unsteady flow of a fractional Maxwell fluid ^[45], and describing the behavior of an Oldroyd-B fluid, which has been used to simulate the response of many dilute polymeric liquids ^[22].

1.1.   Laplace transform

In this section, the Laplace transform is employed on the multi-term time fractional mixed sub-diffusion and diffusion-wave equation in order to reduce the problem into an equivalent time-independent problem. The Laplace transform of $u(\mathit{\boldsymbol{\bar{\xi}}}, t)$ is denoted and defined as in ^[44]

The Laplace transform of Caputo's derivative $\frac{\partial^{\alpha}u(\mathit{\boldsymbol{\bar{\xi}}}, t)}{\partial t^{\alpha}}$ of fractional order $\alpha \in (m-1, m]$ is defined as in ^[44]

Applying Laplace transform on Eqs (1.1)–(1.3), we have

and

which implies

where $\mathcal{\widehat{H}}(\mathit{\boldsymbol{\bar{\xi}}}, s) = \sum_{k = 1}^{p} \varrho_{1, k} s^{\alpha_{k}-1}g_{1}(\mathit{\boldsymbol{\bar{\xi}}})+ \sum_{k = 1}^{p} \varrho_{1, k} s^{\alpha_{k}-2}g_{2}(\mathit{\boldsymbol{\bar{\xi}}})+\varrho_{2}g_{1}(\mathit{\boldsymbol{\bar{\xi}}}) +\sum_{r = 1}^{q} \varrho_{3, r} s^{\beta_{r}-1} g_{1}(\mathit{\boldsymbol{\bar{\xi}}})\\ -\varrho_{6} s^{\gamma-1} \mathit{\boldsymbol{\mathcal{L}}}g_{1}(\mathit{\boldsymbol{\bar{\xi}}}) +\mathcal {\widehat{G}}(\mathit{\boldsymbol{\bar{\xi}}}, s),$ $\mathit{\boldsymbol{\mathcal{L}}} = \Delta$, and $I$ is the identity operator. In the proposed approach, first we discretize the linear differential operator $\mathit{\boldsymbol{\mathcal{L}}}$ via the pseudospectral method, then the full-discrete system (Eqs (1.4) and (1.5)) is solved in Laplace transform space. Finally the solution of Eqs (1.1)–(1.3) is obtained via inversion of the Laplace transform. Our solution method is highly suitable for parallel computations; it belongs to the class of parallel in time methods for TFPDEs (see ^[46]). The pseudospectral method is discussed in next section.

1.2.   Pseudospectral method

The pseudospectral method is an accurate and extremely precise approach for the numerical solution of TFPDEs. The pseudospectral method uses the Chebyshev points for collocation that are nonzero over the entire domain, whereas finite element methods use basis functions that are nonzero only on small subintervals ^[35]. In the pseudospectral method, the expansion of solutions is characterized by some global basis functions, such as Lagrange's interpolation polynomials. The concept of interpolation and differentiation matrices ^[47] is very important in the pseudospectral method. To provide a comprehensive description of the pseudospectral method based on Lagrange's interpolation polynomial basis, the main aspects of the differentiation matrices are reviewed in the next section.

1.2.1.   Differentiation matrices

In the pseudospectral method, the solution is considered over $[-1, 1]$ and the data $\bigg\{\bigg(\xi_j, \widehat{u}(\xi_j)\bigg)\bigg\}_{j = 0}^{m}$ is interpolated by the Lagrange polynomial (LP) $\eta_j(\xi)$ of degree $\leq m$ ^[33,48]

where $\eta_j(\xi)$ is the LP at the point $\xi_{j}(j = 0, 1, ..., m)$, which is

where $\widehat{u}_{j} = \widehat{u}(\xi_{j}).$ The Chebyshev nodes are defined as

and are used to discretize the domain $[-1, 1].$ The $1^{st}$ derivative $\frac{\partial \widehat{u}(\xi)}{\partial \xi }$ is approximated as

and the matrix $\mathit{\boldsymbol{\Phi}}_m$ has elements in the following form

The non-diagonal elements of $[\mathit{\boldsymbol{\Phi}}_m]_{i, j}$ have the following form

where $\alpha_j^{-1} = \prod^{m}_{i\neq j}(\xi_i-\xi_j),$ and the elements on diagonal entries are expressed as

The elements of the $\mu th$-order derivative of $\mathit{\boldsymbol{\Phi}}^{\mu}_{m}$ are analytically obtained as

In ^[47,49], more accurate evaluation of the differentiation matrices is elaborated. For the differentiation matrices, Welfert ^[47] deduced a handy recursion relation as follows

Chebyshev points are remarkable for their ability to enable spectral convergence when appropriate analytic assumptions are made.

1.2.2.   The discrete spectral operator

Let us consider the square domain $\Gamma = [-1, 1]^2$. Generally, the point in $\Gamma$ is denoted by $\mathit{\boldsymbol{\bar{\xi}}}$ and is expressed as

The LPs associated to $\mathit{\boldsymbol{\bar{\xi}}}_{ij}$ can be written as

where $\eta_{ij}(\mathit{\boldsymbol{\bar{\xi}}}_{ij}) = \delta_{ij}.$ The $2^{nd}$-order derivatives of the LPs Eq (1.6) are given as

where $\mathit{\boldsymbol{\Phi}}^2_m$ represents the second order differentiation matrix based on Chebyshev points. Applying the operator $\mathit{\boldsymbol{\mathcal{L}}}$ on the LPs Eq (1.6) based on the points $\{\mathit{\boldsymbol{\bar{\xi}}}_{rs}\}$ is

Consequently, the approximation $\mathit{\boldsymbol{\mathcal{L}}}$ via the pseudospectral method is obtained as

The conditions in Eq (1.5) are incorporating by considering the interpolation matrix $\mathit{\boldsymbol{\mathcal{L}}}_{\mathit{\boldsymbol{M}}}$ and considering all points $\mathit{\boldsymbol{\bar{\xi}}}$. Furthermore, the rows of $\mathit{\boldsymbol{\mathcal{L}}}_{\mathit{\boldsymbol{M}}}$ in correspondence with boundary nodes are replaced with unit vectors that have a one in accordance with the diagonal elements of $\mathit{\boldsymbol{\mathcal{L}}}_{\mathit{\boldsymbol{M}}}$. Hence, the boundary conditions $\mathit{\boldsymbol{\mathcal{L}}}_{\mathcal{B}}\widehat{u}(\mathit{\boldsymbol{\bar{\xi}}}, s) = \widehat{h} (\mathit{\boldsymbol{\bar{\xi}}}, s)$ in Eq (1.5) will be implemented directly ^[33]. By rearranging the columns and rows of the matrix $\mathit{\boldsymbol{\mathcal{L}}}_{\mathit{\boldsymbol{M}}}$, the following block matrix is obtained

where $W$ and $I$ are the nonzero square blocks of order $(m-m_\mathcal{B}) \times (m-m_\mathcal{B})$ and $(m_\mathcal{B} \times m_\mathcal{B}),$ respectively. However, $m_\mathcal{B}$ represents the boundary points. The solution of the system Eqs (1.4) and (1.5) can be attained by solving the linear block system

where $\mathcal{\widehat{H}}$ and $\widehat{h}$ collect the values at interior and boundary collocation points, respectively. In the final step, the inverse Laplace transform is used to obtain the solution of Eqs (1.1)–(1.3).

1.2.3.   Error analysis

The interpolation operator is based on Chebyshev collocation points Eq (1.7) and Lagrange polynomials Eq (1.6) as follows:

The steps proposed in ^[50] will be followed for the construction of the interpolation polynomial error bound, for a constant $\mathcal{M}_{m}$, which satisfies the following estimate

Additionally,

It is possible to show that for Chebyshev interpolation,

Based on $m$, the constant of stability increases very slowly. For $u \in C^{m+1}[-1, 1],$ we have the following bound ^[50]

Theorem 1. ^[50] If Eqs (1.8) and (1.9) hold, and $u \in C^{m+1}[-1, 1],$ we have

with the stability constant

Proof: By using Eqs (1.9) and (1.10) for Eq (1.1) in the one-dimension case, the governing operator is written as $\mathit{\boldsymbol{\mathcal{L}}} = \frac{\partial^{2}}{\partial \xi^{2}};$ thus, the error estimate is given as

since the time derivatives are accurately computed. Therefore, the error bound of $\|D^{\alpha}_{t}(u-\mathbf{\mathcal{I}}_{m}(u))\|_{\infty}, \|D_{t}(u-\mathbf{\mathcal{I}}_{m}(u))\|_{\infty}, \|D^{\beta}_{t}(u-\mathbf{\mathcal{I}}_{m}(u))\|_{\infty}$ and $\|u-\mathbf{\mathcal{I}}_{m}(u)\|_{\infty}$ are of the same order and the error bound of $\|D^{\gamma}_{t}(u_{\xi \xi}-\mathbf{\mathcal{I}}_{m}(u)_{\xi \xi})\|_{\infty}$ and $\; \; \|u_{\xi \xi}-\mathbf{\mathcal{I}}_{m}(u)_{\xi \xi}\|_{\infty}$ are of the same order. Thus, the following stability bound is obtained:

where the constant $\mathcal{N}$ is determined by computing the coefficients of $\|u^{(m+1)}\|_{\infty}.$ A similar stability estimate can be obtained for two-dimensional problems by using the tensor product interpolation operators.

1.3.   Inversion of Laplace transform

In this section, we utilize numerical inverse Laplace methods to transform the pseudospectral method solution $\widehat{u}(\mathit{\boldsymbol{\bar{\xi}}}, s)$ from the Laplace domain to the time domain $u(\mathit{\boldsymbol{\bar{\xi}}}, t)$ as follows:

Here, $\widehat{u}(\mathit{\boldsymbol{\bar{\xi}}}, s)$ needs to be inverted and the converging abscissa is $\rho_0$ and $\rho > \rho_0.$ Thus, the open half plane $Re(s) < \rho$ contains all the singularities of $\widehat{u}(\mathit{\boldsymbol{\bar{\xi}}}, s).$ Our goal is to approximate the integral defined in Eq (1.11). In most cases, the integral defined in Eq (1.11) is quite difficult to be evaluated analytically; therefore, a numerical method needs to be employed. The integral defined in Eq (1.11) may be evaluated by several numerical algorithms available in literature. Every approach has a distinct application and is appropriate for a certain type of function. In this article, we use the two popular inversion algorithms, the improved Talbot's method ^[51] and the Stehfest's method ^[52], which are presented as follows.

1.3.1.   Talbot's method

Here, we utilize the Talbot's method to approximate $u(\mathit{\boldsymbol{\bar{\xi}}}, t)$

where $\Lambda$ is a suitably chosen contour. In the Talbot's method, the numerical quadrature is applied to the integral in Eq (1.12). The trapezoidal and midpoint rule are the two effective rules used in conjunction with the deformation of contour ^[53]. The purpose of contour deformation is to handle the exponential factor. Particularly, the path of integration can be deformed to a Hankel contour, i.e., a contour whose real part starts at $-\infty$ in the 3rd quadrant and winds around all the singularities of the transform function going again to $-\infty$ in the 2nd quadrant. The exponential component decays rapidly on such contour, making the Bromwich integral appropriate for approximation and using the trapezoidal and midpoint rule. Cauchy's theorem justifies such deformation, provided that the contour remains in the region where the transformed function $\widehat{u}(\mathit{\boldsymbol{\bar{\xi}}}, s)$ is analytic. Furthermore, some mild restrictions are required in the left complex plane on the decay of the transformed function $\widehat{u}(\mathit{\boldsymbol{\bar{\xi}}}, s)$^[54,55]. We consider the contour in the following parametric form as^[51]

We have

where $\eta_{1}, \; \eta_2, \; \eta_3,$ and $\eta_4$ are to be selected by the user. Plugging Eq (1.13) in Eq (1.12), we have

Midpoint rule with uniform step $h = \frac{2\pi}{m_{T}}$ is utilized to approximate Eq (1.14) as

1.3.2.   Error analysis

The error analysis of the improved Talbot's approach is based on the following theorem.

Theorem 1.1. ^[51] Let $\omega_k$ be defined as in Eq (1.15). Let $g:\Xi \rightarrow \mathbb{C}$ be an analytic function in the set

when $r, s > 0,$ then

where

and

$\forall \; 0 < \phi < r, \; 0 < \psi < s, \; \; \mathit{\text{and}}\; \; m_{T}\; \; \mathit{\text{even}}$ if $m_{T}$ is an odd number; we can replace $\tan(\frac{m_{T}\omega}{2})$ with $-\cot(\frac{m_{T}\omega}{2})$ if $g(\omega)$ is real valued, that is, $g(\bar{\omega}) = \overline{g(\omega)}$ and if $r$ and $s$ can be taken to be equal, then

By examining the complex tangent function's behavior, this may be bounded as

The above process has been done for even $m_{T}$ and $\mathcal{C}$ and $r$ are some positive constants. A similar approach can be used for an odd $m_{T}.$

The optimal values of the parameters included in Eq (1.13) can be utilized to find the optimal contour of integration, which is necessary to obtain the best results. The authors of ^[51] have obtained the optimal values of the parameters as follows

The corresponding error estimate is given as

1.4.   Stehfest's method

One of the most effective and straightforward techniques for Laplace transform inversion is the Gaver-Stehfest approach. The latter part of the 1960s saw its design. Because of its simplicity and efficacy, it has become more and more popular in a variety of fields, including computational physics, finance, economics, and chemistry. The basis of the Gaver-Stehfest approach is the series of Gaver approximants, as found by Gaver ^[56]. Since the convergence of the Gaver approximants was essentially logarithmic, acceleration was necessary. A linear acceleration approach was provided by Stehfest ^[52] using the Salzer acceleration method. Using a series of functions, the Gaver-Stehfest method approximates $u(\mathit{\boldsymbol{\bar{\xi}}}, t)$ as

where $\theta_{k}$ are given as

Solving the system Eqs (1.4) and (1.5) for the corresponding Laplace parameters $s = \frac{ln2}{t} k, \; k = 1, 2, 3, ..., m_{S},$ the approximate solution $u_{App}(\mathit{\boldsymbol{\bar{\xi}}}, t)$ of the problem in Eq (1.1) can be obtained via Eq (1.16). The Gaver-Stehfest algorithm has a few noteworthy qualities, such as: (ⅰ) $u(\mathit{\boldsymbol{\bar{\xi}}}, t)$ are linear in the context of values of $\widehat{u}(\mathit{\boldsymbol{\bar{\xi}}}, s);$ (ⅱ) the values of $\widehat{u}(\mathit{\boldsymbol{\bar{\xi}}}, s)$ are required merely for real value of $s$; (ⅲ) the procedure of determining the coefficients is fairly effortless; (ⅳ) for constant functions, this approach results in significantly precise approximations, i.e., if $u \equiv c, \; \text{then} \; u_{App}\equiv \; c$ for all $m_{S} \geq 1.$ In literature, this methodology has been employed by many researchers in ^[57,58], in which it is revealed that this strategy converges promptly to $u_{App}(\mathit{\boldsymbol{\bar{\xi}}}, t)$ (given $u(\mathit{\boldsymbol{\bar{\xi}}}, t)$ is non-oscillatory).

Convergence

The convergence of $u_{App}(\mathit{\boldsymbol{\bar{\xi}}}, t)$ has been derived by the author in ^[57]. The results are based on the following theorem.

Theorem 1.2. Let $u:(0, \infty) \rightarrow \mathbb{R}$ be a locally integrable function. Let $s > 0,$ define the Laplace transform $\widehat{u}(\mathit{\boldsymbol{\bar{\xi}}}, s)$, and let $u_{App}(\mathit{\boldsymbol{\bar{\xi}}}, t)$ be the numerical solution as given by Eq (1.16).

1. $u_{App}(\mathit{\boldsymbol{\bar{\xi}}}, t)$ converges given $u(\mathit{\boldsymbol{\bar{\xi}}}, t)$ near $t$.

2. Let for some real number $\phi$ and $0 < \psi < 0.25,$

then $u_{App}(\mathit{\boldsymbol{\bar{\xi}}}, t)\rightarrow \phi$ as $m_{S} \rightarrow +\infty.$

3. Let $u(\mathit{\boldsymbol{\bar{\xi}}}, t)$ be of bounded variation near $t,$ then

Corollary 1.3. Using the assumptions of the above theorem, if

$\forall \; \eta,$ and some $\vartheta,$ then $u_{App}(\mathit{\boldsymbol{\bar{\xi}}}, t) \rightarrow u(\mathit{\boldsymbol{\bar{\xi}}}, t)$ as $m_{S} \rightarrow +\infty.$

Moreover, the authors in ^[59] conducted a number of experiments to determine how parameters affected the numerical scheme's correctness. Their conclusions are as follows: "For $\nu_{1}$ significant digits, select a $m_{S}$ positive integer $\lceil2.2 \nu_{1}\rceil$: After setting the system precision to $\nu_{2} = \lceil 1.1 m_{S}\rceil$, compute $\theta_i, 1 \leq i \leq m_{S}$ for a given $m_{S}$ using Eq (1.17). Next, compute the $u_{App}(\mathit{\boldsymbol{\bar{\xi}}}, t)$ in Eq (1.16) for the provided transformed function $\widehat{u}(\mathit{\boldsymbol{\bar{\xi}}}, s)$ and the argument $t$." These conclusions indicate that the error is $10^{-(\nu_{1}+1)}\leq \frac{u_{App}(\mathit{\boldsymbol{\bar{\xi}}}, t)-u(\mathit{\boldsymbol{\bar{\xi}}}, t)}{u(\mathit{\boldsymbol{\bar{\xi}}}, t)}\leq 10^{-\nu_{1}},$ where $m_{S} = \lceil 2.2 \nu_{1}\rceil$ ^[40].

2.   Application

In this section, three test problems are considered to assess the effectiveness and accuracy of the Laplace transformed pseudospectral method. We compute the maximum absolute error $({Err}_{\infty}),$ the relative error $({Err}_{2}),$ and the root mean square error $({Err}_{rms})$ between the numerical and the exact solutions, which are defined as follows:

where $u_{App}(\mathit{\boldsymbol{\bar{\xi}}}_k, t)$ is the approximate solution and $u(\mathit{\boldsymbol{\bar{\xi}}}_k, t)$ is the exact solution.

Problem 1

We consider Eq (1.1) with exact solution

and the source term is

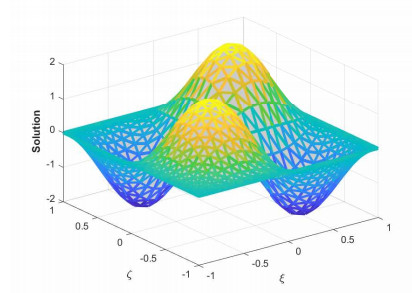
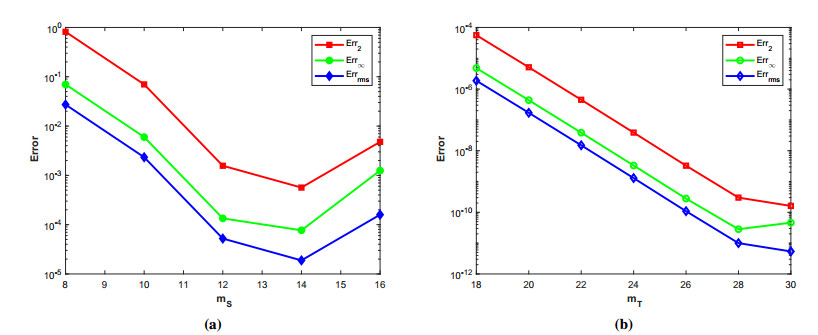
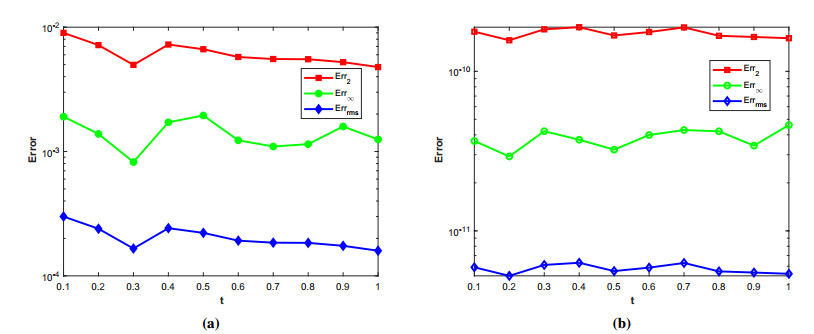
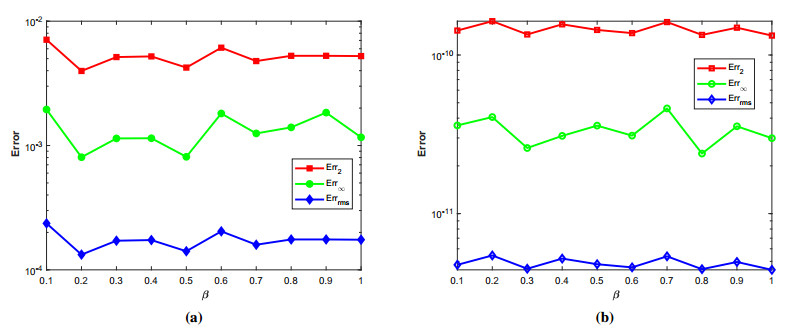
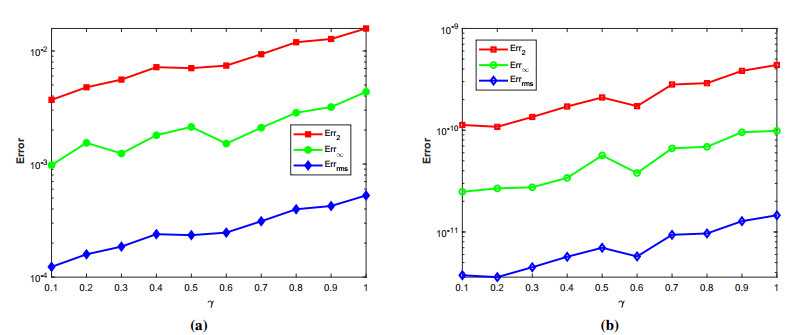
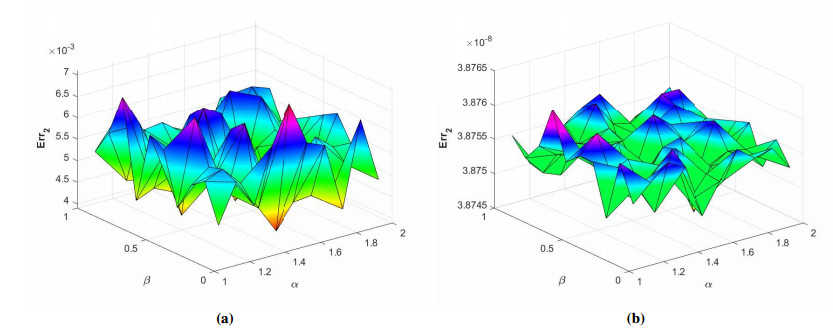
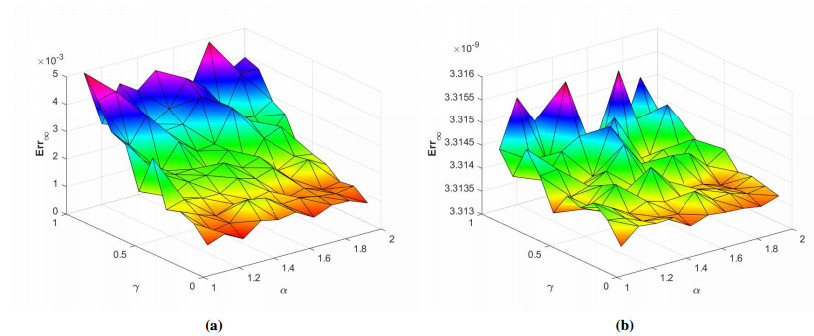
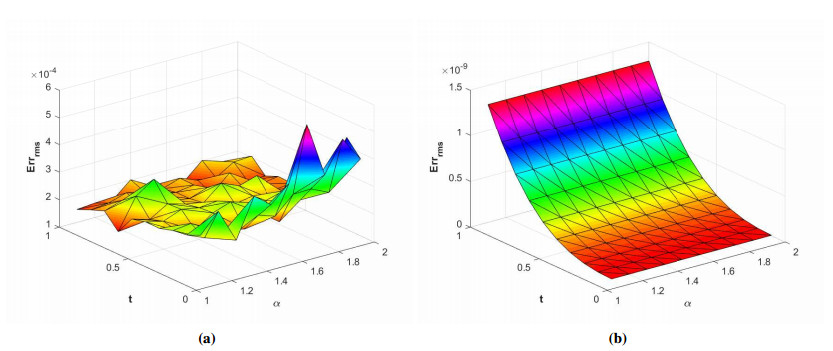
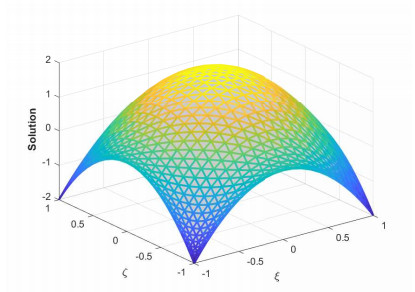
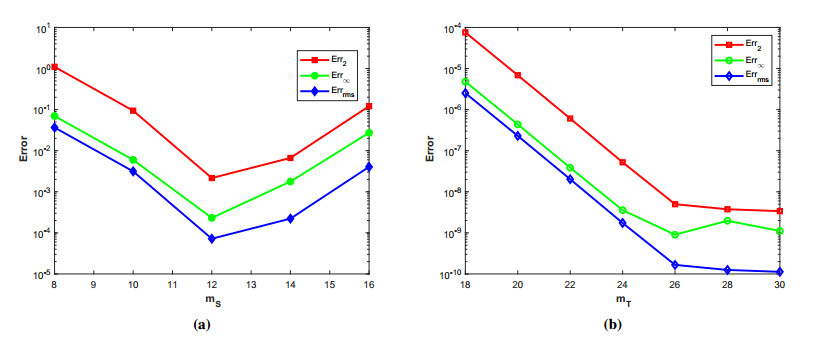
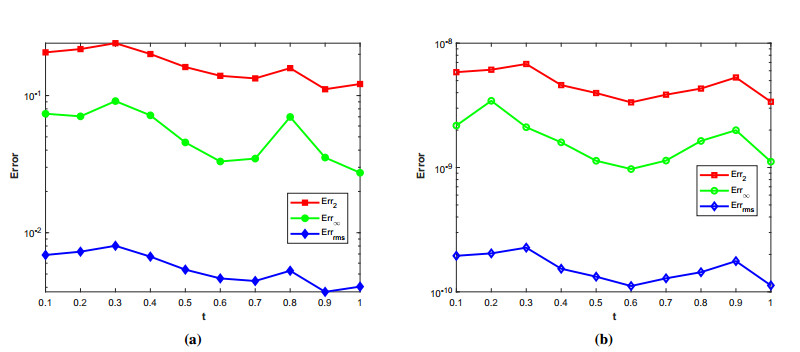
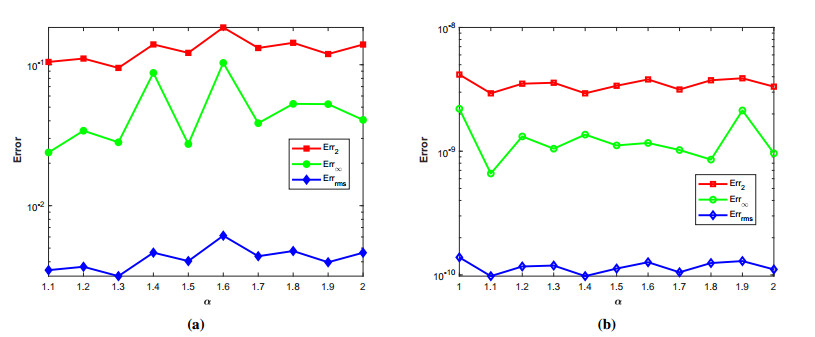
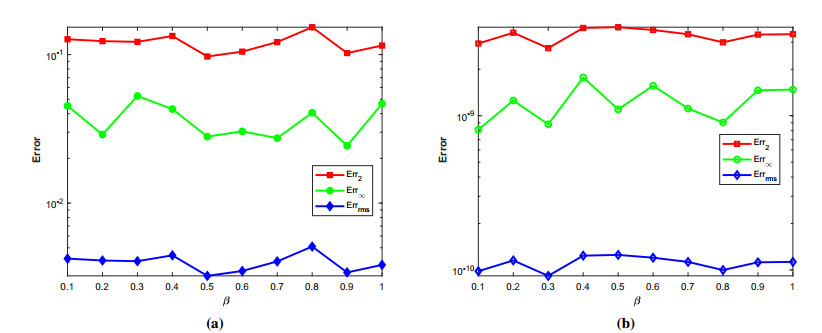
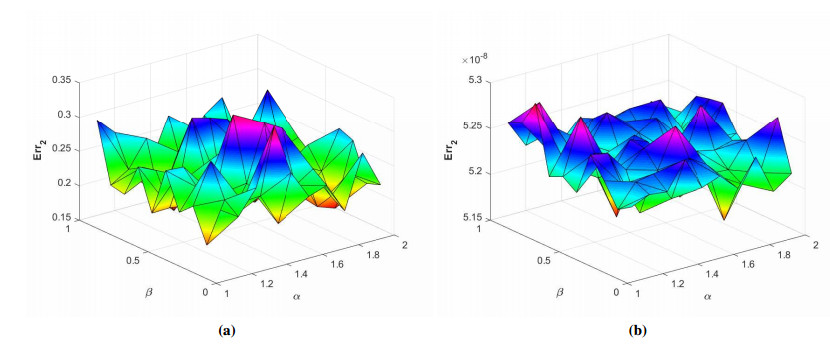
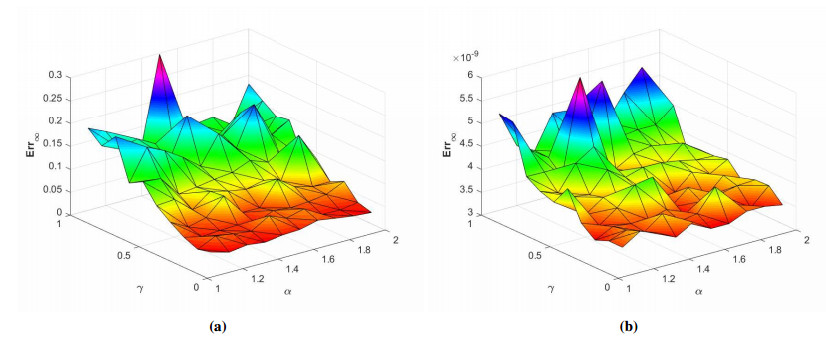
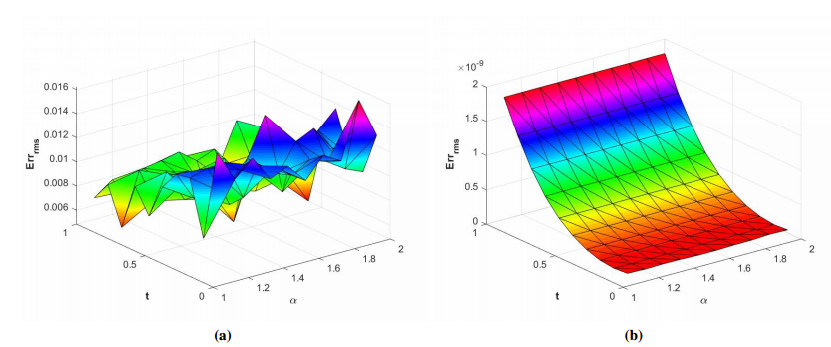
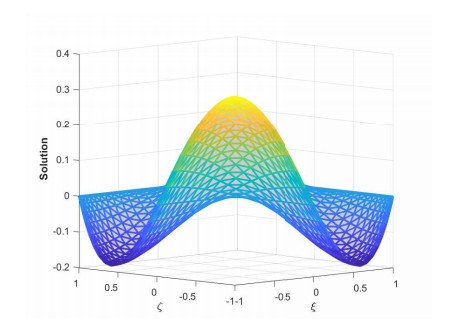
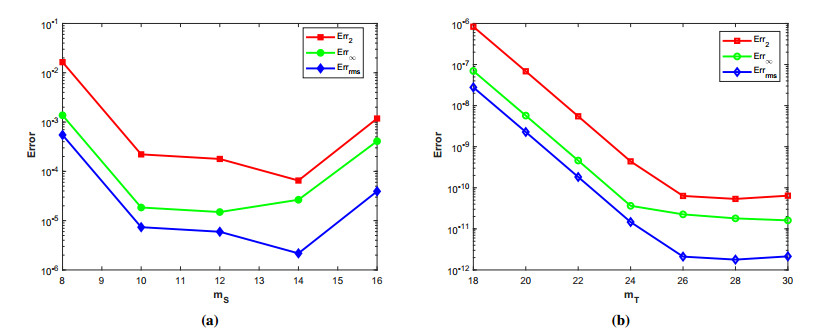
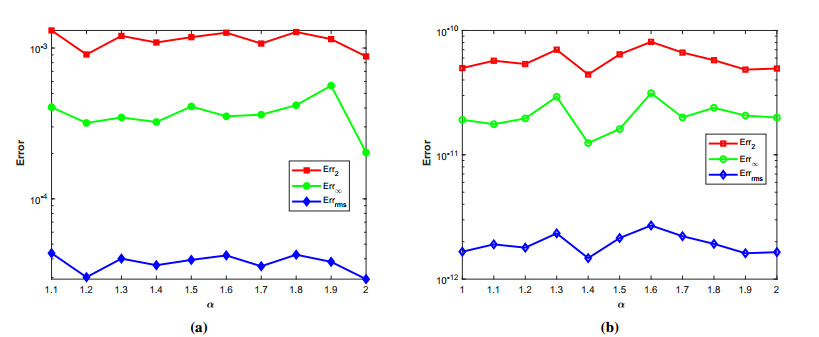
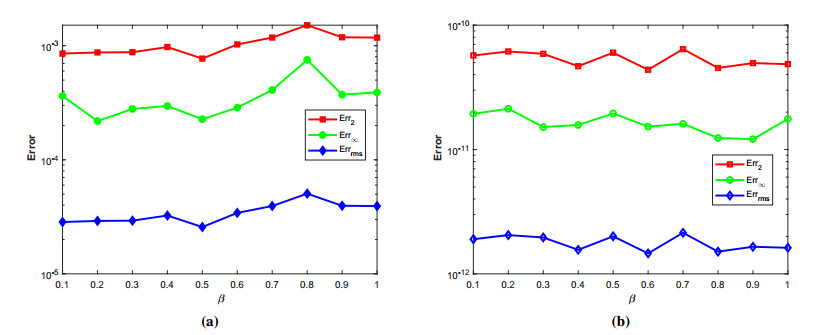
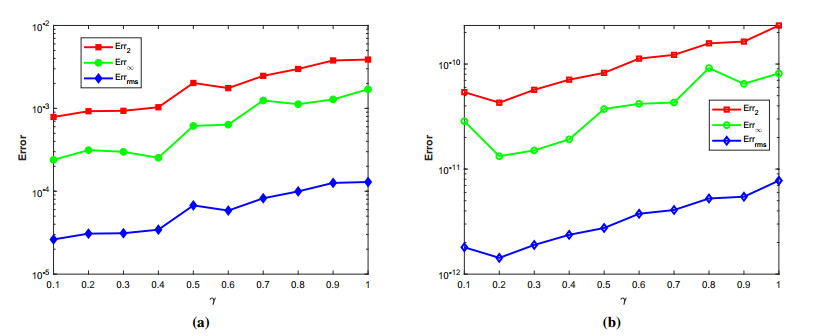
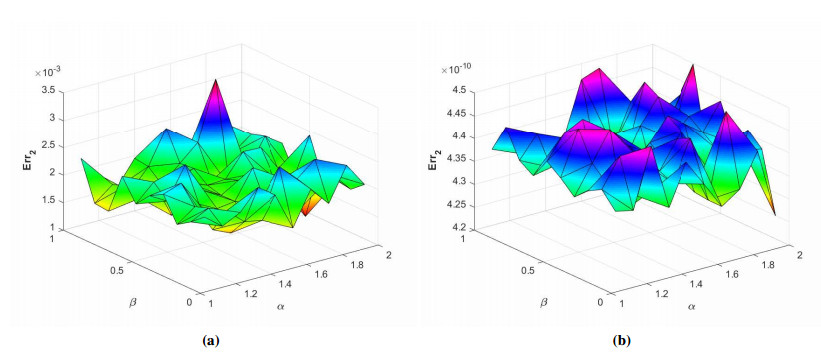
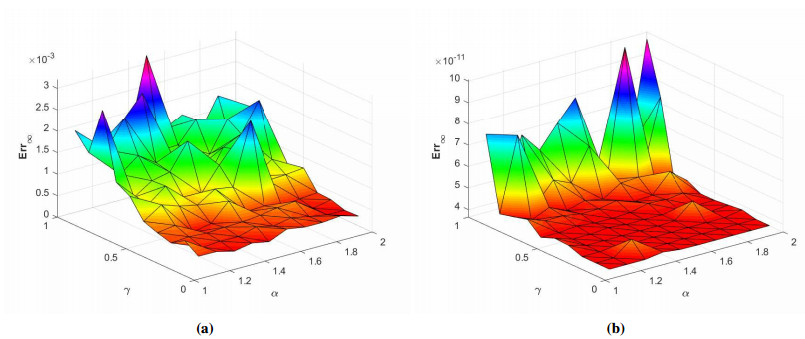
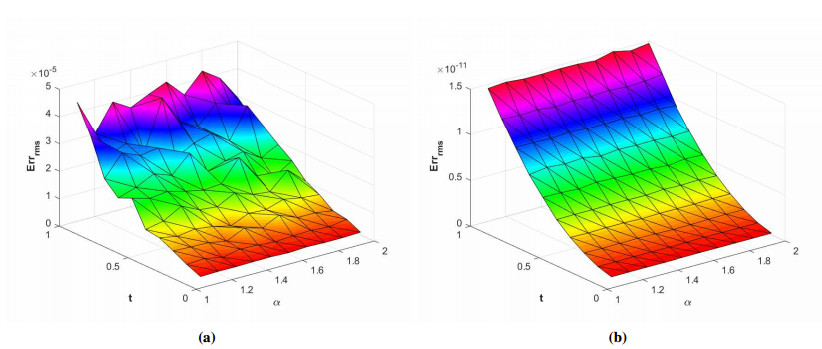
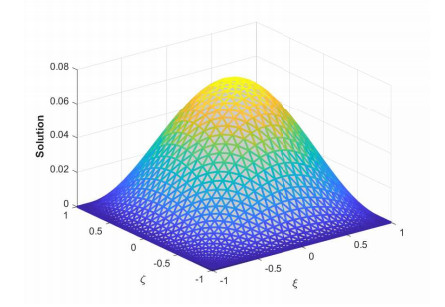
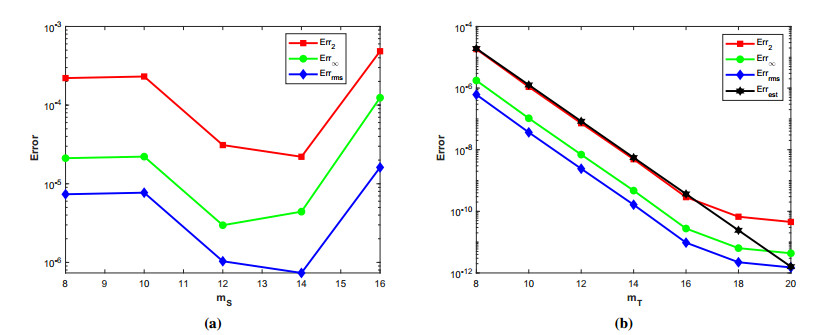
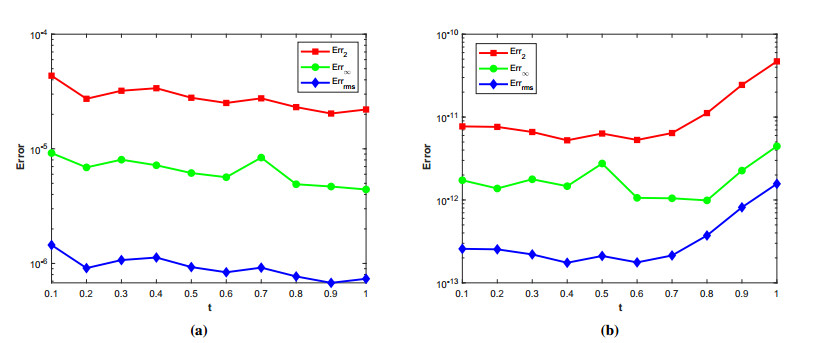
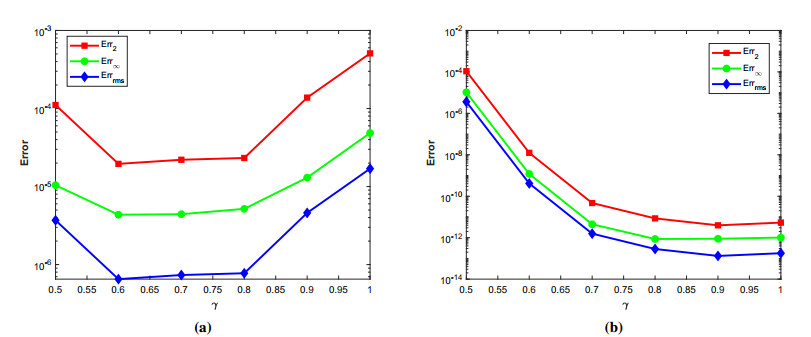
where $\varrho_{1, 1} = \varrho_{2} = \varrho_{3, 1} = \varrho_{4} = \varrho_{5} = \varrho_{6} = 1$ and $(\xi, \zeta) \in [-1, 1]^{2}.$ The initial-boundary conditions are obtained from the analytical solution. The $Err_{2}, Err_{\infty},$ and $Err_{rms}$ errors of the proposed method for problem 1 obtained via the Stehfest's and the Talbot's methods by using various values of $m, \; m_{T}, \; m_{S}, \; \alpha, \; \beta, \; \gamma,$ and $t = 1$ are presented in Tables 1 and 2, respectively. The numerical solution to problem 1 is shown in Figure 1. Figure 2 presents a comparison of error norms $Err_{2}, Err_{\infty},$ and $Err_{rms}$ computed using the Stehfest's and the Talbot's methods for various values of $m_{S}$ and $m_{T}$ with $\alpha = 1.5, \; \beta = 0.7, \; \gamma = 0.3, \; m = 30,$ and $t = 1$. The comparison of $Err_{2}, Err_{\infty},$ and $Err_{rms}$ computed by the Stehfest's and the Talbot's methods for different values of $t$ with $\alpha = 1.5, \; \beta = 0.7, \; \gamma = 0.3, \; m_{S} = 14, \; m_{T} = 30,$ and $m = 30$ is shown in Figure 3. The comparison of $Err_{2}, \; Err_{\infty},$ and $Err_{rms}$ computed using the Stehfest's and the Talbot's methods versus $\alpha$ with $\beta = 0.7, \; \gamma = 0.3, \; m = 30, \; m_{S} = 14, \; m_{T} = 30,$ and $t = 1$ is presented in Figure 4. The comparison of $Err_{2}, Err_{\infty},$ and $Err_{rms}$ computed via the Stehfest's and the Talbot's methods versus $\beta$ with $\alpha = 1.5, \gamma = 0.7, m = 30, m_{S} = 14, m_{T} = 30,$ and $t = 1$ is presented in Figure 5. The comparison of $Err_{2}, Err_{\infty},$ and $Err_{rms}$ computing by the Stehfest's and the Talbot's methods versus $\gamma$ with $\alpha = 1.5, \beta = 0.7, m = 30, m_{S} = 14, m_{T} = 30,$ and $t = 1$ is presented in Figure 6. The plot of $Err_{2}$ obtained via the Stehfest's and the Talbot's methods for $\alpha \in [1, 2]$ and $\beta \in [0, 1]$ with $\gamma = 0.3, \; t = 1, \; m_{S} = 16, m_{T} = 30,$ and $m = 30$ is shown in Figure 7. In Figure 8, the plots of $Err_{\infty}$ obtained using the Stehfest's and the Talbot's methods for $\alpha \in [1, 2]$ and $\gamma \in [0, 1]$ with $\beta = 0.7, \; t = 1, \; m_{S} = 16, \; m_{T} = 30,$ and $m = 30$ are shown. Similarly, Figure 9 presents the plots of $Err_{rms}$ obtained using the Stehfest's and the Talbot's methods for $\alpha \in [1, 2]$ and $t \in [0, 1]$ with $\beta = 0.7, \gamma = 0.3, m_{S} = 16, \; m_{T} = 30,$ and $m = 30.$ It is observed that the accuracy of the Stehfest's method steadily decreases for $m_{S}\geq 14$. From the results presented in tables and figures, we conclude that the proposed method is accurate, stable, and efficient. The numerical results demonstrate that the Talbot's method is more accurate than the Stehfest's method.

Problem 2

We consider Eq (1.1) with exact solution

and the source term is

where $\varrho_{1, 1} = \varrho_{2} = \varrho_{3, 1} = \varrho_{4} = \varrho_{5} = \varrho_{6} = 1,$ $(\xi, \zeta) \in [-1, 1]^{2}$ and the initial-boundary conditions are obtained from the analytical solution.

The $Err_{2}, Err_{\infty},$ and $Err_{rms}$ errors of the proposed method for problem 2 obtained via the Stehfest's and the Talbot's methods by using various values of $m, \; m_{T}, \; m_{S}, \; \alpha, \; \beta, \; \gamma,$ and $t = 1$ are presented in Tables 3 and 4, respectively.

The numerical solution of problem 2 is shown in Figure 10. Figure 11 presents a comparison of error norms $Err_{2}, \; Err_{\infty},$ and $Err_{rms}$ computed via the Stehfest's and the Talbot's methods versus $m_{S}$ and $m_{T}$ with $\alpha = 1.5, \; \beta = 0.7, \; \gamma = 0.3, \; m = 30,$ and $t = 1$. The comparison of $Err_{2}, Err_{\infty},$ and $Err_{rms}$ obtained using the Stehfest's and the Talbot's methods versus $t$ with $\alpha = 1.5, \; \beta = 0.7, \; \gamma = 0.3, \; m_{S} = 14, \; m_{T} = 30,$ and $m = 30$ is shown in Figure 12.

The comparison of $Err_{2}, \; Err_{\infty},$ and $Err_{rms}$ obtained using the Stehfest's and the Talbot's methods versus $\alpha$ with $\beta = 0.7, \; \gamma = 0.3, \; m = 30, \; m_{S} = 14, \; m_{T} = 30,$ and $t = 1$ is presented in Figure 13. The comparison of $Err_{2}, Err_{\infty},$ and $Err_{rms}$ computed using the Stehfest's and the Talbot's methods versus $\beta$ with $\alpha = 1.5, \gamma = 0.7, m = 30, m_{S} = 14, m_{T} = 30,$ and $t = 1$ is shown in Figure 14.

The comparison of $Err_{2}, Err_{\infty},$ and $Err_{rms}$ obtained using the Stehfest's and the Talbot's methods versus $\gamma$ with $\alpha = 1.5, \beta = 0.7, m = 30, m_{S} = 14, m_{T} = 30,$ and $t = 1$ is presented in Figure 15. The plots of $Err_{2}$ obtained using the Stehfest's and the Talbot's methods for $\alpha \in [1, 2]$ and $\beta \in [0, 1]$ with $\gamma = 0.3, \; t = 1, \; m_{S} = 16, m_{T} = 30,$ and $m = 30$ are shown in Figure 16.

In Figure 17, the plots of $Err_{\infty}$ obtained using the Stehfest's and the Talbot's methods for $\alpha \in [1, 2]$ and $\gamma \in [0, 1]$ with $\beta = 0.7, \; t = 1, \; m_{S} = 16, \; m_{T} = 30,$ and $m = 30$ are shown. Similarly, Figure 18 shows the plot of $Err_{rms}$ obtained via the Stehfest's and the Talbot's methods for $\alpha \in [1, 2]$ and $t \in [0, 1]$ with $\beta = 0.7, \gamma = 0.3, m_{S} = 16, \; m_{T} = 30,$ and $m = 30.$ Comparable performances like the one we witnessed in Problem 2 are observed.

Problem 3

We consider Eq (1.1) with analytical solution as

and the source term is

where $\varrho_{1, 1} = \varrho_{2} = \varrho_{3, 1} = \varrho_{4} = \varrho_{5} = \varrho_{6} = 1$ and $\mathit{\boldsymbol{\bar{\xi}}} = (\xi, \zeta) \in [-1, 1]^{2}.$ The initial-boundary conditions are obtained from the analytical solution. The $Err_{2}, Err_{\infty},$ and $Err_{rms}$ errors obtained using the proposed method for problem 3 obtained via the Stehfest's and the Talbot's methods by using various values of $m, \; m_{T}, \; m_{S}, \; \alpha, \; \beta, \; \gamma,$ and $t = 1$ are presented in Tables 5 and 6, respectively.

The numerical method solution to problem 3 is shown in Figure 19. Figure 20 represents a comparison of error norms $Err_{2}, Err_{\infty},$ and $Err_{rms}$ computed by the Stehfest's and the Talbot's methods versus $m_{S}$ and $m_{T}$ with $\alpha = 1.5, \beta = 0.7, \; \gamma = 0.3, \; m = 30$, and $t = 1$. The comparison of $Err_{2}, Err_{\infty},$ and $Err_{rms}$ obtained using the Stehfest's and the Talbot's methods versus $t$ with $\alpha = 1.5, \; \beta = 0.7, \; \gamma = 0.3, \; m_{S} = 14, \; m_{T} = 30,$ and $m = 30$ is shown in Figure 21.

The comparison of $Err_{2}, \; Err_{\infty},$ and $Err_{rms}$ obtained using the Stehfest's and the Talbot's methods for different values of $\alpha$ with $\beta = 0.7, \; \gamma = 0.3, \; m = 30, m_{S} = 14, \; m_{T} = 30,$ and $t = 1$ is shown in Figure 22. The comparison of $Err_{2}, Err_{\infty},$ and $Err_{rms}$ obtained using the Stehfest's and the Talbot's methods for different values of $\beta$ with $\alpha = 1.5, \gamma = 0.7, m = 30, m_{S} = 14, m_{T} = 30,$ and $t = 1$ is presented in Figure 23.

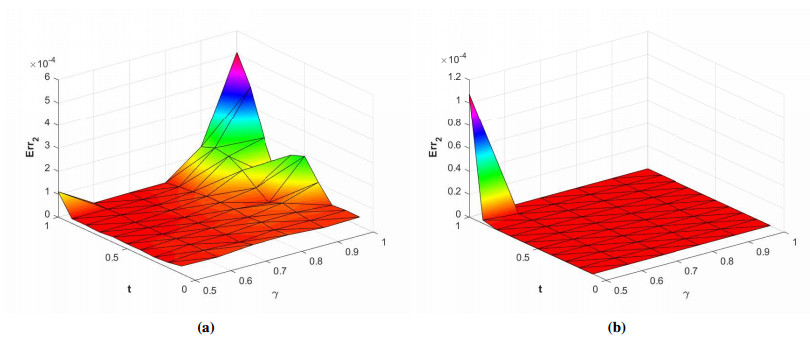
The comparison of $Err_{2}, Err_{\infty},$ and $Err_{rms}$ obtained using the Stehfest's and the Talbot's methods versus $\gamma$ with $\alpha = 1.5, \beta = 0.7, m = 30, m_{S} = 14, m_{T} = 30,$ and $t = 1$ is presented in Figure 24. The plot of $Err_{2}$ using the Stehfest's and the Talbot's methods for $\alpha \in [1, 2]$ and $\beta \in [0, 1]$ with $\gamma = 0.3, \; t = 1, \; m_{S} = 16, m_{T} = 30,$ and $m = 30$ is shown in Figure 25.

In Figure 26, the plots of $Err_{\infty}$ obtained using the Stehfest's and the Talbot's methods for $\alpha \in [1, 2]$ and $\gamma \in [0, 1]$ with $\beta = 0.7, \; t = 1, \; m_{S} = 16, \; m_{T} = 30,$ and $m = 30$ are shown. Similarly, Figure 27 shows the plots of $Err_{rms}$ using the Stehfest's and the Talbot's methods for $\alpha \in [1, 2]$ and $t \in [0, 1]$ with $\beta = 0.7, \gamma = 0.3, m_{S} = 16, \; m_{T} = 30,$ and $m = 30.$

It is observed that the accuracy of the Stehfest's method steadily decreases for $m_{S}\geq 14$. From the results presented in tables and figures, we conclude that the proposed method is accurate, stable, and efficient. The numerical results demonstrates that the Talbot's method is more accurate than the Stehfest's method.

Problem 4

We consider a limiting case of Eq (1.1) with analytical solution as

and the source term is

where $\varrho_{1, 1} = \varrho_{3, 1} = \varrho_{2} = 0,$ $\varrho_{6} = \varrho_{4} = \varrho_{5} = 1,$ $(\xi, \zeta) \in [-1, 1]^{2},$ and the initial-boundary conditions are obtained from the analytical solution. $E_{\gamma}(t) = \sum_{n = 0}^{\infty} \frac{t^{n}}{\Gamma(n \gamma+1)}, \; (\gamma \in \mathbb{C}, Re({\gamma}) > 0)$ is the Mittag Leffler function. The $Err_{2}, Err_{\infty},$ and $Err_{rms}$ errors of the proposed method for problem 4 by using various values of $m, \; m_{T}, \; m_{S}, \; \gamma,$ and $t = 1$ are presented in Tables 7 and 8, respectively. The numerical solution of problem 4 is shown in Figure 28. Figure 29 presents a comparison of error norms $Err_{2}, Err_{\infty},$ and $Err_{rms}$ obtained via the Stehfest's and the Talbot's methods versus $m_{S}$ and $m_{T}$ with $\gamma = 0.7, \; m = 30,$ and $t = 1$. The comparison of $Err_{2}, Err_{\infty},$ and $Err_{rms}$ obtained using the Stehfest's and the Talbot's methods versus $t$ with $\gamma = 0.7, \; m_{S} = 14, \; m_{T} = 25,$ and $m = 30$ is shown in Figure 30. The comparison of $Err_{2}, Err_{\infty},$ and $Err_{rms}$ using the Stehfest's and the Talbot's methods versus $\gamma$ with $m = 30, m_{S} = 14, m_{T} = 25,$ and $t = 1$ is presented in Figure 31. The plot of $Err_{2}$ using the Stehfest's and the Talbot's methods for $\gamma \in [0.5, 1]$ and $t \in [0, 1]$ with $m_{S} = 14, m_{T} = 25,$ and $m = 30$ is shown in Figure 32. In Figure 33, the plots of $Err_{\infty}$ computed using the Stehfest's and the Talbot's methods with $\gamma \in [0.5, 1], \; t \in [0, 1], \; m_{S} = 14, \; m_{T} = 25,$ and $m = 30$ are shown. Similarly, Figure 34 shows the plot of $Err_{rms}$ obtained using the Stehfest's and the Talbot's methods with $\gamma \in [0.5, 1], \; t \in [0, 1], \; m_{S} = 14, \; m_{T} = 25,$ and $m = 30.$ The computational results undeniably demonstrate that Talbot's method is greater in precision than Stehfest's method.

3.   Conclusion

In the current work, we have developed an efficient and stable numerical method, which combines the numerical Laplace transform method in time with the pseudospectral method in space for the numerical solution of the two-dimensional time fractional multi-term mixed sub-diffusion and diffusion-wave equation. The proposed method offers an excellent approach to the solution process of the considered equation. In our technique, first, the Laplace transform was employed, which reduced the problem into an elliptic problem in the Laplace transform domain, then the pseudospectral method was utilized to obtain the approximate solution to the transformed problem. Finally, the improved Talbot's method and the Stehfest's method were used to convert the obtained solution in Laplace transform domain back into time domain. The improved Talbot's method and the Stehfest's method provide a numerical inversion process that is accurate, stable, easy to implement, and does not suffer from stability issues which occur with finite difference time stepping methods. From the results presented in tables and figures, it can be observed that the Stehfest's method provides optimal results for $m_{S} < 14,$ and for $m_{S} \geq 14,$ its accuracy decreases. Furthermore, the obtained numerical results clearly demonstrate that the Talbot's method is considerably more precise than the Stehfest's method.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

The authors D. Santina and N. Mlaiki would like to thank the Prince Sultan University for paying the publication fees for this work through TAS LAB. This research is supported by Prince Sultan University, Saudi Arabia.

Conflicts of interest

The authors declare that they have no conflicts of interest.