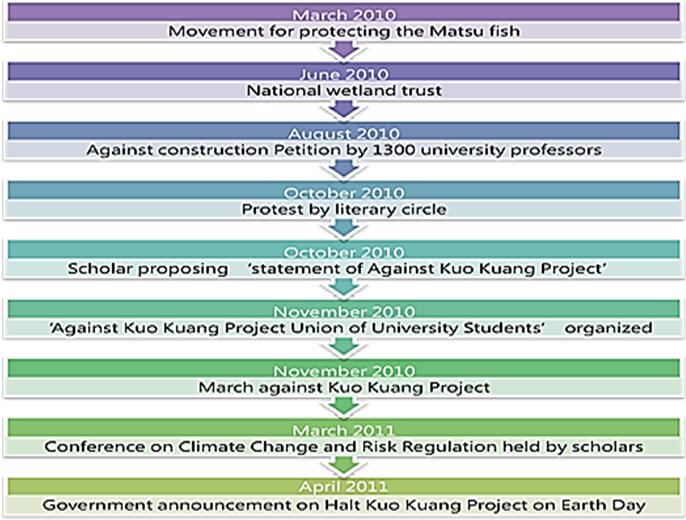
In the past two decades, despite seemingly violating its policy of sustainable development, the government of Taiwan has continued to develop its petrochemical industry. As a result of which public resistance has emerged. This study examines the social robustness and sub-politics capacity of the movement against Kuo Kuang Petrochemical Corp. from 2010 to 2011. Among the various civil groups engaged in the movement, the anti-expert coalition was formed by local environmental, literary and medical groups as well as universities and university professors. These groups mobilized independently, while supporting one another; leading to a multi-risk movement coalition. One significant difference between this anti-expert coalition and past environmental movements was that it not only constructed systematic risk knowledge and resisted official discourse from a professional perspective, but also developed perceptual literary thought, triggering a response from the general public. Therefore, no matter whether it be through systematic, rational participation in the environmental assessment process, proposing socio-economic assessment and health risk paths or their more perceptual initiation of green thought processes (generation justice, land subsidence, good and agriculture safety and the sustainability of villages) and methods of promoting civil trust, the sub-political pluralism has been able to break through authoritative expert politics, and seek for a dynamic reflexive governance of social sustainable development.
1.
Introduction
Monkeypox (Mpox) is caused by the monkeypox virus [1,2], which has its natural reservoir in animals such as monkeys and rodents [3,4]. The virus was first identified in humans in 1970 [5,6]. Human transmission occurs through close contact with an infected person via non-sexual (skin-to-skin) and sexual routes (anal, vaginal, or oral sex) [7]. Mpox is endemic in several African countries, including the Democratic Republic of the Congo (DRC), Ghana, Nigeria, Cameroon, and the Central African Republic (CAR) [8,9]. Transmission in these regions is often driven by zoonotic spillover from animal hosts to humans [10,11] or through direct human-to-human skin contact [8,12].
In April 2022, an outbreak of Mpox occurred in multiple countries where the disease is not endemic [13,14], thus presenting clinical and epidemiological features distinct from previous outbreaks. Notably, the virus is believed to have spread predominantly through sexual contact [15,16]. The outbreak disproportionately affected men who have sex with men (MSM), with the highest number of cases reported within this population [17,18,19]. Changes in sexual behavior, alongside the roll-out of vaccination campaigns, led to a decline in Mpox cases. However, a recent resurgence in Western countries, such as Canada, and other regions, including African countries such as Burundi, Kenya, Rwanda, and Uganda, where Mpox has not been previously reported [20,21,22], has highlighted the need to understand the disease's dynamics in human populations. This resurgence, coupled with the emergence of a new, more virulent and deadly strain (clade I MPXV) [23,24] which has spread even beyond the MSM population, prompted the World Health Organization (WHO) to declare it a Public Health Emergency of International Concern (PHEIC) [25,26].
In addition to Mpox, the MSM population is disproportionately affected by several sexually transmitted infections, including the human immunodeficiency virus (HIV). By the end of 2023, approximately 39 million people were living with HIV/AIDS worldwide [27,28,29], with around 44% of these individuals belonging to the MSM community [30]. Despite the availability of numerous preventive and treatment interventions, HIV continues to spread globally [31,32,33], with approximately 1.5 million new cases and one million HIV-related deaths annually [34,35]. In 2022, the annual incidence rate of HIV in Canada was 4.7 per 100,000 people, with 129 HIV-related deaths reported. About 47% of those living with HIV in Canada are part of the MSM community [36,37].
During the 2022 Mpox outbreak, 40% of the global reported cases were among people living with HIV (PWH) [17,38,39]. Notably, PWH are more susceptible to several infections, including Mpox, due to their compromised immunity [40,41]. Given that both HIV and Mpox can be sexually transmitted and considering the high-risk sexual behaviors often associated with the MSM community [42,43], it remains unclear whether the high prevalence of Mpox in this population is primarily due to the endemicity of HIV or other contributing factors [17,44]. Furthermore, HIV-positive individuals are more likely to undergo diagnostic testing for Mpox relative to HIV-negative individuals [45,46]. This underscores the importance of understanding the concurrent spread of both diseases within the MSM population.
Mathematical models that explore the co-dynamics of Mpox and HIV within a population have been studied [47,48,49,50]. Specifically, Bhunu et al. [47] analyzed a co-dynamics model for Mpox and HIV when both diseases are endemic in a general population. Their results suggest that each disease can enhance the transmission of the other. Moreover, they highlighted that both Mpox and HIV can co-exist within the population when their respective reproduction numbers are above one. In another study, Marcus et al. [48] developed an Mpox-HIV co-infection model, which they used to assess the impact of different control measures on the dynamics of both diseases. Peace et al. [49] proposed and analyzed a co-infection model for Mpox, coronavirus 2019 (COVID-19), and HIV. They considered different interventions to curtail the co-spread of the triple viral infections in a given population. Many of the aforementioned articles considered scenarios where both HIV and Mpox are endemic in a given population, which is not the case in the 2022 Mpox outbreaks, as the outbreaks occurred in populations where solely HIV was already endemic. In addition, the articles looked at the entire population without much attention to the MSM community, which is the most affected by the 2022 outbreaks. In [50], we developed a novel compartmental mathematical model to investigate the impact of HIV on the spread of Mpox in an MSM community. Unlike in the previously mentioned articles, our model mimicked the 2022-2023 Mpox outbreak, where HIV was already circulating within the MSM community at the onset of the outbreak. We showed that HIV endemicity in the MSM community can enhance the spread of Mpox. We considered scenarios were HIV infected individuals may be more susceptible to Mpox due to their compromised immune systems. Our results showed that the use antiretroviral therapy (ART) by these individuals may not be sufficient to curtail the transmission of Mpox. However, a reduction in sexual activities or a moderate use of condom, combined with ART may be beneficial to control the spread of Mpox in the population. These results were obtained by numerical simulations of our model [50].
In this study, we analyze the mathematical model developed in [50]. We aim to verify some of the results obtained therein through stability and bifurcation analyses of the model, and also study other important mathematical properties of the model, with more emphasis on understanding the impact of HIV endemicity and treatment on the spread of Mpox. To the best of our knowledge, stability analysis of the equilibria for an endemic-invasive model for HIV and Mpox has not yet been investigated in the literature. Thus, we hope to fill this gap using our existing model [50].
2.
Mathematical model
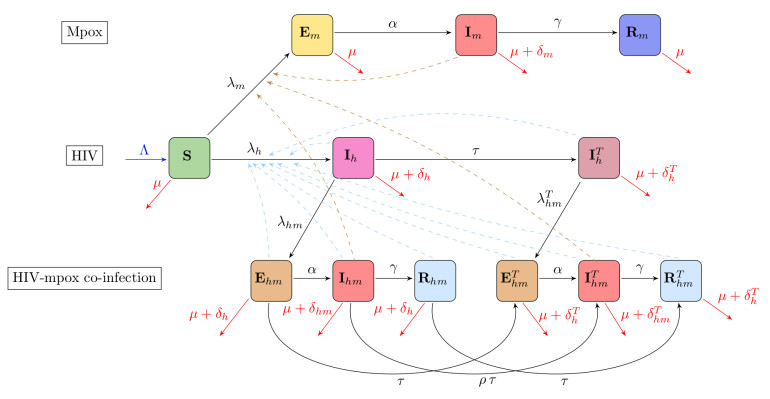
We analyze the compartmental model of HIV-Mpox co-dynamics developed in [50]. The model incorporates the dynamics of individuals infected with HIV only, Mpox only, and HIV-Mpox co-infection (see Figure 1) with 12 compartments. These compartments are individuals susceptible to HIV and Mpox $ (S) $, Mpox-exposed $ (E_{m}) $, Mpox-infectious $ (I_{m}) $, Mpox-recovered $ (R_{m}) $, HIV-infected $ (I_{h}) $, HIV-infected and Mpox-exposed $ (E_{hm}) $, HIV-infected and Mpox-infectious ($ I_{hm} $), HIV-infected and Mpox-recovered ($ R_{hm} $), HIV-infected on ART $ (I^T_{h}) $, HIV-infected on ART and Mpox-exposed $ (E^T_{hm}) $, HIV-infected on ART and Mpox-infectious $ (I^T_{hm}) $, and HIV-infected on ART and Mpox-recovered ($ R^T_{hm} $).
In this model, it is assumed that transmission of Mpox occurs at the infectious stage via sexual contacts. Individuals in the exposed stage of Mpox do not spread the infection. The current model does not capture individuals who contracted HIV while Mpox-exposed, Mpox-infectious, or Mpox-recovered. In addition, the HIV exposed stage and Mpox reinfection are not considered in the model [50]. The model incorporates HIV treatment, whereby ART usage has the likelihood to reduce susceptibility to Mpox. HIV-infected individuals not on ART may initiate treatment at any point in time while they are infected with Mpox. Since Mpox infection has the potential to make an individual visit the hospital or seek medical attention, we assume that individuals with HIV that are in the infectious stage of Mpox have a higher likelihood to initiate ART during their infection. The model assumes that an Mpox-related death only occurs at the infectious stage of the infection, and HIV-related mortality occurs among all HIV-infected individuals, irrespective of their Mpox infection stage, though the rate is reduced for those on ART. Lastly, the model incorporates immigration into the MSM population only through the susceptible compartment $ (S) $, while an exit from the population occurs from any compartment of the model. The differential equations of the model are as follows:
where $ \alpha $ is the progression rate from Mpox-exposed to Mpox-infectious compartment, $ \gamma $ is the Mpox recovery rate, $ \delta_m $ and $ \delta_h $ are the Mpox and HIV related mortality rates, respectively, and $ \delta_{hm} $ is the HIV or Mpox related death rate for co-infected individuals. The death rate for HIV-infected on ART is $ \delta^T_h $, while $ \delta^T_{hm} $ is the mortality rate for co-infected individuals on ART. The model assumes that HIV-infected at the Mpox exposed stage or have recovered from Mpox, initiate treatment for HIV at the same rate ($ \tau $). However, individuals with HIV at the infectious stage of Mpox may start ART at a comparatively higher rate $ \rho \tau $, with $ \rho > 1 $. Here, $ \Lambda $ is the immigration rate into the MSM population and $ \mu $ is the rate at which people leave the MSM population, either by natural death or emigration.
The forces of infection for the transmission of Mpox ($ \lambda_m $) and HIV ($ \lambda_h $) are given by
where $ c $ is the average sexual contact per day and $ p_{m} (p_{h}) $ is the transmission probability of Mpox (HIV) per contact. Based on these definitions, the transmission rate of Mpox $ (\beta_m) $ and HIV ($ \beta_h $) are defined by $ \beta_m = c \, p_{m} $ and $ \beta_h = c \, p_{h} $, respectively. The effectiveness of intervention measures, such as condom usage, is incorporated into the model via the above forces of infection (2.2). This was performed by scaling the probability of transmission $ p_m $ and $ p_h $, by the factor $ 1- \nu \varepsilon $, where $ 0 \leq \nu \leq 1 $ is defined as the compliance rate for condom usage and $ 0 < \varepsilon < 1 $ is the condom efficacy. The product of these two parameters ($ \xi = \nu \varepsilon $) is defined as the condom-associated preventability level. The model assumes that ART reduces the infectiousness of HIV [51,52]. This is incorporated into the model with the help of the scaling parameter $ 0 \leq \eta \leq 1 $ in the force of infection $ \lambda_h $ (2.2b). Lastly, the model assumes higher susceptibility to Mpox as a result of HIV infection [40], with those on ART having a comparatively lower increase in susceptibility [41]. This mechanism was captured in the model by scaling the force of infection $ \lambda_m $ by $ \sigma \geq 1 $ in order to obtain $ \lambda_{hm} = \sigma \, \lambda_m $ for HIV-infected not on ART, and $ \lambda^T_{hm} = \sigma^T \lambda_{m} $ with $ \sigma^T \geq 1 $ for HIV-infected individuals on ART, where $ \sigma \geq \sigma^T $. It is important to note that $ \sigma = \sigma^T = 1 $ implies that there is no higher vulnerability to Mpox due to HIV infection. Additionally, the parameter $ \sigma^T $ may be viewed as the effectiveness of ART in reducing/preventing an increase in the vulnerability to Mpox by HIV, where $ \sigma^T = 1 $ implies that ART prevents increase in vulnerability, and HIV-infected persons on ART have the same susceptibility level to Mpox as those not infected with HIV. On the other hand, values of $ \sigma^T > 1 $ imply that HIV-infected individuals enrolled on ART have a higher vulnerability to Mpox as a result of their HIV infection. In other words, treatment with ART does not successfully prevent an increase in the vulnerability to Mpox. Our goal in this work is to study the mathematical properties of the co-infection model (2.1) as it relates to the Mpox control in the MSM community, in addition to analyzing the stability of its equilibria.
3.
Model analysis
3.1. Basic features of the model
We begin our analysis of the co-dynamical model (2.1) by studying the basic properties of the model, which includes proving the non-negativity and boundedness of its solutions. These proofs are necessary for the well-posedness of the model.
3.1.1. Non-negativity of the model solutions
For the model (2.1) to be epidemiologically meaningful, it is important to show that the model solutions are non-negative. To show this, we begin by stating the following theorem.
Theorem 3.1. Given the initial conditions
the solution
of the co-infection model (2.1) is non-negative for all time $ t > 0 $.
Proof. From the first equation of the ordinary differential equation (ODE) system (2.1), we have the following:
By applying the integrating factor method on (3.3), and simplifying, we obtain the following:
Therefore, $ S(t) \ge 0 $ for all $ t > 0 $. Using a similar analysis, it can be shown that
for all $ t > 0 $.
3.1.2. Boundedness of the model solutions
To study the boundedness of the solutions of the co-infection model (2.1), we state the following theorem.
Theorem 3.2. The closed set $ \mathcal{D} $ given by the following:
where $ N(t) = S + E_{m} + I_{m} + R_{m} + I_{h} + I^T_{h} + E_{hm} + I_{hm} + R_{hm} + E^T_{hm} + I^T_{hm} + R^T_{hm} $ is the total population, which is positively invariant with respect to the model (2.1).
Proof. By adding all the equations of the ODE system (2.1), we obtain the following:
Since the solution of the ODE system (2.1) is non-negative (From Theorem 3.1), from (3.5), we have the following inequality:
Using the integrating factor method to solve (3.6), we obtain the following:
This implies that
Therefore, the total population $ N(t) $ is bounded by $ \Lambda/\mu $ as $ t\to \infty $. This implies that the ODE system (2.1) has its solution in $ \mathcal{D} $. Given that the solutions of this system are always positive for the positive initial conditions, as shown in Section 3.1.1, we conclude that the solutions of the model (2.1) are positively invariant.
3.2. Mpox invasion reproduction number
Next, we derive the Mpox invasion reproduction number for the co-infection model (2.1). The invasion reproduction number of a disease gives the mean number of new infections of the disease caused by one infectious individual in a population entirely susceptible to that disease, but where another disease is already endemic. Here, using the next-generation matrix approach [64], we derive the Mpox invasion reproduction number of our model in an HIV endemic regime. Let $ \Psi_{eh} $ be the Mpox-free equilibrium of the model (2.1) at an HIV endemic regime:
where $ S^*, I_{h}^* $, and $ I^{T*}_{h} $ are given by the following:
Here, $ \mho = \varphi_{h}(\delta^T_{h} + \mu)\left(\mathcal{R}^h_{c} - 1\right) + \mu \, \chi $ with $ \varphi_{h} = \tau + \delta_{h} + \mu $, $ \chi = \delta^T_{h} + \mu + \tau $, and $ \mathcal{R}^h_{c} $ is the control reproduction number for HIV (which is always greater than one for the existence of an HIV endemic equilibrium). It is given by the following:
where $ \Upsilon_{h} = c \, p_{h} (1- \nu \varepsilon) $ (see Appendix A.2 for details).
From (2.1), we consider the compartments that contribute to an Mpox infection. The equations for these compartments are as follows:
where $ \varphi_{m}, \varphi^{\alpha}_{h}, \varphi_{hm}, \varphi_{h}^T $, and $ \varphi_{hm}^T $ are defined as follows:
Using the above equations together with the next-generation matrix method, the Mpox invasion reproduction number is given by the following:
where
with $ \mathcal{H} = 1/\varphi_{hm} + (\rho \tau)/(\varphi_{hm} \, \varphi^T_{hm}) + \tau/(\varphi_{h}^T \varphi^T_{hm}) $. The above invasion reproduction (3.13) defines the mean number of new Mpox infections generated by one Mpox infectious individual in a population totally susceptible to Mpox, but endemic with HIV. The terms $ \mathcal{R}_{c, 1}^{mh} $, $ \mathcal{R}_{c, 3}^{mh} $ and $ \mathcal{R}_{c, 3}^{mh} $ represents the mean number of new Mpox infections generated among the susceptible population, HIV-infected population not on ART, and HIV-infected population on ART, respectively. Additionally, it is important to emphasize that the Mpox invasion reproduction number ($ \mathcal{R}_{c}^{mh} $) reflects what happens at an Mpox-free but HIV endemic regime.
3.3. Local asymptotic stability of the Mpox-free equilibrium at HIV endemic regime
In this section, we study the local asymptotic stability of the Mpox-free equilibrium ($ \Psi_{eh} $, given in (3.8)). We begin our analysis by stating the following theorem.
Theorem 3.3. At an HIV endemic regime, where $ \mathcal{R}^{h}_{c} > 1 $, the Mpox-free equilibrium of the model (2.1) is locally asymptotically stable whenever the Mpox invasion reproduction number $ \mathcal{R}^{mh}_{c} < 1 $ and unstable whenever $ \mathcal{R}^{mh}_{c} > 1 $.
Proof. We consider the Jacobian matrix of the ODE system (2.1) evaluated at the Mpox-free and HIV-endemic equilibrium, $ \Psi_{eh} $. This matrix is written in a compact form as follows:
where
In these matrices, $ \lambda_{h}^* $ is the force of infection for HIV at the Mpox-free equilibrium (3.8). In addition, the total population at this equilibrium is defined as $ N^{*} $. Both quantities are given by the following:
The Jacobian matrix $ J(\Psi_{eh}) $ in (3.14) has twelve eigenvalues, which are used to determine the local asymptotic stability of the Mpox-free equilibrium of the co-infection model (2.1) (at an HIV-endemic regime). The first three eigenvalues of the Jacobian matrix $ J(\Psi_{eh}) $ are $ \Phi_1 = - \varphi_{h} $, $ \Phi_2 = - (\delta^T_{h} + \mu) $, and $ \Phi_3 = - \mu $. The remaining nine eigenvalues satisfy the following equations:
and
It is important to note that the polynomial Eq (3.19) is associated with the stability of the HIV endemic aspect of the equilibrium in (3.8), while the equation in (3.20) is associated with the stability of the Mpox aspect of the same equilibrium.
The coefficients of the polynomial in (3.19) are as follows:
while those of the polynomial in (3.20) are as follows:
where $ \mathcal{G} = \varphi_{m} + \varphi_{hm} $, $ \mathcal{G}^T = \varphi^{T}_{h}+ \varphi^{T}_{hm} $, and $ \mathcal{M}^{\alpha}, \mathcal{M}^{T} $, and $ \mathcal{M}^{\mu} $ are defined as follows:
We observe that the coefficients $ A_{0}, A_{1}, A_{2} $, and $ A_{3} $ are positive for $ \mathcal{R}^{h}_{c} > 1 $. It can easily be shown that the coefficients $ B_{0} $, $ B_{1} $, $ B_{2} $, $ B_{3}, B_{4} $, and $ B_{5} $ are all positive for $ \mathcal{R}^{mh}_{c} < 1 $. We shall use these coefficients together with the Routh-Hurwitz criterion to determine the stability of the equilibrium $ \Psi_{eh} $.
First, we show that the HIV-endemic regime is stable for $ \mathcal{R}^{h}_{c} > 1 $. The Routh-Hurwitz criterion for all the solutions of the polynomial Eq (3.19) to have negative real parts, which guarantees the local asymptotic stability of the HIV-endemic regime, is that $ A_{0} A_{3} > 0 $, $ A_{2} A_{3} > 0 $ and $ A_{1} A_{2} - A_{0} A_{3} > 0 $. Since $ A_{0}, A_{2} $, and $ A_{3} $ are positive when $ \mathcal{R}^{h}_{c} > 1 $, the conditions: $ A_{0} A_{3} > 0 $, $ A_{2} A_{3} > 0 $ are satisfied when $ \mathcal{R}^{h}_{c} > 1 $. For the last condition, we have the following:
which is also positive for $ \mathcal{R}^{h}_{c} > 1 $. Therefore, the HIV-endemic regime is stable for $ \mathcal{R}^{h}_{c} > 1 $
For the Mpox-free aspect of the equilibrium (3.8), we consider the Routh-Hurwitz criterion for all roots of a polynomial of degree six to have a negative real part. This criterion requires that the determinants of the Hurtwitz matrices associated with the characteristic Eq (3.20) are positive [65,66]. That is,
It can be verified that the conditions in (3.22) are satisfied when $ \mathcal{R}^{mh}_{c} < 1 $. However, we do not show the details here due to the length of the resulting expressions. Based on Routh-Hurwitz criterion, we are guaranteed that the roots of the polynomial equations in (3.19) and (3.20) have negative real parts when $ \mathcal{R}^{h}_{c} > 1 $ and $ \mathcal{R}^{mh}_{c} < 1 $, respectively. Additionally, these results guarantee the local asymptotic stability of the Mpox-free equilibrium of the model (2.1) at an HIV-endemic regime when $ \mathcal{R}^{mh}_{c} < 1 $.
To prove the instability of the Mpox-free equilibrium $ \Psi_{eh} $ when $ \mathcal{R}^{mh}_{c} > 1 $ (at an HIV-endemic regime), it is sufficient to show that one of the Routh-Hurwitz criteria required for the stability of this equilibrium is not satisfied for $ \mathcal{R}^{mh}_{c} > 1 $. Since the stability of the Mpox free equilibrium requires that $ B_0 > 0 $, we observe that this condition is not satisfied when $ \mathcal{R}^{mh}_{c} > 1 $. Therefore, the Mpox-free equilibrium is unstable for $ \mathcal{R}^{mh}_{c} > 1 $. Thus, we conclude that, at an HIV-endemic regime, where $ \mathcal{R}^{h}_{c} > 1 $, the Mpox-free equilibrium, $ \Psi_{eh} $, of the model (2.1) is locally asymptotically stable whenever $ \mathcal{R}^{mh}_{c} < 1 $ and unstable whenever $ \mathcal{R}^{mh}_{c} > 1 $.
3.4. Mpox-endemic equilibrium at HIV-endemic regime
Several models have been formulated to independently investigate the dynamics of Mpox and HIV [67,68,69,70]. For many of these models, the existence and stability of Mpox-endemic equilibrium (in the absence of HIV) were studied [67,68], and similarly for HIV [69,70]. In this section, we study the existence and stability of the Mpox-endemic equilibrium of the model (2.1) at an HIV-endemic regime. Specifically, we aim to have a good understanding of the impact of HIV endemicity on the stability of Mpox-endemic equilibrium.
Since only a few Mpox-induced deaths were reported during the 2022 outbreak [71] and HIV treatment with ART has significantly reduced deaths from HIV [36,72], we consider a scenario of our model, where the disease-induced death for both Mpox and HIV are negligible. In other words, we set the Mpox and HIV death rates to zero in our model (i.e., $ \delta_m = \delta_h = \delta_{hm} = \delta_h^T = \delta_{hm}^{T} = 0 $) in Eq (2.1). In this case, the total population becomes constant ($ N = \Lambda/\mu $) and the Mpox and HIV transmission rates are $ \bar{\beta}_m = (c \, p_{m} \, \mu)/ \Lambda $ and $ \bar{\beta}_h = (c \, p_{h} \, \mu)/\Lambda $, respectively.
Let $ \Psi_{e} $ be an arbitrary Mpox-endemic equilibrium, given by the following:
and let $ \lambda^{e}_{m} $ and $ \lambda^{e}_{h} $, given by the following:
be the forces of infection for Mpox and HIV, respectively, at the Mpox-endemic equilibrium. The equilibrium solutions of the model (2.1), without disease-induced deaths at an Mpox-endemic equilibrium are given by the following:
where $ \hat{\lambda}^{e}, \hat{\lambda}^{e}_{hm}, \hat{\varphi}^{\alpha}_{h}, $ and $ \hat{\varphi}_{hm} $ are defined as follows:
By substituting the equilibrium solutions in (3.25) into the force of infection for Mpox in (3.24), we construct the following polynomial:
whose coefficients are given by the following:
Here, $ \varrho = \hat{\varphi}^{\alpha}_{h}\, (\alpha + \mu)^2 (\gamma + \mu)^2 (\gamma + \rho \tau + \mu) $, and $ \hat{\mathcal{H}} $ and $ \mathcal{W} $ are given by the following:
The components of the Mpox-endemic equilibrium in (3.23) are obtained from the polynomial in (3.26) upon solving for $ \lambda^{e}_{m} $ and substituting the positive values of $ \lambda^{e}_{m} $ into the expressions in (3.25). It is important to note that the coefficients of polynomial (3.26) determine the existence of the Mpox-endemic equilibrium. We observe from (3.27) that the coefficient $ a_{3} $ is always positive, and $ a_{0} $ is positive (negative) if the Mpox invasion reproduction number $ \bar{\mathcal{R}}^{mh}_{c} $ is less (greater) than one. It can easily be verified that $ a_{2} > 0 $ when the Mpox invasion reproduction number is less than one ($ \bar{\mathcal{R}}^{mh}_{c} < 1 $). This shows that the existence of the Mpox-endemic equilibrium depends on the sign of $ a_1 $. We summarize the potential scenarios for the existence of this equilibrium in Theorem 3.4.
Theorem 3.4. The co-infection model (2.1) (without disease-induced deaths for both Mpox and HIV) at an HIV-endemic regime has the following:
(i) two Mpox endemic equilibria if $ \bar{\mathcal{R}}^{mh}_{c} < 1 $ and $ a_{1} < 0 $;
(ii) a unique Mpox endemic equilibrium if $ \bar{\mathcal{R}}^{mh}_{c} > 1 $ and $ a_{1} > 0, \, a_{2} < 0 $; and
(iii) no Mpox endemic equilibrium if $ \bar{\mathcal{R}}^{mh}_{c} < 1 $ and $ a_{1} > 0 $.
Item (ⅰ) of Theorem 3.4 suggests the possibility of the model exhibiting a backward bifurcation, in which case, there will be two positive Mpox-endemic equilibria when $ \bar{\mathcal{R}}^{mh}_{c} < 1 $. We summarize this result in the theorem below.
Theorem 3.5. The co-infection model (2.1) (without disease-induced deaths for both Mpox and HIV) at an HIV-endemic regime will exhibit a backward bifurcation (co-existence of a stable Mpox-free equilibrium and a stable Mpox-endemic equilibrium when $ \bar{\mathcal{R}}^{mh}_{c} < 1 $) whenever the following condition holds:
where $ \nu \varepsilon < 1 $ and $ \bar{\mathcal{R}}^{h}_{c} > 1 $.
Remark 3.1. It is important to highlight that although the local stability analysis of both the Mpox-free and Mpox-endemic equilibria around the HIV endemic regime of the model (2.1) have been used to obtain the key analytical results of the current study, the global stability analysis can also be obtained for a special case of the model (2.1), where the dynamics of the two diseases are decoupled. This special case of the model corresponds to a scenario where both HIV and Mpox independently circulate within the population without co-infection. However, in the present study, this scenario is not qualitatively analyzed, as it is almost an unrealistic reflection of real-world scenarios where such a decoupling is unlikely. However, a future study shall aim to explore the global dynamics of the coupled system using some novel techniques.
4.
Model simulation
We numerically generate the bifurcation diagram for the model (2.1) by solving the polynomial Eq (3.26) using MATLAB, version R2024a [73], for different values of the invasion reproduction number of Mpox $ \bar{\mathcal{R}}^{mh}_{c} $. The remaining model parameters are fixed at the values shown in Table 1, except otherwise stated in the figure captions. We set the HIV control reproduction number $ \bar{\mathcal{R}}^{h}_{c} = 1.2325 $, such that HIV is already endemic in the population at the beginning and during the Mpox outbreak. Our aim is to obtain solutions of the cubic polynomial Eq (3.26) when $ \bar{\mathcal{R}}^{mh}_{c} $ is varied. These solutions will be used to determine the existence and stability of the endemic equilibrium of the model (2.1). It is important to note that $ a_1 < 0 $ based on our parameters. When $ \bar{\mathcal{R}}^{mh}_{c} < 1 $, we found that the polynomial equation has two positive solutions (the third solution has negative real part). This suggests the existence of a backward bifurcation based on item (i) of Theorem 3.4. Note that this bifurcation only exists when the inequality in Theorem 3.5 holds. For $ \bar{\mathcal{R}}^{mh}_{c} > 1 $, the polynomial Eq (3.26) has only one solution with a positive real part, which suggests the existence of a stable endemic equilibrium. The root ($ \lambda^{e}_{m} $) of the polynomial equation is plotted with respect to the invasion reproduction number of Mpox $ \bar{\mathcal{R}}^{mh}_{c} $ as our bifurcation diagram.
Figure 2 shows the existence of a backward bifurcation for the co-infection model (2.1). The bifurcation diagrams in this figure are plotted for different values of the parameters $ \sigma $ and $ \sigma^T $, representing increase in vulnerability to Mpox as a result of HIV infection for HIV-infected individuals not on ART ($ I_{h} $) and those on ART ($ I^T_{h} $), respectively. The occurrence of a backward bifurcation in an epidemic model implies that the requirement associated with the reproduction number less than one, although still necessary, is not sufficient for the control of the disease [74,75]. Thus, the control of the disease becomes more difficult in the population. This feature is usually signaled by the appearance of two endemic equilibria co-existing with a stable disease-free equilibrium whenever the threshold quantity, called the reproduction number, is below one. In the left panel of Figure 2, we present our result for scenarios where an HIV infection leads to a higher vulnerability to Mpox. We assume this increase in susceptibility in our model to account for the potential compromise in the immune systems of those infected with HIV. We observe that the endemic equilibrium lobe in the bifurcation diagrams presented in this figure increase as the susceptibility of HIV-infected individuals to Mpox increases. These results suggest that an increase in the vulnerability to Mpox for HIV-infected individuals in the population will negatively impact Mpox control in the population. To identify the main factor contributing to the existence of a backward bifurcation, we consider a scenario where HIV does not increase vulnerability to Mpox (i.e., $ \sigma = \sigma^T = 1 $) with result shown in the right panel of Figure 2. We observe that the backward bifurcation still exists for this scenario, thus suggesting that the existence of a backward bifurcation is not due to increase in the susceptibility to Mpox for those infected with HIV.
We hypothesize that the existence of the backward bifurcation shown in Figure 2 is due to the co-circulation of Mpox and HIV, and more importantly, the endemicity of HIV in the population during the Mpox outbreak. To verify this, we set $ \sigma = 0 $ and $ \sigma^T = 0 $ to mathematically decouple the infection process of Mpox and HIV in our model. As a result, the cubic polynomial Eq (3.26) reduces to the following:
This implies no sign change (in the sense of Descartes' rule of signs [76]) in the coefficients of the polynomial for $ \bar{\mathcal{R}}^{mh}_{c}|_{\sigma = \sigma^T = 0} < 1 $, since all the coefficients in this case are positive, which completely rules out the possibility of a backward bifurcation in the model. Using the reduced polynomial equation in (4.1), we generate the bifurcation diagram in Figure 3, which gives a forward bifurcation as predicted.
To gain an intuition for the existence of the forward bifurcation shown in Figure 3, when $ \sigma = \sigma^T = 0 $, we consider the Mpox force of infection for individuals infected with HIV who are not on ART ($ \lambda_{hm} = \sigma \, \lambda_m $) and those on ART ($ \lambda^T_{hm} = \sigma^T \lambda_{m} $), where $ \lambda_m $ is the Mpox force of infection for the general susceptible population. We observe that $ \lambda_{hm} = 0 $ and $ \lambda_{hm}^T = 0 $ when $ \sigma = 0 $ and $ \sigma^T = 0 $, respectively (i.e., there is no co-infection in this case). In addition, the HIV and Mpox dynamics decouple under this assumption. As a result, the bifurcation diagram in Figure 3 represents the dynamics of a model for the sole spread of Mpox in the population (no HIV infections). Additionally, this observation aligns with the results in Appendices A.1 and A.2, where the separate analyses of Mpox and HIV submodels also reveal the absence of a backward bifurcation.
The results in Figure 4 emphasize the importance of an HIV treatment in the control of Mpox. The results in the left panel of this figure were generated using $ \sigma^T = 1.0 $. In terms of HIV treatment, this implies that HIV the treatment is effective enough to prevent HIV-infected individuals on treatment from becoming more susceptible to Mpox. Comparing the results in this panel to those in the right panel, which were generated with the same values of $ \sigma $ but with $ \sigma^T = 1.3 $ (which can be interpreted as HIV treatment being not effective enough to prevent an increase in the vulnerability to Mpox), we observe that the endemic equilibrium lobe is larger when $ \sigma^T = 1.3 $ compared to when $ \sigma^T = 1.0 $. This suggests that Mpox will be more difficult to control when the HIV treatment is not effective enough to reduce the susceptibility of those on ART. Although, we interpreted this result in terms of the treatment not being effective, the results may also be interpreted as individuals not being consistent with taking their medication, since ART has been shown to significantly reduce the viral levels when taken consistently as required [77]. These results highlight the potential consequence of HIV treatments on the control of Mpox spread.
Lastly, we study the potential effect of sexual contact on the control of Mpox in the MSM population. Given the high level of sexual activities associated with the MSM community [78,79], it is important to investigate the effect of sexual contacts on the spread of Mpox in the community. In Figures 2–4, we have used a fixed sexual contact rate, $ c = 0.85 $. To have a good understanding of the effect of this parameter on the model dynamics, we vary its value while the remaining model parameters are fixed (Figure 5, left panel). The result from this analysis shows a transition from a forward bifurcation to a backward bifurcation as the sexual contact rate increases, which suggest that Mpox will be more difficult to control in the MSM population as the sexual contacts increase in the population. Here, we assume that HIV increases the vulnerability to Mpox in HIV-infected individuals not on ART ($ \sigma = 1.8 $) and has no effect on the susceptibility of those on treatment ($ \sigma^T = 1.0 $). This assumption can also be interpreted as the HIV treatment being effective enough to prevent those on ART from having an increased vulnerability to Mpox like those not on ART. To have a good understanding of the the impact of sexual contacts and HIV treatment on Mpox control, we computed the critical sexual contact rate ($ c^{*} $) at which there was a switch from a backward bifurcation to a forward bifurcation (vice versa) for different values of $ \sigma^T $. Our result shows that $ c^{*} $ decreases non-linearly as $ \sigma^T $ increases (Figure 5, right panel), which signifies that the critical contact rate at which the transition from a backward to a forward bifurcation happens to decrease as the vulnerability to Mpox for HIV infected individuals on ART increases.
Numerical simulations of the co-infection model (2.1) showing the total population of individuals infected with Mpox ($ I_m + I_{hm} + I^T_{hm} $) over time is presented in Figure 6 for different values of the Mpox invasion reproduction number ($ \bar{\mathcal{R}}^{mh}_{c} $). These simulations are used to confirm the existence of a backward bifurcation as revealed in our analysis. We used an initial total population $ N(0) = 4\% \times CN_{pop} $, which corresponds to the MSM population in Canada at the beginning of the 2022-2023 Mpox outbreak (May 2022) [53], where $ CN_{pop} = 38,929,902 $, as defined in Table 1. The other initial conditions are set as follows: $ E_m(0) = 43, I_m(0) = 25, I_h(0) = 15,795 $, and $ I_h^T(0) = 15,795 $. Additionally, we assumed that there were no individuals in the rest of the model compartments at the beginning of the 2022 Mpox outbreak (compartments for individuals infected with Mpox), and we set the initial population of susceptible $ S(0) = N(0) - \big{[}E_m(0) + I_m(0) + I_h(0) + I^T_h(0) \big{]} $. The parameters used for these simulations are presented in Table 1, except otherwise stated in the figure caption. The values of $ \bar{\mathcal{R}}^{mh}_{c} $ used in these simulations ($ \bar{\mathcal{R}}^{mh}_{c} = 1.0606 $, $ \bar{\mathcal{R}}^{mh}_{c} = 0.9710 $, and $ \bar{\mathcal{R}}^{mh}_{c} = 0. 8515 $) were selected from the bifurcation diagram in the right panel of Figure 2, for $ \sigma = 1.8 $ and $ \sigma^T = 1.0 $, to show the model solution in different regions of the diagram. As predicted by our analysis, there is no Mpox-endemic solution in the system when $ \bar{\mathcal{R}}^{mh}_{c} = 0.8515 $ (green curve), which corresponds to having a stable Mpox-free equilibrium for this value of $ \bar{\mathcal{R}}^{mh}_{c} $. In addition, there is a stable Mpox-endemic equilibrium for $ \bar{\mathcal{R}}^{mh}_{c} = 0.9710 $, which is less than one (blue curve). This confirms the existence of a backward bifurcation in the system, as the stable endemic equilibrium co-exists with the Mpox-free equilibrium. Lastly, we show the existence of the stable Mpox-endemic equilibrium for $ \bar{\mathcal{R}}^{mh}_{c} = 1.060 $, which is greater than one (red curve).
5.
Discussion of results
The MSM population was extremely affected during the 2022 Mpox outbreak. Given that the MSM community is also adversely affected by HIV, it is imperative to understand the transmission of both diseases in the population. Recently, we developed a novel compartmental model [50] to study the co-interaction between HIV and Mpox in the MSM community. Specifically, this model was used to investigate the impact of HIV on the spread of Mpox within the MSM community through numerical simulations and a sensitivity analysis. Here, we studied the mathematical properties of the model. Specifically, we established the non-negativity and boundedness of the co-infection model. In addition, we performed bifurcation and stability analyses on the Mpox-free and Mpox-endemic equilibria of the model. Although only a few compartmental models have been proposed to investigate the co-interaction between Mpox and HIV [47,48,49,50], to the best of our knowledge, the stability analysis of equilibria for an endemic-invasive model for HIV and Mpox has not yet been investigated in the literature. Thus, we investigated this for the model developed in [50].
A local stability analysis of the Mpox-free equilibrium at an HIV-endemic regime revealed that the Mpox-free equilibrium of our model was locally asymptotically stable whenever the invasion reproduction number of Mpox $ \mathcal{R}^{mh}_{c} $ was below 1 and unstable whenever $ \mathcal{R}^{mh}_{c} > 1 $. We established this using the Jacobian matrix of the system evaluated at the HIV endemic regime, and then applied the Routh-Hurwitz criterion for stability. This result is essential as it emphasizes that at an Mpox-free and HIV-endemic regime, with a little perturbation of the system around the Mpox-free equilibrium (which can be interpreted as the introduction of a few Mpox-infected individuals into a population that is completely susceptible to Mpox), will not lead to an Mpox outbreak as long as the invasion reproduction number of Mpox $ \mathcal{R}^{mh}_{c} $ is below 1. However, Mpox will become endemic in the population whenever $ \mathcal{R}^{mh}_{c} > 1 $.
Next, we investigated the stability of the Mpox-endemic equilibrium at an HIV-endemic regime. Since only a few cases of Mpox-induced deaths were reported during the 2022 Mpox outbreak [71] and HIV treatments with ART significantly reduced deaths from HIV [36,72], we considered a special case of our model where the disease-induced deaths for both Mpox and HIV were negligible. In other words, we set the Mpox and HIV death rates to zero in our model. Using the polynomial equation for the Mpox-endemic equilibrium, we obtained conditions under which positive solutions could exist. Particularly, we observed a scenario when two positive Mpox-endemic equilibria could exist when the Mpox invasion reproduction number was less than one, thus pointing towards the occurrence of a backward bifurcation in the model. In addition, we showed that the backward bifurcation was due to the endemicity of HIV in the MSM population, and will not occur in a population where only Mpox is spreading. Numerical simulations of the co-infection model were used to verify our analysis.
Furthermore, we considered different scenarios to assess the effect of HIV on Mpox control. Our results were presented in terms of bifurcation diagrams. We considered potential scenarios whereby HIV infection could increase the susceptibility to Mpox, and found that the backward bifurcation lobe becomes larger as HIV-infected individuals became more susceptible to Mpox. This signifies that Mpox will become more difficult to control as HIV-infected individuals become more and more susceptible to Mpox due to a potential compromise in their immune system. To understand the effect of sexual contact on Mpox control, we varied the sexual contact rate while fixing all the remaining model parameters. We found that our co-infection model exhibited a transition from a forward bifurcation to a backward bifurcation as the sexual contact rate increased, which suggests that Mpox becomes more difficult to eradicate in the population as sexual contacts increases. In addition, it signifies that there is a critical sexual contact rate above which Mpox will be more difficult to eradicate in the population. Given the high level of sexual activities common among the MSM population [78,79], it is important to investigate the effect of these activities on the control of Mpox in the population.
Lastly, we investigated the effect of HIV treatment on the control of Mpox. We computed the critical contact rate at which a backward bifurcation becomes a forward bifurcation, as the contact rate decreases, for different susceptibility levels to Mpox for HIV-infected individuals on ART. We found that the critical contact rate decreased as the susceptibility to Mpox increased. This result shows that sexual contact in the MSM population would need to be decreased for Mpox to be easily eradicated from the population, as the effectiveness of HIV treatment to reduce the susceptibility of HIV-infected individuals to Mpox decreases. In other words, as HIV-infected individuals on treatment become more susceptible to Mpox (treatment effectiveness decreases or individuals are increasingly not consistent with taken their medications), sexual contact would need to be decreased for Mpox to be easily controlled in the population. In other words, for the Mpox spread to be easily controlled, we need to ensure that the HIV treatment is effective enough to prevent those on treatment from having a higher vulnerability to Mpox (in other words, HIV-infected enrolled on ART consistently take their medications so as to prevent higher vulnerability to Mpox) if we want to maintain a high sexual contact rate in the MSM population.
6.
Conclusions
Overall, our study investigated the potential detrimental effect of HIV endemicity on the control of Mpox in the MSM community using rigorous stability and bifurcation analyses. The study emphasizes the importance of HIV treatments and moderation in sexual activities on the control of Mpox spread within the MSM community. The results in this study will help inform public health officials and policymakers on interventions that could help facilitate the control of Mpox in the MSM population. A limitation of our study included considering only the MSM population instead of the entire population, which will enable a comprehensive understanding of the disease outbreak and interventions to implement and control the spread of Mpox in the entire population. With that said, considering only the MSM population is also a good idea since the majority of Mpox cases reported in the 2022 outbreak were in the MSM population (95%) [54,80]. Another limitation of our study involved using model parameters associated with the Canadian scenario of the 2022 Mpox outbreak. Although, this implies that our results are more aligned to Canada, the generalization of our modelling techniques and framework to other populations can easily be implemented, and our results can easily be used to infer the scenarios for other populations with a similar demography. We do not expect the results to differ much from those presented here. Additionally, parts of our analysis (endemic equilibrium analysis) did not consider an Mpox-induced mortality since only a very few Mpox-induced deaths were reported for the 2022 outbreak. However, studies on the current Clade 1b outbreak in Africa should incorporate Mpox-induced deaths due to the high mortality rate associated with this strain of the virus [23,81]. A death rate of $ 5\% $ for adults and up to $ 10\% $ on average for children has been reported in DR Congo due to the Clade 1b Mpox outbreak [82,83]. While the emergence of new Mpox clades and new patterns of transmission have been reported in recent outbreaks, they were not the focus of our current study, which is limited to the 2022-2023 outbreak scenario. In future studies, we plan to extend our model to incorporate these broader transmission routes and the more recent developments involving other clades. Additionally, we will investigate the co-interaction between HIV and Mpox beyond the MSM community. In addition, future studies will explore the global dynamics of an improved version of the model, using some novel techniques [84,85,86,87].
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Funding statement
This research is funded by NSERC Discovery Grant (Grant No. RGPIN-2022-04559), NSERC Discovery Launch Supplement (Grant No: DGECR-2022-00454), New Frontier in Research Fund- Exploratory (Grant No. NFRFE-2021-00879), the Canadian Institute for Health Research (CIHR) under the Mpox and other zoonotic threats Team Grant (FRN. 187246), and Canada's International Development Research Centre (IDRC) (Grant No. 109981). W.A.W acknowledges financial support from the NSERC Discovery Grant (Appl No.: RGPIN-2023-05100).
Portions of this work were performed at the Los Alamos National Laboratory under the auspices of the US Department of Energy contract 89233218CNA000001 and supported by NIH grant R01-OD011095. W.A.W., J.D.K, and N.L.B. acknowledge financial support from the CIHR (FRN. 187246). N.L.B acknowledge funding from the European Union Horizon 2021 EUVABECO (grant 101132545). X.W. acknowledge funding support from NSERC of Canada (RGPIN-2020-06825 and DGECR-2020-00369) and the 2023-2026 National Natural Science Foundation of China (12271431).
Conflict of interest
The authors declare no conflict of interest.
Data availability
The MATLAB code used to generate the plots in the paper is available on GitHub at https://github.com/aomame2020/Mpox_HIV.
A.
Appendix
In this section, we provide detailed proofs to some important results stated within the main manuscript.
A.1. Mpox submodel
The Mpox submodel is obtained from the co-infection model (2.1) by setting the variables related to HIV and co-infection dynamics $ (I_{h}, I^T_{h}, E_{hm}, I_{hm}, R_{hm}, E^T_{hm}, I^T_{hm} $, and $ R^T_{hm}) $ to zero. The model is applicable to a scenario where only Mpox is introduced and is spreading in a population. The equations are given by the following:
where $ \lambda_{ms} $ is the force of infection given by the following:
We derive the control reproduction number for the Mpox submodel (A.1) using the next-generation matrix approach. The matrix $ \mathcal{F}_m $, which describes the new infections and matrix $ \mathcal{V}_m $ which describes all other transitions within the infectious stages of the model are defined as follows:
Taking the partial derivatives of $ \mathcal{F}_m $ and $ \mathcal{V}_m $ with respect to the disease classes $ E_{m} $ and $ I_{m} $ and evaluating at the disease free equilibrium $ \Psi_{0m} = \left(\frac{\Lambda}{\mu}, 0, 0, 0 \right) $, we have the following:
Thus, the control reproduction number for the Mpox submodel is given by the following:
The endemic equilibrium of the Mpox submodel (A.1) is defined by the following:
where the equilibrium points $ S^*, E_{m}^*, I_{m}^* $, and $ R^{*}_{m} $ are given by the following:
where the force of infection at the endemic equilibrium is as follows:
and $ \mathcal{R}^m_{c} $ is the control reproduction number for the Mpox submodel, which is defined in (A.2).
The polynomial equation associated with the endemic equilibrium of the Mpox submodel is given by the following:
where $ \lambda^{e}_{ms} $ is the force of infection for Mpox at the endemic equilibrium. It can be easily observed that Eq (A.5) has no sign changes whenever $ \mathcal{R}^{m}_{c} < 1 $, thus completely ruling out the possibility of a backward bifurcation in the Mpox submodel. However, Eq (A.5) has one sign change whenever $ \mathcal{R}^{m}_{c} > 1 $, thus pointing towards the existence of a forward bifurcation in the Mpox submodel.
A.2. HIV submodel (Mpox free model)
In this section, the HIV submodel, which corresponds to the Mpox free model is obtained from the co-infection model (2.1). This is derived by setting the variables related to Mpox and co-infection dynamics $ (E_{m}, I_{m}, R_{m}, E_{hm}, I_{hm}, R_{hm}, E^T_{hm}, I^T_{hm} $, and $ R^T_{hm}) $ to zero. This model describes the dynamics of HIV in the population when there is no Mpox. Its equations are as follows:
where $ \lambda_{hs} $ is the force of infection for this model given by the following:
Next, we compute the control reproduction number for the HIV submodel (A.6) following a similar approach used in Section A.1. In this case, the matrix $ \mathcal{F}_{h} $ and $ \mathcal{V}_{h} $ are defined as follows:
Taking the partial derivatives of $ \mathcal{F}_h $ and $ \mathcal{V}_h $ with respect to the disease classes $ I_{h} $ and $ I^T_{h} $ and evaluating at the disease free equilibrium $ \Psi_{0h} = \left(\frac{\Lambda}{\mu}, 0, 0 \right) $, we have the following:
Thus, the control reproduction number for the HIV submodel is given by the following:
The endemic equilibrium of the HIV submodel (A.6) is defined by the following:
where the equilibrium points $ S^*, I_{h}^* $, and $ I^{T*}_{h} $ are given by the following:
where $ \Upsilon = (\tau + \delta_{h} + \mu)(\delta^T_{h} + \mu) $. Here, $ \mathcal{R}^h_{c} $ is the control reproduction number for the HIV submodel, defined in (A.7).
The polynomial equation associated with the endemic equilibrium of the HIV submodel is given by the following:
where $ \lambda^{e}_{hs} $ is the force of infection for HIV at the endemic equilibrium. It can be easily observed that Eq (A.9) has no sign changes whenever $ \mathcal{R}^{h}_{c} < 1 $, thus completely ruling out the possibility of a backward bifurcation in the HIV submodel. However, the equation has one sign change whenever $ \mathcal{R}^{h}_{c} > 1 $, thus pointing towards the existence of a forward bifurcation in the HIV submodel.
A.3. Mpox submodel at the HIV endemic regime
In this section, we present the Mpox submodel at the HIV endemic regime. This is derived from the main model (2.1) by replacing the HIV associated variables $ I_{h} $ and $ I^{T}_{h} $ with their corresponding solutions at the HIV endemic regime, that is $ I^{*}_{h} $ and $ I^{T*}_{h} $, respectively. The associated equations are given by the following:
where $ I_{h}^* $, and $ I^{T*}_{h} $ are given by the following:
Here, $ \mho = \varphi_{h}(\delta^T_{h} + \mu)\left(\mathcal{R}^h_{c} - 1\right) + \mu \, \chi $ with $ \varphi_{h} = \tau + \delta_{h} + \mu $, $ \chi = \delta^T_{h} + \mu + \tau $, and $ \mathcal{R}^h_{c} $ is the HIV associated control reproduction number, which is greater than one for the HIV endemic regime to exist. It is given by the following:
where $ \Upsilon_{h} = c \, p_{h} (1- \nu \varepsilon) $.
Lemma A.1. [88] Suppose there exists a disease model, where $ \mathcal{A} $ is the set of resident pathogens and $ \mathcal{A}_c $ is the set of invading pathogens. Assume that all the reproductive numbers in the $ \mathcal{A} $-only subsystem exceed 1. If $ x_{0} $ is an $ \mathcal{A}_c $-infection free equilibrium of the model, then $ x_{0} $ is locally asymptotically stable if $ {}_\mathcal{A} \tilde{R}_{0} < 1 $, but unstable if $ {}_\mathcal{A} \tilde{R}_{0} > 1 $, where $ {}_\mathcal{A} \tilde{R}_{0} $ is the overall invasion reproduction number (IRN) when all pathogens in $ A $ are resident.









 DownLoad:
DownLoad: