Dermatology disease prediction based on firefly optimization of ANFIS classifier

1.   Introduction

The mathematical models with uncertainty properties take the forms fuzzy differential equations (FDEs), fuzzy integral equations (FIEs), or fuzzy integro-differential equations (FIDEs). Therefore, the solution of integro-differential equations (IDEs) that have been considered the main core of some physical systems play a significant role in science and engineering ^{[1,2,3,4,5,6]}. Some of these systems are linear and nonlinear Fredholm IDEs, and their solutions are continuously growing in many physical problems that arise naturally under uncertainty properties. The study of FDEs and fuzzy integral equations is currently the focus of much research. The starting point of fuzzy sets was first introduced by Zadeh ^[7]. The fuzzy integral equations were previously derived by Kaleva and Seikkala ^[8,9]. Lately, a lot of academics have focused on this topic and produced a ton of studies that are published in the literature ^[10]. As a result, fuzzy models constrained by FSIDEs behave more like the actual process because the after effect is incorporated into it by using the concepts of fuzzy derivatives and fuzzy integrals ^[11,12], which have several benefits, including the ability to incorporate additional conditions into the problem structure and the ability to structure realistic problems. However, the idea of Hukuhara derivatives that FDEs were developed ^[13]. FDEs and FIEs were extended to FIDEs, which first appeared in 1999 ^[14]. That study paved the way for future research on FSIDEs by applying principles from fuzzy sets theory to the analysis of FDEs and FIEs.

Typically, it is difficult and limiting to obtain the exact analytical solutions for linear FIDEs. Unfortunately, there isn't an analytical solution for the majority of the intricate physical phenomena that can be explained by nonlinear FSIDEs ^[15]. Analytical solutions are not found in many cases. However, there is always a need for the solutions to these equations because of their practical applications, such as the fuzzy Riccati differential equation ^[16]. Therefore, in order to handle such fuzzy situations, it is frequently important to suggest effective approximate techniques. In the meantime, the approximate-analytic class of methods under the approximation techniques can directly evaluate the solution accuracy for the systems involving high-order FIDEs. In addition to being applicable to nonlinear systems of FIDEs without the need for linearization or discretization as numerical approximate techniques ^[17]. Although some numerical class techniques and approximate analytical class techniques are employed and analyzed to obtain the approximate solution of a system of second-kind Fredholm-integro differential equations in the crisp domain ^{[8,9,10,11,12]}, also in the fuzzy domain, the learning algorithm approximate method (LAM) is used to obtain the solution of these systems in 2017 ^[12].

Nevertheless, the series solution's convergence cannot be guaranteed by some current approximate-analytical techniques. However, perturbation-based methods such as the standard fuzzy HAM approach ^[17] exist to solve fuzzy problems and have the capacity to control convergence. The idea of HAM first appeared in Liao PhD thesis 1992 ^[18] to deal with approximate solutions for linear and nonlinear mathematical engineering models. It was found that the HAM provides a solution in series form with a degree of polynomial function HAM that converges to the close form solution; otherwise, the solution is approximated to some degree of accuracy to the open form solution ^[17,19]. Also, the basic idea of HAM provides a great technique to rate the solution convergence through the convergence control parameter. The standard HAM has been modified and used to solve a variety of mathematical problems in the fuzzy domain, such as fuzzy FDEs ^[19], fuzzy partial differential equations ^[20], fuzzy fractional differential equations ^[21,22], fuzzy integral equations ^[17], and fuzzy integro-differential equations ^[23]. According to the aforementioned survey, the majority of the research that used numerical and approximation analytical techniques was applied on crisp system Fredholm IDEs, with only one implementation on FFSIDEs. As a result, we believe it is vital to propose new approximation analytical techniques to overcome such challenges, as we will demonstrate in the next sections. HAMFF, would give significant contribution toward overcoming obstacles of existing methods such as the Variational iteration method (VIM), the Adomian decomposition method (ADM) etc for example the proposed methods will help us to simplify the complexity of the uncertain nonlocal derivative when solving FFSIDEs. Furthermore, unlike all existing methods HAMFF provides the convergence parameter to control the accuracy of the solution, thus ensuring the convergence of the approximate series solutions. Also, the series solutions provided by the HAMFF have the ability to show the graphical designs of the solutions. Consequently, the goal of this research is to create a new convergence-controlled approximate analytical technique, HAMFF, for solving problems that are subject to boundary and initial conditions. The formulation and analysis of this study involving a theoretical framework and methodology relies on some well-known concepts of fuzzy sets theory that have been used to help build our recommended technique to solve FFSIDEs. These concepts include properties of fuzzy numbers ^[24], fuzzy extension principles ^[25], the α-cuts ^[26], fuzzy function ^[27], fuzzy differentiations, and the context of fuzzy integration ^[28,29,30].

2.   Fuzzy analysis of FSFIDEs

The following terms must be defined in order to analyze the suggested system in this work.

Definition 2.1. ^[24] A triangular fuzzy number is a fuzzy set $\tilde{A} = \left({s}_{1}, {s}_{2}, {s}_{3}\right)$that, satisfies the membership function,

where the crisp interval can be defined by $\alpha$-cut operation where $\alpha \in \left[\mathrm{0, 1}\right]$, such that,

where at $\alpha = 1$ the lower and upper bound of ${\tilde{A}}_{\alpha }$ are equal and this is the original crisp number.

Moreover, according to ^[24] the triangular fuzzy number satisfies the following properties:

(1) It is convex (the line by $\alpha$-cut is continuous and the $\alpha$-cut interval satisfies for ${A}_{\alpha } = \left[{{s}_{1}}^{\left(\alpha \right)}, {{s}_{3}}^{\left(\alpha \right)}\right]$, if there is two different ${s}_{1} < {s}_{2}\Rightarrow {{s}_{1}}^{\left({\alpha }_{1}\right)}\le {{s}_{1}}^{\left({\alpha }_{2}\right)}$ and ${{s}_{3}}^{\left({\alpha }_{1}\right)}\ge {{s}_{3}}^{\left({\alpha }_{2}\right)}$).

(2) It is normalized (the maximum membership value is 1, $\exists x\in \mathbb{R}, {\mu }_{A}\left(x\right) = 1$).

(3) Its membership function is piecewise continuous.

(4) It is defined in the real number.

Definition 2.2. ^[28] The integral of the fuzzy function $\tilde{f}$ in $[a, b]$ is the fuzzy number with α-levels denoted by,

where ${\int}_{a}^{b}\underline{f}\left(x; \alpha \right)dx$ and ${\int}_{a}^{b}\bar{f}\left(x; \alpha \right)dx$ are the Riemann integrals of the real functions $\underline{f}\left(x; \alpha \right)$, $\underline{f}\left(x; \alpha \right)$in the interval $[a, b]$.

Now, the general form of the fuzzy system of Fredholm integro-differential equations (FSFIDEs) of the second kind ^[10] is defined as

the initial conditions

where $0\le \alpha \le 1,$ ${\tilde{\lambda }}_{ij}$ are positive fuzzy parameters, ${\tilde{k}}_{ij}$ is an arbitrary fuzzy function called the kernal of integral and ${\tilde{f}}_{i}(x, \alpha)$ is the given fuzzy function of $x\in [a, b]$ with ${\tilde{u}}_{i}(x, \alpha)$ as the unknown fuzzy functions

then we can write Eq (1) as

3.   Formulation and analysis of HAMFF

For the analysis of HAM in ^[18], we can have the substantive of the solution of Eq (1) for all $\alpha$-level sets values where $\alpha \in \left[\mathrm{0, 1}\right]$ is the following process.

The zeroth-order deformation is

and by taking $q = 0$ and $q = 1$ we get.

From Eq (2), the fuzzy initial guess${\tilde{u}}_{i, 0}(x, \alpha)$can be determined from${\tilde{f}}_{i}(x, \alpha)$, then the taylor series of$q$for ${\tilde{u}}_{i}(x, q, \alpha)$is

where

the $m$-th order deformation $f$ or $q = 1$ in Eq (4) is as follows;

and the series solution of Eq (1) takes the following forms

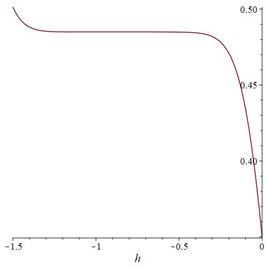
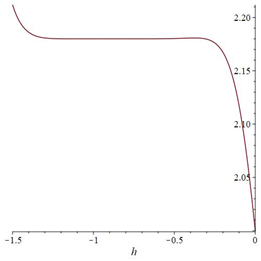
A convenient selecting of $\tilde{h}\left(\alpha \right)$ obtains the convergence of Eq (6) therefore, the solution in series form (homotopy solution).

4.   Convergence analysis HAMFF

The approximate solution of Eq (1) is convergence based on best values of the parameter $\tilde{h}\left(\alpha \right)$ therefore, $\tilde{h}\left(\alpha \right)$ should be discussed to supply enough accuracy for ascertain order of the HAMFF series solution. Therefore, an accurate convergent solution is guaranteed when the convergence parameter is chosen appropriately. Finding the approximate solution with the least amount of residual error is one common method for choosing $\tilde{h}\left(\alpha \right)$. Assume that the residual of Eq (6) is denoted by $\tilde{RE} = \left[\underline{RE}, \overline{RE}\right]$, then defined the following residual form

the mean square residual error (MSRE) of Eq (6) is define in the following form:

by using the least square method to optimize the values of ${\tilde{h}}_{i}\left(\alpha \right)$ such that

and the nonlinear equation coming from Eq. (8) for any $\alpha \in \left(\mathrm{0, 1}\right]$ is derived such that

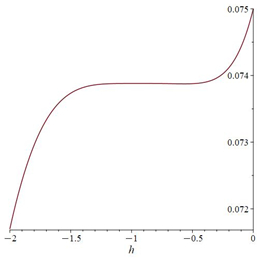
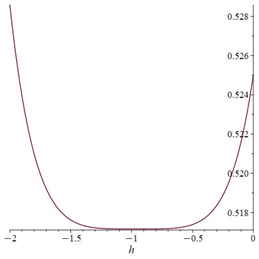
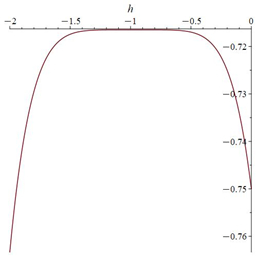
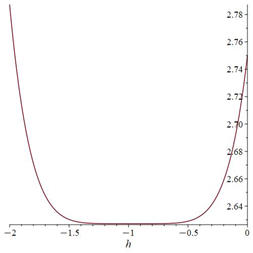
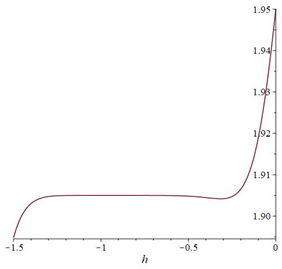
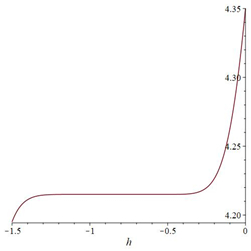
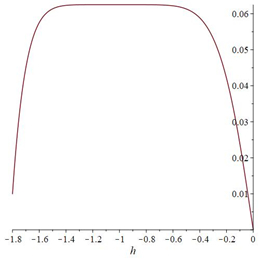
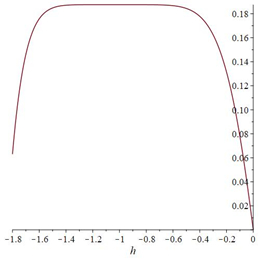
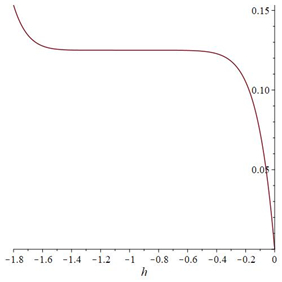
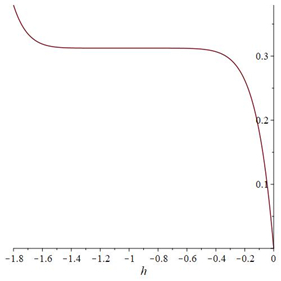
Finally, the equation is solved for ${\tilde{h}}_{i}\left(\alpha \right)$ in each $\alpha$-level set to obtain the best value of $\tilde{h}$ by plotting curves called h-curves such that horizontal line segment with respect to ${\tilde{u}}_{i}^{\left(n\right)}\left(x, \alpha \right)$ to illustrate the best region of the $\tilde{h}\left(\alpha \right)$values, which are the for ${x}_{0} < x < X$. It is familiar in the fuzzy environment to display the contract $h$-curves, and to find the optimal value $\tilde{h}\left(\alpha \right)$ for each$\alpha \in \left[\mathrm{0, 1}\right]$. The choice the best value of $\tilde{h}\left(\alpha \right)$provides the best accurate solution of the FFSIDEs with its corresponding fuzzy level set $\tilde{\alpha } = \left[\underline{\alpha }, \overline{\alpha }\right]$, and then applied $\underline{\alpha }$ for each lower level set gets the best lower approximate solution. A similar step is applied to $\overline{\alpha }$ to determine the best upper solution. The following algorithm is summarizing the dynamic convergence of HAMFF:

Step 1: Set ${\tilde{u}}_{i, 0}\left(x, \alpha \right) = {\tilde{u}}_{i, 0}, \left({\tilde{u}}_{i, 0} = \left\{{\underline{u}}_{i, 0}, {\bar{u}}_{i, 0}\right\}\right), {{\tilde{u}}_{i}}^{'}\left(0, \alpha \right) = \left({{\underline{a}}_{i}}^{'}\left(\alpha \right), {{\bar{a}}_{i}}^{'}\left(\alpha \right)\right), \dots., {{\tilde{u}}_{i}}^{(n-1)}\left(0, \alpha \right) = \left({{\underline{a}}_{i}}^{(n-1)}\left(\alpha \right), {{\bar{a}}_{i}}^{(n-1)}\left(\alpha \right)\right)$.

Step 2: Set $\tilde{\lambda }\left(\alpha \right) = \left[\underline{\lambda }\left(\alpha \right), \bar{\lambda }\left(\alpha \right)\right].$

Step 3: Set $m = \mathrm{1, 2}, 3, \dots, n.$

Step 4: Set $m = m+1$ and for $m = 1$ to $m < n$ evaluate

Step 5: Compute

Step 6: Set the value of ${\alpha }_{0}\in \left[\mathrm{0, 1}\right], x\in [a, b]$ and evaluate

then plot the $h$-curve.

Step 7: Define the residual form in Eqs (6)–(8) and substitute the $\tilde{h}\left({\alpha }_{0}\right)$ in Eq (9) to compute the optimal value of $\tilde{h}\left({\alpha }_{0}\right)$.

Step 8: Replace-again the optimal values of $\tilde{h}\left(\alpha \right)$ for the lower and upper levels in Eq (10).

5.   Applications and numerical results

In this section, the HAMFF is applied to achieve an approximate-exact solution for FSFIDEs in three problems. We defined the maximum errors as follows to demonstrate the high accuracy of the solution when compared with the exact solution.

where:

${\tilde{u}}_{E}\left(x, \alpha \right)$: Fuzzy exact solution,

$\tilde{u}\left(x, \alpha \right)$: Fuzzy approximate solution (HAM).

Moreover, giving the residual error (RE), the computation associated with the problem were performed using the Maple 18 package with a precision of 30 digits.

Problem 1. Consider the following the crisp second kind linear SFIDEs ^[10]

Subject to initial conditions (ICs).

Since this problem is crisp SFIDEs, we will first present fuzzification of the equation. In this study, the fuzzy version of system (9) is created. Such that from Definition 2.2 the fuzzy version of the integral operator is follows:

Now according to the fuzzy analysis in ^[17] the fuzzy version of system (9) is as follows:

From the Definition 2.1 of the triangular fuzzy numbers, we can defuzzify the ICs. Let ${\left[\tilde{0}\right]}_{\alpha }$ and ${\left[\tilde{1}\right]}_{\alpha }$be triangular fuzzy numbers corresponding with the ICs (10) for all $\alpha \in \left[\mathrm{0, 1}\right]$ such that

According to the $\alpha$-cut of triangular fuzzy number in Definition 2.1 the following fuzzy ICs of system (11) are defined as follows

where ${\tilde{f}}_{1}\left(x, \alpha \right) = \left[{\underline{f}}_{1}\left(x, \alpha \right), {\overline{f}}_{1}\left(x, \alpha \right)\right]$ and ${\tilde{f}}_{2}\left(x, \alpha \right) = \left[{\underline{f}}_{2}\left(x, \alpha \right), {\overline{f}}_{2}\left(x, \alpha \right)\right]$ are given by

The exact solutions of the system (11) are

To solve the fuzzy system (11) according to the ICs (12) by means of the HAMFF to obtain the initial approximations. from section 3, the iterations of HAMFF are determined in the following recursive way:

and choosing the linear operators

with the property $L\left[{c}_{1}+{c}_{2}x\right] = 0,$ where ${c}_{1}$ and ${c}_{2}$ are constants. Furthermore, formulation of system (9) according to HAMFF in Section 3 involved the embedding parameter $q\in \left[\mathrm{0, 1}\right]$ and the parameter can be defined with the nonlinear operators as follows:

Using the above definition, with the assumption $H\left(x\right) = 1$ we construct the zeroth-order deformation equation

Obviously, when $q = 0$ and $q = 1$

Thus, we obtain the $mth-$order deformation equations for $m\ge 1$ which are

where

Now, for $m\ge 1,$ the solutions of the mth-order deformation Eq (17) are

Thus, the approximate solutions in a series form are given by

From Section 4, the residual function with respect to this solution for the system (9) is obtained by the substitution of the series solution (19) into the original system (9) such that

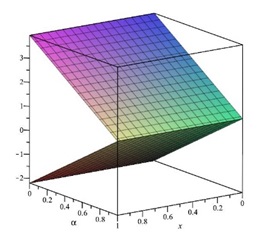
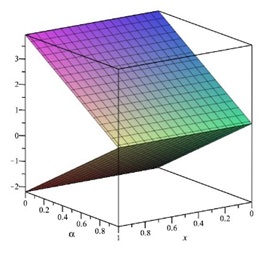
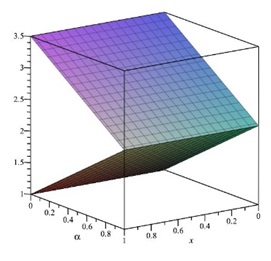
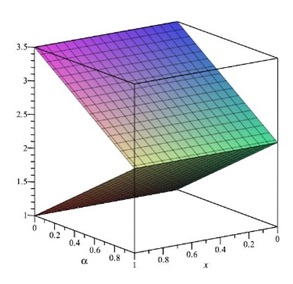
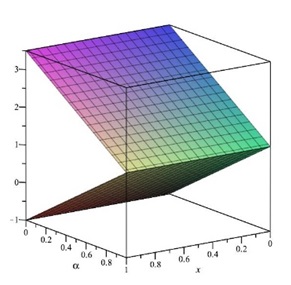
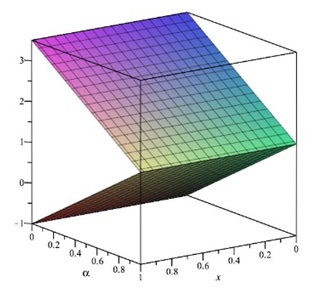
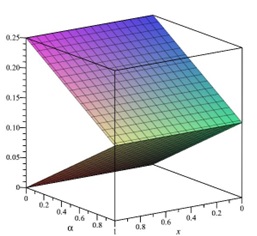
The ${\tilde{h}}_{i}\left(\alpha \right)$-curves of sixth-order HAMFF upper and lower bound solutions $\tilde{u}\left(x, \alpha \right)$ and $\tilde{v}\left(x, \alpha \right)$ at $x = 0.3$ and $\alpha = 0.5$ for system (9) are shown in the following Tables 1 and 2 and Figures 1–4.

By comparing the Tables 3–6, we can see how the results improve after the minimization process.

Tables 3 and 4 show a comparison of the absolute errors applying the HAMFF $(m = 6)$ with the exact solutions (11) within the interval $0\le \alpha \le 1$ at $x = 0.5$ with best values of the convergence control parameter ${\tilde{h}}_{i}$ after minimization which are listed in the following tables (see Tables 5 and 6).

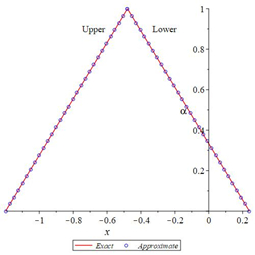
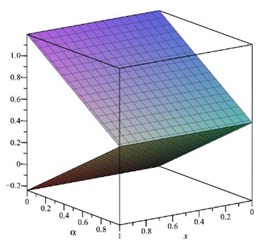
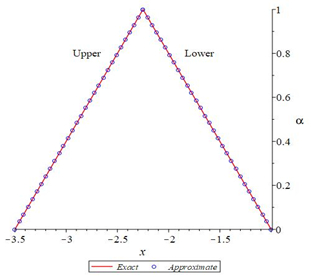
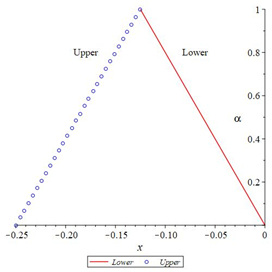
In the following Figures 5–10 shows the exact solutions (${\tilde{u}}_{E}\left(x, \alpha \right)$, ${\tilde{v}}_{E}\left(x, \alpha \right)$) and the fuzzy approximate solutions by HAM ($\tilde{u}\left(x, \alpha \right)$, $\tilde{v}\left(x, \alpha \right)$) of the system (11) are in the form of fuzzy numbers for any $0\le \alpha \le 1$ at $x = 0.3$ and ${\tilde{h}}_{i} = -1$.

According to Figures 5–10, one can summarize that the sixth-order HAMFF solutions of system (9) satisfied the fuzzy solution in triangular fuzzy number forms. To show HAMFF accuracy of Eq (11) crisp version was solved via the Euler polynomials (EP) ^[10] and Laguerre polynomials methods ^[11] (MLP), comparison between sixth-order HAMFF solution EP with $N = 6$ iterations MLP ^[11] with $N = 5$ iterations can be made when$\alpha = 1$ which is equivalent to the crisp version of Eq (11) at the same values of$x\in \left[\mathrm{0, 1}\right]$ that illustrated in Tables 7 and 8 and are displayed in Table 9 below.

Indeed, the sixth- order HAMFF solution system (9) obtained better solution in terms of accuracy over EP ^[10] and MLP ^[11] at $\alpha = 1$ as illustrated in Table 9 above.

Problem 2. Consider the fuzzy version following second kind linear FSFIDEs as follows:

with the boundary conditions (BCs)

System (24) was derived utilizing the same fuzzy analysis in problem 1 from the crisp version SFIDEs in ^[11],

where

${\tilde{f}}_{1}\left(x, \alpha \right) = \left[{\underline{f}}_{1}\left(x, \alpha \right), {\overline{f}}_{1}\left(x, \alpha \right)\right]$ and ${\tilde{f}}_{2}\left(x, \alpha \right) = \left[{\underline{f}}_{2}\left(x, \alpha \right), {\overline{f}}_{2}\left(x, \alpha \right)\right]$ are given by

The exact solutions of the system (24) are

To solve system (24) approximately, the HAMFF is applied to system (24) such that the method iterations are determined in the following recursive way:

where $\tilde{u}^{'}\left(0, \alpha \right) = {\tilde{C}}_{1},$ and $\tilde{v}^{'}\left(0, \alpha \right) = {\tilde{C}}_{2},$ calculated from the BCs (25).

Choosing the linear operators

with the property $L\left[{c}_{1}+{c}_{2}x\right] = 0,$ where ${c}_{1}$ and ${c}_{2}$ are constants.

As in Problem 1, nonlinear operators of system (21) are defined as follows

Using the above definition, with the assumption $H\left(x\right) = 1$ we construct the zeroth-order deformation equation

Obviously, when $q = 0$ and $q = 1$

Thus, we obtain the $mth-$order deformation equations for $m\ge 1$ which are

where

Now, for $m\ge 1,$ the solutions of the mth-order deformation system (24) are

Thus, the approximate solutions in a series form are given by

The residual error function with respect to this solution for the system (21) is

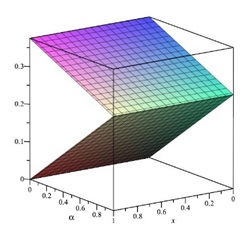
The ${\tilde{h}}_{i}\left(\alpha \right)$-curves of ninth-order HAMFF upper and lower bound solutions $\tilde{u}\left(x, \alpha \right)$ and $\tilde{v}\left(x, \alpha \right)$ at $x = 0.1$ and $\alpha = 0.5$ for system (21) are shown in the following Tables 10 and 11 and Figures 11–14.

By comparing the Tables 12–15, we can see how the results improve after the minimization process.

Tables 12 and 13 show a comparison of the absolute errors applying the HAMFF $(m = 9)$ with the exact solutions within the interval $0\le \alpha \le 1$ at $x = 0.5$ with best values of the convergence control parameter ${\tilde{h}}_{i}$ after minimization which are listed in the following tables (see Tables 14 and 15).

The values of ${\tilde{C}}_{1},$ and ${\tilde{C}}_{2},$ at $x = 1$ for $0\le \alpha \le 1$ with optimal values of ${\tilde{h}}_{i}$ calculated from the BCs (25) are as follows

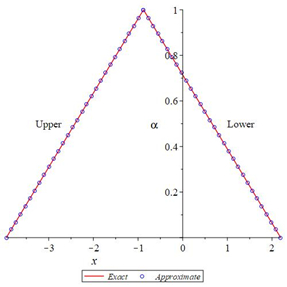
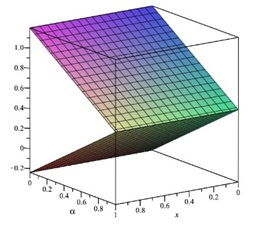
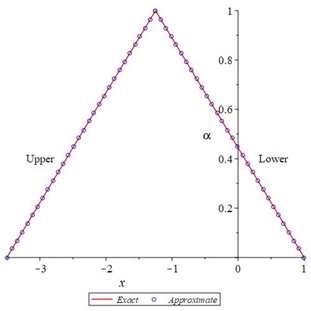
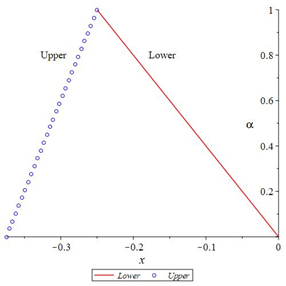
In the following Figures 15–20 shows that the exact solutions (${\tilde{u}}_{E}\left(x, \alpha \right)$, ${\tilde{v}}_{E}\left(x, \alpha \right)$) and the fuzzy approximate solutions by HAMFF ($\tilde{u}\left(x, \alpha \right)$, $\tilde{v}\left(x, \alpha \right)$) of the system (24) are in the form of fuzzy numbers for any $0\le \alpha \le 1$ at $x = 0.1$ and ${\tilde{h}}_{i} = -1$.

According to Figures 15–20, one can summarize that the ninth-order HAMFF solutions of system (24) satisfied the fuzzy solution in triangular fuzzy number forms are illustrated in Tables 16 and 17. Next, a comparison between ninth-order HAMFF solution and the MLP ^[11] are displayed in Table 18 in terms of accuracy at different values of $x\in \left[\mathrm{0, 1}\right]$ and $\alpha = 1$.

The values of ${C}_{1},$ and ${C}_{2},$ at $x = 1$ for $\alpha = 1$ calculated from the BCs (22) are as follows

The values of ${C}_{1},$ and ${C}_{2},$ at $x = 1$ for $\alpha = 1$ with optimal values of ${h}_{i}$calculated from the BCs (22) as follows

From Table 18, the ninth-order HAMFF solution system (9) obtained better solution in terms of accuracy MLP ^[11] at

$\alpha = 1$ at different values of $x$.

Problem 3. From ^[4] the fuzzy version of second kind linear SFIDEs is defined as below:

with the ICs

where

and

Section 3 of the HAMFF analysis of system (35) states the following:

and choosing the linear operators

with the property $L\left[{c}_{1}\right] = 0,$ where ${c}_{1}$ is a constant. Furthermore, the system (35) suggests that we define the nonlinear operators as

Using the above definition, with the assumption $H\left(x\right) = 1,$we construct the zeroth-order deformation equation

Obviously, when $q = 0$ and $q = 1$

Thus, we obtain the $mth-$order deformation equations for $m\ge 1$ which are

where

Now, for $m\ge 1,$ the solutions of the mth-order deformation system (35) are

Thus, the approximate solutions in a series form are given by

The residual error function with respect to this solution for the system (32) is

The ${\tilde{h}}_{i}\left(\alpha \right)$-curves of ninth-order HAMFF upper and lower bound solutions $\tilde{u}\left(x, \alpha \right)$ and $\tilde{v}\left(x, \alpha \right)$ at $x = 0.5$ and $\alpha = 0.5$ for system (35) are shown in the following Tables 19 and 20 and Figures 21–24.

In order to validate the ninth-order HAMFF solution of system (32), a comparative analysis with the learning algorithm iteration (LAI) ^[4] corresponding with 200 iteration is displayed in Tables 21 and 22 in terms of residual errors $\left({\widetilde{RE}}_{1}\right)$ and $\left({\widetilde{RE}}_{2}\right)$ respectively for different values of $0\le \alpha \le 1$ at $x = 0.5$.

By comparing the Tables 21–23, we can see how the results improve after the minimization process. A comparison between ninth-order HAM solution and the fuzzy neural network ^[4] with 200 numerical iterations is given.

Tables 21 and 22 show a comparison of the REs applying the HAMFF $(m = 9)$ with the errors ^[4] within the interval $0\le \alpha \le 1$ at $x = 0.5$ with best values of the convergence control parameter ${\tilde{h}}_{i}$ after minimization which are listed in the following tables (see Table 23).

In the following Figures 25–28 show that the fuzzy approximate solutions by HAMFF ($\tilde{u}\left(x, \alpha \right)$, $\tilde{v}\left(x, \alpha \right)$) of the system (32) are in the form of fuzzy numbers for any $0\le \alpha \le 1$ at $x = 0.5$ and ${\tilde{h}}_{i} = -1$.

The fuzzy solution in triangular fuzzy number forms was satisfied by the ninth-order HAMFF solutions of system (35) as shown in Figures 25–28.

6.   Conclusions

The method of approximate analytical class for solving FSIDEs, known as HAMFF, is the main topic of this work. Using the HAMFF technique, the convergence of the series solution can be efficiently managed by selecting the best convergence parameter for each fuzzy level set. In this study, the FSFIDEs were proposed as utilized as an experimental study to demonstrate the HAMFF technique's precision in solving linear systems with initial conditions. The technique was found to produce a polynomial series solution in close-analytical form that converges to the exact solution as the series order increases. The novelty of HAMFF derived from basic concepts of the standard HAM and some popular definitions and properties of fuzzy sets theory. The study also used the HAMFF to find the series solution in nonlinear terms and suggested a new fuzzy version of FSFIDEs. The HAMFF technique was discovered to offer the series solution FSFIDEs subject to boundary conditions. The optimal convergence parameters for the suggested problems were also ascertained by utilizing the HAMFF's convergence behavior in fuzzy environments to increase the accuracy of the technique. A comparison analysis between the HAMFF and other approximate techniques is presented, showing that the HAMFF obtained a better solution in terms of accuracy. It is noteworthy to note that all the problems in this study that were solved with HAMFF obtained the series solution in the triangular fuzzy numbers.

Author contributions

Zena Talal Yassin: Conceptualization, validation, investigation, writing original draft preparation; Waleed Al-Hayani: Conceptualization, validation, investigation, writing original draft preparation; Ala Amourah: methodology, validation, writing review and editing; Ali F. Jameel: methodology, for-mal analysis, writing review and editing; Nidal Anakira: methodology, investigation, supervision; All authors have read and agreed to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare no conflict of interest.