Identification of marine micro algae in correlation with water quality assessment of coastal region of Maharashtra, India

1.   Introduction

Let $\Omega$ be a convex polygonal domain in $\mathbb{R}^2$. In this paper, we consider the following Dirichlet boundary optimal control problem,

subject to the advection-diffusion equation

Here, $y(x)$ denotes the state variable, $\hat y(x)$ is the desired state, $\rm (1.2a)$ and $\rm (1.2b)$ are called the state equation, $q(x)$ is the control, $\Gamma = \partial\Omega$.

We assume the given functions $f(x), \hat y(x)\in L^2(\Omega)$, $\vec{\beta}(x)\in [W^1_{\infty}(\Omega)]^2$, $c(x)\in L^{\infty}(\Omega)$ with the assumption

and $\alpha > 0$ is a given scalar.

This problem is important in many applications, for example distribution of pollution in air ^[1] or water ^[2] and for problems in computational electro-dynamics, gas and fluid dynamics ^[3]. However, there are several challenges involved in solving this problem numerically. One problem arises for higher order elements and nonsmooth Dirichlet data which can cause serious problems in using standard finite element methods (see ^[4,5]). Another difficulty lies in the fact that Dirichlet boundary conditions do not enter the bilinear form naturally and that causes problems for analyzing the finite element method (see ^[6,7,8,9,10] for further discussion).

One faces another challenge in the presence of layers which are the regions where the gradient of the solution is large. Usually, the boundary layers occur because of the fact that problem has reduced to the first order PDEs and requires boundary conditions on inflow part of the boundary only. In this case, standard Galerkin methods fail when $h{|\vec{\beta}|} > 1$, where $h$ is mesh size, producing highly oscillatory solutions. A lot of research has been done in last 40 years to address this difficulty (see ^{[3,4,11,12,13]}).

We have an example to illustrate this difficulty in the following simple example,

Example 1.1.

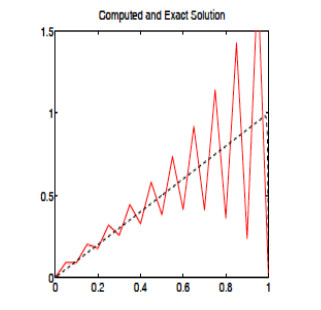
The Figure 1 shows nonphysical oscillations of the standard Galerkin solution for $h = 0.1$ and $\epsilon = 0.0025$.

One way to solve this problem is to use stabilized methods (see ^[14]). We will mention some of them. One of the first stable method of arbitrary order is SUPG (Streamline Upwind Petrov Galerkin) ^[11,15,16]. In this method, the space of test function is different from the space of trial function and chosen such that the method is stable and consistent. Other stabilized methods where the space of trial and test functions are the same and used upwind stabilization are HDG (Hybridizable Discontinuous Galerkin), ^{[17,18,19,20,21]}, SIPG (Symmetric Interior Petrov Galerkin) ^[5,7,10], and LDG (Local Discontinuous Galerkin) ^[22,23,24]. Another popular stabilized method where the space of trial and test functions are the same is edge stabilization ^[25,26].

DG methods are shown to be robust for the advection-diffusion-reaction problem (see ^[7,27]) even for the advection-dominated case. DG methods were not only analyzed for the advection-diffusion-reaction problem but also for the optimal control problem of the advection-diffusion-reaction equation ^[28], (see other stabilized methods for the optimal control problem of the advection-diffusion-reaction equation ^[26,29,30]). In addition to being stable, the discontinuous Galerkin methods, such as SIPG, usually treat the boundary conditions weakly. The SIPG method was also analyzed for distributed optimal control problems and optimal local and global error estimates were obtained (see ^[28] but not for the boundary control problems. We would like to investigate the performance of the SIPG method applied to Dirichlet boundary control problem ($1.1$), ($1.2a$) and ($1.2b$) and prove a priori error estimates. We would also like to perform a number of numerical experiments to confirm our theoretical result which is the main subject of the current work.

In this paper, we analyze the SIPG solution of Dirichlet boundary control problem and the difficulties with dealing with the stability issues as well as with the difficulty of the treatment of Dirichlet boundary conditions. This method has some attractive features and offers some advantages. This method is stable and accurate, can be of arbitrary order and has been shown analytically that the boundary layers do not pollute the solution into the subdomain of smoothness ^[28]. Another attractive feature of the method is that Dirichlet boundary conditions are enforced weakly through the penalty term and not through the finite dimensional subspace ^[25]. As a result of the weak treatment of the boundary conditions, Dirichlet boundary control enters naturally into the bilinear form and makes analysis more natural ^[6,7,8,31]. Finally, the SIPG method has the property that two strategies optimize-then-discretize and discretize-then-optimize produce the same discrete optimality system (see ^[10,23]), which is not the case for other stabilized methods, for example, SUPG method (see ^[15]).

Let us show some features of SIPG method with Figure 2 in the previous example. Consider the problem 1.3 in the example 1 with the much more smaller diffiusion parameter $10^{-9}$ instead of $- 0.0025$. Figure 2 shows the behavior of the SIPG solution for $h = 0.1$ and $\epsilon = 1e-9$. As one can see the solution is stable. The Dirichlet boundary condition at $x = 1$ is almost ignored by the method as a result of weak treatment.

Our choice of this particular DG method was motivated by good approximation and stabilization properties of the method. Additional attractive feature of the method is the weak treatment of the boundary conditions which allows us to set Dirichlet optimal control problem in natural the finite element frame work and to prove optimal convergence rates for on general convex polygonal domain. Moreover, we state the main result of the paper is valid for any general convex domain, there exists a positive constant $C$ independent of $h$ for the error between exact solution of the control function $\bar q$ and its approximation $\bar q_{h}$ such that

for $h$ small enough. Also, we performed several numerical examples to support our theoretical results, and additionally when we investigate numerically performance of the method in the advection-dominated case.

2.   Elliptic equations with Dirichlet boundary conditions

2.1.   Preliminaries

Throughout the paper, we will use standard notation for spaces, completeness and norms. We will use the standard notation for Lebesgue and Sobolev space, their suitable norms, and $L^2$- inner product. Thus,

● $(u, v)_{\Omega} = \int_{\Omega} uvdx$ and $\langle u, v\rangle_{\Gamma} = \int_{\Gamma}uvds$ are the inner products on the domain $\Omega$ and its boundary $\Gamma$, respectively.

The corresponding norms respectively are

● $H^{1/2}(\Gamma) = \{u\in L^2(\Gamma)|\exists \tilde u\in H^1(\Omega):u = tr(\tilde u)\}$.

● $\|u\|_{H^{1/2}(\Gamma)} = inf\{\|\tilde u\|_ {H^1(\Omega)}| tr(\tilde u) = u\}$.

● $|u|_{H^{1/2}(\Gamma)} = inf\{|\tilde u|_ {H^1(\Omega)}| tr(\tilde u) = u\}$.

2.2.   Setting the problem

First, let us consider the state equation,

We review some regularity results for various conditions on data which we will use later in the analysis. The first result is standard and found in ^[32].

Theorem 2.1. Let $f\in H^{-1}(\Omega)$ and $q\in H^{1/2}(\Gamma)$. Then Eq $(2.1)$ admits a unique solution $y\in H^1(\Omega)$. Moreover, the following estimate holds

In the case of $q = 0$ on $\Gamma$, $f\in L^2(\Omega)$, and convex $\Omega$, we can obtain a higher regularity of the solution (see ^[33]).

Theorem 2.2. Let $f\in L^2(\Omega)$ and $q = 0$ on $\Gamma$. Then, the Eq $(2.1)$ admits a unique solution $y\in H^2(\Omega)$ and the following estimate holds

Remark 2.1. Since the adjoint equation defined by

it is also an advection-diffusion equation and the results of the above theorems are valid for the adjoint equation with similar estimates as well. Also, notice that $-\vec{\beta}\cdot\nabla z+(c-\nabla\cdot\vec{\beta})z = - \nabla\cdot(\vec{\beta}z)+cz$.

The theory in the case of $q \in L^2(\Gamma)$ is more technical and to obtain the desired regularity result, we use the transposition method ^[34], which we will briefly describe next.

2.3.   The transposition method

Suppose q is smooth enough having continuous derivatives up to the desired order, $\phi\in L^2(\Omega)$ and let $y_{1}$ and $y_{2}$ be the solutions of the following equations,

respectively. Then, by the integration by parts and using the fact that $y_{2} = 0$ on $\Gamma$, we obtain

where in the last step we use that $-\Delta y_{2} -\nabla\cdot(\vec{\beta}y_{2})+cy_{2} = \phi$ in $\Omega$ and $y_{1} = q$ on $\Gamma$. Hence we obtain

The above formula defines a mapping $\Lambda:\phi\rightarrow -\frac{\partial y_{2}}{\partial n}$ that is linear and continuous from $L^2(\Omega)$ to $H^{1/2}(\Gamma)$. Since the embedding $H^{1/2}(\Gamma)\hookrightarrow L^2(\Gamma)$ is compact, $\Lambda$ is a compact operator from $L^2(\Omega)$ to $L^2(\Gamma)$. Hence, its adjoint $\Lambda^{*}$ is a compact operator from $L^2(\Gamma)$ to $L^2(\Omega)$.

Since $(y_{1}, \phi)_{\Omega} = -\int_{\Gamma} q\frac{\partial y_{2}}{\partial n} = \langle q, \Lambda\phi\rangle_{\Gamma}$ and $\langle q, \Lambda\phi\rangle_{\Gamma} = (\Lambda^{*}q, \phi)_{\Omega}$, we conclude that $y_{1} = \Lambda^{*}q$. Using the above, we can define an "ultra-weak" solution for the Eq $(2.1)$ for Dirichlet data in $L^2(\Gamma)$ as follows.

Definition 2.1. We say that $y\in L^2(\Omega)$ is a unique ultra-weak solution of the Eq $(2.1)$ if

where $p$ satisfies

Now we are ready to provide the following regularity result.

Theorem 2.3. For any $f\in H^{-1}(\Omega)$ and $q\in L^2(\Gamma)$, the Eq $(2.1)$ admits a unique ultra-weak solution $y\in L^2(\Omega)$. Moreover, the following estimate holds,

Proof. Existence follows from the Definition ($2.1$). For the uniqueness, we assume that $y_{1}$ and $y_{2}$ are distinct solutions of the Eq $(2.1)$ and let $u = y_{1}-y_{2}$, then

Since $H^1(\Omega)$ is dense in $L^2(\Omega)$, it is enough to consider $u\in H^1(\Omega)$. By the Theorem ($2.1$), we have

As a result $u = 0$, hence $y_{1} = y_{2}$ and this contradiction proves the uniqueness.

To show the desired estimate $(2.2)$, we use a duality argument. Let $w$ be the solution of the problem

By using the above duality argument and using integration by parts and the fact that $w = 0$ on $\Gamma$, we obtain

where in the last step we use $-\Delta y +\vec{\beta}\cdot\nabla y+cy = f$.

By the trace and the Cauchy-Schwarz inequalities, and by using the Theorem (2.2), we have the following estimate

Canceling $\|y\|_{L^2(\Omega)}$ on both sides, we prove the desired estimate $(2.2)$.

3.   First order optimality system and the regularity of the optimal solution

Next we will provide the first order optimality conditions for the problem $(1.1)$

Theorem 3.1. Assume that $f, \hat y\in L^2(\Omega)$ and let $(\bar y, \bar q)$ be the optimal solution of the Eq $(2.1)$. Then, the optimal control $\bar q$ is given by $\frac{\partial\bar z}{\partial n} = \alpha \bar q$, where $\bar z$ is the unique solution of the equation,

Proof. Let $(\bar y, \bar q)$ be an optimal solution of the Eq $(1.1)$. We set

where $y(q)$ is the solution of the Eq $(2.1)$ for a given $q\in L^2(\Gamma)$. Let $y_{q}$ be the solution of the problem

By the optimality of $(\bar y, \bar q)$ and convexity of $\Omega$, we have that $\frac{1}{\lambda}(F(\bar q+\lambda q)- F(\bar q))\ge 0$ for all $q$ and $\lambda\in(0, 1]$ ^[35]. For $\lambda = 1$, $y_{q} = q+\bar q$, and so $F(\bar q+q)-F(\bar q)\ge 0$.

Equivalently, if $F(\bar q+q)-F(\bar q)\ge 0$ for all $q$ in $L^2(\Gamma)$, then $\bar q$ is an optimal solution of the problem. We find

Let $\bar z$ be the solution of the Eq $(3.1)$. Then, we can estimate the third term of the right hand side by using the Green's formula and using the fact that $y_{q} = \bar q+q$ and $\bar z = 0$ on $\Gamma$. Thus, we obtain

Notice that $\int_{\Omega}\nabla\bar z\cdot\nabla(y_{q}-\bar y) = (\frac{\partial y_{q}}{\partial n}-\frac{\partial \bar y}{\partial n})\bar z\Big|_{\Gamma}-\int_{\Omega}\bar z\Delta (y_{q}-\bar y)$ by using integration by parts. By setting $\frac{\partial\bar z}{\partial n} = \alpha\bar q$, we have

Putting all results together, we have

i.e., $(\bar y, \bar q)$ is the optimal solution to the Eq $(2.1)$ with $\bar q = \frac{1}{\alpha}\frac{\partial\bar z}{\partial n}$ where $\alpha > 0$ given any scalar in the problem (1.1)

3.1.   Strong form of the first order optimality conditions

The first order optimality conditions in the strong form are as the following

3.2.   Regularity

In the next theorem, we establish the regularity of the optimal solution of the problem (1.2a) and (1.2b).

Theorem 3.2. Let $(\bar y, \bar q)\in L^2(\Omega) \times L^2(\Gamma)$ be the optimal solution to the optimization problem $(1.1)$ subject to the problem $\rm (1.2a)$ and $\rm (1.2b)$, and $\bar z$ be the optimal adjoint state $(3.1)$. Then,

Proof. For $\bar q\in L^2(\Gamma)$, from the state Eq (3.4), $\bar y\in L^2(\Omega)$ holds by Theorem (2.3).

Since $\bar y, \hat y\in L^2(\Omega)$ and $\Omega$ is a convex domain, from the adjoint Eq ($3.2$), $\bar z\in H^2(\Omega)$ holds by Theorem ($2.2$).

Since $\bar z\in H^2(\Omega)$, we have $\frac{\partial\bar z}{\partial n}\in H^{1/2}(\Gamma)$, from the gradient Eq $(3.3)$, $\frac{\partial\bar z}{\partial n} = \alpha q$ implies $\bar q\in H^{1/2}(\Gamma)$.

Since $\bar q\in H^{1/2}(\Gamma)$, from the state Eq $(3.4)$, $\bar y\in H^1(\Omega)$ holds by Theorem ($2.1$).

Remark 3.1. Using regularity results, we can generalize the regularity which depends on the largest interior angle of the polygonal domain in $\mathbb{R}^2$ ^[36].

4.   Discontinuous Galerkin discretization

The idea of the FEM is to construct $V_{h}$ and $Q_{h}$ defined on a finite dimensional space that is well approximate the solution spaces $V$ and $Q$. The Galerkin FEM is to find $y_{h}\in V_{h}$ and $q_{h}\in Q_{h}$ such that

where $V_{h}$ is a finite dimensional space and $h$ is a discretization parameter. We can easily see that if $a_{h}(\cdot, \cdot)$ satisfies the conditions of Lax-Milgram Lemma, the Eq ($4.1$) has a unique solution for each $h$.

To construct $V_{h}$, we consider a family of conforming quasi-uniform shape regular triangulations $T_{h}$ of $\Omega$ such that $\bar{\Omega} = \cup_{\tau_{i} \in T_{h}}\tau_{i}$ and $\tau_{i}\cap\tau_{j} = 0$ $\forall \tau_{i}, \tau_{j}\in T_{h}, \ i\neq j$ with a mesh size

We define $E_{h}$ as a collection of all edges $E_{h} = E_{h}^{0}\cup E_{h}^{\partial}$ where $E_{h}^{0}$ and $E_{h}^{\partial}$ are the collections of interior and boundary edges, respectively, and we decompose the boundary edges as

where $E_{h}^{-}: = \{e\in E_{h}^{\partial}: e\subset\{x\in\Gamma:\vec{\beta}(x)\cdot\vec{n}(x) < 0\}\}$ and $E_{h}^{+}: = E_{h}^{\partial}\backslash E_{h}^{-}$ i.e. these are the collections of the edges that belong to the inflow and outflow part of the boundary, respectively. In other words, for a given elements $\tau\in T_{h}$ and $n_{\tau}$ indicates the outward normal to $\tau$, then we can decompose its boundary $\partial\tau$ as $\partial\tau_{-} = \{x\in\partial\tau: \vec{\beta}(x)\cdot\vec{n_\tau}(x) < 0\}$ and $\partial\tau_{+} = \{x\in\partial\tau: \vec{\beta}(x)\cdot\vec{n_\tau}(x)\ge 0\}.$

We define the standard jumps and averages on the set of interior edges by

where $\vec{n}_{1}$ and $\vec{n}_{2}$ are outward normal vectors at the common boundary edge of neighboring elements $\tau_{1}$ and $\tau_{2}$, respectively. If $e\in E_{h}^{\partial}$, then $\{\varphi\} = [[\varphi]] = \varphi|_{e}$ ^[37,38]. Define the discrete state and control spaces as

respectively. We denote by $\mathcal{P}_k$, $\mathcal{P}_l$ the space of polynomials of degree at most $k$ on each element and at most $l$ on each edge, respectively. In general, the state and control variables can be approximated by polynomials of different degrees $k$, $l$$\in\mathbb{N}$.

Here, we use the symmetric interior penalty Galerkin (SIPG) method to approximate to the problem. In deriving the SIPG method, we use the following identity

The SIPG solutions $q_{h}\in Q_{h}$, $y_{h}\in V_{h}$ and a constant advection field $\vec\beta$ satisfies the Eq (4.1) for all $v_{h}\in V_{h}$ where

where $\gamma$ is the penalty parameter, which should be chosen sufficiently large to ensure the stability of the SIPG scheme ^[37,39,40], and $y_{h}^{-} = {\lim\limits_{\zeta\to 0^+} y_{h}(x-\zeta\vec\beta})$, $y_{h}^{+}(x) = {\lim\limits_{\zeta\to 0^+} y_{h}(x+\zeta\vec\beta)}$,

Then, DG solution is defined as a solution of $a_{h}(y_{h}, v_{h}) = \ell_{h}(f; q_{h}, v_{h})$ for al all $v_{h}\in V_{h}$, and mesh dependent norm

which is equivalent to the energy norm ^[38].

4.1.   Well-posed

It has been shown, for example ^[7], that the bilinear form (4.5) is coercive and bounded on $V_{h}$ i.e., $a_{h}(v_{h}, v_{h})\ge C{\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert {v_{h}} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}^2$ and $a_{h}(y_{h}, v_{h})\le C{\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert {y_{h}} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}{\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert {v_{h}} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}$, respectively. Thus, Lax-Milgram Lemma guarantees the existence of a unique solution $y_{h}\in V_{h}$ of the Eq (4.1) for all $v_{h}\in V_{h}$.

4.2.   Discrete optimality system

We apply the SIPG discretization to the optimal control problem $(1.1)$. Now, define the discrete Lagrangian as

Then, setting the partial Frechet derivatives with respect to $y_{h}, q_{h}$ and $z_{h}$ to be zero, we obtain the discrete optimality system.Then, the discretized optimal control problem has a unique solution $(y_{h}, q_{h})\in V_{h}xQ_{h}$ if only if there exists $z_{h}\in V_{h}$ holds the following system:

5.   DG error estimates

5.1.   Auxiliary estimates

We will need some auxiliary estimates that we will use in the proof of the main result. First, we have some standard estimates which are trace and inverse inequalities and the proofs can be found in ^[41,42,43].

Lemma 5.1. There exist positive constants $C_{tr}$ and $C_{inv}$ independent of $\tau$ and $h$ such that for $\forall\tau\in T_{h}$,

for integer $k\ge 0$

Then, we need some basic estimates for $L^2$-Projection where $P_{h}:L^2(\Omega)\rightarrow V_{h}$ is the orthogonal projection such that $(P_{h}v, \chi)_{\tau} = (v, \chi)_{\tau}$ for all $v\in L^2(\tau)$ and $\chi\in V_{h}$.

Lemma 5.2. Let $P_{h}$ be $L^2$-projection. Then, we have that $\exists P_{h}: H^{k+1}\rightarrow V_{h}$ such that for any $\tau\in T_{h}$,

where integer $k\ge 0$.

Proof. From $\it{Local\ Approximation}$ used in ^[30], we know that there exists a local interpolant operator $\it{P_{h}}: H^{k+1}\rightarrow V_{h}$ such that for any $\tau\in T_{h}$ and $\forall v\in H^{k+1}(\tau)$,

Since $h\|\nabla(v-P_{h}(v))\|_{\tau}\le h\|\nabla(v-P_{h}(v))\|_{\tau}+\|v-P_{h}(v)\|_{\tau}\le Ch^{k+1}\|v\|_{H^{k+1}(\tau)}$, we have

Thus,

Likewise, we obtain $\|v-P_{h}v\|_{L^{2}(\tau)}\le Ch^{k+1}\|v\|_{H^{k+1}(\tau)}.$

Now, we are ready to show the error estimate of SIPG solution in the energy norm.

Lemma 5.3. Let $v$ be the unique solution of the Eq $(2.1)$ to satisfy $v\in H^{k+1}(\Omega)$ and $v_{h}\in V_{h}$ be the SIPG solution of the discretized state equation with piecewise polynomials of degree k. Then,

for integer $k\ge 0$.

The proof can be easily seen by using the well-posedness of the bilinear form $(4.5)$, Lemmas (5.1) and (5.2), and it can be also found for example in ^[44,45]. Next, we will need the estimate of $L^2$-Projection on the boundary $\Gamma$ where $P^{\partial}_{h}: L^2(\Gamma)\rightarrow Q_{h}$ is defined by $\langle q-P_{h}^{\partial}q, \phi_{h}\rangle_{e} = 0$ for all $\phi_{h}\in\mathcal{P}_s(e)$.

Lemma 5.4. Let $P^{\partial}_{h}$ be $L^2-$projection defined on the boundary. Then, for any edge $e\in E_{h}^{\partial}$,

where $E_{h}^{\partial}$ is the set of boundary edges which is described in the Eq $(4.2)$, $q\in W^{s, p}(e)$, $0\le s\le 1$, and $1 < p < \infty$.

The proof can be found in ^[6].

Note that Lemmas (5.1)–(5.4) state for general reqularity which depends on the polynomial degree k used in SIPG, the regularity on the solution of the optimal control problem is $(\bar y, \bar q, \bar z) \in H^1(\Omega)\times H^{1/2}(\Gamma)\times H^2(\Omega)$ by Theorem ($3.2$). Thus, the following estimates and the main result will be done by using the regularity on the solution of the problem in Theorem (3.2).

Since SIPG method treats the boundary conditions weakly, SIPG solution is not zero on the boundary even if its continuous solution z is. However, the following result says that the norm of SIPG solution $z_{h}$ on the boundary is rather small.

Lemma 5.5. Let us define auxiliary variable $\tilde{z}$ to be a solution of the Eq $(3.2)$

and $\tilde z_{h}\in V_{h}$ be the SIPG approximation solution. Then,

Proof. Let $\tilde{z}$ be a solution to the Eq $(3.2)$. Since

we can estimated that

by using the definition of the energy norm. Thus, by Theorems ($2.2$), ($3.2$) and Lemma ($5.3$), we have that

The estimate of ${\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert {y-y_{h}} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}$ is more involved because $(y-y_{h})$ does not satisfy the Galerkin orthogonality by $(y-y_{h})\notin V_{h}$ and $a_{h}(y-y_{h}, v_{h})\not = 0$ for $v_{h}\in V_{h}$. First, we can show the following result.

Lemma 5.6. Let $y$ and $y_{h}$ satisfy

Then,

Proof. By the coersivity, adding and subtracting $P_{h}y$, we have

$II:$

By using the boundedness of $a_{h}(., .)$, Theorem (3.2) and Lemma ($5.3$), $k = 0$ and we obtain

$I:$

Since$(P_{h}y-y_{h})\in V_{h}$, we have $a_{h}(y-y_{h}, P_{h}y-y_{h}) = \ell_{h}(0;q-q_{h}, P_{h}y-y_{h}).$ Then, we have

By the definition of $\ell_{h}(, )$, we can see that $\sum_{e}\frac{\gamma}{h}(q-q_{h}, [[P_{h}y-y_{h}]])_{e}$ is the dominating term by being $\frac{\gamma}{h}$ large. Using the fact that $\|[[P_{h}y-y_{h}]]\|_{L^2(\Gamma)}$ is a part of the energy norm and Lemma ($5.3$) for $k = 0$ since $y\in H^1(\Omega)$, we have

The other terms in $\ell_{h}(0;q-q_{h}, P_{h}y-y_{h})$ can be estimated with the similar way. Thus,

By first taking the square root and then canceling ${\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert {y-y_{h}} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}$, we obtain

Using a duality, we can show better estimate in $L^2$ norm.

Lemma 5.7. Let $y$ be the solution of the Eq $(2.1)$ and $y_{h}$ in $V_{h}$ satisfy the bilinear form ($4.5$). Then,

Proof. Since $y_{h}$ is not a Galerkin projection of $y$, let us define $\tilde y_{h}$ by $a_{h}(y-\tilde y_{h}, \chi) = 0$ for $\chi\in V_{h}.$ Then, by the triangle inequality, we have

$K_{1}$

Consider the following equation,

By the boundedness of the bilinear form and using the Galerkin orthogonality,

By using Theorem ($2.2$) and Lemma ($5.3$), we obtain

By canceling $\|y-\tilde{y}_{h}\|^2_{L^2(\Omega)}$, we obtain that

$K_{2}:$

Let us define another dual equation,

$K_{21}:$

Likewise $K_{1}$,

By using Theorem (2.2) and Lemma (5.3), we obtain

$K_{22}:$

$K_{22} = a_{h}(y-y_{h}, v) = \underbrace{a_{h}(y-y_{h}, v-P_{h}v)}_{K_{221}} + \underbrace{a_{h}(y-y_{h}, P_{h}v)}_{K_{222}}.$

By using the boundedness of the bilinear form, Theorem ($2.2$) and Lemma ($5.3$),

By using Lemma ($5.6$), we obtain

$K_{222}:$

Using the fact that $v = 0$ on $\Gamma$, Theorems ($2.2$), ($3.2$) and Lemma ($5.3$), we have that

Then, we obtain

Thus, we have

By canceling $\|\tilde{y}_{h}-y_{h}\|^2_{L^2(\Omega)}$, we obtain

Finally, we obtain

By taking the square root, we conclude

5.2.   Main results

Now, we are ready to prove the main result of the paper. We will state it in the next theorem.

Theorem 5.1. Let $\Omega$ be a convex polygonal domain, $\bar q$ be the optimal control of the problem $(1.1)$ and $\bar{q}_{h}$ be its optimal SIPG solution. Then, for $h$ sufficiently small, there exists a positive constant $C$ independent of $h$ such that

where $(\bar y, \bar q, \bar z) \in H^1(\Omega)\times H^{1/2}(\Gamma)\times H^2(\Omega)$ and $\hat y\in L^2(\Omega)$.

Proof. Since $\bar q$ is the optimal solution of the problem $(1.1)$ and $\bar q$ satisfies the Eq $(3.3)$, we have

Since $\bar q_{h}$ is the approximate solution of the problem $(1.1)$ and $\bar q_{h}$ satisfies the Eq $(4.8)$, we have

Subtracting the Eq $(5.4)$ from the Eq $(5.5)$, for any $\phi_{h}\in Q_{h}$, we have

Taking $\phi_{h} = P^{\partial}_{h}(\bar q-\bar q_{h}) = P^{\partial}_{h}\bar q-P^{\partial}_{h}\bar q_{h} = P^{\partial}_{h}\bar q-\bar q_{h}$ in the Eq $(5.6)$ and splitting

we obtain

Now, we shall estimate each term separately. Most terms can be estimated by using the estimate of the $L^2$-projection. However, the term $(\bar z- \bar z_{h})$ in $J_{2}$ and $J_{5}$ is not in the discrete space, so additional arguments are needed to treat these terms.

Estimate for $J_{1}$: By the Cauchy-Schwarz inequality and using Lemma $(5.4)$,

where $C_{1}$ depends on $\alpha$.

Estimates for $J_{3}$ and $J_{6}$: Using Lemma (5.5) to estimate $\|\bar z_{h}\|_{L^2(\Gamma)}$, the Cauchy-Schwarz inequality, Lemma (5.7) and the regularity of $\bar y$, then we have

Likewise,

where $C_{3}$ and $C_{6}$ depend on $\gamma$.

Estimates for $J_{4}$ and $J_{7}$: By using the Cauchy-Schwarz inequality, Lemmas ($5.5$) and (5.7), we have

Likewise,

Estimate for $J_{5}$: By the Cauchy-Schwarz inequality,

Let us define $\tilde {z}_{h}\in V_{h}$ to be the SIPG solution to $\bar z$ i.e. $a_{h}(\chi, \tilde z_{h}) = (\hat y-\bar y, \chi)$, $\forall\chi\in V_{h}$.

In particular, $a_{h}(\chi, \bar z-\tilde{z}_{h}) = 0$ by the Galerkin orthogonality. Thus, we continue as following,

$J_{51}$:

By the triangle inequality, we have

$J_{511}:$

By the trace inequality, Theorem ($2.2$) and Lemma (5.2), we obtain

Thus,

$J_{512}:$

Since $(P_{h}\bar z-\tilde{z}_{h})\in V_{h}$, we can apply the trace theorem for discrete function and by using the inverse inequality and Lemma (5.2), we obtain that

where we have used Lemma ($5.3$) for $k = 1$ by Theorem ($2.2$) and Lemma (5.2).

Thus,

Since $J_{51} = J_{511}+J_{512}$, we obtain

$J_{52}:$

Since we have

where $\forall\chi\in V_{h}$. We obtain

Now, let us define the following equation

By using the Eq $(5.8)$,

The above equality shows that $w_h = \tilde{z}_{h}-\bar z_{h}$.

Now, using the inverse inequality and the fact that $w = 0$ on $\Gamma$, we obtain

where we have used Theorem ($2.2$) and Lemma ($5.3$) for $k = 1$ by Lemmas (5.2) and (5.7) in the last step.

Thus,

Finally, we obtain

Estimate for $J_{2}$: By using the the estimation of $\|\frac{\partial (\bar z-\bar z_{h})}{\partial n}\|_{L^2(\Gamma)}$ in $J_{5}$, Cauchy-Schwarz inequality and Lemma (5.4), we have

Thus,

After using Lemma (5.7) to estimate $\|\bar y-\bar y_{h}\|_{L^2(\Omega)}$ and combining $J_{1}, J_{2}, J_{3}, J_{4}, J_{5}, J_{6}, J_{7}$ in the Eq (5.7), we obtain

Notice that we can rewrite the above inequality as

After all simplification, we obtain

where $h$ is sufficiently small such that $C'h\le\frac{\alpha}{2}$ to absorb $C'h\|\bar q-\bar q_{h}\|^2_{L^2(\Gamma)}$ to the left hand side. Thus, we conclude that there exists a positive constant $C$ such that

provided h is sufficiently small.

6.   Numerical examples

In this section, we show the features of the method and some numerical examples to support our theoretical results by the method described for the main problem $(1.1)$, $\rm (1.2a)$ and $\rm (1.2b)$. Here, we present numerical results depending on different kinds of domain as the following.

6.1.   $\Omega$ is a line segmenent

Since the domain is one dimensional and the boundary is consisting of two points, there is no regularity limitation due to geometry restriction. Thus, we do not expect an optimal convergence rate, but we observe that the method is still stable and convergent in Tables 1–3 and Figures 3–4.

By setting $\Omega = [0, 1]$, $\epsilon = 1$, $\alpha = 1$, $\vec{\beta} = [1]$, $\bar q = (1-x)^2(x^2)$, $c = 0$, $\bar y = x^4-\frac{e^{\frac{x-1}{\epsilon}}-e^{\frac{-1}{\epsilon}}}{1-e^{\frac{-1}{\epsilon}}}$, and $\bar z = \frac{\alpha}{\epsilon}(1-x)^2x^2$.

6.2.   $\Omega$ is a unit square domain

By setting the problem as the following,

Here, we consider piecewise linear continuous functions to approximate the optimal control.

6.2.1.   Numerical results for the regular case ($\epsilon\gg h$ where h is mesh size) on the unit square domain

The first order conditions allow us deduce the regularity results of the optimal control and so the expected convergence rate has agreed well with the rate in ^[6] as $\|\bar q-\bar q_{h}\|_{L^2(\Gamma)}\le {\it Ch}$ by the square domain with the largest interior angle $w_{max} = \frac{\pi}{2}$.

Lemma (5.7) and $\|\bar q-\bar q_{h}\|_{L^2(\Gamma)}\le {\it Ch}$ yield $\|\bar y-\bar y_{h}\|_{L^2(\Omega)}\le{\it Ch^{3/2}}$. Since the power of h on the right-hand side drops for one for each derivative of the error $(\bar y-\bar y_{h})$, $\|\bar y-\bar y_{h}\|_{H^1(\Omega)}\le{\it Ch^{1/2}}$ by Lemma (5.2). Likewise, From Lemma (5.2) and $z\in H^2$, $\|\bar z-\bar z_{h}\|_{L^2(\Omega)}\le{\it Ch^2}$, and so $\|\bar z-\bar z_{h}\|_{H^1(\Omega)}\le{\it Ch}$ as our expected convergence rates indicated in Tables 4 and 5. Also, the expected rates have agreed well with the rates for the different densities of the meshes in ^[6]. Also, we can see the stability of the method in Figure 5.

6.2.2.   Numerical results for the advection-diffusion dominated case ($h\gg\epsilon$ where h is mesh size) on the unit square domain

Since $\epsilon$ is too small for this case such as $\epsilon = 10^{-5}$, $\frac{h{|\vec{\beta}|}}{\epsilon} > 1$ which means the advection-diffusion dominated case occurs. The norm of y depends on $\epsilon$ such that $\|\bar y\|_{H^{k+1}(\Omega)}\le\frac{C}{\epsilon^{k+1/2}}$. Since the convergence rate of $\bar q$ depends on data of $\bar y$ from the main result, we do not expect any convergence rate and so this case does not contradict with our main result. Also, the feature of the method shows itself that Dirichlet boundary condition is almost ignored by the method as a result of weak treatment and it does not resolve the layers and causes oscillations on the boundary. It can be seen in Figure 6 and Tables 6 and 7 that some oscillatory solutions and non-convergent rate of q appear on the inflow boundary, caused by non-stabilized terms of boundary edges $E_{h}^{\partial}$ represented by $E_{h}^{-}$ in the bilinear form (4.6) and (4.5), whereas it is stable on both the interior edges $E_{h}^0$ and the stabilized boundary edges $E_{h}^{\partial}$ by the penalty term in the form.

6.3.   $\Omega$ is a diamond shaped domain

By a transformation from the unit square domain to obtain a diamond shaped domain $\Omega$ with $\frac{\pi}{4}$, $\frac{\pi}{8}$ and $\frac{\pi}{10}$ angles, while the angle of the domain is getting smaller, we expect that the error rate is getting close to the predicted optimal error rate.

6.3.1.   Numerical results for the regular case on the diamond shape domain with angles $\pi/4$, $\pi/8$ and $\pi/10$

After the transformation from the unit square domain to obtain a diamond shaped domain $\Omega$ with $\frac{\pi}{4}$, $\frac{\pi}{8}$ and $\frac{\pi}{10}$ angles, we can observe from tables 8–10 that the regularity of the state is reducing sharply close to 1 and that we will obtain the predicted rate i.e., $\|\bar q-\bar q_{h}\|_{L^2(\Gamma)}\le {\it Ch^{1/2}}$ yields $\|\bar y-\bar y_{h}\|_{L^2(\Omega)}\le{\it Ch^1}$ by Theorem (5.7). There are many researches, see ^[6,31,46], which obtained an error estimate for the optimal control of order depends on the largest angle of the boundary polygon. Also, we can see the stable behavior of the method in Figures 7–9.

6.3.2.   Numerical results for the advection-diffusion dominated case on the diamond shape domain with angle $\pi/4$

While the method still works, likewise the frame in the unit square domain, it can be seen in Figure 10 and Table 11 that some oscillatory solutions and non-convergent rate of q appear on the inflow boundary whereas it is stable on the interior edges and the stabilized boundary edges as a result of weak treatment because of not resolving the layers and causing oscillations on the boundary.

7.   Conclusions

In this paper, we consider Dirichlet boundary optimal control problem governed by the advection-diffusion equation and apply the DG methods to the problem. We show some attractive features of the method such as the stable behavior of the SIPG method into the domain of the smoothness and for the advection dominated case except on the boundary as a result of the boundary weak treatments. We have proven that the convergence rate for the SIPG method is optimal in the interior of the general convex domain. However, all convergence rates in numerical examples are higher than predicted by the main result because the predicted order exists for general convex domain, but obtaining the predicted optimal convergence rate depends on the maximal angle of the domain because of the regularity ^[6,36,47], which is an interesting topic for future work. Also, for general polygonal domains and Laplace equations it has been shown ^[6] that

where $p > 2$ depends on the largest angle, and obtaining optimal convergence rates for the $p = 2$ case is another interesting topic for future work.

Acknowledgments

I would like to thank to Prof. Dmitriy Leykekhman, my thesis advisor, for helpful discussions and his advisement on my academic journey.

Conflict of interest

The author declares no conflict of interest.