In this paper, within the so called “neuro-visceral integration model”, it is reviewed the ability of the heart to secrete numerous endocrine mediators, neurotransmitters and substances that regulate the immune function with repercussions on the central nervous system. The heart would also seem to be able to process various information independently, influencing the brain work through the “intrinsic cardiac nervous system” and baroreceptor pathways. In reviewing this matter, further physical mechanisms are also described, including mechanical contractions and deformations, that are involved in the “heart-brain symphony” based on intra-cardiac formation and propagation of blood vortices coupled to electrical signals. The relevance of the role of vorticity of the blood flow in the molecular dynamics and physiological activity is stressed. By resorting to some conceptual and formal aspects of the dissipative quantum model of brain, mechanisms such as the spontaneous breakdown of symmetry in many-body physics, the dynamical formation of long range correlations and their associated Nambu-Goldstone quanta, coherent states and fractal self-similarity are discussed with reference to the heart-brain dialog. Our discussion supports the view that the heart role is more than the one of a muscle responsible of the blood flow. Further related topics such as the formation of aneurysms and vein varices which in our modeling seem to be related to the weakening or loss of vorticity of the blood flow, the role of the recently discovered fluid-filled interstitial structure and the complex network of thick collagen bundles are finally briefly mentioned in the concluding remarks.
1.
Introduction
As described by Francisco Torrent-Guasp [1], and recently reviewed and illustrated [2], the heart can be viewed as a muscle-tube folded into a helix shape: its contraction determines a continuous change in the propeller pitch. The heart as it contracts in systole also rotates producing torsion, which was recognized by both Artistotle and Harvey [3]. A beating heart, with its helical myofiber architecture and twisting-untwisting motion, produces spiraling streams of blood flow [4] that propagates in blood vessels, as described by Leonardo Da Vinci [5] and nowadays visualized with 4D magnetic resonance methods [6].
The change in cardiac volumes, stroke volume and coronary flows with a relaxation-oriented psychological activity have been described in our recent work [7]. In this work, the physical mechanisms that are involved in heart-brain communication are reviewed and few novel considerations are added. Mechanical contractions and deformations and intra-cardiac formation and propagation of blood vortices coupled to electrical signals will be considered. Our discussion rests on a growing body of research indicating that the afferent information processed by the intrinsic cardiac nervous system [8] can influence activity in the fronto-cortical areas [9],[10] and motor cortex, affecting psychological factors, such as attention level, motivation [11], perceptual sensitivity, and emotional processing [12]–[15]. According to the model of neurovisceral integration [9],[16]–[19], the information shared by the heart with the brain may also be coded by rhythmic [20] and electromagnetic patterns [21] which may represent the basis of intuitive-emotional processes [22],[23], awareness and feelings [24],[25], and a rational, detached and “less egocentric” reasoning [26].
In our analysis the formation is considered of physical electromagnetic patterns supporting the net of heart communication with brain and body organs, as described, e.g., by Rahman et al. [27]:
“Heart generates an electromagnetic field which is most powerful and extensive than the magnetic field produced by the brain [28]. It also expands in all direction into the space surrounding the body which can be detected nearby to the individual. Using these magnetic fields, heart communicates with the body organs [29]. The hearts magnetic field is 5000 times stronger than that of the brain magnetic field. The heart field which can be detected like ECG is about 60 times greater in amplitude than the field produced by the brain, spread in each cell of the body. The heart field acts as a carrier wave for information that synchronizes the entire body [28]”.
Such a carrier wave may act as a “waveguide” and underlie the molecular and biochemical heart communication spreading in the whole body (cf. e.g. the quotation by Pribram in section 6 below). It is, on the other hand, a common clinical procedure in intensive care units, when an electroencephalogram [EEG] is needed to document brain death, to record the cardiac electrical signal (which anyhow must be filtered in normal EEGs). Moreover, the connection between heart and brain showed by the research activity about the physiology of these two organs has important implications for the treatment of neurological and cardiovascular diseases [30]. As commented in section 2, it appears that in a disease state the heart and the brain are both affected confirming the strict communication between the two organs. The resulting question of whether cardiovascular and neurologic diseases are two sides of the same coin motivates the discussion in the remaining sections 3–6. Section 3 is focused on the dynamics of the brain functional activity and its dissipative quantum model. In section 4 and 5 heart contractions and the underlying coherent molecular dynamics are discussed. Our efforts are to support that the role of heart is more than the one of a muscle-tube folded into a helix shape [2] determining and sustaining the blood flow. Section 6 and 7 are devoted to further remarks, perspective scenarios, open questions and concluding comments.
2.
In a disease state, the heart and the brain are affected at the same time. The cardiovascular and neurologic diseases are two sides of the same coin?
Below, some evidences, detailed in our previous reviews (with related bibliography) [2],[31]–[33], are summarized.
Central neuropeptides regulate cardiovascular responses to stress: vasopressin, angiotensin II and interleukin-1beta (IL-1 beta) appear to increase the cardiovascular tone whereas oxytocin seems to act in the opposite way [31].
Cardiac arrhythmias [such as atrial fibrillation] and/or congestive heart failure frequently lead to cerebrovascular accidents or transient ischemic attacks. On the other hand, cerebrovascular dysfunction may lead to cardiac rhythm disturbances. For example, in the case of subarachnoid bleeding dramatic electrocardiographic changes [ventricular fibrillation] may occur due to QT-interval prolongation [31]. During a cardiac arrest, the brain shows a peculiar high-frequency coherent electrical activity [31].
Even psychological stress alone can induce cardiac arrhythmias and electrocardiographic T waves' changes [at lower heart rates than observed with exercise]. Furthermore, mental stress can release troponin in blood from myocardiocytes, independently of the presence of coronary atherosclerosis and could lead to the so-called mental stress myocardial ischemia [2].
Panic disorders and strong emotional distress may give rise to fatal arrhythmias with transient left ventricular dysfunction [the so-called “Tako-Tsubo” and “Happy Heart” syndrome] with troponin release from myocardiocytes and symptoms similar to those of myocardial infarction [2]. Amyotrophic lateral sclerosis and several central nervous system disorders can produce a ‘pseudo-infarction’ pattern on the electrocardiogram, with ST-elevation followed by biphasic T and inverted T without any detectable myocardial mechanical abnormality [31].
In case of Brugada syndrome, long QT syndrome, and catecholaminergic polymorphic ventricular tachycardia, the differences in autonomic patterning are critical to explaining sudden death in presence of the same genetic ion channel abnormality since birth. This may be interpreted that the genetic mutation creates the substrate of the arrhythmia, but the autonomic nervous system activity may be a key modulating factor in triggering a sudden adrenergic drive for example during anger, exercise or unexpected acoustic stimuli during rest or sleep. Moreover, patients with long QT syndrome have abnormal electroencephalograms (for more details, please see [31] pages 147–151).
Diabetes mellitus can be complicated by autonomic neuropathy and is a condition with increased cardiovascular mortality. Spinal cord stimulation imparts cardioprotection under neuronally dependent cardiac stress and mitigates transient ischemia-induced myocardial infarction. Moreover, myocardial infarction is followed by an intra- and extra-cardiac neuronal remodelling.
In the case of chronic vascular and congenital heart disease, a peculiar neuronal activity decline can be observed among the major effects of coronary artery bypass surgery. Exercise, with its biomechanical, cardiovascular and nervous stimulations, may prevent or slow down the neurological activity decline in elderly patients with heart failure. It has been demonstrated the strict connection between cerebral activity and cardiorespiratory synchronization and baroreflex control of heart rate. Parkinson's disease could lead to autonomic failure with cardiac and extracardiac sympathetic denervation and orthostatic hypotension. “Catecholamine autotoxicity” plays an important role both in Parkinson and in cardiovascular diseases. Mental stress, activating the sympathetic-adrenal-medullary axis, eliciting the release of catecholamines, determines the release of Danger Associated Molecular Patterns (DAMPs) and the activation of the cardiac immune system [32]. In turn, DAMPs can activate the innate immune response leading to sterile inflammation, which can result in myocarditis and cardiomyopathy, as well as atherosclerosis, even in animal models [2],[32].
Heart failure seems to be a risk factor for Alzheimer's disease. Decreased cerebral blood flow and neurohormonal activation due to heart failure may contribute to the dysfunction of the neurovascular unit and cause an energy crisis in neurons [31]. This leads to the impaired clearance of amyloid-beta and hyperphosphorylation of tau protein, resulting in the formation of amyloid-beta plaques and neurofibrillary tangles. Heart failure seems to relate with dementia being vascular dementia the most common dementia disorder. A common network of genes [and metabolic pathways] is altered both in Alzheimer's disease and myocardial infarction [31].
As already reviewed in details [31], many psychological affections are present in case of neurological and cardiac pathologies. For example, dementia and depression are common findings in Parkinson's and Alzheimer's diseases; depression is an important risk factor for cardiovascular diseases because it causes and in the meantime is worsened by immune dysregulation that in turn is related to atherosclerosis, endothelial dysfunction, coronary artery disease and calcification, myocardial infarction and heart failure. In all the aforementioned neurological and cardiovascular diseases, endothelial dysfunction is present [33].
In summary, in a disease state, the heart and the brain are both affected. They involve physiology, biomolecular activity, psychological responses, etc., as described above. Beyond specific biochemical, physiological and functional correlations in each specific disease, their different nature and origin and their wide manifestation spectrum suggest that the cardiovascular and neurologic diseases might be two sides of the same coin. Such a possibility is of course of great theoretical and practical relevance and motivates our analysis in the following sections. In the next one, the attention is focused on brain functional activity.
3.
The dynamical level underlying the functional activity of the brain
Clinical observations, physiological studies, biochemical analysis are at the basis of the knowledge of body organs and their harmonious functional activity. In full generality, the study of biological systems proceeds indeed according to two main complementary and interconnected “moments” or phases. In the first phase, the system is split into its many components or building blocks and the focus is on the recognition of their properties. The study of the interactions among the components is left to the second phase.
The first phase of the study, although necessary, is not sufficient for the understanding of the “coordinated functioning” of the system components because does not focus on the dynamics ruling their interactions and functional correlations. Scientific knowledge requires the merging of the two research phases in a “unified working scheme”. In brain studies, for example, since the early forties, Karl Lashley introduced the concepts of “mass of excitation” and “general fields of activity” when, based on his laboratory observations, he remarked that “...Here is the dilemma. Nerve impulses are transmitted ...form cell to cell through definite intercellular connections. Yet, all behavior seems to be determined by masses of excitation...within general fields of activity, without regard to particular nerve cells... What sort of nervous organization might be capable of responding to a pattern of excitation without limited specialized path of conduction? The problem is almost universal in the activity of the nervous system.” [34] (see also [35] p.9).
Lashley's dilemma points to the fact that the understanding of the observed coordinated neural cell activity is only possible by integrating the two research phases mentioned above. The second phase can in fact account for what is out of reach of the first one, namely the dynamical emergence of collective modes or waves spanning the large assemblies of the system individual components, the “mass of excitation” and “general fields of activity” in Lashley's words.
Lashley's laboratory observations triggered an intense research activity. From one side, for example, Karl Pribram introduced the hypothesis that a “coherent” dynamic could be at the basis of some characteristic properties of memory. By resorting to the results reached in laser physics, he proposed that a phenomenon similar to the hologram formation in quantum optics could be at work in the brain [35]. On the other side, Walter J. Freeman proposed an extended quantitative analysis of EEG signal pointing to the understanding of the neural interaction and transmission by using tools typical of nonlinear dynamical systems, laying the basis for modern neurodynamics and mass action in the nervous system [36],[37]. Of course, the work by these two neuroscientists was made possible by the research activity of many other scientists and by the progress in biology, experimental laboratory machinery and tools, statistical methods in data analysis, etc.
Moreover, taking advantage of the progress in condensed matter and elementary particle physics, Ricciardi and Umezawa proposed in 1967 to apply the body of knowledge of many-body physics to the study the brain [38].
In many-body physics, the merging of the study of the individual properties of the elementary matter constituents, from one side, and of their mutual interactions and correlations, from the other side, was, indeed, and it is, very successful, both from the theoretical understanding and the practical applications standpoints [39]–[41].
For example, the experimentally successful quantum field theory (QFT) description of a magnet, a crystal, or the elementary particle world in high energy physics, is not made in terms of the elementary constituents alone. To be specific, consider the magnet. The elementary constituents carrying a magnetic dipole (e.g. electrons) are the magnet building blocks, but they are not sufficient to describe its macroscopic properties, such as e.g., its magnetization. Other dynamically generated components, must be considered to describe the magnet behavior. These dynamically generated components are the spin waves and the quanta or particles to them associated, the magnons [40],[41].
Magnons behave as real components of the system when considered in its “functional activity”. They are observed “within the magnet” utilizing neutron scattering. When the magnet is split into its components (a “dead” magnet), magnons disappear, they are not found among the magnet building blocks. They do not exist anymore. In the “functioning” magnet, i.e. when magnetization is not zero (below a critical temperature TC), the observation of magnons quanta signal the presence of collective modes within the magnet: the spin waves, indeed, spanning the whole system (in quantum theory, according to the de Broglie relation, to any wave of wave-length λ is associated a quantum or particle whose momentum is inversely proportional to λ, and vice-versa). Considering the crystal as another example, one has the elastic waves and their associated quanta are the phonons [40],[41].
A general theorem in QFT, widely confirmed by experiments, states that the coordinated (‘functional’) activity of the elementary constituents of a system is dynamically generated by long-range correlation waves (the Goldstone theorem [39]–[41]). These correlation waves are responsible for the ordering of the components and span the system or domains of infinitely larger size than the individual component sizes. The associated quanta (called the Nambu-Goldstone (NG) boson quanta or particles) are massless in order to propagate without inertia over the large ordered domains. In the magnet example, among its (macroscopic) “functional activities” there is the one of getting oriented “as a whole” by an external magnetic field (like the compass needle gets oriented by the earth magnetic field). Such a macroscopic behavior is due to the magnetization, which is called “order parameter” since it is a measure of the ordering of the elementary constituents (i.e. a measure of the average difference between the number of elementary magnetic dipoles pointing along a given direction and the number of those pointing along the opposite direction). In the case of the crystal, one of the “functional activities” is, e.g., the crystal stiffness, which is a (whole) system property. The order parameter is the density which depends on the crystal lattice length and specific crystal form, thus on the spatial ordering of the constituent atoms.
Within convenient boundary conditions, e.g. below critical temperatures TC and for large number N of the system constituents, the Goldstone theorem shows that long-range correlations waves are generated by the dynamical process of the spontaneous breakdown of symmetry (SBS), by which, due to an external triggering input or stimulus, the system inner dynamics enters in an energetically favorable state (least energy state or ground state, also called vacuum state) where the ordering of the system components is generated and substitutes their uncorrelated (disordered, indeed) behavior. In the example of the elementary magnetic dipoles, they can be oriented with equal probability in any direction and oscillate out of phase (not at unison) in a state with spherical rotational symmetry (rotations around three orthogonal axes). This is the symmetric or disordered state. Dipoles can be arbitrarily rotated and such a change does not have observable effects on the state. This is not what happens in the magnet, where a preferred dipole orientation exists for the majority of the dipoles and then the spherical rotational symmetry is broken. The dipole ordering in the magnet is, therefore, lack of the spherical rotational symmetry. In the crystal example, the symmetry under continuous space translation is broken and the lattice order arises [39]–[41].
In conclusion, SBS generates the long-range correlation waves (NG collective modes) within the system, which is also expressed by saying that the NG quanta are condensed in the system ground state. The formalism of QFT provides the quantitative description of the SBS phenomenon with extraordinary good prediction and fitting of experimental observations [40],[41].
Ricciardi and Umezawa (RU) proposed to apply the SBS mechanism to model the brain, in particular, the processes of memory recording and recalling [38],[42]. Umezawa observed [43]:
“In any material in condensed matter physics any particular information is carried by certain ordered pattern maintained by certain long range correlation mediated by massless quanta. It looked to me that this is the only way to memorize some information; memory is a printed pattern of order supported by long range correlations...”. Moreover, “...at which level should the brain be studied and described? In other words, is it essential to know the behavior in time of any single neuron in order to understand the behavior of natural brains? Probably the answer is negative. The behavior of any single neuron should not be significant for the functioning of the whole brain, otherwise higher and higher degree of malfunctioning should he observed,..” [38] (in full agreement with Lashely remarks, cf. above).
An input “similar” to the one that produced the recording of one specific memory may excite NG quanta out of the vacuum condensate. In the RU model, such excited NG quanta (or correlation waves) are (“consciously”) felt by the brain as “recalled memory” [38].
One shortcoming of the RU model is the extremely reduced memory capacity: recording of a new memory would induce a new NG boson condensate in the vacuum state, thus cancelling the previously recorded memory (overprinting). To enlarge the memory capacity, by observing that the brain is open to its environment (i.e. it is a dissipative system), the RU model has been extended to the “dissipative quantum model of brain” [44]. In fact, in a dissipative system, all the infinitely many vacuum states existing in QFT (each vacuum state is orthogonal to the other ones) may be accessed by the system in its time evolution. In the dissipative model of the brain, each vacuum may be then used for the recording a different memory, not interfering with other memories recorded in other vacua. The manifold of the memory states constitutes the “memory space”.
Water molecules, that constitute more than 90% in number among the brain molecular constituents (about 80% in weight), and other constituent biomolecules present in the brain are characterized by their electric dipole moment. They constitute the bath in which neural cells, their dendrites, axons, etc., are embedded. Long-range correlations among molecular dipoles would, therefore, facilitate and sustain neural cell organization, both in their permanent (anatomical) interaction net and in their dynamically changeable correlation network. The quantum degrees of freedom described by the QFT formalism are the ones of the molecular dipole vibrational field. Neural cells and their biological components are instead considered to be classical objects. This is a distinctive difference between the dissipative quantum model of the brain and other quantum brain models existing in the literature.
In the dissipative quantum model of the brain, the symmetry that is broken by the external input is the spherical rotational molecular dipole symmetry and the NG quanta are the dipole waves quanta [dwq].
The dissipative model accounts for many observed features of the brain functional activity, which for brevity are not discussed here. A full account of the model and its QFT formalism may be found in the literature [44]–[46]. However, here it has to be observed that the dissipative character of the brain dynamics requires to consider in the model also the environment (“the world”) in which the subject (the brain) is embedded. Since at the equilibrium the fluxes of energy, information, etc. between the brain and its environment need to be balanced [relative, e.g., to the brain, fluxes “in” must be balanced with fluxes “out”], the brain perceives the in-fluxes as the “time-reversed images” of the out-fluxes (the exchange in ↔ out is formally obtained by changing the sign of time variable t ↔ - t). The brain thus perceives its environment as its own image in the “time-mirror”, its Double [47]–[50]. Since the environment “as seen” by the subject (the brain) carries the subject's standpoint and values, the continual dynamic reciprocal relation, sometimes even conflictual reciprocal relation, subject/Double defines the subject (dynamic) identity. It has been proposed that consciousness resides in the dialog of the subject with his Double [47]–[50].
Since all body's flows and chemical reactions take place in water, by extending our considerations to a general frame, an active protagonist of cell biology [51]–[53] can be conceived as a set of correlated-in-phase molecular dipoles, tuned by external inputs and endogenous electromagnetic (em) fields. The associated dipole correlation waves, within their frequency spectrum, govern the interaction of biomolecules, cells and other biological units embedded in the water bath [45],[51],[52].
Before closing this section let us remark that contrarily to some “believes”, experimental observations and explicit calculations show that SBS and the consequent coherent NG condensation is a quite robust phenomenon. It is observed in a wide range of temperatures, from thousands of degrees to very low temperature. For example, the melting point (loss of crystal ordering and symmetry restoration) of a diamond is at TC = 3547 °C (3820 K), at atmospheric pressure. In the absence of oxygen, its melting point is about 4027 °C (4300.15 K). The cobalt magnetization is lost at 1075 °C (1348.15 K). For iron, magnetization loss is at 770 °C (1043.15 K), the kitchen salt (sodium chloride crystal) melts at 804 °C (1077.15 K). The transition of phase is observed at very low temperature (below −252 °C (21.15 K)) in superconductors containing compounds of niobium, at −153 °C (120.15 K) for copper and bismuth superconductor compounds. When the proper framework of QFT is used coherence is thus a quite stable property of matter, including living matter, as it has been observed, e.g., in photosynthesis studies [54].
In the following, the dynamics underlying the functional activity of the heart and the communication between the heart and brain are considered.
4.
The dynamical level underlying the functional activity of the heart
As observed in section 1, our effort in this work is to provide arguments supporting that the role of heart is more than the one of a muscle-tube folded into a helix shape [2] whose contraction and beating determine and sustain the blood flow.
Let's recall that already Aristotle and Harvey [3] realized that heart as it contracts in systole also rotates in torsion with twisting-untwisting motion due to its helical myofibers, thus triggering vorticity in the blood flow. Leonardo Da Vinci [5] observed that a spiraling stream of blood flow [4] propagates in blood vessels [55], as today visualized with 4D magnetic resonance methods [6].
Despite common sense, the brain does not seem hierarchically “superior” to the heart, nor does command it. The helical heart, if adequately nourished, beats alone, regardless of the brain. Moreover, from embryology it is known that the heart begins to beat before the brain is formed. A transplanted heart is not connected to the host nervous system, but can immediately satisfy the physiological demands of its new host [56]. The heart rate is predominantly triggered by the rate of discharge of its dominating pacemaker (mainly the sinus atrial (SA) node and the atrium-ventricular (AV) node) whose action is fine-tuned in vivo from the balance between the sympathetic and parasympathetic nervous systems. The higher heart rate variability, the better heart health.
Like the gastrointestinal system, the heart possesses an extensive neuronal network to be characterized as its own “little brain” [57]. The so-called “intrinsic cardiac nervous system” is connected to intrathoracic nervous ganglia, extra-thoracic ganglions, spinal cord and cortical nerve centers. Cardiac activity is not regulated only at the central level but is predominantly established by beat-to-beat neuro-hormonal loops within autonomous intrathoracic nerve centers [57]. The emerging picture is that the heart represents a sophisticated endocrine and immune station capable of receiving and releasing in the bloodstream complex hormonal signals, cytokines and microvesicles with which to refine its dialog with the brain and the whole body [2],[31]–[33].
Therefore, also the heart can be modelled as a physical system open to its environment, namely a dissipative system. Such a characterizing dynamical feature is of crucial relevance in modelling the heart functional activity.
The anatomical and physiological details of the intrinsic cardiovascular system and its connections with the brainstem, the hypothalamus, thalamus, the amygdala, and the cerebral cortex can be found in two of our recent reviews [2]–[31].
Non-Newtonian fluid models and numerical simulations, or also combined use of Newtonian and non-Newtonian modeling [58], do not provide yet a complete account for all the properties of the blood flow and its vorticity.
We remark that plasmatic water is about 55% of blood volume and it constitutes the bath where other blood components are embedded. As observed in the previous section, water molecules are characterized by their electric dipole moments. The basic associated symmetry is the dipole spherical rotational symmetry where no preferred rotation direction exists. However, it gets broken by the heart systole contraction and rotation motion which induces the vorticity in the flow, thus singling out the preferred direction associated with the vortex core. The general SBS mechanism discussed in the previous section then may apply, with consequent generation of long-range dipole correlations waves spanning the blood flow. Moreover, the heart twisting-untwisting motion acts not only as symmetry breaking trigger, but introduces also a topologically non-trivial structure in the SBS dynamics, indeed the topological singularity at the vortex core.
The formation of vortices with their singularity at the core is well studied in condensed matter physics [40],[41],[59]–[63]. It is a problem of great theoretical and applicative interest and relevance. Starting from the microscopic quantum degrees of freedom of the molecular dipole vibrational field, one may derive, by use, e.g. of time-dependent-Ginzburg-Landau equation, the vortex equation associated with the non-homogeneous condensation of NG dwq. Such a non-homogeneous condensation describes the vortex singularity at r = 0, e.g., in the z direction along the vortex core, of radius r2 = x2 + y2. In stationary case, the boson condensation function is f(x,y) = arctan(y/x). For brevity, the detailed mathematical formalism is not reported here. It can be easily found in refs. [59]–[62] and [63], although for applications in different contexts. The macroscopic vortex flow is described as the envelope of the non-homogeneous, topologically non-trivial NG boson condensation and its observable properties are derived from the microscopic molecular dynamics. The Navier Stokes equation leading to a time-dependent (non-Newtonian) viscosity is also related to the microscopic quantum dipole vibrational field. The role of the free energy minimization at each stationary stage is made explicit.
Another important result is the derivation of Lorentz force acting on ions and charged blood corpuscular components [63]. Their motion appears thus dynamically controlled, they are not just passively carried in the current of the blood flow. The blood pH is thus similarly controlled by the microscopic dynamics.
The flow vorticity is “mechanically” caused at the heart level by the heart torsion motion. Then it becomes “the characteristic regime” of blood flow, since, once originally triggered by the heart contraction, it persists as a result of the microscopic coherent, topologically non-trivial condensation process sustained by the dipole correlation dynamics. As mentioned, the condensation function f(x,y,t) describes indeed the space-time dependent condensation envelope with the vortex singularity at r = 0.
The vorticity of blood flow is dynamically protected from decaying by the coherence and by the conservation of the topological number or charge associated to the singularity, called the winding number n (n denotes the degree of vorticity, i.e. the number of “turns” around the line at r = 0, and labels the homotopy class to which the n-vortex belongs). In the absence of perturbing actions, the conservation of topological charges (numbers) is a strict one. Thus, in the absence of spurious forces or impurities, the vorticity is predicted to be preserved, which is confirmed by observations showing that the blood flow vorticity persists for a long time and far from the heart, through the many arterial ramifications and branches, reaching capillaries and returning to the heart from veins [64]–[68] circulating throughout the body. Moreover, consistently with the conservation law of the topological charge, the singularity of the condensation function f(x,y,t) guaranties that the condensation cannot be ‘washed away’ (the technical word is ‘gauged away’) without drastic changes in the system behavior). This shows how important is the role played by the vorticity of the blood flow even for the general stability of the system, apart, of course, from the stability of specific ‘local’ functional and biomolecular activity.
On the other hand, the coherence of the dynamics of the blood flow ensures that the “in-phase” correlation of the dipole vibrational fields is sustained in time and space in all the districts reached by the blood flow. Of course, counteracting forces, due to external or endogenous agents, may affect coherence, which will turn in some form of physiological and/or biomolecular discomfort or pathology.
In the healthy state, the propagation of coherent correlation waves, tuned with neuronal coherent correlation waves (see the discussion on the dissipative model of the brain in section 3), is the prerequisite for the heart and brain dialog and communications mentioned above. Since the correlations of the dipole vibrational fields are phase-correlations, and phase velocity is not limited by the speed of light, the time needed to establish coherence does not need to be larger than some minimum time. This may account for the immediateness of the heart-brain system response to perceptual experiences. Of course, this does not exclude delays due to biochemical activity triggered by the perception.
One further element connecting the molecular dipole correlation and the vortex flow structure arises from the fact that the electromagnetic (em) field due to external or endogenous agents (e.g. due to charge distributions in the system, ions, molecular dipole deformations and oscillations, etc.) acquires a mass M, whose square is proportional to the polarization density P(x,t) (generated by the dipole vibrational fields as a consequence of the SBS), with M(P) = 0 at P = 0. According to general mechanism and formalism in QFT (called the Anderson-Higgs-Kibble (AHK) mechanism [59]–[63],[69],[70]), the em field gets confined, in a self-focusing or filamentary propagation, within the core of the vortex blood flow. An em filamentary network is thus generated, participating in the complex heart-brain communication and to the perceptual experiences of the body open to its environment.
The radius d of the channel, corresponding to the core of the vortex, through which the em propagates is related to the mass of the field as d = h /2πcM, for non-zero M and non-zero P [52]. h is the Planck constant, and c the speed of light. The strict interdependence is thus seen to exist between the mass of the em field and the size of the core of the blood vortex flow and that they are controlled in definitive by the polarization density P(x,t), which is a measure of the coherence of the dipole wave condensate. The picture emerging from our discussion is the one of complex equilibrium between the body and its environment and the heart-brain correlation.
Remarkably, the SBS formalism also predicts that the size of the vortex core goes as e±γt, with t the time [47],[48],[71]. According to what just observed above, the shrinking of the vortex core signals that long-range correlation (ordering) is prevailing. On the contrary, its enlargement denotes that local correlations (disorder) prevail. Functional anomalies and pathologies appear in the extreme cases of both the possibilities.
Loss of vorticity means a transition to a non-turbulent flow. The presence of the vortex core and its dynamical shrinking or enlarging constitute an important degree of freedom for the vessel system, defending it from important “malfunctionings” at many physiological and biochemical levels. The dynamical control of the vortex core transverse dimension may counter-act, by enlargements, against the vessel closure, due, e.g., to an increase of vessel rigidity or other reasons. Also, flow vorticity provides defense against unwanted anomalous vessel enlargements due to non-vorticose flow overloads.
As observed above, the em field is confined within the vortex core of the blood flow. This means that there is a transverse field gradient on the vortex core boundary which acts on molecular agammaegates, blood cells and other corpuscular components in the surrounding blood flow. The transverse field gradient force is shown to be a selective (frequency resonant) force, able to attract these corpuscular objects in the flowing blood near the vortex core or to repeal them far from it, in regions closer to the vessel walls, depending on the sign of differences between the frequency of the corpuscular object and the em field frequency. In these processes of attraction and repulsion, the same em field frequency is affected by the changes in the corpuscular densities in the blood, with the result of a high nonlinearity of the active interactions. Moreover, the presence of the non-zero mass of the confined em field also implies the presence of a longitudinal force which contributes in “keeping open” the vortex core, counter-acting against unwanted shrinking agents, internal or from the outside environment.
The mentioned possibilities of shrinking of the vortex core might produce the “squeezing out” of the em field when it has too much week intensity. Similarly, a stronger em field might destroy the surrounding vortex (the condensed envelope of dwq). The intermediate situation between these two contrasting extremes is the one of the equilibrium where the self-focusing em field propagation occurs, as described above.
In section 7 a comment is presented on the vorticity of the blood flow and the em filamentary propagation in connection with unwanted molecular deposits on the vessel walls and on the formation of aneurism and vessel varices, clearly important subjects from the standpoint of therapeutic applications.
The persistence of such a “healthy” dynamical equilibrium is characterized by the topological singularity at r = 0. Accordingly, related to the topological winding number n, a fractal self-similarity exists [49],[63],[69], so that the generalized viscosity ρ(t)n = ρ0nendθ, with d the fractal dimension, can be introduced. Consistently with our discussion on the microscopic coherent structure of the NG condensate, the fractal self-similarity is, in fact, isomorph to a deformed coherent state, with the deformation parameter controlled by the fractal dimension [49],[63],[69]. The topological characterization of the dynamics also leads us to consider the expression for the winding number n in term of the gradient of the boson condensation function f(x,y): ∮∇f·dl = 2πn, with integer n and the integration performed along the closed circle [0,2π].
Such an expression provides the magnetic flux quantization given the relationship between the gradient of f(x,y) and the magnetic field [59]–[62],[72]. This suggests to us a possible link with the observed magnetic field referred to by Rahman et al. [27] quoted in the Introduction section.
In conclusion, the pieces of evidence reported so far show that the heart-brain correlation plays a multidimensional role that is central to the normative functioning of the body. Central to the heart functional activity is the triggering and rhythmic reinforcing of the vortex blood flow in the left ventricle. The consequent SBS dynamically produces the coherent dynamics sustaining the vortex blood flow in the body and tuning the heart activity with the brain coherent neural dynamics. In the following section, the heart muscle contractions and its relation with microscopic coherent dynamics are discussed.
5.
Coherent biomolecular dynamics underlying heart muscle contractions
Self-oscillations are ubiquitous in nature, in particular in biological systems. These exhibit processes regulated by self-oscillations which very often are traced back to glycolytic oscillators. The study of self-oscillations is generally aimed at finding simple and unifying basic mechanisms possibly explaining complex behaviors observed at a macroscopic level starting from cell properties. Heartbeat due to its biological and clinical relevance is surely one of the most studied cyclic behavior amenable to basic self-oscillations.
Many studies have been focused on relevant aspects of heart self-oscillations, ranging from the “master” oscillator regime and the sinoatrial node (the natural pacemaker) to the heart macroscopic electric activity measured using electrocardiogram (ECG) monitoring. The electric activity is considered to be the basic agent responsible for producing observed heart self-oscillations. As for muscles in general, also the cardiac muscle contraction is modelled as being generated by the exchange between cells of charged ions, such as Na+, K+, Ca2+, Cl+, etc., ruled by the Hodgkin-Huxley equations.
Although it appears that the electric heart activity is due to the ionic exchange between the two sides of ventricular myocytes, the clear understanding of the quantitative connection of this microscopic level with the (macroscopic) functional ECG level is still lacking.
The observation methodologies and their specific experimental features are in the two cases quite different, namely when looking at glycolytic oscillators one experiments on and observes the biomolecular processes at the cellular level, while at macroscopic level one makes only global observations of the heart activity of the patients, constructing statistics with many of such observations and/or comparing a variety of patients. In any case, transduction of electric field oscillations from the microscopic level to the (mechanical) muscle heart contractions and vice-versa is already a very complex problem to solve (usually, the mechanical behavior is associated to the basic kinetic oscillations, i.e. to the ionic motion for the heart). Then, one may conclude that, firmly stated and recognized the relevance of the electric activity and the study of ECG signals, nevertheless the direct study of muscle contractions, mechanical deformations and oscillations is of great interest (cf. e.g. the role played by the systole contraction producing torsion discussed in previous sections). In this connection, it has to be recalled that the old, widely spread out, diagnostic analysis through auscultation-palpation is focused on these mechanical oscillations. Undeniably, trained physicians can make refined and reliable diagnosis by resorting to these direct auscultation-palpation observations.
As mentioned, observations of mechanical oscillations, as well as the electric activity, can contribute to giving information about the transition mechanism between macro-micro levels. By assuming such a standpoint, in this section the results are reviewed which are derived from a set of measurements [73] of the mechanical vibrations of the chest in the sites typically considered by physicians for the heartbeat analysis. These vibrations were measured by using the Laser Doppler Vibrometry (LDV) and their analysis leads us to recognize coherent dynamical regimes at the basic cellular biomolecular level.
LDV cardiovascular signals have been already used as biometric markers for dynamic physiological behaviors, also in comparative studies concerining conventional analysis and methodologies. The carotid pulse has turned out to be a particularly good marker and LDV techniques have been found much useful in the study of cardiac arrhythmia [74],[75].
Vibrocardiography (VCG) is based on LVD. It is a non-invasive, non-contact observational technique displaying accuracy (1%), high resolution (1 nm) and a high sampling rate. The optical videocardiography (OVC), used for the heart rate (HR) monitoring and the heart rate variability (HRV) [74],[75], has been also used to measure the chest wall and trachea mechanic vibrations [76],[77]. Due to their high sensibility and dense sampling, LDV signals contain information on a large range of space-time parameters, with high-resolution power. For example, LDV measurements can discriminate between chest oscillations due to breathing, so to detect general self-oscillating effects at the macroscopic scale originating from the complex circulation/respiration interactive apparatus. On the other hand, LDV signals contain information on the heart muscle activity as a whole, so to provide comparative insights for traditional physician observations by auscultation-palpation techniques.
In the following, a summary of our measurements is reported. A full account is given in ref. [73]. All the measurements were done in the anechoic chamber of the acoustic laboratory of Salerno University (Italy), which is compliant with UNI EN ISO 3745 in the range frequency 80Hz-20kHz.
The mechanical oscillations (velocity) along the chest and the standard ECG field of fifteen male volunteers and eighteen females volunteers were synchronously measured. The following instrumentations were used: one single-point laser Doppler vibrometers Polytec Laser (PDV-100): frequency band acquisition up to 20KHz, full-scale ± 4V, sensitivity 5 mm s V; the real-time analyzer SoundBook MK2-Expander, 8 channels, sampling frequency 25600 Hz; and the portable ECG device.
Both sensors (laser and ECG) were connected to two channels of the Soundbook acquisition board to obtain synchronous measures. The mechanic oscillations of the 4 pericardial areas were measured using the laser: 1. Aortic region (between the 2nd and 3rd intercostal spaces at the right sternal border) (RUSB right upper sternal border). 2. Pulmonic region (between the 2nd and 3rd intercostal spaces at the left sternal border) (LUSB left upper sternal border). 3. Tricuspid region (between the 3rd, 4th, 5th, and 6th intercostal spaces at the left sternal border) (LLSB left lower sternal border). 4. Mitral region (near the apex of the heart between the 5th and 6th intercostal spaces in the mid-clavicular line, apex of the heart).
The four pericardial areas relate to the heart sounds and can detect various abnormalities in the heart such as the valve stenosis or incompetence which are diagnostic for many diseases in the cardiovascular system.
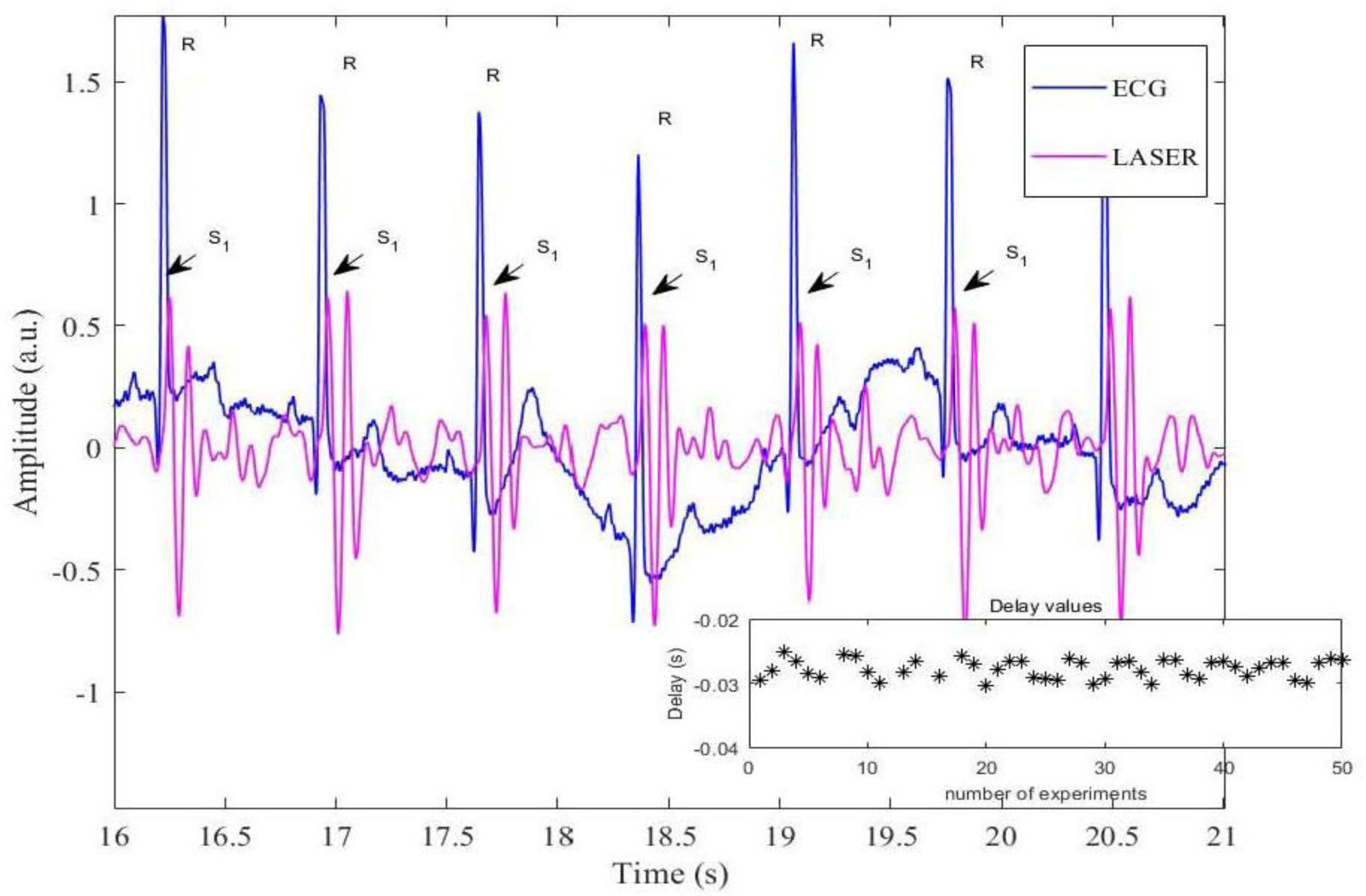
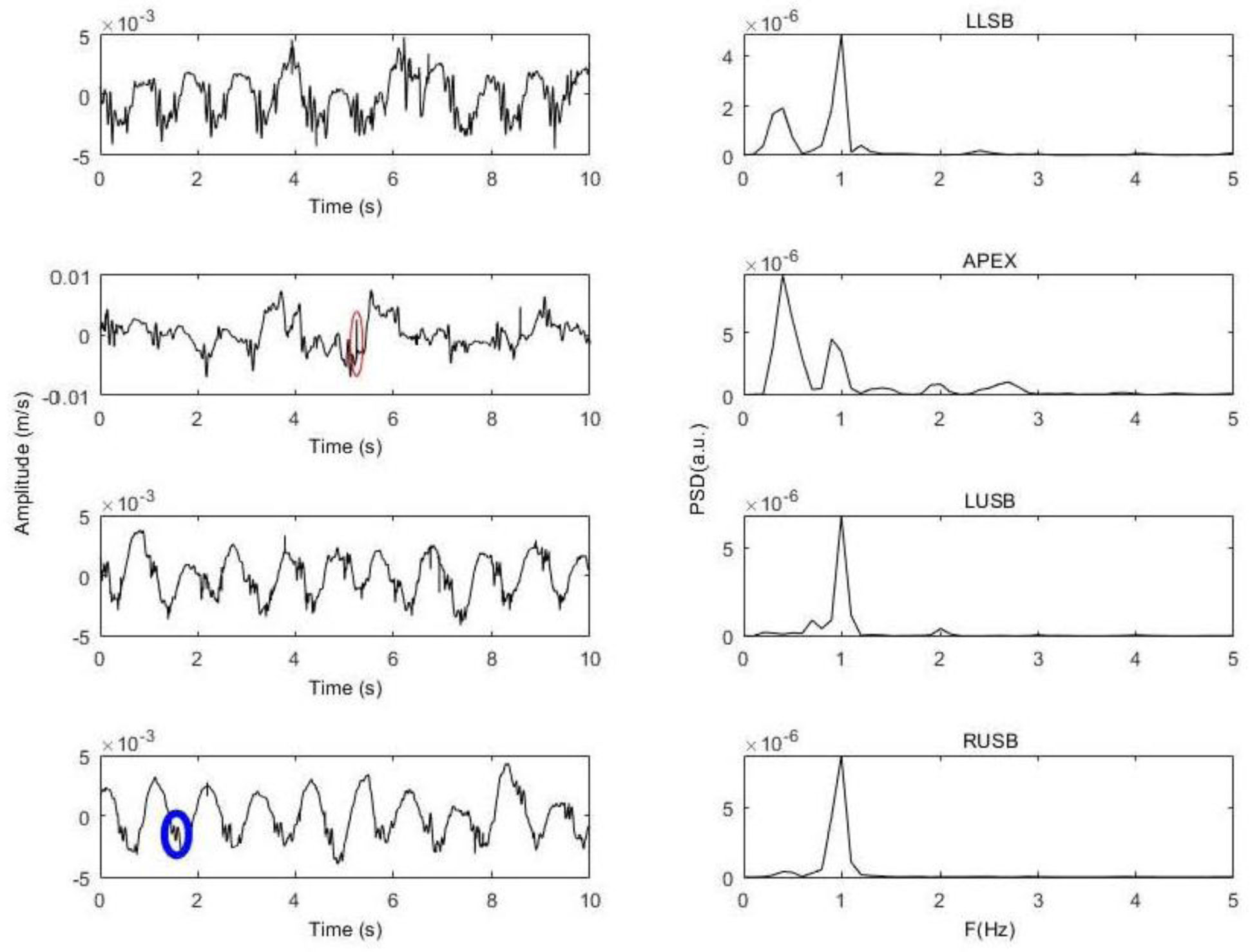
An example of mechanical signals together with the relative spectral content is shown in Figure 1. It was acquired at the selected points by PDV 100 from a 65 years old man. The mechanical vibrations reflect the contributions of both blood pressure and respiration effects together with meaningful information about the cardiac activity. The dominant contribution is relative to the periodicity of 1s, which is the inter-time between two successive heartbeats; the respiration effects are instead on the scale of a few seconds (see the Figure 1 caption). A typical problem in adopting LDV is the presence of the speckle noise due to a splitting of the beam laser because of a non-planar surface. To overcome this problem, it was used a reflecting strip on the skin of the thorax of each subject just focusing the beam. The speckle noise is circled in red in Figure 1. To reduce this effect, the signals were pass-band filtered in the range 3–30 Hz; the results with the power spectral densities are in Figure 2. Characteristic peaks in the range 9–16 Hz, the first (S1) and second (S2) heart sounds are evident.
The superposition of the synchronous acquisitions of both LDV and ECG traces is reported in Figure 3. LDV signals contain all the information held in the ECG, such as R wave and the heart rate, and show more information than ECG, more complex waveforms than ECG and appear to be self-sustained oscillating signals. The first maximum in the mechanical vibration (S1), which corresponds to the aortic valve closure, follows the maximum in ECG (R) with a time delay of about 0.03s, corresponding to the pre-ejection period (PEP) [78]. This delay is estimated in Figure 3. As it can be seen, its variation follows the respiration activity, i.e. it varies over a minimum and a maximum in a lapse of 3.5 s, considering each experiment lasting 0.8 s (similarly, Desjardins et al. [79] calculated a blood-pulse waveform by LDV).
Additional information is obtained by analyzing the basic components present in the time series by applying the Independent Component Analysis (ICA) [80]. It is an entropy-based technique, which can find underlying components [sources] from multivariate statistical data based on their statistical independence. The latter is evaluated by using fourth-order statistical properties. ICA has been already successfully applied to a variety of experimental signals such as in the field of volcano seismology and oceanography [81]–[84].
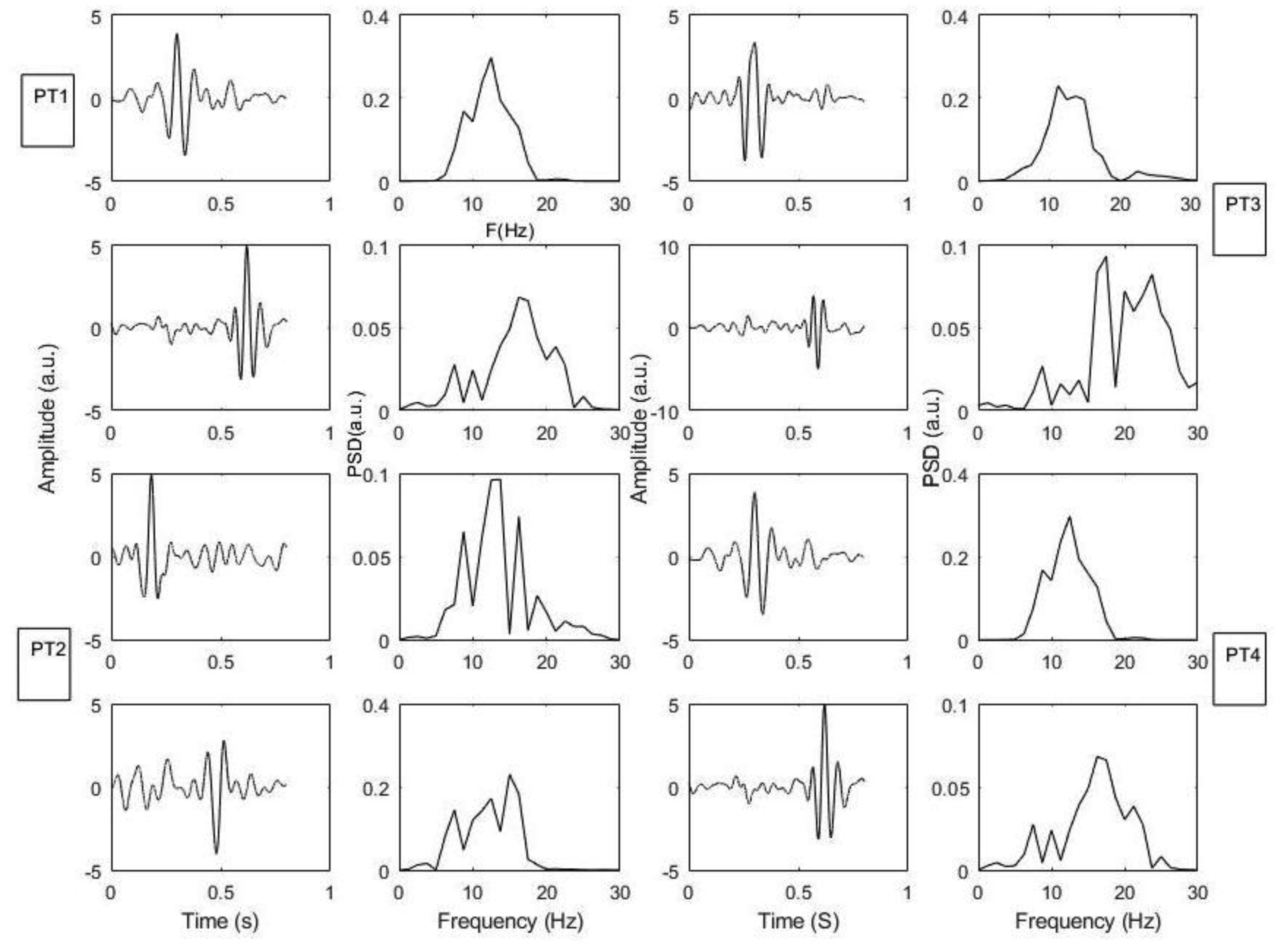
The application of ICA specifically shows that mechanical signals can be decomposed into two components in all the cases (Figure 4).
Our results show that two separated signals in LDV give information about two dynamical modes of the heart, i.e. the rotational and longitudinal modes, with dominant frequencies at 12 and 15 Hz respectively. They are independent modes, separate in time and lay in separate two-dimensional phase spaces. This allows performing the study of each mode separately, which can be crucial in prompt diagnosis of specific anomalies and cardiac diseases [85].
Interesting results come from the analysis of the spectrum on a log-log scale because it reveals both periodic structures and scaling laws.
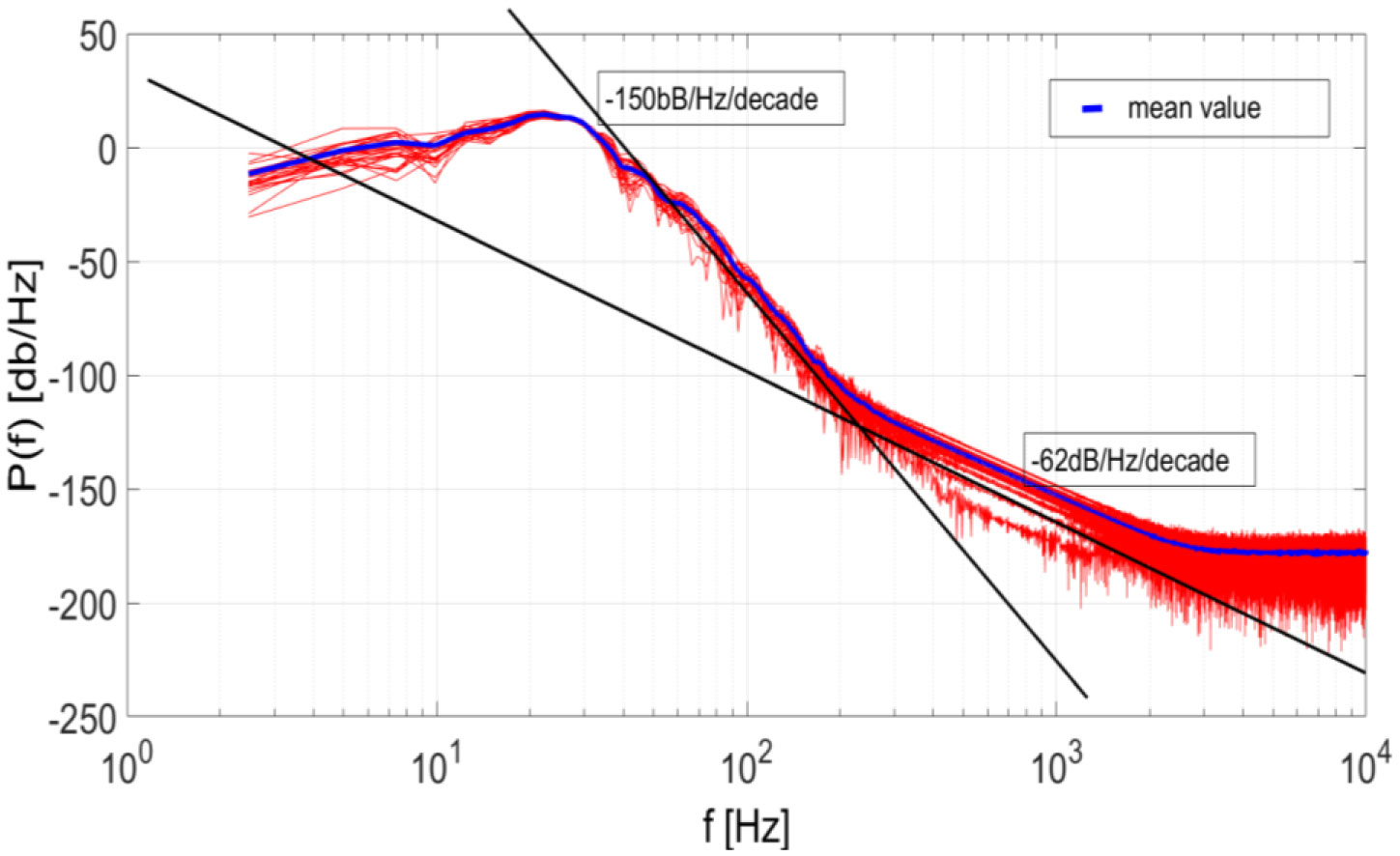
The power spectra in dB/Hz are reported in red in Figure 5. They are relative to 100 mechanical traces (having filtered out the frequencies associated with the breath) and superposed. The traces were acquired at one of the four auscultation points for 0.8 s each. A “periodic” structure in correspondence of the maximum (about 10–30 Hz) and a roll-off in two distinct regions of the spectra were recognized. Specifically, in the frequency range 60–250 Hz there is a first power-law (scaling law) behavior with an estimated decreasing rate of 150 dB/Hz/decade. From 250 to 2000 Hz there is a second power-law with an estimated decreasing rate of 62 dB/Hz/decade, i.e. about a half of the first power law decreasing rate behavior. By using the Grassberger e Procaccia method (an approximate box-counting method), over the trace of 0.8 s the scaling exponent appears to be equal to 1.7 and 0.8.
The two different power laws could denote two different coherent regimes of the microscopic activity. Because of the isomorphism between self-similar fractal structures and deformed coherent states (mentioned in the previous section, see also [86]), the log-log plots in the two frequency ranges in Figure 5 show indeed that two dynamical coherent regimes exist that denote long-range correlation modes at microscopic levels.
In conclusion, the existence of these two linear log-log plots suggests that the heartbeat and its contraction activity are ruled by a coherent basic dynamics at the microscopic level. The “syntony” of the coherent dynamics in the body, which amounts to the “tuning” within a common frequency band of the correlation waves of the different body “districts” and organs, appears to be the prerequisite for the healthy biomolecular and physiological activity.
6.
Perspective scenarios and open questions
The features of the interplay between heart and brain discussed in previous sections have been intuitively perceived since a long time in the mankind history. Let's limit ourselves to mention only one among the many available sources, the Shabaka stone of the VIII-VII century BCE (at British Museum). It is written on it: “[What] the eyes see, hear the ears and sniff the nose are sent to the heart and this brings out all understanding. The language thus repeats the thought of the heart”.
In recent times, Karl Pribram, for example, writes [35]:
“...At the same time, the endogenous processes in each of the other organs, structures, and systems, including those at the micro-scale of cells and membranes, also generate patterns of dynamic activity. These patterns of dynamic activity radiate out into the body's internal environment as energy oscillations, and they interact with the energy waves from the heart and to some degree with the energy waves of other organs and structures. In each of these interactions, the energy waves encode the features of the objects and their dynamic activity as interference patterns”.
As already said, heart and brain are dissipative systems, open to their environment. This means that the heart-brain “system” is in interaction and correlation with other body organs and the whole “external” environment in which the body is embedded. Therefore, the analysis made in neuroscience concerning the brain perceptual experience, its elaboration and the action-perception cycle underlying the functional brain activity in the relation with its operating and “being-in-the-world” may be extended with convenient necessary changes to the interaction of the heart-brain system with the environment. In this way heart, and not only heart, participates in a continuous feedback-action-feedback activity with and within the environment, with the regulation of movements, emotions, physiological changes. In the dissipative quantum model of the brain, it has been proposed that the act of consciousness resides indeed in such an unavoidable dialog with the subject Double. The Double is indeed the mirror (in time) image of the subject depicting the world as seen, perceived and understood by the subject [44]–[46],[50]. The heart, not just the brain, appears thus to be involved in the dynamic process of the self mirroring in the Double in a continual dialogical relation.
Based on our discussion in the previous sections, the meaningfulness appears of the common way of saying that every human being “speaks within himself” constantly in front of the events he experiences, namely he speaks with his Double. The words he pronounces, expressing his relationship with reality, precisely reflect his personality [87] and in fact, it has been recently described [87] how a subjective change in the use of language can bring about the biochemical changes and vice-versa. This leads us also to conclude that psychic activity and its precise language could have a biological impact on specific diseases and therapies [87]. In addition to the data collected “in-vivo”, it has been demonstrated in an in-vitro model how some sound vibrations can directly influence cell growth, structure and behavior [88]. The problem then arises whether the subject response to experienced events is adaptive or maladaptive (vital or mortal) for his own well-being, psychic and biochemical.
In this connection, a possible disease may develop through oxidative stress-generation/DNA-mutations [31],[89],[90] due to the interaction discrepancy (information deficiency (biochemical deficiency)) and/or correlation de-coherence (loss of meaningfulness (symmetry restoration)) between the heart and the brain (excessive-inappropriate tension) and/or between the heart-brain and the environment (the other organs and/or the external world).
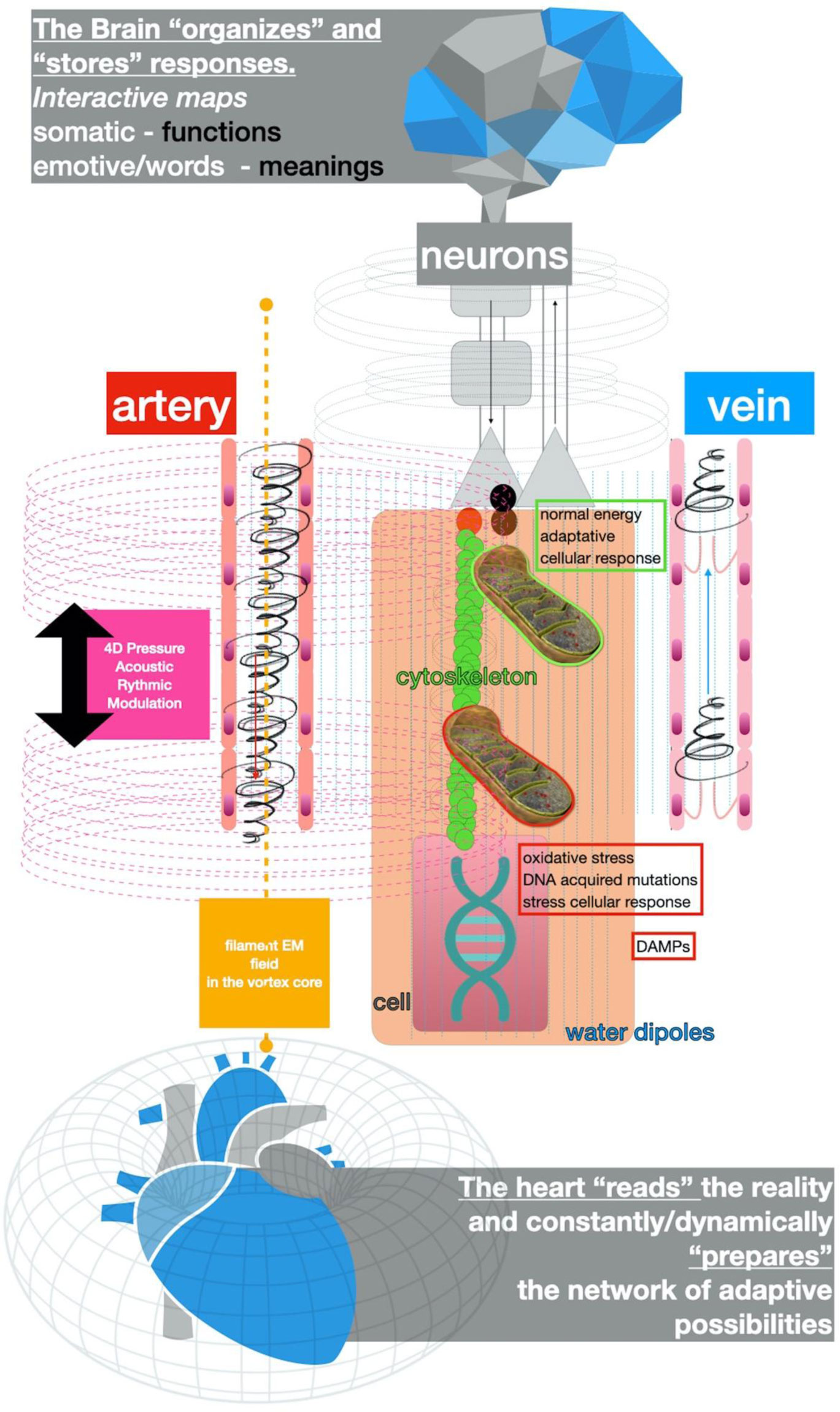
This could lead to a localized “cellular universal stress response” [31] with exposure of danger signals (DAMPS), in the site of de-coherence, and immune system activation [31] with the onset of an organic disease if the signal of the maladaptive response is neglected by the subject (which would continue to act badly, “freezing” an unbalanced response to the environment [91],[92] (unbalance between psyche, desires, beliefs, values etc. and events; a conflict with the Double)), Figure 6.
In this sense, the body seems designed as a structure (self-)conscious of all its parts, which naturally tends to balance integrity and restoration. Its genome, therefore, would not be a management center that gives instructions to the body, but rather an adaptive device that responds to psycho-environmental needs by regulating gene expression [93], ultimately restoring coherent correlations, a vehicle of the basic law of coherence [94].
Besides environmental factors, mental stress alone could trigger a disease (object of psycho-somatic research) [87],[95]. Mental stress damages the brain and the immune system, influencing hormonal activity and metabolism and represents an important etiopathogenetic factor of many pathologies including various cardiovascular diseases, in particular myocardial infarction, stroke and their risk factors [2],[96]. Mental stress alone can result in myocardial ischemia [2],[32].
As Crousos [97] describes: “all organisms must maintain a complex dynamic balance, or homeostasis, which is constantly challenged by internal or external adverse forces called stressors. Stress occurs when homeostasis is threatened or is perceived to be; homeostasis is restored by various physiological and behavioral adaptive responses”.
Over time, a condition of chronic mental stress often results in health problems [31]. In this context, it should be emphasized that the disease, especially if chronic, is not necessarily synonymous with injury: a dysfunction frequently occurs before it.
In a pictorial form, Figure 6 suggests that all cellular structures might be coherently tuned with the heart-centered em [98]/acoustic [88],[99] “grid” at a speed much faster than biochemical signal propagation processes [100],[101] (cf. section 7) and could influence the entire body [102].
The stimuli reaching the brain are organized in frames of meanings [46],[50],[103]. The brain has the role of organizing the body's response to the environment. If the stimulus sent to a group of target cells involved functionally in the behavioral response is consistent with pre-activation/grid tuning, the response will be adaptive, otherwise, cytoskeletal distortions can be generated with the loss of coherence in the cell em field, and possible disease onset. The aim is to signal a maladaptive response, to change it.
Thus, the brain activity (“the way of thinking”) in facing certain stimuli-events [104] could produce illness according to the meanings of the elaborated thoughts [105]. These would affect the body functions which are necessary to respond to the world, i.e. the “reality” as seen on the basis of the meaning that the subject has given it. A connection thus arises between neuronal activity associated to somatic, emotional, phonetic and perceptual experiences [46],[50],[106]–[108] and a biological network [109], to the formation of whose structure the heart has contributed in a not a little part. The waves (acoustic and electromagnetic like those of the heart-brain axis) may determine the shape [110],[111], the dynamics [112], the functions and the final structure of the cells [113]–[115] and its components [116]. Even proteins (currently studied as electromagnetic vibrations [117]), whose functions depend on their shape and folding [118], are affected by em waves, e.g. in the presence of changes and excess of intracellular negative charges (oxidation) [118],[119], which, in turn, can depend on mental stress and associated meanings [31],[120].
As observed by A.J Crum, it is not necessarily events that automatically stress, but how each individual deals with a certain situation [121], resulting in an adaptive or maladaptive response, potentially pathogenic [104].
In the case of adaptive response, the microtubules maintain cellular shape [and therefore the cellular function] suitable for the response to the environment [122]–[124]. The mitochondria will do their job correctly by staying mainly at the cellular periphery [88],[120]. In the opposite case, cytoskeletal distortions can be created with a loss of coherence in the cell inner dynamics. This could cause the mitochondria to collapse towards the cell nucleus [88], and vary the yield of the chemical reactions within them with the production of oxygen radicals [120]. In this way, a cellular stress response is generated which will be signaled (to be corrected) to the immune system, through the exposure of DAMPs [32],[120].
As just observed, given the quantitative unbalance and the alteration of the arrangement of electric charges inside the cell (the electric polarization density, cf. section 3), the protein molecules could conform in space incorrectly and lose their function [125], as well as alterations in gene expression may occur [126].
Of course, other disturbing agents for the correct cell behavior/response are em field and magnetic field disturbances which may interfere with the cell electret formation (cf. section 3), produce stress effects on mitochondria, modify the yield of chemical reaction interfering with the singlet/triplet electron distribution states (so-called Radical Pair Mechanism [89]), with the resulting production of oxygen radicals, inflammatory, metabolic and transcriptional responses [127].
It is remarkable that the majority of the pathologies known to date are determined by the same biomolecular mediators. The question of why, in their circulation, they selectively target a specific district of the body among many different ones remains an open question. A possibility, which however needs to be carefully examined, is that coherent correlation waves present a deficiency or weakness in such a district.
7.
Conclusions
In this paper, the biochemical and biophysical mechanisms underlying the dialog between the heart and the brain have been discussed. Beyond specific biochemical and physiological aspects of specific diseases, heart and brain appear to be both affected in a disease state so that reciprocal feedback effects relate them in a highly nonlinear interaction. The theoretical and the practical relevance of such a cardiovascular and neurological correlation has motivated our subsequent analysis of the dynamical level underlying the functional activity of the brain and the heart. In both cases, it appears that the microscopic dynamics of the system is characterized by coherent correlations among the molecular dipoles of water, which provides the far largest number of molecular components, and macromolecules.
The emerging picture is that coherent correlation waves span the brain and the heart relating their specific functional activity in a unified complex level. In our analysis a relevant role has been played by the dissipative character of the dynamics of the brain and the heart, namely of their “openness”, being systems open to the environment in which they are embedded. Such a feature provides, from one side, the possibility to establish reciprocal complex nonlinear “interactions” at the body level. These interactions are responsible for reciprocal biochemical effects [informational effects] among the body organs induced by biochemical mediators in the general metabolic activity. From the other side, openness allows establishing a generalized “correlation” at the body level, responsible of the “coherent functional binding”, namely of the “in-phase” correlation, within a given frequency band spectrum, carrying the “meaningfulness” of the subject “being-in-the-world”.
Here it must be stressed the distinction between “interactions” and “correlations”.
Interactions are mediated by messengers specific of certain forces (electromagnetic, chemical, mechanical, etc.) and are subject to physical limits, e.g. locality (causality principle) and speed of information messengers not larger than the speed of light. Correlations, on the contrary, are not mediated by messengers, i.e. are not due to forces, but are established by in-phase motion [unison motion], namely collective coherent motion generated by the mechanism of spontaneous breakdown of symmetry (SBS) as described in sections 3–5. In technical terms one says that correlated modes are entangled modes (see e.g. ref. [94] for details on the entanglement). Correlations can be instantaneously established, in contrast, e.g., with the slow spreading of chemical mediators in the interactions.
The conclusion is that “information”, which is carried by a messenger, is exchanged through interactions. They cannot be exchanged through correlations (the messenger would travel at a speed higher than light speed, which cannot be). However, “meanings” are established by correlations. Correlations arise indeed from symmetry breakdown and therefore, as explained in section 3, are responsible for ordered patterns, namely of forms, “correlations among elementary components”, therefore of the macroscopic behavior of assemblies of components as a whole, of their “meaningful” (functional) activity. In linguistics, this is equivalent to the transition from the syntactic level to the semantic one [128].
Finally, it has been extensively discussed in section 4 how the formation of vortices triggered by the heart can then self-propagate in the vessels by virtue of the intrinsic long-range correlations between the serum water molecules organized in coherent domains. The dynamical shrinking or enlarging of the vortex core constitutes an important degree of freedom for the vessel system. Enlargements of the transverse dimension of the vortex core may act against the vessel closure, due to an increase of vessel rigidity or other reasons. On the other hand, the flow vorticity provides a defense against anomalous vessel enlargements, which, instead, might be caused by non-vorticose flow overloads.
Moreover, as observed in section 4, the electromagnetic field propagates in filamentary, self-focusing fashion within the vortex core. The transverse field gradient force acts then as a selective (frequency resonant) force attracting corpuscular objects in the flowing blood near the vortex core or repelling them far from it, pushing them in regions closer to the vessel walls.
This suggests a completely new scenario for the formation of vessel obstructions due to deposits of substances, such as, e.g., cholesterol deposits on the vessel walls. Such deposits are not the cause, but the effects of the vessels malfunctioning which is to be searched in the loss of the dynamic coherence controlling the blood flow vorticity and em field self-focusing propagation. The frequencies of the em self-focusing field need to be tuned in such a way to avoid to repel towards the vessel wall unwanted molecules, possibly circulating in the blood flow. Rather these forces should attract towards the core these unwanted molecules keeping them in circulation till their elimination by the metabolism. It is the loss of proper vorticity of the blood flow that produces the matter deposits on the vessel wall. In the presence of adequate vorticity such deposits would be removed, better, they would not even have the chance to be formed, also considering the “pushing” action of the longitudinal component of the em field, generated by its non-zero mass, directed along the vortex core axis, as explained in section 4. It is a common experience in vascular and cardio-surgery that the duration and the efficiency of artificial channel prosthesis used to repair malfunctioning vessels parts is favored by the vorticity regime of the blood flowing within them [64].
These results of the modelling of molecular dynamics, out of reach in other phenomenological approaches, have much relevance from the standpoint of therapeutic applications.
Relevant for its possible applicative consequences is also the conjecture supported by our modelling that lowering or loss of the blood flow vorticity and the associated self-focusing propagation of the em field is at the origin of the formation of aneurysms and vein varices. This might be consequent to vessel enlargements due to exciding pressure from blood flow non-whirling regime. In a whirling regime, possible overflows would produce shrinking of the vortex core thus avoiding higher pressure on the vessel walls.
A similar vortex and em field dynamics has been modelled to occur also inside the cell and it has been shown that it generates coating of the em filaments whose radius is of an order of the observed microtubules radius (12.5 nm). It is, therefore, a good candidate model for the dynamical formation of microtubules that make up the cell skeleton [51],[52],[129],[130].
In this connection it also interesting to note how anatomically arterial, venous and nerve branches run together, parallel in the human body, forming a network that surrounds each organ, tissue and cells. The recently discovered fluid-filled interstitial structure and the complex network of thick collagen bundles [131] suggest that a similar self-focusing mechanism for the em field propagation and the coherent topologically non-trivial condensation of vortex type are at work also in such cases (cf. section 3 and 4) (see also [132]).
In section 4 it has been also commented on the isomorphism between the fractal self-similarity in the vortex structure and the deformed coherent state, with the deformation parameter controlled by the fractal dimension [49],[63],[69], thus establishing again the connection with the coherence character of the molecular dynamics. The connection between coherence and fractal properties has been also considered in section 5 where muscle contractions of the heart have been studied and two power laws have been found in correspondence to two coherent dynamical regimes (Figure 5).
In the case of the blood vortices and of the heart muscle contraction a central role is played by the molecular displacement field (sound wave), whose quantum is the phonon.
In the heart, these sound waves come primarily from the sequential closing of the mitral and aortic valves [99]. The heart sounds are so ubiquitous that they are almost ignored when, in fact, they provide a continuum of sound and vibrational energy for the whole body throughout the entire lifespan.
At a cellular level, as seen in section 5, muscle contractions could organize the molecular interactions in space and time [73].
According to Bentov [133], the pulse pressure wave of blood also creates a resonant system of interference pattern in the vessel system.
Starting from these considerations, at Padua University several subjects were followed for a year after myocardial infarction in a path focused on adequate stress management. Rapid molecular variations have been documented [7] in response to relaxation-oriented psychic activity (decrease in inflammatory and oxidative-stress markers along with stress hormones (such as cortisol, adrenaline and noradrenaline)).
This seems to be accompanied by different expression of the genetic code (decrease in the expression of NF-kB, p53 and Toll-like Receptor-4 genes) [7] based on epigenetic mechanisms (variation of circulating microRNAs) [96]. There seems to be also a slowdown in the cellular ageing process [126],[134] and a possible post-transcriptional modification of some protein compounds [7],[126].
At the same time, cardiac volumes, contractility of the left ventricle and coronary flows seem to vary favorably with the modification of the psychic activity of the subjects studied [7].
The blood physically changes its appearance (Figure 7). Recently, indeed, it has been documented [135] in vivo that during psycho-induced relaxation, the serum pH tends to increase, the electrical conductivity of plasma decreases and an “ordered” emission of Delayed Luminescence (DL) occurs, due to the emission of biophotons.
The precise meaning of this spontaneous light radiation is still unclear but it seems to be able to affect various biological effects both in terms of intercellular communication, genetic activation or brain and psychological activity [136]. The genesis of this light energy has been proposed to be linked to the oxidative-reductive reactions present in the various tissues of the human body, as a transient in the presence of criticalities of the dynamics, both, with an increase in case of oxidative stress [137], or with less oxidative-stress as documented in [135].
An interesting question related to DL is whether could be related to cavitation (micro-bubbles formation within the blood) and sonoluminescence (micro-bubbles collapse and light emission due to the application of an acoustic field) [138]–[141] but the occurrence of this phenomenon in biology needs to be carefully analyzed and supported by observations.
A further aspect which waits to be clarified is the nature of the “dialog” between the heart and the brain. One possibility is that, in tune with the coherent dynamics mentioned in previous sections, an “in-phase correlation” regime could “entangle” heart and brain so that “order parameters” could be shared among them for the synchronization of the bodily functions involved in the environmental response [142]. In addition to that, effective wave signals could be conveyed by water dipole network and nervous feedback via nonlinear non-dissipative propagation (solitary waves or solitons) [51],[52].
Based on the physical and chemical mechanisms described up to now at the basis of the heart-brain dialog, in the future it would be also possible to better clarify the role of the heart in some neurophysiological processes. A cardio-thoracic neurological sub-system has been described [2],[143], called “intrinsic cardiac nervous system” able 1) to self-regulate independently from the central nervous system 2) probably to manage information coming from the outside (possibly of an electromagnetic nature) [27]–[30]. In the field of psycho-physiology, linear and non-linear analysis are applied to heart and brain signals (mainly heart rate variability (HRV), cerebral functional magnetic resonance and electroencephalogram (EEG) [143]) for brain engaged in functional activity. At the current state of knowledge, the intrinsic cardiac nervous system [8] seems to be able to influence activity in the fronto-cortical areas [9],[10] and motor cortex, affecting factors such as attention level, motivation [11], perceptual sensitivity, and emotional processing [12]–[15]. According to the model of neurovisceral integration [9],[16]–[19], the heart may share with the brain rhythmic [20] and electromagnetic patterns [21] which may support intuitive-emotional processes [22],[23], awareness and feelings [24],[25], and a rational, detached and “less egocentric” reasoning [26]. In these research fields, studying the vorticity of blood as a coherence inducer/regulator with 4D magnetic resonance methods could be very interesting. For example, it has been found [14] that, depending on whether a “fearful” stimulus is presented while the heart is in diastole or systole, the emotional fear response changes dramatically. At the basis of this, baroceptor signals would be implicated [13] which in turn could be affected by different patterns of blood vorticity produced by the heart.
These observations and comments may well extend to animal models, where, although much needs to be discovered and analyzed, it could be very useful in understanding links between psychosocial processes and cardiovascular function and health, and viceversa [144]. It will be necessary to find precise biophysical parameters as a non-invasive marker of coherence-decoherence in the heart-brain dialog from a diagnostic and therapeutic point of view. This issue will be of paramount importance because neuro-cardiologic disease progression in relation to neuro-physiological disorders might be retarded if the pathogenetic process were detected early in a pre-symptomatic phase [145].
Having biophysical non-invasive and accurate follow-up methods would therefore make it possible to integrate the most adequate and individualized strategies, such as mind-body and behavioral techniques and education, into the current models of prevention and treatment (Integrative Medicine model, for more details see [2],[31],[33]).









 DownLoad:
DownLoad: