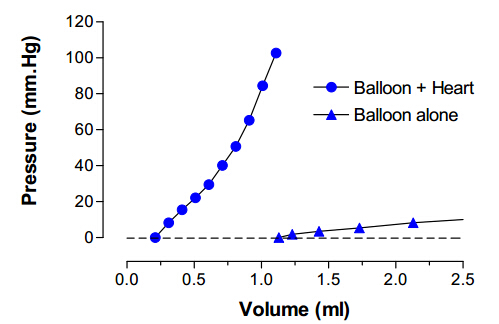
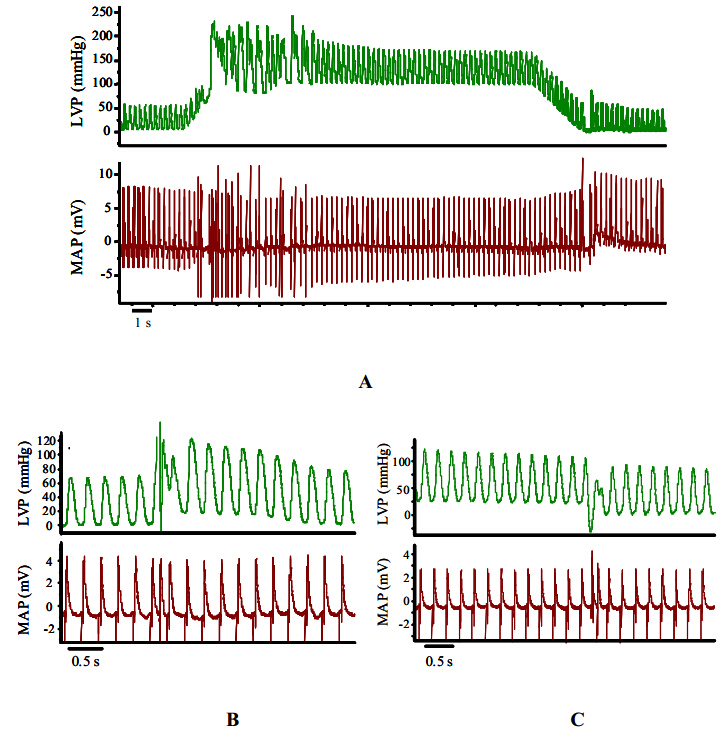
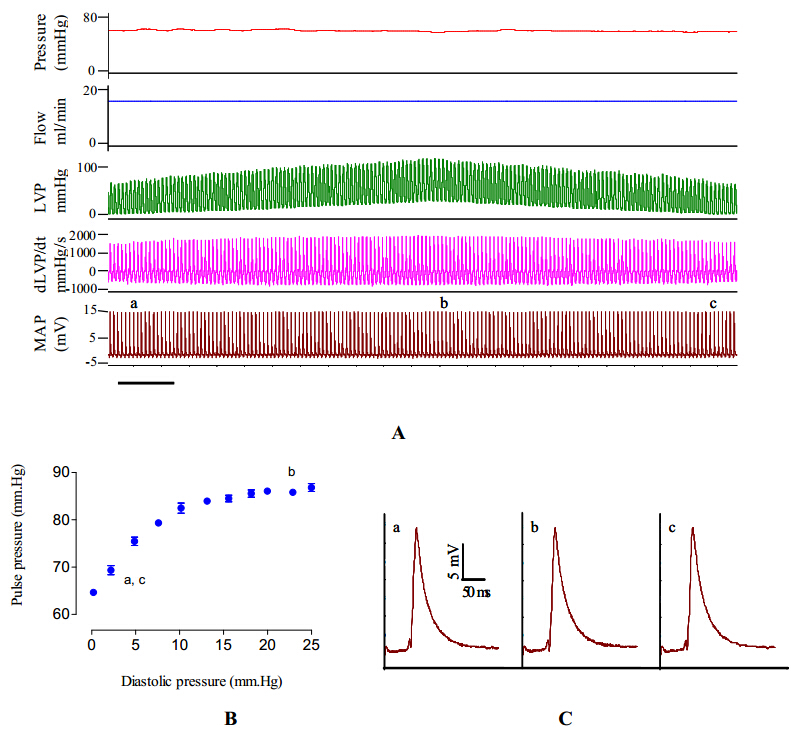
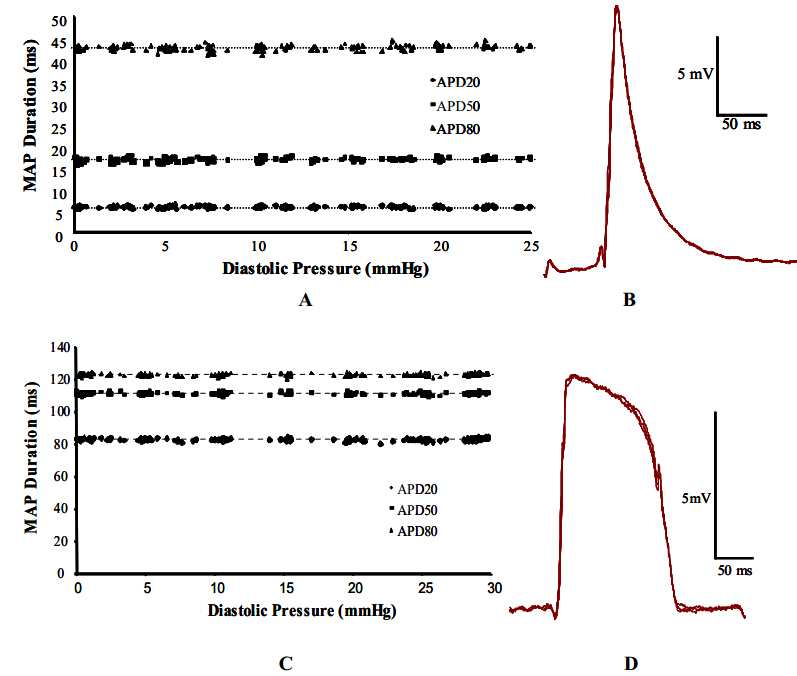
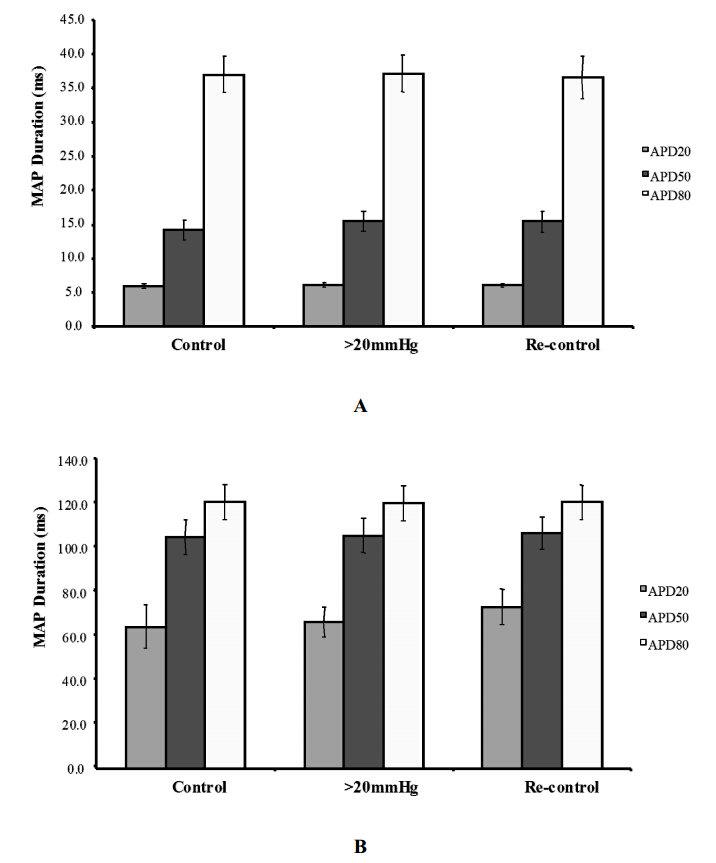
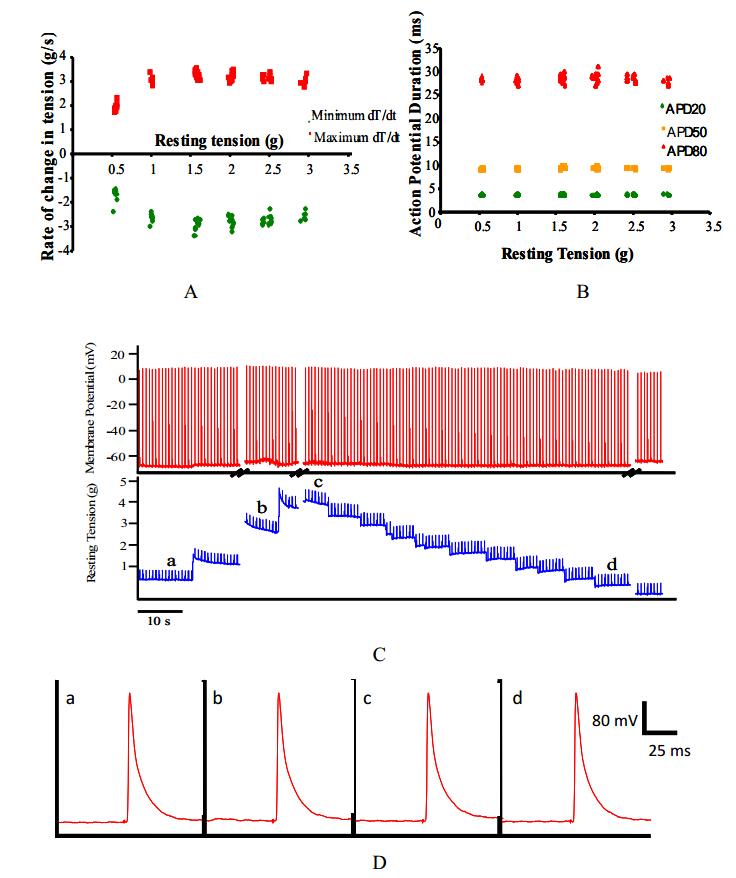
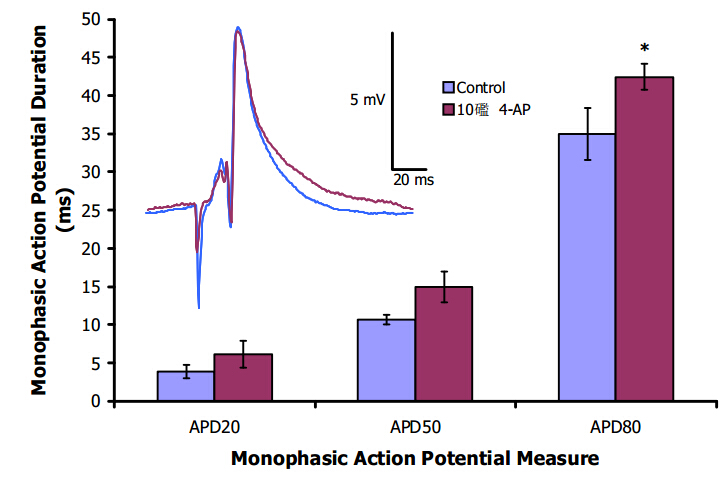
Mechanoelectric feedback (MEF) is the process by which mechanical forces on the myocardium can alter its electrical properties. The effect can be large enough to induce ectopic beats or fibrillation. However, the role of MEF at physiological levels of mechanical stress is not clear. We have investigated alteration in action potential morphology in rat and guinea pig ventricle and in rat atrial tissue at levels of stretch near the plateau of the Frank-Starling curve. Stretch of >100 mm.Hg End Diastolic Left Ventricular Pressure (EDLVP) or rapidly applied stretch (EDLVP increased by 25 mm.Hg within 100 ms) often triggered ectopic beats in isolated rat and guinea-pig hearts. However, ventricular epicardial monophasic action potentials (MAPs) recorded during stretch to EDLVP up to 30 mm. Hg showed no consistent changes in action potential duration (at APD20, APD50 or APD80) in either species. MAP recording detected APD prolongation with very small concentrations of 4-AP (10 μM), confirming the discrimination of the recording technique. In isolated rat atrial strips, no changes in intracellular action potential morphology or membrane potential were seen when stretched to levels producing an optimum increase in contractility. We conclude that alteration in action potential morphology with stretch does not contribute to the Frank-Starling relation in ventricle of rat or guinea-pig isolated heart, or in rat atrial tissue.
1.
Introduction
Animal vocalization is a fascinating topic and contains valuable evidence about animal behaviors and ecosystems. Giant pandas (Ailuropoda melanoleuca) are monestrous mammals and can make 19 different calls in their first 4-5 weeks of life or during their rather short breeding periods [1,2,3,4,5,6,7,8,9,10]. Each call has a specific meaning and the mixture of different calls expresses a certain emotion [1,2,3].
In the 80s', the most representative system Sphinx [11] was developed by Lee Kaifu et al. of California Miramar University (CMU) based on hidden Markov model (HMM) [12], Gaussian mixture model (GMM) [13] and multivariate grammar model (N-gram) [14]. It is the first speech recognition system which is available to nonspecific person.
One of the earliest works applied a convolution neural network (CNN) to identifying 10 anuran species by bio-acoustic data [15]. In the same year, three of the six teams in the 2016 BirdCLEF challenge submitted CNN systems taking spectrograms as input, including the highest-scoring team [16]. Stowell investigated computational bioacoustics with deep learning and indicated at least 83 of the surveyed articles made use of CNNs until 2021 [17].
Recurrent neural network (RNN) [18,19] brought a new breakthrough for acoustic modeling of speech recognition. RNN created memory through the superposition of speech in time. Moreover, long-short term memory (LSTM) solved the problem of gradient vanishing of RNN [20]. The CS-CLDNN (CBAM-Switch-CLDNN) combined the CNN and LSTM models with the convolutional block attention module (CBAM). The recognition accuracy of CS-CLDNN on 20 bird species reached 0.975 [21]. Bergler et al. proposed an orca call types classification based on ResNet18 [22] and Waddell et al. classified six fish call types in the northern Gulf of Mexico Stowell based on ResNet-50 [23].
However, training LSTM was not a trivial task because of its many parameters. Gated recurrent unit (GRU) [24] reduced computation cost through updated gates and reset gates while keeping "memory". Zhang et al. presented a framework composed by convolution module and GRU module, to predict GP's mating success using their vocalizations. However, the recognition accuracy is only about 85% [25].
According to the investigation in [21], there were many efforts on computational Bioacoustics using deep neural networks (DNNs). However, most of works focused on the species classifications based on animal calls, which were easier than the vocalization recognition since the sound differences among species were greater than the differences of the same species vocalizations. Few works devoted to call types classification [22,23,25] with classification accuracy about 85% and still had gaps between existing methods and vocalization recognition.
In summary, although animal vocalization recognition is a very important in animal behaviors analysis and conservation, it is an unsolved open problem even now. Especially, for GP's vocalization recognition, the difficulties are:
1) Sound data collection and labeling is very difficult. The giant panda is a silent animal, only producing calls within four weeks of birth and during a very short mating season. The sound data were all manually labeled by the staff of Chengdu Research Base of Giant Panda Breeding (CRBGPB). Thus, it required long time to collect GP's calls and very heavy workload to manually label the sound data.
2) There were a lot of ambient noises (such as people talking, opening and closing doors etc.) and calls such as peacocks and other birds.
3) Existing methods cannot be used directly to GP's vocalization recognition because of their low recognition accuracy.
Therefore, we should propose a new framework both in feature extraction and vocalization recognition using DNN to improve the performance of existing methods. After analyzing the GP's sound, we found that it is a broad frequency signal. Thus, two new filters, medium Mel filter bank (MFbank) and reversed Mel filter bank (RFbank), were proposed to extract medium and high frequency features. Combined above two band features with the low-frequency feature extracted by Mel filter bank (Fbank) [17], the three banks' features were sent to a deep network composed by GRUs, named 3Fbank-GRU. 3Fbank indicated the inputs of the DNN were the features extracted by three filter banks and GRUs were the main components of the DNN keeping the 'memory' while reducing computation cost of LSTM.
The main contributions of this paper are:
1) Proposed a new feature-extraction scheme that not only used Fbank to extract low frequency features but also introduced new RFbank and MFbank to extract high and medium frequency features.
2) Proposed a novel DNN composed by GRUs to process the three-bank features of GP's sound data.
3) The proposed 3Fbank-GRU method achieved a high recognition accuracy rate of over 95%, and was suitable for labeling large data sets of GP vocalizations collected by camera traps or other recording methods.
The remainder of this paper is as follows: in the second section, the materials and methods are presented; Experiments and discussion will be given in Sections 3 and 4.
2.
Materials and methods
2.1. Sample collection
The data set of GP vocal samples was collected from 176 pandas at the CRBGPB. The subjects include cubs, sub-adult and adult GPs. We used a ShureVP89M directional microphone and a TascamDR-100MK3 handheld recorder (10 Hz~192 0.1/-0.5 dB) to record vocalizations made by GPs. When recording, sampling frequency was set to 48 KHz and 16 bits, since high sampling rate can reduce the distortion of audio and ensure the high frequency vocalizations that were recorded. The audio was saved in WAV format.
At the same time, SONY FDR-AX60 video cameras were used to capture all the video and sound data of the subjects as the basis for classification of vocalization types. The experienced animal husbandry staff of the CRBGPB labeled the vocalizations of the GPs.
20h 20min of data plus the data set previously collected, formed a total of 35h 50min data set. After data collection, the segments containing GP vocalizations were selected from the original datasets manually. Then, the selected segments were classified into 16 types (Table 1). If there was data that could not be labeled accurately because of noises or data missing, it was discarded.
The data was edited with Goldwave audio editing software. The length of each sound clip was 2-4 seconds including at least two peaks of the original signal in order to observe dependency among neighboring vocalizations. Finally, we obtained a total of 12, 800 samples which were divided into 16 categories. Each category contains 800 samples.
2.2. Preprocessing
The sound data contained many systems and environmental noises. Therefore, the noise suppression was carried out to reduce the influence of background noises. We used the minimum mean square error (MMSE) estimation to suppress background noises (see Figure 1 and Table 2).
2.3. Feature extraction
Voiceprint is the acoustic spectrum that carries speech information. The most commonly used voiceprint in sound recognition is Mel filter bank (Fbank) coefficient [21]. However, the classical Fbank cannot get satisfied recognition results for GP vocalization recognition because it only extracts low-frequency information but the frequency spectrum of GP vocalization is very wide. In order to utilize more information from GP's calls, two new filters were proposed to extract other two band coefficients, reverse Mel (RMel) coefficients and medium Mel (Mmel) coefficients, to improve the performance of the whole system.
2.3.1. Fbank feature
A typical framework of Fbank goes through a pre-emphasis filter, is sliced into overlapping frames and a window function is applied to each frame. Afterwards, Fourier transform is performed on each frame (or more specifically a short-time Fourier transform) and then the power spectrum is calculated. Next, convert the linear frequency to Mel frequency and then designs equispaced triangular filters on Mel-scale and coverts it to a linear frequency using Eq (3) to get dense triangles on low frequencies while sparse on other frequencies (Figure 2). Finally, converted triangular filters are applied to the power spectrum to extract the frequency bands [11].
Fbank aims to mimic the non-linear human ear perception of sound by being more discriminative at lower frequencies and less discriminative at higher frequencies. However, designing filters directly on linear frequency to mimic human ears is not an in trivial task. The most useful function of Fbank is the equispaced triangular filters designed on Mel-scale. Then, the filters are converted to linear frequency to form dense filters on low-frequencies while sparse filters on medium and high frequencies (Figure 2). We designed Rmel and Mmel according to this method. The formula of converting linear frequency (f) to Mel frequency m is as follows:
Then, the equispaced triangular filters are designed on Mel-scale and the mth triangular filter is:
Generally, a group of M (usually 22-26) triangular filters is used. The m represents the mth filter on Mel-scale, $ 0\le m\le M $. $ f\left(m-1\right) $, $ f\left(m\right) $, $ f\left(m+1\right) $ represent the lower, central and upper Mel frequencies respectively.
And then, the Mel-scale on Eq (2) is converted to linear frequency using Eq (3) to get filters $ {H}_{f}\left(k\right), f = 1, \cdots, M $ on linear frequency.
The logarithmic energy is calculated as follows:
where p(k) denotes to power spectrum of the sound signal. The obtained value $ {E}_{m} $ is the Fbank feature.
2.3.2. New voiceprint features (Rfbank, Mfbank features)
1) Rfbank feature
The high-frequencies could be extracted by a group of non equispaced triangular filters which were dense on high frequency and sparse on other frequencies (Figure 3). According to the discussion in subsection 2.3.1, the non equispaced triangular filters could be designed as equispaced on a scale similar to Mel, named reversed Mel-scale first. Then, these equispaced triangular filters were converted to linear frequency to form non equispaced filters.
Here, reversed Mel frequency $ {m}_{R} $ is:
where f is the linear frequency.
The triangular filter banks designed on reversed Mel-scale is equispaced and the $ {m}_{R} $th triangular is:
And then, covert the reversed Mel-scale on Eq (6) to linear frequency-scale using following equation to get filters $ {H}_{f}\left(k\right), f = 1, \cdots, M $ on linear frequency.
The logarithmic energy calculated using Eq (4) is the Rfbank feature.
2) Mfbank
According to the discussion in subsection 2.3.1, the medium-frequencies could be extracted by a group of non equispaced triangular filters which were dense on mediun frequency and sparse on other frequencies (Figure 4). The non equispaced triangular filters were designed as equispaced on a scale, named medium Mel-scale first. Then, these equispaced triangular filters will be converted to linear frequency (Hz) to form non equispaced filters.
Here, medium Mel frequency $ {m}_{m} $ is:
where f is the linear frequency.
The triangular filter banks designed on reversed Mel-scale is equispaced and the $ {m}_{m} $th triangular is:
And then, covert the medium Mel-scale on Eq (9) to linear frequency-scale using following Equation to get filters $ {H}_{f}\left(k\right), f = 1, \mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\cdots, M $ on linear frequency.
The logarithmic energy calculated using Eq (4) is the Mfbank feature.
2.4. Proposed method: 3Fbank-GRU
A novel DNN model: 3Fbank-GRU model were proposed based on GRUs. That is, Fbank feature, Mfbank feature and Rfbank feature, whose lengths were n, were processed by three independent 4-layer GRUs with red, blue and green colors respectively (Figure 5). The final processed results of three 4-layer GRUs were fed into h and merged there. Then the merged features were sent to the full connected layers (Dense) and the Softmax layer to get vocalization labels of the sound clips. The labels were encoded by onehot encoder to define the differences of the loss in training.
3Fbank-GRU model was trained using datasets labeled by senior animal husbandry staffs of the CRBGPB. The loss was cross-entropy. During training, the initial value of hyperparameters was: dropout was 0.5, parameter initialization used uniform initialization, batch-size was set to 64 in minibatch training, initial learning rate was set to 0.0001 with variable learning rates and step attenuation (see subsection 3.3). We used 10-fold cross validation to train and test. That is, the samples were randomly divided into 10 equal parts in each category. For each unique group, took the group as a test data set and the remaining 9 groups as a training data set. Fit 3Fbank-GRU on the training set and evaluate it on the test set. The average value of 10 experiments was taken as the final result.
2.5. Method overview
The target of this research is: to provide an automatic recognition system of GP's sound clips to ecological researchers, which can help researchers to find more about the relationship between GP's sound and their behaviors. The recognition can be carried out automatically according to follow procedures (see Figure 6):
1) The collected sound data formed sound database. Clips in the sound database are preprocessing (denoising) firstly. And then, the features were extracted from the preprocessed signals by three banks: Fbank, Mfbank and Rfbank.
2) Given the extracted multi acoustic features: Fbank coefficients, Mfbank coefficients and Rfbank coefficients, the features were fed into 3Fbank-GRU to learn more discriminative features.
3) The proposed model predicted the labels of GP's vocalizations by using fully connected layers (dense layers) with Softmax activation function based on the acoustic merged features extracted at the 3 independent 4-layer GRUs. Specifically, GRUs generated a probability vector $ P\in {R}^{16\times 1} $. The label was assigned as the category with the highest probability.
3.
Results
3.1. data
There are 12, 800 labeled GP vocalization samples, which were divided into 16 categories, each with 800 samples. The test and training data set are chosen according to 10-fold cross validation, which is explained at the end of subsection 2.4.
3.2. Feature selection
MFCC added discrete cosine transform to Fbank filter. In this subsection, we used MFFC features and Fbank features to verify the influence of these two types of voiceprint features on recognition accuracy. The experimental data was set as subsection 3.1 and 2.5. The recognition model was a single-layer GRU network, the hidden layer dimension was 300 and the dropout was 0.5. The initialization was normal initialization, the learning rate was 0.0001, the training process used minibatch, batch size was 64 and the training was 100 epochs.
From Figure 7, the accuracy of the MFCC feature on the training set was 88.54%, the accuracy on the test set was 81.50% and the average accuracy of the 10-fold cross validation on the test set was 82.06%. While the accuracy of Fbank on the training set was 92.65%, the accuracy on the test set was 85.05% and the average accuracy of 10-fold cross validation on the test set was 85.74%.
The experimental results showed that the recognition accuracy of MFCC was 3.68% higher than that of Fbank. Thus, the MFCC feature had better recognition performance than the Fbank feature when using the GRU for giant panda vocalization recognition. Therefore, we used MFCC feature in our recognition framework.
3.3. Hyper-parameter selection
3.3.1. Network layer
In order to specify the layer of DNN composed by GRUs, we kept the model parameters except for the layers of DNN constant and observed the recognition accuracies of the different layers (see Figure 8). From Figure 8, we can conclude that the four layers had the best performance in five models and the network layer was set to 4.
3.3.2. Initialization
From above discussion, when the number of layers of DNN was 4, the recognition accuracy reached 88.85%. Here, we fixed the model parameters and investigated parameter. Three commonly used parameter initialization methods, normal, uniform and orthogonal, were used to conduct experiments, and the experimental results were shown in Table 3.
From Table 3, the uniform Initialization had the highest accuracy of 90.72%. Thus, the uniform was chosen as our initialization method.
3.3.3. Batch size
Batch size was generally 2 to the power of n, such as 16, 32, 64, etc. Here, the model structure was kept unchanged and uniform initialization was used with batch sizes of 16, 32, 64, 128 respectively (see Table 4). From Table 4, the batch size 64 had the best the recognition accuracy and was selected as the batch size of proposed model.
3.3.4. Dropout
The dropout values were 0.2, 0.5, 0.7 and "without dropout". The dropout 0.5 had the highest recognition accuracy and was the dropout of proposed model (see Table 5).
3.3.5. Summary
In summary, the feature of the ablation experiment was the Fbank feature and hyper-parameters were: four layers of DNN, 64 batch size, 0.5 dropout and uniform initialization.
3.4. Model comparison
Proposed 3Fbank-GRU were compared with Gaussian mixture model-hidden Markov model (GMM-HMM) [12,13], Fbank-GRU, Fbank-LSTM [19], 3Fbank-LSTM and KD-CLDNN [21]. All three models used 16 categories (800 samples each) of GP labeled vocal samples in experiments and used 10-fold cross validation to train and test the system.
3Fbank-GRU/3Fbank-LSTM (proposed method) extracted three kinds of features: Fbank, Rfbank, Mfbank and automatically gave labels of GP test sound clips (Figure 5). It had three independent GRUs whose parameters were not shared with each other. Each GRU's layer was four and its hidden layer dimension was 300.
Fbank-GRU/Fbank-LSTM's feature was its Fbank coefficients and the recognition model was a one-layer GRU/LSTM with 300 hidden layer dimension. The other hyperparameters of training initialization both of Fbank-GRU, Fbank-LSTM, 3Fbank-LSTM and 3Fbank-GRU were set as described in subsection 3.3.
We built an HMM for each category of samples. The number of states of an HMM was three, the number of Gaussian mixture elements for each state was three, the covariance matrix was the diagonal matrix and the number of iterations was 2000 times.
CS-CLDNN proposed in [21] was a CNN-LSTM-DNN model. The low-frequency features of bird voices were extracted by Mel FBank and sent to two CNN modules. In each module, the convolutional layer was activated by Swish function, followed by a convolutional block attention module (CBAM) and MaxPooling. Then, the low frequency features and features extracted by two CNN modules were fed to LSTM and full-connected DNN to classification. CS-CLDNN was considered as a state-of-art method in bird voice classification because of its high accuracy.
Table 6 showed average recognition accuracies of GP's 16 vocalization categories using 6 models. Not surprisingly, GMM-HMM had the lowest recognition accuracy 87.1%. The performance of GRU and LSTM were very similar both using features extracted by Fbank and 3Fbank. That is, the recognition accuracy of Fbank-GRU was 92.6% while Fbank-LSTM was 92.8%. The difference between two models was 0.2%. Moreover, the recognition accuracy of 3Fbank-GRU (96.9%) was 0.4% higher than the 3Fbank-LSTM (96.5%). Considering the training LSTM was more complex than the GRU, GRU was the more cost-effective model of the two.
Although the average classification accuracy of 20 kinds of bird sounds using CS-CLDNN achieved 97.5%, the average recognition accuracy of GP's 16 vocalization categories was only 93.9%. However, CS-CLDNN was with the highest recognition accuracy in models whose features were extracted only by Fbank. The other two models, Fbank-GRU and Fbank-LSTM were with recognition accuracies 92.6% and 92.8% respectively. The recognition accuracy of CS-CLDNN was higher 1.3% than Fbank-GRU while 1.1% than Fbank-LSTM. Thus, CS-CLDNN was the best model in models using Fbank features.
When 3Fbank features were introduced, the recognition accuracies were improved by nearly 3% even compared to CS-CLDNN with the highest accuracy using Fbank features. That is, the accuracy of 3Fbank-LSTM was 2.6% higher than CS-CLDNN while 3Fbank-GRU was 3% higher than CS-CLDNN. It was a big improvement.
Just as above discussion, LSTM and GRU have very similar recognition performance and models with 3Fbank features are big improvements over models with Fbank features. Thus, in order to observe the performance of different kinds of models in each of GP's 16 vocalizations recognition, GMM-HMM, Fbank-GRU and 3Fbank-GRU are chosen to observe the recognition performance.
The vocalizations with high recognition accuracies using the Fbank-GRU model included the cub's "goo" and "chirping" and "gasp" of the adult GPs (see Table 7). The recognition accuracies of the above-mentioned three calls were higher than 96%. There were eight calls with low recognition accuracies: "squeak" of GPs' cub, "mm-hmm" of sub-adult GPs and "hum", "bird scream", "scream", "hiss" of adult GPs. Among them, the recognition accuracies of the six calls were lower than 91% while the classification of "bark" and "strong bark" was vague with more cases of miscommunication. The recognition accuracy rates for the remain six vocalizations were between 92% and 95% respectively.
It is obviously that the recognition accuracies using Fbank-GRU for all categories were improved comparing with the accuracies using HMM-GMM. The average improvement rate was 5.47%. This implies that DNNs composed by GRUs are promising methods in GP's automatic vocalization recognition.
The recognition accuracies using 3Fbak-GRU were improved in all GP's vocalization compared with both GMM-HMM and Fbank-GRU. As discussed in the previous paragraph, the performance of Fbank-GRU was better than GMM-HMM. Thus, we will only compare the proposed method (3Fbank-GRU) with Fbank-GRU.
Six vocalizations with low recognition rate using Fbank-GRU: "squeak", "mm-hmm", "hum", "bird scream", "scream" and "hiss" whose recognition accuracies were about 90% are significantly improved with more than 6% improvement rates and their recognition accuracies were all over 96%. The improvement of recognition accuracies for "barking" and "strong bark" were relatively small. There were still misclassifications, but recognition accuracies were increased more than 3%. Three calls: "goo", "chirping" and "gasp" which had high recognition accuracies also had a slight improvement and their recognition accuracies exceed 98%. The recognition accuracies of the other kinds of vocalizations were also improved.
In summary, all recognition accuracies using the proposed model were over 95% and the proposed model was best among the three recognition methods. The proposed DNN improved average accuracy by 4.3% compared with Fbank-GRU and by 9.77% compared with GMM-HMM.
4.
Discussion
Both for the infant and adult GPs, vocalizations convey important information of breeding or needs to the mother. Considering captive GP's, their low success rate of natural mating and low birth rate of newborns, vocalization recognition is very important to the management of captive GPs.
4.1. Spectrogram characters of GP's voice
When Fbank features were used in speech recognition, the low frequency components of speech signals usually reflect the essential information of speech well. Nevertheless, for the GPs, the recognition accuracy of only using the Fbank feature and the GRUs was unsatisfied because of broad spectrum of animal calls.
From Table 8, we can see that the frequency distribution of GP's vocalizations is wide. Baby panda "cuckoo" sound, adult pandas "chirping" and "gasp" are the lowest frequency over all calls and their frequencies of concentrated energy are below 2000 Hz. The baby giant panda's "goo", the young giant panda's "mm", the adult giant panda's "hum", "bird scream", "scream" and "hiss" have high frequency, whose average frequency is above 2000 Hz. The frequency of "squeak" is the highest, and can reach about 10.2 kHz. The average frequency of the vocalizations of the rest types is between 1500 and 2000 Hz.
In order to observe the change trends between the recognition accuracy of Fbank-GRU and the average frequency of GP's vocalizations, the GP's vocalizations were coded to their serial numbers defined in Table 1. Moreover, the recognition accuracy of Fbank-GRU and 3Fbank-GRU was magnified by 40, 000 times and subtracted by 35, 000 to show it with the same order of the average accuracy's values (see Figure 9).
Observing Figure 9, we can conclude:
1) The recognition accuracy of Fbank-GRU (the red curve) and the average frequency (the blue curve) had opposite trends. That is, the minimum of the recognition accuracy curve was the maximum of the average frequency curve, which mean the GP's vocalizations with high average frequency were with low recognition accuracy while the low average frequency were with high recognition accuracy. In other words, Fbank-GRU had good performance only in low frequency signal.
2) The orange curve of 3Fbank-GRU floated above the red curve of Fbank-GRU, which mean the recognition accuracy of 3Fbank-GRU was higher than the Fbank-GRU. In addition, the orange curve was smoother than the red curve. Thus, the 3Fbank-GRU can handle wide average frequency signals better than the Fbank-GRU.
As mentioned above, the GP's vocalization frequency is very wide. Therefore, extracting high frequency and medium frequency features can help us increase the recognition accuracy. Two new features, Mfbank and Rfbank, were proposed to improve the performance of Fbank features and the GRUs. In order to handle three features, three GRUs with not shared parameters were designed in our framework. The output of the three GRUs were spliced into one output finally (Figure 6). Experimental results were obviously improved compared with the Fbank-GRU model and the GMM-HMM. All accuracies of 16 vocalizations using the proposed model were over 95%, which mean that the system based on the proposed model can be used directly for the automatic recognition of GP's vocalizations.
4.2. Robustness in noise
There are environmental and device noises in collected sound dataset. Fortunately, the highest energy of these noises concentrated on the low frequency. Thus, the most of noises can be suppressed by traditional high-passed filters. The MMSE was used to reduced noises (see subsection 2.2 and Table 2).
4.3. Weakness
However, there are some weaknesses that need further study.
1) There are 16 categories of sample data in our paper, some kinds of calls are not included because of the small amount of data, such as "single call" and "low ow".
2) Although the recognition results of 16 kinds of panda calls are satisfactory, but the differences between each type of calls are not analyzed.
3) The number of layers, Initialization and other parameters of the identification model have been discussed in this paper. However, the limited number of panda calls samples cannot fully reflect the statistical characteristics of all kinds of parameters. More data are needed to optimize the model.
4.4. Future works
1) Collect more types and numbers of giant panda calls to train and design new DNN model.
2) Analyze the differences between the frequency features of different kinds of panda calls and study the voiceprint features more suitable for panda voice signals.
3) Focus on both automatically recognize, locate and segment the PD's vocalizations.
5.
Conclusions
This paper is mainly based on using the voiceprint features and deep learning to identify GP vocalizations. Two new voiceprint features, Mfbank features and Rfbank features, were extracted by designing two new filters. These two types of voiceprint features were combined with the Fbank voiceprint features to improve GP vocalization recognition. We designed a DNN model named 3Fbank-GRU to realize the automatic recognition of GP vocalizations based on the features of Fbank, Mfbank and Rfbank. Finally, our experiments showed that the recognition accuracies of 16 vocalizations were over 95% and improved average accuracy by 4.3% compared with the Fbank-GRU and by 9.77% compared with GMM-HMM. As the first effort to design a system for the automatic recognition of GP vocalizations, the proposed model will help researchers to better understand the role that vocalizations play in giant panda behavior. Moreover, since the system based on 3Fbank-GRU can label sound clips automatically, it will greatly reduce the work burden of manually analyzing vocalizations.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This research is supported by the Program of Natural Science Foundation of Sichuan Province (2022NSFSC0020), National and Regional Studies Archival Center for Higher Education, Ministry of Education, Japan and South Korea Institute, Sichuan Normal University (2022RHZD003), Chengdu Science and Technology Program (2022-YF09-00019-SN) and the Program of Chengdu Research Base of Giant Panda Breeding (NO. 2020CPB-C09, NO. 2021CPB-B06).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: