Coarse-grained molecular dynamics simulations of biomolecules

1.   Introduction

Undoubtedly, the current era of networking is characterized by novelty. The rapid expansion of networks is giving rise to an unprecedented volume of data, contributing to heightened complexity in terms of data dimensions and features. Within this extensive dataset, when there is a need to analyze and detect specific data, the presence of numerous non-essential redundant features emerges. This proliferation of redundant features intensifies the challenges in network intrusion detection, akin to a pathological condition. As a consequence, a pivotal strategy for enhancing the efficacy and performance of network intrusion detection involves the elimination of duplicate characteristics. Network intrusion detection detects attack patterns by analyzing network traffic, with machine learning algorithms such as artificial neural networks, naive Bayes, and decision trees being predominantly utilized in current practices. Traditional machine learning methods are particularly valuable for solving small-scale data and simple tasks, offering better interpretability. Novel deep learning methods exhibit superior performance in handling large-scale data and complex tasks, albeit requiring more computational resources. Given the immense volume of current network traffic, attempting to identify the most suitable features through a systematic search is generally impractical due to the limitations of direct computation in practice. Although evaluating all possible subsets is costly in practice, the emergence of intelligent optimization algorithms provides a solution. Intelligent optimization algorithms are classified into four categories: evolution-based algorithms, swarm intelligence-based algorithms, physics-based algorithms, and human behavior-related algorithms. These algorithms can approach the optimal solution of a problem, are simple to implement, and exhibit high flexibility. The algorithms can be modified depending on the requirements of the problem to efficiently search the space and avoid falling into local optimum. Hence, many feature selection methods utilize intelligent optimization algorithms to mitigate increasing computational complexity, handle invalid or duplicate features, and aid in analyzing data behavior, thereby reducing computational and storage costs ^[1,2,3,4].

In this context, numerous studies have been conducted, yielding a plethora of viable solutions. These include traditional feature selection methods (such as relevance feature selection and information gain) and population intelligence optimization algorithms (e.g., Harris hawk optimization (HHO) ^[5], particle swarm optimization (PSO) ^[6], gray wolf optimization (GWO) ^[7], and whale optimization algorithm (WOA) ^[8]), all aimed at addressing the feature problem in network intrusion detection.

Despite the establishment of a substantial number of intelligent optimization algorithms for handling feature selection in network intrusion detection, there remains an optimization space in the selection of these algorithms. While there are numerous outstanding options available, their outcomes are not perfect ^[9].

Artificial rabbits optimization (ARO) ^[10], introduced by L. Wang et al. in 2022, is a novel intelligent optimization algorithm. Its robust optimality-seeking ability makes it particularly well-suited for addressing the feature selection challenges in network intrusion detection. When handling large-dimensional data, ARO is prone to settling into the local optimum, leading to unsatisfactory results. The bottlenose dolphin aptimizer (BDO) ^[11], introduced by A. Srivastava et al. in 2022, stands out for its strong pre-probing ability and remarkable convergence speed.

Given the exceptional performance of ARO, scholars have extended its applicability to practical scenarios. To extend network life by reducing energy consumption rates, R. Ramalingam et al. integrated ARO with WSNs, designing the energy efficient cluster formation based on the ARO ^[12]. Y. Wang et al. synergized the aquila optimizer (AO) with ARO, utilizing the hybrid algorithm to address five industrial engineering design problems and photovoltaic model parameter identification challenges ^[13]. Additionally, the ARO, introduced by D. Dangi et al., plays a crucial role in enhancing the performance of robust random vector functional link networks (RRVFLN) by efficiently mitigating hidden layer bias and optimizing the input weights of the RRVFLN model ^[14].

Furthermore, the research in network traffic intrusion detection aims to enhance detection capabilities, striving for both strength and speed to yield superior results in practical applications ^[15]. Notably, H. Alazzam et al. introduced a feature selection method designed for an IDS. The suggested method efficiently reduces the number of features required to construct a robust IDS, preserving a high level of accuracy. Moreover, the proposed cosine similarity method exhibits superior convergence speed compared to the standard sigmoid method ^[16]. Q. M. Alzubi et al. introduced a novel IDS utilizing an enhanced hybrid algorithm that combines binary GWO and PSO. The system efficiently employs a support vector machine for dataset classification and experimentally evaluates the significant enhancement in intrusion detection accuracy using the NSL-KDD dataset ^[17]. A. Alzaqebah et al. employed a modified GWO, incorporating filter and wrapper approaches during the initialization phase. The parameters of the extreme learning machine are subsequently fine-tuned using the enhanced GWO. The final proposed model can minimize data dimensions and eliminate irrelevant and noisy data, effectively enhancing the performance of the IDS ^[18]. M. Injadat et al. proposed a multi-level optimization NIDS framework based on machine learning. The framework utilizes oversampling techniques to determine the minimum suitable training sample size, investigates the impact of various feature selection techniques, and employs hyperparameter optimization to enhance performance. Final experiments demonstrate that the framework effectively reduces computational complexity while maintaining detection performance ^[19]. J. Lee et al. proposed a deep sparse autoencoder (DASE) for extracting and compressing important features, which was then combined with random forest (RF) to form the DASE-RF model. Experimental comparisons demonstrate that the model significantly enhances both detection speed and performance ^[20]. D. Mauro et al. focus on feature selection in machine learning for network intrusion detection. The article introduces and investigates various feature selection algorithms and datasets, validated using a correlation-based feature selector as the objective function. A comprehensive analysis demonstrates that reducing redundant features is practically lossless for feature selection, leading to accelerated training processes and enhanced detection speed ^[21].

Y. Li et al. introduced a hybrid intrusion detection method that incorporates adaptive synthesis and a decision tree based on the ID3. The approach involves employing multiple criteria and comparing various models. Experimental results suggest that this method effectively increases the intrusion detection rate ^[22]. T. Wang et al. introduced a multi-label feature selection method utilizing the Hilbert-Schmidt independence criterion (HSIC) and the sparrow search algorithm. This method aims to identify optimal features by capturing dependencies between features and all labels, employing HSIC as a feature selection criterion. The proposed method demonstrates some effectiveness ^[23]. A. Dahou et al. utilized the reptile search algorithm (RSA) to enhance the IDS in the context of Internet of Things (IoT) environment data. In this approach, the CNN model is employed to filter the optimal subset of features, effectively boosting the performance of the detection system ^[24]. M. Imran et al. proposed a novel approach for anomaly detection that involves optimizing an artificial neural network with a cuckoo search algorithm. The NSL-KDD dataset was employed for real data simulation, and the experiments were assessed through a multi-algorithm comparison to achieve optimal results ^[25].

Next, we present the prior work done by our group. Initially, our team proposed an enhanced butterfly optimization algorithm combined with black widow optimization. The experimental dataset was selected from the UNSW-NB15 dataset, and the results demonstrated that the proposed approach significantly enhances performance while successfully minimizing feature dimensions in the context of feature selection for network intrusion detection ^[26]. Then, our group integrated the classification optimization results of weighted K-nearest neighbor (KNN) with the outcomes of the feature selection algorithm. We proposed a combination strategy of feature selection and weighted KNN based on the integrated optimization algorithm. Experiments demonstrated that this proposed strategy significantly enhances the efficiency and accuracy of network intrusion detection ^[27]. Finally, our group introduced a jumping spider optimization approach, combining the HHO with the tiny hole imaging algorithm (HHJSOA). The experimental section verified the classification accuracy and performance of the HHJSOA using both the UNSW-NB15 dataset and the KDD99 dataset. The experimental findings revealed that it can significantly enhance the classification effect and address performance issues in feature selection applications ^[28]. Furthermore, our team proposed a modified version of the golden jackal optimization (mGJO), which combines two strategies and applies them to intrusion detection in software-defined networks (SDN). Our experiments utilized the novel InSDN dataset, resulting in improved performance across various classification metrics and feature selection ^[29].

Building upon the studies and considerations mentioned above, this paper introduces LBARO, a hybrid algorithm that combines BDO and ARO. Additionally, four strategies are incorporated to collaboratively enhance the original algorithm. Subsequently, the LBARO is employed in the feature selection of network intrusion detection, facilitating the construction of a robust network intrusion detection model. The experiments involve a range of network intrusion detection datasets, along with recent superior algorithms and traditional classical algorithms, for comparative testing and evaluation. The aim is to verify the effectiveness and excellence of the LBARO. The main contributions of this paper are as follows.

1) A novel feature selection model for network intrusion detection is proposed. Four main modules exist in this model. This model is used to solve the feature redundancy problem of the intrusion detection dataset, reduce the feature dimension, and enhance the intrusion detection efficiency and accuracy.

2) In this paper, four strategies are used to synergistically modify ARO. The mud ring feeding strategy helps to enhance the exploration rate. The adaptive switching strategy effectively balances the combined algorithm. The levy flight strategy can provide larger strides to escape from the local optimum. The dynamic lens-imaging learning strategy enhances population richness. The benchmarking function is used to test the performance of LBARO by comparing it with other algorithms.

3) In this paper, the feature selection model incorporating LBARO is proposed, using a binary version of LBARO to search for the optimal subset of features. The experiments are conducted using four UCI datasets (the NSL-KDD dataset, the UNSWNB-15 dataset, and the InSDN dataset) to test the superiority of the proposed model in this paper by comparing the models combined with other algorithms.

2.   Basic algorithms

2.1.   Artificial rabbits optimization algorithm

The ARO is primarily proposed by referencing two survival laws observed in the natural world: meandering foraging and random hiding of rabbits. Specifically, meandering foraging serves as an exploration strategy preventing rabbits from being detected by natural predators, allowing them to graze near their nests. Random hiding is another strategy in which rabbits move to other burrows to hide further away.

2.1.1.   Exploration phase

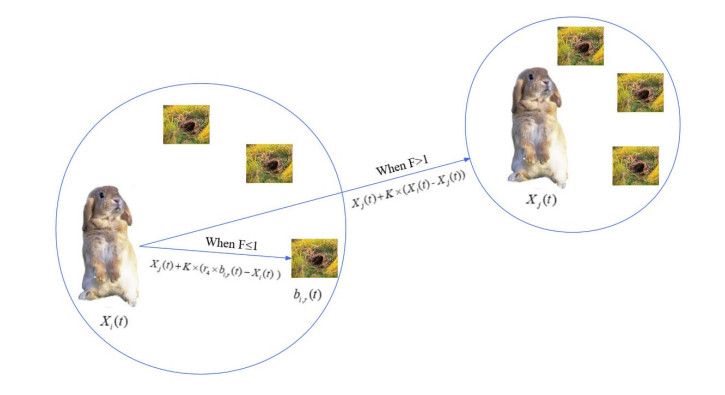
In detour foraging (exploration) within the ARO, it is assumed that each rabbit in the population has its own area with some grass and burrows. During foraging activities, rabbits tend to randomly move far away from other individuals in search of food and ignore nearby food. This behavior is known as meandering foraging, and its mathematical model is expressed as

where $ X_i^{t + 1} $ represents the potential location of the ith rabbit in iteration t + 1; the rabbits' positions in the current iteration t are shown by the symbols $ X_i^t $ and $ X_j^t $, respectively; $ N $ represents the population's size; $ {T_{\max }} $ is the maximum number of iterations, while $ t $ is the current iteration; the size of the dimensions is indicated by $ d $; the randomly selected integer between 1 and D is indicated by $ g $; three random values in the interval [0, 1] are $ {r_1} $, $ {r_2} $, and $ {r_3} $; $ {n_1} $ has a typical normal distribution; and $ L $ is the distance covered by a step in a meandering foraging performance.

2.1.2.   Transition from exploration to exploitation

The energy factor F gradually decreases to maintain a satisfactory equilibrium between exploration and exploitation. The mathematical model for this is expressed as

where $ {r_6} $ is an arbitrary number in the range of 0–1 and the value of the energy factor $ F $ fluctuates between 0 and 2. The search mechanism based on the energy factor $ F $ is depicted in Figure 1.

Figure 1.  Search mechanism based on the energy factor $ F $.

DownLoad: Full-Size Img PowerPoint

2.1.3.   Exploitation phase

Facing chases and attacks from predators is the norm for rabbits. To survive, they dig various holes around their nests as shelters. In each iteration, rabbits always generate burrows along the dimension of the search space and then choose one of them randomly to hide, reducing the probability of being captured. The mathematical model is simulated as follows:

where the parameter $ K $ can be calculated using Eqs (2)–(4), $ {b_{i, r}}^t $ denotes the burrow of the ith rabbit randomly selected among the $ D $ burrows utilized for hiding in the current iteration $ t $, $ {r_4} $ and $ {r_5} $ are two arbitrary values in the range of 0–1, and $ {n_2} $ has a normal distribution.

2.2.   Bottlenose dolphin optimizer algorithm

The hunting technique of the bottlenose dolphin, which mimics the mud ring feeding strategy, serves as the inspiration for the BDO. Dolphins utilize a special hunting tactic called mud ring feeding to both feed and trap fish. Dolphins that live in groups collaborate to find prey early in the hunt. Driver dolphins will guide the population in team hunts to surround the shoal of fish. During the encirclement, the dolphins move their tails along the sand so that they form a plume. The purpose of the plume, which resembles a fishing net, is that the fish become disorientated. At the same time, fish trapped in the plume attempt to jump out of the plume. Due to the jumping behavior of the fish, other members of the dolphin population will surround the position of the plume and capture any fish that reach the plume position. To increase the efficiency of the attack, the dolphins reduce the encirclement. Eventually, as the dolphins approach the location of the captured fish, more fish will jump out to be hunted by the dolphins. During this hunt, other dolphins in the group also generate plumes simultaneously for hunting, enhancing search efficiency.

3.   Modified strategies

In this study, the defects of the ARO are modified from the perspective of synergy, which can make the ARO effective in enhancing the convergence speed, escaping the local optimum and stability. The strategies utilized to modify the performance of the ARO include the mud ring feeding strategy, adaptive switching mechanism strategy, levy flight strategy, and dynamic lens-imaging learning strategy, which utilize the complementary properties of these four strategies to synergistically optimize the original algorithm in all aspects to maximize the gains achieved, as shown in Figure 2.

Figure 2.  Modified approach diagram of the ARO.

DownLoad: Full-Size Img PowerPoint

Initially, a faster search is conducted for the global exploration phase by incorporating the mud ring feeding strategy of the BDO. Then, to better balance the LBARO, the adaptive switching mechanism is introduced to better equilibrate and guide individual search directions. Next, the levy flight strategy is introduced in the local exploitation phase by utilizing the resulting perturbations for variational updates on the original algorithmic positions. Lastly, for better escaping from the local optimum, the dynamic lens-imaging learning strategy is introduced to enhance the exploitation capability.

3.1.   Mud ring feeding strategy

In addition to sluggish convergence and low population diversity in the early exploration phase of the ARO, the detour foraging mechanism lacks the ability to produce enough volatility so that it allows the search agent to completely explore the whole field of search. The mud ring feeding strategy of the BDO is then added to the exploitation phase aimed at enhancing the original algorithm constraints and obtaining superior overall optimization performance. The dolphins collaborate to locate their prey during the exploration phase. The driving dolphin begins to circle the prey area as soon as it has been identified. The movement of the driver dolphin towards the prey location. It is assumed that the current position of the driver dolphin represents the location of the prey. During the search process, this position is searched for a better solution. Therefore, the mud ring feeding strategy of the BDO has excellent exploration ability and fast contraction speed, which can effectively make up for the shortcomings of the ARO ^[30]. The mathematical model for this is expressed as

where $ X_{DD}^{t + 1} $ denotes the updated position of the driver dolphin, $ X_{DD}^t $ denotes the position of the driver dolphin, rand is a random number between [-1, 1], which helps to spread out the search capability, and $ \theta $ is a constant that aids in encircling the place during the search by haphazardly decreasing. $ X_{FD}^{t + 1} $ denotes the updated position of the follower dolphin, $ X_{FD}^t $ denotes the current position of the follower dolphin, denotes the position of the driver dolphin, and $ {a_f} $ is an acceleration factor that accelerates the movement of the follower dolphin towards the driver dolphin.

3.2.   Adaptive switching mechanism strategy

The meandering foraging strategy of the ARO can still provide some guarantee for the survival of the rabbits, although it suffers from the problems of poor volatility and slow convergence to a certain extent. The mud ring feeding strategy introduced is not a direct replacement for the detour foraging strategy. To further optimize the balance between the two, an extra parameter that directs the search direction must be added to the combined algorithm. Therefore, this paper introduced an adaptive switching mechanism of one kind ^[31]. The mathematical model for this is expressed as

where $ {E_0} $ is a random value that ranges between -1 and 1, $ {E_1} $ is a control parameter that decreases linearly, $ t $ is the current iteration number, and $ {T_{\max }} $ is the maximum iteration number. The global exploration phase of the algorithm occurs when |$ E $| ≥ 1, while the local exploitation phase occurs when |$ E $| < 1. $ {E_1} $ drops consistently to improve the balance between the phases of exploration and exploitation.

3.3.   Levy flight strategy

When rabbits face predators, they will use the holes dug around the nest as hiding places out of the need for survival. At this point, the random number $ {r_4} $ utilized to generate the perturbation can, to some extent, provide a small range of changes in the location of the update mutation so that the rabbit's choice of hiding place has a certain degree of randomness. However, as the ARO iterates, the fluctuation of random numbers shows relatively weak performance and may not provide sufficient leaps when facing the local optimum. Consequently, the ARO might lead to the capture of the rabbit, resulting in getting trapped in the local optimum. Thus, at this point, the levy flight strategy can generate random numbers with larger spans, providing more variables for replacing the random number $ {r_4} $ ^[32]. Since the stochastic hiding phase is the exploitation phase, levy flight enhances the spatial search capability and the ability of the ARO to escape from the local optimum. This effectively searches for the global optimal solution in the iterations of the ARO ^[33]. The mathematical model for this is expressed as

where $ \alpha $ is fixed at 0.15; $ u $ and $ v $ follow Gaussian distributions with mean 0 and variances $ {\sigma _u}^2 $ and $ {\sigma _v}^2 $, respectively; The conventional gamma function is represented by $ \Gamma $; and the correlation parameter, which is set to 1.5, is represented by $ \gamma $.

3.4.   Dynamic lens-imaging learning strategy

In this paper, the levy flight strategy is adopted to disturb the position update to enhance the exploitation ability of the ARO locally and to enhance the rabbit's chance of survival. Nevertheless, if one only uses the levy flight strategy, the goal of preventing the ARO from reaching the local optimum is defeated by a probabilistic solution. Therefore, the dynamic lens-imaging learning strategy is introduced after each algorithm iteration. It improves the local optimal ability of the ARO and prevents sliding into iterative stagnation. The survival potential of the rabbits has been effectively boosted. The dynamic lens-imaging learning strategy has been recently proposed ^[34,35]. It is derived from the opposition-based learning method. This strategy derives the law of convex lens imaging from the law of optics. It is based on the principle of refracting a solid from one side to the other through a convex lens to generate an inverted image.

where $ub$ and $lb$ are the upper and lower bounds, respectively, and $ X $ and $ {X^{'}} $ are the individual and its opposing individual, called the scale factor, respectively. The scaling factor $ \varphi $ improves the local exploitation of the original algorithm. The scaling factor is typically regarded as a constant in the original lens imaging learning strategy, which reduces the convergence performance of the original algorithm. Therefore, a new nonlinear dynamically decreasing scale factor based on nonlinear dynamics is introduced, which allows for larger values to be obtained in the early iterations of the modified algorithm. Thus, the modified algorithm is able to search in a wider range of different dimensional regions and enhance the diversity of the population. Smaller values are obtained towards the end of the modified algorithm iterations, enabling a refined search in the proximity of optimal individuals to further enhance the resolution of the local optimum.

As the population is more likely to fall into the local optimum during the exploitation phase, the dynamic lens-imaging learning strategy was adopted for the iterated population of the LBARO. In each iteration, the positions of the population are randomly altered based on both the total number of individuals in the current population and the fitness of the best solution, which is computed and maintained. This is done to further enhance population variety and prevent local optimum.

3.5.   Proposed algorithm

The LBARO is constructed based on the ARO and consists of four main components. First, by combining the mud ring feeding strategy with ARO, which takes advantage of the rapid convergence rate of strategy in updating the position, the global exploration capability is improved. The introduction of an adaptive switching mechanism facilitates the adjustment between the exploration and exploitation phases. To prevent subsequently falling into the local optimum, the levy flight strategy is also implemented during the local exploitation phase of the ARO. Lastly, the dynamic lens-imaging learning strategy is presented to provide better positional variability while also improving population variety and stochastically optimizing the population. This helps the population avoid stagnating in the local optimum. The execution phases of the LBARO are displayed below. The flowchart of LBARO is depicted in Figure 3, and its pseudo-code description is provided in Algorithm 1.

Figure 3.  Flow chart of the LBARO.

DownLoad: Full-Size Img PowerPoint

3.6.   Time complexity

The time complexity can effectively measure the running efficiency of the algorithm. Time complexity is undoubtedly one of the very important performance metrics. An in-depth discussion of time complexity can provide a better understanding of the performance characteristics of algorithms and provide guidance for practical applications. The excellence of an algorithm depends not only on the quality of individual metrics but also on whether the complexity of the algorithm has increased. In the feature selection of network intrusion detection, an excess of redundant features can decrease detection efficiency, while the algorithm's operational speed also impacts the overall system performance. Therefore, one of the requirements for enhancing the algorithm is to minimize increases in complexity while building upon the original algorithm. According to the pseudo-code in Algorithm 1, the overall time complexity is determined by the population size (N), the maximum number of iterations (T), and the dimensionality (D). The time complexity of ARO can be expressed as O(1 + N + T × N +× T × N × D +× T × N × D), which is O(N + NT + NDT). During the initialization phase of LBARO, the rabbit locations are randomly generated, requiring a time complexity of O(N). Throughout the iterative phase of LBARO, the time complexity of evaluating the rabbit's frontal fitness and updating its position is O(N × T + N × D × T). Hence, the time complexity of LBARO remains O(N + NT + NDT), indicating no increase compared to ARO.

4.   Proposed model

For network intrusion detection, the corresponding feature selection model was constructed with the LBARO, as illustrated in Figure 4. Feature selection of network intrusion detection model based on the LBARO can be divided into four core modules according to their functional roles: the data acquisition module, the data pre-processing module, the feature selection module, and the model evaluation module ^{[36,37,38,39]}.

Figure 4.  Feature selection model based on LBARO.

DownLoad: Full-Size Img PowerPoint

1) Data acquisition module

The rapid development of the Internet era results in a substantial and cumbersome redundancy of network data, necessitating its analysis. Therefore, it is necessary to collect the network reality traffic data through relevant tools. To generate a dataset for further analysis of the data, the network data collection component primarily gathers the network data packets that the host obtains from the network. In the study, four datasets (UCI, NSL-KDD, UNSW-NB 15, and InSDN) are utilized as simulations of realistic network data.

2) Data pre-processing module

The data collected in the actual network is generally dirty data, and there are usually problems such as missing numbers, data noise, data inconsistency, data redundancy, unbalanced data sets, outliers, and data duplication. Therefore, before using the data, effective data cleaning must be carried out.

The first phase involves cleaning the data, which includes identifying and eliminating anomalous data, handling missing or incorrect data, and getting rid of duplicate data. The data is consistently classified as numerical in the second stage. This is done to prevent the occurrence of later experimental input value format inconsistency by transforming the character type or other types of data using label coding. The third step of the normalization process is carried out, utilizing the normalization function to process the data to tackle the problem of the substantial disparities in the dimensions of the attributes of the dataset species utilized in this work. The procedure maps all the data values into the [0, 1] interval, which can achieve the aim of converting the un-normalized data into normalized data to increase the accuracy of feature selection.

3) Feature selection module

After the dataset is crawled from the web and undergoes data cleaning, simple data filtering has been performed to some extent. There will still be an overwhelming number of redundant features that are invisible to the unaided eye, though, because network data is typically very vast. These characteristics greatly increase the complexity of detecting network intrusions, decreasing the rate of detection and taking an unnecessary amount of time. Thus, the existence of feature selection provides further processing of the dataset before intrusion detection. This effectively reduces redundant features, reduces the amount of data, and improves the detection correctness.

Next, the preprocessed dataset undergoes an iterative optimization search conducted by an intelligent optimization algorithm. The population of rabbits forages and avoids obstacles in search of a better place with each generation. When the iteration concludes, the algorithm obtains where the current ideal location exists, which is the index of the optimal subset. At this point, the module obtains the optimal feature subset selection to achieve the aim of de-redundant feature subsets and data dimensionality reduction.

4) Model evaluation module

Evaluating the classifiers means estimating the average degree of correctness of the classifiers' decisions at the time of prediction. Common classifiers are SVM classifier, KNN classifier, K-means classifier, and plain Bayesian classifier. Therefore, it is necessary to select or design the classification effect evaluation metrics according to the characteristics of the scene. In the paper, a suitable KNN classifier is utilized for evaluation.

Following the feature selection by the algorithm, the dataset is obtained concerning dimensionality reduction. At this point, the KNN classifier is invoked and the dataset of the optimal feature subset optimized by LBARO is provided as an input parameter to the classifier. After the prediction by the classifier, the data relevant to the classification is collected. Finally, to evaluate the overall model performance, metrics such as accuracy, recall, precision, and F1-score are employed, all of which are commonly utilized to assess classification effectiveness.

5.   Experimental results

5.1.   LBARO capability test

5.1.1.   Experimental environment

The experimental tests were carried out in a single setting to guarantee the objectivity and fairness of experiments. The Intel Core i5-12490F CPU@3.00 GHz processor type, the Windows 11 operating system, and the MATLAB 2022b programming language are all utilized in the experimental setup.

5.1.2.   Benchmark function

For this experiment, eight common benchmark test functions were selected, comprising four single-peak functions (f1–f4) and four multi-peak functions (f5–f8), chosen with moderate concentrations ^[40]. The experiment involves a degree of randomness. The test functions in the experiment were run independently multiple times. The benchmark test functions are depicted in Table 1.

Table 1.  Benchmark function expressions.

Function expressions	Dimension	Range	fmin
$ {f_1}(x) = \sum\limits_{i = 1}^n {x_i^2} $	30	[-100,100]	0
$ {f_2}(x) = \sum\limits_{i = 1}^n {\left| {{x_i}} \right|} + \prod\limits_{i = 1}^n {\left| {{x_i}} \right|} $	30	[-10, 10]	0
$ {f_3}(x) = \sum\limits_{i = 1}^n {{{\left({\sum\limits_{j - 1}^i {{x_j}} } \right)}^2}} $	30	[-100,100]	0
$ {f_4}(x) = {\max _i}\left\{ {\left| {{x_i}} \right|, 1 \leqslant i \leqslant n} \right\} $	30	[-32, 32]	0
$ {f_5}(x) = \sum\limits_{i = 1}^n { - {x_i}} \sin (\sqrt {\left| {{x_i}} \right|}) $	30	[-500,500]	-418.9829 × D
$ {f_6}(x) = - 20\exp \left({ - 0.2\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {x_i^2} } } \right) - \exp \left({\frac{1}{n}\sum\limits_{i = 1}^n {\cos (2\pi {x_i})} } \right) + 20 + e $	30	[-32, 32]	0
$ $$\begin{array}{l} {f_7}(x) = \frac{\pi }{n}\left\{ {10\sin (\pi {y_i}) + \sum\limits_{i = 1}^{n - 1} {{{({y_i} - 1)}^2}\left[{1 + 10{{\sin }^2}(\pi {y_{i + 1}})} \right] + {{({y_n} - 1)}^2}} } \right\} \hfill \\ + \sum\limits_{i = 1}^n {u({x_i}, 10,100, 4)} \hfill \\ {y_i} = 1 + \frac{{{x_i} + 1}}{4} \hfill \\ u({x_i}, a, k, m) = \left\{ \begin{array}{l} k{({x_i} - 1)^m}, {x_i} > a \hfill \\ 0, - a < {x_i} < a \hfill \\ k{(- {x_i} - a)^m}, {x_i} < - a \hfill \end{array}$$ \right\} \hfill \end{array} $	30	[-50, 50]	0
$ {f_8}(x) = - \sum\nolimits_{i = 1}^7 {{{\left[{(X- {a_i}){{(X- {a_i})}^T} + {c_i}} \right]}^{ - 1}}} $	4	[0, 10]	-10.5363

---

 | Show Table

DownLoad: CSV

5.1.3.   Benchmark function results

Table 2 provides the parameters of each algorithm. The average optimal value, average worst value, average value, and standard deviation of the four algorithms, AO, GWO, ARO, and LBARO, are calculated independently and run thirty times on single-peak and multi-peak test functions.

Table 2.  Parameterization.

Algorithms	Parameter values
AO	α = 0.1, δ = 0.1
PSO	c1 = 2, c2 = 2
ARO	—
LBARO	d1 = 100, d2 = 10, af = 3.5

---

 | Show Table

DownLoad: CSV

The fitness graph in Figure 5 illustrates how the LBARO converges more rapidly and accurately than alternative algorithms. Further evidence of LBARO's superior stability and results is presented in Table 3. This demonstrates that the LBARO can balance exploration and development while achieving a faster and more accurate convergence rate throughout the global exploration stage. It can enhance the population richness in the local exploitation phase and effectively avoid falling into the local optimum. As a result, the LBARO has better ability and more robustness under the iterative optimization of the same algorithm.

Figure 5.  Convergence curves of fitness.

DownLoad: Full-Size Img PowerPoint

Table 3.  Benchmark function results.

Function	Algorithms	Min	Max	Ave	Std
F1	AO	1.79E-158	1.32E-103	4.44E-105	2.41E-104
	PSO	9.79E-01	4.36E+00	2.58E+00	8.57E-01
	ARO	6.75E-70	1.93E-55	7.85E-57	3.62E-56
	LBARO	0.00E+00	0.00E+00	0.00E+00	0.00E+00
F2	AO	4.47E-84	2.49E-67	8.30E-69	4.55E-68
	PSO	2.21E+00	8.09E+00	4.41E+00	1.49E+00
	ARO	6.14E-39	5.16E-29	1.73E-30	9.41E-30
	LBARO	0.00E+00	1.76E-188	5.87E-190	0.00E+00
F3	AO	1.53E-155	1.74E-102	6.53E-104	3.18E-103
	PSO	9.91E+01	2.83E+02	1.86E+02	5.00E+01
	ARO	2.63E-55	1.62E-42	1.25E-43	4.05E-43
	LBARO	0.00E+00	0.00E+00	0.00E+00	0.00E+00
F4	AO	1.09E-80	9.30E-53	3.10E-54	1.70E-53
	PSO	1.52E+00	2.36E+00	2.00E+00	2.00E-01
	ARO	2.16E-29	8.77E-23	6.05E-24	1.98E-23
	LBARO	6.15E-143	4.03E-110	1.34E-111	7.36E-111
F5	AO	-4.03E+03	-2.76E+03	-3.35E+03	2.84E+02
	GWO	-8.66E+03	-3.30E+03	-6.12E+03	1.26E+03
	ARO	-1.02E+04	-8.53E+03	-9.28E+03	4.36E+02
	LBARO	-1.24E+04	-9.02E+03	-1.05E+04	1.09E+03
F6	AO	4.44E-16	4.44E-16	4.44E-16	0.00E+00
	GWO	1.66E+00	3.44E+00	2.66E+00	4.72E-01
	ARO	4.44E-16	4.44E-16	4.44E-16	0.00E+00
	LBARO	4.44E-16	4.44E-16	4.44E-16	0.00E+00
F7	AO	7.35E-09	1.80E-05	3.12E-06	5.13E-06
	GWO	7.97E-03	4.19E-01	6.22E-02	7.89E-02
	ARO	1.18E-05	2.13E-04	5.63E-05	4.11E-05
	LBARO	1.57E-32	1.57E-32	1.57E-32	5.57E-48
F8	AO	-1.04E+01	-1.03E+01	-1.04E+01	2.45E-02
	PSO	-1.04E+01	-2.75E+00	-8.47E+00	2.96E+00
	ARO	-1.04E+01	-2.77E+00	-9.39E+00	2.33E+00
	LBARO	-1.04E+01	-1.04E+01	-1.04E+01	0.00E+00

---

 | Show Table

DownLoad: CSV

5.2.   Feature selection fitness function

Combining feature selection with intelligent optimization algorithms is a superior approach because of the advancement and growth of these algorithms in recent years, which has increased their effectiveness. The performance of the feature subset is significantly affected by the number of selected features and the classification error rate. The evaluation function in question is displayed as follows:

where $Er$ is the classification error rate of the specified classifier, Fitness is the ideal value of a workable solution as represented by a single member of the population, $ Se $ is the quantity of chosen feature subsets, Fe represents the total features, $\alpha $ and $\beta $ denote the two weights, with $\alpha $ set to 0.99 and $\beta $ to 0.01.

This work presents the introduction of the sigmoid function to LBARO, enabling its conversion to binary LBARO for discrete situations. The binary version of the LBARO is utilized in this study for feature selection. The population members act as the seeking agents, and the locations of agents are obtained through the iterations of the algorithm. The population is transformed into a binary encoded population with individuals described as ${{\text{X}}_{id}}$, where $d$ is the feature dimension, via the conversion function. The characteristics of this workable solution are chosen when ${{\text{X}}_{id}}$ = 1. Otherwise, it is not chosen ^[41]. The following formula displays its transformation function:

5.3.   Experimental parameters

In the experimental context, the experimental algorithms are AO, GWO, ARO, and LBARO, and different datasets will be generated to examine the overall performance of the respective models. The experiment selects a variety of datasets, offering varied test conditions and data as much as feasible. It can verify the ability of redundant features and inspect the perfection of the overall model performance. The experimental settings were set: the K-fold cross-validation multiplier was 10, the population size N = 30, and the number of iterations T_max = 50.

Table 4.  Parameterization.

Parameters	Numbers
K-fold cross-validation multiplier	10
Population size	30
Maximum iterations	50

---

 | Show Table

DownLoad: CSV

5.4.   UCI dataset

The UCI dataset is employed to evaluate the efficacy of the LBARO in dimensionality reduction ^[42]. Four UCI datasets are selected as test objects, and their complete information is provided in Table 5. Table 6 indicates the experimental outcomes of UCI datasets.

Table 5.  UCI dataset.

Number	Dataset name	Sample size	Number of features
1	Ionosphere	351	34
2	Vehicle	846	18
3	Heatstatlog	270	13
4	Sonar	208	61

---

 | Show Table

DownLoad: CSV

Table 6.  Test results of the UCI.

Algorithms	Metrics	Ionosphere	Vehicle	Heatstatlog	Sonar
AO	Accuracy	0.933	0.759	0.864	0.887
	Recall	0.970	0.828	0.758	0.871
	F1-score	0.948	0.873	0.820	0.885
	Precision	0.928	0.923	0.893	0.900
PSO	Accuracy	0.867	0.779	0.877	0.871
	Recall	0.955	0.857	0.758	0.903
	F1-score	0.900	0.909	0.833	0.875
	Precision	0.851	0.968	0.926	0.848
ARO	Accuracy	0.905	0.762	0.864	0.920
	Recall	0.970	0.812	0.758	0.935
	F1-score	0.928	0.881	0.820	0.921
	Precision	0.889	0.963	0.893	0.906
LBARO	Accuracy	0.943	0.778	0.889	0.935
	Recall	0.985	0.867	0.758	0.968
	F1-score	0.956	0.912	0.847	0.938
	Precision	0.929	0.963	0.962	0.909

---

 | Show Table

DownLoad: CSV

The LBARO achieved the highest scores across all four classification metrics on the Ionosphere, Heatstatlog, and Sonar datasets in the experiment. Its classification performance is significantly superior to the other algorithms.

The accuracy and precision of the vehicle dataset are marginally worse than those of the PSO, but generally, the effect is the best and the other metrics remain fantastic. Though the classification performance is still inferior to the three comparison methods, the LBARO achieves an outstanding overall ranking in terms of score.

5.5.   NSK-KDD dataset

The NSL-KDD dataset is the modified edition of the KDD99 dataset ^{[43,44,45,46]}. It emerged as the solution to several intrinsic issues, for instance the duplicate record issue. The NSL-KDD dataset is divided into two subsets: a training set and a test set.

The NSL-KDD dataset, which consists of 41 features with one column of labelled characteristics, is utilized for classification testing. The dataset includes four attack types: denial of service (DoS), probing, user to root (U2R), and remote to local (R2L). The labels for the typical type of data are assigned to 0, while the labels for the four types of aberrant attacks are set to 1. Following the deletion of the features in columns 10–22 of the dataset, all the data are normalized. The features of non-essential network connection records are also removed. Additionally, 10% and 5% of the training and testing sets, respectively, are randomly chosen for testing. ROC curve is presented in Figures 6 and 7, while corresponding test data is provided in Tables 7 and 8.

Figure 6.  ROC curve of 5% NSL-KDD.

DownLoad: Full-Size Img PowerPoint

Figure 7.  ROC curve of 10% NSL-KDD.

DownLoad: Full-Size Img PowerPoint

Table 7.  Classification results of 5% NSL-KDD.

Metrics	AO	PSO	ARO	LBARO
Accuracy	0.813	0.802	0.797	0.831
Recall	0.957	0.938	0.973	0.951
F1-score	0.815	0.804	0.805	0.829
Precision	0.710	0.703	0.687	0.734
Number of features	10	14	12	6

---

 | Show Table

DownLoad: CSV

Table 8.  Classification results of 10% NSL-KDD.

Metrics	AO	PSO	ARO	LBARO
Accuracy	0.803	0.843	0.806	0.846
Recall	0.969	0.958	0.970	0.969
F1-score	0.809	0.840	0.812	0.845
Precision	0.694	0.748	0.700	0.749
Number of features	10	15	15	11

---

 | Show Table

DownLoad: CSV

The results gathered from the experiments on the 5% dataset are indicated in Table 7. The LBARO outperformed the other three algorithms in all three metrics, except for recall. Additionally, accuracy has increased by 1.8–3.4% when compared to the other algorithms. These findings suggest that the modified algorithm has a clear accuracy in classification and does not exhibit any glaring classification errors. With a 1.4–2.5% increase in the F1-score, it can be said that the updated method more effectively balances recall and precision and can benefit from both effects simultaneously. LBARO is precisely accurate in classifying the data samples as positive classes, and the occurrence of incorrect predictions is significantly minimized. The precision is enhanced by 2.4–4.7%. Additionally, by reducing the number of chosen feature values to six, a significant number of redundant features are eliminated, which lessens the workload associated with intrusion detection and boosts its efficiency. This suggests that for the effect of feature selection on a 5% dataset, the LBARO performs best overall.

The results gathered from the experiments on the 10% dataset are indicated in Table 8. The data in the table illustrates that while the recall of the AO and LBARO is the same, the accuracy and F1-score of the LBARO are significantly higher than those of the AO. The modified algorithm performs better overall and has a more comprehensive effect than the original PSO and ARO, which were the least effective and ranked low for the number of features selected. This suggests that the feature selection of the LBARO on the 10% dataset yields the best overall performance. The results indicate that with feature selection on 10% of the dataset, the LBARO output reflects its best overall performance.

The ROC curve is intuitively effective in reflecting the excellence of the classifier's performance. The extent to which the ROC curve is leaning towards the upper-left corner determines the excellence of the classifier. The comparison indicates that, for different numbers of subsets taken from the NSL-KDD dataset, the results are all that the curve curvature of LBARO is more towards the upper left corner. Its classification accuracy is the most superior.

5.6.   UNSW-NB 15 dataset

The UNSW-NB15 dataset is available for network intrusion detection. It is a public dataset. It is provided by the Network Security Laboratory at the University of New South Wales in Sydney ^[47,48]. The dataset simulates network traffic in a real network environment and contains a variety of common network attacks and normal traffic. The UNSW-NB 15 dataset contains 175,341 network connection records, which include summary information, network connection characteristics, and traffic statistics. The network connections in the dataset are labelled as normal traffic or with different types of attacks such as DoS, scanning, intrusion, etc. In addition, it contains a detailed description of the attacks and a categorization of the attack types.

UNSW-NB 15 dataset preparation. Firstly, deleting superfluous features, and removing ID features in the dataset, is only the data serial number. Secondly, the data is numericized, comprising the features proto, service, status, and attack_cat, and their numerical values are processed. In the proto attribute, since its values are too varied and yet certain data are too little, the three most essential values of network traffic TCP, UDP, and ICMP are mapped to 1, 2, and 3, respectively, and the rest of the values are mapped to 4. The rest of the non-numerical properties are changed according to the natural number ordering. The data is then normalized.

Table 9 shows the data results of the experiments on the UNSW-NB 15 dataset 10,000 dataset. Based on the data, LBARO scores higher than the other three algorithms in all three metrics except the precision rate, and the comparison shows that the improvement exists at most 0.6%, 2.19%, and 0.85% effect enhancement in the accuracy, recall, and F1-score respectively. Additionally, the final method reduces feature values to 12, thereby filtering out superfluous redundant features and decreasing intrusion detection effort while also increasing intrusion detection efficiency. According to the statistics, the LBARO performs the best overall when it comes to how feature selection affects the UNSW-NB 15 dataset.

Table 9.  Classification results of UNSW-NB 15.

Metrics	AO	PSO	ARO	LBARO
Accuracy	0.9210	0.9217	0.9260	0.9270
Recall	0.9303	0.9130	0.9302	0.9349
F1-score	0.8966	0.8956	0.9024	0.9041
Precision	0.8652	0.8788	0.8763	0.8753
Number of features	12	21	13	12

---

 | Show Table

DownLoad: CSV

The iterative fitness curve results of the algorithms are presented in Figure 8. The number of folds in the fitness curve can indicate the LBARO's effectiveness in avoiding local maxima, while the curve's steepness and height can reflect its ability to find iterative maxima in a given environment. The fitness curve in the figure illustrates that LBARO can achieve a higher fitness value and a reduced error with the same population size and number of repetitions. The frequency of zigzags in the curve indicates that LBARO consistently navigates out of the local optimum and approaches the optimal solution more efficiently during the procedure.

Figure 8.  Fitness curves of UNSW-NB 15.

DownLoad: Full-Size Img PowerPoint

The LBARO has the best classification accuracy, as demonstrated by the comparison of the ROC curve in Figure 9, which indicates superior results. With a value range of [0, 1], the AUC value can also, to some extent, represent the classifier's performance. As can be seen from the bar chart in Figure 10, the AUC values of the modified algorithm are also all higher than the other algorithms and are closer to 1. These results signify the authenticity of its detection method, rendering it notably valuable.

Figure 9.  ROC curves of UNSW-NB 15.

DownLoad: Full-Size Img PowerPoint

Figure 10.  AUC results of UNSW-NB 15.

DownLoad: Full-Size Img PowerPoint

5.7.   InSDN dataset

The SDN concept was introduced by Prof Mckeown in 2009. It has been gaining more and more acceptance and has also been utilized and implemented in numerous data centers ^[49,50]. It can be challenging for manufacturers to address the numerous vulnerabilities and dangers posed by developing technology. Consequently, the deployment of IDS is an important component of the network architecture. The aim is to monitor the network for the presence of malicious activities. No existing publicly available dataset can be directly utilized for anomaly detection systems applied in SDN networks. InSDN by Nhien-An Le-Khac first generated a comprehensive SDN dataset to validate IDS's performance. The new dataset includes benign and various attack categories that can occur in different elements of the SDN platform. 343,939 instances total are included in the dataset for both normal and attack traffic, with 68,424 instances coming from normal data and 27,515 instances from attack traffic.

Classification test on the InSDN dataset. There are three files in the InSDN dataset, in which Normal_data.csv is the normal data, and the remaining two files, metasploitable-2.csv, and OVS.csv are the anomalous attack information. The label "normal" is assigned the value 0, while the remaining anomalous data is labelled with 1. After normalizing the data, 10,000 random data points are taken from the data set for testing.

Table 10 presents the results of the experiments on the 10,000-item InSDN dataset. From the presented data, it is evident that LBARO performs well overall. Although it ranks second in the number of selected features, there is no significant difference compared to AO, and both achieve better results. Furthermore, the score data for the other four performance indicators surpasses that of other algorithms, all showing improvements in their metrics. The comprehensive evaluation reveals that LBARO enhances detection accuracy by effectively reducing redundant features and improving detection rates. Therefore, it can be concluded that LBARO’s feature selection effect on the InSDN dataset is relatively superior and leads to certain performance improvements.

Table 10.  Classification results of InSDN.

Metrics	AO	PSO	ARO	LBARO
Accuracy	0.9857	0.9860	0.9863	0.9900
Recall	0.9837	0.9837	0.9845	0.9861
F1-score	0.9825	0.9829	0.9833	0.9877
Precision	0.9813	0.9821	0.9821	0.9894
Number of features	5	15	14	6

---

 | Show Table

DownLoad: CSV

The iterative fitness curve results of the algorithm are presented in Figure 11. At this point, for the zigzag frequency of the fitness curves, the test results in the InSDN dataset are similar to those in the UNSWNB-15 dataset. It indicates that the excellence of LBARO can be effectively demonstrated in different datasets as well. Moreover, upon zooming in on Figure 12, the discernible ROC curve exhibits a more pronounced upper-left corner, indicating a superior classification effect based on the evaluation criteria. As depicted in the bar chart in Figure 13, while all four algorithms exhibit improved effectiveness, the AUC value of the modified algorithm remains the highest, underscoring the authenticity of its detection method.

Figure 11.  Fitness curve of InSDN.

DownLoad: Full-Size Img PowerPoint

Figure 12.  ROC curve of InSDN.

DownLoad: Full-Size Img PowerPoint

Figure 13.  AUC results of InSDN.

DownLoad: Full-Size Img PowerPoint

6.   Conclusions

This work synergistically modifies the ARO by utilizing four approaches. By absorbing the mud ring feeding strategy of the BDO, the advantages of its global exploration ability and fast convergence speed are taken advantage of. The shortcomings of the ARO, with poor global exploration ability and slow convergence speed, are compensated. In the meantime, an adaptive switching mechanism is presented to guide the equilibrium between the original algorithm and the mud ring feeding strategy. Also, to take advantage of its capacity to produce giant strides and cause the algorithm to deviate as much as possible from the local optimum, the levy flight strategy is implemented during the local exploitation phase. Then, the dynamic lens-imaging learning strategy is introduced to further enhance the perturbation ability. This strategy aims to improve the ARO's overall performance by increasing the population richness of the populations. At this point, the LBARO is adopted to construct a feature selection model for network intrusion detection, which effectively overcomes the issue of the existence of unduly duplicated features in the network intrusion detection dataset. The experimental design examines the model integrated with various algorithms, and the conclusions are as follows:

1) The exploration ability of the ARO can be effectively enhanced by the LBARO, ensuring that the iteration process can converge rapidly. Additionally, the exploration and exploitation of the LBARO are more balanced, and the last larger volatility and population richness enhancement can make it easier for the LBARO to escape the local optimum.

2) Four benchmark functions, four single-peaks, and four multi-peaks, are utilized to evaluate the performance of the LBARO. The findings indicate that, compared with other algorithms, the LBARO obtains the minimum values and lowest standard deviation and converges more rapidly. It exhibits superior stability and an improved ability to approach the ideal.

3) The study presents a novel LBARO-based feature selection model for network intrusion detection. It excels in both dimensionality reduction and detection rate enhancement, securing the top-ranking position in overall tests conducted on four distinct types of network datasets simulating real network traffic data.

In the era of big data, data analysis is imperative. Differences in analyzed data can directly affect the generation of economic value and the yield of social benefits. However, the data contains unnecessary characteristic features. This undoubtedly causes a significant impact on the accuracy of data prediction and analysis, among other issues. To improve the quality of data, a significant volume of duplicated network traffic must be subjected to data dimensionality reduction. The research demonstrates that the processing of network traffic data can be solved using feature selection in the network intrusion detection model.

The network traffic data that has undergone dimensionality reduction processing can significantly improve the accuracy and prediction time of the ensuing prediction and offer a certain implementation baseline for actual data processing. Currently, this research only considers the experimental comparison of binary classification on four network datasets. To improve the performance of the proposed model and strengthen its stability, additional network datasets will be employed in further research to provide a more complete data classification scenario.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work has been supported by the National Natural Science Foundation of China under Grant 61602162 and Hubei Provincial Science and Technology Plan Project under Grant 2023BCB041.

Conflict of interest

The authors declare no conflict of interest.