Cytosine methylation is one of the most studied epigenetic modifications and its occurrence has been deeply studied in mammals and plants. DNA methylation (together with other epigenetic modifications of DNA and histones) plays an important role in different processes. Indeed, several morphological and/or behavioural traits may origin as a consequence of the epigenetic modulation of genes so that identical genes can results in different “morphs”. Despite considerable progress during recent years, many questions remain since it is largely unknown how the environment triggers alterations in the epigenome. In the present review we discuss the use of aphids and honey bees as epigenetic experimental model to understand how cytosine methylation is directly or indirectly linked to environmental factors. Indeed, the epigenetic changes of DNA could be at the basis of unexpected morphological differences explaining also complex traits.
1.
Introduction
Networks arise in all areas of science and engineering whenever we study the interactions between discrete actors [4]. To understand the functioning of the brain, it is critical to know which regions are sending signals to which other regions [8]. In ecology, the goal may be to understand the structure of the food web, that is, to identify which organisms depend on which others for sustenance [10]. In social science or epidemiology, the question may be to identify links between people along which information or disease might spread [14]. Similarly, financial regulators often wish to understand the interdependence of financial institutions that are enmeshed by a web of investments and loans, in order to determine how a shock might ripple through the community [26].
The network topology is not known explicitly in most of these real-world examples, thereby calling for data-driven computational methods to identify links from time-series collected at each node. In this process of network inference, one seeks to determine which actors influence the dynamics of which other actors, from the joint time evolution of their states. Despite considerable progress in network inference, the precise quantification of the errors associated with the implementation of these methods remain elusive. This is the motivating question for the present study.
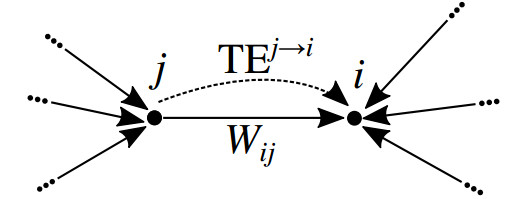
In mathematical terms, a network is modeled by a graph $ \Gamma = (\mathcal{V}, \mathcal{E}) $, a collection $ \mathcal{V} $ of vertices (or nodes), some subset of which are connected pairwise by a set $ \mathcal{E} $ of edges (or links) [12]. In particular, we consider weighted directed networks, in which each edge is interpreted as beginning at a node $ j $ and end ending at a node $ i $, and to which there is associated a scalar weight $ W_{ij} $. With respect to network inference, given two nodes $ i $ and $ j $, one seeks to infer if node $ j $ influences the behavior of node $ i $ and, in addition, the strength $ W_{ij} $ of that influence. In particular, the interest is in direct influence, that is, if node $ i $ depends on node $ j $ and node $ j $ on node $ k $, then node $ k $ influences node $ i $, but perhaps only indirectly, and it is important to distinguish this from the direct influence of $ j $ on $ i $.
In an authentic model-free vein, information theory provides a mathematical framework for drawing such inferences based solely on time-series [5]. Information theory grew out of the effort to understand the transmission of signals along noisy communication channels and has strong connections both with statistical physics and with optimal strategies for gambling and investment [9]. The information in an event is associated with the uncertainty in its outcome, with unlikely events possessing more information. Information may flow among the units of a network, and can be used to reconstruct its topology. For example, Squartini and colleagues [26] have recently reviewed information-theoretic results for network inference, focusing on financial networks, and Wibral and colleagues [30] have presented an overview of the state-of-the-art of information-theoretic methods in neuroscience.
Introduced almost twenty years ago by Schreiber [25] to quantify asymmetries in coupled dynamical systems, transfer entropy is emerging as an approach of choice to guide the process of network inference from time-series. A thorough survey of its mathematical properties and many applications is provided in [6]. Given a pair of time-series, transfer entropy measures the reduction in uncertainty in predicting the future state of one of the time-series from its present value, compared with predicting its future state from both its present value and that of the second series. In the context of network inference, one predicts that a link is present from node $ j $ to node $ i $ given a value of transfer entropy from node $ j $ to node $ i $ that is statistically different from zero.
While network inference based on transfer entropy is intuitive and computationally inexpensive, it is not free of technical limitations that may beget false positive and negative results. Most of these limitations are rooted in the pairwise definition of transfer entropy that does not contemplate the existence of indirect influence from any other node in the network. Extending the transfer entropy definition to multivariate interactions could address some of these limitations, but it would require the estimation of high dimensional probability mass functions that could be computationally unfeasible beyond simple motifs [6]. While Runge [24] and Sun and colleagues [28] pinpoint several pathological instances in which transfer entropy-based network reconstruction can fail, we currently lack analytical results that can help assess the accuracy of the inference and determine scenarios where false results should be expected. Filling this gap in knowledge is the chief aim of this study.
Specifically, we continue the mathematically-principled treatment of a random Boolean network (RBN) model proposed in [20] as a minimalistic representation of policy diffusion. The model is a simplification of the more general setup presented in [2,13] to describe enactment and changes to alcohol-related policies in the 50 state of the United States of America from 1980. In the RBN, each node is assigned a Boolean variable, whose probability of activation at a given time-step depends on both the state of its neighboring nodes and on its own internal dynamics, each of which is specified by weighting parameters. The model possesses a small parameter that allows for the use of perturbation methods to compute closed-form equations approximating the relations between system parameters and the transfer entropy, allowing the reconstruction of the former from the latter. In [19], the analysis was completed and extended to the case in which the parameters vary with a prescribed temporal period $ \tau $, while here we assume, for simplicity, that it is time-independent.
The model provides an interesting test case for a number of reasons. Foremost is that its explicit and linear mathematical formulation allows for closed-form analysis that is not possible for real-world datasets, nor for most nonlinear mathematical models. Second is that because it is defined in terms of predetermined parameters, the ground truth is known and deviations from that ground truth can be exactly measured. It is exceptionally simple and fast to evaluate, allowing us to compute long time-series that would be unavailable in most experimental settings. Finally, because the state space of the model is binary, computation of the transfer entropy is especially fast and inexpensive.
The RBN model consists of $ N $ nodes with state $ X^{i}, i = 1\ldots N $, each of which can take the two states zero or one. The system's state at a given time depends on its previous state according to the linear transition law
where the constants $ \Theta $ and $ W_{ij} $ are chosen to ensure that the right-hand side of the equation lies in $ [0, 1] $. The right-hand side consists of two terms. The first, $ \Theta $ is simply the spontaneous probability of node activation. The second is the increased probability of activation due to the activation of the other nodes connected to it. Specifically, the term $ W_{ij} $ represents the nonnegative weighted influence on node $ i $ from its neighbor $ j $. We assume for simplicity that the network contains no self-connected edges, that is,
In the context of policy diffusion, $ \Theta $ measures the tendency of a legal unit to spontaneously enact or change a policy in the absence of any interaction with other legal units. With reference to real policy-making in the United States of America, adopting a time-step of one month would yield small values of $ \Theta $ for policies that have a high start-up cost and unknown, long-term, benefits as well as for policies that attend rare, specific problems that could have significant opposition [2,13]. The RBN shares similarities with synapsis models in theoretical neuroscience, where influence between neurons is represented through excitatory networks [23]. This is the case of slowly-varying dynamics on which we focus, thereby enabling a perturbation argument that treats $ \Theta $ as a small parameter.
The primary analytical result of [19] is a closed-form expression relating the transfer entropy from $ j $ to $ i $ with the weight $ W_{ij} $, namely,
where $ G^{(2)} $ is the map
which is one-to-one for $ x > 0 $. This expression was derived earlier in [20] where $ W_{ij} $ was assumed to take only the binary values zero or one. In [19], it is proposed that truncating this expression and solving for $ W_{ij} $ should be an effective way to estimate the network weights. This is shown via a handful of examples to largely reproduce the network structure of several small time-dependent networks and of a larger random network. These examples include networks with as few as two and as many as 100 nodes.
In the present work, we compute the next-order, $ \mathcal{O}\left({\Theta^3}\right) $, term in this approximation, providing an estimate of the error associated with indirect influence from other nodes in the network. Approximation (1.3) is local in the sense that the weight corresponding to a link $ (i, j) $ is determined entirely by the transfer entropy from $ j $ to $ i $. The correction, by contrast, depends on the difference between the total weighted inputs incident on each of the nodes $ i $ and $ j $, revealing the effect of the more global network structure on the transfer entropy.
This paper is organized as follows. In Section 2 we introduce our motivating example, whose surprising behavior we wish to explain. In Section 3, we summarize additional mathematical background to this problem. In Section 4, we calculate the next order term in the expansion (1.3) to understand the errors made in the example calculation. Then in Section 5 we return to this example, which is illuminated by our calculation. To offer evidence in favor of the generality of the analysis, we numerically study a network of coupled chaotic maps in Section 6. Finally, we present our main conclusions in Section 7.
2.
A surprising example
We begin by describing the network at the center of the example. The Barabási-Albert (BA) network was introduced in 1999 to model the network structure of the internet, although related models date back at least to Yule's work in 1925 [1,31]. Such a network is constructed by an algorithm exhibiting preferential attachment that proceeds as follows. Begin with a small "seed'' graph, which we take to be the complete network with $ m_0 $ nodes. Then at step $ k = m_0+1, \ldots N $, choose $ m $ existing nodes at random according to the weights
where $ d_i $ is the in-degree of node $ i $ (the number of links pointing toward $ i $), and create links between node $ k+1 $ and the $ m $ chosen nodes. By construction, the network have no self-directed edges connecting a node to itself (assuming that the seed network satisfies this property.)
The standard BA network is undirected; Prettejohn et al. describe a directed network variation [21]. In their model, the links added at each step are directed edges from node $ k $ to node $ j $, corresponding to a nonzero weight above the diagonal. If that were the entire model all links would point toward the seed graph, and none would point away from it. In the modified version, once such a directed edge is chosen, then with the same probability $ p_j $ another directed edge is created in the opposite direction (i.e., from $ j $ to $ k $), corresponding to a nonzero entry below the diagonal in the weight matrix.
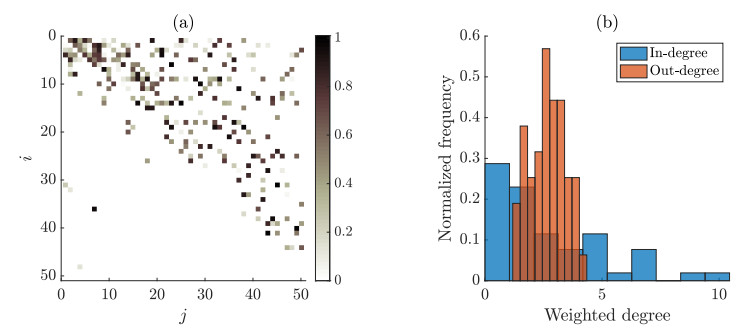
After constructing such a network $ \Gamma $ we introduce a random weight $ W_{ij} $, chosen from the uniform distribution on $ [0, 1] $, to each link from a node $ j $ to a node $ i $. By the above construction, most of the nonzero weights lie above the diagonal. The elements of the weight matrix $ W $ in (1.1) represent the influence of $ j $ on $ i $. The matrix $ W $ visualized in Figure 1. Due to the method of construction, the out-degree of each node, that is, the number of nonzero entries in each column is fairly homogeneous: 40 of the 50 nodes have out-degree equal to five, while the in-degree (number of nonzero entries per row) is much more heterogeneous, with 15 different values ranging from 0 to 20.
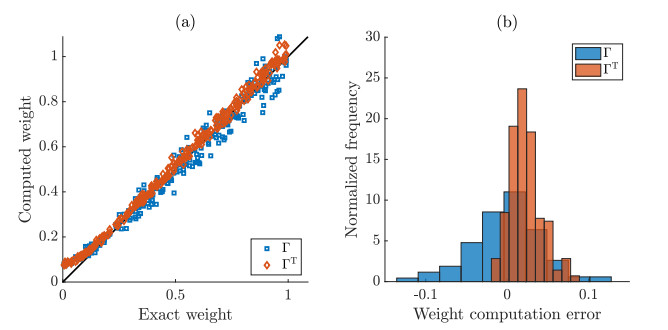
In the computational example we apply the result of [19] to reconstruct two distinct but related networks. The first is described above and the second is its transpose $ \Gamma^ \mathsf{T} $, obtained by reversing the orientation of each directed link. The weight matrix for $ \Gamma^ \mathsf{T} $ is simply the transposed weight matrix $ W^ \mathsf{T} $. The in-degree of a node $ i $ of $ \Gamma^ \mathsf{T} $ is equal to the out-degree of the same node in $ \Gamma $, and vice-versa.
To analyze the model, we run $ 100 $ time-series each of $ 10^5 $ steps. For each of the 2,450 pairs $ (i, j) $ (excluding the terms with $ i = j $ since there are no self-loops by construction), we compute the transfer entropy $ \mathrm{TE}^{j\to i} $ via a simple plug-in estimation [17] where we count the occurrences of the possible states that define the interaction between the node pair. Then we calculate, using the leading-order term in (1.3), an approximate value of the corresponding weight. We utilize $ \Theta = 0.05 $, which is sufficiently small to ensure that the probability on the right-hand side of (1.1) is less than one for all $ i $, since no row of the matrix has more than 20 nonzero entries. We average the computed value of the transfer entropy over the 100 realizations. If the $ \mathcal{O}\left({\Theta^3}\right) $ error term in (1.3) is negligible, then the inferred influence of $ j $ on $ i $ in $ \Gamma $ should be identical to the influence of $ i $ on $ j $ in $ \Gamma^ \mathsf{T} $.
In Figure 2, we plot the inferred weights as a function of their exact values for both these matrices, here showing only the 262 nonzero entries. When the weight is small, the computation significantly overestimates it in both cases. For larger weights, there is an increased amount of variation in the predicted values, but it is distributed in markedly different ways for the two matrices. For the network $ \Gamma $, the variation appears to be distributed evenly above and below the exact value. For the network $ \Gamma^ \mathsf{T} $, the error in the inference is nearly always positive, and appears to be much smaller. This is confirmed in the right panel of the figure, which shows histograms of the errors, normalized to have unit area. The histogram for the network $ \Gamma $ has mean close to zero and is considerably broader than the histogram for $ \Gamma^ \mathsf{T} $, which has a positive mean value.
Since most of the entries of the weight matrix $ W $ are zero, a critical measure of success in the network reconstruction is minimizing false positives, that is, links that are inferred between disconnected nodes. The overestimation of weights lower than 0.1 evident in Figure 2 suggests that some false positives are unavoidable. Of the 262 largest inferred weights for both $ \Gamma $ and $ \Gamma^ \mathsf{T} $, 11 entries for $ W $ and 13 for $ W^ \mathsf{T} $ would be classified as false positives. Note that this computation was performed using the value of the transfer entropy averaged over 100 realizations. Significantly more false positives were found if the calculation was performed using a single realization.
Clearly, the calculated errors in the weights in the calculation for $ \Gamma $ are larger than for the similar calculation using $ \Gamma^ \mathsf{T} $, despite the fact that equation (1.3) predicts the same leading-order accuracy. The analysis of this paper aims to determine what topological features of the two networks conspire to create this difference and to determine how to correct it.
3.
Mathematical background
3.1. Markov chains
We assume familiarity with the basics of Markov chains and use this section mainly to set notation [7]. We consider a discrete-time finite-state Markov chain $ Z(t), \, t \in \mathbb{N} $ evolving in a sample space $ \mathcal{Z} $ whose generic element is denoted as $ z_i, \, i = 1 \ldots \left\lvert{\mathcal{Z}}\right\rvert $ where $ \left\lvert{\mathcal{Z}}\right\rvert $ is the cardinality of the set. Lower case letters will be used to denote realizations of random variables. The transition matrix is a matrix $ P \in \mathbb{R}_+^{\left\lvert{\mathcal{Z}}\right\rvert\times\left\lvert{\mathcal{Z}}\right\rvert} $, whose columns each sum to one. The entry $ P_{ij} $ represents the probability that the the Markov chain will transition from state $ z_i $ to state $ z_j $ at any given step,
Considered as a row vector, the distribution $ \nu(t) $ evolves according to the following recursion,
for $ t \in \mathbb{N} $ and initial distribution $ \nu(0) = \nu_0 $.
The solution to this recursion is a probability distribution for all times $ t $, such that its entries are non-negative and sum to one. Given mild assumptions on the transition matrix $ P $, the recursion converges exponentially as $ t\to\infty $ to a unique limiting distribution denoted $ \pi $, called the stationary distribution[7]. This is given by the left eigenvector with unit eigenvalue,
3.2. Elements of information theory
Our goal is to reconstruct the network $ \Gamma $ from a time-series of finite duration generated by the dynamics of (1.3). Since this time series is finite, it is impossible to determine with certainty the matrix used to create it. The object, then, is to find the network that is consistent with the data while requiring the fewest unsupported assumptions. Loosely speaking, we can say that it should not be too surprising [9]. The idea of surprise is that unlikely events convey more information, so a "surprise function'' should assign a large value to unlikely events and a small value to expected events.
The information associated with the event that a random variable $ X $ drawn from a sample space $ \mathcal{X} $ takes the value $ x $ is
Here, we make use of natural logarithms, so that information is measured in nats. The (Shannon) entropy of the random variable $ X $ is then the expectation of the information
which quantifies the amount of uncertainty in $ X $, where $ \mathrm{E} $ denotes expectation. The entropy is the unique functional over probability distributions that satisfies the Shannon-Khinchin axioms [15], making it the best choice for measuring the uncertainty of a distribution. Since the entropy is the expectation of $ I(X) $, it is generically non-negative.
Given another random variable $ Y $, the notions of joint and conditional entropies are similarly defined by
where $ \mathcal{Y} $ is the sample space of $ Y $.
These notions can be readily extended to stochastic processes, such that given two stationary processes $ X $ and $ Y $, transfer entropy from $ Y $ to $ X $ is defined as [25]
Transfer entropy measures the reduction in the uncertainty of predicting $ X(t+1) $ from both $ X(t) $ and $ Y(t) $ relative to predicting it from $ X(t) $ alone. As a simple consequence of its definition, transfer entropy is non-negative.
We acknowledge that building on this definition, a variety of ameliorations could be undertaken. For example, one may consider delayed interactions between the two processes, such that $ Y(t) $ in (3.5) should be replaced with $ Y(t-\delta) $ with $ \delta $ being a suitable time-delay [29]. Also, one may attempt a symbolic treatment of the time-series [27], or pursue an analysis in terms of recurrence plots [22]. In this work, we focus on the classical definition in (3.5) toward gathering analytical insight into the role of the topology on the accuracy of transfer entropy-based network inference.
4.
Analysis
We briefly present the computation of the next-order correction in the transfer entropy formula (1.3) and of the probabilities used to construct it. This necessarily builds on the calculation in [19], the details of which are summarized below. As in most perturbative calculations [16], the number and complexity of terms greatly increases as the order of the calculation increases. The details of this calculation were assisted and verified using Mathematica.
4.1. The stationary distribution
System (1.1) can be reformulated as a Markov chain, with $ \left\lvert{\mathcal{Z}}\right\rvert = 2^N $ states $ z = [X^1, \ldots, X^N] \in {\{0, 1\}}^N $, such that each state is a binary vector whose entries take the value one or zero depending on whether that node is active. Letting $ Z(t) = [X^1(t), \ldots, X^N(t)] $, then the transition probability in (1.1) can be written as
where the unit vector $ e_i $ is column $ i $ of the identity matrix. For both possible realizations $ x^i_+ $ of $ X^i(t+1) $, this can be written as
Taking a product of such terms yields the transition matrix of this Markov chain
The transition matrix $ P $ can be expanded in powers of $ \Theta $ as follows:
The first three terms are given in [19]. Specifically, the zeroth order term is
Here, the norm of a binary vector is taken to be the number of nonzero entries, namely,
The first order term is
where $ 1_N $ denotes a column vector of $ N $ ones. Finally, the second order term is
where $ \mathcal{I}_1(z_j) $ and $ \mathcal{I}_2(z_j) $ are used to identify the two entries of $ z_j $ that are different from zero for the case $ \left\lVert{z_j}\right\rVert = 2 $.
In a similar manner, we compute $ P^{(3)} $. The calculation below will only need the values of $ P^{(3)} $ for which $ \left\lVert{z_i}\right\rVert = 0 $ (it appears only in Eq. (4.7d)). Accordingly, that is all we report here
We remark that $ P^{(n)}_{ij}\neq 0 $ only in the case that both $ \left\lVert{z_i}\right\rVert\le n $ and $ \left\lVert{z_j}\right\rVert \le n $. There are of course $ \binom{N}{n} $ vectors $ z $ with $ \left\lVert{z}\right\rVert = n $, so that if $ n\ll N $ then the approximate matrix, computed for all transitions with $ \left\lVert{z}\right\rVert\le n $, is low rank. Given a time-series of system (1.1), this provides a way to check whether $ \Theta $ has been chosen small enough that the proposed approximation is reasonable.
Next, we expand the stationary distribution to the third order, in a manner similar to the transition matrix,
By replacing (4.6) into (3.2) and grouping terms of the same power in $ \Theta $, we determine the following chain of relationships:
The left column of equations contains the expansion of the stationary equation, while the right column enforces the condition that $ \pi $ is a probability distribution. The matrix $ \left(I - P^{(0)}\right) $ in each equation is singular, with a one-dimensional null space. The first Eq. (4.7a) is solved by its null vector. The other equations are all solvable, as long as the vectors on their right-hand sides sum to zero, and they all do.
The first three equations in (4.7) for the zeroth, first, and second order terms in the expansion are solved in [19] and are given by
and
To extend the computation to the next order, we replace (4.6) and (4.8) into (4.7d). By solving the equation and imposing the constraint that the perturbation is zero-sum, we determine
where the Hadamard product [3], or element-wise product, $ {(A\circ B)}_{ij} = A_{ij}B_{ij} $, is in the $ \left\lVert{z_j}\right\rVert = 0 $ term.
Marginalizing (4.6) via (4.8) and (4.9), we compute the stationary periodic distribution of each node
This distribution describes the probability that a node is active or non-active at a given time. Should the expansion be truncated at the second order in $ \Theta $, only the row sum of $ W $ at node $ i $ (quantifying the weighted in-degree of node $ i $) will enter the probability distribution in (4.10). These nodes are those that influence node $ i $ with respect to system (1.1). Extending the analysis to the third power in $ \Theta $ brings forward a more complex dependence of node $ i $ on the $ i $th row sum of the square of the matrix $ W $, representing the dependence of the state of $ X $ at time $ t $ on its state at time $ (t-2) $.
Similarly, marginalizing (4.6) with respect to any nodes but node pair $ (i, j) $, we determine the following joint distribution for $ (i, j) $:
While a second order expansion in $ \Theta $ would yield that node $ i $ and $ j $ are independent, retaining the third order power yields a different claim. Specifically, (4.11) cannot be obtained from (4.9) if we are interested in the quantification of the third order term in $ \Theta $.
4.2. Transfer entropy
We now develop the two leading-order terms in the expansion of the transfer entropy, using the definition (3.5) and the expansion (4.6) developed in the last section. Without loss of generality we consider the transfer entropy from node 2 to node 1:
where the probabilities are evaluated using the stationary distributions derived in the previous section.
We can compute the conditional probability in the denominator of the logarithm term using the transition probability (4.2) and properly marginalizing the stationary distribution (4.6), as follows:
Up to terms of order $ \mathcal{O}\left({\Theta^2}\right) $, this expansion matches that given in [19]. In agreement with one's expectation, for small values of $ \Theta $, such that an affine expansion would hold, the probability of a transition does not depend on the network topology. Retaining the second order power in $ \Theta $ introduces a dependence on all the nodes that influence node 1. Increasing further the order of the expansion, we observe a richer influence from the entire network, expressed through the term involving $ W^2 $.
A similar calculation yields the term in the numerator of (4.12). By using (4.11) and (4.6), we establish
Again, the expansion agrees with that found in [19] up to order $ \mathcal{O}\left({\Theta^2}\right) $. Similarly to (4.13), for small values of $ \Theta $, the probability that node 1 transitions to a given state conditional to its present state and the present state of node 2 depends only on $ W_{11} $ and $ W_{12} $. Including to the second power in $ \Theta $ brings about the effect of all the other nodes that influence node $ 1 $ (excluding node 2). The third power in $ \Theta $ depicts a further degree of interaction, wherein the entire network contributes to the probability of transition (4.14), through the term involving $ W^2 $.
The joint probability $ \Pr{\left[X^1(t+1) = x_+^1, X^1(t) = x^1, X^2(t) = x^2\right]} $ in (4.12) is calculated as the product of (4.11) and (4.14), although, remarkably, the $ \mathcal{O}\left({\Theta^3}\right) $ correction terms in these equations do not enter into the calculation to this order. From this joint probability and the conditional probabilities in (4.13) and (4.14), we can calculate an expansion for transfer entropy. Switching from labeling the indices from $ (1, 2) $ to $ (i, j) $ with $ i\neq j $, we establish
where the scalar function $ G^{(2)} $ is defined in (1.4) and the matrix function $ G^{(3)} $ is defined entry-wise as
where
is the weighted in-degree of node $ j $. The calculation presented in this paragraph is the first place that assumption (1.2) is used.
In agreement with the discussion on the effect of the network network topology on local joint and transition probabilities in (4.13) and (4.14), the asymptotic expansion for transfer entropy in (4.15) suggests that increasing the order of the expansion in $ \mathrm{TE}^{j\rightarrow i} $ hampers the possibility of mapping transfer entropy one-to-one with the corresponding weights. Surprisingly, the term in $ \Theta^3 $ depends on the influence of $ j $ on $ i $ along with the in-degree of both $ i $ and $ j $, which encapsulate the overall influence of any other network node on the pair.
4.3. Solving for the weights
In the process of network inference, we should compute all the entries of $ W $ from transfer entropy values estimated from time-series. To accomplish this goal, we must solve the system of Eq. (4.15) with $ i, j = 1, \ldots, N $, $ i\neq j $, for $ W $. For convenience, we scale transfer entropy by $ \Theta^2 $, yielding the following matrix-valued equation for $ W $
where $ T_{ij} = \Theta^{-2} \mathrm{TE}^{j\to i} $.
Formally, we can solve (4.18) for $ W $ as a series in $ \Theta $, as follows:
and find the two equations
These have formal solutions
Ultimately, we compute any element of $ W $ by following these steps: (i) For every pair $ i\neq j $, we solve (4.19a) to compute the value $ W^{(0)}_{ij} $ and we assemble the matrix $ W^{(0)} $ (with zeros on the diagonal). (ii) For every pair $ i\neq j $, we compute the correction $ W_{ij}^{(1)} $ by using the entire matrix $ W^{(0)} $.
To shed light on the topological underpinnings of the correction $ W^{(1)} $ that relate $ \mathrm{TE}^{j\rightarrow i} $ to weights beyond that between $ i $ and $ j $, we can perform a further perturbation analysis. Specifically, we can estimate the correction term in (4.19b) in the case that the entries in $ W $ are small using Taylor series. As shown in [19], $ G^{(2)}(W_{ij})\sim \frac{W_{ij}^2}{2} $. Similarly, expanding (4.16) under the assumption that all elements of $ W $ are small, i.e., $ W_{ij}\ll 1 $, we find
Interestingly, this result holds even if assumption (1.2) is not satisfied. Therefore the correction (4.19b) approximately satisfies
where $ d_i^{(0)} $ is the in-degree of node $ i $ with respect to matrix $ W^{(0)} $, which, based on (4.19a) encapsulates the overall information transfer to node $ i $ from its neighbors. The same expansion holds, with a different remainder, if $ W_{ij}\ll1 $ but the other weights in (4.16) are $ \mathcal{O}\left({1}\right) $.
Overall, (4.21) indicates that $ W^{(1)}_{ij} $ depends on all the transfer entropy values associated with incoming information to nodes $ i $ and $ j $. Note that $ d_i^{(0)} $ and $ d_j^{(0)} $ have opposite signs in the term (4.21). Specifically, the correction in the inference of the weight between nodes $ i $ and $ j $ can be split into two terms $ W^{\rm link}_{ij} = \frac{1}{2}{\left(W_{ij}^{(0)} \right)}^2 $ and $ W^{\rm topology}_{ij} = \frac{1}{2} W_{ij}^{(0)}(d_j^{(0)}-d_i^{(0)}) $. The first of these, $ W^{\rm link}_{ij} $, represents a correction that depends only on the computed transfer entropy for the pair $ (i, j) $. The second, by contrast, depends on the mismatch between their weighted in-degrees from $ W^{(0)} $ measures the differing rate at which information is transferred to the two nodes from the network. Stretching the thermodynamics analogy, we could refer to this mismatch as a common uncertainty bath upon which we must tackle the inference problem. The computation of $ W^{(0)}_{ij} $ treats the pair $ (i, j) $ in isolation, while the correction term $ W^{\rm topology}_{ij} $ accounts for the information which both nodes $ i $ and $ j $ receive from the rest of the network; see Figure 3. We attribute the different behaviors of the simulations reported in Section 2 to this observation, as we relate in the next Section.
We further comment that to this order in the expansion, Eq. (4.16) yields that if $ W_{ij} = 0 $ then $ T_{ij} = 0 $. Since transfer entropy $ \mathrm{TE}^{j\rightarrow i} $ computed by time series is never exactly zero, this suggests that the third order approximation will do no better than the second-order approximation at discriminating between $ W_{ij} = 0 $ and $ W_{ij} $ positive but small. However, it can contribute to the accuracy of the identification of nonzero weights, in terms of both the mean and variance of the prediction.
5.
Continued numerical example
If transfer entropy $ \mathrm{TE}^{j \to i} $ were a function solely of the weight $ W_{ij} $ and not of further topological properties of the graph, then the inferred weights for a network $ \Gamma $ and its transpose, computed to leading order, should be identical. That they were not found to be identical in Section 2 motivated the computation, via perturbation expansion, of the next order correction terms, detailed in Section 4. Eq. (4.21) provides an intuitive explanation for the differing behaviors. The correction term $ W^{\rm topology}_{ij} $ is proportional to the mismatch between the weighted in-degrees of nodes $ i $ and $ j $, with an additional factor of $ W_{ij} $. Figure 1(b) shows that the weighted in-degrees for $ \Gamma $ vary more widely than the weighted in-degrees of $ \Gamma^ \mathsf{T} $ (which equal the weighted out-degrees of $ \Gamma $). Therefore, the range in their mismatch is larger, giving rise to the wider variation in the inferred weights for $ \Gamma $ than for $ \Gamma^ \mathsf{T} $.
We now apply the correction (4.19b) to the numerical simulations described in Section 2. In Figure 4 we compare the second and third order approximations for the computation with the networks $ \Gamma $ and $ \Gamma^ \mathsf{T} $. Subfigures (a) and (b) show the second and third order approximations to the weights for the network $ \Gamma $. With respect to $ \Gamma $, the variance of the error is reduced in the improved approximation, while the mean error, which was already close to zero, stays about the same. For the network $ \Gamma^ \mathsf{T} $, as shown in Subfigures (c) and (d), the mean error is reduced while the error variance is improved only slightly. After the correction is applied, the inferred weights for both the networks $ \Gamma $ and $ \Gamma^ \mathsf{T} $ are computed to about the same accuracy.
Clearly, the correction term accounts for the marked difference between the inferred weights seen in the initial numerical experiment. When the correction term is included in the computation, then transfer entropy, already demonstrated to be a useful tool for network reconstruction, only improves. A notable study by Sun et al. demonstrates that $ \mathrm{TE}^{j \to i} $ is in itself insufficient for reconstructing $ W_{ij} $ since it fails to condition on the dynamics of the remaining nodes in the network [28]. That paper proposes an alternative measure of influence which the authors call causation entropy, and which is conditioned on a higher number of terms. The terms exerting influence are then identified by an optimization over the terms included. The procedure outlined in Section 4.3 provides an alternative method to measure indirect influence while relying only on dyadic interactions, allowing us to nonlinearly combine the transfer entropies of all node-pairs in order to effectively approximate such a conditioning.
6.
Additional numerical example
The analysis performed in this paper applies only to the RBN model (1.1). It is tempting, however, to draw from it a more general conclusion about transfer entropy. Namely, consider models in which the coupling between the nodes of the network is weak. To leading-order, transfer entropy between two nodes should depend only on the strength of the coupling between them, but this is subject to a correction like that given in (4.20), dependent on the difference in total weighted in-degree of the two nodes forming the pair.
In this section, we explore this hypothesis with a numerical example. We consider a coupled system of chaotic tent maps subject to additive noise. The evolution of the $ i $th state is given by the following equation:
Here, $ n^i(t) $ is additive noise drawn from a normal distribution, with small multiplier $ \sigma $ and the nonlinear function $ F $, known as the tent map, is
In the absence of noise—that is, when $ \sigma = 0 $—solutions to (6.2) may synchronize, so that their trajectories will tend to be identical and follow the individual dynamics of single tent map, bounded in the $ [0, 1] $ interval. A condition for the existence of stable synchronous solutions for this system can be derived, based on the earlier work of [18], as follows. The condition is derived as follows. Define an $ N\times N $ matrix $ L $ by
Then stable solutions exist if, for all nonzero eigenvalues $ \lambda $ of $ L $,
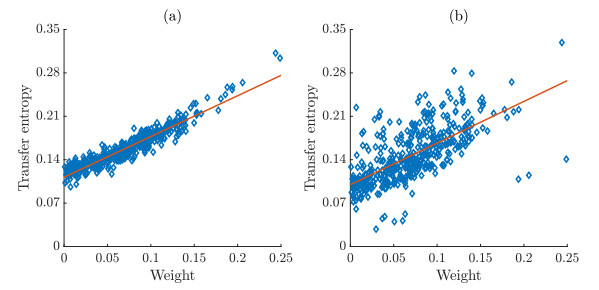
We were unable to find any examples of networks of the type used in Section 2 for which synchronization was possible for both the weighted network $ \Gamma $ and its transpose $ \Gamma^ \mathsf{T} $. Instead, we construct the following simple family of weighted networks that may lead to synchronization. Let $ \Gamma $ be a directed Erdős-Rényi network [11]. In this class of networks, the nodes are connected randomly such that a directed link exists from $ j $ to $ i \neq j $, with a fixed probability $ p < 1 $. Then, for each node $ i $, we choose random weights $ W_{ij} $ such that $ d_i = \sum_{j} W_{ij} = 1 $.
Thus, the term $ W_{ij}^{\rm topology} $ is identically zero for $ \Gamma $ but nonzero for the network $ \Gamma^ \mathsf{T} $. We expect from (4.21) that the computed transfer entropy for (6.2) using $ \Gamma^ \mathsf{T} $ will be have larger variance than the computed transfer entropy for $ \Gamma $. Figure 5 shows the results of this computation, performed with $ N = 30 $, $ p = \frac{1}{2} $, $ \Theta = 0.96 $, which satisfies the synchronization condition for both networks, and $ \sigma = 0.1 $. The in-degree of each node of $ \Gamma $ equals one by construction, while for $ \Gamma^ \mathsf{T} $, the in-degree has mean one and variance $ 0.049 $. It is clear from the simulations that the computed transfer entropy is more widely scattered for $ \Gamma $ than for $ \Gamma^ \mathsf{T} $.
Therefore, we conclude that the wider variation in in-degree for $ \Gamma $ than for $ \Gamma^ \mathsf{T} $ is responsible for the difference in the behaviors. This supports the idea that the claims analytically derived for the RBN apply to a wider class of coupled dynamical systems. The main message of this work is that the success of pairwise inference through transfer entropy depends on the topological features of the network to be discovered. Networks with homogeneous in-degree can be more accurately inferred than those with heterogeneous in-degree. The out-degree plays a surprisingly marginal role on the quality of the inference.
7.
Conclusion
Transfer entropy is emerging as a promising approach to carry out network reconstruction from the time-series of the network nodes. In this vein, one utilizes the value of transfer entropy between a pair of network nodes to decide whether a link exists between them and, potentially, predict its weight. This process is based on the premise that transfer entropy maps one-to-one with the weight of the link between two nodes, which is in general difficult to guarantee. In fact, the definition of transfer entropy between two nodes deliberately excludes the effect of any other node in the network, thereby neglecting indirect influence between the two nodes that could be supported by the entire network.
In this work, we seek to offer a precise quantification of the topological features that challenge transfer-entropy network reconstruction in the context of a simple Boolean network model, inspired by policy diffusion. Through perturbation analysis of the high-dimensional Markov chain associated with the model evolution on the entire network, we establish a closed-form expression for the stationary distribution. This is, in turn, utilized to derive our main result, consisting of a third-order accurate form of transfer entropy between any two nodes in the network.
Our closed-form result indicates that, for sufficiently slow dynamics, transfer entropy between two nodes maps injectively to the corresponding weight of the link between them. As the perturbation parameter increases to encompass dynamics that could evolve at a faster scale, the one-to-one map breaks down, in favor of a more complex relationship between topology and transfer entropy. Specifically, we discover that inferring the weight between two nodes calls for examining transfer entropy from any other node in the network to the node pair under scrutiny. The higher the mismatch between the two nodes in terms of their total incoming transfer entropy, the less accurate is the one-to-one mapping between transfer entropy and influence.
This finding is particularly important when studying heterogeneous networks, such as scale-free models where wide variations in the incoming information flow should be expected as we seek to discover links around potential hubs. To detail this aspect, we have examined two instances of a weighted, directed scale-free network: one in which heterogeneity manifests in terms of out-degree and, the other, constructed through simple matrix transposition that displays heterogeneity in terms of the in-degree distribution. In the former case, transfer entropy between each pair of nodes offers an unbiased measure of the mutual influence between the nodes, such that one might estimate the corresponding weight from transfer entropy reading with an uncertainty of zero mean. In the latter case, we observe a systematic bias of transfer entropy-based inference, such that the uncertainty in the estimation has a non-zero mean, although it is characterized by a narrower variance. Accounting for the high-order correction derived in this paper, we successfully address network inference in both cases, attaining an unbiased, tight reconstruction of every weight in the network from transfer entropy measures.
Although numerical results on coupled chaotic tent maps seem to align with our analytical predictions, the generality of our results remains an open question for future research. Specifically, our future work should seek to establish a general framework for error quantification in transfer entropy-based network inference, beyond the case of Boolean network model examined herein. While it is unlikely that one could determine a closed-form expression of transfer entropy for general dynamics in terms of the network topology as proposed in this paper, it may be tenable to establish conservative bounds on information transfer associated with indirect influence between nodes. Another area of future inquiry includes the extension of the analytical framework to encompass time-varying dynamics, leading to a non-stationary Markov process, and self-loops in the network, which would likely exacerbate the role of heterogeneity on transfer entropy.
Acknowledgments
This work was undertaken while RG was on sabbatical at the NYU Tandon School of Engineering. He thanks them for their hospitality. MP acknowledges the support of the National Science Foundation under Grant nos. CMMI 1433670, CMMI 1561134, and CBET 1547864.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: